Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 ноября 2020 года; проверки требует 1 правка.
Теплоёмкость определяется суммой поступательных, вращательных и удвоенным числом колебательных степеней свободы.
Теплоёмкость идеального газа — отношение количества теплоты, сообщённой газу 
, к изменению температуры 
, которое при этом произошло 
[1].
Удельная и молярная теплоёмкость[править | править код]
Молярная теплоёмкость — теплоёмкость 1 моля вещества [2]:
где 
— масса, 
— молярная масса вещества.
Теплоёмкость единичной массы вещества называется удельной теплоёмкостью и, в системе СИ, измеряется в Дж/(кг·К)[1].
Формула расчёта удельной теплоёмкости[1][2]:
- где c — удельная теплоёмкость, m — масса нагреваемого (охлаждающегося) вещества.
Теплоёмкость идеального газа в изопроцессах[править | править код]
Адиабатический[править | править код]
В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть 
. Однако, объём, давление и температура меняются, то есть 
[3].
Следовательно, теплоёмкость идеального газа в адиабатическом процессе равна нулю: 
.
Изотермический[править | править код]
В изотермическом процессе постоянна температура, то есть 
. При изменении объёма газу передаётся (или отбирается) некоторое количество тепла[3]. Следовательно, теплоёмкость идеального газа равна плюс-минус бесконечности: 
Изохорный[править | править код]
В изохорном процессе постоянен объём, то есть 
и, следовательно газ не совершает работы. Первое Начало Термодинамики для изохорного процесса имеет вид[1]:
А для идеального газа
Таким образом,
где 
— число степеней свободы частиц газа.
Другая формула:
где 
— показатель адиабаты, 
— газовая постоянная газа.
Изобарный[править | править код]
Молярная теплоёмкость при постоянном давлении обозначается как 
. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера 
[1].
Уравнение Майера вытекает из первого начала термодинамики[4]:
.
В рассматриваемом случае, согласно определению теплоёмкости:
Учитываем, что работа газа равна [4]:
Согласно уравнению Менделеева-Клапейрона для одного моля газа[1]:
Подставляя уравнение (4) в (3) получаем:
Так как энергия одной молекулы равна 
(6)[Комм 1][5], то и внутренняя энергия в целом и при изобарном процессе будет определяться по соотношению (1). Следовательно, подставляя уравнения (1) и (5) в (2) получаем соотношение Майера.
Молекулярно-кинетическая теория позволяет вычислить значения молярной теплоёмкости для классического идеального газа газов через значение универсальной газовой постоянной исходя из уравнения (6) и предположения, что молекулы газа не взаимодействуют между собой[5]:
Теплоёмкости можно также определить исходя из уравнения Майера, если известен показатель адиабаты, который можно измерить экспериментально (например, с помощью измерения скорости звука в газе или используя метод Клемана — Дезорма).
Теплоёмкость реального газа может значительно отклонятся от теплоёмкости идеального газа. Так при температуре в 25 °С и атмосферном давлении атомарный водород имеет теплоёмкость 2,50R , а атомарный кислород — 2,63R. Также теплоёмкость реального газа зависит от температуры[5].
См. также[править | править код]
- Идеальный газ
- Первое начало термодинамики
- Теплоёмкость
Комментарии[править | править код]
- ↑ i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы
- ↑ 1 2 При жёсткой связи между атомами, то есть колебательные степени свободы исключены из рассмотрения. Примером трёхатомной линейной молекулы служит цианистый водород HCN.
Примечания[править | править код]
- ↑ 1 2 3 4 5 6 Савельев, 2001, с. 26—30.
- ↑ 1 2 Базаров И. П., Термодинамика, 2010, с. 41.
- ↑ 1 2 Савельев, 2001, с. 30—31.
- ↑ 1 2 Савельев, 2001, с. 18-20.
- ↑ 1 2 3 Савельев, 2001, с. 61-63.
Литература[править | править код]
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.— Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Белоконь Н. И. Основные принципы термодинамики. — М.: Недра, 1968. — 110 с.
- Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
В случае, если результатом теплообмена становится передача телу некоего количества теплоты Q, то его температура и внутренняя энергия претерпевают изменения.
Необходимое для нагревания 1 кг вещества на 1 К количество теплоты Q носит название удельной теплоемкости вещества c, а ее формула выглядит следующим образом:
c=Qm∆T.
В большом количестве ситуаций удобной для использования является молярная теплоемкость C:
C=M·c, где M представляет собой молярную массу вещества.
Теплоемкость, полученная таким способом, не является однозначной характеристикой вещества. Исходя из первого закона термодинамики, можно сказать, что изменение внутренней энергии тела зависимо не только от количества полученной теплоты, но и от величины совершенной телом работы. В разных условиях осуществления процесса теплопередачи тело может совершать различную работу. Таким образом, переданное телу одинаковое количество теплоты способно провоцировать изменения его внутренней энергии и, соответственно, температуры.
Подобной неоднозначностью при определении теплоемкости характеризуются только газообразные вещества. Объем в процессе нагрева практически не меняет своей величины, что сводит работу расширения к нулю. По этой причине вся полученная телом теплота уходит на изменение его внутренней энергии. Газ в процессе теплопередачи может значительно менять свой объем и совершать работу, чем отличается от твердых тел и жидкостей. Таким образом, теплоемкость газообразного вещества имеет зависимость от характера термодинамического процесса.
Изопроцессы в газах
Чаще всего рассматриваются два значения теплоемкости газов:
- CV являющаяся молярной теплоемкостью в изохорном процессе (V=const);
- Cp представляющая собой молярную теплоемкость в изобарном процессе (p=const).
При условии постоянного объема газ не совершает работы: A=0. Исходя из первого закона термодинамики для 1 моля газа, можно сказать, что справедливым является следующее выражение:
QV=CV∆T=∆U.
Изменение величины ΔU внутренней энергии газа прямо пропорционально изменению значения ΔT его температуры.
В условиях процесса при постоянном давлении первый закон термодинамики дает такую формулу:
Qp=∆U+p(V2-V1)=CV∆T+pV.
В котором ΔV является изменением объема 1 моля идеального газа при изменении его температуры на ΔT. Таким образом, можно заявить, что:
Cp=Qp∆T=CV+p∆V∆T.
Из уравнения состояния идеального газа, записанного для 1 моля, может выражаться отношение ΔVΔT:
pV=R.
В котором R представляет собой универсальную газовую постоянную. При условии постоянства давления p=const, можно записать следующее:p∆V=R∆T или ∆V∆T=Rp.
Из этого следует, что выражающее связь между молярными теплоемкостями Cp и CV соотношение имеет вид (формула Майера):
Cp=CV+R.
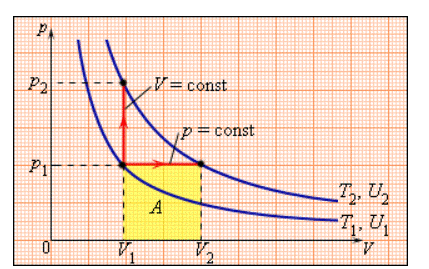
В процессе с неизменным давлением молярная теплоемкость Cp газа всегда превышает молярную теплоемкость CV в процессе с не подверженным изменениям объемом, что демонстрируется на рисунке 3.10.1.
Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT=T2 –T1. При p=const газ совершает работу A=p1(V2 – V1). Поэтому Cp>CV.
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом занимает важное место в термодинамике и обозначается в виде греческой буквы γ.
γ=CpCV.
Данное отношение включено в формулу для адиабатического процесса.
Между двумя изотермами, обладающими температурами T1 и T2 на диаграмме (p, V) реальны различные варианты перехода. Так как для всех подобных переходов изменение величины температуры ΔT=T2 –T1 является одним и тем же, выходит, что изменение значения
ΔU внутренней энергии тоже одинаково. С другой стороны, совершенные при этом работы A и количества теплоты Q, полученные в результате теплообмена, выйдут разными для различных путей перехода. Из этого следует, что газа имеет относительно приближенное к бесконечности число теплоемкостей. Cp и CV представляют собой частные, однако, очень важные для теории газов, значения теплоемкостей.
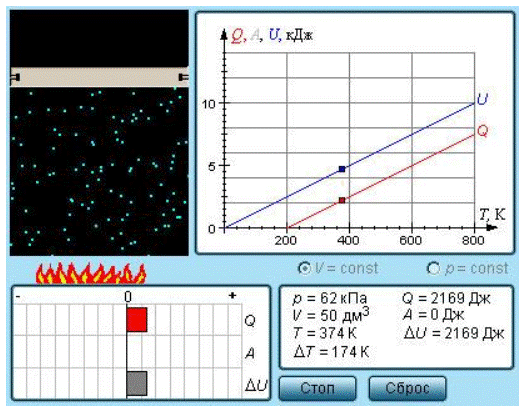
Рисунок 3.10.2. Модель теплоемкости идеального газа.
Термодинамические процессы, в которых теплоемкость газа не подвергается изменениям, носят название политропических.
Каждый изопроцесс являются политропическим. В изотермическом процессе ΔT=0, из-за чего CT=∞. В адиабатическом процессе ΔQ=0, выходит, что Cад=0.
Стоит обратить внимание на то, что «теплоемкость» и «количество теплоты» являются крайне неудачными терминами, доставшимися современной науке в качестве наследства теории теплорода, которая господствовала в XVIII веке.
Данная теория представляла теплоту в виде содержащегося в телах особого невесомого вещества. Считалось, что оно не подвержено уничтожению и не может быть созданным. Явление нагрева объясняли повышением, а охлаждение – понижением содержания в телах теплорода. Однако теория теплорода оказалась несостоятельной, так как не смогла дать ответа на вопрос, почему одинаковое изменение внутренней энергии тела возможно получить, приводя ему разное количество теплоты в зависимости от совершаемой им работы. По этой причине утверждение, что в данном теле содержится некоторый запас теплорода лишено смысла.
Молекулярно-кинетическая теория
В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией E→ поступательного движения молекул и абсолютной температурой T:
E→=32kT.
Внутренняя энергия 1 моля идеального газа эквивалентна произведению E→ на число АвогадроNА:
U=32kNAT=32RT.
При условии изменения температуры на величину ΔT внутренняя энергия изменяется на величину:
U=32R∆T=CV∆T.
Коэффициент пропорциональности между ΔU и ΔT эквивалентен теплоемкости CV в условиях постоянного давления:
CV=32R=12,47 ДЖ/моль·К.
Данное выражение подтверждается экспериментами с газами, которые состоят из одноатомных молекул вроде гелия, неона или аргона. При этом для двухатомных (водород, азот) и многоатомных (углекислый газ) газов такое соотношение не согласуется с полученными в результате опытов данными. Причина этого расхождения заключается в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать энергию как поступательного, так и вращательного их движения.
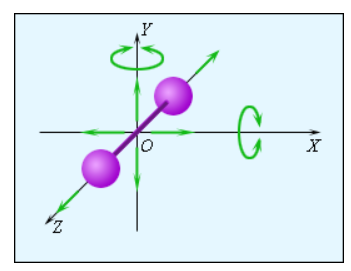
Рисунок 3.10.3. Модель двухатомной молекулы. Точка O совпадает с центром масс молекулы.
Рисунок 3.10.3 иллюстрирует модель двухатомной молекулы. Молекула имеет возможность производить пять независимых типов движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y.
Опытным путем выяснено, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких значениях температуры. В условиях обычных температур вращение вокруг оси Z не происходит.
Каждое независимое движение в молекуле носит название степени свободы.
Выходит, что одноатомная молекула обладает 3 поступательными степенями свободы, «жесткая» двухатомная молекула 5 степенями, то есть 3 поступательными и 2 вращательными, а многоатомная молекула 6 степенями свободы, из которых 3 приходятся на поступательные и 3 на вращательные.
В классической статистической физике доказывается теорема о равномерном распределении энергии по степеням свободы:
Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна 12kT.
Из данной теоремы следует, что для молярных теплоемкостей газа Cp и CV и их отношения
γ справедлива запись в следующем виде:
CV=i2R, Cp=Cv+R=i+22R, γ=CpCV=i+2i,
где i представляет собой количество степеней свободы газа.
Для газа, состоящего из одноатомных молекул (i=3)
CV=32R, Cp=Cv+R=52R, γ=CpCV=53=1,66.
Для газа, состоящего из двухатомных молекул (i=5)
CV=52R, Cp=Cv+R=72R, γ=CpCV=75=1,4.
Для газа, состоящего из многоатомных молекул (i=6)
CV=3R, Cp=Cv+R=4R, γ=CpCV=43=1,33.
В обычных условиях экспериментально измеренные теплоемкости многих газов неплохо согласуются с приведенными выражениями, но в целом классическая теория теплоемкости газов вполне удовлетворительной не является. Существует колоссальное число примеров со значительной разницей между результатами эксперимента и теорией. Данный факт объясняется тем, что классическая теория не может полностью учесть, связанную с внутренними движениями в молекуле энергию.
Теорема о равномерном распределении энергии по степеням свободы может быть применена и по отношению к тепловому движению частиц в твердом теле. Входящие в состав кристаллической решетки атомы колеблются около положений равновесия. Энергия данных колебаний представляет собой внутреннюю энергию твердого тела. Каждый конкретный атом может колебаться в кристаллической решетке в трех взаимно перпендикулярных направлениях. Выходит, что каждый атом имеет 3 колебательные степени свободы. При условии гармонических колебаний средняя кинетическая энергия эквивалентна средней потенциальной энергии. По этой причине в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT.
Внутренняя энергия 1 моля твердого вещества равна следующему выражению:
U=3RNAkt=3Rt.
Следовательно, молярная теплоемкость вещества в твердом состоянии равняется:
С=3R=25,12 Дж/моль·К.
Данное выражение носит название закона Дюлонга–Пти. Для твердых тел почти нет различия между Cp и CV по причине пренебрежительно малой работы при сжатии или расширении.
Опыт показывает, что молярная теплоемкость у многих твердых тел (химических элементов) при обычных температурах на самом деле близка к 3R. При этом, в условиях низких температур заметны довольно сильные расхождения между теорией и экспериментом. Таким образом, гипотеза о равномерном распределении энергии по степеням свободы может считаться лишь приближением. Заметная в опыте зависимость теплоемкости от температуры объясняется только при условии использования квантовых представлений.
Молярная и удельная теплоемкость газа.
Молярная
теплоемкость
Молярная
теплоемкость — теплоемкость 1 моля
идеального газа.
Теплоемкость
идеального газа в изопроцессах
Адиабатический
В
адиабатическом процессе теплообмена
с окружающей средой не происходит, то
есть 
.
При изменении объема температура и
давление меняются, то есть 
.
Следовательно, теплоемкость идеального
газа в адиабатическом процессе также
равна нулю: Садиаб=0.
Изотермический
В
изотермическом процессе постоянна
температура, то есть 
.
При изменении объема газу передается
(или отбирается) некоторое количество
тепла. Следовательно, теплоемкость
идеального газа стремится к бесконечности: 
Изохорный
В
изохорическом процессе постоянен объем,
то есть 
.
Элементарная работа газа равна
произведению изменения объема на
давление, при котором происходит
изменение (δA =
δVP).
Первое Начало Термодинамики для
изохорического процесса имеет вид:
А
для идеального газа
Таким
образом,
где i —
число степеней свободы частиц газа.
Изобарный
В
изобарном процессе (
):
CP=δQ/νΔT=CV+R=((i+2)/2)*R
Уде́льная
теплоёмкость (Удельная
теплота нагревания на один градус,
обозначается как c)
вещества определяется как
количество тепловой энергии,
необходимой для
повышениятемпературы одного килограмма вещества
на один градус.
Единицей СИ для
удельной теплоёмкости
является Джоуль на килограмм–Кельвин.
Следовательно, удельную теплоёмкость
можно рассматривать
как теплоёмкость единицы массывещества.
На значение удельной теплоёмкости
влияет температура вещества. К примеру,
измерение удельной теплоёмкости воды
даст разные результаты при 20 °C и
60 °C.
Формула
расчёта удельной теплоёмкости: 
,
где 
—
удельная теплоёмкость, 
— количество
теплоты,
полученное веществом при нагреве (или
выделившееся при охлаждении),
—
масса нагреваемого (охлаждающегося)
вещества, 
—
разность конечной и начальной температур
вещества.
Связь
Cv
и Cp:
т.
е. молярная теплоемкость газа при
постоянном объеме СV равна
изменению внутренней энергии одного
моль газа при повышении его температуры
на 1 К. Поскольку Um=(i/2)RT
, то
(5)
Если
газ нагревается при постоянном давлении,
то выражение (3) можно представить в
виде
Учитывая,
что (Um/dT)
не зависит от вида процесса (внутренняя
энергия идеального газа не зависит ни
от p, ни от V, а определяется лишь
температурой Т) и всегда равна СV (см.
(4)), и дифференцируя уравнение Клапейрона
— Менделеева pVm=RT
(42.4) по T (p=const), получаем
(6)
Выражение
(6) называется уравнением
Майера;
оно говорит о том, что Сp всегда
больше СV ровно
на величину молярной газовой постоянной.
Это объясняется тем, чтобы осуществить
нагревание газа при постоянном давлении
требуется еще дополнительное количество
теплоты на совершение работы расширения
газа, так как постоянство давления
обеспечивается увеличением объема
газа. Использовав (5), формулу (6) можно
записать в виде
(7)
При
исследовании термодинамических процессов
важно знать характерное для каждого
газа отношение Сp к
СV :
(8)
Из
формул (5) и (7) следует, что молярные
теплоемкости зависят лишь от числа
степеней свободы и не зависят от
температуры. Это утверждение
молекулярно-кинетической теории
справедливо в довольно широком интервале
температур лишь для одноатомных газов.
Уже у двухатомных газов число степеней
свободы, которое проявляется в
теплоемкости, зависит от температуры.
Молекула двухатомного газа обладает
тремя поступательными, двумя вращательными
и одной колебательной степенями
свободы.
По
закону равномерного распределения
энергии по степеням свободы, для комнатных
температур СV =
(7/2)R. Из качественной экспериментальной
зависимости молярной теплоемкости
СV водорода
(рис. 1) следует, что СV следующим
образом зависит от температуры: при
низкой температуре (≈50 К) СV =
(3/2)R, при комнатной — CV =
(5/2)R (вместо расчетных (7/2)R) и при очень
высокой — СV=
(7/2)R. Это можно объяснить, сделав
предположение, что при низких температурах
наблюдается только поступательное
движение молекул, при комнатных —
добавляется их вращение, а при высоких
— к данным двум видам движения добавляются
еще колебания молекул.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Теплоёмкость определяется суммой поступательных, вращательных и удвоенным числом колебательных степеней свободы.
Теплоёмкость идеального газа — отношение количества теплоты, сообщённой газу [math]displaystyle{ delta Q }[/math], к изменению температуры [math]displaystyle{ dT }[/math], которое при этом произошло [math]displaystyle{ C = frac{delta Q}{dT} }[/math] [1].
Удельная и молярная теплоёмкость
Молярная теплоёмкость — теплоёмкость 1 моля вещества [2]:
- [math]displaystyle{ C_M = frac{C}{nu} = frac{1}{nu} frac{delta Q}{Delta T}, }[/math]
где [math]displaystyle{ nu = m/M, }[/math] [math]displaystyle{ m }[/math] — масса, [math]displaystyle{ M }[/math] — молярная масса вещества.
Теплоёмкость единичной массы вещества называется удельной теплоёмкостью и, в системе СИ, измеряется в Дж/(кг·К)[1].
Формула расчёта удельной теплоёмкости[1][2]:
[math]displaystyle{ c=frac{C_M}{M} = frac{delta Q}{ mdT}, }[/math]
- где c — удельная теплоёмкость, m — масса нагреваемого (охлаждающегося) вещества.
Теплоёмкость идеального газа в изопроцессах
Адиабатический
В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть [math]displaystyle{ dQ=0 }[/math]. Однако, объём, давление и температура меняются, то есть [math]displaystyle{ dTneq 0 }[/math][3].
Следовательно, теплоёмкость идеального газа в адиабатическом процессе равна нулю: [math]displaystyle{ C = {0 over dT} = 0 }[/math].
Изотермический
В изотермическом процессе постоянна температура, то есть [math]displaystyle{ dT=0 }[/math]. При изменении объёма газу передаётся (или отбирается) некоторое количество тепла[3]. Следовательно, теплоёмкость идеального газа равна плюс-минус бесконечности: [math]displaystyle{ C to pm infty }[/math]
Изохорный
В изохорном процессе постоянен объём, то есть [math]displaystyle{ delta V=0 }[/math] и, следовательно газ не совершает работы. Первое Начало Термодинамики для изохорного процесса имеет вид[1]:
- [math]displaystyle{ dU=delta Q = nu C_V dT. qquad (1) }[/math]
А для идеального газа
- [math]displaystyle{ dU=frac i2 nu R Delta T. }[/math]
Таким образом,
- [math]displaystyle{ C_V=frac i2 R, }[/math]
где [math]displaystyle{ i }[/math] — число степеней свободы частиц газа.
Другая формула:
- [math]displaystyle{ C_{V}=frac{R}{gamma – 1}, }[/math]
где [math]displaystyle{ gamma }[/math] — показатель адиабаты, [math]displaystyle{ R }[/math] — газовая постоянная газа.
Изобарный
Молярная теплоёмкость при постоянном давлении обозначается как [math]displaystyle{ C_p }[/math]. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера [math]displaystyle{ C_p = C_v + R }[/math][1].
Уравнение Майера вытекает из первого начала термодинамики[4]:
- [math]displaystyle{ delta Q = mathrm{d} U + delta A, qquad(2) }[/math].
В рассматриваемом случае, согласно определению теплоёмкости:
- [math]displaystyle{ delta Q = C_p mathrm{d} T, }[/math]
Учитываем, что работа газа равна [4]:
- [math]displaystyle{ delta A = mathrm{d} (pV) = nRmathrm{d} T qquad = p mathrm{d} V qquad + V mathrm{d} p qquad=p mathrm{d} V qquad, (V mathrm{d} p qquad=0) (3) }[/math]
Согласно уравнению Менделеева-Клапейрона для одного моля газа[1]:
- [math]displaystyle{ p mathrm{d} V = R mathrm{d} T. qquad (4) }[/math]
Подставляя уравнение (4) в (3) получаем:
- [math]displaystyle{ delta A = R mathrm{d} T qquad (5) }[/math]
Так как энергия одной молекулы равна [math]displaystyle{ lt egt = frac{i}{2}kT }[/math] (6)[Комм 1][5], то и внутренняя энергия в целом и при изобарном процессе будет определяться по соотношению (1). Следовательно, подставляя уравнения (1) и (5) в (2) получаем соотношение Майера.
Молекулярно-кинетическая теория позволяет вычислить значения молярной теплоёмкости для классического идеального газа газов через значение универсальной газовой постоянной исходя из уравнения (6) и предположения, что молекулы газа не взаимодействуют между собой[5]:
- для общего случая [math]displaystyle{ C_p = frac{i+2}{2}R, }[/math]
- для одноатомных газов [math]displaystyle{ C_p = frac{5}{2}R, }[/math] то есть около 20.8 Дж/(моль·К);
- для двухатомных газов и многоатомных газов с линейными молекулами[Комм 2] [math]displaystyle{ C_p = frac{7}{2}R, }[/math] то есть около 29.1 Дж/(моль·К);
- для многоатомных газов с нелинейными молекулами[Комм 2] [math]displaystyle{ C_p = 4R, }[/math] то есть около 33.3 Дж/(моль·К).
Теплоёмкости можно также определить исходя из уравнения Майера, если известен показатель адиабаты, который можно измерить экспериментально (например, с помощью измерения скорости звука в газе или используя метод Клемана — Дезорма).
Теплоёмкость реального газа может значительно отклонятся от теплоёмкости идеального газа. Так при температуре в 25 °С и атмосферном давлении атомарный водород имеет теплоёмкость 2,50R , а атомарный кислород — 2,63R. Также теплоёмкость реального газа зависит от температуры[5].
См. также
- Идеальный газ
- Первое начало термодинамики
- Теплоёмкость
Комментарии
- ↑ i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы
- ↑ 2,0 2,1 При жёсткой связи между атомами, то есть колебательные степени свободы исключены из рассмотрения. Примером трёхатомной линейной молекулы служит цианистый водород HCN.
Примечания
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 Савельев, 2001, с. 26—30.
- ↑ 2,0 2,1 Базаров И. П., Термодинамика, 2010, с. 41.
- ↑ 3,0 3,1 Савельев, 2001, с. 30—31.
- ↑ 4,0 4,1 Савельев, 2001, с. 18-20.
- ↑ 5,0 5,1 5,2 Савельев, 2001, с. 61-63.
Литература
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.— Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Белоконь Н. И. Основные принципы термодинамики. — М.: Недра, 1968. — 110 с.
- Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
Теплоемкость идеального газа – это отношение тепла, сообщенного газу, к изменению температуры δТ, которое при этом произошло.
Молярная теплоемкость
Молярная теплоемкость – теплоемкость 1 моля идеального газа.
Теплоемкость идеального газа в процессах
Адиабатический
В адиабатическом процессе теплообмена с окружающей средой не происходит, т.е. δQ=0. Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: Садиаб=0.
Изотермический
В изотермическом процессе постоянна температура, т.е. . Следовательно, теплоемкость идеального газа стремится к бесконечности: 
Изохорический
В изохорическом процессе постоянен объем, т.е. . Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение (
). Первое Начало Термодинамики для изохорического процесса имеет вид:
А для идеального газа
Таким образом,
где – число степеней свободы частиц газа.
Изобарический
В изобарическом процессе (
):
CP=δQ/νΔT=CV+R=(5/2)*R
Вывод формулы для теплоемкости в данном процессе
Согласно 1 началу термодинамики существует 2 способа изменить внутреннюю энергию тела (в нашем случае идеального газа): передать ему тепло или совершить над ним работу.
dU=δQ+δA, где δA – работа окр. среды над газом.
δAокр.среды=-δAгаза
δQ=dU+δAгаза
В расчете на 1 моль:
С=δQ/ΔT=(ΔU+pΔV)/ΔT
ΔU=CV*ΔT
C=CV+(pΔV/ΔT)в данном процессе
См. также
- Идеальный газ
- Первое начало термодинамики
- Теплоемкость
Ссылки
1. Открытый Колледж
2. CГГА
3. Статья в “Кванте”, формат djvu
