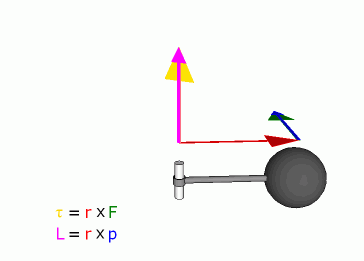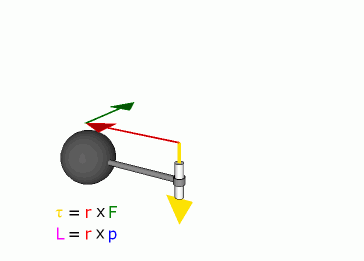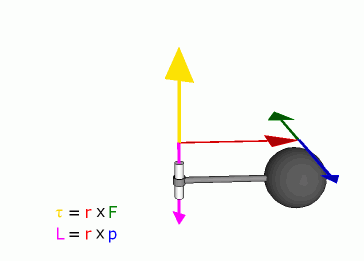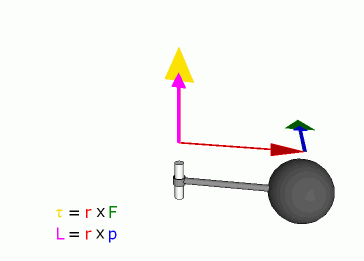Как найти момент импульса частицы

Как найти момент импульса частицы

Кроме энергии и импульса существует
ещё Одина физическая величина. С которой
связан закон сохранения — это момент
импульса. Моментом импульса частицы
относительно точки О называется векторравный,-радиус;
-импульс.

Т.е.
является ??? вектором. Его направление
выбрано так, что вращение вокруг О в
направлениии векторобразует правовинтовую систему. Модульугол
междуи

плечо вектораотносительно О.

Найдем с какой величиной связано
изменение вектора
во времени:

.

Т.к
т.о неподвижна, торавно скорости частицы, т.е. совпадает
с,
т.е..
Далее— второй закон Ньютона и;
Величина—момент
силы аксиальный вектор.,—плечо
силыотносительно т.О.

Т.о производная по
момента импульсачастицы, относительно некоторой т.О
выбранной системы отсчета равна моменту
равнодействующей силыотносительно этой точки.
Это уравнение называют уравнением
моментов.

Если система отсчета является
неинерциальной, то в момент силы
включает в себя как момент сил
взаимодействия, так и момент сил инерции
(относительно той же т.О). Из уравнения
моментов следует что если,
то—равномерное
вращательное движение. Т.е. если момент
всех сил относительно т.О системы отсчета
равен О, в течение интересующего нас,
то момент импульса частицы относительно
этой точки остается постоянным.

Уравнение моментов позволяет найти
точки относительно О в любой момент
времени если известначастицы относительно точки. Для этого
достаточно продифференцировать уравнение.
Кроме этого, если известна зависимость,
то можно найти приращение момента
импульса частицы относительно т.О за
любой промежуток времени. Для этого
необходимо проинтегрировать уравнение,
тогда

Выражение
—импульс
момента силы подобно,
т.е. приращение момента импульса частицы
за любой промежуток времени равно
импульсу момента силы за э

то время.

4.3. Момент импульса и момент силы относительно оси.

Возьмем
в интересующей нас системе отсчета
произвольную неподвижную ось.
Пусть относительно некоторой т.О осимомент импульса частицы равен,
а момент сил.
Момент импульса относительно осиназывается проекция на эту ось вектора,
определенного относительно произвольной
точки О данной оси. Аналогично вводится
понятие момента силы относительно оси.
Уравнение момента относительно осит.е. производная ототносительноравнаотносительно
этой оси. В частности при.
Т.е. если момент илы относительно
некоторой осиравен 0, тоотносительно этой оси остаеся постоянным.
При этом векторменяется.

4.4. Закон сохранения момента импульса системы.

Рассмотрим систему состоящую из 2 частиц,
на которые действуют также силы
и.
Момент импульса является аддитивной
величиной. Для системы равен векторной
сумме моментов импульса отдельных
частиц относительно одной и той же точки.

Нам известно, что
—моменту
всех сил, действующих на частицу, а
изменение момента системы,
тогда;;

—
суммарный момент всех внутренних сил
действующих на частицы.

—
суммарный момент всех внешних сил
действующих на частицы.

Значит для двух частиц:

.

Суммарный момент внутренних сил
относительно любой точки равен 0. силы
взаимодействия между частицами
по 3му закону Ньютона
действуют по одной прямой, значит имеют
одинаковое плечо, поэтому момент каждой
пары внутренних сил равен 0.

Т.о.
;
т.е. системы изменяются под действием
внешних сил.
Если внешние силы отсутствуют,,
то,
является аддитивным сохраняющейся
величиной. Т.е. момент импульса замкнутой
системы частиц остается постоянным, не
меняется со временем. Это справедливо
относительно любой точки инерциальной
системы отсчета:т.е. моменты импульса отдельных частейодной части системы происходят за счет
убылидругой части (относительно одной точки).

Закон справедлив и в неинерциальной
системе отсчета в тех случаях когда
суммарный момент всех внешних сил,
включая силы инерции равен нулю.

Закон
играет такую же роль как закон сохранения
энергии импульса. Он позволяет решать
разные задачи, не рассматривая детально
внутренние процессы. Пример: разгоняют????

Момент импульса
;т.е.уменьшается как.
Этот эффект широко используют гимнасты,
фигуристы и т.д. здесь мы интересуемся
силами взаимодействия и т.д. у незамкнутых
систем может сохраняться не сам,
а его проекция на некоторую неподвижную
ось.
Это бывает, когдавсех внешних сил.

;;

В физике понятие момента импульса
расширяют на немеханические системы
(с электромагнитным излучением, в атомах,
ядра и др.) где не действуют законы
Ньютона. Здесь закон сохранения момента
импульса уже не является следствием
законов Ньютона, а представляет собой
самостоятельныйпринцип, является
обобщением опытных фактов и является
одним из фундаментальных законов наряду
с законами сохранения энергии и импульса.

Источник
Момент импульса
{displaystyle {vec {L}}={vec {r}}times {vec {p}},}
Размерность L2MT−1
Единицы измерения
СИ м2·кг/с
СГС см2·г/с
Примечания
псевдовектор

Моме́нт и́мпульса (момент импульса относительно точки, также: кинетический момент, угловой момент, орбитальный момент, момент количества движения) — физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение[1].

Для одной материальной точки момент импульса равен векторному произведению радиус-вектора точки на её импульс, для системы точек — сумме таких произведений. Стандартное обозначение: mathbf{L}, единица измерения в СИ: м2кг/с. Величина mathbf{L} зависит от выбора положения начала отсчёта радиус-векторов O.

Момент импульса замкнутой системы сохраняется. Он является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения. При наличии внешних сил производная момента импульса по времени равна моменту сил (относительно того же начала O).

Основное использование понятия момента импульса относится к задачам, связанным с реальным вращением (особенно при наличии центральной или осевой симметрии; тогда О обычно выбирается в центре или на оси). Но величина mathbf{L} может быть вычислена и в других ситуациях, например для прямолинейного движения частицы мимо произвольной точки O, не лежащей на линии движения и условно принимаемой за центр.

В случае вращения твёрдого тела вокруг фиксированной оси часто используется не сам момент импульса, а его проекция {displaystyle L_{parallel }} на эту ось — такая величина называется моментом импульса относительно оси.

Понятие момента импульса было изначально введено в классической механике, но имеет обобщения в квантовой механике и электродинамике.

Момент импульса в классической механике[править | править код]

Связь между силой F, моментом силы τ, импульсом scriptstyle{mathbf p} и моментом импульса scriptstyle{mathbf L}

Определение[править | править код]

Момент импульса mathbf L материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:

{mathbf {L}}={mathbf {r}}times {mathbf {p}},

где mathbf {r}  — радиус-вектор частицы относительно выбранного неподвижного начала отсчёта, {mathbf p} — импульс частицы.

Из определения момента импульса следует его аддитивность: для системы, состоящей из нескольких материальных точек, выполняется

{displaystyle mathbf {L} =sum limits _{i}mathbf {L} _{i}=sum _{i}mathbf {r} _{i}times mathbf {p} _{i}}.

Количество частиц может быть бесконечным, например в случае твёрдого тела с распределённой массой.

Так как момент импульса задаётся векторным произведением, он является псевдовектором, перпендикулярным обоим векторам mathbf {r} и {mathbf p}.

Момент импульса можно вычислить относительно любого начала отсчета O (получающиеся при этом разные значения mathbf{L} связаны очевидным образом); однако чаще всего (для удобства и определённости) его вычисляют относительно центра масс, закреплённой точки вращения твердого тела или другой чем-то выделенной точки.

Выбор точки O иногда связан с характером задачи. Так, при рассмотрении орбитального движения планеты вокруг Солнца за начало отсчёта естественно взять Солнце, а при анализе её же собственного вращения — центр этой планеты. Естественно, получатся два разных момента импульса: {displaystyle mathbf {L} _{mathrm {orbit} }} и {displaystyle mathbf {L} _{mathrm {spin} }}.

Вычисление в общем случае[править | править код]

Если имеется материальная точка массой m, двигающаяся со скоростью mathbf{v} и находящаяся в точке, описываемой радиус-вектором mathbf {r} , то {displaystyle mathbf {p} =mmathbf {v} } и момент импульса вычисляется по формуле

{displaystyle mathbf {L} =mathbf {r} times mmathbf {v} }.

Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки {displaystyle dm=rho (mathbf {r} )dV} (rho — плотность) и просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:

{displaystyle mathbf {L} =int limits _{V}{mathbf {dL} }=int limits _{V}{mathbf {r} times mathbf {v} ,dm}=int limits _{V}{mathbf {r} times mathbf {v} ,rho dV}}.

На практике rho задаётся как функция трёх координат и необходимо выполнение тройного интегрирования:

{displaystyle mathbf {L} =iiint {(xmathbf {i} +ymathbf {j} +zmathbf {k} )times mathbf {v} ,rho (x,y,z),dx,dy,dz}}.

Если считать, что rho(x,y,z) — обобщённая функция, включающая, возможно, и дельтообразные члены, то эта формула применима и к распределённым, и к дискретным системам.

Случай фиксированной оси[править | править код]

Важным случаем использования понятия «момент импульса» является движение вокруг неизменной оси. В такой ситуации часто рассматривают не сам момент импульса (псевдовектор), а его проекцию на ось как псевдоскаляр, знак которого зависит от направления вращения:

{displaystyle L_{parallel }=pm |mathbf {r_{perp }} times mathbf {p_{perp }} |}.

Параллельность-перпендикулярность (parallel , perp ) имеются в виду по отношению к оси; {displaystyle mathbf {r} =mathbf {r_{perp }} +mathbf {r_{parallel }} }, {displaystyle mathbf {p} =mathbf {p_{perp }} +mathbf {p_{parallel }} }. При этом {displaystyle r_{perp }} — расстояние от оси до материальной точки, называемое «плечом». Величина указанной проекции, в отличие от самого момента, не меняется при сдвиге начала отсчёта O на оси. Для распределённой системы

{displaystyle L_{parallel }=pm left|int {mathbf {r_{perp }} times mathbf {v_{perp }} ,rho dV}right|}.

Если при этом все точки тела движутся по окружностям (вращаются) с одинаковой угловой скоростью omega , то есть численно {displaystyle v=omega r_{perp }}, то для материальной точки массой m или для системы будет, соответственно,

{displaystyle L_{parallel }=pm omega mr_{perp }^{2}quad } или {displaystyle quad L_{parallel }=pm omega int {r_{perp }^{2},rho dV}}.

Величину {displaystyle L_{parallel }} иногда называют моментом импульса относительно оси. Символ параллельности у L и знак перед выражением могут опускаться, если очевидно, о чём идёт речь.

Для абсолютно твёрдого тела, величина последнего интеграла называется моментом инерции относительно оси вращения и обозначается I. Тогда запись обретает вид {displaystyle ,L_{parallel }=pm Iomega ,} или, в векторной форме, {displaystyle mathbf {L} =I{boldsymbol {omega }}}. Если известен момент инерции относительно оси, проходящей через центр масс тела, а вращение происходит вокруг другой, но параллельной ей оси, то необходимый момент инерции находится по теореме Штайнера.

Сохранение момента импульса[править | править код]

Закон сохранения момента импульса: суммарный момент импульса относительно любой неподвижной точки для замкнутой системы остается постоянным со временем.

Производная момента импульса по времени есть момент силы:

{displaystyle {frac {dmathbf {L} }{dt}}=sum _{i}{frac {dmathbf {r} _{i}}{dt}}times mathbf {p} _{i}+sum _{i}mathbf {r} _{i}times {frac {dmathbf {p} _{i}}{dt}}=sum _{i}mathbf {r} _{i}times mathbf {F} _{i}=mathbf {tau _{ext}} },

Таким образом, требование замкнутости системы может быть ослаблено до требования равенства нулю главного (суммарного по всем частицам i) момента внешних сил:

{displaystyle mathbf {L} =mathrm {constant} leftrightarrow mathbf {tau _{ext}} =0},

где {displaystyle mathbf {tau _{ext}} } — момент сил, приложенных к системе частиц. (Но конечно, если внешние силы вообще отсутствуют, это требование также выполняется.) Аналогичный закон сохранения справедлив для момента импульса относительно фиксированной оси.

По теореме Нётер закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол delta varphi, радиус-вектор частицы с номером i изменятся на {displaystyle delta mathbf {r} _{i}=delta varphi times mathbf {r} _{i}}, а скорости — {displaystyle delta mathbf {v} _{i}=delta varphi times mathbf {v} _{i}}. Функция Лагранжа {mathcal L} системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому

delta mathcal L = mathcal L(mathbf{r}_i + deltamathbf{r}_i,; mathbf{v}_i + deltamathbf{v}_i) - mathcal L(mathbf{r}_i,; mathbf{v}_i) = sum limits_i left( frac{partial mathcal L}{partial mathbf r_i} delta varphi timesmathbf r_i + frac{partial mathcal L}{partial mathbf v_i} delta varphi times mathbf v_i right)= 0.

С учётом frac{partial {mathcal {L}}}{partial {mathbf v_{i}}} = mathbf {p_{i}},; frac{partial mathcal {L}}{partial mathbf {r_{i}}} = mathbf {dot p_{i}}, где {mathbf p}_{i} — обобщенный импульс i-той частицы, каждое слагаемое в сумме из последнего выражения можно переписать в виде

dot {mathbf p_i} ,delta varphi times mathbf r_i + mathbf p_i,delta varphi times mathbf {dot r_i}.

Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:

delta mathcal L = delta varphi sum limits_i left( mathbf r_i times dot {mathbf p_i} + dot {mathbf r_i} times mathbf p_i right) = delta varphi frac{d}{dt} sum limits_i (mathbf r_i times mathbf p_i) = delta varphi frac{d mathbf L}{dt} = 0,

где mathbf L = sum mathbf L_i = sum mathbf r_i times mathbf p_i — момент импульса системы. Ввиду произвольности delta varphi, из равенства delta mathcal L = 0 следует {displaystyle {frac {dmathbf {L} }{dt}}=0.}

Смежные понятия[править | править код]

При рассмотрении задач, связанных с вращением, фигурируют понятия, частично упоминавшиеся выше:

  • момент импульса относительно оси (термин состоит из четырёх слов) — проекция момента импульса на ось;
  • момент инерции твёрдого тела (см. также моменты инерции некоторых тел);
  • момент силы (он же: крутящий момент, вращательный момент, вертящий момент);
  • импульс момента силы {displaystyle int limits _{t_{1}}^{t_{2}}mathbf {r} times mathbf {F} (t);dt} (единица измерения — Н·м·с) — мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении).

Несмотря на созвучность с «моментом импульса», эти понятия не синонимичны термину «момент импульса» и несут самостоятельный смысл.

Момент импульса в электродинамике[править | править код]

При описании движения заряженной частицы в электромагнитном поле канонический импульс p не является инвариантным. Как следствие, канонический момент импульса {displaystyle mathbf {L} =mathbf {r} times mathbf {p} } тоже не инвариантен. Тогда берётся реальный импульс, который также называется «кинетическим импульсом»:

{displaystyle mathbf {p} -{frac {emathbf {A} }{c}},}

где e — электрический заряд, c — скорость света, A — векторный потенциал. Таким образом, гамильтониан (инвариантный) заряженной частицы массы m в электромагнитном поле:

H =frac{1}{2m} left( mathbf{p} -frac {e mathbf{A} }{c}right)^2 + evarphi,

где varphi  — скалярный потенциал. Из этого потенциала следует закон Лоренца. Инвариантный момент импульса, или «кинетический момент импульса», определяется следующим образом:

K= mathbf{r} times left( mathbf{p} -frac {e mathbf{A} }{c}right).

Момент импульса в квантовой механике[править | править код]

Оператор момента[править | править код]

В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определёнными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на hbar (h с чертой — постоянная Планка, поделенная на 2 pi ).

Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновый момент импульса всегда кратен hbar/2 для фермионов и hbar для бозонов. Например, электрон в состоянии покоя имеет момент импульса hbar/2.[2]

В классическом определении момент импульса зависит от 6 переменных {displaystyle r_{x}}, {displaystyle r_{y}}, {displaystyle r_{z}}, p_{x}, p_{y}, и p_{z}. Переводя это на квантовомеханические определения, используя принцип неопределенности Гейзенберга, получаем, что невозможно вычислить все шесть переменных одновременно с любой точностью. Поэтому есть ограничение на то, что мы можем узнать или подсчитать о практическом моменте импульса. Это значит, что лучшее, что мы можем сделать — это подсчитать одновременно величину вектора момента импульса и какой-либо одной его компоненты (проекции).

Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:

{displaystyle {hat {mathbf {L} }}={hat {mathbf {r} }}times {hat {mathbf {p} }}},

где hat{mathbf{r}} и hat{mathbf{p}} — координатный и импульсный оператор, соответственно, а второй — на внутренние, спиновые. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:

{displaystyle {hat {mathbf {L} }}=-ihbar (mathbf {r} times nabla )},

где nabla  — оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства:

[L_i,; L_j ] = i hbar varepsilon_{ijk} L_k, quadleft[L_i,; mathbf{L}^2 right] = 0,

где varepsilon_{ijk} — Символ Леви-Чивиты;

и даже более важные подстановки с гамильтонианом частицы без заряда и спина:

left[L_i,; H right] = 0.

Симметрия вращения[править | править код]

Операторы момента импульса обычно встречаются при решении задач сферической симметрии в сферических координатах. Тогда момент импульса в пространственном отображении:

{displaystyle -{frac {1}{hbar ^{2}}}mathbf {L} ^{2}={frac {1}{sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial }{partial theta }}right)+{frac {1}{sin ^{2}theta }}{frac {partial ^{2}}{partial varphi ^{2}}}.}

Когда находят собственные значения этого оператора, получают следующее:

{displaystyle L^{2}mid l,;mrangle ={hbar }^{2}l(l+1)mid l,;mrangle ,}
L_z mid l,; m rang = hbar m mid l,; m rang,

где l, m — целые числа, такие что {displaystyle -lleq mleq l,} а
lang theta ,; varphi mid l,; m rang = Y_{l,;m}(theta,;varphi)
— сферические функции.

Примечания[править | править код]

  1. ↑ Pivarski, Jim Spin. Symmetry Magazine (март 2013). Дата обращения: 28 апреля 2014. Архивировано 15 апреля 2014 года.
  2. ↑ [Информация с сайта Нобелевского комитета (англ.). Дата обращения: 3 ноября 2017. Архивировано 18 мая 2008 года. Информация с сайта Нобелевского комитета (англ.)]

Литература[править | править код]

  • Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. — М.: Мир, 1984. — Т. 1. — 302 с.
  • Блохинцев Д. И. Основы квантовой механики. — М.: Наука, 1976. — 664 с.
  • Боум А. Квантовая механика: основы и приложения. — М.: Мир, 1990. — 720 с.
  • Варшалович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория углового момента. — Л.: Наука, 1975. — 441 с.
  • Зар Р. Теория углового момента. О пространственных эффектах в физике и химии. — М.: Мир, 1993. — 352 с.
Источник

Уравнение моментов для частицы и системы частиц

Закон сохранения момента импульса >>

Уравнение моментов для частицы и системы частиц. dL/dt = M – скорость изменения момента импульса частицы равна моменту силы: dL/dt = [dr/dt,p] + [r,dp/dt] = [r,dp/dt] = [r,F] = M Для системы частиц: dL/dt = Mвнешн – производная по времени от момента импульса системы материальных точек относительно произвольного неподвижного начала равна суммарному моменту всех внешних сил относительно того же начала. dLz/dt = Mz – уравнение моментов относительно неподвижной оси 0Z. Если Mz = 0, то Lz = const.

Слайд 8 из презентации «Момент силы 10 класс»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Момент силы 10 класс.ppt» можно в zip-архиве размером 235 КБ.

Похожие презентации

«Вещества тела частицы» – Твёрдые жидкие газообразные СОЛЬ ВОДА ГАЗ. Любой предмет, любое живое существо можно назвать телом. Тела состоят из Веществ. Тела. Тела, вещества, частицы. Вещества состоят из мельчайших частиц, невидимых глазом. Загадки. Естественные Искусственные. Первый русский ученый – естествоиспытатель, физик, химик, историк, поэт и художник.

«Частица 7 класс» – Частица как часть речи. Правописание частиц. Проблемные вопросы. Создать ситуацию успеха на уроке. Основополагающий вопрос. Представление результатов исследования. Уметь определять роль частиц в предложении. Что такое ЧАСТИЦА. Какие разряды частиц бывают? Зачем нужны части речи? Употребление и разграничение на письме частиц НЕ и НИ.

«Методы наблюдения и регистрации частиц» – Анод. Вильсон Чарлз Томсон Рис. « ….. воспитание творческих способностей в человеке основывается на развитии самостоятельного мышления» П.П. Капица. Пузырьковая камера. Стеклянная трубка. Методы наблюдения и регистрации элементарных частиц. Газоразрядный счётчик Гейгера. Сцинтилляционный метод. Регистрация сложных частиц затруднена.

«Методы регистрации элементарных частиц» – Пролёт частицы вызывает образование цепочки капель, которые можно сфотографировать. Счетчик Гейгера. Разрядные искры строго локализованы. Треки элементарных частиц в толстослойной фотоэмульсии. Расстояние между пластинами от 1-2 см до 10 см. Метод толстослойных фотоэмульсий. 20-е г.г. Л.В.Мысовский, А.П.Жданов.

«Заряжённые частицы» – Метод толстослойных фотоэмульсий позволяет регистрировать редкие явления. Пузырьковая камера. Метод толстослойных фотоэмульсий. Применение изотопов. Счётчик Гейгера позволяет регистрировать только факт пролета частицы. Изотопы. Счетчик Гейгера. Пузырьковая камера позволяет регистрировать траектории заряженных частиц.

«Момент силы» – Тема урока: «Момент силы». Задача. Сделайте расчет, пользуясь правилом моментов сил. Рычаги в технике, быту и природе.

Уравнение моментов: моменты силы, импульса и инерции

Если линейное перемещение тел описывают в классической механике с помощью законов Ньютона, то характеристики движения механических систем по круговым траекториям вычисляют с помощью специального выражения, которое называется уравнением моментов. О каких моментах идет речь и в чем заключается смысл этого уравнения? Эти и другие вопросы раскрываются в статье.

Момент силы

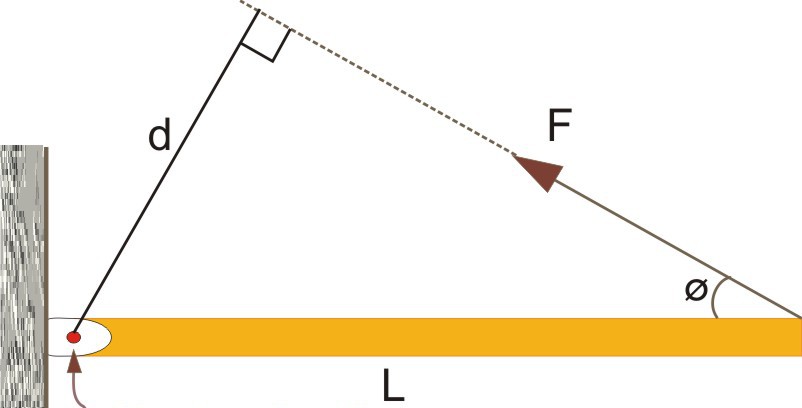
Всем хорошо известна ньютоновская сила, которая, действуя на тело, приводит к сообщению ему ускорения. Когда же такая сила прилагается к объекту, который закреплен на некоторой оси вращения, то эту характеристику принято называть моментом силы. Уравнение момента силы может быть записано в следующем виде:

Рисунок, поясняющий это выражение, приведен ниже.

Здесь видно, что сила F¯ направлена к вектору L¯ под углом Φ. Сам же вектор L¯ полагается направленным от оси вращения (указана стрелкой) к точке приложения F¯.

Приведенная выше формула представляет собой произведение двух векторов, поэтому величина M¯ также является направленной. Куда будет повернут момент силы M¯? Это можно определить по правилу правой руки (четыре пальца направлены вдоль траектории от конца вектора L¯ к концу F¯, а отставленный палец большой показывает направление M¯).

На рисунке выше выражение для момента силы в скалярном виде примет форму:

Если внимательно всмотреться в рисунок, то можно увидеть, что L*sin(Φ) = d, тогда имеем формулу:

Величина d является важной характеристикой при вычислении момента силы, поскольку она отражает эффективность приложенной F к системе. Эту величину принято называть рычагом силы.

Физический смысл M заключается в способности силы совершить вращение системы. Эту способность может ощутить на себе каждый, если будет открывать дверь за ручку, толкая ее около петель, или же попробует открутить гайку коротким и длинным ключом.

Равновесие системы

Понятие о моменте силы оказывается очень полезным, когда рассматривают равновесие системы, на которую действуют несколько сил, и которая имеет ось или точку вращения. В таких случаях применяют формулу:

То есть система будет находиться в равновесии, если сумма всех моментов сил, приложенных к ней, нулевая. Заметим, что в этой формуле присутствует знак вектора над моментом, то есть при решении следует не забывать учитывать знак этой величины. Общепринятым правилом считается, что действующая сила, которая вращает систему против часовой стрелки, создает положительный Mi¯.

Ярким примером задач рассматриваемого типа являются проблемы с равновесием рычагов Архимеда.

Момент импульса

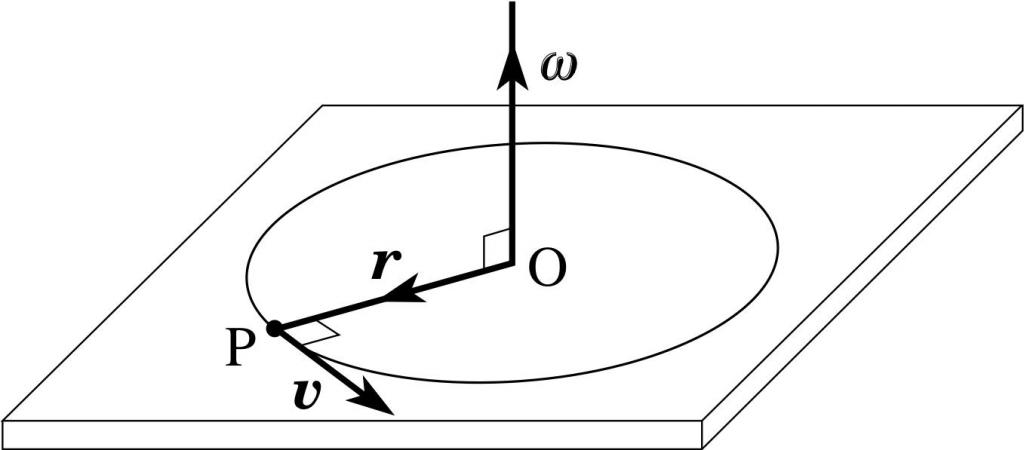
Это еще одна важная характеристика движения по окружности. В физике ее описывают произведением количества движения на рычаг. Уравнение момента импульса имеет такой вид:

Здесь p¯ – вектор импульса, r¯ – вектор, соединяющий вращающуюся материальную точку с осью.

Поясняющий это выражение рисунок приведен ниже.

Здесь ω – угловая скорость, которая дальше появится в уравнении моментов. Заметим, что направление вектора T¯ находится по тому же правилу, что и M¯. На рисунке выше T¯ по направлению будет совпадать с вектором угловой скорости ω¯.

Физический смысл величины T¯ является таким же, как и характеристики p¯ в случае линейного движения, то есть момент импульса описывает количество вращательного движения (запасенную кинетическую энергию).

Момент инерции

Третья важная характеристика, без которой невозможно составить уравнение движения вращающегося объекта, – это момент инерции. Появляется он в физике в результате математических преобразований формулы для момента импульса материальной точки. Покажем, как это делается.

Представим величину T¯ в следующем виде:

T¯ = r¯*m*v¯, где p¯ = m*v¯

Пользуясь связью между угловой и линейной скоростями, можно переписать это выражение следующим образом:

T¯ = r¯*m*r¯*ω¯, где v¯ = r¯*ω¯

Последнее выражение запишем в виде:

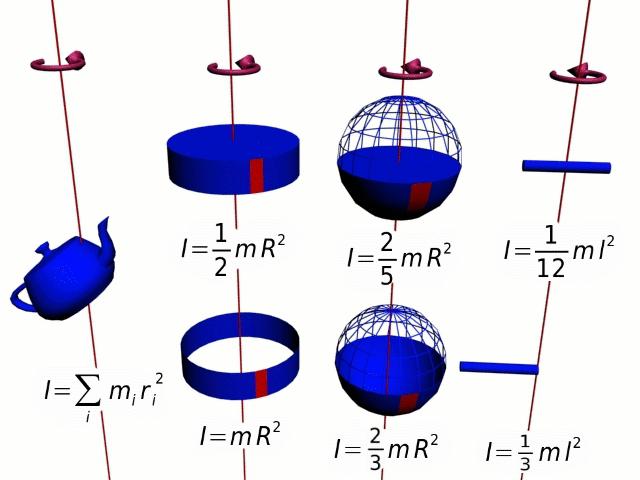
Величина r 2 *m – это момент инерции I для точки массой m, которая совершает круговое движение вокруг оси на расстоянии от нее r. Этот частный случай позволяет ввести общее уравнение момента инерции для тела произвольной формы:

I – это аддитивная величина, смысл которой заключается в инерционности вращающейся системы. Чем больше I, тем труднее раскрутить тело, и необходимо приложить значительные усилия, чтобы его остановить.

Уравнение моментов

Мы рассмотрели три величины, название которых начинается со слова “момент”. Это сделано было намеренно, поскольку все они связаны в одно выражение, получившее название уравнения 3 моментов. Выведем его.

Рассмотрим выражение для момента импульса T¯:

Найдем, как изменяется величина T¯ во времени, имеем:

Учитывая, что производная угловой скорости равна таковой для скорости линейной, деленной на r, а также раскрывая величину I, приходим к выражению:

dT¯/dt = m*r 2 *1/r*dv¯/dt = r*m*a¯, где a¯ = dv¯/dt – линейное ускорение.

Заметим, что произведение массы на ускорение – это не что иное, как действующая внешняя сила F¯. В итоге получаем:

Мы пришли к интересному выводу: изменение момента импульса равно моменту действующей внешней силы. Это выражение принято записывать в несколько иной форме:

M¯ = I*α¯, где α¯ = dω¯/dt – угловое ускорение.

Это равенство называется уравнением моментов. Оно позволяет рассчитать любую характеристику вращающегося тела, зная параметры системы и величину внешнего воздействия на нее.

Закон сохранения T¯

Полученный в предыдущем пункте вывод свидетельствует о том, что если внешний момент сил будет равен нулю, то момент импульса меняться не будет. В таком случае запишем выражение:

Эта формула носит название закона сохранения величины T¯. То есть любые изменения внутри системы суммарный момент импульса не меняют.

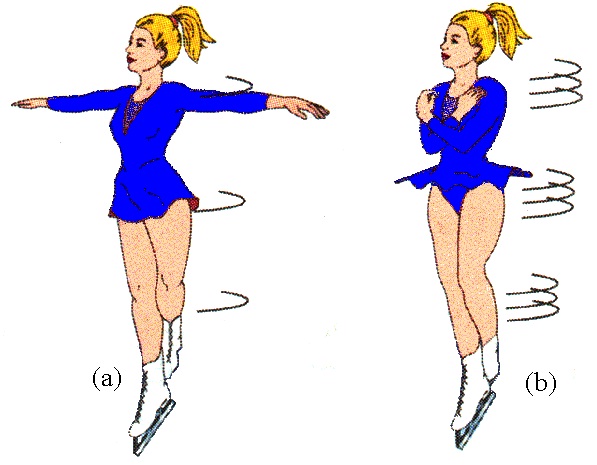
Этот факт используется фигуристами и балеринами во время их выступлений. Также его применяют, если необходимо выполнить поворот вокруг своей оси искусственного спутника, движущегося в космосе.

Уравнение моментов

Определение и уравнение моментов

Пусть O – любая неподвижная точка в инерциальной системе отсчета. Это называется началом или полюсом. Обозначим через радиус-вектор, взятый от этой точки до точки приложения силы (рис.1).

Момент силы относительно точки O является векторным произведением радиус-вектора и силы :

направление выбрано так, что последовательность векторов образует правую систему, т. е. если вы посмотрите вдоль вектора ,то поворот вдоль кратчайшего пути от первого фактора в (1) до вторая выполняется по часовой стрелке, таким образом совпадает с направлением поступательного движения правого штыря, ручка которого вращается от до вдоль кратчайшего пути.

Моментом нескольких сил относительно точки является векторная сумма моментов этих сил относительно одной и той же точки:

Момент импульса материальной точки

Момент импульса материальной точки относительно точки O является векторным произведением радиус-вектора и импульса

где J – момент инерции, – угловая скорость вращения тела.

Система из n материальных точек – это момент количества движения относительно некоторой точки O – векторная сумма моментов импульсов этих точек относительно того же начала:

Временная производная от момента импульса механической системы относительно неподвижной точки (полюса О) равна сумме внешних силовых моментов , действующих на систему:

Для материальной точки уравнение момента написано:

Уравнение (6) называется моментом для системы материальных точек. Это основной закон динамики твердого тела, вращающегося вокруг неподвижной точки.

В проекциях на оси фиксированной декартовой системы координат с началом на полюсе O уравнение моментов системы записывается в виде:

где – проекция момента количества движения на соответствующей оси; – проекции полного момента сил на соответствующую ось.

Уравнение моментов позволяет получить ответ на следующие вопросы:

1. найти момент силы (общий момент внешних сил) относительно интересующей нас точки в любой момент времени, если известна зависимость момента количества движения частицы (системы частиц) от одной и той же точки;

2. определить приращение углового момента частицы (системы частиц) относительно точки O для любого периода времени, если временная зависимость силового момента (полного момента внешних сил), действующего на эту частицу (система частиц) относительно одной и той же точки.

Примеры решения проблем

Сравните угловые скорости, полученные материальной точкой под действием крутящих моментов, графики (a, b) которых показаны на рисунках.

В соответствии с уравнением моментов для материальной точки мы имеем:

поскольку мы имеем дело с материальной точкой, соответственно, J не зависит от времени, получаем:

Вспомните геометрический смысл интеграла.

Вычислить и сравнить площадь треугольников OAB и OCD.

Области треугольников равны соответственно

Угловые скорости, полученные материальной точкой, равны в первом и втором случаях.

Горизонтальный диск с радиусом R = 0,2 м и массой m = 5 кг вращается вокруг оси, проходящей через ее центр. Зависимость угловой скорости вращения диска от времени определяется уравнением w = A + 8t. Найдите значение касательной силы, приложенной к ободу диска. Трение пренебрегалось.

Мы делаем рисунок

Запишем уравнение моментов:

где – искомая сила. Перепишите (2.2), найдите модуль: – угол между вектором и равен , так как силы, касательные к диску, направлены вдоль радиуса диска в точку касания, следовательно, M = RF.

Поскольку мы имеем дело с телом, который не меняет момент инерции со временем, мы имеем:

Где – момент инерции диска относительно оси, проходящей через его центр.

Подставим числовые значения, получим:

Величина (модуль) касательной силы, приложенной к краю диска, равна 4 N.

[spoiler title=”источники:”]

http://fb.ru/article/430454/uravnenie-momentov-momentyi-silyi-impulsa-i-inertsii

http://www.homework.ru/spravochnik/uravnenie-momentov/

[/spoiler]

Источник

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.

Момент импульса замкнутой системы сохраняется.

Момент импульса в классической механике

Torque animation

Связь между импульсом {displaystyle scriptstyle {mathbf {p} }} и моментом {displaystyle scriptstyle {mathbf {L} }}

Определение

Момент импульса {displaystyle mathbf {L} } частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульлор

ъ

{displaystyle ~mathbf {L} =mathbf {r} times mathbf {p} ,}

где {displaystyle ~mathbf {r} } — радиус-вектор частицы относительно выбранного начала отсчёта, {displaystyle ~mathbf {p} } — импульс частицы.

В системе СИ момент импульса измеряется в единицах джоуль–секунда; Дж·с.

Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение:

{displaystyle mathbf {L} _{Sigma }=sum limits _{i}mathbf {L} _{i}}.

Вычисление момента

Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам {displaystyle ~mathbf {r} } и {displaystyle ~mathbf {p} }. Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения. Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на нее можно указать ряд рецептов в соответствии с общими правилами нахождения векторного произведения двух векторов.

{displaystyle L=|mathbf {r} ||mathbf {p} |sin theta _{r,;p},}

где {displaystyle ~theta _{r,;p}} — угол между {displaystyle ~mathbf {r} } и {displaystyle ~mathbf {p} }, определяемый так, чтобы поворот от {displaystyle ~mathbf {r} } к {displaystyle ~mathbf {p} } производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения. Направление поворота важно при вычислении, так как определяет знак искомой проекции.

Запишем {displaystyle ~mathbf {r} } в виде {displaystyle ~mathbf {r} =mathbf {r_{parallel }} +mathbf {r_{perp }} }, где {displaystyle ~mathbf {r_{parallel }} } — составляющая радиус-вектора, параллельная вектору импульса, а {displaystyle ~mathbf {r_{perp }} } — аналогично, перпендикулярная ему. {displaystyle ~mathbf {r_{perp }} } является, по сути, расстоянием от оси вращения до вектора {displaystyle ~mathbf {p} }, которое обычно называют «плечом». Аналогично можно разделить вектор импульса на две составляющие: параллельную радиус-вектору {displaystyle ~mathbf {p_{parallel }} } и перпендикулярную ему {displaystyle ~mathbf {p_{perp }} }. Теперь, используя линейность векторного произведения, а также свойство, согласно которому произведение параллельных векторов равно нулю, можно получить еще два выражения для {displaystyle ~L}.

{displaystyle mathbf {L} =mathbf {r} times mathbf {p} =(mathbf {r_{perp }} +mathbf {r_{parallel }} )times mathbf {p} =mathbf {r_{perp }} times mathbf {p} +mathbf {r_{parallel }} times mathbf {p} =mathbf {r_{perp }} times mathbf {p} .}
{displaystyle mathbf {L} =mathbf {r} times mathbf {p} =mathbf {r} times (mathbf {p_{perp }} +mathbf {p_{parallel }} )=mathbf {r} times mathbf {p_{perp }} .}

Для систем, совершающих вращение вокруг одной из осей симметрии (вообще говоря, вокруг так называемых главных осей инерции), справедливо соотношение

{displaystyle ~mathbf {L} =I{boldsymbol {omega }},}

где {displaystyle ~I} — момент инерции относительно оси вращения, {displaystyle ~{boldsymbol {omega }}} — вектор угловой скорости.

В общем случае вектор момента связан с вектором угловой скорости линейным оператором момента инерции:

{displaystyle mathbf {L} ={hat {I}}{boldsymbol {omega }}}

Сохранение углового момента

Симметрия в физике
Преобразо-
вания 		Инвариант-
ность 		Закон
сохранения
↕ трансляции времени Консервативность …энергии
↔ трансляции пространства Однородность …импульса
○ Вращения Изотропия …момента импульса
× Группа Лоренца Относительность
Лоренц-инвариантность 		инвариантность интервала
(и др. скаляров пространства-времени)

Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.

В замкнутых системах момент импульса постоянен.
Производная момента импульса по времени есть момент силы:

{displaystyle tau ={frac {dmathbf {L} }{dt}}={frac {dmathbf {r} }{dt}}times mathbf {p} +mathbf {r} times {frac {dmathbf {p} }{dt}}=mathbf {r} times mathbf {F} ,}

Таким образом, требование системы быть «замкнутой», означает равенство нулю главного (суммарного) момента внешних сил:

{displaystyle mathbf {L} _{mathrm {system} }=mathrm {constant} leftrightarrow sum tau _{mathrm {ext} }=0,}

где {displaystyle ~tau _{ext}} — момент одной из сил, приложенных к системе частиц.

Математически закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол {displaystyle ~delta varphi }, радиус-вектор частицы с номером {displaystyle ~i} изменятся на {displaystyle ~delta mathbf {r} _{i}=delta varphi times mathbf {r} _{i}}, а скорости — {displaystyle ~delta mathbf {v} _{i}=delta varphi times mathbf {v} _{i}}. Функция Лагранжа {displaystyle ~{mathcal {L}}} системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому

{displaystyle delta {mathcal {L}}={mathcal {L}}(mathbf {r} _{i}+delta mathbf {r} _{i},;mathbf {v} _{i}+delta mathbf {v} _{i})-{mathcal {L}}(mathbf {r} _{i},;mathbf {v} _{i})=sum limits _{i}left({frac {partial {mathcal {L}}}{partial mathbf {r} _{i}}}delta varphi times mathbf {r} _{i}+{frac {partial {mathcal {L}}}{partial mathbf {v} _{i}}}delta varphi times mathbf {v} _{i}right)=0.}

С учетом {displaystyle {frac {partial {mathcal {L}}}{partial mathbf {v} _{i}}}=mathbf {p} _{i},;{frac {partial {mathcal {L}}}{partial mathbf {r} _{i}}}=mathbf {dot {p}} _{i}}, где {displaystyle ~mathbf {p} _{i}} — обобщенный импульс {displaystyle ~i}-той частицы, каждое слагаемое в сумме из последнего выражения можно переписать в виде

{displaystyle {dot {mathbf {p} }}_{i},delta varphi times mathbf {r} _{i}+mathbf {p} _{i},delta varphi times mathbf {dot {r}} _{i}.}

Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:

{displaystyle delta {mathcal {L}}=delta varphi sum limits _{i}left(mathbf {r} _{i}times {dot {mathbf {p} }}_{i}+{dot {mathbf {r} }}_{i}times mathbf {p} _{i}right)=delta varphi {frac {d}{dt}}sum limits _{i}(mathbf {r} _{i}times mathbf {p} _{i})=delta varphi {frac {dmathbf {L} }{dt}}=0,}

где, {displaystyle mathbf {L} =sum mathbf {L} _{i}=sum mathbf {r} _{i}times mathbf {p} _{i}} — момент импульса системы. Ввиду произвольности {displaystyle delta varphi }, из равенства {displaystyle delta {mathcal {L}}=0} следует {displaystyle ~{frac {dmathbf {L} }{dt}}=0}.

На орбитах момент импульса распределяется между собственным вращением планеты и момента импульса ее орбитального движения:

{displaystyle mathbf {L} _{mathrm {total} }=mathbf {L} _{mathrm {spin} }+mathbf {L} _{mathrm {orbit} }.}

Момент импульса в электродинамике

При описании движения заряженной частицы в электромагнитном поле, канонический импульс {displaystyle ~p} не является инвариантным. Как следствие, канонический момент импульса {displaystyle ~mathbf {L} =mathbf {r} times mathbf {p} } тоже не инвариантен. Тогда берем реальный импульс, который также называется «кинетическим импульсом»:

{displaystyle ~mathbf {p} -{frac {emathbf {A} }{c}},}

где {displaystyle ~e} — электрический заряд, {displaystyle ~c} — скорость света, {displaystyle ~A} — векторный потенциал. Таким образом, гамильтониан (инвариантный) заряженной частицы массы {displaystyle m} в электромагнитном поле:

{displaystyle H={frac {1}{2m}}left(mathbf {p} -{frac {emathbf {A} }{c}}right)^{2}+evarphi ,}

где {displaystyle ~varphi } — скалярный потенциал. Из этого потенциала следует закон Лоренца. Инвариантный момент импульса или «кинетический момент импульса» определяется:

{displaystyle K=mathbf {r} times left(mathbf {p} -{frac {emathbf {A} }{c}}right).}

Момент импульса в квантовой механике

Оператор момента

В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определенными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на {displaystyle hbar } ({displaystyle h} с чертой), определяемой, как постоянная Планка, поделенная на {displaystyle 2pi }. Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновой момент импульса всегда кратен {displaystyle hbar /2} . Например, электрон в состоянии покоя имеет момент импульса {displaystyle hbar /2}.

В классическом определении момент импульса зависит от 6 переменных {displaystyle ~r_{x}}, {displaystyle ~r_{y}}, {displaystyle ~r_{z}}, {displaystyle ~p_{x}}, {displaystyle ~p_{y}}, и {displaystyle ~p_{z}}. Переводя это на квантовомеханические определения, используя принцип неопределенности Гейзенберга, получаем, что невозможно вычислить все шесть переменных одновременно с любой точностью. Поэтому есть ограничение на то, что мы можем узнать или подсчитать о практическом моменте импульса. Это значит, что лучшее, что мы можем сделать — это подсчитать одновременно величину вектора момента импульса и его компоненты по осям.

Математически, момент импульса в квантовой механике определяется как количество движения — не количественно, а как оператор физической величины:

{displaystyle {hat {mathbf {L} }}=mathbf {r} times {hat {mathbf {p} }},}

где {displaystyle mathbf {r} } и {displaystyle {hat {mathbf {p} }}} — координатный и импульсный оператор соответственно. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:

{displaystyle mathbf {L} =-ihbar (mathbf {r} times nabla ),}

где {displaystyle nabla } — оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства:

{displaystyle [L_{i},;L_{j}]=ihbar varepsilon _{ijk}L_{k},quad left[L_{i},;mathbf {L} ^{2}right]=0}

и даже более важные подстановки с гамильтонианом частицы без заряда и спина:

{displaystyle left[L_{i},;Hright]=0}

Симметрия вращения

Операторы момента импульса обычно встречаются при решении задач сферической симметрии в сферических координатах. Тогда момент импульса в пространственном отображении:

{displaystyle -{frac {1}{hbar ^{2}}}mathbf {L} ^{2}={frac {1}{sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial }{partial theta }}right)+{frac {1}{sin ^{2}theta }}{frac {partial ^{2}}{partial varphi ^{2}}}}

Когда находят собственные значения этого оператора, получают следующее:

{displaystyle L^{2}mid l,;mrangle ={hbar }^{2}l(l+1)mid l,;mrangle }
{displaystyle L_{z}mid l,;mrangle =hbar mmid l,;mrangle ,}

где

{displaystyle langle theta ,;varphi mid l,;mrangle =Y_{l,;m}(theta ,;varphi )}

— сферические гармоники.

Вычисление момента импульса

Если имеется материальная точка массой {displaystyle ~m}, двигающаяся со скоростью {displaystyle ~mathbf {v} } и находящаяся в точке, описываемой радиус-вектором {displaystyle ~mathbf {r} }, то момент импульса вычисляется по формуле:

{displaystyle ~mathbf {L} =mathbf {r} times mmathbf {v} ,}

где {displaystyle times } — знак векторного произведения.

Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки и векторно просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:

{displaystyle {vec {L}}=int limits _{V}{overrightarrow {dL}}=int limits _{V}{{vec {r}}times {vec {v}},dm}.}

Литература

  • Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. Том 1. М.: Мир, 1984. 302с.
  • Блохинцев Д. И. Основы квантовой механики. 5-ое изд. Наука, 1976. — 664 с.
  • Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720c.
  • Варшалович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория углового момента. Л.: Наука, 1975.

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Момент импульса. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

Источник

Добавить комментарий