Как найти момент импульса относительно точки - Сайт, где вы сможете решить свои вопросы

Момент импульса

Размерность	L²MT⁻¹
Единицы измерения
СИ	м²·кг/с
СГС	см²·г/с
Примечания
псевдовектор

Моме́нт и́мпульса (момент импульса относительно точки, также: кинетический момент, угловой момент, орбитальный момент, момент количества движения) — физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение^[1].

Для одной материальной точки момент импульса равен векторному произведению радиус-вектора точки на её импульс, для системы точек — сумме таких произведений. Стандартное обозначение: , единица измерения в СИ: м²кг/с. Величина зависит от выбора положения начала отсчёта радиус-векторов O.

Момент импульса замкнутой системы сохраняется. Он является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения. При наличии внешних сил производная момента импульса по времени равна моменту сил (относительно того же начала O).

Основное использование понятия момента импульса относится к задачам, связанным с реальным вращением (особенно при наличии центральной или осевой симметрии; тогда О обычно выбирается в центре или на оси). Но величина может быть вычислена и в других ситуациях, например для прямолинейного движения частицы мимо произвольной точки O, не лежащей на линии движения и условно принимаемой за центр.

В случае вращения твёрдого тела вокруг фиксированной оси часто используется не сам момент импульса, а его проекция ${displaystyle L_{parallel }}$ на эту ось — такая величина называется моментом импульса относительно оси.

Понятие момента импульса было изначально введено в классической механике, но имеет обобщения в квантовой механике и электродинамике.

Момент импульса в классической механике[править | править код]

Связь между силой F, моментом силы τ, импульсом и моментом импульса

Определение[править | править код]

Момент импульса материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:

{mathbf {L}}={mathbf {r}}times {mathbf {p}}

где — радиус-вектор частицы относительно выбранного неподвижного начала отсчёта, — импульс частицы.

Из определения момента импульса следует его аддитивность: для системы, состоящей из нескольких материальных точек, выполняется

${displaystyle mathbf {L} =sum limits _{i}mathbf {L} _{i}=sum _{i}mathbf {r} _{i}times mathbf {p} _{i}}$

Количество частиц может быть бесконечным, например в случае твёрдого тела с распределённой массой.

Так как момент импульса задаётся векторным произведением, он является псевдовектором, перпендикулярным обоим векторам и .

Момент импульса можно вычислить относительно любого начала отсчета O (получающиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определённости) его вычисляют относительно центра масс, закреплённой точки вращения твердого тела или другой чем-то выделенной точки.

Выбор точки O иногда связан с характером задачи. Так, при рассмотрении орбитального движения планеты вокруг Солнца за начало отсчёта естественно взять Солнце, а при анализе её же собственного вращения — центр этой планеты. Естественно, получатся два разных момента импульса: ${displaystyle mathbf {L} _{mathrm {orbit} }}$ и ${displaystyle mathbf {L} _{mathrm {spin} }}$ .

Вычисление в общем случае[править | править код]

Если имеется материальная точка массой , двигающаяся со скоростью и находящаяся в точке, описываемой радиус-вектором , то и момент импульса вычисляется по формуле

{displaystyle mathbf {L} =mathbf {r} times mmathbf {v} }

Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки ( rho — плотность) и просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:

${displaystyle mathbf {L} =int limits _{V}{mathbf {dL} }=int limits _{V}{mathbf {r} times mathbf {v} ,dm}=int limits _{V}{mathbf {r} times mathbf {v} ,rho dV}}$

На практике rho задаётся как функция трёх координат и необходимо выполнение тройного интегрирования:

{displaystyle mathbf {L} =iiint {(xmathbf {i} +ymathbf {j} +zmathbf {k} )times mathbf {v} ,rho (x,y,z),dx,dy,dz}}

Если считать, что — обобщённая функция, включающая, возможно, и дельтообразные члены, то эта формула применима и к распределённым, и к дискретным системам.

Случай фиксированной оси[править | править код]

Важным случаем использования понятия «момент импульса» является движение вокруг неизменной оси. В такой ситуации часто рассматривают не сам момент импульса (псевдовектор), а его проекцию на ось как псевдоскаляр, знак которого зависит от направления вращения:

${displaystyle L_{parallel }=pm |mathbf {r_{perp }} times mathbf {p_{perp }} |}$

Параллельность-перпендикулярность (, perp ) имеются в виду по отношению к оси; ${displaystyle mathbf {r} =mathbf {r_{perp }} +mathbf {r_{parallel }} }$ , ${displaystyle mathbf {p} =mathbf {p_{perp }} +mathbf {p_{parallel }} }$ . При этом ${displaystyle r_{perp }}$ — расстояние от оси до материальной точки, называемое «плечом». Величина указанной проекции, в отличие от самого момента, не меняется при сдвиге начала отсчёта O на оси. Для распределённой системы

${displaystyle L_{parallel }=pm left|int {mathbf {r_{perp }} times mathbf {v_{perp }} ,rho dV}right|}$

Если при этом все точки тела движутся по окружностям (вращаются) с одинаковой угловой скоростью omega , то есть численно ${displaystyle v=omega r_{perp }}$ , то для материальной точки массой или для системы будет, соответственно,

${displaystyle L_{parallel }=pm omega mr_{perp }^{2}quad }$

или ${displaystyle quad L_{parallel }=pm omega int {r_{perp }^{2},rho dV}}$

Величину ${displaystyle L_{parallel }}$ иногда называют моментом импульса относительно оси. Символ параллельности у и знак перед выражением могут опускаться, если очевидно, о чём идёт речь.

Для абсолютно твёрдого тела, величина последнего интеграла называется моментом инерции относительно оси вращения и обозначается . Тогда запись обретает вид ${displaystyle ,L_{parallel }=pm Iomega ,}$ или, в векторной форме, . Если известен момент инерции относительно оси, проходящей через центр масс тела, а вращение происходит вокруг другой, но параллельной ей оси, то необходимый момент инерции находится по теореме Штайнера.

Сохранение момента импульса[править | править код]

Закон сохранения момента импульса: суммарный момент импульса относительно любой неподвижной точки для замкнутой системы остается постоянным со временем.

Производная момента импульса по времени есть момент силы:

${displaystyle {frac {dmathbf {L} }{dt}}=sum _{i}{frac {dmathbf {r} _{i}}{dt}}times mathbf {p} _{i}+sum _{i}mathbf {r} _{i}times {frac {dmathbf {p} _{i}}{dt}}=sum _{i}mathbf {r} _{i}times mathbf {F} _{i}=mathbf {tau _{ext}} }$

Таким образом, требование замкнутости системы может быть ослаблено до требования равенства нулю главного (суммарного по всем частицам ) момента внешних сил:

${displaystyle mathbf {L} =mathrm {constant} leftrightarrow mathbf {tau _{ext}} =0}$

где ${displaystyle mathbf {tau _{ext}} }$ — момент сил, приложенных к системе частиц. (Но конечно, если внешние силы вообще отсутствуют, это требование также выполняется.) Аналогичный закон сохранения справедлив для момента импульса относительно фиксированной оси.

По теореме Нётер закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол , радиус-вектор частицы с номером изменятся на ${displaystyle delta mathbf {r} _{i}=delta varphi times mathbf {r} _{i}}$ , а скорости — ${displaystyle delta mathbf {v} _{i}=delta varphi times mathbf {v} _{i}}$ . Функция Лагранжа системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому

$delta mathcal L = mathcal L(mathbf{r}_i + deltamathbf{r}_i,; mathbf{v}_i + deltamathbf{v}_i) - mathcal L(mathbf{r}_i,; mathbf{v}_i) = sum limits_i left( frac{partial mathcal L}{partial mathbf r_i} delta varphi timesmathbf r_i + frac{partial mathcal L}{partial mathbf v_i} delta varphi times mathbf v_i right)= 0.$

С учётом $frac{partial {mathcal {L}}}{partial {mathbf v_{i}}} = mathbf {p_{i}},; frac{partial mathcal {L}}{partial mathbf {r_{i}}} = mathbf {dot p_{i}}$ , где ${mathbf p}_{i}$ — обобщенный импульс -той частицы, каждое слагаемое в сумме из последнего выражения можно переписать в виде

$dot {mathbf p_i} ,delta varphi times mathbf r_i + mathbf p_i,delta varphi times mathbf {dot r_i}.$

Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:

$delta mathcal L = delta varphi sum limits_i left( mathbf r_i times dot {mathbf p_i} + dot {mathbf r_i} times mathbf p_i right) = delta varphi frac{d}{dt} sum limits_i (mathbf r_i times mathbf p_i) = delta varphi frac{d mathbf L}{dt} = 0,$

где — момент импульса системы. Ввиду произвольности , из равенства следует ${displaystyle {frac {dmathbf {L} }{dt}}=0.}$

Смежные понятия[править | править код]

При рассмотрении задач, связанных с вращением, фигурируют понятия, частично упоминавшиеся выше:

момент импульса относительно оси (термин состоит из четырёх слов) — проекция момента импульса на ось;
момент инерции твёрдого тела (см. также моменты инерции некоторых тел);
момент силы (он же: крутящий момент, вращательный момент, вертящий момент);
импульс момента силы ${displaystyle int limits _{t_{1}}^{t_{2}}mathbf {r} times mathbf {F} (t);dt}$ (единица измерения — Н·м·с) — мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении).

Несмотря на созвучность с «моментом импульса», эти понятия не синонимичны термину «момент импульса» и несут самостоятельный смысл.

Момент импульса в электродинамике[править | править код]

При описании движения заряженной частицы в электромагнитном поле канонический импульс не является инвариантным. Как следствие, канонический момент импульса тоже не инвариантен. Тогда берётся реальный импульс, который также называется «кинетическим импульсом»:

${displaystyle mathbf {p} -{frac {emathbf {A} }{c}},}$

где — электрический заряд, — скорость света, — векторный потенциал. Таким образом, гамильтониан (инвариантный) заряженной частицы массы в электромагнитном поле:

$H =frac{1}{2m} left( mathbf{p} -frac {e mathbf{A} }{c}right)^2 + evarphi,$

где varphi — скалярный потенциал. Из этого потенциала следует закон Лоренца. Инвариантный момент импульса, или «кинетический момент импульса», определяется следующим образом:

$K= mathbf{r} times left( mathbf{p} -frac {e mathbf{A} }{c}right).$

Момент импульса в квантовой механике[править | править код]

Оператор момента[править | править код]

В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определёнными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на hbar ( с чертой — постоянная Планка, поделенная на 2 pi ).

Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновый момент импульса всегда кратен hbar/2 для фермионов и hbar для бозонов. Например, электрон в состоянии покоя имеет момент импульса hbar/2 .^[2]

В классическом определении момент импульса зависит от 6 переменных ${displaystyle r_{x}}$ , ${displaystyle r_{y}}$ , ${displaystyle r_{z}}$ , $p_{x}$ , $p_{y}$ , и $p_{z}$ . Переводя это на квантовомеханические определения, используя принцип неопределенности Гейзенберга, получаем, что невозможно вычислить все шесть переменных одновременно с любой точностью. Поэтому есть ограничение на то, что мы можем узнать или подсчитать о практическом моменте импульса. Это значит, что лучшее, что мы можем сделать — это подсчитать одновременно величину вектора момента импульса и какой-либо одной его компоненты (проекции).

Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:

{displaystyle {hat {mathbf {L} }}={hat {mathbf {r} }}times {hat {mathbf {p} }}}

где и — координатный и импульсный оператор, соответственно, а второй — на внутренние, спиновые. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:

{displaystyle {hat {mathbf {L} }}=-ihbar (mathbf {r} times nabla )}

где nabla — оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства:

$[L_i,; L_j ] = i hbar varepsilon_{ijk} L_k, quadleft[L_i,; mathbf{L}^2 right] = 0$

где $varepsilon_{ijk}$ — Символ Леви-Чивиты;

и даже более важные подстановки с гамильтонианом частицы без заряда и спина:

Симметрия вращения[править | править код]

Операторы момента импульса обычно встречаются при решении задач сферической симметрии в сферических координатах. Тогда момент импульса в пространственном отображении:

${displaystyle -{frac {1}{hbar ^{2}}}mathbf {L} ^{2}={frac {1}{sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial }{partial theta }}right)+{frac {1}{sin ^{2}theta }}{frac {partial ^{2}}{partial varphi ^{2}}}.}$

Когда находят собственные значения этого оператора, получают следующее:

${displaystyle L^{2}mid l,;mrangle ={hbar }^{2}l(l+1)mid l,;mrangle ,}$

L_z mid l,; m rang = hbar m mid l,; m rang,

где , — целые числа, такие что а
$lang theta ,; varphi mid l,; m rang = Y_{l,;m}(theta,;varphi)$
— сферические функции.

Примечания[править | править код]

↑ Pivarski, Jim Spin. Symmetry Magazine (март 2013). Дата обращения: 28 апреля 2014. Архивировано 15 апреля 2014 года.
↑ [Информация с сайта Нобелевского комитета (англ.). Дата обращения: 3 ноября 2017. Архивировано 18 мая 2008 года. Информация с сайта Нобелевского комитета (англ.)]

Литература[править | править код]

Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. — М.: Мир, 1984. — Т. 1. — 302 с.
Блохинцев Д. И. Основы квантовой механики. — М.: Наука, 1976. — 664 с.
Боум А. Квантовая механика: основы и приложения. — М.: Мир, 1990. — 720 с.
Варшалович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория углового момента. — Л.: Наука, 1975. — 441 с.
Зар Р. Теория углового момента. О пространственных эффектах в физике и химии. — М.: Мир, 1993. — 352 с.

Источник

Моментом импульса материальной точки
аотносительно неподвижной точки 0
называется физическая величина, равная
векторному произведению

,
(20)

где
– радиус-вектор проведенный из точки 0
в точку а,– импульс материальной точки.

Рис.9.

Направление вектора
совпадает с направлением поступательного
движения правого винта при его вращении
отк.
Модуль вектора момента импульса

(21)

где
– угол между векторамии,– плечо вектораотносительно точки 0. Моментом импульса
системы материальных точек относительно
неподвижной точки 0 называется векторная
сумма моментов импульсов всех материальных
точек системы относительно той же точки
0

(22)

7. Момент импульса относительно неподвижной осиz.

Моментом импульса материальной точки
аотносительно неподвижной осиzназывается скалярная величина,
равная проекции на эту ось вектора
момента импульса, определенного
относительно произвольной точки 0 данной
оси. Значение момента импульса не зависит
от положения точки 0 на осиz.

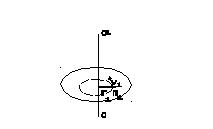
Рис.10.

Рассмотрим вращение твердого тела
вокруг неподвижной оси z(О-О¹). Каждая точка твердого тела
описывает горизонтальную окружность
радиусасо скоростью.
Скорость.и
импульсперпендикулярны этому радиусу,
поэтомурадиус является плечом вектора(угол=90⁰).
Момент импульса каждой точки твердого
тела относительно осиzравен

(23)

и направлен по оси в сторону, определяемую
правилом правого винта. Моменты импульса
всех точек твердого тела будут
сонаправлены, поэтому момент импульса
твердого тела относительно оси есть
сумма моментов импульсов отдельных
частиц

то есть все точки твердого тела вращаются
с одинаковой угловой скоростью, то wможно вынести за знак суммы

то есть

Момент импульса твердого тела относительно
оси вращения равен произведению момента
инерции тела относительно той же оси
на угловую скорость.

Лекция 6. Уравнения динамики вращательного движения.

1. Закон сохранения момента импульса.

Продифференцируем момент импульса
по времени

Величина
есть скорость материальной точки,
связанная с ее импульсом соотношением.
Поэтому первое слагаемоеравно нулю как векторное произведение
коллинеарных векторови,
()
Второе слагаемое можно преобразовать
с помощью уравнения Ньютона

Тогда

.
(1)

Это уравнение моментов относительно
неподвижной точки. Производная по
времени момента импульса материальной
точки (относительно неподвижной точки)
равна моменту силы относительно этой
же точки.

Уравнение моментов (1) можно обобщить
на случай произвольной системы
материальных точек. Пусть система
состоит из nматериальных
точек вращающихся вокруг центра 0.

…………………….

где
– момент внутренних сил,– момент внешних сил.

По третьему закону Ньютона
= 0, так как внутренние силы входят
попарно, сила с которой одно тело
действует на другое равно и противоположно
направлена сила с которой второе тело
действует на первое. Полный момент этих
сил равен нулю (см. рис.)

Исходя из этого уравнение примет вид

где
– момент импульса системы материальных
точек.

=– момент всех сил действующих на систему
материальных точек.

(2)

Основной закон динамики вращательного
движения для системы материальных
точек. Производная по времени от
момента импульса системы материальных
точек относительно неподвижной точки
равна геометрической сумме моментов
всех внешних сил относительно этой
точки.

Если момент всех внешних сил относительно
неподвижной точки равен нулю, то момент
импульса системы относительно той же
неподвижной точки остается постоянным
во времени.

иили(3)

Выражение (3) – математическая запись
закона сохранения момента импульса.
Если мы продифференцируем по времени
момент импульса относительно неподвижной
оси, то получим уравнение моментов
относительно неподвижной оси

(4)

Как было показано ранее, момент импульса
твердого тела относительно оси вращения
равен

Если момент инерции
при
вращении остается постоянным, то

где– угловое ускорение. Тогда

(5).

Произведение момента инерции твердого
тела относительно оси вращения на
угловое ускорение равно моменту внешних
сил относительно той же оси.

Уравнение (5) – основное уравнение
динамики вращательного движения вокруг
неподвижной оси. Оно напоминает уравнение
Ньютона для поступательного движения.

Роль массы mиграет момент
инерцииJ, роль скоростиv– угловая скоростьw,
роль с илыF– момент силыM, роль импульсаp– момент импульсаL. Момент
импульсаLчасто называют
вращательным импульсом системы.

Если момент внешних сил M_zотносительно оси вращения равен нулю,
то вращательный импульс сохраняется:

(6)

Продемонстрировать закон сохранения
импульса можно с помощью скамьи
Жуковского. Скамья Жуковского представляет
собой стул, сиденье которого имеет форму
диска. Диск может свободно вращаться
вокруг вертикальной оси на шариковых
подшипниках.

Человек, оттолкнувшись ногой от пола,
приводит скамью во вращение. Вместе со
скамьей будет вращаться и он сам. Во
время вращения момент импульса системы
скамья плюс человек будет оставаться
постоянным, какие бы внутренние движения
не совершались в системе.

Если человек разведет руки в стороны,
то он увеличит момент инерции системы
J, а потому угловая скорость
вращенияwдолжна
уменьшиться, чтобы оставался неизменным
вращательный импульсL=Jw(см рис 1а и 1б)

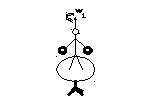
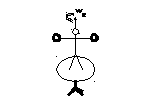
Рис.1а. L=J₁w₁Рис.1бL=J₂w₂

J₁w₁=J₂w₂(J₂>J_1,w₂<w₁)

Если человек, стоя на неподвижной скамье
Жуковского, начинает делать конические
движения над головой, скамья начинает
вращаться в другую сторону (рис.2).

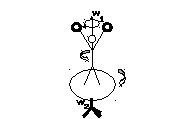
Общий момент импульса системы остается
равным нулю.

Когда винт судна начинает вращаться,
по закону сохранения момента импульса
системы, корпус судна должен вращаться
в противоположную сторону. В обычных
условиях это не страшно, но в критических
ситуациях (сильная боковая волна, легкое
судно) может привести к опрокидыванию
судна. Эта же ситуация всегда реализуется
и для вертолетов. Чтобы этого не
происходило, на хвосте устанавливается
другой винт для гашения вращения.

В заключении сопоставим основные
величины и уравнения определяющие
вращение тела им его поступательное
движение.

Поступательное
движение

Вращательное
движение

Масса m

Скорость v
= dr/dt

Ускорение a
= dv/dt

Сила F

Импульс p
= mv

Основное уравнение динамики F
= ma

F
= dp/dt

Работа dA
= F ds

Кинетическая энергия mv²/2

Момент инерции J

Угловая скорость w
= dφ/dt

Угловое ускорение ε =
dw/dt

Момент силы M
= Fr

Момент импульса L
= Jw

Основное уравнение динамики M
= Jε

M
= dL/dt

Работа вращения dA
= Mdφ

Кинетическая
энергия вращения Jw²/2

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.

Момент импульса замкнутой системы сохраняется.

Момент импульса в классической механике

Связь между импульсом 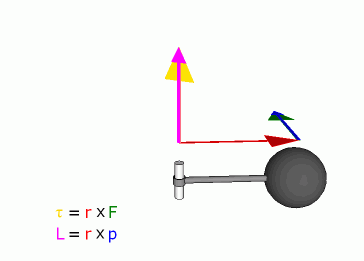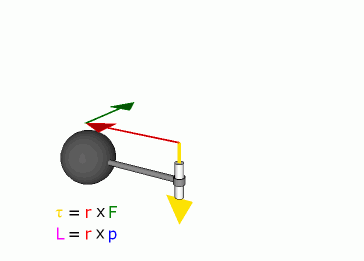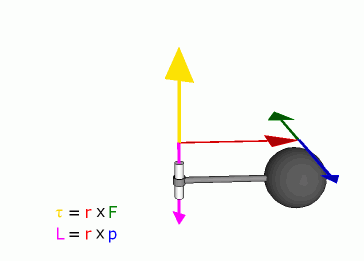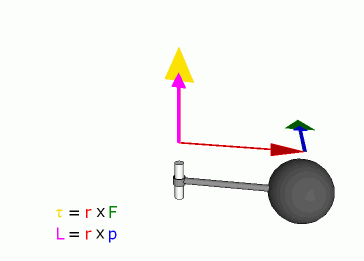и моментом

Определение

Момент импульса частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульлор

{displaystyle ~mathbf {L} =mathbf {r} times mathbf {p} ,}

где — радиус-вектор частицы относительно выбранного начала отсчёта, — импульс частицы.

В системе СИ момент импульса измеряется в единицах джоуль–секунда; Дж·с.

Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение:

${displaystyle mathbf {L} _{Sigma }=sum limits _{i}mathbf {L} _{i}}$ .

Вычисление момента

Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам и . Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения. Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на нее можно указать ряд рецептов в соответствии с общими правилами нахождения векторного произведения двух векторов.

${displaystyle L=|mathbf {r} ||mathbf {p} |sin theta _{r,;p},}$

где ${displaystyle ~theta _{r,;p}}$ — угол между и , определяемый так, чтобы поворот от к производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения. Направление поворота важно при вычислении, так как определяет знак искомой проекции.

Запишем в виде ${displaystyle ~mathbf {r} =mathbf {r_{parallel }} +mathbf {r_{perp }} }$ , где ${displaystyle ~mathbf {r_{parallel }} }$ — составляющая радиус-вектора, параллельная вектору импульса, а ${displaystyle ~mathbf {r_{perp }} }$ — аналогично, перпендикулярная ему. ${displaystyle ~mathbf {r_{perp }} }$ является, по сути, расстоянием от оси вращения до вектора , которое обычно называют «плечом». Аналогично можно разделить вектор импульса на две составляющие: параллельную радиус-вектору ${displaystyle ~mathbf {p_{parallel }} }$ и перпендикулярную ему ${displaystyle ~mathbf {p_{perp }} }$ . Теперь, используя линейность векторного произведения, а также свойство, согласно которому произведение параллельных векторов равно нулю, можно получить еще два выражения для .

${displaystyle mathbf {L} =mathbf {r} times mathbf {p} =(mathbf {r_{perp }} +mathbf {r_{parallel }} )times mathbf {p} =mathbf {r_{perp }} times mathbf {p} +mathbf {r_{parallel }} times mathbf {p} =mathbf {r_{perp }} times mathbf {p} .}$

${displaystyle mathbf {L} =mathbf {r} times mathbf {p} =mathbf {r} times (mathbf {p_{perp }} +mathbf {p_{parallel }} )=mathbf {r} times mathbf {p_{perp }} .}$

Для систем, совершающих вращение вокруг одной из осей симметрии (вообще говоря, вокруг так называемых главных осей инерции), справедливо соотношение

{displaystyle ~mathbf {L} =I{boldsymbol {omega }},}

где — момент инерции относительно оси вращения, — вектор угловой скорости.

В общем случае вектор момента связан с вектором угловой скорости линейным оператором момента инерции:

{displaystyle mathbf {L} ={hat {I}}{boldsymbol {omega }}}

Сохранение углового момента

Симметрия в физике
Преобразо- вания	Инвариант- ность	Закон сохранения
↕ трансляции времени	Консервативность	…энергии
↔ трансляции пространства	Однородность	…импульса
○ Вращения	Изотропия	…момента импульса
× Группа Лоренца	Относительность Лоренц-инвариантность	инвариантность интервала (и др. скаляров пространства-времени)

Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.

В замкнутых системах момент импульса постоянен.
Производная момента импульса по времени есть момент силы:

${displaystyle tau ={frac {dmathbf {L} }{dt}}={frac {dmathbf {r} }{dt}}times mathbf {p} +mathbf {r} times {frac {dmathbf {p} }{dt}}=mathbf {r} times mathbf {F} ,}$

Таким образом, требование системы быть «замкнутой», означает равенство нулю главного (суммарного) момента внешних сил:

${displaystyle mathbf {L} _{mathrm {system} }=mathrm {constant} leftrightarrow sum tau _{mathrm {ext} }=0,}$

где ${displaystyle ~tau _{ext}}$ — момент одной из сил, приложенных к системе частиц.

Математически закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол , радиус-вектор частицы с номером изменятся на ${displaystyle ~delta mathbf {r} _{i}=delta varphi times mathbf {r} _{i}}$ , а скорости — ${displaystyle ~delta mathbf {v} _{i}=delta varphi times mathbf {v} _{i}}$ . Функция Лагранжа системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому

${displaystyle delta {mathcal {L}}={mathcal {L}}(mathbf {r} _{i}+delta mathbf {r} _{i},;mathbf {v} _{i}+delta mathbf {v} _{i})-{mathcal {L}}(mathbf {r} _{i},;mathbf {v} _{i})=sum limits _{i}left({frac {partial {mathcal {L}}}{partial mathbf {r} _{i}}}delta varphi times mathbf {r} _{i}+{frac {partial {mathcal {L}}}{partial mathbf {v} _{i}}}delta varphi times mathbf {v} _{i}right)=0.}$

С учетом ${displaystyle {frac {partial {mathcal {L}}}{partial mathbf {v} _{i}}}=mathbf {p} _{i},;{frac {partial {mathcal {L}}}{partial mathbf {r} _{i}}}=mathbf {dot {p}} _{i}}$ , где ${displaystyle ~mathbf {p} _{i}}$ — обобщенный импульс -той частицы, каждое слагаемое в сумме из последнего выражения можно переписать в виде

${displaystyle {dot {mathbf {p} }}_{i},delta varphi times mathbf {r} _{i}+mathbf {p} _{i},delta varphi times mathbf {dot {r}} _{i}.}$

${displaystyle delta {mathcal {L}}=delta varphi sum limits _{i}left(mathbf {r} _{i}times {dot {mathbf {p} }}_{i}+{dot {mathbf {r} }}_{i}times mathbf {p} _{i}right)=delta varphi {frac {d}{dt}}sum limits _{i}(mathbf {r} _{i}times mathbf {p} _{i})=delta varphi {frac {dmathbf {L} }{dt}}=0,}$

где, ${displaystyle mathbf {L} =sum mathbf {L} _{i}=sum mathbf {r} _{i}times mathbf {p} _{i}}$ — момент импульса системы. Ввиду произвольности , из равенства следует ${displaystyle ~{frac {dmathbf {L} }{dt}}=0}$ .

На орбитах момент импульса распределяется между собственным вращением планеты и момента импульса ее орбитального движения:

${displaystyle mathbf {L} _{mathrm {total} }=mathbf {L} _{mathrm {spin} }+mathbf {L} _{mathrm {orbit} }.}$

Момент импульса в электродинамике

При описании движения заряженной частицы в электромагнитном поле, канонический импульс не является инвариантным. Как следствие, канонический момент импульса тоже не инвариантен. Тогда берем реальный импульс, который также называется «кинетическим импульсом»:

${displaystyle ~mathbf {p} -{frac {emathbf {A} }{c}},}$

${displaystyle H={frac {1}{2m}}left(mathbf {p} -{frac {emathbf {A} }{c}}right)^{2}+evarphi ,}$

где — скалярный потенциал. Из этого потенциала следует закон Лоренца. Инвариантный момент импульса или «кинетический момент импульса» определяется:

${displaystyle K=mathbf {r} times left(mathbf {p} -{frac {emathbf {A} }{c}}right).}$

Момент импульса в квантовой механике

Оператор момента

В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определенными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на ( с чертой), определяемой, как постоянная Планка, поделенная на . Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновой момент импульса всегда кратен . Например, электрон в состоянии покоя имеет момент импульса .

В классическом определении момент импульса зависит от 6 переменных ${displaystyle ~r_{x}}$ , ${displaystyle ~r_{y}}$ , ${displaystyle ~r_{z}}$ , ${displaystyle ~p_{x}}$ , ${displaystyle ~p_{y}}$ , и ${displaystyle ~p_{z}}$ . Переводя это на квантовомеханические определения, используя принцип неопределенности Гейзенберга, получаем, что невозможно вычислить все шесть переменных одновременно с любой точностью. Поэтому есть ограничение на то, что мы можем узнать или подсчитать о практическом моменте импульса. Это значит, что лучшее, что мы можем сделать — это подсчитать одновременно величину вектора момента импульса и его компоненты по осям.

Математически, момент импульса в квантовой механике определяется как количество движения — не количественно, а как оператор физической величины:

{displaystyle {hat {mathbf {L} }}=mathbf {r} times {hat {mathbf {p} }},}

где и — координатный и импульсный оператор соответственно. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:

{displaystyle mathbf {L} =-ihbar (mathbf {r} times nabla ),}

где — оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства:

${displaystyle [L_{i},;L_{j}]=ihbar varepsilon _{ijk}L_{k},quad left[L_{i},;mathbf {L} ^{2}right]=0}$

и даже более важные подстановки с гамильтонианом частицы без заряда и спина:

${displaystyle left[L_{i},;Hright]=0}$

Симметрия вращения

Когда находят собственные значения этого оператора, получают следующее:

${displaystyle L^{2}mid l,;mrangle ={hbar }^{2}l(l+1)mid l,;mrangle }$

${displaystyle L_{z}mid l,;mrangle =hbar mmid l,;mrangle ,}$

где

${displaystyle langle theta ,;varphi mid l,;mrangle =Y_{l,;m}(theta ,;varphi )}$

— сферические гармоники.

Вычисление момента импульса

Если имеется материальная точка массой , двигающаяся со скоростью и находящаяся в точке, описываемой радиус-вектором , то момент импульса вычисляется по формуле:

где — знак векторного произведения.

Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки и векторно просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:

${displaystyle {vec {L}}=int limits _{V}{overrightarrow {dL}}=int limits _{V}{{vec {r}}times {vec {v}},dm}.}$

Литература

Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. Том 1. М.: Мир, 1984. 302с.
Блохинцев Д. И. Основы квантовой механики. 5-ое изд. Наука, 1976. — 664 с.
Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720c.
Варшалович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория углового момента. Л.: Наука, 1975.

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Момент импульса. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

Источник

Момент импульса в классической механике[править | править код]

Определение[править | править код]

Вычисление в общем случае[править | править код]

Случай фиксированной оси[править | править код]

Сохранение момента импульса[править | править код]

Смежные понятия[править | править код]

Момент импульса в электродинамике[править | править код]

Момент импульса в квантовой механике[править | править код]

Оператор момента[править | править код]

Симметрия вращения[править | править код]

Примечания[править | править код]

Литература[править | править код]

7. Момент импульса относительно неподвижной осиz.

Лекция 6. Уравнения динамики вращательного движения.

1. Закон сохранения момента импульса.

Момент импульса в классической механике

Определение

Вычисление момента

Сохранение углового момента

Момент импульса в электродинамике

Момент импульса в квантовой механике

Оператор момента

Симметрия вращения

Вычисление момента импульса

Литература

Вам также может понравиться

Если уже выщипаны брови как исправить

Жижа плюется как исправить

Как найти клиента для холодных звонков

Добавить комментарий Отменить ответ