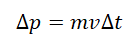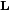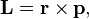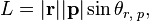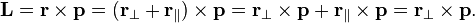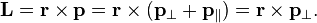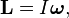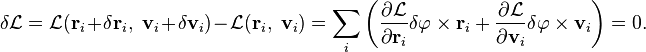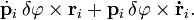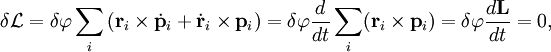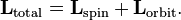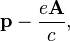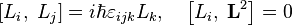П
дана материальная точка, имеющая импульср. Пусть её положение
относительно точки О определяется
радиусом-векторомr.
Движение такой точки характеризуют
моментом импульсаL.
Моментом импульса материальной точки
относительно точки О называется
векторная величина, равная векторному
произведению радиуса-вектораr
и вектора импульсаp:
L=[r,p].
Модуль момента импульса L=rpsin,
где
– угол между векторамиr
и р. Направление вектора
момента импульса определяется по правилу
правого винта.
Размерность момента импульса [L]=кг.м2/с.
М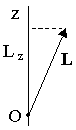
импульса тела относительно точки равен
векторной сумме моментов импульсов
частиц тела относительно той же точки
L=L1+L2+…+LN.
Проекция вектора момента импульса
относительно точки О на ось z,
проходящую через эту точку, называетсямоментом импульса относительно оси:
Lz=[r,p]z.
Момент импульса относительно оси
является скалярной величиной.
Момент импульса тела относительно оси
z равен проекции
момента импульса тела относительно
точки О на осьz,
проходящую через эту точку.
4.3. Связь момента силы и момента импульса
Момент импульса и момент силы связаны
между собой. Найдём выражение, связывающее
их.
Возьмём производную по времени от
выражения, определяющего момент импульса:
Член
равен нулю, так как угол между вектором
скоростиdr/dt и
вектором импульсар равен нулю.
Производная импульса по времени,
имеющаяся во втором члене полученного
выражения, равна силе (второй закон
Ньютона). Поэтому можем записать
полученное выражение в следующей форме:
.
Но [r,F]
есть по определению момент силыF относительно
той же точки О. Поэтому
т.е. скорость изменения момента импульса
частицы равна моменту силы,
действующему на эту частицу.
Проекция последнего уравнения на ось
zвыражает связь
момента импульса относительно осиzи момента силы
относительно той же оси.
.
4.4. Основной закон динамики вращательного движения
Пусть твёрдое тело вращается относительно
неподвижной оси z.
Выразим момент импульса твёрдого тела
относительно оси вращения. Для этого
представим твёрдое тело как совокупность
элементарных масс. Момент
импульса одной элементарной массы
относительно осиz
Момент импульса всего тела равен сумме
моментов импульсов всех элементарных
масс
Скорость vу разных
элементарных масс различна, а угловая
скорость одинакова.
Поскольку v=r,
Поскольку угловая скорость со одинакова
для всех элементарных масс, её можно
вынести за знак суммы
Введём обозначение
.
С учётом этого
Lz=Jz..
Ранее мы получили, что момент импульса
и момент силы связаны следующим
образом:
.
Заменив Lz
наJzωи с учётом того, чтоJz
с течением времени не изменяется,
получаем
Учитывая, что производная угловой
скорости по времени равна угловому
ускорению , получаем
.
Полученное выражение – основной закон
динамики вращательного движения,
связывающий между собой меру внешнего
воздействия – момент силы Mz
с результатом внешнего воздействия
– угловым ускорением.
Коэффициент Jz, стоящий
в этом уравнении, зависит от массы тела
и от того, как она распределена по
объёму тела (это видно из определения
величиныJz).
Чем меньше Jz, тем большее
угловое ускорение получит тело при
воздействии момента силыMz.
Это говорит о том, что коэффициентJz.
характеризует инертность вращающегося
тела. ПоэтомуJz называют
моментом инерции тела относительно осиz.
Знание величины момента инерции тела
необходимо для описания вращательного
движения. Поэтому обсудим более подробно,
что такое момент инерции и как его
вычислить.
Соседние файлы в папке часть 1
- #
- #
- #
- #
- #
- #
| Момент импульса | |
|---|---|
 |
|
| Размерность | L2MT−1 |
| Единицы измерения | |
| СИ | м2·кг/с |
| СГС | см2·г/с |
| Примечания | |
| псевдовектор |
Моме́нт и́мпульса (момент импульса относительно точки, также: кинетический момент, угловой момент, орбитальный момент, момент количества движения) — физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение[1].
Для одной материальной точки момент импульса равен векторному произведению радиус-вектора точки на её импульс, для системы точек — сумме таких произведений. Стандартное обозначение: 

Момент импульса замкнутой системы сохраняется. Он является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения. При наличии внешних сил производная момента импульса по времени равна моменту сил (относительно того же начала O).
Основное использование понятия момента импульса относится к задачам, связанным с реальным вращением (особенно при наличии центральной или осевой симметрии; тогда О обычно выбирается в центре или на оси). Но величина 
В случае вращения твёрдого тела вокруг фиксированной оси часто используется не сам момент импульса, а его проекция 
Понятие момента импульса было изначально введено в классической механике, но имеет обобщения в квантовой механике и электродинамике.
Момент импульса в классической механике[править | править код]
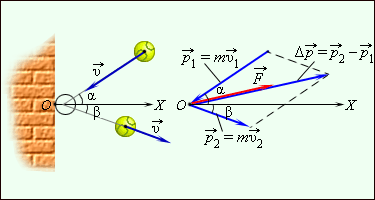
Связь между силой F, моментом силы τ, импульсом 
Определение[править | править код]
Момент импульса 
,
где 

Из определения момента импульса следует его аддитивность: для системы, состоящей из нескольких материальных точек, выполняется
.
Количество частиц может быть бесконечным, например в случае твёрдого тела с распределённой массой.
Так как момент импульса задаётся векторным произведением, он является псевдовектором, перпендикулярным обоим векторам 

Момент импульса можно вычислить относительно любого начала отсчета O (получающиеся при этом разные значения 
Выбор точки O иногда связан с характером задачи. Так, при рассмотрении орбитального движения планеты вокруг Солнца за начало отсчёта естественно взять Солнце, а при анализе её же собственного вращения — центр этой планеты. Естественно, получатся два разных момента импульса: 

Вычисление в общем случае[править | править код]
Если имеется материальная точка массой 



.
Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки 

.
На практике 
.
Если считать, что 
Случай фиксированной оси[править | править код]
Важным случаем использования понятия «момент импульса» является движение вокруг неизменной оси. В такой ситуации часто рассматривают не сам момент импульса (псевдовектор), а его проекцию на ось как псевдоскаляр, знак которого зависит от направления вращения:
.
Параллельность-перпендикулярность (




.
Если при этом все точки тела движутся по окружностям (вращаются) с одинаковой угловой скоростью 


или
.
Величину 

Для абсолютно твёрдого тела, величина последнего интеграла называется моментом инерции относительно оси вращения и обозначается 


Сохранение момента импульса[править | править код]
Закон сохранения момента импульса: суммарный момент импульса относительно любой неподвижной точки для замкнутой системы остается постоянным со временем.
Производная момента импульса по времени есть момент силы:
,
Таким образом, требование замкнутости системы может быть ослаблено до требования равенства нулю главного (суммарного по всем частицам 
,
где 
По теореме Нётер закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол 




С учётом 


Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:
где 



Смежные понятия[править | править код]
При рассмотрении задач, связанных с вращением, фигурируют понятия, частично упоминавшиеся выше:
- момент импульса относительно оси (термин состоит из четырёх слов) — проекция момента импульса на ось;
- момент инерции твёрдого тела (см. также моменты инерции некоторых тел);
- момент силы (он же: крутящий момент, вращательный момент, вертящий момент);
- импульс момента силы
(единица измерения — Н·м·с) — мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении).
Несмотря на созвучность с «моментом импульса», эти понятия не синонимичны термину «момент импульса» и несут самостоятельный смысл.
Момент импульса в электродинамике[править | править код]
При описании движения заряженной частицы в электромагнитном поле канонический импульс 

где 



где 
Момент импульса в квантовой механике[править | править код]
Оператор момента[править | править код]
В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определёнными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на 


Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновый момент импульса всегда кратен 


В классическом определении момент импульса зависит от 6 переменных 





Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:
,
где 

,
где 
,
где 
и даже более важные подстановки с гамильтонианом частицы без заряда и спина:
.
Симметрия вращения[править | править код]
Операторы момента импульса обычно встречаются при решении задач сферической симметрии в сферических координатах. Тогда момент импульса в пространственном отображении:
Когда находят собственные значения этого оператора, получают следующее:
где 


— сферические функции.
Примечания[править | править код]
- ↑ Pivarski, Jim Spin. Symmetry Magazine (март 2013). Дата обращения: 28 апреля 2014. Архивировано 15 апреля 2014 года.
- ↑ [Информация с сайта Нобелевского комитета (англ.). Дата обращения: 3 ноября 2017. Архивировано 18 мая 2008 года. Информация с сайта Нобелевского комитета (англ.)]
Литература[править | править код]
- Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. — М.: Мир, 1984. — Т. 1. — 302 с.
- Блохинцев Д. И. Основы квантовой механики. — М.: Наука, 1976. — 664 с.
- Боум А. Квантовая механика: основы и приложения. — М.: Мир, 1990. — 720 с.
- Варшалович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория углового момента. — Л.: Наука, 1975. — 441 с.
- Зар Р. Теория углового момента. О пространственных эффектах в физике и химии. — М.: Мир, 1993. — 352 с.
Выберем на оси времени малый интервал , в течение которого сила остается практически неизменной. Импульс силы за время будет равен площади заштрихованного столбика. Если всю ось времени на интервале от до разбить на малые интервалы , а затем просуммировать импульсы силы на всех интервалах , то суммарный импульс силы окажется равным площади, которую образует ступенчатая кривая с осью времени. В пределе () эта площадь равна площади, ограниченной графиком и осью . Этот метод определения импульса силы по графику является общим и применим для любых законов изменения силы со временем. Математически задача сводится к интегрированию функции на интервале .
Импульс силы, график которой представлен на рис. 1.16.1, на интервале от до равен:
В этом простом примере
В некоторых случаях среднюю силу можно определить, если известно время ее действия и сообщенный телу импульс. Например, сильный удар футболиста по мячу массой может сообщить ему скорость . Время удара приблизительно равно .
Импульс , приобретенный мячом в результате удара есть:
Следовательно, средняя сила , с которой нога футболиста действовала на мяч во время удара, есть:
Это очень большая сила. Она приблизительно равна весу тела массой .
Если движение тела во время действия силы происходило по некоторой криволинейной траектории, то начальный 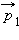
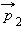
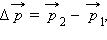
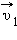
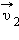
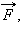
 |
| Рисунок 1.16.2.
При нормальном падении мяча массой на упругую стенку со скоростью Импульс тела, закон сохранения импульсатеория по физике 🧲 законы сохраненияИмпульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость: Единица измерения импульса — килограмм на метр в секунду (кг∙м/с). Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0). Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь. Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ: p = mv = 0,01∙300 = 3 (кг∙м/с) Относительный импульсОтносительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость: p 1отн2— импульс первого тела относительно второго, m1 — масса первого тела, v 1отн2 — скорость первого тела относительно второго, v 1и v 2 — скорости первого и второго тела соответственно в одной и той же системе отсчета. Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем. Сначала переведем единицы измерения в СИ: Изменение импульса тела∆ p — изменение импульса тела, p — конечный импульс тела, p 0 — начальный импульс тела Частные случаи определения изменения импульса телаАбсолютно неупругий ударКонечный импульс тела: Модуль изменения импульса тела равен модулю его начального импульса: Абсолютно упругий ударМодули конечной и начальной скоростей равны: Модули конечного и начального импульсов равны: Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: Пуля пробила стенкуМодуль изменения импульса тела равен разности модулей начального и конечного импульсов: Радиус-вектор тела повернул на 180 градусовМодуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормалиМодули конечной и начальной скоростей равны: Модули конечного и начального импульсов равны: Угол падения равен углу отражения: Модуль изменения импульса в этом случае определяется формулой: |
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
F ∆t — импульс силы, ∆ p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
Отсюда скорость равна:
Импульс частицы до столкновения равен − p 1, а после столкновения равен − p 2, причём p1 = p, p2 = 2p, − p 1⊥ − p 2. Изменение импульса частицы при столкновении Δ − p равняется по модулю:
Алгоритм решения
Решение
Запишем исходные данные:
Так как угол α = 90 о , вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δ p = √ p 2 1 + p 2 2
Подставим известные данные:
Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5
pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Закон cохранения импульса
О чем эта статья:
9 класс, 10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела
p — импульс тела [кг · м/с]
m — масса тела [кг]
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса
Векторная сумма импульсов тел в замкнутой системе постоянна
А выглядит — вот так:
Закон сохранения импульса
pn — импульс тела [кг · м/с]
Простая задачка
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
— это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
— это импульс мальчика после прыжка,
— это импульс лодки после прыжка.
Изобразим на рисунке, что происходило до и после прыжка.
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
Подставим формулу импульса.
, где:
— масса мальчика [кг]
— скорость мальчика после прыжка [м/с]
— масса лодки [кг]
— скорость лодки после прыжка [м/с]
Выразим скорость лодки :
Подставим значения:
м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
Задачка посложнее
Тело массы m1 = 800 г движется со скоростью v1 = 3 м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы m2 = 200 г со скоростью v2 = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.
Решение: Для данной системы выполняется закон сохранения импульса:
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
Спроецируем импульсы на ось х:
После неупругого удара получилось одно тело массы , которое движется с искомой скоростью:
Отсюда находим скорость тела, образовавшегося после удара:
Переводим массу в килограммы и подставляем значения:
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на получившееся значение.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
Применим выражение для ускорения
В этих уравнениях слева находится величина a. Так как левые части уравнений равны, можно приравнять правые их части
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
В правой части находится — это разница между конечной и начальной скоростью.
Преобразуем правую часть
Раскрыв скобки, получим
Заменим произведение массы и скорости на импульс:
То есть, вектор – это вектор изменения импульса .
Тогда второй закон Ньютона в импульсной форме запишем так
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме
Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
Сила называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.
Закон сохранения импульса позволяет оценить скорость ракеты.
vг — скорость горючего,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
Скорость ракеты при реактивном движении
vг — скорость горючего [м/с]
mр — масса ракеты [кг]
vр — скорость ракеты [м/с]
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
[spoiler title=”источники:”]
http://skysmart.ru/articles/physics/zakon-sohraneniya-impulsa
[/spoiler]
Главная
»
Самолетостроение
»
Физика
»
Момент импульса. Закон сохранения момента импульса. Основной закон динамики вращательного движения.
Момент импульса. Закон сохранения момента импульса. Основной закон динамики вращательного движения.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.
Момент импульса замкнутой системы сохраняется.
Момент импульса в классической механике
Связь между импульсом 
Определение
Момент импульса 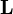
где 
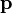
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.
Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение:
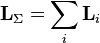
Вычисление момента
Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам 
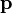
где 

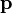

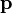
Запишем 
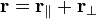
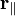


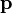
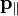

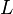
Для систем, совершающих вращение вокруг одной из осей симметрии (вообще говоря, вокруг так называемых главных осей инерции), справедливо соотношение
где 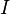
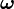
В общем случае вектор момента связан с вектором угловой скорости линейным оператором момента инерции:
Сохранение углового момента
Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.
Производная момента импульса по времени есть момент силы:
Таким образом, требование системы быть «замкнутой», означает равенство нулю главного (суммарного) момента внешних сил:
где 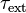
Математически закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол 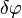
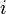
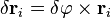

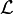
С учетом 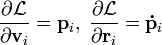
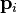
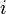
Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:
где, 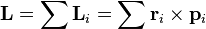


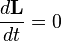
На орбитах момент импульса распределяется между собственным вращением планеты и момента импульса ее орбитального движения:
Момент импульса в электродинамике
При описании движения заряженной частицы в электромагнитном поле, канонический импульс 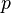

где 


где 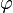
Момент импульса в квантовой механике
Оператор момента
В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определенными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на 


В классическом определении момент импульса зависит от 6 переменных 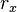
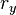
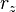
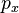
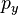
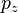
Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:
где 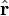

где 
и даже более важные подстановки с гамильтонианом частицы без заряда и спина:
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.






















![[L_i,; L_j ] = i hbar varepsilon_{ijk} L_k, quadleft[L_i,; mathbf{L}^2 right] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc71cd271eeabf833358dbaf02930a174d88e1f0)
![left[L_i,; H right] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbcc5ef1a6821f34a74fdf4ab2b1767ad83a639d)




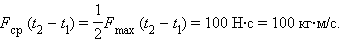
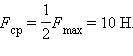
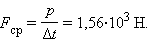
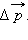
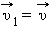 после отскока мяч будет иметь скорость
после отскока мяч будет иметь скорость 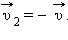 Следовательно, изменение импульса мяча за время отскока равно
Следовательно, изменение импульса мяча за время отскока равно 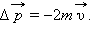 В проекциях на ось этот результат можно записать в скалярной форме . Ось направлена от стенки (как на рис. 1.16.2), поэтому и . Следовательно, модуль изменения импульса связан с модулем скорости мяча соотношением .
В проекциях на ось этот результат можно записать в скалярной форме . Ось направлена от стенки (как на рис. 1.16.2), поэтому и . Следовательно, модуль изменения импульса связан с модулем скорости мяча соотношением .