Подведу итог рассматриваемой темы.
Основное уравнение динамики вращательного движения
говорит о том, что угловое ускорение, приобретаемое телом, прямо пропорционально результирующему моменту действующих на тело сил и обратно пропорционально моменту инерции тело.
Этот закон можно записать ещё в таком виде:
Если момент внешних сил равен нулю (когда внешними силами пренебрегаем или когда линия их действия проходит через ось вращения), то получаем уравнение, называемое законом сохранения момента импульса:
Смысл этого закона такой: уменьшая момент инерции тела увеличиваем угловую скорость его вращения, и наоборот.
Ярким примером демонстрации закона сохранения момента импульса является вращение фигуриста. Когда он приближает руки к корпусу, то уменьшает свой момент инерции, увеличивая скорость вращения. Об этом же говорит следующий рисунок:
Закон сохранения момента импульса выполняется и для системы тел, вращающихся вокруг общей оси, при условии, что эта система замкнута, то есть когда момент внешних сил равен нулю.
Например, когда система состоит из человека и платформы, при вращении которой силой трения можно пренебречь. Сначала человек и платформа неподвижны и их общий момент импульса равен нулю.
Когда человек двигается по платформе по окружности, платформа начинает вращаться в обратную сторону. Общий момент импульса системы остаётся равным нулю.
Закон сохранения момента импульса в рассматриваемом примере запишется так:
Подробно о рассматриваемом случае говорится в решении задачи 7.
Подумайте над решением следующих задач:
1. Однородный стержень длиной 1 м и массой 0,3 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением вращается стержень, если вращающий момент (момент силы) равен 0,05 Нм? Ответ:2 рад/с2
2. Диск массой 1 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Найти кинетическую энергию диска. Ответ: 12 Дж
3. Кинетическая энергия вала, вращающегося с постоянной скоростью , соответствующей 6 м/с, равна 45 Дж. Найти момент импульса вала. Ответ: 2,4 кг м2/с
4. Диск массой 1 кг и диаметром 50 см вращается вокруг оси, проходящей через его центр перпендикулярно плоскости диска, делая 25 об/с. Какую работу надо совершить, чтобы остановить диск? Ответ: 385 Дж
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Задачи 18 – 20 на законы сохранения.
Следующая запись: Задачи 1 – 4 на вращательное движение
Ссылки на другие занятия найдёте в Занятие 1.
Данная задача находится в разделе
Решебник Волькенштейн на странице № 4
<<< Предыдущая задача из Волькенштейн
3.21 Диск диаметром D = 60 см и массой m = 1 кг вращается вокруг оси, проходящей через центр перпендикулярно к его плоскости с частотой n = 20 об/с. Какую работу А надо совершить, чтобы остановить диск?
Следующая задача из Волькенштейн >>>
3.23 Найти кинетическую Wк энергию велосипедиста, едущего со скоростью v = 9 км/ч. Масса велосипедиста вместе с велосипедом m = 78 кг, причем на колеса приходится масса m0 = 3 кг. Колеса велосипеда считать обручами.
[14.07.2014 17:00]
Решение 8514:
Номер задачи на нашем сайте: 8514
ГДЗ из решебника:
Тема:
Глава 1. Физические основы механики
§ 3. Вращательного движение твердых тел
Нашли ошибку? Сообщите в комментариях (внизу страницы)
|
Раздел: Физика Полное условие: 3.22 Кинетическая энергия вала, вращающегося с частотой n = 5 об/с, Wк = 60 Дж. Найти момент импульса L вала.Решение, ответ задачи 8514 из ГДЗ и решебников: Этот учебный материал представлен 1 способом:
|
||
| Счетчики: 10563 | Добавил: Admin |
Для просмотра в натуральную величину нажмите на картинку
| Добавить комментарий
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
Готовое решение: Заказ №8335
Тип работы: Задача
Статус: Выполнен (Зачтена преподавателем ВУЗа)
Предмет: Физика
Дата выполнения: 07.08.2020
Цена: 227 руб.
Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
№2-2 Условие 1 5. Кинетическая энергия вала, вращающегося с частотой n = 5 об/с, равна Wк = 60 Дж. Найти момент импульса L вала. Условие 2 1.87. Кинетическая энергия вала, вращающегося с постоянной скоростью, соответствующей частоте 5 об/с, равна 60 Дж. Найти момент количества движения этого вала.
Решение.
Угловая скорость вращения вала: , где – частота вращения скамьи. Кинетическая энергия вращающегося вала: .
- Кинетическая энергия вала, вращающегося с постоянной частотой 5 с-1, равна 60 Дж. Найти момент импульса вала. (3,82 кг•м2/с)
- Тело массой m = 10 г движется по окружности радиусом R = 6,4 см. Найти тангенциальное ускорение aτ тела, если известно, что к концу второго оборота после начала движения его кинетическая энергия Ек = 0,8 мДж.
- Найти момент импульса Jw вала, вращающегося с частотой n = 10 с-1. Кинетическая энергия вращающегося вала Wк = 100 Дж.
- Кинетическая энергия вала, вращающегося с частотой n = 5 об/с, Eк = 60 Дж. Найти момент импульса вала.
П
усть
дана материальная точка, имеющая импульср. Пусть её положение
относительно точки О определяется
радиусом-векторомr.
Движение такой точки характеризуют
моментом импульсаL.
Моментом импульса материальной точки
относительно точки О называется
векторная величина, равная векторному
произведению радиуса-вектораr
и вектора импульсаp:
L=[r,p].
Модуль момента импульса L=rpsin,
где
– угол между векторамиr
и р. Направление вектора
момента импульса определяется по правилу
правого винта.
Размерность момента импульса [L]=кг.м2/с.
М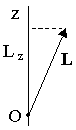
омент
импульса тела относительно точки равен
векторной сумме моментов импульсов
частиц тела относительно той же точки
L=L1+L2+…+LN.
Проекция вектора момента импульса
относительно точки О на ось z,
проходящую через эту точку, называетсямоментом импульса относительно оси:
Lz=[r,p]z.
Момент импульса относительно оси
является скалярной величиной.
Момент импульса тела относительно оси
z равен проекции
момента импульса тела относительно
точки О на осьz,
проходящую через эту точку.
4.3. Связь момента силы и момента импульса
Момент импульса и момент силы связаны
между собой. Найдём выражение, связывающее
их.
Возьмём производную по времени от
выражения, определяющего момент импульса:
Член
равен нулю, так как угол между вектором
скоростиdr/dt и
вектором импульсар равен нулю.
Производная импульса по времени,
имеющаяся во втором члене полученного
выражения, равна силе (второй закон
Ньютона). Поэтому можем записать
полученное выражение в следующей форме:
.
Но [r,F]
есть по определению момент силыF относительно
той же точки О. Поэтому
т.е. скорость изменения момента импульса
частицы равна моменту силы,
действующему на эту частицу.
Проекция последнего уравнения на ось
zвыражает связь
момента импульса относительно осиzи момента силы
относительно той же оси.
.
4.4. Основной закон динамики вращательного движения
Пусть твёрдое тело вращается относительно
неподвижной оси z.
Выразим момент импульса твёрдого тела
относительно оси вращения. Для этого
представим твёрдое тело как совокупность
элементарных масс. Момент
импульса одной элементарной массы
относительно осиz
Момент импульса всего тела равен сумме
моментов импульсов всех элементарных
масс
Скорость vу разных
элементарных масс различна, а угловая
скорость одинакова.
Поскольку v=r,
Поскольку угловая скорость со одинакова
для всех элементарных масс, её можно
вынести за знак суммы
Введём обозначение
.
С учётом этого
Lz=Jz..
Ранее мы получили, что момент импульса
и момент силы связаны следующим
образом:
.
Заменив Lz
наJzωи с учётом того, чтоJz
с течением времени не изменяется,
получаем
Учитывая, что производная угловой
скорости по времени равна угловому
ускорению , получаем
.
Полученное выражение – основной закон
динамики вращательного движения,
связывающий между собой меру внешнего
воздействия – момент силы Mz
с результатом внешнего воздействия
– угловым ускорением.
Коэффициент Jz, стоящий
в этом уравнении, зависит от массы тела
и от того, как она распределена по
объёму тела (это видно из определения
величиныJz).
Чем меньше Jz, тем большее
угловое ускорение получит тело при
воздействии момента силыMz.
Это говорит о том, что коэффициентJz.
характеризует инертность вращающегося
тела. ПоэтомуJz называют
моментом инерции тела относительно осиz.
Знание величины момента инерции тела
необходимо для описания вращательного
движения. Поэтому обсудим более подробно,
что такое момент инерции и как его
вычислить.
Соседние файлы в папке часть 1
- #
- #
- #
- #
- #
- #
