Как найти момент импульса всей системы - Сайт, где вы сможете решить свои вопросы

Если
в задаче рассматривается не одна
материальная точка, а система точек, то
момент импульса системы равен векторной
сумме моментов импульсов всех материальных
точек системы

где
все векторы

определены относительно одной и той же
точки заданной системы отсчета.

Сумма
моментов всех внутренних сил будет
равна нулю, так как силы, с которыми
взаимодействуют любые две материальные
точки системы, удовлетворяют третьему
закону Ньютона и действуют вдоль одной
прямой, поэтому их плечи одинаковые, а
направления противоположные.

Закон изменения
момента импульса для системы тел имеет
вид

то
есть изменение момента импульса системы
равно сумме моментов всех внешних сил
относительно той же точки.

Если сумма моментов
всех внешних сил равна нулю, то момент
импульса системы сохраняется

Как
и в случае закона сохранения импульса,
момент импульса незамкнутой системы
сохраняется при условии что:

1) суммарный момент
внешних сил равен нулю,

2)
если момент внешних сил относительно
точки отличен от нуля, но относительно
некоторой оси равен нулю, то момент
импульса относительно этой оси
сохраняется,

3)
если действие внешних сил ограничено
во времени

(удар, взрыв), то изменением момента
импульса

за время удара можно пренебречь.

Ранее
было показано, что в некоторых случаях
решение задач, связанных с импульсом
системы, упрощается, если их решать в
системе центра масс (раздел IV).
Решение задач на момент импульса также
упрощается в этой системе отсчета. Это
связано с тем, что полный импульс системы
частиц в системе центра масс равен нулю,
и поэтому момент импульса системы не
зависит от выбора точки, относительно
которой его определяют. Поэтому этот
момент называют собственным моментом
импульса и обозначают
.
Момент импульса

системы частиц в произвольной системе
складывается из ее собственного момента
импульса

и момента
,
обусловленного движением системы частиц
как целого

Решение задач

6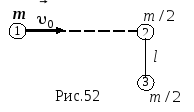.4.
Шарик массы
m,
двигавшийся со скоростью

испытал упругое лобовое столкновение
с одним из шариков покоившейся жесткой
гантели (рис.52). Масса каждого шарика
гантели равна m/2,
длина легкого соединительного стержня
гантели – l.
Считая шарики материальными точками,
найдите:

а)
скорость каждого шарика сразу после
соударения,

б)*
скорость центра масс системы после
соударения,

в)*
собственный момент импульса

гантели (в системе центра масс).

Решение.
а) Рассмотрим момент импульса системы
относительно точки соударения (шарик
2 рис.52). Относительно этой точки момент
импульса системы до столкновения равен
нулю. Рассматриваемая система является
замкнутой, поэтому момент импульса
сохраняется и остается равным нулю.
Следовательно, после столкновения
скорость нижнего шарика гантели равна
нулю

(т.к. плечо импульса 3 шарика не равно
нулю, а плечи импульсов 1 и 2 шариков
равны нулю).

Поскольку
удар абсолютно упругий, импульс и
кинетическая энергия системы также
сохраняются:

,
(1)

,
(2)

где

и

– скорости отлетевшего шарика (шарик 1
рис.52) и верхнего шарика гантели (шарик
2 рис.52) сразу после удара. Решая совместно
уравнения (1) и (2), найдем скорость верхнего
шарика гантели и скорость отлетевшего
шарика сразу после удара

и
.

б)
Момент импульса системы частиц
складывается из ее собственного момента
импульса

и момента, обусловленного движением
системы частиц как целого
:

,
(3)

где
и

– радиус-вектор центра масс и суммарный
импульс системы частиц соответственно.
Так как момент импульса системы после
столкновения равен нулю, из уравнения
(3) следует, что собственный момент
импульса гантели после столкновения
равен:

Центр
масс гантели после столкновения (также
как и до столкновения) находится
посередине соединительного стержня,
т.е.
,
скорость ее центра масс

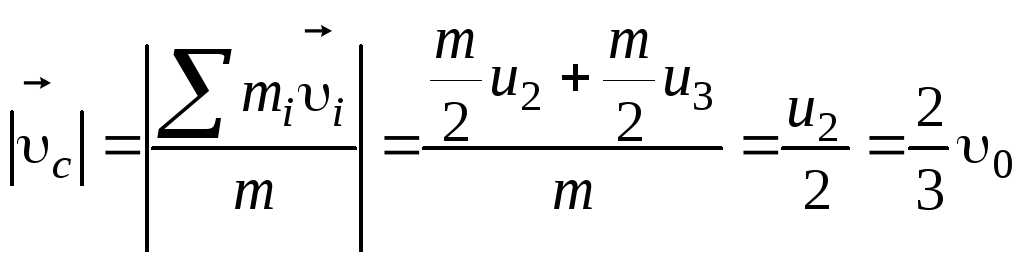в)
Учитывая, что

получим искомую величину:

6.5.
Гладкий
горизонтальный диск вращают относительно
Земли, вращение которой не учитывается,
с угловой скоростью

вокруг вертикальной оси, проходящей
через его центр – точку 0. Из этой точки
в момент

пустили небольшую шайбу массой m
со скоростью
.
Найдите момент импульса шайбы

относительно точки 0 в системе отсчета
связанной с диском.

Решение.
Система отсчета, связанная с вращающимся
диском, является неинерциальной системой
отсчета. В этой системе момент импульса
шайбы относительно точки 0 равен

где
–
скорость шайбы относительно диска.
Раскрыв векторное произведение, получим

где

– угол между векторами
и
.
Из условия задачи известна скорость
шайбы относительно Земли, которая
является инерциальной системой отсчета
–
.
Запишем связь между скоростями шайбы
в этих системах отсчета

В
ыразим
из последнего выражения

и определим ее направление (рис.53). Из
рисунка видно, что вектор

является диагональю прямоугольника,
значит
.
Учитывая, что
,
найдем момент
импульса шайбы

относительно точки 0 в системе отсчета
связанной с диском, подставив найденные
величины в исходное выражение

А
направление вектора

покажем на рис.53.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Момент импульса

Размерность	L²MT⁻¹
Единицы измерения
СИ	м²·кг/с
СГС	см²·г/с
Примечания
псевдовектор

Моме́нт и́мпульса (момент импульса относительно точки, также: кинетический момент, угловой момент, орбитальный момент, момент количества движения) — физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение^[1].

Для одной материальной точки момент импульса равен векторному произведению радиус-вектора точки на её импульс, для системы точек — сумме таких произведений. Стандартное обозначение: , единица измерения в СИ: м²кг/с. Величина зависит от выбора положения начала отсчёта радиус-векторов O.

Момент импульса замкнутой системы сохраняется. Он является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения. При наличии внешних сил производная момента импульса по времени равна моменту сил (относительно того же начала O).

Основное использование понятия момента импульса относится к задачам, связанным с реальным вращением (особенно при наличии центральной или осевой симметрии; тогда О обычно выбирается в центре или на оси). Но величина может быть вычислена и в других ситуациях, например для прямолинейного движения частицы мимо произвольной точки O, не лежащей на линии движения и условно принимаемой за центр.

В случае вращения твёрдого тела вокруг фиксированной оси часто используется не сам момент импульса, а его проекция ${displaystyle L_{parallel }}$ на эту ось — такая величина называется моментом импульса относительно оси.

Понятие момента импульса было изначально введено в классической механике, но имеет обобщения в квантовой механике и электродинамике.

Момент импульса в классической механике[править | править код]

Связь между силой F, моментом силы τ, импульсом и моментом импульса

Определение[править | править код]

Момент импульса материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:

{mathbf {L}}={mathbf {r}}times {mathbf {p}}

где — радиус-вектор частицы относительно выбранного неподвижного начала отсчёта, — импульс частицы.

Из определения момента импульса следует его аддитивность: для системы, состоящей из нескольких материальных точек, выполняется

${displaystyle mathbf {L} =sum limits _{i}mathbf {L} _{i}=sum _{i}mathbf {r} _{i}times mathbf {p} _{i}}$

Количество частиц может быть бесконечным, например в случае твёрдого тела с распределённой массой.

Так как момент импульса задаётся векторным произведением, он является псевдовектором, перпендикулярным обоим векторам и .

Момент импульса можно вычислить относительно любого начала отсчета O (получающиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определённости) его вычисляют относительно центра масс, закреплённой точки вращения твердого тела или другой чем-то выделенной точки.

Выбор точки O иногда связан с характером задачи. Так, при рассмотрении орбитального движения планеты вокруг Солнца за начало отсчёта естественно взять Солнце, а при анализе её же собственного вращения — центр этой планеты. Естественно, получатся два разных момента импульса: ${displaystyle mathbf {L} _{mathrm {orbit} }}$ и ${displaystyle mathbf {L} _{mathrm {spin} }}$ .

Вычисление в общем случае[править | править код]

Если имеется материальная точка массой , двигающаяся со скоростью и находящаяся в точке, описываемой радиус-вектором , то и момент импульса вычисляется по формуле

{displaystyle mathbf {L} =mathbf {r} times mmathbf {v} }

Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки ( rho — плотность) и просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:

${displaystyle mathbf {L} =int limits _{V}{mathbf {dL} }=int limits _{V}{mathbf {r} times mathbf {v} ,dm}=int limits _{V}{mathbf {r} times mathbf {v} ,rho dV}}$

На практике rho задаётся как функция трёх координат и необходимо выполнение тройного интегрирования:

{displaystyle mathbf {L} =iiint {(xmathbf {i} +ymathbf {j} +zmathbf {k} )times mathbf {v} ,rho (x,y,z),dx,dy,dz}}

Если считать, что — обобщённая функция, включающая, возможно, и дельтообразные члены, то эта формула применима и к распределённым, и к дискретным системам.

Случай фиксированной оси[править | править код]

Важным случаем использования понятия «момент импульса» является движение вокруг неизменной оси. В такой ситуации часто рассматривают не сам момент импульса (псевдовектор), а его проекцию на ось как псевдоскаляр, знак которого зависит от направления вращения:

${displaystyle L_{parallel }=pm |mathbf {r_{perp }} times mathbf {p_{perp }} |}$

Параллельность-перпендикулярность (, perp ) имеются в виду по отношению к оси; ${displaystyle mathbf {r} =mathbf {r_{perp }} +mathbf {r_{parallel }} }$ , ${displaystyle mathbf {p} =mathbf {p_{perp }} +mathbf {p_{parallel }} }$ . При этом ${displaystyle r_{perp }}$ — расстояние от оси до материальной точки, называемое «плечом». Величина указанной проекции, в отличие от самого момента, не меняется при сдвиге начала отсчёта O на оси. Для распределённой системы

${displaystyle L_{parallel }=pm left|int {mathbf {r_{perp }} times mathbf {v_{perp }} ,rho dV}right|}$

Если при этом все точки тела движутся по окружностям (вращаются) с одинаковой угловой скоростью omega , то есть численно ${displaystyle v=omega r_{perp }}$ , то для материальной точки массой или для системы будет, соответственно,

${displaystyle L_{parallel }=pm omega mr_{perp }^{2}quad }$

или ${displaystyle quad L_{parallel }=pm omega int {r_{perp }^{2},rho dV}}$

Величину ${displaystyle L_{parallel }}$ иногда называют моментом импульса относительно оси. Символ параллельности у и знак перед выражением могут опускаться, если очевидно, о чём идёт речь.

Для абсолютно твёрдого тела, величина последнего интеграла называется моментом инерции относительно оси вращения и обозначается . Тогда запись обретает вид ${displaystyle ,L_{parallel }=pm Iomega ,}$ или, в векторной форме, . Если известен момент инерции относительно оси, проходящей через центр масс тела, а вращение происходит вокруг другой, но параллельной ей оси, то необходимый момент инерции находится по теореме Штайнера.

Сохранение момента импульса[править | править код]

Закон сохранения момента импульса: суммарный момент импульса относительно любой неподвижной точки для замкнутой системы остается постоянным со временем.

Производная момента импульса по времени есть момент силы:

${displaystyle {frac {dmathbf {L} }{dt}}=sum _{i}{frac {dmathbf {r} _{i}}{dt}}times mathbf {p} _{i}+sum _{i}mathbf {r} _{i}times {frac {dmathbf {p} _{i}}{dt}}=sum _{i}mathbf {r} _{i}times mathbf {F} _{i}=mathbf {tau _{ext}} }$

Таким образом, требование замкнутости системы может быть ослаблено до требования равенства нулю главного (суммарного по всем частицам ) момента внешних сил:

${displaystyle mathbf {L} =mathrm {constant} leftrightarrow mathbf {tau _{ext}} =0}$

где ${displaystyle mathbf {tau _{ext}} }$ — момент сил, приложенных к системе частиц. (Но конечно, если внешние силы вообще отсутствуют, это требование также выполняется.) Аналогичный закон сохранения справедлив для момента импульса относительно фиксированной оси.

По теореме Нётер закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол , радиус-вектор частицы с номером изменятся на ${displaystyle delta mathbf {r} _{i}=delta varphi times mathbf {r} _{i}}$ , а скорости — ${displaystyle delta mathbf {v} _{i}=delta varphi times mathbf {v} _{i}}$ . Функция Лагранжа системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому

$delta mathcal L = mathcal L(mathbf{r}_i + deltamathbf{r}_i,; mathbf{v}_i + deltamathbf{v}_i) - mathcal L(mathbf{r}_i,; mathbf{v}_i) = sum limits_i left( frac{partial mathcal L}{partial mathbf r_i} delta varphi timesmathbf r_i + frac{partial mathcal L}{partial mathbf v_i} delta varphi times mathbf v_i right)= 0.$

С учётом $frac{partial {mathcal {L}}}{partial {mathbf v_{i}}} = mathbf {p_{i}},; frac{partial mathcal {L}}{partial mathbf {r_{i}}} = mathbf {dot p_{i}}$ , где ${mathbf p}_{i}$ — обобщенный импульс -той частицы, каждое слагаемое в сумме из последнего выражения можно переписать в виде

$dot {mathbf p_i} ,delta varphi times mathbf r_i + mathbf p_i,delta varphi times mathbf {dot r_i}.$

Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:

$delta mathcal L = delta varphi sum limits_i left( mathbf r_i times dot {mathbf p_i} + dot {mathbf r_i} times mathbf p_i right) = delta varphi frac{d}{dt} sum limits_i (mathbf r_i times mathbf p_i) = delta varphi frac{d mathbf L}{dt} = 0,$

где — момент импульса системы. Ввиду произвольности , из равенства следует ${displaystyle {frac {dmathbf {L} }{dt}}=0.}$

Смежные понятия[править | править код]

При рассмотрении задач, связанных с вращением, фигурируют понятия, частично упоминавшиеся выше:

момент импульса относительно оси (термин состоит из четырёх слов) — проекция момента импульса на ось;
момент инерции твёрдого тела (см. также моменты инерции некоторых тел);
момент силы (он же: крутящий момент, вращательный момент, вертящий момент);
импульс момента силы ${displaystyle int limits _{t_{1}}^{t_{2}}mathbf {r} times mathbf {F} (t);dt}$ (единица измерения — Н·м·с) — мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении).

Несмотря на созвучность с «моментом импульса», эти понятия не синонимичны термину «момент импульса» и несут самостоятельный смысл.

Момент импульса в электродинамике[править | править код]

При описании движения заряженной частицы в электромагнитном поле канонический импульс не является инвариантным. Как следствие, канонический момент импульса тоже не инвариантен. Тогда берётся реальный импульс, который также называется «кинетическим импульсом»:

${displaystyle mathbf {p} -{frac {emathbf {A} }{c}},}$

где — электрический заряд, — скорость света, — векторный потенциал. Таким образом, гамильтониан (инвариантный) заряженной частицы массы в электромагнитном поле:

$H =frac{1}{2m} left( mathbf{p} -frac {e mathbf{A} }{c}right)^2 + evarphi,$

где varphi — скалярный потенциал. Из этого потенциала следует закон Лоренца. Инвариантный момент импульса, или «кинетический момент импульса», определяется следующим образом:

$K= mathbf{r} times left( mathbf{p} -frac {e mathbf{A} }{c}right).$

Момент импульса в квантовой механике[править | править код]

Оператор момента[править | править код]

В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определёнными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на hbar ( с чертой — постоянная Планка, поделенная на 2 pi ).

Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновый момент импульса всегда кратен hbar/2 для фермионов и hbar для бозонов. Например, электрон в состоянии покоя имеет момент импульса hbar/2 .^[2]

В классическом определении момент импульса зависит от 6 переменных ${displaystyle r_{x}}$ , ${displaystyle r_{y}}$ , ${displaystyle r_{z}}$ , $p_{x}$ , $p_{y}$ , и $p_{z}$ . Переводя это на квантовомеханические определения, используя принцип неопределенности Гейзенберга, получаем, что невозможно вычислить все шесть переменных одновременно с любой точностью. Поэтому есть ограничение на то, что мы можем узнать или подсчитать о практическом моменте импульса. Это значит, что лучшее, что мы можем сделать — это подсчитать одновременно величину вектора момента импульса и какой-либо одной его компоненты (проекции).

Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:

{displaystyle {hat {mathbf {L} }}={hat {mathbf {r} }}times {hat {mathbf {p} }}}

где и — координатный и импульсный оператор, соответственно, а второй — на внутренние, спиновые. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:

{displaystyle {hat {mathbf {L} }}=-ihbar (mathbf {r} times nabla )}

где nabla — оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства:

$[L_i,; L_j ] = i hbar varepsilon_{ijk} L_k, quadleft[L_i,; mathbf{L}^2 right] = 0$

где $varepsilon_{ijk}$ — Символ Леви-Чивиты;

и даже более важные подстановки с гамильтонианом частицы без заряда и спина:

Симметрия вращения[править | править код]

Операторы момента импульса обычно встречаются при решении задач сферической симметрии в сферических координатах. Тогда момент импульса в пространственном отображении:

${displaystyle -{frac {1}{hbar ^{2}}}mathbf {L} ^{2}={frac {1}{sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial }{partial theta }}right)+{frac {1}{sin ^{2}theta }}{frac {partial ^{2}}{partial varphi ^{2}}}.}$

Когда находят собственные значения этого оператора, получают следующее:

${displaystyle L^{2}mid l,;mrangle ={hbar }^{2}l(l+1)mid l,;mrangle ,}$

L_z mid l,; m rang = hbar m mid l,; m rang,

где , — целые числа, такие что а
$lang theta ,; varphi mid l,; m rang = Y_{l,;m}(theta,;varphi)$
— сферические функции.

Примечания[править | править код]

↑ Pivarski, Jim Spin. Symmetry Magazine (март 2013). Дата обращения: 28 апреля 2014. Архивировано 15 апреля 2014 года.
↑ [Информация с сайта Нобелевского комитета (англ.). Дата обращения: 3 ноября 2017. Архивировано 18 мая 2008 года. Информация с сайта Нобелевского комитета (англ.)]

Литература[править | править код]

Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. — М.: Мир, 1984. — Т. 1. — 302 с.
Блохинцев Д. И. Основы квантовой механики. — М.: Наука, 1976. — 664 с.
Боум А. Квантовая механика: основы и приложения. — М.: Мир, 1990. — 720 с.
Варшалович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория углового момента. — Л.: Наука, 1975. — 441 с.
Зар Р. Теория углового момента. О пространственных эффектах в физике и химии. — М.: Мир, 1993. — 352 с.

Источник

В статье обсуждается, как рассчитать импульс системы по импульсам каждого объекта.

Импульс системы определяется движением количества объектов, которыми обладает система. Одни из них движутся со своими скоростями внутри системы, другие покоятся. Следовательно, мы можем вычислить импульс системы, суммируя все импульсы объектов в системе.

Узнать больше о Momentum.

Вычислите импульс системы, содержащей движущиеся объекты, например объект А массой 5 кг, движущийся со скоростью 2 м/с, и объект В массой 3 кг, движущийся со скоростью 5 м/с.

Данный:

m₁ = 5 кг

m₂ = 3 кг

u₁ = 2 м / с

u₂ = 5 м / с

Найти: П_{система} =?

Формула:

Σ P_{система} = P₁+ Р₂ +…

Решения:

Импульс системы рассчитывается путем сложения импульсов двух движущихся объектов.

P_{система} = P₁+ Р₂

P_{система} = м₁u₁ + м₂u₂

Подставляя все значения,

P_{система} = 5 х 2 + 3 х 5

P_{система} = 25

Импульс системы, состоящей из двух движущихся тел, равен 25 кг·м/с.

Узнать больше о Net Force

Как рассчитать импульс системы

Каков импульс системы?

Импульс системы – это движение всей массы системы, включающей несколько объектов.

Когда система включает в себя движение многих объектов, понятие центр массы вводится. Это среднее положение всех объектов в системе, вес по отношению к их массе. Таким образом, импульс системы есть произведение полной массы и скорости центра масс.

Общий импульс системы
(Кредит: Shutterstock)

Импульс системы равен P^→см = Мв^→_cm

Где v^→_cm есть скорость центра масс.

Mv^→_cm = Мд/дтр^→_cm ……… .. (1)

Где r^→_cm это положение центра масс.

Формула центра масс такова,

r^→_cm = м₁r^→1/м2р^→2

Уравнение (1) принимает вид

Mv^→_cm = Md/dt (m1r^→1/м2р^→2)

Mv^→_cm = м₁д/дтр₁^→ +m₂д/дтр₂^→ + …

Mv^→_cm = м₁v₁^→ + м₂v₂^→

Mv^→_cm = P^→₁+P^→₂

Р см = Р^→₁+P^→₂

Вот почему мы говорим, импульс системы есть вектор сумма всех импульсов каждого объекта в системе.

Подробнее о Как рассчитать моментум?

Мы видим три движущихся транспортных средства, таких как автомобиль массой 150 кг, движущийся со скоростью 50 км/ч, мотоцикл массой 80 кг, движущийся со скоростью 80 км/ч, и грузовик массой 250 кг, движущийся со скоростью 30 км/ч. Вычислите импульс системы, в которой автомобиль и мотоцикл движутся в одном направлении, а грузовик — в противоположном.

Данный:

m₁ = 150 кг

m₂ = 80 кг

m₃ = 250 кг

v₁ = 50 км / ч

v₂ = 80 км / ч

v₃ = 30 км / ч

Найти: П_{система}=?

Формула:

P^→_cm= P^→₁+P^→₂ +…

Решения:

Импульс системы рассчитывается как

P^→_cm = P^→₁+P^→₂ +…

P_{система}= P₁ + Р₂ + Р₃

P_{система}= м₁v₁+ м₂v₂ + (-м₃v₃)

Подставляя все значения,

P_{система}= 150 х 50 + 80 х 80 – 250 х 30

P_{система}= 7500 + 6400 – 7500

P_{система}= 6400 кг.км/час

P_{система}= 6400 х 1000/3600

P_{система}= 1777.7

Импульс системы, состоящей из движущегося автомобиля, мотоцикла и грузовика, равен 1777.7 кг.м/с.

Узнайте больше о начальном импульсе.

Как рассчитать полный угловой момент системы?

Полный угловой момент системы рассчитывается с использованием ее момента инерции и угловой скорости.

При расчете полного углового момента нам нужно предположить только объекты, движущиеся под углом в системе. Инерция вращения и угловая скорость объекта предлагают его угловой момент для расчета полного углового момента путем сложения всех угловых моментов объекта в системе.

Мы обсуждали только импульс объекта, который движется прямолинейно или линейно со скоростью v. В системе также присутствует объект, движущийся под углом со скоростью ω. Объект имеет линейный импульс (P) или угловой момент (L) в зависимости от движения.

Для линейное движение, линейный импульс объекта равен P = mv.

Для угловое движение, угловой момент объекта

L = Iω ………………(*)

Где я = момент инерции определяется как

“сумма массы объекта с системой с квадратом его расстояния от оси вращения системы ‘.

Момент инерции для различных форм (Кредит: Shutterstock)

я = Σм_ir_i²

я = мистер².

Соотношение между угловая скорость ω и линейная скорость v равна ω = v/r

Подставляя значения I и ω в уравнение (*), получаем

L = v/r мр²

L ^→ = р^→ *мв^→ or

L ^→ = г^→ * П^→ ……………… (2)

Из приведенного выше соотношения между угловой момент и импульса, мы можем вычислить угловой момент для неорбитальных движущихся объектов внутри системы.

Линейный импульс против углового момента

Связь между линейным и угловым моментом
(Фото: Википедия)

Полный угловой момент системы представляет собой сумму углового момента каждого объекта в системе.

л = л₁ + л₂ + л_N ………………. (3)

Второй закон движения Ньютона говорит

Σ F = d/dt P^→

Дифференцируя уравнение (2) по t,

д/дт л^→ = V^→ * д/дт П^→

д/дт л^→ = г^→* Σ Ф^→ ……… .. (4)

Правая часть представляет собой формулу крутящего момента, которая также называетсямомент силыд., что заставляет тело вращаться вокруг неподвижной оси.

Σ = г^→ * Σ Ф^→ ……………… .. (5)

Используя уравнения (3), (4) и (5),

д/дт л^→ =Σⁱdl_i/дт = Σⁱτ^→_i

Приведенное выше уравнение выражает сумма крутящего момента на каждом объекте в системе дает чистый внешний крутящий момент Στ^→ на систему, чтобы изменить ее полный угловой момент. Следовательно,

dL^→/dt= Στ^→

Но если нет крутящий момент, действующий на вращающийся объекты, Στ^→ = 0 , тогда

dL^→/дт = 0,

Так сохраняется угловой момент системы.

Это означает, что угловой момент отдельного объекта может измениться во время столкновения, но общий угловой момент системы останется прежним.

Для системы двух вращающихся тел

L_{перед столкновением}= л_{после столкновения}

I_1iω_1i + Я_2iω_2i = Я_1fω_1f + Я_2fω_2f ………………….. (6)

Сохранение углового момента (Кредит: Shutterstock)

Подробнее об угловой скорости.

Рассчитайте угловой момент системы, состоящей из двух конькобежцев с моментом инерции 5 кг·м2 и 8 кг·м2, которые скользят под углом со скоростью 10 и 15 рад/с соответственно, тяня их за руки. Кроме того, если они протягивают руки, чтобы уменьшить движение, первый фигурист скользит со скоростью 2 рад/с. Тогда какова скорость второго скольжения фигуриста?

Данный:

I₁ = 5кг.м²

I₂ = 8кг.м²

ω_1i = 10 рад / с

ω_2i = 15 рад / с

ω_1f = 2 рад/с

Найти:

L_общий =?
ω_2f =?

Формула:

L_общий = л₁ + L₂
I_1iω_1i + Я_2iω_2i = Я_1fω_1f + Я_2fω_2f

Решения:

Момент количества движения системы обоих конькобежцев рассчитывается как

L_общий = л₁ + L₂

L_общий = Я_1iω_1i + Я_2iω_2i

Подставляя все значения,

L_общий = 5 х 10 + 8 х 15

L_общий = 50 + 120

L_общий = 170

Угловой момент системы конькобежцев 170кг.м.²/ S

Конечная скорость второго фигуриста рассчитывается по формуле закон сохранение момента импульса.

I_1iω_1i + Я_2iω_2i = Я_1fω_1f + Я_2fω_2f

Подставляя все значения,

5 х 10 + 8 х 15 = 5 х 2 + 8 х ω_2f

170 = 10 + 8ω_2f

8ч_2f = 160

ω_2f = 20

Скорость, с которой скользит второй фигурист после вытягивания рук, составляет 20 рад/с.

Узнайте больше об относительном движении.

Источник

Решение задач

Момент импульса в классической механике[править | править код]

Определение[править | править код]

Вычисление в общем случае[править | править код]

Случай фиксированной оси[править | править код]

Сохранение момента импульса[править | править код]

Смежные понятия[править | править код]

Момент импульса в электродинамике[править | править код]

Момент импульса в квантовой механике[править | править код]

Оператор момента[править | править код]

Симметрия вращения[править | править код]

Примечания[править | править код]

Литература[править | править код]

Каков импульс системы?

Как рассчитать полный угловой момент системы?

Вам также может понравиться

Как найти человека по фамилии имени отчество

Как исправить флеш память телефона

Firebird msg not found как исправить ibexpert

Добавить комментарий Отменить ответ