Как найти момент инерции для тела

Как найти момент инерции для тела

Момент инерции
{displaystyle J=int limits _{(m)}r^{2}mathrm {d} m}
Размерность L2M
Единицы измерения
СИ кг·м²
СГС г·см²

Моме́нт ине́рции — тензорная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле. Момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества, которое, формально, может представлять собой не обязательно ось вращения (т.е. прямую), но и точку или плоскость. В последних случаях говорят о моменте инерции относительно точки или плоскости, а возникать такие величины могут в формальных вычислениях, например, при расчете тензора инерции.

Единица измерения в Международной системе единиц (СИ): кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.

Осевой момент инерции[править | править код]

Осевые моменты инерции некоторых тел

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси[1]:

{displaystyle J_{a}=sum _{i=1}^{n}m_{i}r_{i}^{2},}

где:

  • mi — масса i-й точки,
  • ri — расстояние от i-й точки до оси.

Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

{displaystyle J_{a}=int limits _{(m)}r^{2}dm=int limits _{(V)}rho r^{2}dV,}

где:

dm = ρ dV — масса малого элемента объёма тела dV,
ρ — плотность,
r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

{displaystyle J_{a}=rho int limits _{(V)}r^{2}dV.}

Теорема Гюйгенса — Штейнера[править | править код]

Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями[1]:

{displaystyle J=J_{c}+md^{2},}

где m — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

{displaystyle J=J_{c}+md^{2}={frac {1}{12}}ml^{2}+mleft({frac {l}{2}}right)^{2}={frac {1}{3}}ml^{2}.}

Осевые моменты инерции некоторых тел[править | править код]

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения

Тело Описание Положение оси a Момент инерции Ja
Traegheit a punktmasse.png Материальная точка массы m На расстоянии r от точки, неподвижная mr^{2}
Traegheit b zylindermantel.png Полый тонкостенный цилиндр или кольцо радиуса r и массы m Ось цилиндра mr^{2}
Traegheit c vollzylinder.png Сплошной цилиндр или диск радиуса r и массы m Ось цилиндра {frac {1}{2}}mr^{2}
Traegheit d hohlzylinder2.png Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 Ось цилиндра m{frac {r_{2}^{2}+r_{1}^{2}}{2}}[Комм 1]
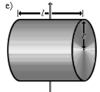
Traegheit e vollzylinder 2.png Сплошной цилиндр длины l, радиуса r и массы m Ось перпендикулярна образующей цилиндра и проходит через его центр масс {1 over 4}mcdot r^{2}+{1 over 12}mcdot l^{2}
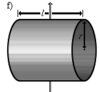
Traegheit f zylindermantel 2.png Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m Ось перпендикулярна к цилиндру и проходит через его центр масс {1 over 2}mcdot r^{2}+{1 over 12}mcdot l^{2}
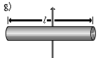
Traegheit g stab1.png Прямой тонкий стержень длины l и массы m Ось перпендикулярна к стержню и проходит через его центр масс {frac {1}{12}}ml^{2}
Traegheit h stab2.png Прямой тонкий стержень длины l и массы m Ось перпендикулярна к стержню и проходит через его конец {frac {1}{3}}ml^{2}
Traegheit i kugel1.png Тонкостенная сфера радиуса r и массы m Ось проходит через центр сферы {frac {2}{3}}mr^{2}
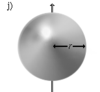
Traegheit j kugel1.png Шар радиуса r и массы m Ось проходит через центр шара {frac {2}{5}}mr^{2}
Cone (geometry).svg Конус радиуса r и массы m Ось конуса {frac {3}{10}}mr^{2}
Равнобедренный треугольник с высотой h, основанием a и массой m Ось перпендикулярна плоскости треугольника и проходит через вершину (при высоте) {frac {1}{24}}m(a^{2}+12h^{2})
Правильный треугольник со стороной a и массой m Ось перпендикулярна плоскости треугольника и проходит через центр масс {frac {1}{12}}ma^{2}
Квадрат со стороной a и массой m Ось перпендикулярна плоскости квадрата и проходит через центр масс {frac {1}{6}}ma^{2}
Прямоугольник со сторонами a и b и массой m Ось перпендикулярна плоскости прямоугольника и проходит через центр масс {frac {1}{12}}m(a^{2}+b^{2})
Правильный n-угольник радиуса r и массой m Ось перпендикулярна плоскости и проходит через центр масс {displaystyle {frac {mr^{2}}{6}}left[1+2cos(pi /n)^{2}right]}
Torus 3d.png Тор (полый) с радиусом направляющей окружности R, радиусом образующей окружности r и массой m Ось перпендикулярна плоскости направляющей окружности тора и проходит через центр масс {displaystyle I=mleft({frac {3}{4}},r^{2}+R^{2}right)}

Вывод формул[править | править код]

Тонкостенный цилиндр (кольцо, обруч)

Вывод формулы

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда

{displaystyle J=sum dJ_{i}=sum R_{i}^{2}dm.qquad (1).}

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

J=sum R^{2}dm=R^{2}sum dm=mR^{2}.

Толстостенный цилиндр (кольцо, обруч)

Вывод формулы

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

dm=rho dV=rho cdot 2pi rhdr;qquad dJ=r^{2}dm=2pi rho hr^{3}dr.

Момент инерции толстого кольца найдём как интеграл

J=int _{R_{1}}^{R}dJ=2pi rho hint _{R_{1}}^{R}r^{3}dr=
{displaystyle =2pi rho hleft.{frac {r^{4}}{4}}right|_{R_{1}}^{R}={frac {1}{2}}pi rho hleft(R^{4}-R_{1}^{4}right)={frac {1}{2}}pi rho hleft(R^{2}-R_{1}^{2}right)left(R^{2}+R_{1}^{2}right).}

Поскольку объём и масса кольца равны

V=pi left(R^{2}-R_{1}^{2}right)h;qquad m=rho V=pi rho left(R^{2}-R_{1}^{2}right)h,

получаем окончательную формулу для момента инерции кольца

J={frac {1}{2}}mleft(R^{2}+R_{1}^{2}right).

Однородный диск (сплошной цилиндр)

Вывод формулы

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):

J={frac {1}{2}}mR^{2}.

Сплошной конус

Вывод формулы

Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен

r={frac {Rh}{H}},

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска.
Масса и момент инерции такого диска составят

dm=rho dV=rho cdot pi r^{2}dh;
dJ={frac {1}{2}}r^{2}dm={frac {1}{2}}pi rho r^{4}dh={frac {1}{2}}pi rho left({frac {Rh}{H}}right)^{4}dh;

Интегрируя, получим

{begin{aligned}J=int _{0}^{H}dJ={frac {1}{2}}pi rho left({frac {R}{H}}right)^{4}int _{0}^{H}h^{4}dh={frac {1}{2}}pi rho left({frac {R}{H}}right)^{4}left.{frac {h^{5}}{5}}right|_{0}^{H}=={frac {1}{10}}pi rho R^{4}H=left(rho cdot {frac {1}{3}}pi R^{2}Hright){frac {3}{10}}R^{2}={frac {3}{10}}mR^{2}.end{aligned}}

Сплошной однородный шар

Вывод формулы

Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

r={sqrt {R^{2}-h^{2}}}.

Масса и момент инерции такого диска составят

dm=rho dV=rho cdot pi r^{2}dh;
dJ={frac {1}{2}}r^{2}dm={frac {1}{2}}pi rho r^{4}dh={frac {1}{2}}pi rho left(R^{2}-h^{2}right)^{2}dh={frac {1}{2}}pi rho left(R^{4}-2R^{2}h^{2}+h^{4}right)dh.

Момент инерции шара найдём интегрированием:

{begin{aligned}J&=int _{-R}^{R}dJ=2int _{0}^{R}dJ=pi rho int _{0}^{R}left(R^{4}-2R^{2}h^{2}+h^{4}right)dh=\&=pi rho left.left(R^{4}h-{frac {2}{3}}R^{2}h^{3}+{frac {1}{5}}h^{5}right)right|_{0}^{R}=pi rho left(R^{5}-{frac {2}{3}}R^{5}+{frac {1}{5}}R^{5}right)={frac {8}{15}}pi rho R^{5}=\&=left({frac {4}{3}}pi R^{3}rho right)cdot {frac {2}{5}}R^{2}={frac {2}{5}}mR^{2}.end{aligned}}

Тонкостенная сфера

Вывод формулы

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

J_{0}={frac {2}{5}}MR^{2}={frac {8}{15}}pi rho R^{5}.

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

{displaystyle {begin{aligned}J&={frac {dJ_{0}}{dR}}dR={frac {d}{dR}}left({frac {8}{15}}pi rho R^{5}right)dR=\&={frac {8}{3}}pi rho R^{4}dR=left(rho cdot 4pi R^{2}dRright){frac {2}{3}}R^{2}={frac {2}{3}}mR^{2}.end{aligned}}}

Тонкий стержень (ось проходит через центр)

Вывод формулы

Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

dm={frac {mdr}{l}};qquad dJ=r^{2}dm={frac {mr^{2}dr}{l}}.

Интегрируя, получим

J=int _{-l/2}^{l/2}dJ=2int _{0}^{l/2}dJ={frac {2m}{l}}int _{0}^{l/2}r^{2}dr={frac {2m}{l}}left.{frac {r^{3}}{3}}right|_{0}^{l/2}={frac {2m}{l}}{frac {l^{3}}{24}}={frac {1}{12}}ml^{2}.

Тонкий стержень (ось проходит через конец)

Вывод формулы

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l⁄2. По теореме Штейнера новый момент инерции будет равен

J=J_{0}+mr^{2}=J_{0}+mleft({frac {l}{2}}right)^{2}={frac {1}{12}}ml^{2}+{frac {1}{4}}ml^{2}={frac {1}{3}}ml^{2}.

Безразмерные моменты инерции планет и их спутников[2][3][4]

Безразмерные моменты инерции планет и спутников[править | править код]

Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра[5][6].

Центробежный момент инерции[править | править код]

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины[1][7]:

{displaystyle J_{xy}=int limits _{(m)}xydm=int limits _{(V)}xyrho dV,}
{displaystyle J_{xz}=int limits _{(m)}xzdm=int limits _{(V)}xzrho dV,}
{displaystyle J_{yz}=int limits _{(m)}yzdm=int limits _{(V)}yzrho dV,}

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела[7].

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции[7].

Геометрические моменты инерции[править | править код]

Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:

{displaystyle J_{Va}=int limits _{(V)}r^{2}dV,}

где, как и ранее r — расстояние от элемента dV до оси a.

Размерность JVa — длина в пятой степени (mathrm {dim} J_{Va}=mathrm {L^{5}} ), соответственно единица измерения СИ — м5.

Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:

{displaystyle J_{Sa}=int limits _{(S)}r^{2}dS,}

где интегрирование выполняется по поверхности S, а dS — элемент этой поверхности.

Размерность JSa — длина в четвёртой степени (mathrm {dim} J_{Sa}=mathrm {L^{4}} ), соответственно единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката часто указывается в см4.

Через геометрический момент инерции площади выражается момент сопротивления сечения:

{displaystyle W={frac {J_{Sa}}{r_{max}}}.}

Здесь rmax — максимальное расстояние от поверхности до оси.

Геометрические моменты инерции площади некоторых фигур
Прямоугольника высотой h и шириной b: J_{y}={frac {bh^{3}}{12}}

J_{z}={frac {hb^{3}}{12}}

Прямоугольного коробчатого сечения высотой и шириной по внешним контурам H и B, а по внутренним h и b соответственно J_{z}={frac {BH^{3}}{12}}-{frac {bh^{3}}{12}}={frac {1}{12}}(BH^{3}-bh^{3})

J_{y}={frac {HB^{3}}{12}}-{frac {hb^{3}}{12}}={frac {1}{12}}(HB^{3}-hb^{3})

Круга диаметром d J_{y}=J_{z}={frac {pi d^{4}}{64}}

Момент инерции относительно плоскости[править | править код]

Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости[9].

Если через произвольную точку O провести координатные оси x,y,z, то моменты инерции относительно координатных плоскостей xOy, yOz и zOx будут выражаться формулами:

{displaystyle J_{xOy}=sum _{i=1}^{n}m_{i}z_{i}^{2} ,}
{displaystyle J_{yOz}=sum _{i=1}^{n}m_{i}x_{i}^{2} ,}
{displaystyle J_{zOx}=sum _{i=1}^{n}m_{i}y_{i}^{2} .}

В случае сплошного тела суммирование заменяется интегрированием.

Центральный момент инерции[править | править код]

Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) {displaystyle J_{O}}  — это величина, определяемая выражением[9]:

{displaystyle J_{a}=int limits _{(m)}r^{2}dm=int limits _{(V)}rho r^{2}dV,}

где:

Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей[9]:

{displaystyle J_{O}={frac {1}{2}}left(J_{x}+J_{y}+J_{z}right),}
{displaystyle J_{O}=J_{xOy}+J_{yOz}+J_{xOz}.}

Тензор инерции и эллипсоид инерции[править | править код]

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором {displaystyle {vec {s}}=leftVert s_{x},s_{y},s_{z}rightVert ^{T},leftvert {vec {s}}rightvert =1}, можно представить в виде квадратичной (билинейной) формы:

{displaystyle I_{s}={vec {s}}^{T}cdot {hat {J}}cdot {vec {s}},qquad } (1)

где {displaystyle {hat {J}}} — тензор инерции. Матрица тензора инерции симметрична, имеет размеры 3times 3 и состоит из компонент центробежных моментов:

{displaystyle {hat {J}}=leftVert {begin{array}{ccc}J_{xx}&-J_{xy}&-J_{xz}\-J_{yx}&J_{yy}&-J_{yz}\-J_{zx}&-J_{zy}&J_{zz}end{array}}rightVert ,}
{displaystyle J_{xy}=J_{yx},quad J_{xz}=J_{zx},quad J_{zy}=J_{yz},quad }{displaystyle J_{xx}=int limits _{(m)}(y^{2}+z^{2})dm,quad J_{yy}=int limits _{(m)}(x^{2}+z^{2})dm,quad J_{zz}=int limits _{(m)}(x^{2}+y^{2})dm.}

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора {displaystyle {hat {J}}}:

{displaystyle {hat {J}}_{d}={hat {Q}}^{T}cdot {hat {J}}cdot {hat {Q}},}
{displaystyle {hat {J}}_{d}=leftVert {begin{array}{ccc}J_{X}&0&0\0&J_{Y}&0\0&0&J_{Z}end{array}}rightVert ,}

где {displaystyle {hat {Q}}} — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины {displaystyle J_{X},J_{Y},J_{Z}} — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

{displaystyle I_{s}=J_{X}cdot s_{x}^{2}+J_{Y}cdot s_{y}^{2}+J_{Z}cdot s_{z}^{2},}

откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на {displaystyle I_{s}}

{displaystyle left({s_{x} over {sqrt {I_{s}}}}right)^{2}cdot J_{X}+left({s_{y} over {sqrt {I_{s}}}}right)^{2}cdot J_{Y}+left({s_{z} over {sqrt {I_{s}}}}right)^{2}cdot J_{Z}=1}

и произведя замены:

{displaystyle xi ={s_{x} over {sqrt {I_{s}}}},eta ={s_{y} over {sqrt {I_{s}}}},zeta ={s_{z} over {sqrt {I_{s}}}},}

получаем канонический вид уравнения эллипсоида в координатах {displaystyle xi eta zeta }:

{displaystyle xi ^{2}cdot J_{X}+eta ^{2}cdot J_{Y}+zeta ^{2}cdot J_{Z}=1.}

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

{displaystyle r^{2}=xi ^{2}+eta ^{2}+zeta ^{2}=left({s_{x} over {sqrt {I_{s}}}}right)^{2}+left({s_{y} over {sqrt {I_{s}}}}right)^{2}+left({s_{z} over {sqrt {I_{s}}}}right)^{2}={1 over I_{s}}.}

См. также[править | править код]

  • Кинематика твёрдого тела
  • Метод главных компонент
  • Сопротивление материалов
  • Теорема Штейнера
  • Теорема Кёнига (механика)
  • Механические приложения тройного интеграла
  • Механические приложения двойного интеграла
  • Полярный момент инерции
  • Список моментов инерции
  • Момент силы
  • Момент импульса

Комментарии[править | править код]

  1. ↑ При получении этой формулы путём вычитания момента инерции сплошного цилиндра радиусом r1 из цилиндра радиусом r2 необходимо обратить внимание, что их массы при этом не будут одинаковыми или равны m. При этом должно выполняться условие {displaystyle m_{2}-m_{1}=m}. Из формулы для массы соответствующего цилиндра можно определить, что в этом случае {displaystyle m_{1}=m{frac {r_{1}^{2}}{r_{2}^{2}-r_{1}^{2}}}} и {displaystyle m_{2}=m{frac {r_{2}^{2}}{r_{2}^{2}-r_{1}^{2}}}}. В правильности использования знака «+» в этой формуле также можно убедиться, если сравнить моменты инерции полого толстостенного и сплошного цилиндров с одинаковыми массами. Действительно, у первого из этих цилиндров масса в среднем сосредоточена дальше от оси, чем у второго, поэтому и момент инерции этого цилиндра должен быть больше, чем у сплошного. Именно такое соотношение моментов инерции и обеспечивает знак «+». С другой стороны, в пределе при стремлении r1 к r2 формула для полого толстостенного цилиндра должна приобрести тот же вид, что и формула для полого тонкостенного цилиндра. Очевидно, что такой переход происходит только при использовании формулы со знаком «+».

Примечания[править | править код]

  1. ↑ 1 2 3 Тарг С. М. Момент инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 206—207. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
  2. ↑ Planetary Fact Sheet. Дата обращения: 31 августа 2010. Архивировано 14 марта 2016 года.
  3. ↑ Showman, Adam P.; Malhotra, Renu. The Galilean Satellites (англ.) // Science. — 1999. — Vol. 286, no. 5437. — P. 77—84. — doi:10.1126/science.286.5437.77. — PMID 10506564.
  4. ↑ Margot, Jean-Luc; et al. Mercury’s moment of inertia from spin and gravity data (англ.) // Journal of Geophysical Research  (англ.) (рус. : journal. — 2012. — Vol. 117. — doi:10.1029/2012JE004161.
  5. ↑ Галкин И.Н. Внеземная сейсмология. — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X.
  6. ↑ Пантелеев В. Л. Физика Земли и планет. Гл. 3.4 — Гравитационное поле планеты. Дата обращения: 31 августа 2010. Архивировано 3 октября 2013 года.
  7. ↑ 1 2 3 Тарг С. М. Краткий курс теоретической механики. — М.: «Высшая школа», 1995. — С. 269—271. — 416 с. — ISBN 5-06-003117-9.
  8. ↑ 1 2 Бухгольц Н. Н. Основной курс теоретической механики. — 4-е изд. — М.: «Наука», 1966. — Т. 2. — С. 131.
  9. ↑ 1 2 3 Яблонский А. А. Динамика // Курс теоретической механики. — 3-е изд. — М.: «Высшая школа», 1966. — Т. II. — С. 102—103. — 411 с.

Литература[править | править код]

  • Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
  • Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
  • Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Архивная копия от 7 января 2014 на Wayback Machine Издательство Физического факультета МГУ, 1997.
  • Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
  • Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
  • Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с.
  • Беляев Н. М. Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.

Ссылки[править | править код]

  • Определение момента инерции тел простой формы.
Источник

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

Масса - мера инертности тела

 

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

физика инерция формулы

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

определение момента инерции

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

момент инерции для чайников

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Формулы для момента инерции

 

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Решение:

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

определение момента инерции тела

Массу кольца можно представить в виде:

инерция тела физика

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

момент инерции формула физика

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Решение:

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Пример решения задачи на нахождение момента инерции

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Иван

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник
фото из интернета
фото из интернета

В нашем обиходе довольно часто встречаются выражения « он совершенно инертный» или «его инертность заставляет задуматься». Их применяют в отношении человека, который не обладает инициативой и не привык двигаться. Существуют другие понятия такого лица, но думаю, что они больше относятся к медицине. В общем понимании это человек не любящий принимать собственных решений. Или возьмем пример из цирка, где силач под аплодисменты зрителей выдерживает валун огромной массы. Данный объект лежит совершенно спокойно и не совершает никаких движений. Напарник бьет по камню и атлету совершенно не больно. Вся причина кроется в том, что объект инертен по отношению к цирковому артисту. Если бы на месте огромного валуна был маленький камушек, был бы тот же эффект.

Также можем применить пример из жизни, когда пешеход стоит на проезжей части и наблюдает за несущимся автомобильным потоком. Тяжелогруженная машина, если решила совершить остановку начинает тормозить раньше, чем легковая и совершает движение по инерции под влиянием груза. Естественно, что грузовик продвинется гораздо дальше по сравнению с легковушкой.

Момент инерции простыми словами: определение, формулы, примеры решения задач

Что такое инерция

В научном понимании это свойство тел находится в состоянии покоя, при этом внешние силы никакого воздействия не осуществляют. Понятие момента инерции вызывает определенный вопрос. Не каждому обывателю понятно это выражение, поэтому разберем его подробнее. Инерция, это свойство отдельного тела, лежать в спокойном состоянии при отсутствии на него внешних действий различной силы. Также объект может воспрепятствовать изменчивости скоростных показателей. Из жизни мы можем привести такой пример, когда машина находится на льду и начинает тормозить, то она не сразу останавливается, а совершает поступательное движение благодаря льду. Весь тормозной путь будет считаться инерцией. Или размешивая чай в стакане после того, как перестанем мешать, жидкость продолжает совершать вращательное движение. Это будет считаться инерцией.

Определение момента инерции

Еще со школьной скамьи нам было известно, что масса, это масса инертности тела. Если к примеру, мы совершим толчок двух вагонов у которых разный вес, то совершенно понятно, что остановить труднее будет тот вагон, у которого масса тяжелее. Одним словом, чем больше вес, тем нужно большее усилие для совершения движения. В данной ситуации мы рассматриваем поступательное движение, когда вагон совершает движение прямо.

Понятие момента инерции, включает в себя меру инертности тела при вращении вокруг своей оси. Момент инертности является физическим значением и обозначается буквой J. Измеряемость данной величины кг умноженный на метр в квадрате.

Высчитывают момент инертности при помощи следующей формулы.

Момент инерции простыми словами: определение, формулы, примеры решения задач

Применяется она обычно в научной физике, при вычислении момента инерции тела. Если представить объект, разбившийся на несколько кусков, то момент инерции будет равняться сумме этих кусков, умноженный на квадрат расстояния к оси вращения. Так определяют момент инерции в физике. Если брать реальность, то определение происходит в результате расчетов, произведенных по формуле Штейнера.

Теорема Штейнера

Прежде всего, нам нужно понять, отчего зависит момент инерции. Ответ достаточно прост: от веса, оси вращения, формы и габаритов объекта. Теорема Штейнера имеет важное значение и студенты часто ее используют для решения различных задач. Что же она обозначает? Она имеет следующую формулировку. Момент инерции объекта относительно оси равен сумме момента инерции тела относительно оси, которая проходит через центр параллельно оси и произведения массы тела на квадрат расстояния между осями.

Момент инерции простыми словами: определение, формулы, примеры решения задач

Немного мудреное понятие, но именно так объясняется теорема. В физике существуют разнообразные виды инерции: например, центральный или геометрический. Момент инерции является единицей измерения для тела, которое совершает вращательное движение вокруг своей оси.

Момент инерции простыми словами: определение, формулы, примеры решения задач

Пример решения задачи

Вашему вниманию представим 2 варианта. В первом случае мы попытаемся найти момент инерции, а во втором, применим знания полученные при изучении теоремы Штейнера.

Упражнение 1. Установить момент инерции диска весом М и радиусом Р. Ось вращения соответственно расположена по центру объекта.

Оптимальное решение:

Диск делится на маленькие колечки, радиус которых изменяется от 0 до Р. Разберем более подробно отдельное кольцо. Обозначим, что его вес равен значение м, а радиус показателю р. Тогда получим момент инерции равный: DJ= DMR в квадрате.

Момент инерции простыми словами: определение, формулы, примеры решения задач

Массу кольца можно представить в виде:

Момент инерции простыми словами: определение, формулы, примеры решения задач
Момент инерции простыми словами: определение, формулы, примеры решения задач

Упражнение 2. Установить момент инерции диска с массой М и радиусом Р.

Оптимальное решение:

Момент инерции простыми словами: определение, формулы, примеры решения задач

Используя формулу Штейнера решаем упражнение, J = Jc+ мd в квадрате. Подставляем полученные данные в формулу и получаем решение.

Момент инерции неотъемлемо имеет связь с другими популярными физическими законами. Например, со вторым законом Ньютона. В данном случае момент инерции принимает значение массы.

Остались вопросы или нужна помощь, есть замечания по данной статье пишите в комментариях будем рады подискутировать, так же подписывайтесь на наш канал или другие соц сети:

ПОДПИСАТЬСЯ НА КАНАЛ I Сайт Антиплагиату НЕТ I ВКОНТАКТЕ

Источник

Момент
инерции —
скалярная
физическая величина, характеризующая
распределение масс в теле, равная сумме
произведений элементарных масс на
квадрат их расстояний до базового
множества (точки, прямой или плоскости).

Единица
измерения СИ: кг·м².

Обозначение:
I
или J.

Для
расчета моментов
инерции
тонкого диска
массы m
и радиуса R
выберем систему координат так, чтобы
ее оси совпадали с главными центральными
осями (рис.32). Определим момент инерции
тонкого однородного диска относительно
оси z
, перпендикулярной к плоскости диска.
Рассмотрим бесконечно тонкое кольцо с
внутренним

радиусом
r
и наружным r+dr.
Площадь такого кольца ds=2r
$pi$ dr, а его
масса
,
гдеS= $pi$ R2
– площадь всего диска. Момент инерции
тонкого кольца найдется по формуле
dJ=dmr2.
Момент инерции всего диска определяется
интегралом

Вычисление
момента
инерции тонкого стержня:

Пусть
тонкий стержень имеет длину l
и массу m.
Разделим его на малые элементы длины
dx
(рис.27), масса которых
.
Если выбранный элемент находится на
расстоянии x от оси, то его момент инерции,
т.е.    
Интегрируя
последнее соотношение в пределах от 0
до l/2
и удваивая полученное выражение (для
учета левой половины стержня), получим

Момент
инеpции обручаотносительно оси,
пpоходящей чеpез центp кольца пеpпендикуляpно
к его плоскости. В этом случае все
элементаpные массы обруча удалены от
оси на одинаковое pасстояние, поэтому
в сумме (3.18) r2 можно вынести за знак
суммы, т. е.    

Теорема
Штейнера:

В
общем случае вращения тела произвольной
формы вокруг произвольной оси, вычисление
момента инерции может быть произведено
с помощью теоремы Штейнера: момент
инерции относительно произвольной оси
равен сумме момента инерции J0 относительно
оси, параллельной данной и проходящей
через центр инерции тела, и произведения
массы тела на квадрат расстояния между
осями: J=J0+ma^2.

Например,
момент инерции диска относительно оси
О’ в соответствии с теоремой Штейнера:

17. Момент инерции однородного тела вращения. Моменты инерции конуса, шара.

Линия
– ось вращения.

– масса на квадрат радиуса окружности,
по которой движется материальная точка.

Все
тело мысленно разбиваем на маленькие
объемы. Масса этого кусочка
.

Твердое
тело представляется как совокупность
системы точечных масс.

– расстояние, на котором находится точка
от оси вращения.

– общий алгоритм определения собственного
момента инерции твердого тела, относительно
оси проходящей через центр инерции
данного тела.

Момент
инерции шара.

    
Сплошной шар массы
m
и радиуса R
можно рассматривать как совокупность
бесконечно тонких сферических слоев с
массами dm
, радиусом r,
толщиной dr
(рис.35).

    
Рассмотрим
малый элемент сферического слоя $delta$
m с координатами
x, y, z.
Его моменты инерции относительно осей
проходящих через центр слоя – $delta$
Jx,
$delta$ Jy,
$delta$ Jz,
равны

Т.
е. можно записать
    (п.26)

    
Так как для
элементов сферического слоя x2+y2+z2=r2
то

    
После
интегрирования по всему объему слоя
получим
    (п.27)

    
Так как, в силу
симметрии для сферического слоя
dJx=dJy=dJz=dJ
, а
,
тоИнтегрируя по всему объему шара,
получаем
    
Окончательно
(после интегрирования) получим, что
момент инерции шара относительно оси,
проходящей через его центр равен

Разобьём
КОНУС
на цилиндрические слои  
ось
толщиной dr.
Масса такого слоя 
 dm
= r2dr,

где
ρ – плотность
материала, из которого изготовлен конус.
Момент инерции этого слоя
dI = dm.r2.

Момент
инерции всего конуса  
складывается
из моментов инерции всех слоёв: 

 I
=
=

ρπ
r
4
dr
=
ρR5.

Остаётся выразить
его через массу всего цилиндра:
m
=
=

=

R3,

отсюда    ρ
=
,
I
=
 =

mR2.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Когда тело продолжает двигаться при отсутствии на него воздействия каких-либо сил, говорят о проявлении инерции. Именно ею объясняются трудности удержаться на ногах при резком торможении автобуса или усидеть в седле велосипеда, когда под колеса резко выбегает кот. Кроме инерции, проявляющейся при движении тел по прямой, аналогичное явление бывает при вращении вокруг оси. В таком случае в физике говорят о моменте инерции – скалярной величине, измеряющей инертность тела при осевом вращении.

Момент инерции и его физический смысл

Обеспечить поступательное движение предмета при его толкании будет тем тяжелее, чем больше он весит. Аналогичные эксперименты предусматривались школьной программой и относились к прямо направленному действию.

Момент инерции

Источник: encrypted-tbn0.gstatic.com

Было понятно, что именно масса тела характеризует  степень его инертности и является ее мерой.

При совершении предметом вращательных движений наблюдается иной вид зависимости. В данном случае мерой инертности выступает момент инерции.

Момент инерции – скалярная измеряемая характеристика инертности тела в момент совершения осевого вращения.

Задачи по определению величины момента инерции решаются с помощью теоремы Гюйгенса-Штейнера, смысл которой заключается в следующем:

МИ для тела, вращающегося вокруг какой-либо оси, равна сумме слагаемых единиц: момент инерции предмета, который вращается вокруг оси, параллельной данной, и проходящей через центр масс, а также произведения массы на расстояние между осями, возведенное в квадрат.

Теорма Штейнера

Источник: theslide.ru

В приведенной формуле используются следующие обозначения: d – расстояние между осями, m – масса тела, Iz – момент инерции относительно рассматриваемой оси, а Ic – относительно оси, которая проходит через центр масс. В профильной литературе и учебниках буква I может заменяться J.

Формулировка способа количественного измерения момента инерции при осевом вращении предмета стала возможной в результате работы двух ученых-математиков: Гюйгенса и Штейнера. Теорема дает возможность быстрого решения задач на определение инерции предмета любой формы, для которого уже просчитана центробежная сила. Формула Штейнера позволяет вычислить момент инерции этого предмета относительно выбранной оси, проходящей параллельно прямой, следующей через центр фигуры.

Единицы измерения в системе СИ

Единицей измерения момента инерции, принятой в системе СИ, является кг, умноженный на метр в квадрате – кг·м². В еще одной системе измерения (СГС) единицей измерения является грамм на квадратный сантиметр – г·см².

Как рассчитать момент инерции, формула

Измерение значения момента инерции можно произвести теоретически, согласно формуле. Для этого условно движущийся предмет разбивается на мелкие составляющие, масса которых обозначается  dm. В конечном итоге момент инерции (МИ) равняется сумме произведений всех образовавшихся масс на расстояние до оси, возведенное в квадрат.

Формула

Источник: works.doklad.ru

Исходя из этой формулы, момент инерции, кроме массы тела, определяется положением оси, вокруг которой предмет вращается, а также его формой и габаритами.

Возможность рассчитать моменты инерции полезна, к примеру, при исследованиях свойств и структуры элементов Солнечной системы. Это так называемый безразмерный момент инерции. Высчитанная по формуле величина дает представление о распределении массы по глубине.

Виды моментов инерции

Кроме безразмерного момента инерции, в физике существуют понятия:

  • центробежный МИ;
  • главный МИ;
  • геометрический МИ;
  • МИ относительно плоскости;
  • центральный МИ;
  • тензор инерции;
  • эллипсоид инерции.

Центробежными МИ относительно прямоугольных осей координат (декартовой системы) считаются Jxy, Jxz, Jyz. Ось ОХ является главной, когда центробежные моменты инерций Jxy и Jxz равняются нулям.

Любая точка тела может являться центром трех главных осей инерции. Они характеризуются взаимной перпендикулярностью. МИ относительно них считается главным для данного предмета. Главные оси, которые пролегают через центр масс, – являются главными центральными осями инерции предмета. МИ относительно них – главные центральные МИ. Для однородного тела ось симметрии всегда является главной центральной осью инерции.

Для геометрических МИ существуют формулы, основывающиеся на объеме относительно оси и площади относительно оси.

Твердое тело может иметь МИ относительно плоскости. Тогда это – скалярная величина, которая рассчитывается суммированием произведений массы каждой точки предмета и расстояния от нее до плоскости, возведенного в квадрат.

Понятие «Центрального МИ» связано с точкой О, МИ относительно полюса либо полярным МИ.

Момент инерции тела относительно оси вращения

МИ служит единицей измерения инерции тела, которое вращается вокруг оси, подобно тому, как масса является мерой при поступательном движении.

Определить МИ предметов касательно оси вращения позволяет формула Штейнера.

Пример:

Наглядное подтверждение применения формулы Штейнера – расчет МИ стержня, ось вращения которого проходит через конец.

Формула 2

 

Моменты инерции простейших объектов

Момент инерции некоторых однородных тел, имеющих простую форму, в зависимости от характеристик осей вращения можно определить по следующим формулам:

  1. МИ точечного предмета либо полого цилиндра с тонкими стенками (с массой m и радиусом r) = mr2
  2. МИ диска или сплошного цилиндра = 1/2 mr2
  3. МИ цилиндра с толстыми стенками, у которого внешний радиус обозначен r2, а внутренний – r1, :

    Формула 3

     
    В указанных случаях ось вращения является осью цилиндра.
  4. МИ сплошного цилиндра с осью вращения, перпендикулярной образующей цилиндра, расположенной по центру масс:

    Формула 4

     
  5.  МИ полого цилиндра с тонкими стенками и осью, перпендикулярной к цилиндру и проходящей через центр масс:

    Формула 5

     
  6. МИ прямого тонкого стержня с осью, перпендикулярной к нему и проходящей через центр масс:

    Формула 6

     
  7. МИ сферы с тонкими стенками и осью по центру = 2/3 mr2
  8. МИ шара с осью по центру = 2/5 mr2
  9. МИ равнобедренного треугольника с осью, перпендикулярной его плоскости и проходящей через вершину:

    Формула 9

     

Примеры решения задач

Применение на практике приведенных формул происходит, например, для решения следующих задач.

Пример №1

Задано найти МИ однородного диска с известными массой и радиусом. Из дополнительных сведений: ось вращения – через центр диска.

Для решения диск разбивается на тонкие кольца, радиусы которых равняются от 0 до R. Взяв одно из них и обозначив его радиус буквой (r), а массу – (dm), формула для расчета МИ  (согласно теореме Гюйгенса-Штейнера) выглядит следующим образом: (dJ=dmr2.)

С учетом подстановки в конечную формулу для определения МИ формулы для массы кольца получаем:

Задача1

 

Пример № 2

Задано найти у того же диска МИ относительно оси, которая проходит через середину радиуса.

Из предшествующего задания используем найденную величину МИ относительно оси, которая проходит через центр масс. Используя формулу Штейнера, решаем задачу.

Задача 2

 

Если решать аналогичные задачи нет желания или времени, а контрольную работу нужно сдать в срок, на помощь придут сотрудники Феникс.Хелп. 

Источник

Добавить комментарий