Как найти момент инерции для уголка

Центробежный момент инерции уголка

мм⁴

Центробежный
момент инерции всего сечения относительно
осей Z_cY_c:

I_yczc=(300669+(-10)∙(-99)∙1390)+(0+102∙(-35)∙2340)+(0+(-56)∙55∙4000)

I_yczc=
19761573
мм⁴

Для
проверки правильности выбора знака
угла 
следует разбить уголок на два прямоугольника
(рис.3) пересчитать и сравнить их
расхождение в центробежном моменте
инерции. Если расхождение велико это
означает, что угол выбран не с тем знаком.

рис.3

Центробежный
момент для всего сечения с уголком,
разделенным на два простых прямоугольника
равен:

F_1x=560
мм²
– площадь поперечного сечения

F_1xx=880
мм²
– площадь поперечного сечения

a_1x=8.4
мм – координата от оси Z_c1x
до Z_с

b_1x=-131
мм – координата от оси Y_c1x
до Y_с

a_1xx=-76
мм – координата от оси Z_c1xx
до Z_с

b_1xx=-22.5
мм – координата от оси Y_c1xx
до Y_с

I_yczc=(I_yc1zc1+((a_1x∙
b_1x∙F_1x)+(a_1xx∙
b_1xx∙F_1xx)))+(I_yc2zc2+a₂∙
b₂∙F₂)+(
I_yc3zc3+a₃∙
b₃∙F₃)

I_yczc=(0+((8.4)∙(-131)∙560)+((-76)∙(-22.5)∙880))+(0+102∙(-35)∙2340)+(0+(-56)∙55∙4000)

I_yczc=19785224
мм⁴

Как видно из расчетов центробежные
моменты инерции вычисленные разными
способами расходятся в значениях не
более чем на 0.12%. Это означает, что знак
угла α выбран правильно.

3. Нахождение положения главных осей и моментов инерции:

Угол
наклона главных осей инерции, проходящих
через центр тяжести составного сечения,
к центральным осям инерции Z_cY_cопределим по формуле:

Так
как угол >0, то
откладываем его по осиZпротив
движения часовой стрелки.

Определение
величин главных моментов инерции I_uи I_vсечения:

Верхние знаки следует брать при I_zc
> I_yc , а нижниеI_zc < I_yc

=69204276мм⁴

=29060227 мм⁴

Проверка

I_U + I_V = I_zc
+ I_yc 
69204276+29060227 = 52648839+4561566498264503=98264503

Главная
центральная ось Uполучается на
чертеже поворотом осиZ_cпротив часовой стрелки, так как>0
и осьUбудет являться осью относительно
которой момент инерции будет максимальным.

Раздел II

ЦЕНТРАЛЬНОЕ
РАСТЯЖЕНИЕ (СЖАТИЕ ) СТЕРЖНЕЙ .

СТАТИЧЕСКИ
НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ.

Основные понятия и зависимости.

Центральным
растяжением (сжатием)
называется такой вид деформации, при
котором в поперечных сечениях стержня
возникает только нормальная (продольная)
сила N
остальные силовые факторы равны нулю.
В дальнейшем центральное растяжение
(сжатие) коротко называется просто
растяжением (сжатием). Нормальная
(продольная) сила
в поперечном сечении представляет собой
равнодействующую нормальных внутренних
сил распределенных по площади поперечного
сечения и связана с нормальными
напряжениямив этом сечении зависимостью:.
Принято считатьположительной
нормальную силу, вызывающую растяжение,
отрицательной нормальную силу, вызывающую
сжатие.
Нормальные силы в поперечных сечениях
определяют методом сечений. Считается
что при растяжении (сжатии) справедлива
гипотеза плоских сечений (гипотеза
Бернулли) следовательно, нормальные
напряжения в поперечных сечениях стержня
распределены равномерно и
,
где–
площадь поперечного сечения. Положительным
считается растягивающее нормальное
напряжение. Согласно гипотезе плоских
сечений материал стержня при растяжении
(сжатии) находится в линейном напряженном
состоянии. На основании закона Гука
относительное удлинение бесконечно
малого участка стержня:,
где модуль продольной упругости
материала (модуль Юнга). Полное удлинение
стержня в общем случае, когда нормальная
сила и площадь поперечного сечения
меняются по длине: ,
где –
длина стержня. В частном случае, когда
нормальная сила и площадь по длине
постоянны: .
Для ступенчатого стержня полное
удлинение вычисляется как сумма удлинений
его участков: ,
где
соответственно длина, площадь поперечного
сечения, нормальная сила на i
– том участке.

Растяжение
(сжатие) сопровождается изменением
поперечных размеров стержня. Между
относительной поперечной –
и относительной продольной –
деформациями при растяжении (сжатии)
существует связь ,
где
– коэффициент Пуассона (коэффициент
поперечной деформации) является
константой материала. Знак «-» в уравнении
отражает тот факт, что
и
всегда имеют противоположные знаки.

Условия
прочности
для стержней работающих на растяжение
сжатие записываются для опасных сечений
стержня, в которых действуют наибольшие
по величине растягивающие и сжимающие
напряжения. В случае, когда материал
стержня имеет одинаковую прочность на
растяжение и сжатие достаточно одного
условия прочности
,
где допускаемое напряжение для материала
стержня. Если материал стержня имеет
разную прочность при растяжении и сжатии
необходимо выполнение одновременно
двух условий прочности:,,
где,–
допускаемые напряжения для материала
стержня соответственно на растяжение
и сжатие.

Статически
неопределимыми системами
называются такие системы, в которых
количество неизвестных сил (реакций,
внутренних силовых факторов) превышает
число уравнений равновесия. Степенью
статической неопределимости n
называется разность между r
– количеством неизвестных и u
– числом уравнений статики: .
В статически неопределимых задачах не
удается определить силовые факторы из
условий равновесия и прежде чем решать
задачи прочности и жесткости необходимо
раскрыть статическую неопределимость.
Общий принцип
раскрытия статической неопределимости
заключается в том, что в дополнении к
имеющимся уравнениям равновесия всегда
можно составить n
условий совместности деформаций
(совместности перемещений). Условия
совместности деформаций (перемещений)
связывают между собой деформации
отдельных элементов системы или
перемещения ее точек. Затем в условиях
совместности деформации (или перемещения)
выражаются через внутренние усилия,
которые в свою очередь могут быть
выражены методом сечений через внешние
силы. После решения условий совместности
вместе с уравнениями равновесия
относительно неизвестных усилий,
статическая неопределимость будет
раскрыта.

Для
реальных стержней на основании принципа
Сен-Венана гипотеза плоских сечений
справедлива лишь вдали от мест приложения
внешних сосредоточенных нагрузок и
мест изменения размеров и формы
поперечного сечения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Расчет моментов инерции онлайн

При выполнении расчетов часто приходится вычислять моменты инерции сложных сечений относительно различных осей, лежащих в плоскости фигуры. Для стандартных поперечных сечений стержней моменты инерции даны в таблицах ГОСТ 8509-93, ГОСТ 8510-86, ГОСТ 57837-2017, ГОСТ 8240-97. В остальных случаях, для выполнения онлайн расчета момента инерции круга, кольца, треугольника, прямоугольного контура, нестандартных сварных швеллера, уголка и двутавра можно воспользоваться данной страницей нашего сайта.

Момент инерции треугольника

МОМЕНТ ИНЕРЦИИ ТРЕУГОЛЬНИКА

Момент инерции Ix₀, м 4

Момент инерции Ix₁, м 4

Момент инерции Ix₂, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Момент инерции треугольника относительно центральной оси, параллельной одной из его сторон вычисляется по формуле:
I_x0 = b×h 3 / 36;
Момент инерции треугольника относительно оси, совпадающей с одной из его сторон:
I_x1 = b×h 3 / 12;
Момент инерции треугольника относительно оси, параллельной одной из его сторон и проходящей через противоположную вершину:
I_x2 = b×h 3 / 4.

Момент инерции кольца

МОМЕНТ ИНЕРЦИИ КОЛЬЦА

Момент инерции Ix, м 4

Полярный момент инерции Ip, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Момент инерции кольца относительно главной центральной оси:
I_x = π×D 4 /64 – π×d 4 /64;
Полярный момент инерции кольца:
I_p = π×D 4 /32 – π×d 4 /32.

Момент инерции прямоугольника

МОМЕНТ ИНЕРЦИИ ПРЯМОУГОЛЬНИКА

Момент инерции Ix, м 4

Момент инерции Iy, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Момент инерции прямоугольника относительно главных центральных осей:
I_x = (b×h 3 – b1×h1 3 )/12;
I_y = (h×b 3 – h1×b1 3 )/12.

Момент инерции двутавра

МОМЕНТ ИНЕРЦИИ ДВУТАВРА

Толщина полки t, мм

Толщина стенки s, мм

Момент инерции Ix, м 4

Момент инерции Iy, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Моменты инерции двутавра относительно главных центральных осей:
I_x = (B×H 3 – (B – s)×(H – 2t) 3 ) / 12;
I_y = (2t×B 3 + (H – 2t)×s 3 ) / 12.

Момент инерции уголка

МОМЕНТ ИНЕРЦИИ УГОЛКА

Момент инерции Ix, м 4

Момент инерции Iy, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Моменты инерции уголка относительно центральных осей:
I_x = (d×(H – y) 3 + B×y 3 – (B – d)×(y – d) 3 ) / 3;
I_y = (d×(B – x) 3 + H×x 3 – (H – d)×(x – d) 3 ) / 3,
где x и y – расстояния от наружных сторон уголка до центральных осей Y и X соответственно.

Момент инерции швеллера

МОМЕНТ ИНЕРЦИИ ШВЕЛЛЕРА

Толщина полки d, мм

Толщина стенки s, мм

Момент инерции Ix, м 4

Момент инерции Iy, м 4

Площадь сечения F, м 2

©Copyright Кайтек 2020

Моменты инерции швеллера относительно главных центральных осей:
I_x = (B×H 3 – (B – s)×(H-2d) 3 ) / 12;
I_y = (H×x 3 – (H – 2d)×(x – s) 3 + d×(B – x) 3 )/3,
где x – расстояния от наружной сторон швеллера до центральной оси Y.

Расчеты моментов инерции по умолчанию выполнены относительно центральных и главных центральных осей сечения. Моменты инерции относительно осей, параллельных главным центральным осям можно вычислить, прибавив к полученному результату произведение квадрата расстояния между соответствующими осями на площадь сечения.

Момент инерции сечения

Меня часто спрашивают: «…а что такое моменты инерции в сопротивлении материалов и зачем они вообще?» Об этом в сегодняшней теме

Моменты инерции сечения из простых фигур

Начнем с моментов инерции простых фигур и на их примере выясним для сложных фигур и составных сечений из стандартных профилей.

Начать объяснение о том, что такое моменты инерции нужно с того, что спросить, а что такое площадь?

Обычная площадь квартиры, огорода сечения стержня? Зачем она и почему?

Так вот площадь это характеристика которую придумали и вывели для разных фигур, чтобы была возможность сравнивать земельные наделы. Не всегда они были прямоугольные или квадратные. А сравнить кто сколько получил в надел было нужно. Вот и вывели такую закономерность для прямоугольника, что если перемножить стороны — получим величину, которую можно будет сравнить с перемноженной высотой на основание деленное пополам для треугольника или для круга Пи умножить на эр в квадрате )). Т.е. площади простых фигур

Что касается моментов инерции в сопротивлении материалов, то тут они появились, когда стало понятно, что есть какая то геометрически измеримая величина для разных форм сечения, которая позволит сравнить сопротивляемость этих сечений изгибу.

Проще говоря бревно, которое выполняет роль балки и изгибается может иметь форму прямоугольника, квадрата или круга, а нам нужно сравнить их сопротивляемость изгибу. Вот для этих целей выводили формулу напряжений и оказалось, что в числителе оказался изгибающий момент, а в знаменателе момент инерции:

на балке изображены главные центральные оси z y

прогибы для таких балок будут разными относительно осей z и y, т.к. моменты инерции будут разные.

Вывод моментов инерции для простых фигур

Так вот ниже я приведу видео уроки, плейлист, в котором один за одним выведены моменты инерции для простых фигур, а именно для прямоугольника, треугольника и круга. А затем приводится стандартный расчет моментов инерции для более сложной фигуры, которая состоит из нескольких простых. Всегда сложную фигуру можно разбить на несколько простых. Исходя из этого расчет и ведется.

Моменты инерции измеряются в единицах длины в 4 степени, т.е. см⁴ или м⁴. Чаще всего используется см⁴, т.к. такие единицы измерения приведены в сортаменте прокатной стали.

Момент инерции, это величина, которая показывает сопротивляемость сечения изгибу. На примере линейки хорошо понятно что изгиб в одной плоскости и изгиб в другой плоскости будут сильно отличаться, хотя площадь сечения не меняется. Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.

Центральными осями называют оси, которые проходят через центр тяжести сечения

Главные оси располагаются в сечении таким образом, что центробежный момент относительно них равен нулю. Т.е. это максимальный и минимальный осевые моменты инерции

Оси, которые проходят через центр тяжести сечения и центробежный момент инерции относительно них равен нулю. При этом данные осевые моменты инерции являются экстремальными, т.е. имеют максимальное и минимальное значение. Именно относительно этих осей ведут расчет и к ним приводят нагрузки. Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.

При вычислении моментов инерции осевых, при переходе от одних осей к другим появляется центробежный момент инерции, как составляющая пары осевых моментов инерции. И только для главных осей центробежные моменты инерции равны нулю. Именно эти оси мы и отыскиваем в наших расчетах. Поэтому мы ищем величину центробежного момента инерции для не главных осей и из свойства, что главные центральные оси это такие оси, относительно которых центробежный момент инерции равен нулю, находим положение главных центральных осей.

Моменты инерции для прямоугольника

#Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.

Сопротивление материалов и Моменты инерции для прямоугольника. Понятие моментов инерции, формулы и вывод для прямоугольника. Осевые центробежный моменты инерции. для треугольника вывод моментов инерции в этом видео: https://www.youtube.com/embed/_pixohVoc-4?vq=hd720 Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2018-04-09

моменты инерции для прямоугольника для главных центральных осей равны, формула

моменты инерции для прямоугольника для осей проходящих через основные размеры равны, формула

Моменты инерции для треугольника

Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции

Сопротивление материалов и Моменты инерции для треугольника. Сопромат вывод моментов инерции для простых фигур. Моменты инерции для треугольника. Моменты инерции для осей в треугольнике, которые проходят через основные размеры. Вывод и пояснение к этой теме сопротивления материалов. для прямоугольника вывод моментов инерции в этом видео: https://www.youtube.com/watch?v=v1TE1UW_sRE&feature=youtu.be‎ Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2018-04-09

Моменты инерции треугольника относительно произвольых осей

Момент инерции круга. Моменты инерции простых фигур. #сопромат

Вывод моментов инерции для круга. Видео урок из темы «Моменты инерции простых фигур». В видео приведен вывод момента инерции полярного, в полярной системе координат Ip Затем выведены моменты инерции осевые Iz, Iy. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2019-09-14

Моменты инерции. Оси центральные и главные. Что это и где. #сопромат

Центральные оси — любая пара взаимно перпендикулярных осей, которые проходят через центр тяжести фигуры Главные оси — оси для которых центробежный момент инерции равен нулю, а осевые моменты имеют максимум и минимум. Об этом и многом другом в видео уроке по моментам инерции в сопротивлении материалов Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2019-09-14

Примеры расчетов моментов инерции для сечений

Ниже приводятся примеры расчетов моментов инерции относительно главных центральных осей, объяснение, что такое центробежный момент инерции и почему оси называются главными центральными для примеров:

• простейшие фигуры — прямоугольник, треугольник
• составные сечения из простейших треугольника и прямоугольника
• составные из прокатных профилей

Пример расчета моментов инерции относительно главных центральных осей для простейших фигур

Подробно объясняется как найти центробежный момент инерции, как найти осевые моменты инерции, как относительно центральных и как относительно главных осей для простых фигур.

Пример расчета моментов инерции для сечения состоящего из прямоугольника и треугольника

Сечения балок может быть составным, т.е. таким, которое складывается из нескольких фигур. В примере, в видеоуроке ниже рассказыватся как найти моменты инерции относительно главных центральных осей для такого сечения балки

Расчет моментов инерции сечения составного из стандартных прокатных профилей

В видеоуроке ниже разбирается порядок расчета моментов инерции относительно главных центральных осей для сечения составленого из трех прокатных профилей уголков

Моменты инерции простых сечений

Моменты инерции относительно осей Оx, Оx₁, Оy, Оy₁:

.

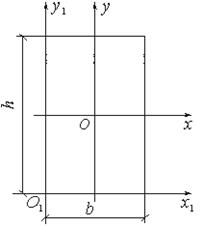
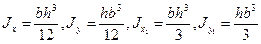
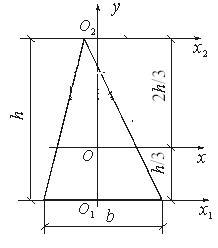
моменты инерции относительно осей Оx, О₁x₁ и О₂x₂,:

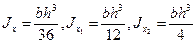
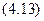
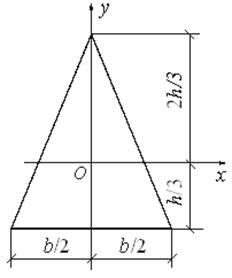
Прямоугольный и равнобедренный треугольники.

Для прямоугольного треугольника определим центробежный момент инерции J_xy относительно центральных осей Ox и Oy, параллельных катетам:

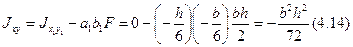
Момент инерции равнобедренного треугольника относительно оси

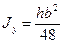
Круг. Полярный момент инерции круга:

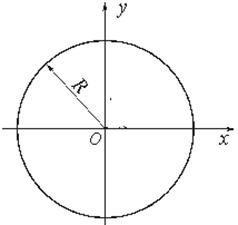
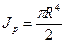
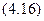
Учитывая, что для круга J_x = J_y и полярный момент согласно равен сумме двух осевых моментов, получим:

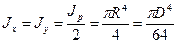
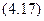
Кольцевое сечение. Моменты инерции кольца находятся как разность моментов инерции двух кругов с радиусами R₂ и R₁ :

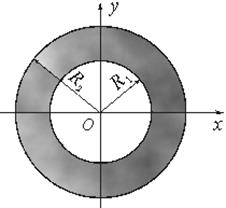
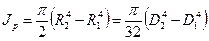
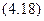
Относительно осей O₁x₁ и O₁y₁, которые являются главными осями для полукруга, осевые моменты инерции равны половине момента инерции круга:

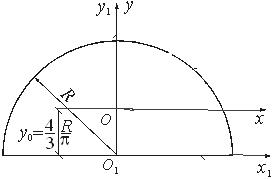
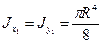
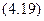
Момент инерции относительно главной центральной оси определяется с помощью первой формулы:

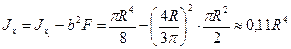
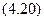
Геометрические характеристики сечений прокатных профилей (двутавры, швеллеры, уголки) приведены в таблицах сортамента прокатной стали.

Моменты инерции составных сечений. При определении моментов инерции составного сечения последнее разбивают на простые фигуры, у которых известны положения центров тяжести и моменты инерции относительно собственных центральных осей. По формулам (4.6) находят координаты центра тяжести всего сечения в системе произвольно выбранных вспомогательных осей. Параллельно этим осям проводят центральные оси, относительно которых определяют осевые и центробежный моменты инерции по формулам (4.7). Моменты инерции относительно главных центральных осей определяются по формуле (4.11), а положение главных центральных осей – по формулам (4.10).

Далее рассмотрены примеры задач.

5. Примеры решения задач

Пример 1. Определим положение центра тяжести и моменты инерции относительно главных центральных осей сечения, состоящего из полукруга и прямоугольника с вырезом. Размеры сечения на рисунке даны в сантиметрах.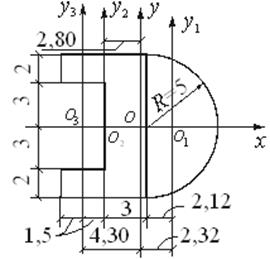

Разобьем сечение на три простые фигуры: полукруг с радиусом R=5 см, прямоугольник с размерами сторон 6×10 см, прямоугольный вырез с размерами 3×6 см и определим площади и моменты инерции этих фигур относительно собственных центральных осей.

Для полукруга по формулам (2.21) и (2.22) имеем:

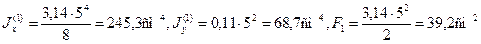
Положение центра тяжести О₁ полукруга определяется по формуле (2.20) и равно 0,424·5 = 2,12 см (рис.2.15).

Для прямоугольника и прямоугольного выреза по формулам (2.13) получим

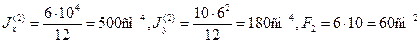
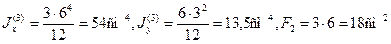
Площадь всего сечения равна F = 39,2 + 60 – 18 = 81,2 см 2 .

Центр тяжести О сечения лежит на горизонтальной оси симметрии. Для определения его положения выберем в качестве вспомогательной оси центральную ось прямоугольника O₂y₂ . Тогда получим

.

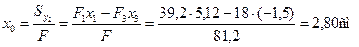Отложим эту величину от оси О₂y₂ вправо и проведем ось Оy, которая вместе с осью Ох составит пару главных центральных осей всего сечения. Определим координаты центров тяжести отдельных фигур в системе координат Оxy: а₁ = 2,32 см, а₂ = – 2,80 см, а₃ = – 4,30 см .

По формулам (2.6) найдем моменты инерции сечения относительно осей Ох и Оy:

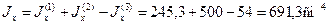
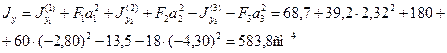
Пример 2.Для стержня несимметричного сечения, составленного из швеллера [ 30 и неравнобокого уголка L180х110х12, определим центр тяжести сечения, моменты инерции относительно главных центральных осей и положение этих осей. На рисунке размеры даны в сантиметрах.

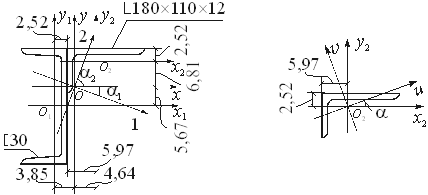
Выпишем геометрические характеристики сечения швеллера:

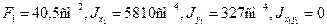
Геометрические характеристики сечения неравнобокого уголка:

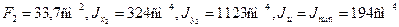
Величину центробежного момента инерции уголка 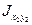(в сортаменте она не приведена) определим по второй из формул (2.11):

,

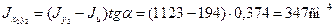где tga = 0,374 – тангенс угла наклона главной оси u к оси Ох₂ , величина которого приведена в сортаменте.

Площадь всего сечения равна F = 40,5 + 33,7 = 74,2 см 2 .

Для определения положения центра тяжести выберем в качестве вспомогательных осей оси швеллера О₁x₁ и О₁y₁. Тогда по формулам (2.5) получим

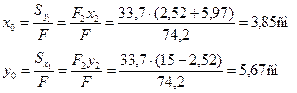
Эти величины и координаты центров тяжести швеллера и уголка в системе координат Охy показаны на рисунке и соответственно равны:

Определим по формулам (2.6) моменты инерции сечения относительно центральных осей Ох и Оy.

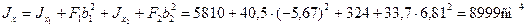
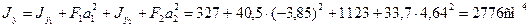
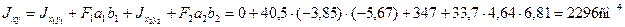
По формулам (2.12) и (2.11) найдем величины главных моментов инерции и углы наклона главных осей 1 и 2 к оси Ох :

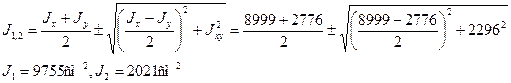
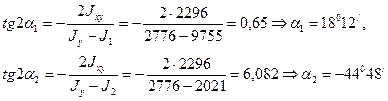
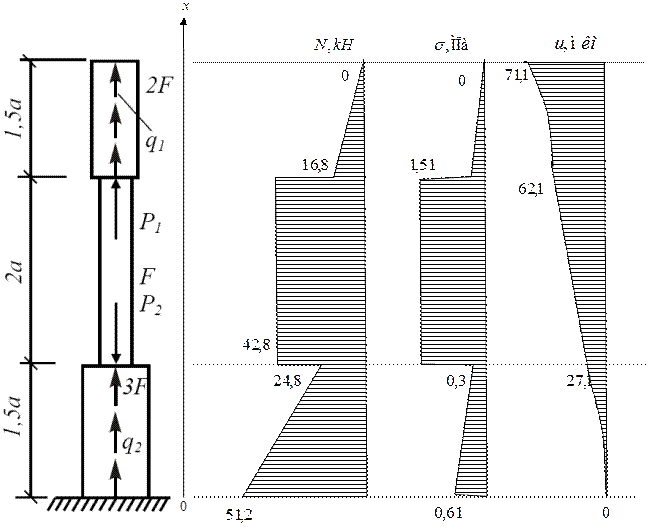
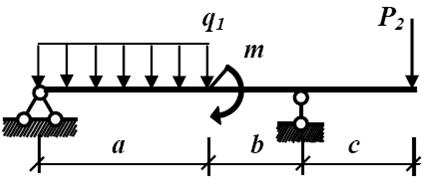
Пример 3. Для статически определимого стержня ступенчато постоянного сечения при заданных осевых нагрузках и геометрических размерах по строке требуется:

1.Определить опорную реакцию в месте закрепления стержня.

2.Вычислить значения продольных сил и нормальных напряжений в характерных сечениях и построить эпюры этих величин.

3.Найти величины абсолютных удлинений (укорочений) участков стержня и величину общего удлинения (укорочения) стержня в целом.

4.Определить значения осевых перемещений характерных сечений и построить эпюру осевых перемещений.

a, м	F, см 2	Р1, кН	Р2, кН	q1, кН/м	q2, кН/м	Е, МПа
0,8	2,0·10 5

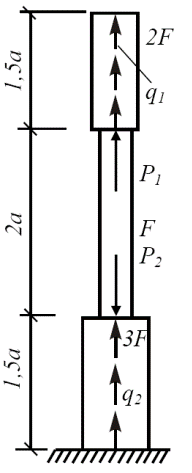
1. Составим уравнение равновесия: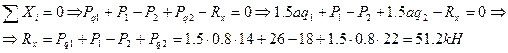

2. Вычислим значения продольных сил:

Участок 1: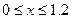

При ;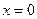

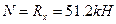
При ;

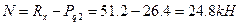
Значение продольной силы линейно уменьшается

Участок 2: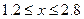

При ;

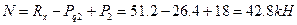
При ;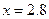

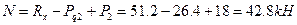
Значение продольной силы не изменяется

Участок 3: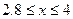

При ;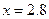

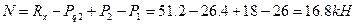
При ;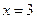

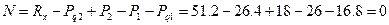
Значение продольной силы линейно уменьшается.

Найдем величины нормальных напряжений в характерных сечениях:

Участок 1: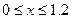

При ;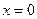

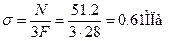
При ;

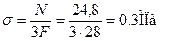
Участок 2: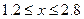

При ;

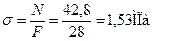
Участок 3: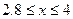

При ;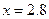

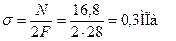
При ;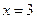

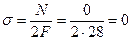
Величины абсолютных удлинений каждого их участков стержней найдем по формуле:

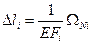, где 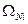– площадь под эпюрой продольных сил на каждом участке.

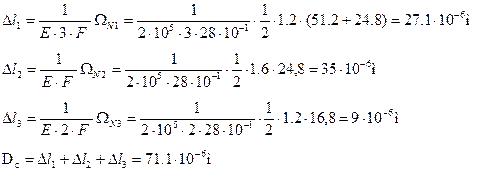
Определим величины осевых перемещений характерных сечений.

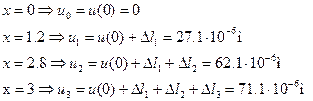
На участках 1 и 3 эпюра осевых перемещений имеет вид квадратичной параболы, на участке 2 изменяется линейно.

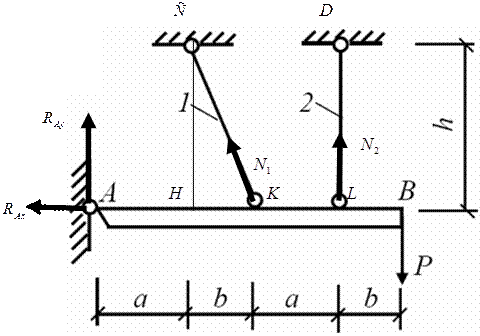
Пример 4. Для статически неопределимой стержневой системы, состоящей из абсолютно жесткой балки AB и поддерживающих ее стальных стержней 1 и 2 по схеме №…. при геометрических размерах, соотношениях площадей поперечных сечений стержней F₂/F₁ и величине нормативной нагрузки Р, указанных в строке № …. табл.2, требуется:

1.Определить расчетное значение нагрузки, приняв коэффициент надежности по нагрузке γ_f = 1,2.

2.Определить усилия в стержнях системы. Собственную массу элементов стержневой системы не учитывать.

3.Подобрать сечения стрежней в виде двух стальных прокатных равнобоких уголков, используя метод расчета по предельным состояниям. При подборе сечений обеспечить заданное соотношение площадей F₂/F₁. Расчетное сопротивление по пределу текучести стали марки ВСТ3 принять равным 210 МПа, коэффициент условий работы γ_с = 0,9.

4.Определить величины нормальных напряжений в поперечных сечениях стержней и проверить выполнение условий прочности.

5.Определить величины удлинений стержней, приняв Е=2,1·10 5 МПа.

6.Определить нагрузку Р_т, при которой в системе возникают первые пластические деформации, считая, что материал стержней следует диаграмме Прандтля и имеет предел текучести σ_т = 240 МПа.

7.Определить разрушающую нагрузку Р_разр, при которой система полностью исчерпывает свою несущую способность.

a, м	b, м	h, м	F2/F1	Р, кН
1,4	0,8	1,3	1,3

1. Определим расчетные значения нагрузки:

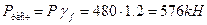
2. Определим усилия в стержнях. Система является статически неопределимой. Представим систему в деформированном виде. Рассмотрим:

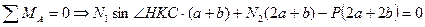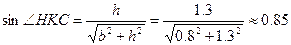
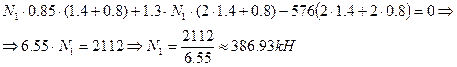
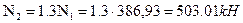
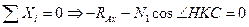, где

, где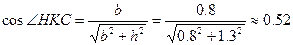

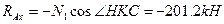
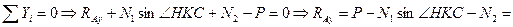-256kH

Отрицательные знаки говорят о том, что действительные направления сил противоположны указанным на чертеже.

Вычисляем напряжения в стержнях 1 и 2

,

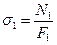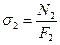
Определяем требуемые по условию прочности площади поперечных сечений

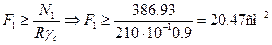
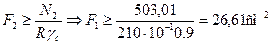
Проверим соотношение 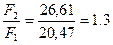, условие выполняется.

Принимаем по сортаменту сечения стержней в виде двух стальных прокатных равнобоких уголков.

Стержень 1: профиль №7, ,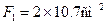

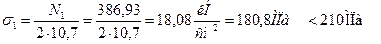
Стержень 2: профиль №10, ,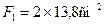

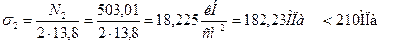
Определим удлинения стержней при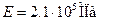

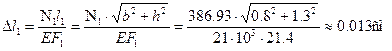
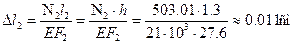
Определим нагрузку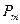

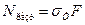, σ_т = 240 МПа

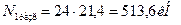
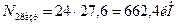
Находим из уравнения равновесия величину Р_разр:

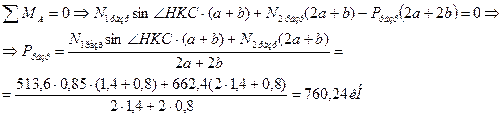
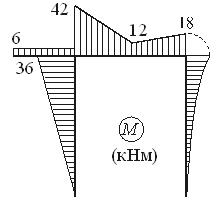
Пример 5. Для рамы с шарнирными опорами построим эпюры N,Q, и M.

Определяем величины опорных реакций.

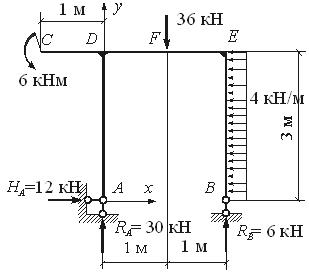
SX = 0 ,	– 4·3 + HА = 0 ,	HА = 12 кН ;
SMА = 0	6 – 36·1 + 4·3·1,5 + 2RВ = 0 ,	RВ = 6 кН ;
SMВ = 0 ,	6 + 36 + 4·3·1,5 – 2RА = 0 ,	RА = 30 кН ;
SU = 0 (проверка) ,	– 36 + 30 + 6= – 36 + 36 = 0 .

Определяем внутренние усилия в характерных сечениях каждого участка рамы.

Участок АD
Сечение А:	N = – RА = – 30 кН (сжатие),	Q = – HА= – 12 кН , M = 0
Сечение D:	N = – 30 кН , Q = – 12 кН ,	M = – 12*3 = – 36 кНм
(растянуты левые волокна).
Участок ВЕ
Сечение В:	N = – RА = – 6 кН ,	Q = 0 , M = 0 ,
Сечение E:	N = – 6 кН , Q = 4·3 = 12 кН ,	M = – 4·3·1,5 = – 18 кНм
(растянуты правые волокна).
Участок CE
Сечение C:	N = 0 , Q = 0 ,	M = – 6 кНм
(растянуты верхние волокна) .
Сечение D (слева):	N = 0 , Q = 0 ,	M = – 6 кНм .
Сечение D (справа):	N = – HА = – 12 кН , Q = RА = 30 кН ,	M = – 6 – 12·3= – 42 кНм
Сечение F (слева):	N = – 12 кН , Q = 30 кН ,	M= –42+30·1= – 12 кНм .
Сечение F (справа):	N = – 12 кН , Q = 30 – 36 = – 6 кН ,	M = – 12 кНм .
Сечение Е:	N = – 12 кН , Q = – RВ = – 6 кН ,	M = – 18 кНм .

Построим эпюры N , Q , и M:

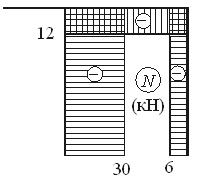
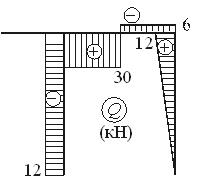
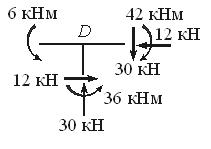
Вырежем мысленно узел D и покажем его равновесие под действием внутренних усилий в стержнях, сходящихся в узле. Нетрудно видеть, что узел находится в равновесии:

Пример 6. Рассчитать на прочность по методу предельных состояний двутавровую прокатную балку.

Материал балки сталь ВСт 3. Предел текучести σ_т = 240 МПа, расчетное сопротивление по пределу текучести R= 210 МПа, расчетное сопротивление при сдвиге R_s = 130 МПа. Коэффициент условий работы γ_с = 0,9. В табл. 2 приведены нормативные значения нагрузок. Коэффициент надежности по нагрузке γ_f = 1,2.

1.Определить опорные реакции;

2.Вычислить величины внутренних усилий в характерных сечениях и построить эпюры внутренних усилий.

3.Подобрать сечение балки из двутавра, используя условие прочности по первой группе предельных состояний.

1. Определим опорные реакции.

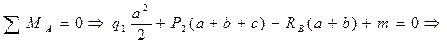
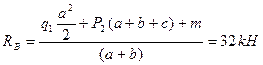
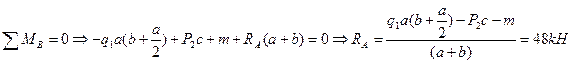
2. Проверка: 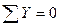, получаем

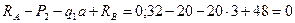
Реакции найдены правильно.

3. Построим эпюры Q и M.

Разобьем нашу балку на три участка и найдем суммы сил и моментов, действующих на каждом участке.

I участок: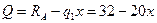

II участок: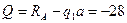

III участок: ,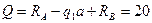

В конце балки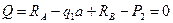

I участок: 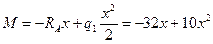; где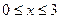

II участок: 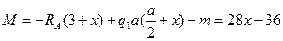, где ;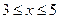

III участок: 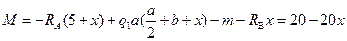, где ;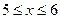

На участке 1 эпюра М имеет вид квадратичной параболы, ветви которых направлены вверх.

Построим схему конструкции и эпюры Q и M:

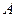
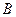
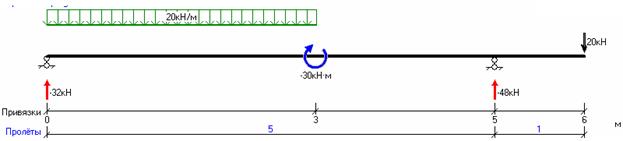
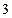
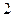
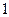
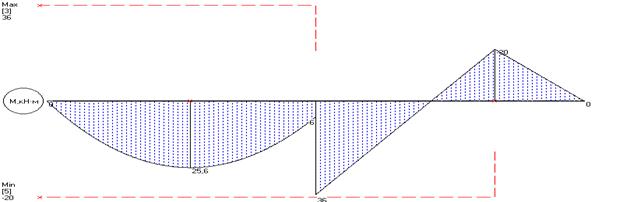
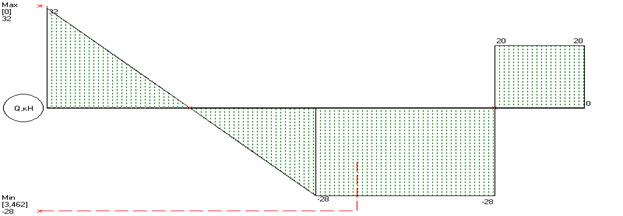
Значения М и Q в характерных сечениях балки указаны на эпюрах.

Опасным является сечение в точке с координатой 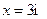, где 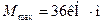. Расчетное значение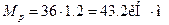

Требуемый момент сопротивления равен

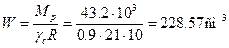
По сортаменту прокатной стали принимаем двутавровый профиль № 22

h=220мм, b=110мм, d=5.4мм, t=8.7мм, J_x=2550см 4 , W=232см 3 , S_x=131см 3

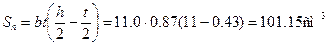
Вычислим значения наибольших нормальных напряжений в опасном сечении балки:

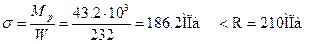
Прочность балки обеспечена.

6. Задания для контрольной работы

Для сечений, имеющих одну ось симметрии, по схемам №1-16 при размерах, указанных в таблице 2, требуется определить:

1) положение центра тяжести;

2) положение главных центральных осей инерции и величины главных моментов инерции.

Первая буква фамилии студента	а, см
А	П
Б	Р
В	С
Г	Т
Д	У
Е	Ф
Ж	Х
З	Ц
И	Ч
К	Ш
Л	Щ
М	Э
Н	Ю
О	Я

Схемы сечений стержней:

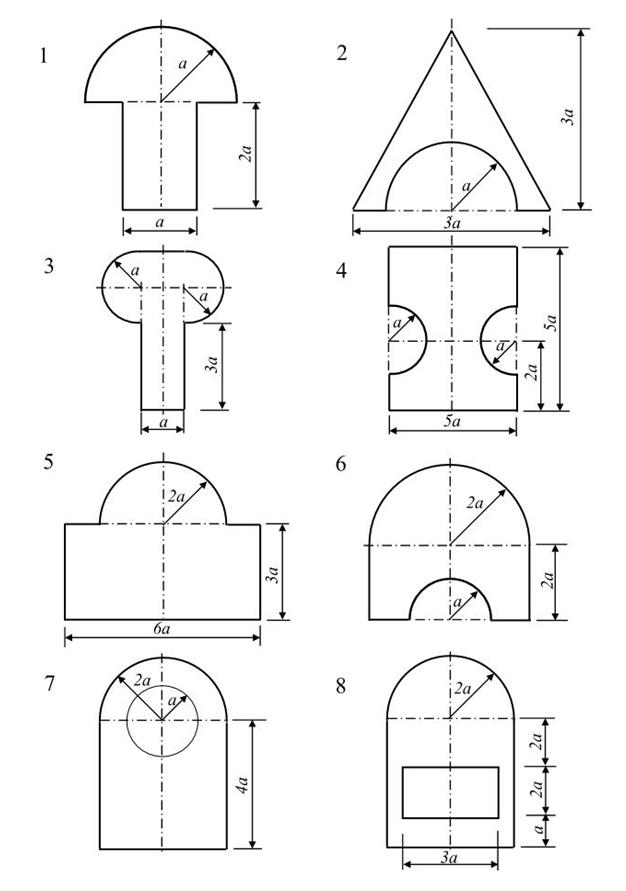
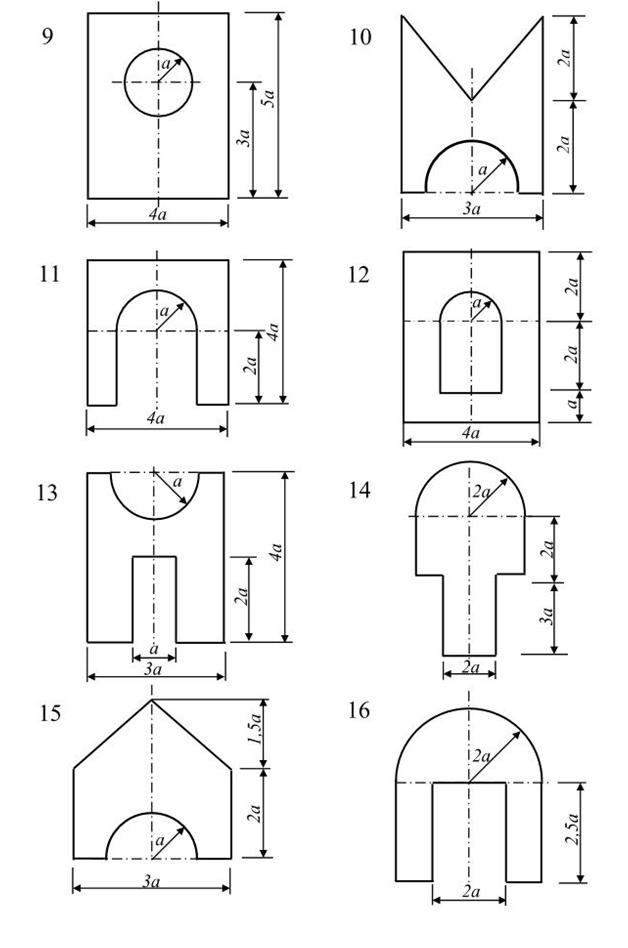
Для несимметричных сечений по схемам №1-16 при размерах, указанных в таблице 3, требуется:

1) определить положение центра тяжести;

2) вычислить осевые и центробежные моменты инерции относительно центральных осей;

3) определить положение главных центральных осей инерции и величины главных моментов инерции;

4) построить круг инерции и определить графически величины главных моментов инерции и направления главных центральных осей;

5) сравнить результаты аналитического и графического расчетов.

[spoiler title=”источники:”]

http://stroymex.online/sopromat/momenty-inercii-secheniy/all-about-moments-of-inertia

http://mydocx.ru/10-131542.html

[/spoiler]