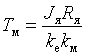Как найти момент инерции двигателя постоянного тока

Составим уравнения
динамики и статики электрического
двигателя постоянного тока, который
приводит в движение рабочий механизм.
Будем считать, что двигатель и рабочий
механизм соединены жесткой кинематической
связью (например, редуктором), и поэтому
они могут рассматриваться как единое
целое. Питание двигателя электрической
энергией осуществляется от источника
с регулируемым напряжением. Этот источник
выполняет функции исполнительного
устройства. В качестве исполнительного
устройства может быть использован
рассмотренный выше генератор постоянного
тока, тиристорный преобразователь,
силовой магнитный усилитель.

Схема замещения
такой электромеханической системы
показана на рис. 4.3.

Рис. 4.3. Схема замещения двигателя
постоянного тока

Основной управляемой
величиной является частота вращения
вала двигателя Д
n,
1/с. Частоту вращения можно регулировать
изменением
э. д. с.
,
создаваемой исполнительным устройствомИУ,
и изменением напряжения возбуждения
.
Чаще используется первый способ –
изменение напряжения, приложенного к
якорю двигателя, при постоянном напряжении.
Основное возмущающее воздействие
двигателя – момент сопротивления,
возникающий при взаимодействии рабочего
механизмаРМ
с внешней средой. В общем случае этот
момент зависит от частоты вращения.
Зависимость
может иметь довольно сложный характер.

Так как в двигателе
происходят и механический, и электрические
переходные процессы, то его состояние
в каждый момент времени описывается
двумя уравнениями равновесия:

уравнением моментов

(4.17)

и уравнением
напряжений в цепи якоря

(4.18)

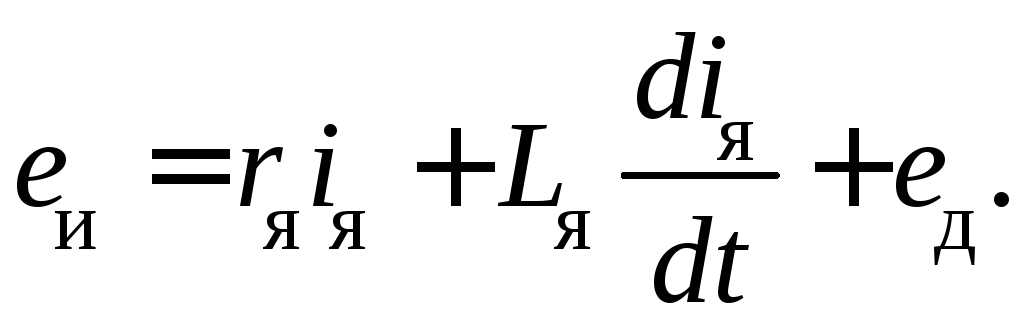
В этих уравнениях
приняты следующие обозначения:
–
движущий момент двигателя, Н ∙ м;– сумма момента инерции двигателяи приведенного на вал двигателя момента
инерции рабочего механизма,
кг ∙м²;
– суммарное активное сопротивление
цепи якоря, Ом;–
индуктивность цепи якоря, Гн;–
ток в цепи якоря, А;– противодействующая э. д. с. двигателя,
В.

Момент
,
создаваемый двигателем, пропорционален
току в цепи якоря и магнитному потоку
возбуждения Ф, Вб:

(4.19)

где
– конструктивная постоянная двигателя,
Н∙м/А∙Вб [символы,
иимеют такое же значение, как в формуле
(4.5)].

Э. д. с.
,
возникающая в обмотке якоря при вращении,
пропорциональна частоте вращения и
потоку возбуждения:

(4.20)

где
– конструктивная постоянная, В/Вб (1/с).

Магнитный поток
возбуждения двигателя, так же как у
генератора, является нелинейной функцией
тока возбуждения, которую в практических
расчетах заменяют линейной.

Уравнения (4.17) –
(4.20) совместно описывают двигатель как
единую физическую систему. Они могут
быть представлены в виде алгоритмической
схемы двигателя
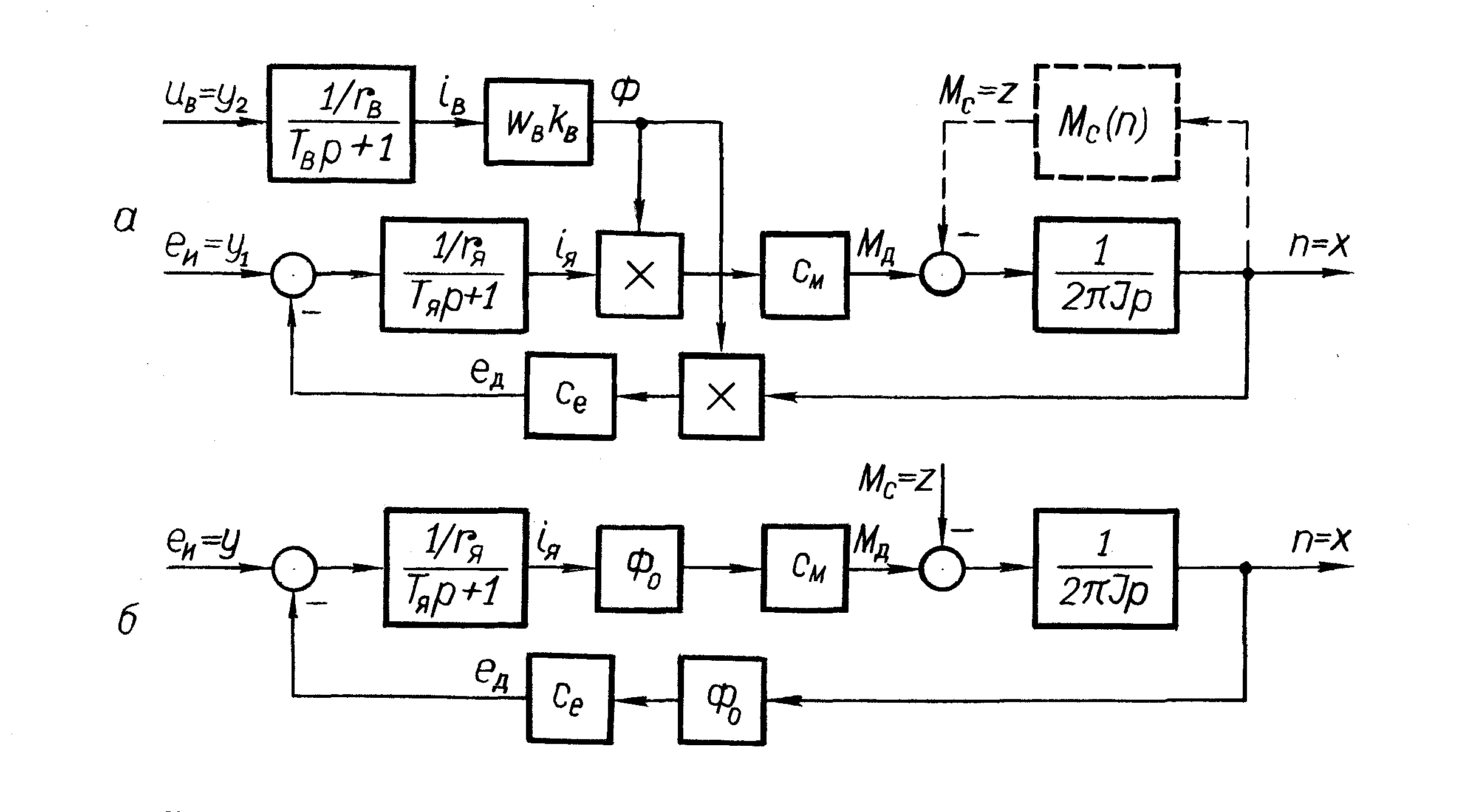
(рис. 4.4, а).
В схеме имеется два множительных звена.
Это означает, что при изменяющемся
потоке возбуждения двигатель является
нелинейным объектом.

Если напряжение
возбуждения
не
используется в качестве управляющего
воздействия и магнитный поток возбуждения
Ф в процессе управления постоянен
(Ф=Ф₀=const),
то алгоритмическая схема (рис. 4.4, а)
может быть упрощена (рис. 4.4, б).

Рис. 4.4. Алгоритмическая схема двигателя
постоянного тока:

а– с регулируемым возбуждением;б– с постоянным возбуждением

Составим общее
уравнение двигателя для наиболее часто
применяемого варианта управления –
изменением напряжения якорной цепи при
постоянном возбуждении. Подставим
выражения (4.19) и (4.20) в уравнения (4.17) и
(4.18) и объединим последние в одно
уравнение. Для этого выразим из уравнения
моментов (4.17) ток и его производную:

(4.21)

(4.22)

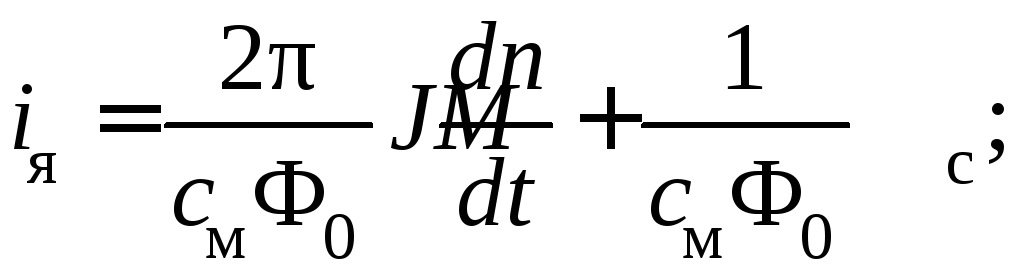
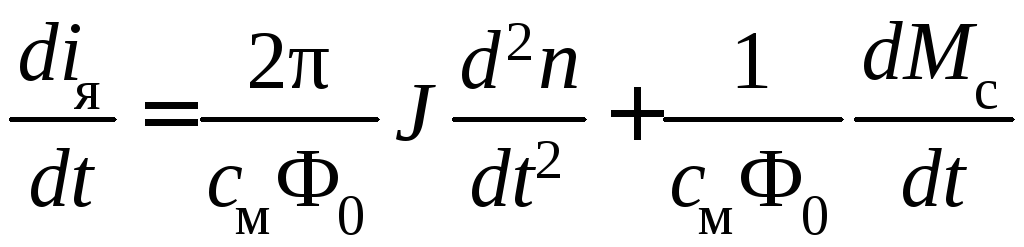
и подставим их в
уравнение напряжений (4.18). Тогда получим

(4.23)

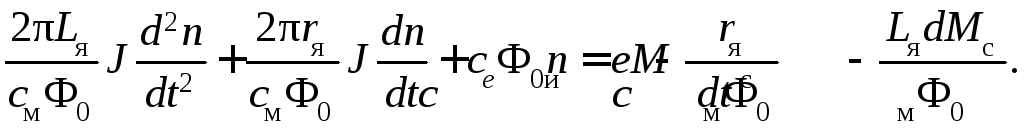
Введем следующие
обозначения:

–электромеханическая
постоянная времени двигателя, с;

–
электромагнитная постоянная времени,
с;

–передаточный
коэффициент двигателя по управляющему
воздействию – напряжению, (1/с)/В;

– передаточный
коэффициент двигателя по возмущающему
воздействию – моменту, 1/с/(Н∙м)

Разделив
предварительно левую и правую части
уравнения (4.23) на
и используя введенные обозначения,
получим
уравнение динамики двигателя в
стандартной форме

(4.24)

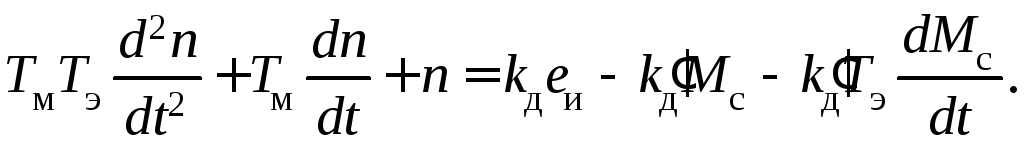
Переходя к
изображениям по Лапласу, можно из
уравнения (4.24) получить передаточные
функции двигателя:

по управляющему
воздействию – напряжению

(4.25)

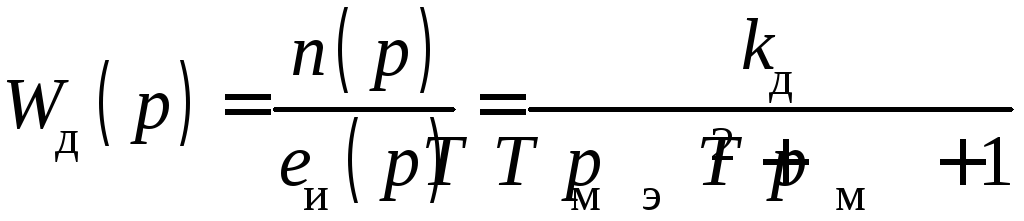
и по возмущающему
воздействию – моменту сопротивления

(4.26)

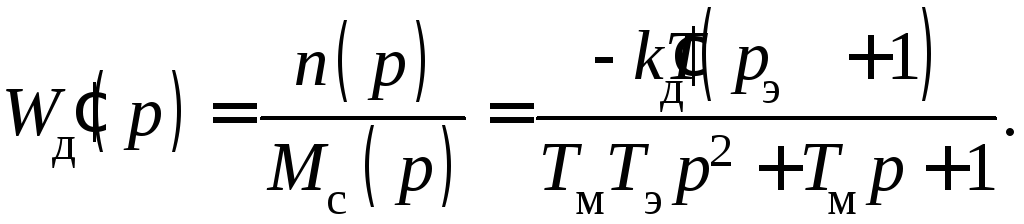
Приравнивая в
уравнении (4.24) производные по времени
нулю, получим уравнение
статики двигателя:

(4.27)

Выражение (4.27)
представляет собой уравнение механической
характеристики двигателя с независимым
возбуждением. Первое слагаемое
соответствует частоте вращения при
идеальном холостом ходе, а второе –
снижению частоты под нагрузкой.

Конструктивные
постоянные
и,
входящие в выражения передаточных
коэффициентов, определяют по номинальным
данным двигателя:

(4.28)

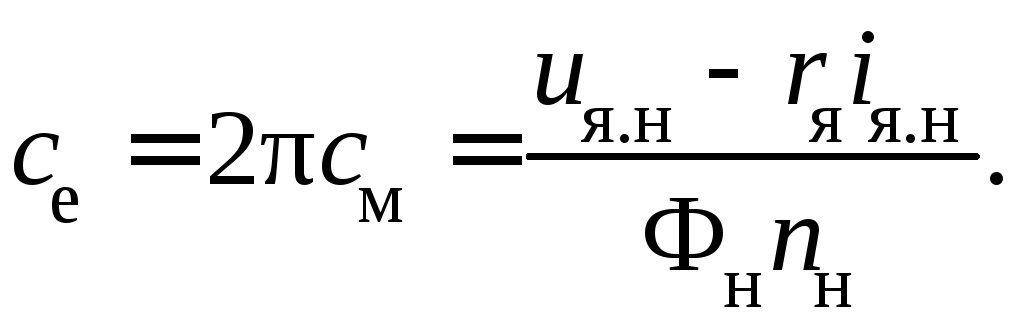
Так как индуктивность
якорной цепи в каталогах обычно не
указана, то постоянную времени
определяют экспериментально или
вычисляют по приближенной формуле проф.
В. Б. Уманского

(4.29)

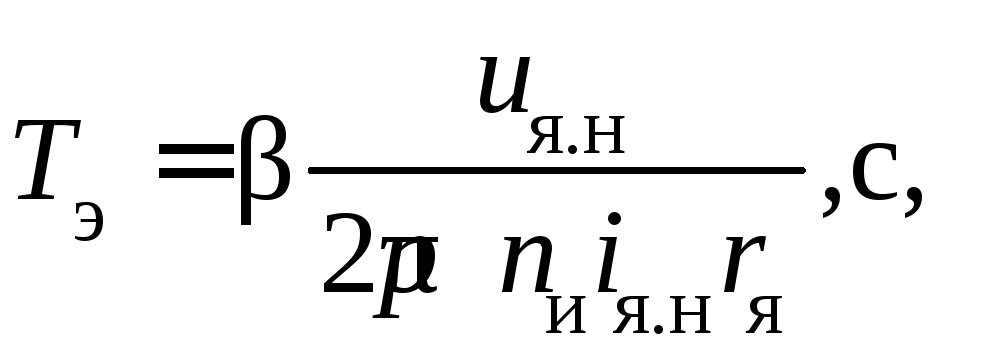
где
=
0,25 – для двигателей с компенсационной
обмоткой;=
0,6 – без компенсационной обмотки.

Постоянная времени
якорной цепи двигателей составляет
обычно 0,1 – 0,5 с, а электромеханическая
постоянная может принимать значения
от 0,5 до 5 с.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Двигатель постоянного тока

Для двигателя постоянного тока (ДПТ) основными уравнениями являются:

– уравнение электрического равновесия ;

– уравнение механического равновесия ;

– уравнение связи .

Рис.5.1. Структурная схема двигателя постоянного тока

Данным уравнениям соответствует структурная схема рис.5.1.

Если , то , (Ке = Км в системе СИ).

Из структурной схемы можно вывести ряд передаточных функций, поскольку есть входные сигналы U, MC, Ф, есть внутренние координаты I, M, есть выходная координата w.

Выведем следующие передаточные функции при Ф = const:

, , , .

,

где .

;

;

Характеристический полином

Корни полинома

При корни вещественные отрицательные ;

При корни комплексные.

В первом случае полином может быть записан в следующем виде:

Во втором случае имеем комплексные корни:

.

Характеристический полином получает вид:

,

где , .

На рис. 5.2, 5.3, 5.4 представлены ЛАЧХ для четырех выше выведенных передаточных функций ДПТ при . Учтено, что

; .

Рис.5.2. ЛАЧХ для передаточных функций ДПТ

Рис. 5.3. ЛАЧХ для передаточной функции ДПТ

Рис. 5.4. ЛАЧХ для передаточной функции ДПТ

При комплексных корнях характер ЛАЧХ будет аналогичным, но может появиться небольшой резонансный пик ( находится в пределах от 0,4 и более).

Цепь намагничивания ДПТ можно представить структурной схемой по рис. 5.5, где

– постоянная времени ОВ (находится в пределах 0,5 ··· 4 сек.)

Tвт – постоянная времени вихревых токов в станине и полюсах

(Твт = (0,1 ··· 0,2)Тв);

– находится из кривой намагничивания;

Рис.5.5. Структурная схема цепи возбуждения ДПТ.

При регулировании потоком ДПТ существенно нелинейное звено. Во – первых, в структуре рис. 5.1 появляются два блока произведения, во-вторых, надо учитывать нелинейность кривой намагничивания.

Следует отметить, что структурная схема ДПТ при Ф = const рассматривается при постоянстве параметров, т. е. в предположении, что реакция якоря полностью скомпенсирована, активное сопротивление и индуктивность якорной цепи постоянны. Для кривой намагничивания пренебрегаем петлей гистерезиса (при регулировании потоком). Обычно пренебрегаем зависимостью МС от скорости вращения. Однако реально все эти влияния есть и они существенны.

Рассчитаем изменения RЯ при изменении температуры обмотки с 20 °С до 90 °С :

Таким образом, активное сопротивление якорной цепи изменяется на 28 % при переходе от начального включения до рабочей температуры в 90 °С.

Сопротивление может быть найдено из каталогов (при приведении к рабочей температуре ).

Сопротивление якорной цепи можно приближенно определить по данным на щитке электрической машины. Полагая, что при работе двигателя в номинальном режиме его постоянные РПОСТ и переменные РПЕР потери равны, получим

;

ρд = (1 ··· 2) % при Р > 100 кВт;

ρд = (2 ··· 5) % при Р = (100 ··· 5) кВт;

ρд = (5 ··· 10) % при Р = (5 ··· 0,5) кВт;

ρд > 10 % при Р = (0,5 ··· 0,1) кВт.

Экспериментально RЯ находится методом амперметра – вольтметра.

Индуктивность якоря изменяется еще больше, чем сопротивление якорной цепи. Ее рассчитывают

,

где: n = 0,1 – 0,2 для машин с компенсационной обмоткой (0,25 – для крупных машин); n=0,6 для машин без компенсационной обмотки; рп – число пар полюсов.

Опыты оказывают, что с изменением тока якоря от 0 до пускового индуктивность якоря уменьшается на 30 – 45%.

Экспериментально LЯ определяется по кривой гашения поля [25]. Обмотка якоря подключается к источнику постоянного тока и в некоторый момент замыкается накоротко.

По осцилографируемой кривой IЯ = f(t) (рис. 5.6) можно рассчитать LЯ по уравнению: ,

откуда .

Рис. 5.6. Экспериментальное определение ТЯ по кривой гашения поля

Индуктивность обмотки якоря при включенной цепи возбуждения на 15 -20 % меньше, чем при отключенной (сказывается насыщение магнитной цепи). Поэтому опыт желательно проводить при включенной цепи возбуждения.

Определение момента инерции двигателя по геометрическим размерам отдельных вращающихся деталей трудоемок и неточен. Поэтому момент инерции определяется экспериментальным путем по кривой выбега и потерям холостого хода. Двигатель разгоняется до некоторой скорости, а затем отключается от сети, осциллографируется кривая выбега (рис. 5.7.).

Рис. 5.7. Определение момента инерции двигателя по кривой выбега.

Затем определяются потери холостого хода при ряде значений скорости, рассчитывается и строится кривая

Момент инерции определяется следующим образом: .

Значение J определяется для нескольких точек, усредняется, в результате достигается достоверность результатов. Данная методика используется в том числе при определении момента инерции всей системы «двигатель – рабочая машина».

Идентификацию (определение математической модели объекта по экспериментальным данным) удобно производить на ЭВМ, вводя в нее массив точек переходных процессов. В настоящее время в наладочных организациях имеются приборы на основе микроЭВМ, в которые через АЦП данные вводятся автоматически и рассчитываются параметры объекта.

Постоянные времени электромеханической системы могут быть определены методами активной идентификации при подаче на вход воздействия периодического характера. В результате получают ЛАЧХ, по сопрягающим частотам которой определяют постоянные времени.

УДК 621.313.2.001.57

И. А. Орловский

ИДЕНТИФИКАЦИЯ МОМЕНТА ИНЕРЦИИ И МОМЕНТА СОПРОТИВЛЕНИЯ В ЭЛЕКТРОПРИВОДЕ ПОСТОЯННОГО ТОКА

Рассмотрен способ идентификации в реальном времени момента инерции и момента сопротивления механизма с приводом постоянного тока, значения которых зависят от угла поворота вала двигателя. Получены уравнения для расчета моментов инерции и сопротивления по показаниям датчиков тока и частоты вращения. Моделирование работы электропривода и идентификации параметров подтвердили высокую точность предложенного способа.

Для повышения качества управления и реализации оптимальных систем управления все более важными становятся вопросы идентификации параметров электропривода. Использование в настоящее время микропроцессоров в электроприводе позволяет выполнять необходимые для идентификации вычисления.

В ряде механизмов, выполняющих циклическую работу (опрокидыватели, роботы-манипуляторы, экскаваторы, моталки и др.), момент инерции механизма и статический момент сопротивления механизма (далее момент сопротивления) являются нелинейными и зависят от угла поворота вала двигателя. Эта зависимость может оставаться неизменной в течение нескольких циклов работы. Расчет регуляторов классическими способами выполняется для определенных фиксированных параметров объекта и не учитывает изменения его параметров. Полученные при идентификации в процессе работы параметры объекта используются в математических выражениях классически определенных регуляторов, что позволяет повысить качество переходных процессов.

Вопросам идентификации параметров привода постоянного тока посвящено большое количество работ. В [1] авторы отмечают, что из условий наблюдаемости параметры электромеханической системы могут быть определены только в динамическом режиме. Рассматривается вопрос идентифицируемости параметров электропривода за счет гармонического изменения напряжения, приложенного к якорю двигателя. Определяются необходимые минимальные значения амплитуд гармонических составляющих выходного напряжения тиристорного преобразователя для обеспечения идентифицируемости параметров электропривода. В [2] отмечается сложность идентификации параметров привода постоянного тока при наличии гармонических составляющих в напряжении питания двигателя. Идентификацию предлагается выполнять из

уравнений энергетического баланса. Для вычисления параметров принимается достаточно узкий диапазон изменения момента инерции (±6 %). В [3] идентификация параметров двигателя реализуется автоматизированным диагностическим комплексом. Измерения выполняются с частотой 10 кГц. Отмечаются сложности реализации, связанные с дискретностью измерений. Установлено, что максимум ошибки идентификации электромагнитной постоянной времени совпадает с максимумом второй производной тока. Ошибка идентификации составляла от 5 до 35 %. При этом момент инерции и момент сопротивления механизма считались неизменными. В [4] рассмотрен способ определения момента сопротивления и электромеханической постоянной времени привода постоянного тока при работе регулятора скорости в режиме отсечки без использования информации от датчика скорости. Для этого во время пуска двигателя измеряются токи и напряжения при двух разных значениях напряжения отсечки тока. Для получения необходимых зависимостей принимается, что моменты инерции и сопротивления во время пуска остаются неизменными. В [5] рассмотрено применение нечеткой нейронной рекуррентной много модельной сети для систем идентификации сложных нелинейных объектов на примере электропривода постоянного тока. Такая система позволяет обеспечить высокую точность (порядка 2 %) получения модели привода через несколько периодов задающего сигнала, однако требует значительных вычислительных ресурсов и не обеспечивает идентификацию параметров, необходимых для настройки регуляторов.

Целью статьи является идентификация с высокой точностью в процессе работы привода зависимостей момента инерции и момента сопротивления механизма от угла поворота вала двигателя.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ

Пусть в реальном механизме, исходя из его устройства и технологии, существуют нелинейные зависимости момента инерции ] = /(а) и момента сопротивления Мс = /(а) от угла поворота вала двигателя а. Описание этих зависимостей удобно выполнять для нормированных значений момента инерции и момента сопро-

тивления. Введем коэффициенты, характеризующие нелинейность

к/(а) = ^

н

кМ(а) =

Мс(а)

м

н

где ]н, Мн – номинальные значения момента инерции привода и момента двигателя, /(а), Мс(а) – реальные значения момента инерции и момента сопротивления механизма; к/(а), км(а) – значения нелинейных коэффициентов момента инерции и момента сопротивления механизма.

Уравнение движения привода при изменяющихся моментах инерции и сопротивления имеет вид

М (Ь) – Мс(а) =

— й/( а ) • со ( Ь ) 1

(1)

где М (Ь), <о( Ь) – момент и частота вращения двигателя. Угол поворота а при движении также является функцией времени.

Уравнение (1) с учетом введенных коэффициентов и после дифференцирования произведения примет вид

= /

г(Ь)• См — кМ(а)- Мн =

йк/(а) й<( Ь)

(2)

где г(Ь) – ток якоря двигателя, См – постоянная момента двигателя. В уравнение (2) соответствует двигателю постоянного тока с постоянным магнитным потоком возбуждения. При использовании другого вида двигателя необходимо использовать соответствующее выражение момента двигателя. Дальнейшие расчеты, приведенные ниже, остаются такими же.

Для выполнения расчетов в дискретной системе представим (2) в виде разностного дифференциального уравнения

г(Ь1 )• см— км(а1 )• мн = — / н ‘ < ( Ь 1) ‘ к/(а2) – к/(а 1 ) 1 + Ь2 – Ь1

/н • к/ (а 1 ) • < ( Ь2) – < ( Ь1) 1

Ь2 – Ь1

(3)

где а1 и а2 – значения углов поворота в моменты времени ¿1 и ¿2. Обозначим такт счета Д—1 — ¿2 — ¿1. При описании движения уравнением (3) принимается, что на всем промежутке времени Д^ производные момента инерции и частоты вращения остаются неизменными. Неизвестными в данном уравнении являются

км(а1), к/(а1) и к/(а2), остальные величины являются константами либо измеряются.

В момент времени ¿2 уравнение движения имеет вид

г (Ь2) • см — км(а2)• мн — — / н • < ( Ь2) ‘ к/ ( аз ) — к/ ( а 2 ) 1 +

¿3 — ¿2

/ н • к/ ( а 2 ) • < ( Ь3) — < ( Ь2 ) 1

¿3 — ¿2

(4)

где а3 – значение угла поворота в момент времени ¿3.

При реализации интервал времени ДЬ одинаков в уравнении (3) и (4), т. е. Д^ — ^ — ¿1 — ¿3 — ¿2. Для возможности вывода относительно простых аналитических выражений, не смотря на вносимую погрешность идентификации, лианеризуем зависимость момента инерции от а на малом интервале 2Д-1 (от ¿1 до ¿3). С учетом этого можно принять к/(а1) — к/(а2) — — к/(а2) — к/(а3), тогда уравнение (4) можно записать следующим образом

г (Ь2) • см — км(а2мн — — /н • < ( Ь2) ‘ к/ (а2 ) — к/ (а 1 ) 1 +

¿О —

/н- к/ ( а 2) • < ( Ь3 < ( Ь2 1 Ь2 — Ь1

(5)

В уравнениях (3) и (5) неизвестными являются четыре параметра км(а1), км(а2), к/(а1) и к/(а2). Необходимые для вычисления этих величин два уравнения можно получить при движении механизма через углы а1, а2 и а3 в том же направлении, но при другом значении частоты вращения, либо при движении механизма в обратном направлении. Уравнения имеют вид

г2(Ь1 ‘)• см — км(а1мн — — / н • <2 ( Ь 1 ‘ ) • к/( а 2) — к/( а 1) 1 +

Ь ‘ — Ь ‘

Ь2 Ь1

/ н • к/(а 1 ) • < 2 ( Ь2′ ) — < 2 ( Ь1 ‘ ) 1

Ь2 — Ь1′

(6)

г2(Ь2> СМ — кМ(а2) • Мн — — / н • <2 ( ¿2′) • к/ ( а3) — к/( а 2) 1

Ь3 Ь2′

/ н • к/ (а2) • <0 2 ( ¿3 ‘ ) — < 2 ( ¿2 ‘ ) 1

¿3′ — Ь2

(7)

где ¿1′, ¿2′, ¿3′ – моменты времени, когда механизм проходит соответственно углы положения а1, а2 и а3.

Если принять аналогично, что Д ¿2 — ¿2′ — ¿1′ — — ¿3′ — ¿2′, то система уравнений примет вид

Ч(¿1)- См- км(а1)- Мн =

= /Н • Ю 1( Ч) ■ [ к1 (а2 ) – кАа 1)].

м.

] н ■ (а 1 ) ■ [ со 1 ( ¿2) – Ю 1 ( ¿1) ]

А^

¿1( ¿2)■ СМ – АМ(а2) ■ МН =

= ^н ■ Ю 1 ( ¿2) ■ [ ^/(а2) – ^/(а1)]

А£,

] Н ■ kJ(а2 ) ■ [ Ю 1 ( ¿3 ) – Ю 1 ( ¿2 )]

А£,

«2(¿1СМ – ^М(а1)^ МН =

= Jн ■ Ю 2 ( ¿1 ) ■ [ У0^ – иДа1)]

А^

J н ■ kJ (а 1 ) ■ [ Ю 2 ( ¿2 ) – Ю 2 ( ¿1 )]

А^

«2(¿2)■ СМ – АМ(а1)^ Мн = = J н ■ Ю 2 ( ¿2 ) ■ [ к J( а 2) – а 1 )]

Аи

н ■ kJ ( а 2 ) ■ [ Ю 2 ( ¿3 ) – Ю 2 ( ¿2 ) ]

А^

2

(8)

Из первого уравнения системы (8), используя (9) и (10), найдем коэффициент момента сопротивления

где

им(а1)

Ь – М ■ N – Р

М

н

Ь 11 (¿1) ■ СМ,

М=

^^ н ■ Ю 1( ¿1 ) Аt, ,

N =

А -^(а^■С

(11)

р = ^^н ■ ^ (а 1 ) ■ [ Ю 1 ( ¿2 ) – Ю 1 ( ¿1 )] Р = А ¿ .

По выражениям (10) и (11) из результатов измерений вычисляются искомые коэффициенты для угла поворота а1. Для получения зависимостей АДа1), Ам^) расчеты выполняются для различных углов поворота с заданным шагом.

Вычтем из первого уравнения системы (8) третье уравнение и из второго уравнения четвертое, получим

где

С = J

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

ГЕ ■ [^Да2) – АДа1)] + АДа^ ■ С = А; [р ■ [иДа2) – и^(а1)] + £Да2) ■ Д = В,

А = [¿1(¿1) – ¿2(¿1 ‘)]■ См, В = [ ¿1( ¿2) – ¿2( ¿2 ‘)]■ См, Ю1 ( ¿2 ) Ю1( ¿1) Ю2( Ц) Ю2(

н

А^

Аt,

А и

А1

2 -I

Б = J

н

‘Ю1 ( Ч ) Ю1( ¿2) Ю2( ¿3^ ®2 ( ¿2 ‘>

Аt,

Аt,

Аи

А

2 -I

Е = J

н

Р = J

н

Ю1(¿1) – Ю2(¿1′ )’ А А ¿2

Ю1( ¿2) Ю2( ¿{У

Аt,

А и

Из системы (9), найдем

и (а ) = А ■ (Д – р)+в ■ Е

kJ(аl) (Е + С) ■(Б – Р) + Р ■ Е’

(9)

(10)

ПРОВЕРКА АНАЛИТИЧЕСКИХ РЕЗУЛЬТАТОВ НА ПУТЕМ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Проверка идентификации моментов сопротивления и инерции выполнялась на модели электропривода постоянного тока со следующими параметрами двигателя: ин = 220 В, 1н = 80,5 А, юн = 104,72 рад, Jн =

сек

2

= 0,9 кг ■ м2, См = 1,9 Н/А, Ея = 0,618 Ом, Ья = = 0,105 Гн. Использовались имеющиеся в электроприводе положения показания датчиков тока, частоты вращения и угла поворота. Зависимости момента инерции и момента сопротивления от угла поворота взяты следующими

АДа) = 0, 5 + е

-0, 2а

им (а) = 1 – е

-0, 1а

(12)

(13)

Выполнялась полная отработка цикла работы механизма. Запоминались значения токов, частоты вращения в дискретные моменты времени для всех значений угла положения а при движении, как в прямом, так и обратном направлении. Измерения параметров в обоих направлениях выполнялись с одинаковым шагом дискретизации, что удобно при практической реализации измерений. Использование одинакового шага дис-

к Зависимость момента инерции от угла поворота

1.5 1.4 1.3 1.2 1.1 1

0.9 0.8 0.7 0.6 0.5 Ь

1 итанное значение явленное значение

– —– устан

—

—

10

15

20

25 30 а, рад

Рисунок 1 — Графики цикла работы механизма (угол поворота вала двигателя, частота вращения, ток двигателя)

Рисунок 2 — Зависимости момента инерции и момента сопротивления от угла поворота для рассчитанных и замеренных значений

кретизации привело к необходимости вычисления А^ и пересчета значений ¿2′), ®2(¿2′), ®2(¿э’)

Результаты моделирования цикла работы механизма приведены на рисунке 1 – Здесь показаны зависимости угла поворота, частоты вращения и тока якоря двигателя от времени. Результаты идентификации зависели от шага дискретизации, так как пересчет значений ¿2(), ю2(¿2′), ю2(¿3′) в местах перегиба тока и частоты вращения приводит к неточному вычислению этих значений при линейной интерполяции. Повышение точности достигается интерполяцией более высокого порядка и уменьшением шага дискретизации. Для шага 10-5 секунды и линейной интерполяции результаты идентификации момента инерции и момента сопротивления представлены на рисунке 2. Увеличенные фрагменты этих зависимостей показаны на рисунке 3. На рисунках штриховыми линиями

обозначены принятые зависимости согласно (12) и (13) момента инерции и момента сопротивления от угла поворота. Непрерывными линиями показаны результаты идентификации этих параметров. Имеющиеся ошибки оценки для большей части диапазона для момента инерции и момента сопротивления не превышали 0,1 %. Использование в системе управления идентифицированных параметров с такой точностью позволяет значительно повысить качество управления.

ВЫВОДЫ

Рассмотрен способ идентификации в электроприводе постоянного тока момента инерции и момента сопротивления, значения которых зависят от угла поворота вала двигателя. Идентификация осуществляется в

TEOPIЯ I METOДИ ABTOMATИЧHOГO УПPABЛIHHЯ

Увеличенный участок зависимости к от а

0.6062 0 606 0 6058 0 6056 0.6054 0.6052

-рассчитанное значение —–установленное значение

^

ч

л

11.21 11.22 11.23 11.24 11.25 11.26 11.27 11.28

а, рад

км Увеличенный участок зависимости км от а

0 9074 0.9072 0.907 0.9068 0.9066 0.9064 0.9062

/у

у

/ У

✓

…. j.

– ‘jt

_-рассчитанное значение —-установленное значение

23.66 23.68 23 7 23.72 23.74 23.76 23.78 23 Е

а, рад

ПЕРЕЧЕНЬ ССЫЛОК

1. Cиcюк Г. Ю., Родькин Д. И., Королев Ю. Г. К вопросу об идентификации параметров тиристорных электроприводов постоянного тока на основе моделей энергообразования // Проблемы создания новых машин и технологий, Научные труды КГПИ. Кременчуг.

– 1999. – № 2. – С. 47-50.

2. Родькин Д. И., Хараджян А. А., Михайлов C. В. Диагностика параметров двигателя постоянного тока при испытаниях // Проблемы создания новых машин и технологий. Научные труды КГПИ. Кременчуг. – 1998. -№ 1. – 10 с.

3. Бешта О. C., Балахонцев О. В., Xyдoлiй C. C. 0мови тдвишення точност ^ентифтацп динaмiчниx пapaмeтpiв електропривода // Вюник Кременчуцького Державного полтехшчного ушверситету. – 2002. -№ 1. – С. 426-427.

4. Орловский И. А. Определение параметров привода постоянного тока в режиме ограничения тока якоря / / Електротехшка та електроенергетика. – 2002. – № 1.

– С. 63-66.

5. Baruch I. S., Flores J. M., Garrido R. A fuzzy neural recurrent multi-model for systems identification and control // Proceeding of the European Control Conference. – 2001.

– Pp. 3540-3545.

ШАтшла 14.06.04 Шсля доробки 3.05.05

Розглянуто засiб iдентuфiкацiï у реальному часi моменту терцп i моменту опору мехатзму з приводом посттного струму, значення котрих залежать вiд кута повертання валу двигуна. Отримант рiвняння розрахунку моментiв iнерцïï та опору з показань давачiв струму та частоти обертання. Моделювання роботи електроприводу та iдентuфiкацiï параметрiв тдтвер-дили високу точтсть запропонованого засобу.

Рисунок 3 — Увеличенные фрагменты зависимостей момента инерции и момента сопротивления от угла поворота

течение цикла работы механизма. Результаты моделирования при малом шаге дискретизации показали высокую точность идентификации.

In real time has been considerate mode of identification inertia moment and resistance moment of mechanism with the direct current gear, there are meaning depend on angle of turn shaft of the motor. Taken equations for the calculation inertia moment and resistance moment by reading current pick-up and frequency rotation pick-up. Simulation of the work electric drive and the identification of parameters have confirmed high accuracy offered mode.

Цель лабораторной работы: изучение статических
характеристик и характера переходных процессов в двигателе постоянного тока с
независимым возбуждением от постоянных магнитов при изменении управляющего
напряжения, внешнего силового воздействия, а также в зависимости от соотношения
значений основных параметров двигателя.

Задачи лабораторной работы

·       
приобретение навыков формирования математических
моделей исполнительных двигателей электромеханических систем как динамических
объектов с помощью средств системы визуального моделирования Simulink на примере модели коллекторного
двигателя постоянного тока (ДПТ) с возбуждением от постоянного магнитного поля;

·       
изучение характера переходных процессов в ДПТ и
определение электромагнитной и электромеханической постоянных времени двигателя
путем проведения вычислительных экспериментов;

·       
исследование свойств ДПТ в установившихся
режимах работы;

·       
определение регулировочной характеристики ДПТ
при непрерывном регулировании напряжения, подаваемого на якорную цепь
двигателя;

·       
определение механической характеристики ДПТ при
изменении назрузочного момента;

·       
исследование зависимости динамических свойств
ДПТ от момента инерции ротора и приведенного момента инерции объекта
управления.

Порядок выполнения лабораторной работы

1.     Запустите
Matlab и
откройте окно для создания модели Simulink. С помощью мыши «перетащите» нужные модули из
библиотеки Simulink на рабочее поле модели и
соедините их линиями связи в соответствии со структурной схемой модели
двигателя постоянного тока. Присвойте имя программной модели и сохраните ее в
каталоге, указанном преподавателем.

 Рис.1

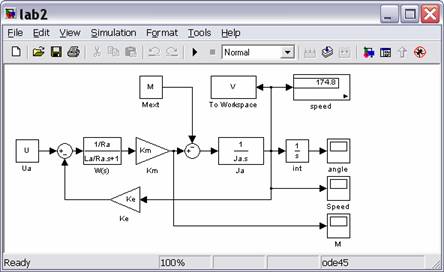
Числовые значения параметров модели ДПТ для своего варианта задайте
как переменные в окне Command Window[1] в
соответствии с в таблицей.

clear       % Очистка
Workspase

Ra=4.0;     % Активное
сопротивление обмотки якоря

La=0.004;   %
Индуктивность обмотки якоря

Ja=0.00002; % Момент инерции ротора

Km=0.057;   % Коментный
коэффициент двигателя

Ke=0.057;   %
Коэффициент противоЭДС

Unom=24;    %
Номинальное напряжение двигателя

Umax=40;    %
Напряжение источника энергии

Mnom=0.2;   %
Номинальный момент двигателя

Двигатель	Uном	n ном	Iном	Rя,	Тэ	Jдв,	kе,
В	об/мин	A	Ом	мс	кгм2	Вс/рад
ДПР62Н1-02	27	6000	0,72	4	1	3,60*10-6	0,043
ДПР72Н1-07	12	4500	2,20	0,56	0,65	7,80*10-6	0,025
ПЯ250Ф	36	3000	9,50	1	1	2,92*10-4	0,115
ДПУ200	92	3000	7,40	1,53	1,1	7,80*10-4	0,293
ДП40	24	4000	2,90	1,45	1	1,27*10-4	0,057
ДП50	24	4000	5,30	0,28	1,5	6,08*10-4	0,057

2.     Снимите
переходной процесс изменения угловой скорости вала двигателя w и тока
якоря I_я
при ступенчатом изменении напряжения U_я. Для этого введите номинальное значение U_я, указанное
в табл.1, и задайте нулевое значение возмущающего момента M_в от внешних сил.
Установите необходимые значения параметров процесса моделирования, раскрыв
поочередно разделы Simulation
и Parameters.
Общее время моделирования рекомендуется принимать приблизительно равным 4Т_м.
Предварительно необходимо вычислить значения электромагнитной и
электромеханической постоянных времени рассматриваемого ДПТ.

,           

3.     Получите
и зарисуйте переходные процессы скорости и тока при номинальном значении
напряжения якоря и внешнем моменте, равном нулю.

 

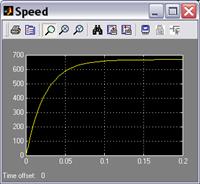
4.     Определите
по полученным графикам время переходного процесса Т_пп[2] скорости двигателя w и
перерегулирование s[3]. Сопоставьте установившееся значение
скорости вала двигателя со значением, которое ожидается на основании
теоретических положений. Дайте объяснение характеру изменения тока якоря.

Примечание: Для
апериодического процесса справедливо соотношение T_пп » 3t.

5.     Определите
значение электромеханической постоянной времени двигателя Т_м
по переходному процессу угловой скорости вращения вала двигателя. Сопоставьте
полученное значение с ожидаемым значением, вычисленным теоретически. Если эти
значения отличаются, объясните, чем это может быть вызвано.

6.     Приложите
к валу внешний момент M_вн=-0.5М_п
и M_вн=0.5М_п,
где М_п – расчетное
значение пускового момента двигателя. Получите переходные процессы скорости и
тока якоря. Приведите графики в отчете.

Как изменяется характер переходных процессов при действии внешнего
возмущающего момента? Как влияет М_в на установившиеся
значения скорости и тока?

7.     Изучите
влияние момента инерции подвижных частей, приведенных к валу двигателя, на
динамические свойства ДПТ (M_вн=0).

Для этого рассмотрите переходные процессы при ступенчатом изменении
напряжения на якоре, при значении момента инерции на валу ротора: J=J_a, J=2J_a  и  J=4J_a .

Последний два варианта означают, что вал двигателя связан с
объектом, обладающим приведенным к валу ДПТ моментом инерции, равным моменту
инерции ротора и превышающим его в 3 раза, соответственно.

Как изменяются Т_пп , s, ω(∞) и
тока якоря ?

Зафиксируйте в отчете и объясните результаты.

8.     Путем
вычислительного эксперимента определите значение электромагнитной постоянной
времени двигателя Т_э. Для этого необходимо рассмотреть
переходные процессы при заторможенном вале двигателя. Поэтому измените
структуру программы моделирования таким образом, чтобы внешний момент был равен
электромагнитному моменту двигателя. Значение Т_э определите
непосредственно по графику переходного процесса тока якоря и сопоставьте со
значением, полученным на основании теоретического расчета. Объясните
результаты.

9.     Повторить
предыдущий опыт при значениях напряжения управления, равных 50% и 25% от
номинального напряжения. Зафиксируйте результаты и сделайте вывод о влиянии
напряжения управления U_я
на скорость и ток двигателя. Изменяются ли значения Т_пп и s
?

10. Постройте по 5
точкам (U_я=-U_ном÷U_ном)
регулировочную характеристику двигателя при M_вн=0.

	-Uном	-0,5Uном	0	0,5Uном	Uном
ω(∞)

11. Постройте по 5
точкам (M_вн
= –M_п÷M_п)
механическую характеристику двигателя при U_я=0.5U_ном.

	–Mп	-0,5Mп	0	0,5Mп	Mп
ω(∞)

12. Постройте семейства
механической и регулировочной характеристик ДПТ. Для этого проведите
автоматизированную серию вычислительных экспериментов при значениях напряжения
якоря и значениях внешнего момента приведенных в таблице:

	-1,5Uном	-Uном	-0,5Uном	0	0,5Uном	Uном	1,5Uном
-1,5Mп
–Mп
-0,5Mп
0
0,5Mп
Mп
1,5Mп

Для этого воспользуйтесь программой:

clear       % Очистка
Workspase

Ra=4.0;     % Активное
сопротивление обмотки якоря

La=0.004;   %
Индуктивность обмотки якоря

Ja=0.00002; % Момент инерции ротора

Km=0.057;   % Коментный
коэффициент двигателя

Ke=0.057;   %
Коэффициент противоЭДС

Unom=24;    %
Номинальное напряжение двигателя

Umax=40;    %
Напряжение источника энергии

Mnom=0.35;  % Номинальный момент двигателя

Nu=7;       % Число
точек Uдв, нечетное

Nm=7;       % Число
точек Mвн, нечетное

% Выполнение расчетов

for j=1:Nu,            
% Цикл изменения Uя

    j1=j-(Nu+1)/2;

      U=Unom*2*j1/(Nu-1);
U1(j)=U;

        for i=1:Nm,     % Цикл изменения Mвн

        i1=i-(Nm+1)/2;

        M=Mnom*2*i1/(Nm-1); M1(i)=M;

      
 sim(‘lab2.mdl’,0.20),

        n=size(V);          % Размерность вектора

       
Au(j,i)=V(n(1)),    % Заполнение
массива

       
Am(i,j)=V(n(1)),    % Заполнение
массива

    end

end

% Вывод графика “Семейство регулировочных
характеристик”

figure(1); set(1,’Name’,’Семейство регулировочных
характеристик’);

plot (U1,Au); GRID;

title (‘Семейство регулировочных характеристик’)

Xlabel(‘Напряжение на якоре двигателя, V’)

Ylabel(‘Установившаяся скорость вращения, 1/s’)

legend(‘Mext=’,’Mext=’,’Mext=’,’Mext=0′,’Mext=’,’Mext=’,’Mext=’)

% Вывод графика “Семейство нагрузочных
характеристик”

figure(2); set(2,’Name’,’Семейство нагрузочных
характеристик’);

plot (M1,Am); GRID;

title (‘Семейство нагрузочных характеристик’)

Xlabel(‘Внешний момент, Nm’)

Ylabel(‘Установившаяся скорость вращения, 1/s’)

legend(‘Ua=’,’Ua=’,’Ua=’,’Ua=0′,’Ua=’,’Ua=’,’Ua=’)

Изучите приведенную программу. Обработайте полученные графики. Если
надписи не читаемы, примените к ним шрифт GOST type A.

Сделайте выводы по результатам построения механической и
регулировочной характеристик ДПТ.

13. Оформите отчет, в
который включите схемы моделирования, исходные данные, все полученные числовые
оценки, графики процессов и выводы по результатам проведенной лабораторной
работы.