Вычисление моментов инерции
Моменты инерции материальной кривой
Моментом инерции материальной точки относительно оси
называется число
, где
— масса точки, а
— ее расстояние от оси. Аналогично определяется момент инерции относительно точки.
Пусть — материальная линия, линейная плотность которой во всех точках равна единице. Тогда масса элементарного участка этой линии равна его длине
, а момент инерции
такого участка относительно оси абсцисс равен
. Интегрируя, получаем момент инерции относительно оси абсцисс всей линии:
. Так же доказывается, что
и
,
где — момент инерции относительно начала координат. Отсюда следует, в частности, что
.
Если линия задана параметрическими уравнениями
, то
Аналогичные формулы справедливы для и
Моменты инерции криволинейной трапеции
Перейдем к вычислению моментов инерции криволинейной трапеции. Будем считать, что ее поверхностная плотность равна единице. Сначала найдем момент инерции прямоугольника со сторонами и
относительно стороны
. Разобьем его на элементарные прямоугольники со сторонами
и
(см. рис. 61). Площадь (а потому и масса) каждого такого прямоугольника равна
. Значит, момент инерции элементарного прямоугольника относительно стороны
равен
, а момент инерции всего прямоугольника относительно этой стороны выражается формулой
Криволинейную трапецию разобьем на элементарные прямоугольники со сторонами и
. Момент инерции каждого из этих прямоугольников относительно оси абсцисс выражается формулой
. Интегрируя, получаем момент инерции всей криволинейной трапеции относительно оси абсцисс:
Аналогично доказывается, что момент инерции криволинейной трапеции относительно оси ординат выражается формулой
(момент инерции элементарного прямоугольника относительно оси ординат равен ).
Полярный момент инерции (т. е. момент относительно начала координат) в этом случае выражается формулой
Пример 9. Вычислить момент инерции равнобедренного треугольника относительно его основания.
Решение. Расположим оси координат так, как показано на рисунке 65.
Пусть основание треугольника , высота
. Прямая
проходит через точки
и
. Ее уравнение
, то есть
.
Ясно, что момент инерции треугольника
относительно оси
равен удвоенному моменту инерции треугольника
относительно той же оси. Значит,
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Приложения криволинейных интегралов
Краткая теория
Длина дуги
Длину дуги
плоской или пространственной линии
определяют по формуле:
Масса дуги
Если
– линейная плотность вещества в точках дуги,
то массу
дуги
определяют по формуле:
Статистические моменты
Статистические
моменты
и
плоской дуги
относительно координатных осей
и
определяют по формулам:
Моменты инерции
Моменты
инерции
,
плоской дуги
относительно координатных осей
и
определяют по формулам:
Полярный момент инерции
Полярный
момент инерции
плоской дуги
относительно начала координат определяют по
формуле:
Площадь фигуры
Площадь
фигуры, расположенной в плоскости
и ограниченной замкнутой линией
, вычисляют по формуле:
Работа, приложенная к точке, при перемещении по дуге
Работу, совершаемую силой
приложенной в точке
при перемещении ее по дуге
, вычисляют по формуле:
Примеры решения задач
Задача 1
Найти
момент инерции относительно оси
четверти однородной окружности
, расположенной в первом
квадранте.
Решение
Окружность
однородна, следовательно
, следовательно искомый
момент инерции:
Для
удобства вычислений перейдем к параметрическим уравнениям окружности
Тогда:
Ответ:
Задача 2
Найти
массу дуги кривой
от точки
до
, если плотность в каждой точке
ее равна абсциссе точки;
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Плотность
дуги:
Искомая масса будет выражаться
криволинейным интегралом 1-го рода:
Производная:
Искомая масса:
Ответ:
.
Задача 3
Найти
массу дуги окружности
, лежащей в первой
четверти, если плотность в каждой ее точке равна абсциссе точки.
Решение
Плотность:
Искомая масса будет
выражаться криволинейным интегралом 1-го рода:
Параметрическое
уравнение окружности:
Окружность лежит в
первой четверти, поэтому
Ответ:
.
Задача 4
Вычислить
работу силы
при обходе точки ее приложения по границе
области
в положительном направлении, начиная от точки
.
Решение
Искомая
работа будет равна криволинейному интегралу 2-го рода:
Для
вычисления интеграла воспользуемся формулой Грина:
Ответ:
.
Задача 5
Вычислить
работу силового поля
при перемещении материальной точки вдоль пути
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Параметр
:
Перейдем к
определенному интегралу:
Искомая работа:
Ответ:
Задача 6
Вычислить
работу силы
при перемещении материальной точки вдоль линии
от точки
до точки
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Криволинейный
интеграл 2-го рода можно свести к определенному интегралу по следующей формуле:
Получаем:
Ответ:
Масса
$mathbf { textit { m } } $ материальной кривой $mathop { AB } limits^cup $ с плотностью $mu (mathbf { textit { x } } $,$mathbf { textit { y } } $,$mathbf { textit { z } } )$ вычисляется по формуле $m=intlimits_ { mathop { AB } limits^cup } { mu (x,y,z)dell } $.
Пример 1
Найти массу четверти лемнискаты $r^2=a^2cos 2varphi $, если плотность выражается формулой $mu (mathbf { textit { x } } $,$mathbf { textit { y } } )=ksqrt { x^2+y^2 } =kr$.
Решение:
$r=asqrt { cos 2varphi } $, $ { r } ‘=-afrac { sin 2varphi } { sqrt { cos 2varphi } } $ , поэтому
$m=intlimits_ { mathop { AB } limits^cup } { krdell } = kintlimits_0^ { pi / 4 } { asqrt { cos 2varphi } } cdot sqrt { a^2cos 2varphi +frac { a^2sin ^22varphi } { cos 2varphi } } dvarphi = frac { 1 } { 4 } pi ka^2$
Статические моменты и координаты центра масс
Пусть плоская материальная кривая $mathop { AB } limits^cup $ имеет плотность $mu (mathbf { textit { x } } $,$mathbf { textit { y } } )$.
Статический момент относительно оси $mathbf { textit { Ox } } $ определяется по формуле $M_x =intlimits_ { mathop { AB } limits^cup } { ymu (x,y)dell } $, относительно оси Oy: $M_y =intlimits_ { mathop { AB } limits^cup } { xmu (x,y)dell } $.
Аналогично, статические моменты пространственной кривой относительно координатных плоскостей вычисляются по формулам $ M_ { xy } =intlimits_ { mathop { AB } limits^cup } { zmu dell } , quad M_ { xz } =intlimits_ { mathop { AB } limits^cup } { ymu dell } , quad M_ { yz } =intlimits_ { mathop { AB } limits^cup } { xmu dell } $
Координаты центра масс могут быть найдены по формулам
$x_c =frac { M_ { y } } { m } ,quad ;y_c =frac { M_ { x } } { m } quad $ – для плоской кривой;
$x_c =frac { M_ { yz } } { m } ,quad ;y_c =frac { M_ { xz } } { m } ,quad ;z_c =frac { M_ { xy } } { m } quad -$ для пространственной кривой, где $mathbf { textit { m } } $ – масса кривой.
Пример 1
Найти центр масс четверти однородной окружности $x^2+y^2=a^2,xgeqslant 0,ygeqslant 0$
Решение:
Можно считать, что $mu =1$. Тогда масса кривой равна ее длине $m=frac { 2pi a } { 4 } =frac { pi a } { 2 } $. Статический момент $M_x $ равен $ M_x =intlimits_ { mathop { AB } limits^cup } { ydell } =intlimits_0^a { sqrt { a^2-x^2 } cdot sqrt { 1+frac { x^2 } { a^2-x^2 } } dx } =a^2. $ Из соображений симметрии $M_y =M_x $, поэтому координаты центра масс равны $ x_c =frac { M_y } { m } =frac { 2a } { pi } ,quad ;y_c =frac { M_x } { m } =frac { 2a } { pi } . $
Моменты инерции
Моменты инерции плоской кривой $mathop { AB } limits^cup $с плотностью $mu $ относительно координатных осей вычисляются по формулам $ I_ { Ox } =intlimits_ { mathop { AB } limits^cup } { y^2mu dell } , quad I_ { Oy } =intlimits_ { mathop { AB } limits^cup } { x^2mu dell } ; $ моменты инерции относительно начала координат $ I_0 =intlimits_ { mathop { AB } limits^cup } { (x^2+y^2)mu dell } =I_x +I_y $ В случае пространственной кривой моменты инерции относительно координатных осей и начала координат определяются по формулам $ I_ { Ox } =intlimits_ { mathop { AB } limits^cup } { (y^2+z^2)mu dell } , quad I_ { Oy } =intlimits_ { mathop { AB } limits^cup } { (x^2+z^2)mu dell } , quad I_ { Oz } =intlimits_ { mathop { AB } limits^cup } { (x^2+y^2)mu dell } , quad I_0 =intlimits_ { mathop { AB } limits^cup } { (x^2+y^2+z^2)mu dell =frac { I_ { Ox } +I_ { Oy } +I_ { Oz } } { 2 } } . $
Пример 1
Найти момент инерции относительно оси $mathbf { textit { Oz } } $ однородной винтовой линии $mu =1mathbf { textit { x } } =mathbf { textit { a } } cos mathbf { textit { t } } , mathbf { textit { y } } =mathbf { textit { a } } sin mathbf { textit { t } } , mathbf { textit { z } } =mathbf { textit { at } } ; 0 leqslant mathbf { textit { t } } leqslant 2pi $
Решение:
$I_ { Oz } =intlimits_ { mathop { AB } limits^cup } { (x^2+y^2)mu dell } =intlimits_0^ { 2pi } { (a^2cos ^2t+a^2sin ^2t)sqrt { a^2+a^2sin ^2t+a^2cos ^2t } dt=a^3sqrt 2 intlimits_0^ { 2pi } { dt=2sqrt 2 pi a^3 } } $.
Рабчук Александр Викторович1, Самигуллина Ракия Гареевна2
1Уфимский государственный авиационный технический университет, к.т.н.. доцент кафедры математики
2Уфимский государственный авиационный технический университет, старший преподаватель каф. математики
Аннотация
Традиционно, такие разделы высшей математики как криволинейные и поверхностные интегралы, особенно их применение, вызывают затруднения у студентов при изучении. Поэтому в данной статье кратко дана теория и приведено много разобранных примеров взятых из различных источников, в частности из [1,2,3].
Rabchuk Aleksandr Viktorovich1, Samigullina Rakiya Gareevna2
1Ufa State Aviation Technical University, PhD in Technical Science, Assistant Professor of the Mathematic Department
2Ufa State Aviation Technical University, Senior teacher of the Mathematic Department
Abstract
By tradition, devides higher mathematics by contour and surface integrals ,particularly application, is difficult by students.Therefor in this article give theori and many look into examples from [1,2,3].
Библиографическая ссылка на статью:
Рабчук А.В., Самигуллина Р.Г. Приложения криволинейных интегралов. Часть 1 // Современная педагогика. 2014. № 10 [Электронный ресурс]. URL: https://pedagogika.snauka.ru/2014/10/2675 (дата обращения: 24.02.2023).
Приложения криволинейного интеграла первого рода
1. Если подынтегральная функция равна единиц, то криволинейный интеграл
![]()
равен длине S кривой L, т.е.
![]()
![]()
2. Пусть в плоскости Оху задана гладкая кривая L, на которой определена и непрерывна функция двух переменных z=f(x,y)≥0. Тогда можно построить цилиндрическую поверхность с направляющей L и образующей, параллельной оси Оz и заключенной между L и поверхностью z=f(x,y). Площадь этой цилиндрической поверхности можно вычислить по формуле
![]()
3. Если L=AB – материальная кривая с плотностью, равной ρ=ρ(х,у), то масса этой кривой вычисляется по формуле
![]()
(физический смысл криволинейного интеграла первого рода).
4. Статистические моменты материальной кривой L относительно координатных осей Ох и Оу соответственно равны
![]()
![]()
![]()
![]()
где ρ(х,у) – плотность распределения кривой L а ![]()
![]() – координаты центра тяжести (центра масс) кривой L.
– координаты центра тяжести (центра масс) кривой L.
5. Интегралы
![]()
![]()
![]()
![]()
выражают моменты инерции кривой L с линейной плотностью ρ(х,у) относительно осей Ох, Оу и начала координат соответственно.
ПРИМЕРЫ:1. Вычислить криволинейный интеграл
![]()
где L – дуга параболы у2 = 2х, заключенная между точками (2, 2) и (8, 4).
![]() Найдем дифференциал дуги dl для кривой
Найдем дифференциал дуги dl для кривой ![]() . Имеем
. Имеем
![]()
![]()
![]()
Следовательно, данный интеграл равен
![]()
Ответ: ![]()
![]()
2. Вычислить криволинейный интеграл
![]()
где L – контур треугольника АВО с вершинами А(1,0), В(0,1), О(0,0)
Поскольку
![]()
то остается вычислить криволинейный интеграл по каждому из отрезков АВ, ВО и ОА :
1) (АВ): так как уравнение прямой АВ имеет вид у=1 – х, то ![]() . Отсюда, учитывая, что х меняется от 0 до 1, получим
. Отсюда, учитывая, что х меняется от 0 до 1, получим
2) (ВО): рассуждая аналогично, находим х=0, 0 ≤ у ≤ 1, ![]() откуда
откуда
.gif)
3) (ОА): ![]()
![]() .
.
.gif)
4) Окончательно
![]()
Ответ: ![]()
![]()
3. Вычислить криволинейный интеграл
![]()
где L – окружность ![]()
![]() Введем полярные координаты
Введем полярные координаты ![]()
![]() Тогда, поскольку
Тогда, поскольку ![]() уравнение окружности примет вид
уравнение окружности примет вид ![]() т.е.
т.е. ![]() а дифференциал дуги
а дифференциал дуги
![]()
При этом ![]() Следовательно,
Следовательно,
.gif)
Ответ: ![]()
![]()
4. Вычислить криволинейный интеграл первого рода от функции с тремя переменными
![]()
где L – дуга кривой, заданной параметрически ![]()
![]()
![]()
![]()
![]() Перейдем в подынтегральном выражении к переменной t. Имеем для подынтегральной функции:
Перейдем в подынтегральном выражении к переменной t. Имеем для подынтегральной функции:
![]()
Теперь выразим через t дифференциал dl:
.gif)
Таким образом,
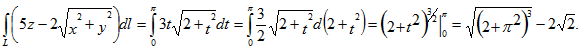
Ответ: ![]()
![]()
5. Вычислить площадь части боковой поверхности кругового цилиндра ![]() , ограниченной снизу плоскостью Оху, а сверху поверхностью
, ограниченной снизу плоскостью Оху, а сверху поверхностью ![]()
![]() Искомая площадь вычисляется по формуле
Искомая площадь вычисляется по формуле
.gif)
где L – окружность x2+y2=R2. Поверхность цилиндра и поверхность ![]() симметричны относительно координатных плоскостей Оxz и Oyz, поэтому можно ограничиться вычислением интеграла при условиях у≥0, х≥0, т.е. вычислить четверть искомой площади и результат умножить на 4. Имеем
симметричны относительно координатных плоскостей Оxz и Oyz, поэтому можно ограничиться вычислением интеграла при условиях у≥0, х≥0, т.е. вычислить четверть искомой площади и результат умножить на 4. Имеем
![]()
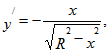
.gif)
Следовательно,
.gif)
![]() Получили определенный интеграл, который берем подстановкой
Получили определенный интеграл, который берем подстановкой ![]() откуда
откуда
![]()
![]()
![]()
.gif)
Ответ: ![]()
![]()
6. Найти массу четверти эллипса
.gif)
расположенной в первой четверти, если линейная плотность в каждой точке пропорциональна ординате этой точки с коэффициентом k.
![]() Поскольку р(х, у)=ky, имеем
Поскольку р(х, у)=ky, имеем
![]()
L – четверть эллипса
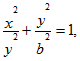 х≥0, у≥0.
х≥0, у≥0.
Переходим к параметрическим координатам эллипса ![]() Напомним, что
Напомним, что ![]() – фокусное расстояние эллипса, а
– фокусное расстояние эллипса, а ![]() – эксцентриситет эллипса. Находим
– эксцентриситет эллипса. Находим
.gif)
Переходим к вычислению массы
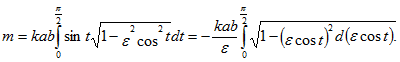
Воспользуемся формулой
![]()
где ![]() Получаем
Получаем
![]()
Учитывая, что 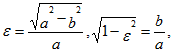 получим окончательно
получим окончательно
.gif)
Ответ: .gif)
![]()
7. Найти координаты центра тяжести дуги окружности x2+y2=R2(0≤ x ≤R, 0≤ y ≤R).
![]() Так как по условию задана четверть дуги окружности, то ее длина
Так как по условию задана четверть дуги окружности, то ее длина ![]() В силу того, что биссектриса I координатного угла является осью симметрии, имеем
В силу того, что биссектриса I координатного угла является осью симметрии, имеем ![]() . Теперь находим
. Теперь находим
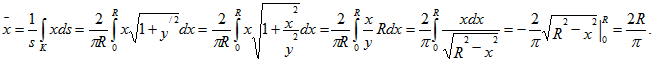
Ответ: ![]()
Приложения криволинейного интеграла второго рода
Интеграл
![]()
можно представить в виде скалярного произведения векторов F=Pi+Qi и ds=idx+jdy:
![]()
В таком случае
![]()
Выражает работу переменной силы F=Pi+Qj при перемещении материальной точки М=М(х,у) вдоль кривой L=AB от точки А до точки В.
При А=В кривая L замкнута, а соответствующий криволинейный интеграл по замкнутой кривой обозначается так:
![]()
В этом случае направление обхода контура иногда поясняется стрелкой на кружке, расположенном на знаке интеграла.
Предположим, что в плоскости Оху имеется односвязная область D (это значит, что в ней нет «дыр»), ограниченная кривой ![]() , (
, (![]() – обозначение границы области D), а в области D и на ее границе
– обозначение границы области D), а в области D и на ее границе ![]() функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными.
функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными.
Теорема: Пусть А и В – произвольные точки области D, AmB и AnB – два произвольных пути (гладкие кривые), соединяющие эти точки (рис. 2).
Тогда следующие условия равносильны:
1. ![]() (условие Грина).
(условие Грина).
2. ![]() (криволинейный интеграл не зависит от пути интегрирования).
(криволинейный интеграл не зависит от пути интегрирования).
3. ![]() (интеграл по любому замкнутому пути равен нулю).
(интеграл по любому замкнутому пути равен нулю).
4. ![]() (выражение
(выражение ![]() представляет собой полный дифференциал некоторой функции
представляет собой полный дифференциал некоторой функции ![]() ).
).
В случае выполнения любого из равносильных условий предыдущей теоремы криволинейный интеграл по любой кривой, соединяющей точки (хо, уо) и (х1, у1) из области D, можно вычислить при помощи формулы Ньютона-Лейбница
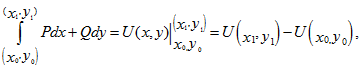
где U(x, y) – некоторая первообразная для P dx + Q dy.
С другой стороны, первообразная U(x, y) выражения P dx + Q dy может быть найдена при помощи криволинейного интеграла
.gif)
В этих же условиях на функции Р(х,у) и Q(х,у), а также на область D, имеет место формула Грина, позволяющая свести криволинейный интеграл по замкнутому контуру к двойному интегралу
![]()
Здесь предполагается, что обход границы ![]() области D в криволинейном интеграле
области D в криволинейном интеграле
![]()
совершается в положительном направлении, т.е. при таком обходе границы область D остается слева; для односвязной области это направление совпадает с направлением против часовой стрелки.
Заметим, что площадь S=S(D) области D может быть вычислена при помощи криволинейного интеграла второговрода:
![]()
(эта формула получается из формулы Грина с ![]() ).
).
ПРИМЕРЫ:1. Даны функции Р(х ,у) = 8х+4у+2, Q(х ,у) = 8у+2 и точки А(3, 6), В(3,0), С(0,6). Вычислить криволинейный интеграл
![]()
где:
1) L – отрезок ОА;
2) L – ломаная ОВА;
3) L – ломаная ОСА;
4) L – парабола, симметричная относительно оси Оу и проходящая через точки О и А;
5) проверить выполнимость условия Грина.
1) Отрезок ОА может быть записан в виде: у=2х, ![]() . Тогда dy=2dx и
. Тогда dy=2dx и
.gif)
2) Используем свойство аддитивности, вычисляя отдельно интеграл по отрезкам ОВ и ВА. Тогда:
а) ОВ: здесь у=0, 0≤х≤3, т.е. dy=0, откуда
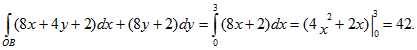
б) ВА: х=3, 0≤у≤6, т.е. dx=0, и
.gif)
Таким образом,
![]()
![]()
3) Этот интеграл вычислим аналогично предыдущему.
а) ОС: х=0, (т.е. dx=0), 0≤y≤6, откуда

б) СА: 0≤х≤3 , у=6, dy=0, следовательно,
.gif)
Окончательно
![]()
4) Подставив координаты точки А(3;6) в равенство у=ах2 найдем уравнение данной параболы ![]() . При этом 0≤х≤3 и
. При этом 0≤х≤3 и ![]() откуда (путь ОА по параболе обозначим
откуда (путь ОА по параболе обозначим ![]() )
)
.gif)
5) Имеем
![]()
т.е. условие Грина не выполняется. Этот факт, а также вычисления в пунктах 1) – 4) этой задачи показывают, что данный криволинейный интеграл второго рода зависит от пути интегрирования.
2. Вычислить интеграл
![]()
где L – верхняя половина эллипса .gif) пробегаемая по ходу часовой стрелки.
пробегаемая по ходу часовой стрелки.
![]() Воспользуемся параметрическими уравнениями эллипса: х=a cost, y=b sin t,
Воспользуемся параметрическими уравнениями эллипса: х=a cost, y=b sin t, ![]() т.е. dx = – a sin t dt, dy = b cos t dt. Подставляя в интеграл и учитывая направление обхода (откуда следует, что t меняется от π до 0), получаем
т.е. dx = – a sin t dt, dy = b cos t dt. Подставляя в интеграл и учитывая направление обхода (откуда следует, что t меняется от π до 0), получаем
.gif) Ответ:
Ответ: ![]()
![]()
3. Вычислить криволинейный интеграл
![]()
где L – отрезок, соединяющий точку С(2, 3, -1) с точкой D(3, -2, 0).
![]() Составим параметрические уравнения отрезка СD, используя уравнения прямой, проходящей через две точки:
Составим параметрические уравнения отрезка СD, используя уравнения прямой, проходящей через две точки:
![]()
Отсюда ![]() . Далее, находим
. Далее, находим ![]() подставляем все нужные выражения в данный интеграл, обозначенный через J, и вычисляем определенный интеграл:
подставляем все нужные выражения в данный интеграл, обозначенный через J, и вычисляем определенный интеграл:
.gif)
Ответ: ![]()
4. Вычислить ![]() где К – отрезок прямой от А(0 ;0) до В (4; 3).
где К – отрезок прямой от А(0 ;0) до В (4; 3).
![]() Уравнение прямой АВ имеет вид у=(3; 4)х. Находим у/= ¾ и, следовательно,
Уравнение прямой АВ имеет вид у=(3; 4)х. Находим у/= ¾ и, следовательно,
.gif)
Ответ: ![]()
5. Вычислить ![]() если
если ![]()
![]() Найдем
Найдем ![]() Тогда
Тогда
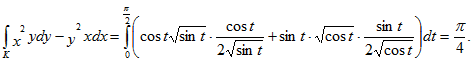
Ответ: ![]()
6. Найти массу М дуги кривой x=t, y=t2/2, z=t3/3 (0≤ t ≤1), линейная плотность которой меняется по закону ![]()
![]()
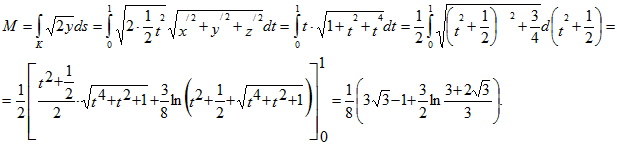
Ответ: 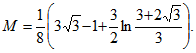
![]()
7. Вычислить криволинейный интеграл ![]() от точки А(1, 0) до точки В(0, 2) (рис. 3):
от точки А(1, 0) до точки В(0, 2) (рис. 3):
1) по прямой 2х+у=2;
2) по дуге параболы 4х+у2=4;
3) по дуге эллипса x=cost, y=2sint.
1) Пользуясь данным уравнением линии интегрирования, преобразуем криволинейный интеграл в обыкновенный определенный интеграл с переменной х, затем вычисляем его:
у=2-2х, dy=-2dx,
.gif)
2) Здесь удобно преобразовать криволинейный интеграл в обыкновенный интеграл с переменной у:
.gif)
3) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем его: x=cost, dx=-sintdt; y=2sint; dy=2costdt:

Ответ: I1=1, I2=-1/5, I3=4/3. ![]()
8. Вычислить криволинейный интеграл ![]() между точками Е
между точками Е
(-1, 0) и Н (0, 1):
1) по прямой ЕН;
2) по дуге астроиды х=cos3t, y=sin3t.
![]() 1) Вначале составляем уравнение линии интегрирования – прямой ЕН, как уравнение прямой, проходящей через две известные точки: у-х=1.
1) Вначале составляем уравнение линии интегрирования – прямой ЕН, как уравнение прямой, проходящей через две известные точки: у-х=1.
Пользуясь этим уравнением и известной формулой для дифференциала дуги плоской кривой преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной х и вычисляем его:
.gif)
2) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем:
![]()
![]() ибо π/2≤ t ≤π;
ибо π/2≤ t ≤π;
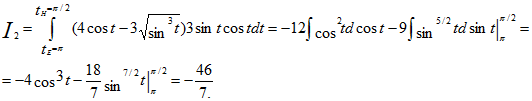
Ответ: ![]()
9. Даны точки А(3, -6, 0) и В(-2, 4, 5). Вычислить криволинейный интеграл ![]()
1) по прямолинейному отрезку ОВ;
2) по дуге АВ окружности, заданной уравнениями x2+y2+z2=45, 2x+y=0.
![]() 1) Вначале составляем уравнения линии интегрирования – прямой ОВ.
1) Вначале составляем уравнения линии интегрирования – прямой ОВ.
Пользуясь общими уравнениями прямой, проходящей через две точки .gif) получим
получим ![]() Приравнивая эти равные отношения параметру t, преобразуем полученные канонические уравнения прямой ОВ к параметрическому виду: x=-2t, y=4t, z=5t.
Приравнивая эти равные отношения параметру t, преобразуем полученные канонические уравнения прямой ОВ к параметрическому виду: x=-2t, y=4t, z=5t.
Далее, пользуясь этими уравнениями, преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной t, затем вычисляем его
.gif)
2) Преобразуем данные уравнения окружности к параметрическому виду. Полагая х=t, получим у=-2t (из второго данного уравнения), ![]() (из первого уравнения). Отсюда
(из первого уравнения). Отсюда .gif) и
и

Ответ: ![]()
![]()
10. Вычислить криволинейные интегралы:
1) ![]()
2) ![]() вдоль периметра треугольника с
вдоль периметра треугольника с
вершинами А(-1,0), В (0,2) и С (2,0)
Составив уравнение прямой АВ, у-2х=2, и исходя из этого уравнения, преобразуем криволинейный интеграл на отрезке АВ в обыкновенный интеграл с переменной х:
у=2х+2, dy=2dx, 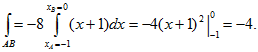
Аналогичным путем вычисляя криволинейный интеграл на отрезках ВС и СА, получим
х=2-у, dx=-dy,
.gif)
Следовательно,
![]()
2) Здесь подынтегральное выражение есть полный дифференциал функции двух переменных, ибо (уcosx)’y =(sinx)’x =cosx. Вследствии этого данный криволинейный интеграл, взятый по периметру данного треугольника равен нулю. Он будет равен нулю и по любому другому замкнутому контуру.
Ответ: ![]()
11. Найти длину кардиоиды x=2acost-acos2t, y=2asint-asin2t.
![]() Применяем формулу
Применяем формулу ![]() , исходя из данных параметрических уравнений кардиоиды и формулы для дифференциала дуги плоской кривой, преобразуем криволинейный интеграл формулы в обыкновенный интеграл с переменной t.
, исходя из данных параметрических уравнений кардиоиды и формулы для дифференциала дуги плоской кривой, преобразуем криволинейный интеграл формулы в обыкновенный интеграл с переменной t.
.gif)
Ответ: L=16a. ![]()
12. Найти площадь, ограниченную замкнутой кривой:
1) эллипсом x=a cost, y=b sint;
2) петлей декартова листа х3+у3-3аху=0.
![]() 1) Применяем формулу
1) Применяем формулу ![]() , исходя из данных параметрических уравнений эллипса, преобразуем криволинейный интеграл в обыкновенный интеграл с переменной t и вычисляем его:
, исходя из данных параметрических уравнений эллипса, преобразуем криволинейный интеграл в обыкновенный интеграл с переменной t и вычисляем его:
.gif)
2) Вначале преобразуем данное уравнение к параметрическому виду. Полагая у=хt, получим ![]()
Геометрический параметр t=y/x есть угловой коэффициент полярного радиуса ОМ (рис. 6), точка М(х, у) опишет всю петлю кривой при изменении t от 0 до +∞.
Преобразуя криволинейный интеграл формулы ![]() в обыкновенный интеграл с переменной t , получим
в обыкновенный интеграл с переменной t , получим
.gif)
Ответ: S=3a2/2. ![]()
13. Найти массу дуги АВ кривой у=lnx, если в каждой ее точке линейная плотность пропорциональна квадрату абсциссы точки: хА=1, хВ=3.
![]() Применяем формулу
Применяем формулу ![]() , исходя из данного уравнения кривой, преобразуем криволинейный интеграл в обыкновенный с переменной х
, исходя из данного уравнения кривой, преобразуем криволинейный интеграл в обыкновенный с переменной х

Ответ: ![]()
14. Найти координаты центра тяжести дуги АВ винтовой линии х=аcost, y=asint, z=bt, если в каждой ее точке линейная плотность пропорциональна аппликате этой точки: tA=0, tB=π.
![]() Применяя формулы
Применяя формулы .gif) вычислим криволинейные интегралы, преобразуя их в обыкновенные интегралы с переменной t:
вычислим криволинейные интегралы, преобразуя их в обыкновенные интегралы с переменной t:
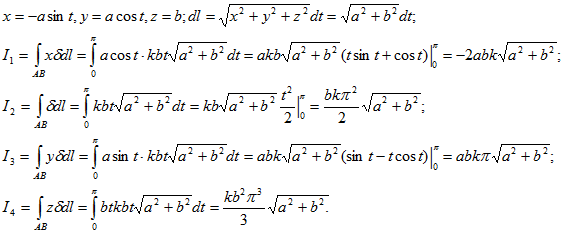
Следовательно, ![]()
Ответ: ![]()
15. Вычислить работу, совершаемую силой тяжести при перемещении точки массы m по дуге АВ некоторой кривой.
![]() Если выбрать прямоугольную систему координат так, чтобы направление оси Оz совпало с направлением силы тяжести, то действующая на точку сила
Если выбрать прямоугольную систему координат так, чтобы направление оси Оz совпало с направлением силы тяжести, то действующая на точку сила ![]() а ее проекции на оси координат Fx=P=O, Fy=Q=0, Fz=R=mg.
а ее проекции на оси координат Fx=P=O, Fy=Q=0, Fz=R=mg.
Искомая работа согласно формуле ![]()
.gif)
Она зависит только от разности аппликат начала и конца пути, но не зависит от формы пути.
16. Найти работу силового поля, в каждой точке (х,у) которого напряжение (сила, действующая на единицу массы) ![]() , когда точка массы m описывает окружность x=accost, y=asint, двигаясь по ходу часовой стрелки.
, когда точка массы m описывает окружность x=accost, y=asint, двигаясь по ходу часовой стрелки.
![]() Подставляя в формулу
Подставляя в формулу ![]() проекции силы
проекции силы ![]() действующей на точку: Fx=m(x+y), Fy= – mx, и преобразуя криволинейный интеграл в обыкновенный с переменной t, получим
действующей на точку: Fx=m(x+y), Fy= – mx, и преобразуя криволинейный интеграл в обыкновенный с переменной t, получим

Ответ: Е=2πma2.
Библиографический список
- Лунгу К.Н. Сборник задач по высшей математике. 1 курс – 7-е изд., – М.: Айрис-пресс, 2008.
- Лунгу К.Н. Сборник задач по высшей математике. 2 курс – 5-е изд., – М.: Айрис-пресс, 2007.
- Письменный Д.Т. Конспект лекций по высшей математике: полный курс – 7-е изд. – М.: Айрис-пресс, 2008.
Все статьи автора «Рабчук Александр Викторович»
16.3. Криволинейные интегралы.

16.3.1. Введение. Рассмотрим следующую физическую задачу. Пусть в пространстве Oxyz вдоль кривой  перемещается материальная точка под воздействием силы
перемещается материальная точка под воздействием силы  ; при этом сила может меняться от точки к точке. Требуется найти работу, которая совершается силой.
; при этом сила может меняться от точки к точке. Требуется найти работу, которая совершается силой.
В случае, когда в качестве берётся
берётся  – прямолинейный отрезок (левая часть рисунка), и
– прямолинейный отрезок (левая часть рисунка), и  – постоянная сила, работа есть скалярное произведение силы на вектор перемещения точки:
– постоянная сила, работа есть скалярное произведение силы на вектор перемещения точки:  . Это выражение можно трактовать двумя способами.
. Это выражение можно трактовать двумя способами.
1. По определению скалярного произведения  . Здесь
. Здесь ,
,  – угол между
– угол между  . Обозначим
. Обозначим  , тогда
, тогда  .
.
2. Если расписать скалярное произведение в координатной форме, то  .
.
Пусть теперь  – произвольная гладкая ограниченная кривая, и сила
– произвольная гладкая ограниченная кривая, и сила  может меняться от точки к точке (правая часть рисунка). Чтобы свести этот случай к предыдущему, разобьём кривую
может меняться от точки к точке (правая часть рисунка). Чтобы свести этот случай к предыдущему, разобьём кривую  точками
точками  на
на  частей, на каждой из дуг
частей, на каждой из дуг  выберем произвольную точку
выберем произвольную точку  , и, считая, что дуга
, и, считая, что дуга  – прямолинейный отрезок – вектор
– прямолинейный отрезок – вектор  длины
длины  , и сила вдоль этого отрезка постоянна и равна
, и сила вдоль этого отрезка постоянна и равна  , получим, что работа вдоль этой дуги близка к
, получим, что работа вдоль этой дуги близка к  (
( ). Как мы видели, это выражение можно представить и в виде
). Как мы видели, это выражение можно представить и в виде 
(где 
 – угол между
– угол между  и
и  ), и в виде
), и в виде  . Суммируя эти выражения по всем
. Суммируя эти выражения по всем  дугам, получим выражения двух интегральных сумм:
дугам, получим выражения двух интегральных сумм:  и
и  . Переход к пределу в этих интегральных суммах при
. Переход к пределу в этих интегральных суммах при  приведёт к двум криволинейным интегралам:
приведёт к двум криволинейным интегралам:  и
и  . Первый из этих интегралов называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги; второй – криволинейным интегралом второго рода, или криволинейным интегралом по координатам. Несмотря на то, что они описывают одну и ту же физическую величину, с математической точки зрения это разные объекты. Они имеют разные определения и разные свойства. В частности, криволинейный интеграл первого рода не зависит от направления прохождения кривой:
. Первый из этих интегралов называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги; второй – криволинейным интегралом второго рода, или криволинейным интегралом по координатам. Несмотря на то, что они описывают одну и ту же физическую величину, с математической точки зрения это разные объекты. Они имеют разные определения и разные свойства. В частности, криволинейный интеграл первого рода не зависит от направления прохождения кривой:  (так как угол
(так как угол  между силой и кривой входит в подынтегральную функцию в явном виде), в то время как криволинейный интеграл второго рода меняет знак при изменении направления прохождения кривой:
между силой и кривой входит в подынтегральную функцию в явном виде), в то время как криволинейный интеграл второго рода меняет знак при изменении направления прохождения кривой:  (вектор
(вектор  , координаты которого входят в интегральную сумму, меняется на вектор
, координаты которого входят в интегральную сумму, меняется на вектор  ).
).
Перейдём к формальным определениям.
Рекомендуемые материалы
16.3.2. Криволинейный интеграл первого рода (по длине дуги).
16.3.2.1. Определение криволинейного интеграла первого рода. Пусть в пространстве переменных x,y,z задана кусочно-гладкая кривая  , на которой определена функция f(x,y,z). Разобьём кривую точками
, на которой определена функция f(x,y,z). Разобьём кривую точками  на
на  частей, на каждой из дуг
частей, на каждой из дуг  выберем произвольную точку
выберем произвольную точку  , найдём
, найдём  и длину
и длину  дуги
дуги  , и составим интегральную сумму
, и составим интегральную сумму  . Если существует предел последовательности интегральных сумм при
. Если существует предел последовательности интегральных сумм при  , не зависящий ни от способа разбиения кривой на дуги
, не зависящий ни от способа разбиения кривой на дуги  , ни от выбора точек
, ни от выбора точек  , то функция f(x,y,z) называется интегрируемой по кривой
, то функция f(x,y,z) называется интегрируемой по кривой  , а значение этого предела называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги от функции f(x,y,z) по кривой
, а значение этого предела называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги от функции f(x,y,z) по кривой  , и обозначается
, и обозначается  (или
(или  ).
).

Теорема существования. Если функция f(x,y,z) непрерывна на кусочно-гладкой кривой  , то она интегрируема по этой кривой.
, то она интегрируема по этой кривой.
Случай замкнутой кривой. В этом случае в качестве начальной и конечной точки можно взять произвольную точку кривой. Замкнутую кривую в дальнейшем будем называть контуром и обозначать буквой С. То, что кривая, по которой вычисляется интеграл, замкнута, принято обозначать кружочком на знаке интеграла:  .
.
16.3.2.2. Свойства криволинейного интеграла первого рода. Для этого интеграла имеют место все шесть свойств, справедливых для определённого, двойного, тройного интеграла, от линейности до теоремы о среднем. Сформулировать и доказать их самостоятельно. Однако для этого интеграла справедливо и седьмое, персональное свойство:
Независимость криволинейного интеграла первого рода от направления прохождения кривой:  .
.
Доказательство. Интегральные суммы для интегралов, стоящих в правой и левой частях этого равенства, при любом разбиении кривой и выборе точек  совпадают (всегда длина дуги
совпадают (всегда длина дуги 
 ), поэтому равны их пределы при
), поэтому равны их пределы при  .
.
16.3.2.3. Вычисление криволинейного интеграла первого рода. Примеры. Пусть кривая  задана параметрическими уравнениями
задана параметрическими уравнениями  , где
, где  – непрерывно дифференцируемые функции, и пусть точкам
– непрерывно дифференцируемые функции, и пусть точкам  , которые задают разбиение кривой, соответствуют значения параметра
, которые задают разбиение кривой, соответствуют значения параметра  , т.е.
, т.е.  . Тогда (см. раздел 13.3. Вычисление длин кривых)
. Тогда (см. раздел 13.3. Вычисление длин кривых)  . По теореме о среднем, существует точка
. По теореме о среднем, существует точка  такая, что
такая, что  . Выберем точки
. Выберем точки  , получающиеся при этом значении параметра:
, получающиеся при этом значении параметра: 
 . Тогда интегральная сумма для криволинейного интеграла
. Тогда интегральная сумма для криволинейного интеграла  будет равна интегральной сумме для определенного интеграла
будет равна интегральной сумме для определенного интеграла  . Так как
. Так как  , то, переходя к пределу при
, то, переходя к пределу при  в равенстве
в равенстве  , получим
, получим
 .
.
Таким образом, вычисление криволинейного интеграла первого рода сводится к вычислению определённого интеграла по параметру. Если кривая задана параметрически, то этот переход не вызывает трудностей; если дано качественное словесное описание кривой, то основной трудностью может быть введение параметра на кривой. Ещё раз подчеркнём, что интегрирование всегда ведётся в сторону возрастания параметра.
Примеры. 1. Вычислить  , где
, где  – один виток спирали
– один виток спирали 
Здесь переход к определённому интегралу проблем не вызывает: находим  , и
, и  .
.
2. Вычислить тот же интеграл по отрезку прямой, соединяющей точки  и
и  .
.
Здесь прямого параметрического задания кривой нет, поэтому на АВ необходимо ввести параметр. Параметрические уравнения прямой имеют вид  где
где  – направляющий вектор,
– направляющий вектор,  – точка прямой. В качестве точки берем точку
– точка прямой. В качестве точки берем точку  , в качестве направляющего вектора – вектор
, в качестве направляющего вектора – вектор  :
:  . Легко видеть, что точка
. Легко видеть, что точка  соответствует значению
соответствует значению  , точка
, точка  – значению
– значению  , поэтому
, поэтому  .
.

3. Найти , где
, где  – часть сечения цилиндра
– часть сечения цилиндра  плоскостью z=x+1, лежащая в первом октанте.
плоскостью z=x+1, лежащая в первом октанте.
Решение: Параметрические уравнения окружности – направляющей цилиндра имеют вид x=2cosj, y=2sinj, и так как z=x+1, то z= 2cosj+1. Итак,
 поэтому
поэтому

16.3.2.3.1. Вычисление криволинейного интеграла первого рода. Плоский случай. Если кривая лежит на какой-либо координатной плоскости, например, плоскости Оху, и задаётся функцией  , то, рассматривая х как параметр, получаем следующую формулу для вычисления интеграла:
, то, рассматривая х как параметр, получаем следующую формулу для вычисления интеграла:  . Аналогично, если кривая задаётся уравнением
. Аналогично, если кривая задаётся уравнением  , то
, то  .
.
Пример. Вычислить  , где
, где  – четверть окружности
– четверть окружности  , лежащая в четвёртом квадранте.
, лежащая в четвёртом квадранте.

Решение. 1. Рассматривая х как параметр, получаем 
 , поэтому
, поэтому 
 .
.
2. Если за параметр взять переменную у, то 
 и
и  .
.
3. Естественно, можно взять обычные параметрические уравнения окружности 
 :
:  .
.
Если кривая задана в полярных координатах  , то
, то  , и
, и  .
.
16.3.2.4. Механические приложения криволинейного интеграла 1-го рода.
16.3.2.4.1. Масса m материальной кривой  с плотностью m(x,y,z) вычисляется по формуле
с плотностью m(x,y,z) вычисляется по формуле  .
.
Пример. Найти массу четверти лемнискаты  , если плотность выражается формулой m(x,y)=
, если плотность выражается формулой m(x,y)= .
.
Решение:  , поэтому
, поэтому 
16.3.2.4.2. Статические моменты и координаты центра масс. Пусть плоская материальная кривая  имеет плотность m(x,y). Статический момент относительно оси Ox определяется по формуле
имеет плотность m(x,y). Статический момент относительно оси Ox определяется по формуле  , относительно оси Oy:
, относительно оси Oy:  .
.
Аналогично, статические моменты пространственной кривой относительно координатных плоскостей вычисляются по формулам
 ,
,  ,
, 
Координаты центра масс могут быть найдены по формулам
 – для плоской кривой;
– для плоской кривой;
 – для пространственной кривой, где m – масса кривой.
– для пространственной кривой, где m – масса кривой.
Пример. Найти центр масс четверти однородной окружности 
Решение: Можно считать, что m=1. Тогда масса кривой равна ее длине  . Статический момент
. Статический момент  равен
равен

Из соображений симметрии  , поэтому координаты центра масс равны
, поэтому координаты центра масс равны
 .
.
16.3.2.4.3. Моменты инерции. Моменты инерции плоской кривой  с плотностью m относительно координатных осей вычисляются по формулам
с плотностью m относительно координатных осей вычисляются по формулам
 ,
, 
моменты инерции относительно начала координат

В случае пространственной кривой моменты инерции относительно координатных осей и начала координат определяются по формулам
 ,
,  ,
,  ,
, 
Пример. Найти момент инерции относительно оси Oz однородной винтовой линии (m=1) x=acos t, y=asin t, z=at; 0 £ t £ 2p
Решение:  .
.
16.3.3. Криволинейный интеграл второго рода (по координатам).

16.3.3.1. Определение криволинейного интеграла второго рода. Пусть в пространстве Oxyz дана кусочно-гладкая кривая  , на которой определена функция
, на которой определена функция  . Разобьём кривую точками
. Разобьём кривую точками 
 на
на  частей, на каждой из дуг
частей, на каждой из дуг  выберем произвольную точку
выберем произвольную точку  , найдём
, найдём  и проекцию
и проекцию  дуги
дуги  на ось Ох, и составим интегральную сумму
на ось Ох, и составим интегральную сумму  . Если существует предел последовательности интегральных сумм при
. Если существует предел последовательности интегральных сумм при  , не зависящий ни от способа разбиения кривой на дуги
, не зависящий ни от способа разбиения кривой на дуги  , ни от выбора точек
, ни от выбора точек  , то функция Р(x,y,z) называется интегрируемой по кривой
, то функция Р(x,y,z) называется интегрируемой по кривой  , а значение этого предела называется криволинейным интегралом второго рода, или криволинейным интегралом по координате х от функции Р(x,y,z) по кривой
, а значение этого предела называется криволинейным интегралом второго рода, или криволинейным интегралом по координате х от функции Р(x,y,z) по кривой  , и обозначается
, и обозначается  (или
(или  ).
).
Теорема существования. Если функция Р(x,y,z) непрерывна на кривой  , то она интегрируема по этой кривой.
, то она интегрируема по этой кривой.
Если на кривой  , вместе с функцией Р(x,y,z), заданы функции Q(x,y,z) и R(x,y,z), то, аналогично интегралу
, вместе с функцией Р(x,y,z), заданы функции Q(x,y,z) и R(x,y,z), то, аналогично интегралу  , определяются интегралы
, определяются интегралы  и
и . В приложениях рассматривается сумма этих интегралов, которая обозначается
. В приложениях рассматривается сумма этих интегралов, которая обозначается  и также называется криволинейным интегралом второго рода. Если кривая, по которой ведётся интегрирование, является контуром (т.е. замкнута), то, как и для криволинейного интеграла по длине дуги, в качестве начальной (и совпадающей с ней конечной) точки можно взять любую точку кривой.
и также называется криволинейным интегралом второго рода. Если кривая, по которой ведётся интегрирование, является контуром (т.е. замкнута), то, как и для криволинейного интеграла по длине дуги, в качестве начальной (и совпадающей с ней конечной) точки можно взять любую точку кривой.
16.3.3.2. Свойства криволинейного интеграла второго рода. Для этого интеграла существенны следующие свойства:
16.3.3.2.1. Линейность. Если функции  интегрируемы по кривой
интегрируемы по кривой  (каждая по своей координате, то по этой кривой интегрируемы функции
(каждая по своей координате, то по этой кривой интегрируемы функции  , и
, и 
16.3.3.2.2. Аддитивность. Если кривая  разбита на две части
разбита на две части  и
и  , не имеющие общих внутренних точек, то
, не имеющие общих внутренних точек, то  .
.
Доказательство этих свойств такое же, как и для других типов интегралов; воспроизвести их самостоятельно. Персональное свойство криволинейного интеграла по координатам:
16.3.3.2.3. Изменение знака криволинейного интеграла второго рода при изменении направления прохождения кривой:  .
.
Доказательство очевидно: при изменении направления прохождения кривой меняет знак каждая проекция  , следовательно, меняет знак интегральная сумма, следовательно, меняет знак предел последовательности интегральных сумм.
, следовательно, меняет знак интегральная сумма, следовательно, меняет знак предел последовательности интегральных сумм.
16.3.3.3. Вычисление криволинейного интеграла второго рода. Примеры. Пусть кривая  задана параметрическими уравнениями
задана параметрическими уравнениями  , где
, где  – непрерывно дифференцируемые функции, и пусть точкам
– непрерывно дифференцируемые функции, и пусть точкам  , которые задают разбиение кривой, соответствуют значения параметра
, которые задают разбиение кривой, соответствуют значения параметра  , т.е.
, т.е.  . Тогда по теореме Лагранжа существуют такие точки
. Тогда по теореме Лагранжа существуют такие точки  , что
, что  . Выберем точки
. Выберем точки  , получающиеся при этих значениях параметра:
, получающиеся при этих значениях параметра: 
 . Тогда интегральная сумма для криволинейного интеграла
. Тогда интегральная сумма для криволинейного интеграла  будет равна интегральной сумме для определенного интеграла
будет равна интегральной сумме для определенного интеграла  . Так как
. Так как  , то, переходя к пределу при
, то, переходя к пределу при  в равенстве
в равенстве  , получим
, получим
 . Аналогично доказываются формулы для интегралов по другим координатам. Окончательно
. Аналогично доказываются формулы для интегралов по другим координатам. Окончательно 
Таким образом, вычисление криволинейного интеграла второго рода ни чем не отличается от вычисления интеграла первого и сводится к интегрированию по параметру. Направление интегрирования определяется условиями задачи.
Примеры. 1. Найти  , где
, где  – виток винтовой линии x=a×cos t, y=a×sin t, z=a×t, 0 £ t £ 2p.
– виток винтовой линии x=a×cos t, y=a×sin t, z=a×t, 0 £ t £ 2p.
Решение: 
Пусть плоская кривая задана в декартовой системе координат уравнением y=y(x), A(a,y(a)), B(b,y(b)). Тогда
 .
.
Пример 2. Найти  по кривой
по кривой  .
.

Решение: Пользуясь свойством аддитивности, разобьем интеграл на сумму двух:

Пример 3. Найти  , где C – окружность, проходимая в отрицательном направлении (по часовой стрелке).
, где C – окружность, проходимая в отрицательном направлении (по часовой стрелке).

Решение: Параметризуем окружность x=2cos t, y=2sin t, 0 £ t £ 2p. Движению по часовой стрелке соответствует уменьшение параметра t, поэтому интегрируем от  до 0:
до 0:

 Пример 4. Вычислить
Пример 4. Вычислить  по каждому из путей, соединяющих точки О(0,0) и А(2,4), и изображённых на рисунке справа:
по каждому из путей, соединяющих точки О(0,0) и А(2,4), и изображённых на рисунке справа:
1. Ломаная ОВА, состоящая из прямолинейных отрезков;
2. Ломаная ОСА;
3. Прямолинейный отрезок ОА;
4-5. Параболы ODA и OEA, симметричные относительно координатных осей.
Решение. 1. 
 (по свойству аддитивности). На ОВ в качестве параметра естественно выбрать переменную х, при этом
(по свойству аддитивности). На ОВ в качестве параметра естественно выбрать переменную х, при этом  , поэтому
, поэтому  . На ВА
. На ВА  , поэтому
, поэтому  . Окончательно,
. Окончательно,  .
.
2.  .
.
 .
.  . Окончательно,
. Окончательно,  .
.
3. На прямолинейном отрезке ОА  , поэтому
, поэтому  .
.
4. Уравнение параболы ОЕА имеет вид  , значение коэффициента k найдём, подставляя в это уравнение координаты точки А:
, значение коэффициента k найдём, подставляя в это уравнение координаты точки А:  , поэтому
, поэтому  .
.
5. Совершенно также убеждаемся, что интеграл по параболе ODA имеет то же значение.
Закономерен вопрос: для любого ли интеграла и любых начальной и конечной точек значение интеграла не зависит от формы пути, соединяющего эти точки? Убедимся в том, что это не так, на примере интеграла  :
:  ;
;  .
.
Следующие разделы будут посвящены ответу на поставленный вопрос: при каких условиях криволинейный интеграл второго рода  не зависит от формы пути, соединяющего начальную и конечную точки, и определяется только этими точками? В трёхмерном случае этот вопрос будет изучаться в теории поля.
не зависит от формы пути, соединяющего начальную и конечную точки, и определяется только этими точками? В трёхмерном случае этот вопрос будет изучаться в теории поля.
16.3.3.4. Формула Грина.
16.3.3.4.1. Связность, односвязность, многосвязность. Напомним определения ряда понятий из теории функций нескольких переменных, которыми нам придется пользоваться.
Множество точек (на прямой, на плоскости, в пространстве) называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.
Область (на плоскости, в пространстве) называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области.
Примеры: односвязны шар, параллелепипед и вообще любой выпуклый объём в пространстве. Односвязен шаровой слой, заключённый между двумя сферами. Пример неодносвязной области: тор. Все пространство односвязно и остаётся односвязным, если из него удалить точку или отрезок. Если же удалить из пространства прямую, оно потеряет свойство односвязности: окружность, охватывающую эту прямую, не удастся стянуть в точку, не пересекая прямую.
Кусочно-гладкая граница ограниченной односвязной области всегда связна, следовательно, является контуром.
16.3.3.4.2. Теорема Грина для односвязной области. Пусть на плоскости Oxy задана односвязная область D, ограниченная кусочно-гладким контуром C. На множестве  определены непрерывные функции
определены непрерывные функции  и
и  , имеющие непрерывные частные производные. Тогда
, имеющие непрерывные частные производные. Тогда  , при этом контур С обходится так, что область D остаётся слева.
, при этом контур С обходится так, что область D остаётся слева.

Док-во. 1. Пусть D – простая область. Докажем сначала, что  . Опишем D неравенствами
. Опишем D неравенствами  Тогда
Тогда 

 . Если контур включает вертикальные участки, такие как EF, то на этих участках dx= 0, поэтому
. Если контур включает вертикальные участки, такие как EF, то на этих участках dx= 0, поэтому  , и
, и  , что и требовалось доказать.
, что и требовалось доказать.

Равенство  доказывается точно также:
доказывается точно также: 

 . Суммируя равенства
. Суммируя равенства  и
и  , получим одну из важнейших формул анализа -формулу Грина
, получим одну из важнейших формул анализа -формулу Грина


2. Пусть теперь D – произвольная, не обязательно простая, область. Разобьём её на простые части. Пусть это разбиение производится отрезком АВ, и пусть подобласти D1 и D2 – результат разбиения. Для этих подобластей формула Грина доказана:
 и
и  . По свойству аддитивности
. По свойству аддитивности  ,
, 
 . Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам АВ и ВА взаимно уничтожаются, а сумма интегралов по кривым ВFA и AEB даёт интеграл по контуру С, т.е. формула Грина верна и для области, не являющейся простой. Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых.
. Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам АВ и ВА взаимно уничтожаются, а сумма интегралов по кривым ВFA и AEB даёт интеграл по контуру С, т.е. формула Грина верна и для области, не являющейся простой. Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых.

16.3.3.4.3. Теорема Грина для многосвязной области. Пусть теперь D многосвязная на плоскости Oxy. Граница многосвязной области состоит из нескольких связных частей, не имеющих общих точек. Рассмотрим случай, когда граница области D (на рисунке область заштрихована) состоит из внешнего контура С и внутренних контуров С1 и С2. Соединим контур С разрезом FM с контуром С1, разрезом BG – с контуром С2. (Под словами “соединим разрезом BG ” подразумевается то, что мы удалим из D отрезок BG). Область  с границей
с границей  односвязна, поэтому для неё справедлива формула Грина:
односвязна, поэтому для неё справедлива формула Грина:
 . Двойные интегралы по областям D и
. Двойные интегралы по областям D и  равны (площадь разрезов равна нулю); в криволинейный интеграл по кусочно-гладкой кривой
равны (площадь разрезов равна нулю); в криволинейный интеграл по кусочно-гладкой кривой  интегралы по разрезам входят с противоположными знаками (
интегралы по разрезам входят с противоположными знаками ( и
и  , например) и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области: пусть на плоскости Oxy дана многосвязная область D с границей
, например) и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области: пусть на плоскости Oxy дана многосвязная область D с границей  . На множестве
. На множестве  определены непрерывные функции
определены непрерывные функции  и
и  , имеющие непрерывные частные производные. Тогда
, имеющие непрерывные частные производные. Тогда  , при этом каждая часть полной границы
, при этом каждая часть полной границы  обходится так, что область D остаётся слева.
обходится так, что область D остаётся слева.
16.3.3.5. Условия независимости криволинейного интеграла от пути интегрирования. В этом разделе будет дан ответ на вопрос: при каких условиях криволинейный интеграл второго рода  не зависит от формы пути, соединяющего точки А и В, а определяется только этими точками? Будем предполагать, что в некоторой односвязной области
не зависит от формы пути, соединяющего точки А и В, а определяется только этими точками? Будем предполагать, что в некоторой односвязной области  на плоскости заданы непрерывно дифференцируемые функции
на плоскости заданы непрерывно дифференцируемые функции  и
и  , и все рассматриваемые точки, контуры и области принадлежат этой области.
, и все рассматриваемые точки, контуры и области принадлежат этой области.

16.3.3.5.1. Теорема 1. Для того, чтобы интеграл  не зависел от формы пути, соединяющего точки А и В, необходимо и достаточно, чтобы интеграл по любому замкнутому контуру был равен нулю.
не зависел от формы пути, соединяющего точки А и В, необходимо и достаточно, чтобы интеграл по любому замкнутому контуру был равен нулю.
Доказательство. Необходимость. Пусть  – произвольный замкнутый контур, лежащий в области
– произвольный замкнутый контур, лежащий в области  , А и В – произвольные точки этого контура. Так как, по условию,
, А и В – произвольные точки этого контура. Так как, по условию,  , то
, то 
 .
.
Достаточность. Пусть для любого контура  выполняется
выполняется  . Пусть
. Пусть  ,
,  – произвольные точки,
– произвольные точки,  и
и  – две различных кривых, соединяющих эти точки.
– две различных кривых, соединяющих эти точки.  – замкнутый контур, поэтому
– замкнутый контур, поэтому 


 , что и требовалось доказать.
, что и требовалось доказать.
16.3.3.5.2. Теорема 2. Для того, чтобы интеграл  по любому контуру С был равен нулю, необходимо и достаточно, чтобы функции
по любому контуру С был равен нулю, необходимо и достаточно, чтобы функции  и их частные производные были непрерывны, и выполнялось условие
и их частные производные были непрерывны, и выполнялось условие  .
.
Доказательство. Необходимость. От противного. Пусть для  выполняется
выполняется  , но существует точка
, но существует точка  такая, что
такая, что  . Предположим для определённости, что
. Предположим для определённости, что  . Так как разность
. Так как разность  непрерывна, существует окрестность точки
непрерывна, существует окрестность точки  такая, что
такая, что  . Выберем контур С, целиком лежащий в этой окрестности. Если D – область ограниченная этим контуром, то, по формуле Грина,
. Выберем контур С, целиком лежащий в этой окрестности. Если D – область ограниченная этим контуром, то, по формуле Грина,  . Но, по теореме об интегрировании неравенств,
. Но, по теореме об интегрировании неравенств,  (
( – площадь области D), т.е.
– площадь области D), т.е.  , что противоречит условиям теоремы. Следовательно, в любой точке
, что противоречит условиям теоремы. Следовательно, в любой точке  выполняется условие
выполняется условие  .
.
Достаточность. Если в любой точке  выполняется условие
выполняется условие  , то для любого контура С
, то для любого контура С  (D – область ограниченная контуром С).
(D – область ограниченная контуром С).
Таким образом, для того, чтобы криволинейный интеграл  не зависел от формы пути, соединяющего начальную и конечную точки (или, что то же самое, интеграл по любому замкнутому контуру был равен нулю), требуется выполнение двух условий:
не зависел от формы пути, соединяющего начальную и конечную точки (или, что то же самое, интеграл по любому замкнутому контуру был равен нулю), требуется выполнение двух условий:
1. Контур и ограниченная им область лежат в некоторой односвязной области, в которой
2.  и их частные производные непрерывны , и
и их частные производные непрерывны , и .
.
Отметим существенность первого условия. Так, для интеграла  второе условие выполняется:
второе условие выполняется:  , в то же время интеграл по окружности радиуса R не равен нулю:
, в то же время интеграл по окружности радиуса R не равен нулю:  . Причина – функции Р и Q непрерывны всюду, кроме начала координат; удаление точки из плоскости лишает её свойства односвязности.
. Причина – функции Р и Q непрерывны всюду, кроме начала координат; удаление точки из плоскости лишает её свойства односвязности.
16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути.
Если выполнены условия независимости от формы пути, соединяющего начальную  и конечную
и конечную  точки кривой, то значение интеграла
точки кривой, то значение интеграла  определяется только точками А и В. Поэтому в этом случае для обозначения интеграла применяется обозначение
определяется только точками А и В. Поэтому в этом случае для обозначения интеграла применяется обозначение  или
или  . Докажем следующую теорему.
. Докажем следующую теорему.

Теорема. Если в односвязной области G выполнено условие  , то существует функция
, то существует функция  такая, что для любых точек
такая, что для любых точек  и
и 
 .
.
Функцию  принято называть потенциальной функцией.
принято называть потенциальной функцией.
Доказательство. Фиксируем произвольную точку  , и докажем, что в качестве искомой функции
, и докажем, что в качестве искомой функции  можно взять
можно взять  . Действительно, по свойству аддитивности
. Действительно, по свойству аддитивности 

 , или
, или  , т.е.
, т.е.  , что и требовалось доказать.
, что и требовалось доказать.
Разность  обозначается символом
обозначается символом  или
или  . Формула
. Формула  является аналогом формулы Ньютона-Лейбница для двухмерного случая; ещё раз отметим, что она имеет место в случае, когда выполняются условия независимости интеграла от формы пути.
является аналогом формулы Ньютона-Лейбница для двухмерного случая; ещё раз отметим, что она имеет место в случае, когда выполняются условия независимости интеграла от формы пути.

Докажем, что для построенной функции  выполняются следующие соотношения:
выполняются следующие соотношения:
 . Действительно, пусть
. Действительно, пусть 
 . Тогда
. Тогда  ,
,

 (на
(на  )
) 
 (по теореме о среднем)
(по теореме о среднем)  . Точка
. Точка  удовлетворяет условиям
удовлетворяет условиям  . Устремим
. Устремим  , тогда
, тогда  , и
, и  .
.
Аналогично доказывается, что  .
.

Условие  теперь означает просто, что
теперь означает просто, что  . Кроме того, из
. Кроме того, из 
 следует, что подынтегральное выражение
следует, что подынтегральное выражение 
 является полным дифференциалом функции
является полным дифференциалом функции  (условие
(условие  есть условие того, что обыкновенное дифференциальное уравнение первого порядка
есть условие того, что обыкновенное дифференциальное уравнение первого порядка  – уравнение в полных дифференциалах). Для отыскания потенциальной функции
– уравнение в полных дифференциалах). Для отыскания потенциальной функции  можно: 1. Решить уравнение в полных дифференциалах; 2. Построить
можно: 1. Решить уравнение в полных дифференциалах; 2. Построить  напрямую по формуле
напрямую по формуле  . В качестве пути интегрирования обычно берётся путь М0АМ, состоящий из отрезков, параллельных координатным осям.
. В качестве пути интегрирования обычно берётся путь М0АМ, состоящий из отрезков, параллельных координатным осям.
Вместе с этой лекцией читают “10. К биографии Кантемира”.
Тогда на М0А 
 ; на АМ
; на АМ  .
.
Продемонстрируем оба метода на примере 4 раздела 16.3.3.3:  . Здесь
. Здесь 
 , т.е. условия независимости выполняются. В качестве точки
, т.е. условия независимости выполняются. В качестве точки  берём начало координат
берём начало координат  .
.
1. Решаем систему уравнений  Из первого уравнения
Из первого уравнения  , подставляем эту функцию во второе уравнение
, подставляем эту функцию во второе уравнение  (потенциал всегда определяется с точностью до произвольной постоянной, физический смысл имеет разность потенциалов в двух точках, которая не зависит от этой постоянной).
(потенциал всегда определяется с точностью до произвольной постоянной, физический смысл имеет разность потенциалов в двух точках, которая не зависит от этой постоянной).
2.  .
.
Теперь, когда потенциальная функция определена, легко находится любой интеграл:  .
.
16.3.3.7. Выражение площади плоской области через криволинейный интеграл. Из формулы Грина  следует неожиданный результат: если функции Р и Q удовлетворяют условию
следует неожиданный результат: если функции Р и Q удовлетворяют условию  , то
, то  (
( – площадь области D). Таким образом, площадь области можно выразить через криволинейный интеграл второго рода по границе этой области. В качестве функций Р и Q можно взять любые непрерывно дифференцируемые функции, такие что
– площадь области D). Таким образом, площадь области можно выразить через криволинейный интеграл второго рода по границе этой области. В качестве функций Р и Q можно взять любые непрерывно дифференцируемые функции, такие что  , например,
, например,  ;
;  ;
;  ;
;  и т.д. В результате
и т.д. В результате  и т.д. При этом контур С (граница области D) обходится в положительном направлении. Чаще всего применяется третья из этих формул. Для примера найдём площадь, ограниченную эллипсом
и т.д. При этом контур С (граница области D) обходится в положительном направлении. Чаще всего применяется третья из этих формул. Для примера найдём площадь, ограниченную эллипсом  . Параметрические уравнения эллипса
. Параметрические уравнения эллипса  , поэтому
, поэтому  ; это, видимо, самый простой способ вычисления площади эллиптической области.
; это, видимо, самый простой способ вычисления площади эллиптической области.
