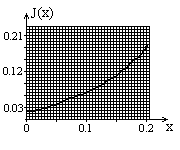Как найти момент инерции маятника обербека

Цель работы

Изучение
законов динамики вращательного движения;
теоретическое и экспериментальное
определение момента инерции крестообразного
маятника Обербека; изучение зависимостей
угловой скорости и момента силы от
момента инерции.

Основные
понятия.

Моментом
силы F относительно точки О называется
векторное произведение радиус-вектора
,
проведенного из точки О в точку приложения
силы, на вектор силы
:
.

Моментом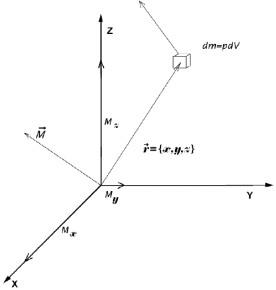
силы относительно оси называется
скалярная величина, равная проекции на
данную ось вектора момента силы
относительно какой-либо точки той же
оси.

Если
рассмотреть отдельную материальную
точку массой dm,
вращающуюся вокруг оси на расстоянии
r,
то ее момент инерции равен J=dmr².
Твердое тело можно мысленно представить
как совокупность большого числа n
материальных точек dm_i
и
просуммировать моменты инерции всех
точек относительно данной оси:

(1)

Если
тело однородно, то dm=dV,
где 
– плотность, dV – элементарный
объем. Тогда момент инерции всего тела
может быть рассчитан по формуле:

(2)

Если
известен момент инерции тела относительно
оси, проходящей через центр инерции
(центр масс) тела J₀,
то можно вычислить момент инерции тела
относительно оси с помощью теоремы
Штейнера:
момент инерции J
относительно произвольной оси вращения
равен сумме моментов инерции J₀
относительно
оси, параллельной данной и проходящей
через центр масс тела, и произведения
массы тела m
на квадрат расстояния a
между
осями:

J=J₀+ma²
(3)

Покажем,
как, пользуясь теоремой Штейнера и
выражением для момента инерции цилиндра,
полученным из (2) после интегрирования
по объему, можно рассчитать момент
инерции крестообразного маятника
Обербека.

Момент
инерции всего маятника относительно
оси вращения равен сумме моментов
инерции четырех стержней с цилиндрическими
грузами на них, момента инерции втулки,
в которой крепятся стержни, и момента
инерции барабана:

J=J_вт+J_б+4(J_ст+J_гр)
(4)

У
втулки и барабана ось вращения проходит
через их центр масс, это цилиндрические
тела, поэтому:

Момент
инерции стержня длиной l_ст,
относительно оси, проходящей через его
конец и перпендикулярный ему

Момент
инерции грузов найдем, считая грузы
материальными точками массой m,
так как их рамеры малы по сравнению с
расстоянием до оси вращения:
J_гр=m_грx²,
где x
–
расстояние от центра груза до оси
вращения. Все части маятника – цилиндры,
поэтому их массы запишутся
,
где =7.810³
кг/м³
– плотность стали, d
– диаметр
цилиндра, l
– его
высота или длина.

(5)

Момент
силы
,
момент инерции J
и угловое
ускорение

связаны основным законом динамики
вращательного движения:
.

Учитывая,
что
,
этот закон можно записать в виде:

(6)

где

– момент
импульса (количества движения) тела.

Методика
эксперимента

Маятник
Обербека состоит из четырех стержней,
расположенных под прямым углом друг к
другу, втулки и барабана, на который
наматывается нить. По стержням могут
перемещаться грузы равной массы, которые
могут быть укреплены в любых точках
стержня.

Маятник
приводится во вращение с помощью груза
m,
подвешенного на шнуре, который наматывается
на барабан. Если груз поднять на некоторую
высоту h,
то он будет опускаться, вращая барабан,
а с ним и весь маятник.

1.
Момент инерции маятника можно определить
из основного закона динамики вращательного
движения
,
где
–
момент
силы, приводящий маятник во вращение,
–
его угловое ускорение. Выразим момент
силы и угловое ускорение через величины,
легко измеряемые на опыте. Момент силы
– это произведение силы на плечо ее
приложения, то есть радиус барабана r_б.
Силой, вращающей маятник, является сила
натяжения шнура. Для определения силы
натяжения шнура рассмотрим силы,
действующие на груз.

Со
стороны Земли действует сила тяжести
mg,
со стороны шнура – сила натяжения F_н.
По второму закону Ньютона
,
где
–
линейное ускорение груза. Спроектируем
на вертикальную ось:

(7)

Ускорение
груза a
найдем из формулы равноускоренного
движения h=at²/2,
где h
– высота, с которой опускается груз, t
– время
движения. Получим a=2h/t².
Окончательно момент силы:

(8)

Угловое
ускорение 
маятника и барабана найдем, связав его
с линейным ускорением груза
a. Так
как шнур плотно намотан на барабан, он
сообщает точкам его поверхности то же
линейное ускорение, которое имеет груз.
Поэтому a=r_б
одновременно
является линейным ускорением груза и
точек поверхности барабана. Тогда:

(9)

Подставив
(10) и (9) в (7), получим
,
откуда

(10)

2.
С помощью маятника Обербека можно
опытным путем получить связь между 
и моментом инерции J.

Меняя
расстояние от грузов на стержнях до оси
вращения, мы тем самым меняем момент
инерции маятника. Поэтому, в соответствии
с основным законом динамики вращательного
движения, если J₁>J₂,
должно получиться ₁<₂.
Угловое ускорение в каждом случае
рассчитывается через время падения
(9). При постоянном моменте силы M:

M=J₁₁=J₂₂.
(11)

.
Установка позволяет определить момент
сил трения, возникающих в трущихся
частях на оси вращения. Груз m,
поднятый на высоту h относительно
нижней точки, сначала опускается до
этой точки, а затем из-за инертности
вращательного движения маятника вновь
поднимается до высоты h₁<h.

Запишем
закон сохранения энергии с учетом сил
трения для одного такого цикла:

mgh=mgh₁+M_Тр,

где

– угол поворота маятника за все время
движения.

Так
как
,
то получим:
.
Отсюда:

(12)

Порядок
выполнения работы

Для
определения момента инерции:

1.
Закрепляем грузы на концах стержней
маятника Обербека и 3 раза измеряем t
– время падения груза с высоты h.

2.
Уменьшаем на одинаковую величину
расстояние от грузов до оси вращения и
повторяем п.1.

x(c)	t1(c)	t2(c)	t3(c)	(c)
0.2	15.5	17	16.5	16.3
0.05	10	11	11	10.6

Для
определения момента сил трения:

1.
Измеряем высоту h
падения
груза относительно нижней точки.

2.
Отпускаем груз и измеряем высоту h₁,
на которую поднимется груз при остановке
маятника.

3.
Повторяем опыт 3 раза и находим среднее
значение
.

h=0.6
м

h1=0.23 м

h1=0.24 м

h1=0.24 м

=0.237 м

Обработка
результатов эксперимента

_стали
=
7,710³
кг/м³;
H =
2,510^-2
м;
a = 2,510^-2
м/c²;
H₀
= 8,310^-2
м;
R = 1,010^-2
м.

1.
По формуле (10) определяем J
для каждого опыта:
J₁=0.057,
J₂=0.068,
J₃=0.064
– при
x=0.2;
J₁=0.024,
J₂=0.028,
J₃=0.028
– при
x=0.05.

Определяем
среднее значение

при каждом положении x:

=0.063
кгм²;

=0.027
кгм².

Строим
график зависимости момента инерции
маятника от положения грузов на стержнях
(x).

2.
По формуле (5) при тех же значениях x
теоретически
рассчитываем и строим зависимость
(x).

x	0,2	0,05
(x)	0,1879	0,0366

3.
По формуле (9) определяем 
и проверяем выполнение соотношения
(11).

J₁₁=2,8510^-2,
J₂₂=2,8810^-2
J₁₁J₂₂

4.
По формуле (12) рассчитываем значение
M_Тр.
M_Тр=1.2510^-2.

Расчет
погрешностей

Абсолютная
погрешность J
измерения
момента инерции рассчитывается по
формуле для косвенных измерений:

Величина
t
определяется как случайная погрешность
прямого измерения.

,

x	t	J
0.2	0.054	0.001
0.05	0.183	0.0014

где
С_N
– коэффициент Стьюдента, t_i
– время,
полученное при i-ом
измерении,
–
среднее время из N
измерений,
–
среднее значение момента инерции.

Погрешность
измерения момента сил трения рассчитывается
по формуле для косвенного измерения:

где
при заданном значении h
величина
h
определяется как приборная погрешность
(половина цены деления измерительной
линейки), а h₁
для N
измерений вычисляется по формуле
Стьюдента:

где

– среднее значение высоты подъема, h_1k
– высота
подъема при k-ом
измерении.

h₁=0.006,
M_Тр=0.002

Проделав все
задания, относящиеся к данной лабораторной
работе и сделав все необходимые
вычисления, мы можем сделать ряд выводов:

• с
  увеличением расстояния между осью
  вращения и положением цилиндров, момент
  инерции маятника J
  увеличивается;

• угловая
  скорость вращения маятника обратно
  пропорционально зависит от величины
  t,
  то есть чем меньше время прохождения
  расстояния h^’
  ,
  тем угловая скорость больше, иначе –
  меньше;

Соседние файлы в папке лабораторная работа

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

  24.01.201413.82 Кб67термопара.xls

При решении уравнений вращательного или колебательного (осциллирующего) движения необходимо знать момент инерции рассматриваемой системы. Данная статья посвящена изучению различного рода маятников и моменту инерции, которым они характеризуются.

Понятие о маятнике. Виды

Перед тем как приводить определение момента инерции маятника, необходимо рассмотреть, что собой представляет этот прибор. В физике под ним понимают абсолютно любую систему, которая может совершать колебания или вращение вокруг некоторой точки или оси под действием гравитационного поля, то есть силы тяжести. Это определение предполагает, что маятник в обязательном порядке должен обладать конечной массой, при этом центр масс системы не должен находиться в точке, через которую проходит ось вращения.

Вам будет интересно:Семинарское занятие: определение, виды, задачи, методика разработки

Существуют различные виды маятников. В данной статье рассмотрим только 3 из них:

• математический, или простой;
• физический (на примере однородного стержня);
• маятник Обербека.

Первые два являются маятниками колебательного типа, третий – вращательного.

Вращение и момент инерции

Когда тело с некоторой массой начинает вращаться вокруг оси, то его движение принято описывать следующим уравнением:

Вам будет интересно:Плотность воды г/мл: физические свойства и зависимость плотности от температуры

M = I*α.

Здесь M – это суммарный, или результирующий, момент всех внешних сил, которые действуют на систему, I – ее момент инерции и α – угловое ускорение.

Момент силы M по определению – это величина, равная произведению действующей силы на плечо, которое равно расстоянию от точки приложенной силы до оси вращения.

Момент инерции – величина, характеризующая инерционные свойства системы, то есть насколько быстро ее можно раскрутить, прилагая некоторый момент M. Также I характеризует запасенную вращающейся системой кинетическую энергию. Момент инерции I для материальной точки (воображаемый объект, масса которого сосредоточена в бесконечно малом объеме пространства), совершающей круговое движение на расстоянии от оси r, можно вычислить по следующей формуле:

I = m*r2.

В общем же случае при определении I для тела произвольной формы следует пользоваться такими выражениями:

1) I = ∑mi*ri2.

2) I = ∫dm *ri2 = ρ*∫dV *ri2.

Первое равенство применяется при дискретном расположении масс в системе, второе – при непрерывном.

Из этих выражений видно, что I является функцией расстояния до оси вращения и распределения массы в системе относительно этой оси и не зависит ни от прикладываемых моментов сил M, ни от скорости вращения ω.

Математический (простой) маятник

Поскольку этот вид колебательной системы является самым простым, то рассмотрим его подробнее. Маятник математический представляет собой материальную точку, которая подвешена на невесомой и нерастяжимой нити. Если эту точку отклонить слегка от положения равновесия, а затем отпустить, то она начнет совершать колебания. Также предполагается, что не существует сил трения в точке закрепления нити, и пренебрегают сопротивлением воздуха.

Как понятно из описания выше, математический маятник представляет собой идеальный случай, который не реализуется на практике. Тем не менее его изучение позволяет получить некоторые важные выводы для рассматриваемого типа движения.

Ниже на рисунке представлен этот маятник, а также обозначены действующие в системе силы при его колебании.

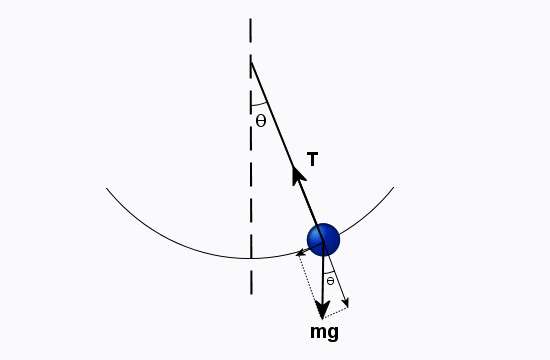
Применяя к нему уравнение движения, получаем следующее равенство:

M = -m*g*sin(θ)*L; I = m*L2; α = d2θ/dt2 =>

=> -m*g*sin(θ)*L = m*L2*d2θ/dt2, откуда:

L *d2θ/dt2 + g*sin(θ) = 0.

Поясним некоторые моменты: момент силы от натяжения нити T (см. рис.) равен нулю, поскольку она действует непосредственно на ось; момент от силы тяжести взят со знаком минус, поскольку он направлен по часовой стрелке; L – длина нити; угловое ускорение α по определению является второй производной от угла поворота по времени либо первой производной по времени от угловой скорости ω; формула момента инерции маятника этого типа совпадает с таковой для материальной точки с массой m, находящейся от оси вращения на расстоянии L.

Полученное выше выражение можно упростить, если принять приближение: sin(θ)≈θ. Оно справедливо, когда углы колебания являются небольшими (до θ=10o ошибка не превышает 0,5 %). В этом случае получаем:

L*d2θ/dt2 + g*θ = 0.

Мы получили классическое дифференциальное уравнение (диф. ур.) второго порядка. Его решением является функция синуса:

θ = A*sin(ω*t+θ0).

Здесь A и θ0 – амплитуда колебаний и начальный угол отклонения от равновесия, соответственно. Если это решение подставить в диф. ур. выше, то можно получить угловую скорость и период колебаний:

ω = √(g/L) и T = 2*pi/ω = 2*pi*√(L/g).

Мы получили удивительный результат: период колебаний математического маятника не зависит от начальных условий (A и θ0), а также от массы m.

Поведение математического маятника впервые начал изучать Галилей. Впоследствии Гюйгенс показал возможность использования полученной формулы для определения ускорения свободного падения Земли.

Физический маятник общего типа

Этот прибор представляет собой твердое тело произвольной формы (его масса может быть неравномерно распределена по его объему), которое совершает колебания относительно горизонтальной оси, не проходящей через центр масс тела.

При решении уравнения движения этого прибора рассматривают идеальный объект, масса которого сосредоточена в его центре тяжести. Такое предположение приводит к следующей формуле для периода его колебания:

T = 2*pi*√(Io/(m*g*h)).

Здесь h – расстояние от центра тяжести до оси вращения O, Io – момент инерции физического маятника. Заметим, что если для расчета момента силы тяжести можно воспользоваться свойством аддитивности этой величины и свести сумму всех моментов к одному, приложенному к центру тяжести, то для вычисления момента инерции Io так поступать нельзя, его следует рассчитывать с использованием общих формул, которые были приведены ранее.

Колеблющийся стержень и его момент инерции

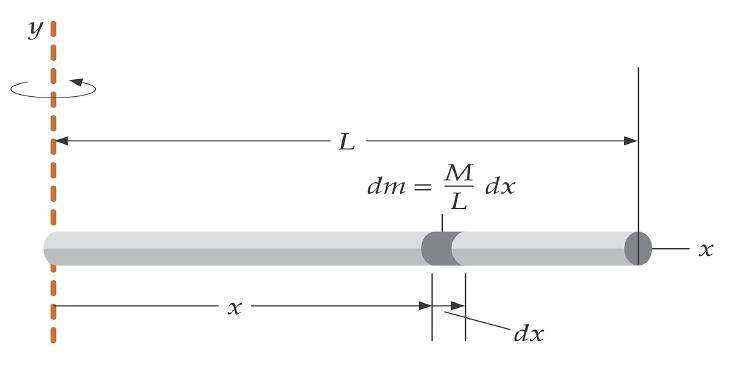
Представим себе, что имеется твердый стержень массой m и длиной L, который подвешен к одному из концов вертикально. Эта конструкция способна совершать колебания под действием земного притяжения.

Если применить интегрирование относительно оси к такому стержню, то можно получить, что момент инерции маятника физического указанной конструкции будет равен:

Io = m*L2/3.

Тогда его период колебаний будет равен:

T = 2*pi*√(2*L /(3*g)).

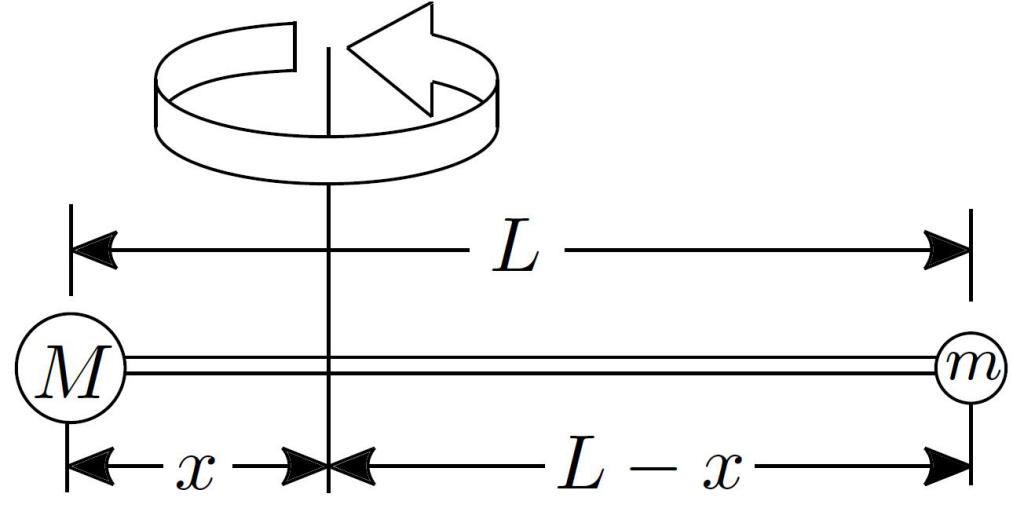
Маятник Обербека

На рисунке ниже приведен этот вид маятника.

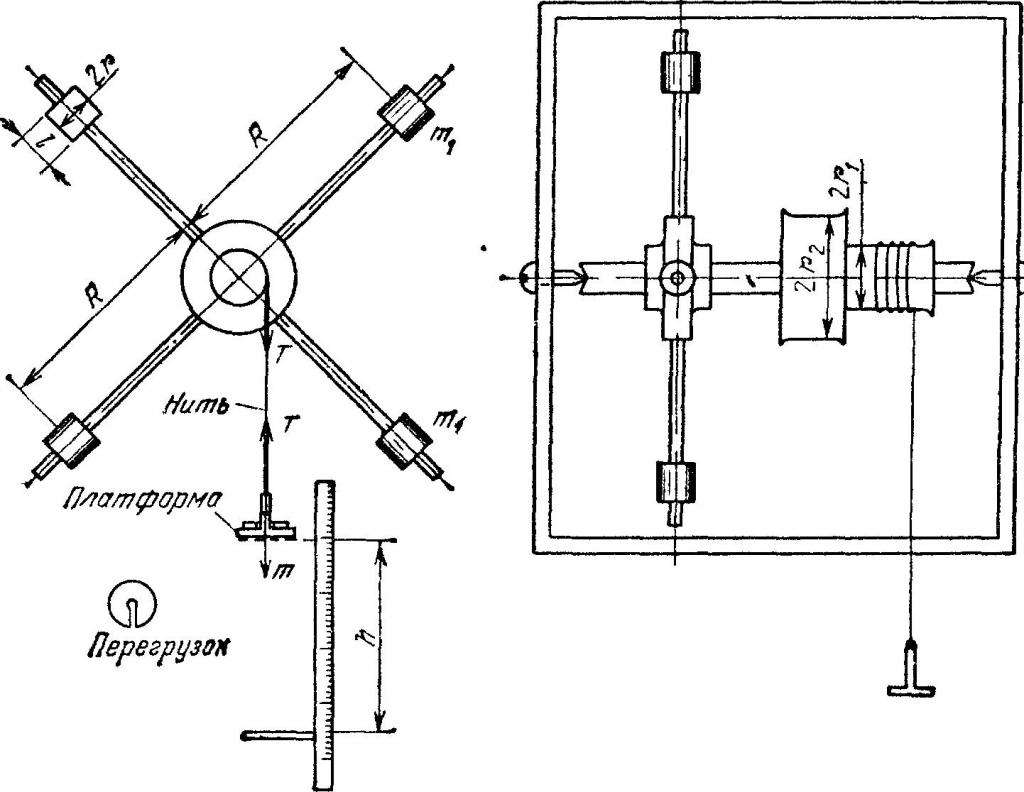
Из рисунка видно, если подвесить груз к нити, то 4 стержня с грузами начинают вращаться с некоторым угловым ускорением.

Маятник Обербека используется для проведения лабораторных работ по физике с целью проверки уравнения вращательного движения.

Определение момента инерции маятника Обербека

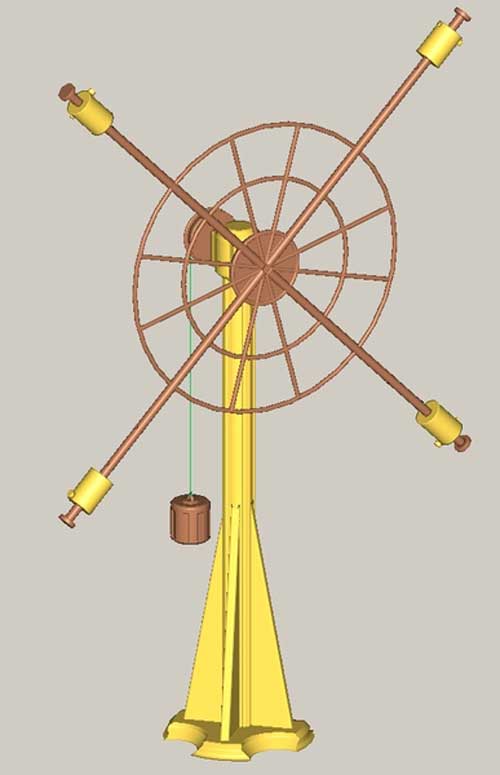
Для решения этой задачи необходимо сделать важное приближение: вес стержней и дисков, к которым подвешивается на нити перегрузок, является пренебрежимо малым по сравнению с весом одного груза m. Учитывая, что размер грузов намного меньше их расстояния до оси вращения, можно воспользоваться формулой для момента инерции материальной точки. Поскольку грузов 4 и все они имеют одинаковую массу, но расположены на разных расстояниях от оси, то получаем следующую формулу для момента инерции маятника Обербека:

I = I1+I2+I3+I4 = m*(R12+R22+R32+R42 ).

Поскольку этот маятник позволяет регулировать положение каждого груза на стержне, то его момент инерции может изменяться.

---

Подборка по базе: ЛБ-2 Определение длительности производственного цикла.pdf, Лабораторная работа №2_Изучение конструкции и определение характ, Тема 4.1. Определение и классификация имени существительного.pdf, 1. Заикание. Определение понятия, исторические аспекты исследова, Тема 1.1-Этика как наука. Определение профессиональной этики.rtf, Скорость света и ее определение физика.doc, Лаб.Раб. Определение режимов ручной дуговой сварки Горячев.doc, РГЗ 3 Определение фильтрационных параметров продуктивного пл.doc, Практическая работа 13. Координаты вектора. Решение задач на опр, Tema №7 Определение неисправностей сизод.docx

---

Лабораторнаяработа№12

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА ОБЕРБЕКА

Дата выполнения Время на подготовку и допуск к лабораторной работе: 30 минут. Время на выполнение экспериментов: 30 минут.

Время на оформление отчета и расчёты: 30 минут.

Цель работы.

Ознакомится с понятием момента инерции вращающегося тела. Определить зависимость момента инерции маятника Обербека от положения грузов и массы подвеса.

Оборудование.

1. Маятник Обербека.
2. Грузы разной массы.
3. Секундомер.
4. Линейка.

Основные сведения.

Любое твердое тело, имеющее ось вращения, будет совершать вращательное движение, если к нему приложить внешнюю силу Fвн., линия действия которой не проходит через ось вращения (Рис. 12.1).

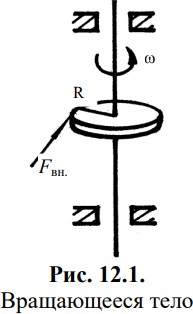
Перпендикуляр, опущенный из оси вращения на линию действия силы, называется плечом силы R.

Произведение силы Fвн. на плечо R называется моментом силы.

M = Fвн. · R.

Итак, чтобы тело вращалось, необходимо приложить момент силы.

Если на тело действует постоянный момент силы, то тело будет вращаться равноускоренно с постоянным угловым ускорением 𝜀.

где J — момент инерции вращающегося тела.

Формула (12.1) выражает второй закон Ньютона для вращательного движения. Момент инерции выполняет роль массы тела, а момент силы — роль силы.

Моментом инерции материальной точки принято называть произведение массы точки на квадрат ее расстояния до оси вращения.

J=mr².

Если тело разбить на n элементов, то момент инерции всего тела будет вычисляться следующим образом

где i — номер элемента тела.

В данной лабораторной работе определяется момент инерции маятника Обербека (Рис. 12.2).

Маятник состоит из четырех стальных стержней, расположенных под прямым углом и вставленных во втулку. На стержнях укреплены грузики одинаковой массы m₀. Эти грузики можно перемещать вдоль стальных стержней.

Изменяя их расстояние от оси вращения, можно изменить момент инерции маятника. На ось вращения насажен шкив, радиусом R. На шкив намотан шнур, свободный конец которого имеет специальную подставку для закрепления на ней различных грузов. Груз массой m, опускаясь на шнуре, приводит во вращение шкив и стержни с грузиками массой m₀.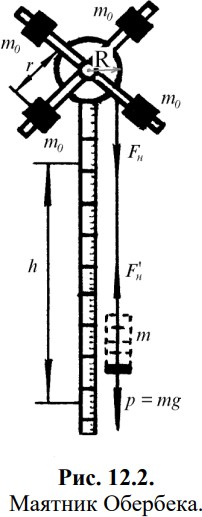

Найдем величину момента силы M, вращающего маятник, и его угловое ускорение 𝜀.

Момент силы M определим по формуле

M = F_нR,

где F_н — сила, вызывающая вращение маятника (сила натяжения шнура), R — радиус шкива (плечо силы).

Если сила тяжести груза P = mg больше силы натяжения F_н, то груз будет опускаться с ускорением под действием силы F_уск. = ma.

P – F_н = F_уск.
Откуда F_н = mg – ma = m(g – a).

Ускорение силы тяжести g (ускорение свободного падения) значительно больше линейного ускорения a , с которым груз движется вниз. Поэтому можно считать приближенно

Величину углового ускорения 𝜀 можно найти из следующих соображений. Шнур, разматываясь со шкива, не скользит по нему и, следовательно, каждая точка шкива в месте соприкосновения со шнуром будет двигаться с тем же линейным ускорением, что и сам спускающийся груз. Между угловым ускорением точки на окружности и ее линейным ускорением существует зависимость.

Величину линейного ускорения спускающегося груза можно определить по формуле равноускоренного поступательного движения. Если t – время, в течение которого груз проходит путь h с ускорением a, то

Таким образом, угловое ускорение

Подставляя в формулу (12.1) значения момента силы M из формулы (12.2) и угловое ускорение из формулы (12.4), получим расчетную формулу для момента инерции маятника Обербека.

Все величины, стоящие в правой части формулы (12.5). m — масса груза, R

• радиус шкива, t — время падения груза и h — высота падения груза, измеряются на опыте.

Формула (12.5) получена в предположении, что a << g. В том, что линейное ускорение груза a действительно мало по сравнению с ускорением свободного падения g, нетрудно убедиться на основании опытных данных.

Подставляя полученные экспериментальные значения h и t в формулу (12.3), можно убедиться, что a << g.

Порядок выполнения работы

1. Определите зависимость момента инерции маятника Обербека от расстояния r грузиков m₀ на стержнях крестовины от оси вращения.

• расположите грузики m0 на стержнях крестовины на расстоянии r₁ от оси вращения;
• намотайте на шкив шнур, свободный конец которого имеет специальную подставку для грузов;
• придерживая крестовину, положите на подставку груз m;
• отметьте деление на линейке, соответствующее основанию подставки с грузом m;
• отпустите груз для свободного падения и одновременно включите секундомер, но не толкайте крестовину;
• выключите секундомер, как только подставка с грузом достигнет нижней отметки на линейке;
• определите по секундомеру время падения груза t₁;
• результат измерения t₁ запишите в Таб. 12.1;
• повторите опыт еще 2 раза, т. е. измерьте время t2 и t3 и из 3-х значений взять среднее tср.;
• расположите грузики m0 на стержнях крестовины на расстоянии r2 от оси вращения;
• определите по той же методике среднее время падения tср. груза m;
• измерьте по линейке высоту падения h груза m. Проделайте те же измерения tср. для расстояний r3, r4, r5. Результаты измерений занесите в Таб. 12.1.

Таб. 12.1.

r, м	m, кг	h, м	t1, с	t2, с	t3, с	tср, с	J, кгм2
10 см	151 г	44 см	4,28	2,85	2,63	3,25	0,028
12 см	151 г	44 см	3,45	3,18	3,48	3,37	0,031
14 см	151 г	44 см	2,89	2,94	3,05	2,96	0,024
16 см	151 г	44 см	2,89	2,94	2,74	2,86	0,022
18 см	151 г	44 см	3,21	3,89	5,11	4,07	0,045
20 см	151 г	44 см	4,65	4,30	3,88	4,28	0,049

R= 4 см

1. Исследуйте зависимость момента инерции маятника Обербека от массы подвеса m, висящего на нити. Для этого:

• установите грузики m0 на стержнях крестовины на расстоянии r5;
• намотайте на шкив шнур;
• придерживая крестовину, положите на подставку груз m1;
• отметьте деление шкалы, соответствующее основанию подставки;
• опустите груз для свободного падения, одновременно включите секундомер;
• выключите секундомер, как только подставка с грузом m1 достигнет нижней отметки на линейке;
• определите по секундомеру время падения груза t1;
• результаты измерения запишите в Таб. 12.2.
• повторите опыт еще два раза и из 3-х значений вычислите значение tср.; Проделайте опыты с грузами m2, m3, m4, m5.

Результаты измерений занесите в Таб. 12.2. Таб. 12.2.

m, кг	r, м	h, м	t1, c	t2, c	t3, c	tср, с	J, кгм2	Ji-Jcp кгм 2	(Ji-Jcp) 2 (кгм2)2
53 г	16 см	44 см	4,91	6,94	5,57	5,81	0,088	-0,051	0,0026
102 г	16 см	44 см	4,95	5,25	5,06	5,09	0,129	-0,01	0,0001
151 г	16 см	44 см	3,00	4,04	3,83	3,62	0,097	-0,042	0,0018
200 г	16 см	44 см	4,60	4,05	4,56	4,40	0,189	0,05	0,0025
249 г	16 см	44 см	3,66	3,36	4,94	3,99	0,194	0,055	0,0030

R= 4 см

Обработка результатов измерения

1. По результатам Таб. 12.1 рассчитайте по формуле

моменты инерции маятника Обербека для пяти положений грузиков на стержнях крестовины. Результаты расчетов занесите в Таб. 12.1.

1. Постройте графики зависимости J = f(r) и J = f (r²) (см. п. 3 Правил оформления…) при постоянной массе m.

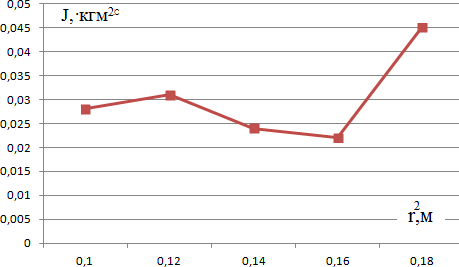
1. По результатам Таб. 12.2 рассчитайте моменты инерции маятника Обербека при постоянном r1 и различных массах груза m1, m2, m3, m4, m5. Результаты расчета занесите в Таб. 12.2.
2. Постройте график зависимости J = f(m) при r₁ = const.

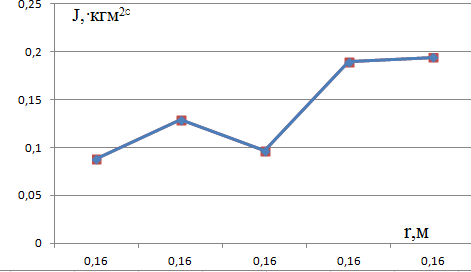
1. Сделайте выводы.

Вывод: момент инерции маятника зависит от массы грузов и расстояния грузов от оси вращения прямопропорционально.

1. По данным расчета момента инерции таблицы 12.2 произведите обработку результатов измерения, вычислите среднее значение момента инерции маятника Jcp и абсолютную погрешность измерения ∆J. Окончательный

=обработке результатов измерений»).

𝐽_ср = 0,139 кг ∙ м²

^∑5 (𝐽_𝑖 − 𝐽_𝑐р)²

_{∆𝐽 = 2√}

𝑖=1

𝑛(𝑛 − 1)
∆𝐽 = 0,044 кг ∙ м²

Тогда 𝐽 = (0,139 ± 0,044) кг ∙ м²

1. Определите относительную погрешность измерения по формуле

𝛿=^0,022 ∙ 100% = 15,8%

0,139
Контрольные вопросы

1. Дайте определение момента инерции. Каков физический смысл момента инерции?

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси.

Момент инерции является мерой инертности тела при вращении (физический смысл)

1. Почему с увеличением расстояния r грузиков m₀ от оси вращения момент инерции возрастает. Какая это зависимость?

Возрастает так как момент инерции зависит от распределения массы в пространстве. Зависимость является прямой пропорциональностью

1. Поясните вид графика зависимости J = f(m) при r = const. Зависимость момента инерции тела от массы является прямой пропорциональностью
2. От чего зависит момент инерции твердого тела?

От массы тела, от квадрата расстояния от оси вращения

1. Сформулируйте основной закон динамики вращательного движения. Основной закон динамики вращения (II закон Ньютона для вращательного движения): Момент вращающей силы, приложенной к телу, равен произведению момента инерции тела на угловое ускорение.

Замечания преподавателя

Оценка за работу:баллов. Подпись преподавателя: