Как найти момент инерции пластинки

Механические приложения двойного интеграла

Будем считать, что $mathbf { textit { D } } $ – неоднородная плоская пластина с поверхностной плотностью материала в точке $P$ равной $mu (P)$. В механике $mu (P)$ определяется так. Точка $P$ окружается малой областью $mathbf { textit { S } } $, находится масса $mathbf { textit { m } } (mathbf { textit { S } } )$ и площадь этой области { площадь тоже будем обозначать буквой $mathbf { textit { S } } $ } и $mu (P)=mathop { lim } limits_ { diam(S)to 0 } frac { m(S) } { S } $.

Для нахождения массы по заданной плотности мы решим обратную задачу. Разобьём $mathbf { textit { D } } $ на малые подобласти $mathbf { textit { D } } _ { 1 } $, $mathbf { textit { D } } _ { 2 } $,$mathbf { textit { D } } _ { 3 } , { ldots } , mathbf { textit { D } } _ { n } $, в каждой из подобластей $mathbf { textit { D } } _ { i } $ выберем произвольную точку $mathbf { textit { P } } _ { i } $, и, считая что в пределах $mathbf { textit { D } } _ { i } $ плотность постоянна и равна $mu (P_i )$, получим, что масса $mathbf { textit { D } } _ { i } $ приближённо есть $mu (P_i )cdot s(D_i )$, а масса всей пластины $sumlimits_ { i=1 } ^n { mu (P_i )cdot s(D_i ) } $.

Это интегральная сумма, при уменьшении $d=mathop { max } limits_ { i=1,2,ldots ,n } diam(D_i )$ точность приближения увеличивается, и в пределе $m(D)=mathop { lim } limits_ { begin{array} { l } dto 0 \ (nto infty ) \ end{array} } sumlimits_ { i=1 } ^n { mu (P_i )cdot Delta s(D_i ) } =iintlimits_D { mu (P)ds } $.

Аналогично находятся другие параметры пластины:

Координаты центра тяжести

$x_c =frac { 1 } { m(D) } iintlimits_D { xcdot mu (P)ds } $, $y_c =frac { 1 } { m(D) } iintlimits_D { ycdot mu (P)ds } $;

Моменты инерции пластины

• $I_x =iintlimits_D { y^2cdot mu (P)ds } $ { относительно оси $mathbf { textit { Ox } } $ } ,
• $I_y =iintlimits_D { x^2cdot mu (P)ds } $ { относительно оси $mathbf { textit { Oy } } $ } ,
• $I_O =iintlimits_D { (x^2+y^2)cdot mu (P)ds } =I_x +I_y $ { относительно начала координат } .

Пластина расположена в области (R) и ее плотность в точке ( { left( { x,y }right) } ) равна ( { rho left( { x,y }right) } ).

Масса пластины

(m = largeiintlimits_Rnormalsize { rho left( { x,y }right)dA } )

Статические моменты пластины

Момент пластины относительно оси (Ox) определяется формулой

( { M_x } = largeiintlimits_Rnormalsize { yrho left( { x,y }right)dA } )

Аналогично, момент пластины относительно оси (Oy) выражается в виде

( { M_y } = largeiintlimits_Rnormalsize { xrho left( { x,y }right)dA } )

Координаты центра масс пластины

• (bar x = largefrac { { { M_y } } } { m } normalsize = largefrac { 1 } { m } normalsize largeiintlimits_Rnormalsize { xrho left( { x,y }right)dA } = largefrac { { iintlimits_R { xrho left( { x,y }right)dA } } } { { iintlimits_R { rho left( { x,y }right)dA } } } normalsize,;)
• (bar y = largefrac { { { M_x } } } { m } normalsize = largefrac { 1 } { m } normalsize largeiintlimits_Rnormalsize { yrho left( { x,y }right)dA } = largefrac { { iintlimits_R { yrho left( { x,y }right)dA } } } { { iintlimits_R { rho left( { x,y }right)dA } } } normalsize ).

Заряд пластины

(Q = largeiintlimits_Rnormalsize { sigma left( { x,y }right)dA } ),

где электрический заряд распределен по области (R) и его плотность в точке ( { left( { x,y }right) } ) равна ( { sigma left( { x,y }right) } ).

Среднее значение функции

(mu = largefrac { 1 } { S } iintlimits_Rnormalsize { fleft( { x,y }right)dA } ,;) где (S = largeiintlimits_Rnormalsize { dA } ).

Пример 1

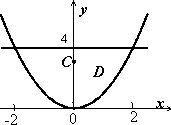
Найти параметры неоднородной плоской пластины, ограниченной кривыми

$D:left[{ begin{array} { l } y=x^2, \ y=4; \ end{array} }right.$ если плотность $mu (x,y)=y+1$.

Решение:

$m(D)=iintlimits_D { (y+1)dxdy } =2intlimits_0^2 { dx } intlimits_ { x^2 } ^4 { (y+1)dy } =2intlimits_0^2 { left. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } =$ $ =2intlimits_0^2 { left( { 12-x^4/2-x^2 }right)dx } =2left. { left( { 12x-x^5/10-x^3/3 }right) }right|_0^2 =2left( { 24-frac { 16 } { 5 } -frac { 8 } { 3 } }right)=frac { 544 } { 15 } . $ $ x_c =frac { 1 } { m(D) } iintlimits_D { x(y+1)dx } dy=frac { 15 } { 544 } intlimits_ { -2 } ^2 { dx } intlimits_ { x^2 } ^4 { x(y+1)dy } =frac { 15 } { 544 } intlimits_ { -2 } ^2 { xleft. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } = $ $=frac { 15 } { 544 } intlimits_ { -2 } ^2 { left( { 12x-x^5/2-x^3 }right)dx } = quad =frac { 1 } { 544 } left. { left( { 6x^2-x^6/10-x^4/4 }right) }right|_ { -2 } ^2 =0$ { что и следовало ожидать, так как область и плотность симметричны относительно оси Оу). $ begin{array} { l } y_c =frac { 1 } { m(D) } iintlimits_D { y(y+1)dx } dy=frac { 15 } { 544 } intlimits_ { -2 } ^2 { dx } intlimits_ { x^2 } ^4 { y(y+1)dy } =frac { 15 } { 272 } intlimits_0^2 { left. { left( { y^3/3+y^2/2 }right) }right|_ { x^2 } ^4 dx } = \ =frac { 15 } { 272 } intlimits_0^2 { left( { 64/3+8-x^6/3-x^4/2 }right)dx } =frac { 15 } { 272 } left. { left( { 88x/3-x^7/21-x^5/10 }right) }right|_0^2 =frac { 15 } { 272 } left( { frac { 176 } { 3 } -frac { 128 } { 21 } -frac { 16 } { 5 } }right)=frac { 15 } { 272 } cdot frac { 1728 } { 35 } approx 2,72. \ end{array} $ $ I_x =iintlimits_D { y^2(y+1)dx } dy=2intlimits_0^2 { dx } intlimits_ { x^2 } ^4 { y^2(y+1)dy } =2intlimits_0^2 { left. { left( { y^4/4+y^3/3 }right) }right|_ { x^2 } ^4 dx } =2intlimits_0^2 { left( { frac { 256 } { 3 } -frac { x^8 } { 4 } -frac { x^6 } { 3 } }right)dx } = $ $ =2left. { left( { frac { 256 } { 3 } x-frac { x^9 } { 36 } -frac { x^7 } { 21 } }right) }right|_0^2 approx 300,7. $ $ I_y =iintlimits_D { x^2(y+1)dx } dy=2intlimits_0^2 { x^2dx } intlimits_ { x^2 } ^4 { (y+1)dy } =2intlimits_0^2 { x^2left. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } =2intlimits_0^2 { x^2left( { 12-frac { x^4 } { 2 } -x^2 }right)dx } = $ $ =2left. { left( { 4x^3-frac { x^7 } { 14 } -frac { x^5 } { 5 } }right) }right|_0^2 approx 32,9. quad I_O =iintlimits_D { left( { x^2+y^2 }right)(y+1)dx } dy=I_x +I_y approx 333,6. $

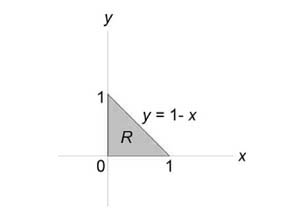
Пример 2

Вычислить моменты инерции треугольника, ограниченного прямыми (x + y = 1,) (x = 0,) (y = 0) и имеющего плотность $rho left( { x,y }right) = xy.$

Решение:

Найдем момент инерции пластины относительно оси (Ox:) $ { { I_x } = iintlimits_R { { y^2 } rho left( { x,y }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { { y^2 } xydy } }right]dx } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { { y^3 } dy } }right]xdx } } = { intlimits_0^1 { left[ { left. { left( { frac { { { y^4 } } } { 4 } }right) }right|_0^ { 1 – x } }right]xdx } } = \ = { frac { 1 } { 4 } intlimits_0^1 { { { left( { 1 – x }right) } ^4 } xdx } } = { frac { 1 } { 4 } intlimits_0^1 { left( { 1 – 4x + 6 { x^2 } – 4 { x^3 } + { x^4 } }right)xdx } } = \ = { frac { 1 } { 4 } intlimits_0^1 { left( { x – 4 { x^2 } + 6 { x^3 } – 4 { x^4 } + { x^5 } }right)dx } } = { frac { 1 } { 4 } left. { left( { frac { { { x^2 } } } { 2 } – frac { { 4 { x^3 } } } { 3 } + frac { { 6 { x^4 } } } { 4 } – frac { { 4 { x^5 } } } { 5 } + frac { { { x^6 } } } { 6 } }right) }right|_0^1 } = { frac { 1 } { 4 } left( { frac { 1 } { 2 } – frac { 4 } { 3 } + frac { 3 } { 2 } – frac { 4 } { 5 } + frac { 1 } { 6 } }right) } = { frac { { 49 } } { { 120 } } . } $

Аналогично вычислим момент инерции относительно оси (Oy:) $ { { I_y } = iintlimits_R { { x^2 } rho left( { x,y }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { { x^2 } xydy } }right]dx } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { ydy } }right] { x^3 } dx } } = { intlimits_0^1 { left[ { left. { left( { frac { { { y^2 } } } { 2 } }right) }right|_0^ { 1 – x } }right] { x^3 } dx } } = { frac { 1 } { 2 } intlimits_0^1 { { { left( { 1 – x }right) } ^2 } { x^3 } dx } } = \ = { frac { 1 } { 2 } intlimits_0^1 { left( { 1 – 2x + { x^2 } }right) { x^3 } dx } } = { frac { 1 } { 2 } intlimits_0^1 { left( { { x^3 } – 2 { x^4 } + { x^5 } }right)dx } } = { frac { 1 } { 2 } left. { left( { frac { { { x^4 } } } { 4 } – frac { { 2 { x^5 } } } { 5 } + frac { { { x^6 } } } { 6 } }right) }right|_0^1 } = { frac { 1 } { 2 } left( { frac { 1 } { 4 } – frac { 2 } { 5 } + frac { 1 } { 6 } }right) } = { frac { 1 } { { 120 } } . } $

Пример 3

Электрический заряд распределен по площади диска ( { x^2 } + { y^2 } = 1) таким образом, что его поверхностная плотность равна $sigma left( { x,y }right) = 1 + { x^2 } + { y^2 } ;left( { text { Кл/м } ^2 }right)$ Вычислить полный заряд диска.

Решение:

В полярных координатах область, занятая диском, описывается множеством (left[{ left( { r,theta }right)|;0 le r le 1,0 le theta le 2pi }right].)

Полный заряд будет равен $ { Q = iintlimits_R { sigma left( { x,y }right)dxdy } } = { intlimits_0^ { 2pi } { left[ { intlimits_0^1 { left( { 1 + { r^2 } { { cos } ^2 } theta + { r^2 } { sin^2 } theta }right)rdr } }right]dtheta } } = { intlimits_0^ { 2pi } { dtheta } intlimits_0^1 { left( { 1 + { r^2 } }right)rdr } } = { 2pi intlimits_0^1 { left( { r + { r^3 } }right)dr } } = \ = { 2pi left. { left( { frac { { { r^2 } } } { 2 } + frac { { { r^4 } } } { 4 } }right) }right|_0^1 } = { 2pi left( { frac { 1 } { 2 } + frac { 1 } { 4 } }right) } = { frac { { 3pi } } { 2 } ;left( { text { Кл } }right). } $

Известно из
механики, что момент инерции материальной
точки
относительно оси(или точкиО)
равен произведению массы точки на
квадрат расстояния от
до(или доО).
Кроме того, момент инерции системы
материальных точек равен сумме моментов
инерции этих точек.

Пусть теперь в
области
имеем распределение массы с поверхностной
плотностью.
Чтобы найти момент инерцииотносительно, например, оси,
как и в предыдущем пункте, разобьёмна части, выберем в каждой частиточкуи сосредоточим всю массув этой точке. Получим систему материальных
точек, и момент инерции этой системы
даст приближённое значение для искомого
момента инерцииобласти:

Точное значение
получим в виде интеграла:

Аналогично для
момента инерции относительно оси
:

Нетрудно догадаться,
что момент инерции
областиотносительно начала координат можно
найти по формуле

Пример 6.
Найти момент инерции однородного круга
радиуса
отно-сительно фиксированного диаметра.

Решение.
Пусть центр круга – в начале координат,
а фиксированный диаметр лежит на оси
.
Однородность означает, что.

Искомый момент
инерции:

VI Вычисление площади поверхности

Прежде всего,
требуется определить само понятие
площади поверхности. В своё время
математики показали, что невозможно
определить это понятие путём вписывания
и описывания многогранных поверхностей
(так это было сделано при определении
площади плоской фигуры и объёма тела).
Был предположен другой подход.

Будем обозначать
поверхность символом
,
а её площадь –.
Такую же систему обозначений примем и
для части поверхностии для плоских фигур.

Разобьём
начастейи в каждой из них выберем точкуЧерез выбранную точку проведем касательную
плоскость к поверхности и спроектируемна эту плоскость. Обозначимполученную проекцию и её площадь. Пусть,
кроме того,.

Определение.
Конечный предел вида

называют площадью
поверхности
.

Можно показать,
что если поверхность
не имеет особых точек (т.е. в каждой её
точке можно провести касательную
плоскость), то данный предел существует
и не зависит от разбиенияна частии от выбора точек.

Напомним, что,
если поверхность
задана явным уравнением,
причемисуществуют в точке,
то существует и касательная плоскость
в точке,
и её нормальный вектор имеет вид.
Заметим, что этот вектор образует острый
угол с осью

Теорема.
Пусть поверхность
задана уравнением,причем частные производныеинепрерывны в.
Тогда площадь данной поверхности можно
вычислить по формуле

Идея
доказательства. Разобьём
область
(проекциюна плоскость)
начастейи через их границы проведем цилиндрические
поверхности с образующими параллельными
оси.
Тогда и поверхностьразобьётся начастей.
В каждой такой части выберем точку,
проведем касательную плоскостьс нормальным век- тором.
Данный вектор составляет с осьюуголтакой, что.Тот
же самый уголсоставляет касательная плоскостьс координатной плоскостью

Пусть
и.
Можно показать, чтопри.
Это означает,

что

.

Отсюда

.

Но тогда сумма
— это интегральная сумма, которая в
пределе и даёт интеграл из формулировки
теоремы.

Пример 7.
Найти площадь части поверхности
,
распо-

ложенную внутри
цилиндра

Решение.
Очевидно, проекцией части конуса,
расположенной в цилиндре, есть “основание“
цилиндра – круг радиуса
с центром.
Предварительные вычисления:

Имеем для
:

Задачи (для
самостоятельного решения)

1. Вычислить объём
тела, ограниченного поверхностями

и
.

2. Найти положение
центра масс однородного полукольца
.

3. Поверхностная
плотность в каждой точке
кругапропор-циональна расстоянию отдо некоторого фиксированного диаметра.
Найти момент инерции круга относительно
конца этого диаметра.

4. Найти площадь
части сферы
,
расположенной внутри цилиндра.

Соседние файлы в папке Лекции по мат.анализу

• #
• #
• #
• #
• #
• #

Рассмотрим
теперь проблему определения момента инерции различных тел. Общая формула для
нахождения момента инерции объекта относительно оси  имеет вид

,

или

.                       (19.4)

Иными
словами, нужно сложить все массы, умножив каждую из них на квадрат ее
расстояния до оси . Заметьте, что это верно даже для
трехмерного тела, несмотря на то, что расстояние имеет такой «двумерный вид».
Впрочем, в большинстве случаев мы будем ограничиваться двумерными телами.

В
качестве простого примера рассмотрим стержень, вращающийся относительно оси,
проходящей через его конец и перпендикулярной к нему (фиг. 19.3). Нам нужно
просуммировать теперь все массы, умноженные на квадраты расстояния  (в этом случае
все  –
нулевые). Под суммой, разумеется, я имею в виду интеграл от , умноженный на
«элементики» массы. Если мы разделим стержень на кусочки длиной , то
соответствующий элемент массы будет пропорционален , а если бы  составляло длину
всего стержня, то его масса была бы равна . Поэтому

и

.                 (19.5)

Размерность
момента инерции всегда равна массе, умноженной на квадрат длины, так что
единственная существенная величина, которую мы вычислили, это множитель .

Фиг. 19.3. Прямой стержень,
вращающийся вокруг оси, проходящей черед один из его концов.

А
чему будет равен момент инерции , если ось вращения проходит через
середину стержня? Чтобы найти его, нам снова нужно взять интеграл, но уже в
пределах от  до
.
Заметим, однако, одну особенность этого случая. Такой стержень с проходящей
через центр осью можно представлять себе как два стержня с осью, проходящей
через конец, причем масса каждого из них равна , а длина равна . Моменты инерции двух
таких стержней равны друг другу и вычисляются по формуле (19.5). Поэтому момент
инерции всего стержня равен

.              (19.6)

Таким
образом, стержень гораздо легче крутить за середину, чем за конец.

Можно,
конечно, продолжить вычисление моментов инерции других интересующих нас тел. Но
поскольку такие расчеты требуют большого опыта в вычислении интегралов (что
очень важно само по себе), они как таковые не представляют для нас большого
интереса. Впрочем, здесь имеются некоторые очень интересные и полезные теоремы.
Пусть имеется какое-то тело и мы хотим узнать его момент инерции относительно
какой-то оси. Это означает, что мы хотим найти его инертность при вращении
вокруг этой оси. Если мы будем двигать тело за стержень, подпирающий его центр
масс так, чтобы оно не поворачивалось при вращении вокруг оси (в этом случае на
него не действуют никакие моменты сил инерции, поэтому тело не будет поворачиваться,
когда мы начнем двигать его), то для того, чтобы повернуть его, понадобится
точно такая же сила, как если бы вся масса была сосредоточена в центре масс и
момент инерции был бы просто равен , где  – расстояние от центра масс до оси
вращения. Однако формула эта, разумеется, неверна. Она не дает правильного
момента инерции тела. Ведь в действительности при повороте тело вращается.
Крутится не только центр масс (что давало бы величину ), само тело тоже должно
поворачиваться относительно центра масс. Таким образом, к моменту инерции  нужно добавить  – момент инерции
относительно центра масс. Правильный ответ состоит в том, что момент инерции
относительно любой оси равен

.                  (19.7)

Эта
теорема называется теоремой о параллельном переносе оси. Доказывается она очень
легко. Момент инерции относительно любой оси равен сумме масс, умноженных на
сумму квадратов  и
, т. е. . Мы сейчас
сосредоточим наше внимание на , однако все в точности можно
повторить и для .
Пусть координата  есть расстояние данной частной точки
от начала координат; посмотрим, однако, как все изменится, если мы будем
измерять расстояние  от центра масс вместо  от начала
координат. Чтобы это выяснить, мы должны написать

.

Возводя
это выражение в квадрат, находим

.

Что
получится, если умножить его на  и просуммировать по всем ? Вынося постоянные
величины за знак суммирования, находим

.

Третью
сумму подсчитать легко; это просто . Второй член состоит из двух
сомножителей, один из которых ; он равен -координате центра масс. Но
это должно быть равно нулю, ведь  отсчитывается от центра масс, а в
этой системе координат среднее положение всех частиц, взвешенное их массами,
равно нулю. Первый же член, очевидно, представляет собой часть  от . Таким образом,
мы и приходим к формуле (19.7).

Давайте
проверим формулу (19.7) на одном примере. Просто проверим, будет ли она
применима для стержня. Мы уже нашли, что момент инерции стержня относительно
его конца должен быть равен . А центр масс стержня, разумеется,
находится на расстоянии . Таким образом, мы должны получить,
что .
Так как одна четвертая + одна двенадцатая = одной третьей, то мы не сделали
никакой грубой ошибки.

Кстати,
чтобы найти момент инерции (19.5), вовсе не обязательно вычислять интеграл.
Можно просто предположить, что он равен величине , умноженной на некоторый неизвестный
коэффициент .
После этого можно использовать рассуждения о двух половинках и для момента
инерции (19.6) получить коэффициент . Используя теперь теорему о
параллельном переносе оси, докажем, что , откуда . Всегда можно найти
какой-нибудь окольный путь!

При
применении теоремы о параллельных осях важно помнить, что ось  должна быть
параллельна оси, относительно которой мы хотим вычислять момент инерции.

Стоит,
пожалуй, упомянуть еще об одном свойстве, которое часто бывает очень полезно
при нахождении момента инерции некоторых типов тел. Оно состоит в следующем:
если у нас есть плоская фигура и тройка координатных осей с началом координат,
расположенным в этой плоскости, и осью , направленной перпендикулярно к ней,
то момент инерции этой фигуры относительно оси  равен сумме моментов инерции
относительно осей  и . Доказывается это совсем просто.
Заметим, что

(поскольку
все ).
Аналогично,

,

по

.

Момент
инерции однородной прямоугольной пластинки, например с массой , шириной  и длиной  относительно оси,
перпендикулярной к ней и проходящей через ее центр, равен просто

,

поскольку
момент инерции относительно оси, лежащей в плоскости пластинки и параллельной
ее длине, равен ,
т. е. точно такой же, как и для стержня длиной , а момент инерции относительно
другой оси в той же плоскости равен , такой же, как и для стержня длиной .

Итак,
перечислим свойства момента инерции относительно данной оси, которую мы назовем
осью :

1.
Момент инерции равен

.

2.
Если предмет состоит из нескольких частей, причем момент инерции каждой из них
известен, то полный момент инерции равен сумме моментов инерции этих частей.

3.
Момент инерции относительно любой данной оси равен моменту инерции относительно
параллельной оси, проходящей через центр масс, плюс произведение полной массы
на квадрат расстояния данной оси от центра масс.

4.
Момент инерции плоской фигуры относительно оси, перпендикулярной к ее
плоскости, равен сумме моментов инерций относительно любых двух других взаимно
перпендикулярных осей, лежащих в плоскости фигуры и пересекающихся с
перпендикулярной осью.

В
табл. 19.1 приведены моменты инерции некоторых элементарных фигур, имеющих
однородную плотность масс, а в табл. 19.2 – моменты инерции некоторых фигур,
которые могут быть получены из табл. 19.1 с использованием перечисленных выше
свойств.

Таблица
19.1 Простые примеры моментов инерции

Таблица
19.2 Моменты инерции, полученные из табл. 19.1