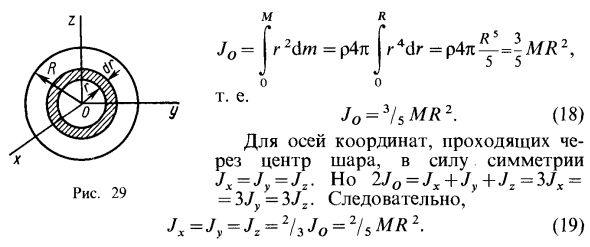Моменты инерции простейших однородных тел
- Момент инерции объекта сложной формы часто можно рассчитать, если он был предварительно разделен на объекты простой формы. Момент инерции сложного объекта получается суммированием моментов инерции этих частей объекта. Получите формулу для расчета момента инерции некоторых однородных простых объектов. Однородный стержень Есть стержень с одинаковой длиной I и массой M (рис. 25). Сориентируйте быка на стержень вдоль оси.
Рассчитайте момент инерции стержня относительно оси Oz, которая проходит перпендикулярно от конца стержня к стержню. Согласно определению момента инерции континуума вокруг оси, Рисунок 25 JOl-f x2dm = p j x2dx. Поскольку dw = pdx, p = M / l — плотность стержня. При расчете интеграла это выглядит так Вот так Момент инерции стержня относительно оси Cz ‘, проходящей через центр тяжести и параллельный оси Oz, определяется по теореме Штейнера. Jo ^ Jc. + Md1 d2 = (// 2) 2 = / 2/4 Это (12) Прямоугольная плита Размеры прямоугольной тонкой пластины — f и h, а масса — M (рисунок 26). Оси Ox и Oy находятся в плоскости пластины, а оси Oz перпендикулярны ей.
В общем случае все шесть уравнений можно рассматривать вместе, так как правая часть этих уравнений зависит от шести параметров и их начальных производных, если сила зависит от скорости.
Людмила Фирмаль
Чтобы определить момент инерции пластины относительно оси Oy, разбейте пластину на основные полосы шириной d.v и массой dwi = pAdx и интегрируйте x от 0 до /. получить Потому что фи = М Выполняя тот же расчет для оси Ox, • ‘.- «и- Эта ось Вол проходит через центр пластины. Определить момент инерции Для оси Oz необходимо сначала вычислить момент инерции одиночной заштрихованной полосы для параллельной оси O’z согласно уравнению стержня (12), а затем применить теорему Штейнера. Для основных полос, Формула интеграции Получить в диапазоне от 0 до I Относительно блюдо.
Поэтому следующая формула получается для момента инерции пластины относительно оси координат. L-AND ^; (13> Круглый диск Существует тонкий однородный диск с радиусом R и массой M (с.27). Рассчитаем момент инерции Джо для точки О. Этот момент инерции тонкого диска совпадает с моментом инерции Jz относительно координатной оси Oz, перпендикулярной плоскости диска. Разделите диск на концентрические полосы шириной dr и ограничьте их в виде материальных кругов. Масса полосы равна плотности p = M / (nR2), т.е. d / u = p-2nrdr, в 2nrdr раз больше ее площади.
- Момент одной полосы относительно точки O равен r2at. Обо всем диске Jo = Jr2dwi = p-2l Jr’dr = p-2l ^ — Вот так. T / Z Tiz Рис. 28 Jt = J0 = MR2! 2. (14) Для координатных осей Ox и Oy в плоскости диска с симметрией Jx = Jr, используя (8) = = JX + Jy + Jz, но Jz-J0 Jx = Jy = ll2Jo = MR2l ^. (15) Для тонких проволочных колец или круглых колес масса распределяется по всему ободу, а не по всей площади. Jt = Jo = MR2-, Jz = Jy = l! 2mr2. (16) Круглый цилиндр Для круглого однородного цилиндра с массой M, радиусом R и длиной I (рис. 28) сначала рассчитайте момент инерции относительно оси симметрии Oz. Для этого мы нарушаем Цилиндр на тонком диске массой dm и толщиной dz с плоскостью, перпендикулярной оси Oz.
Для таких дисков момент Это J. = MR2! 2. (17) Рассчитывается момент инерции относительно поперечной оси Su цилиндра. Для этого цилиндр с поперечным сечением, перпендикулярным вертикальной оси, делится на основные диски толщиной dz. Согласно теореме Штейнера dmR + dmz2, момент инерции основного диска с массой d / u = lL 2pdz относительно оси Si. Чтобы получить момент инерции всего цилиндра вокруг оси Su, полученное выражение должно быть интегрировано по z в диапазоне от 0 до // 2, а результат должен быть удвоен. получить Однако nR2lp = M — масса цилиндра. В результате 7Cy = L / (d2 / 4 + / 2/12).
Прежде чем рассматривать применение некоторой теоремы Карно, необходимо рассчитать кинетическую энергию потерянной скорости твердого тела, движущегося вокруг неподвижной оси или неподвижной точки.
Людмила Фирмаль
Таким образом, момент инерции цилиндра относительно его симметричной горизонтальной оси получается как сумма моментов инерции диска и стержня относительно этой оси, масса которых равна массе цилиндра в отдельности. Диск получается из цилиндра симметричным сжатием с обоих концов до средней плоскости при сохранении радиуса и получается путем сжатия стержня-цилиндра до однородного стержня вдоль оси цилиндра при сохранении длины. Мяч Масса шара равна М, а радиус равен R (рис. 29).
Делит шар на концентрические сферические слои с радиусом r и толщиной Слой равен произведению площади поверхности сферы радиуса r на толщину слоя dr, т.е. dK = 4nr2dr. Следовательно, масса базового слоя равна dm = pd V = p4lg 2dr. Для момента инерции шара относительно центра O шара, Рисунок 29 Jo = Jr2dzn = р4лJ r4dr = р4л ^ — = ^ Л / Я2, _ Т. е. JO = 3! SMR2. (18) Для координатной оси, проходящей через центр шара, из-за симметрии, jx = jy = jz, но 2JO = JX + J „+ JI = 3JX = 3Jy = 3JX. Jx = Jy = Jz = 2/3 Jo = 2 / sMR2. (19)
Смотрите также:
Задачи по теоретической механике
Определение моментов инерции некоторых
однородных тел
Момент инерции однородной тонкой
прямоугольной пластины. Найдем моменты
инерции однородной тонкой прямоугольной
пластины массы m
относительно ее осей симметрии. Длины
сторон пластины равны a
и b, соответственно
(рис. 3.1).

Рис. 3.1
В первую очередь определим момент
инерции пластины относительно оси Сy.
Для этого выделим элементарную массу
в виде полосы шириной dz,
расположенной на расстоянии z
от оси y. Тогда
dm=dS=bdz,
где
– масса единицы площади пластины.
Элементарный момент инерции выделенной
полосы относительно оси Сy
dJCy=(x2+z2)dm=b(x2+z2)dz.
Учитывая малую толщину пластины,
пренебрежем координатой x,
и проинтегрируем по z:
.
Так как =m/ab,
окончательно имеем
. (3.1)
Очевидно, что после аналогичных
рассуждений не трудно получить момент
инерции относительно оси Сz:
. (3.2)
Теперь найдем момент инерции пластины
относительно оси Сx.
Для этого выделим элемент пластины
площадью dS=dydz
и массой dm=dydz
(рис. 3.2). Элементарный момент инерции
относительно оси Сx:
dJCx=(y2+z2)dm=(y2+z2)dz.
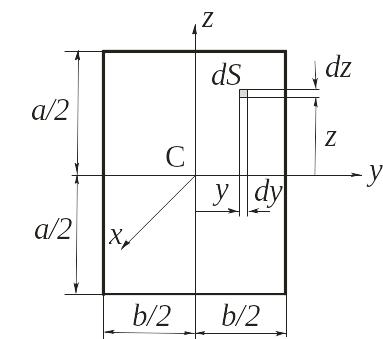
Рис. 3.2
Интегрируем по площади пластины
.
Подставляя =m/ab,
получаем
. (3.3)
Момент инерции однородной круглой
пластины. Определим моменты инерции
однородной тонкой круглой пластины
массы m и радиуса R
относительно оси Cz,
проходящей через центр пластины
перпендикулярно ее плоскости (рис. 3.3).
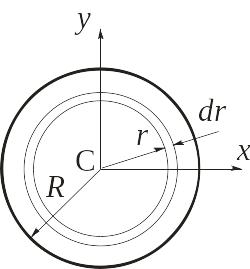
Рис. 3.3
Мысленно выделим в пластине элементарное
кольцо радиуса r и
толщины dr. Масса этого
кольца:
dm=2rdr.
Элементарный момент инерции кольца
относительно оси z:
dJCz=r2dm=2r3dr.
Момент инерции всей пластины относительно
оси z:
.
Принимая во внимание, что
,
окончательно находим
. (3.4)
Определим теперь момент инерции пластины
относительно оси x
(рис. 3.4).
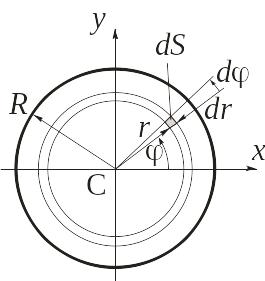
Рис. 3.4
Воспользуемся полярной системой
координат r, .
Выделим элемент площади dS=rddr
массы dm=dS=rddr.
Элементарный момент инерции площадки
dJCx=dm(y2+z2)
включает в себя координату z,
которой в силу малой толщины пластины
можно пренебречь. Так как
y=rsin,
то
dJCx=r2sin2dm=r3sin2
ddr.
Тогда
.
Подставляя значение ,
окончательно получаем:
.
(3.5)
Момент инерции однородного прямого
кругового цилиндра. Определим моменты
инерции однородного прямого кругового
цилиндра массы m,
радиуса R и высоты H
относительно его осей симметрии (рис.
3.5).

Рис. 3.5
Сначала найдем момент инерции цилиндра
относительно оси Cz,
проходящей через его центр масс С.
При выводе формулы (3.4) мы в рассуждениях
не использовали толщину пластины.
Поэтому, рассматривая прямой круговой
цилиндр как однородную круглую пластину,
сразу получаем:
. (3.6)
Для определения момента инерции цилиндра
относительно оси Cx
мысленно рассечем цилиндр двумя
сечениями, перпендикулярными оси Cz
и расположенными на расстояниях z
и z+dz
от плоскости Cxy,
соответственно. Применяя теорему
Гюйгенса-Штейнера, найдем момент инерции
элементарной пластинки относительно
оси Cx:
dJCx=
dmR2/4+dmz2,
где dm=dV=R2dz
– масса элементарной пластинки;
– плотность цилиндра.
Интегрируя по высоте цилиндра, получим
.
После подстановки в это выражение
соотношения m=R2H
имеем
.
(3.7)
Очевидно, что JCx=JCy.
Момент инерции однородного тонкого
стержня. Определим момент инерции
однородного тонкого стержня массы m
и длины l относительно
осей Cx и Cy,
перпендикулярных стержню (рис. 3.6).
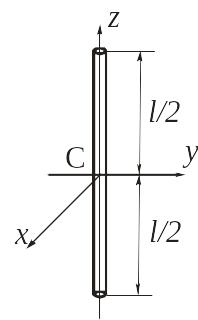
Рис. 3.6
Эти моменты инерции найдем, положив в
формуле (5.7) R=0, а
H=l:
JCx=JCy=ml2/12. (3.8)
Соседние файлы в папке Первый курс Летняя сессия
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
06.07.20214.74 Mб4Статика.docx
- #
В этом уроке посмотрим, как определяются осевые моменты инерции для сложного сечения (состоящего из простых фигур).
Условие задачи
В качестве примера возьмём симметричное сечение, имеющее две оси симметрии:

Определение положения центра тяжести
Первым делом, необходимо определить положение центра тяжести сечения. Как это делается, можешь посмотреть в отдельном уроке, перейдя по указанной ссылке. Здесь же, я приведу только расчёт.
Подготовим сечение к расчёту:
- разобьём сечение на простейшие фигуры;
- обозначим центры тяжести отдельных фигур;
- введём вспомогательные координатные оси (y0, x0).

Площадь сечения
Используя эту страничку, найдём площади отдельных фигур:

Расстояния от центров тяжести отдельных фигур до вспомогательных осей
Статические моменты

Координаты центра тяжести
Покажем центр тяжести всего сечения:

Как видишь, центр тяжести находится ровно посередине сечения. Это свойство симметричного сечения. У такого сечения, которое имеет две оси симметрии, центр тяжести находится на пересечении этих осей. Поэтому для симметричного сечения можно и НЕ рассчитывать положение центра тяжести.
Расчёт осевых моментов инерции
Для выполнения дальнейшего расчёта следует обозначить центральные оси для всего сечения (x, y), а также собственные оси для каждой отдельной фигуры, которые формируют сечение:

Как определить моменты инерции относительно центральных осей?
Осевые моменты инерции (Ix, Iy) относительно центральных осей (x, y) можно определить по следующим формулам:

где Ixi, Iyi – моменты инерции отдельных фигур относительно собственных осей;
Ai – площади отдельных фигур;
yci, xci – расстояния от центров тяжести отдельных фигур до соответствующей центральной оси.
Определение моментов инерции для каждой фигуры
Определим осевые моменты инерции каждой отдельной фигуры, пользуясь справочной информацией:
Определение расстояний от центров тяжести каждой фигуры до центральных осей
Определение моментов инерции относительно центральных осей
Другие уроки, на проекте – ssopromat.ru, по расчёту геометрических характеристик можно найти здесь.