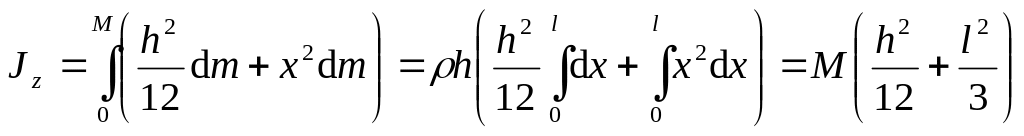Как найти момент инерции прямоугольной пластины

Моменты инерции
тел сложной формы часто удается вычислить,
если их предварительно разбить на тела
простой формы. Моменты инерции сложных
тел получают, суммируя моменты инерции
частей этих тел. Получим формулы для
вычисления моментов инерции некоторых
однородных простейших тел.

О z’ днородный стержень

И

Рис. 21

меем однородный стержень длиной

и массой

(рис. 21). Направим по стержню ось

.
Вычислим момент инерции стержня
относительно оси

,
проходящей перпендикулярно стержню
через его конец. Согласно определению
момента инерции сплошного юла относительно
оси, имеем

,

так
как

,
где

– -плотность стержня.

Вычисляя интеграл,
получаем

. (69)

Момент
инерции стержня относительно оси

,
проходящей через центр масс и параллельной
оси

,
определяется по теореме Штейнера

,
где

.

Следовательно,

. (70)

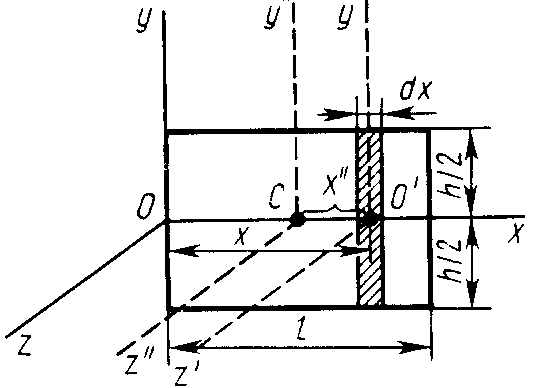
Прямоугольная пластина

Прямоугольная
тонкая пластина имеет размеры

и

и массу

(рис. 22). Оси

и

расположим в плоскости пластины, а ось

– перпендикулярно ей. Для определения
момента инерции пластины относительно
оси

разобьем пластину на элементарные
полоски шириной

и массой

и проинтегрируем по

от 0 до

.
Получим

y”
y‘

,

т

Рис. 22

ак как

.

Аналогичные
вычисления для оси

дадут

,

так
как эта ось проходит через середину
пластины.

Для
определения момента инерции пластины
относительно оси

следует предварительно вычислить момент
инерции отдельной заштрихованной
полоски относительно параллельной оси

по формуле (70) для стержня и применить
затем теорему Штейнера. Для элементарной
полоски имеем

.

Интегрируя
это выражения по

от 0 до

,
получим

.

Для
моментов инерции пластины относительно
осей координат получено:

,

,

. (71)

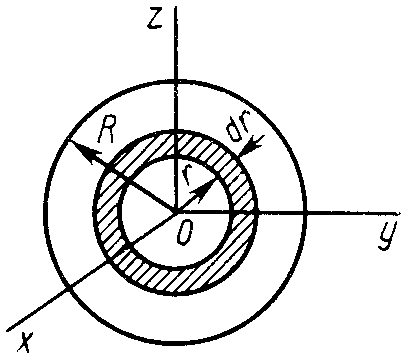
Круглый диск

Имеем
тонкий однородный диск радиусом

и массой

(рис. 23). Вычислим момент его инерции

относительно т
очки

.
Этот момент инерции для тонкого диска
совпадает с моментом инерции

относительно координатной оси

,
перпендикулярной плоскости диска.
Разобьем диск на концентрические полоски
шириной

,
принимаемые в пределе за материальные
окружности. Масса полоски равна ее
площади

,
умноженной на плотность

,
т.е.

.
Момент одной полоски относительно точки

равен

.
Для всего диска

Рис. 23

.

Таким образом

. (72)

Для
осей координат

и

,
расположенных в плоскости диска, в силу
симметрии

.
Используя (66), имеем

,
но

,
поэтому

. (73)

В случае топкого
проволочного кольца или круглого колеса,
у которых масса распределена не по
площади, а по его ободу, имеем

,

. (74)

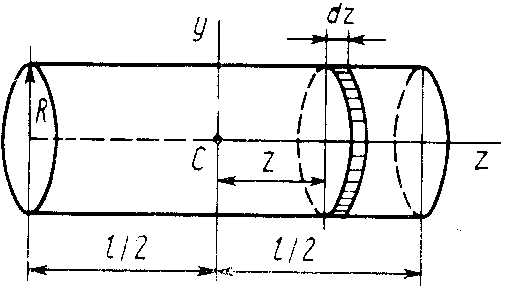
Круглый цилиндр

Для
круглого однородного цилиндра, масса
которого

,
радиус

и длина

(рис. 24), вычислим его момент и
нерции
относительно продольной оси симметрии

:
разобьем цилиндр плоскостями,
перпендикулярными оси

на тонкие диски массой

и толщиной

.
Для такого диска момент инерции
о

Рис. 24

тносительно оси

равен

.
Для всего цилиндра

. (75)

Вычислим
момент инерции цилиндра относительно
его поперечной оси симметрии

.
Для этого разобьем цилиндр поперечными
сечениями, перпендикулярными его
продольной оси, на элементарные диски
толщиной

.
Момент инерции элементарного диска
массой

относительно оси

по теореме Штейнера

.

Чтобы
получить момент инерции всего цилиндра
относительно оси

следует проинтегрировать полученное
выражение по

в пределах от 0 до

и результат удвоить. Получим

Но

– масса цилиндра. Следовательно

.

Таким
образом, момент инерции цилиндра
относительно его поперечной оси симметрии
получается как сумма моментов инерции
относительно этой оси диска и стержня,
массы которых равны по отдельности
массе цилиндра. Диск получается из
цилиндра симметричным сжатием его с
торцов до срединной плоскости при
сохранении радиуса, а стержень – сжатием
цилиндра в однородный стержень,
расположенный по оси цилиндра, при
сохранении длины.

Шар

П

Рис. 25

усть масса шара

,
радиус

(рис. 25). Разобьем шар на концентрические
сферические слои радиусом

и толщиной

.
Масса такого слоя

,
где

,

– объем слоя, равный произведению
площади поверхности сферы радиусом

на толщину слоя

,
т.е.

.
Таким образом, масса элементарного слоя

.

Для
момента инерции шара относительно его
центра

имеем

. (76)

Для
осей координат, проходящих через центр
шара, в силу симметрии

.
Используя (66), имеем

.
Поэтому

. (77)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Механические приложения двойного интеграла

Будем считать, что $mathbf { textit { D } } $ – неоднородная плоская пластина с поверхностной плотностью материала в точке $P$ равной $mu (P)$. В механике $mu (P)$ определяется так. Точка $P$ окружается малой областью $mathbf { textit { S } } $, находится масса $mathbf { textit { m } } (mathbf { textit { S } } )$ и площадь этой области { площадь тоже будем обозначать буквой $mathbf { textit { S } } $ } и $mu (P)=mathop { lim } limits_ { diam(S)to 0 } frac { m(S) } { S } $.

Для нахождения массы по заданной плотности мы решим обратную задачу. Разобьём $mathbf { textit { D } } $ на малые подобласти $mathbf { textit { D } } _ { 1 } $, $mathbf { textit { D } } _ { 2 } $,$mathbf { textit { D } } _ { 3 } , { ldots } , mathbf { textit { D } } _ { n } $, в каждой из подобластей $mathbf { textit { D } } _ { i } $ выберем произвольную точку $mathbf { textit { P } } _ { i } $, и, считая что в пределах $mathbf { textit { D } } _ { i } $ плотность постоянна и равна $mu (P_i )$, получим, что масса $mathbf { textit { D } } _ { i } $ приближённо есть $mu (P_i )cdot s(D_i )$, а масса всей пластины $sumlimits_ { i=1 } ^n { mu (P_i )cdot s(D_i ) } $.

Это интегральная сумма, при уменьшении $d=mathop { max } limits_ { i=1,2,ldots ,n } diam(D_i )$ точность приближения увеличивается, и в пределе $m(D)=mathop { lim } limits_ { begin{array} { l } dto 0 \ (nto infty ) \ end{array} } sumlimits_ { i=1 } ^n { mu (P_i )cdot Delta s(D_i ) } =iintlimits_D { mu (P)ds } $.

Аналогично находятся другие параметры пластины:

Координаты центра тяжести

$x_c =frac { 1 } { m(D) } iintlimits_D { xcdot mu (P)ds } $, $y_c =frac { 1 } { m(D) } iintlimits_D { ycdot mu (P)ds } $;

Моменты инерции пластины

• $I_x =iintlimits_D { y^2cdot mu (P)ds } $ { относительно оси $mathbf { textit { Ox } } $ } ,
• $I_y =iintlimits_D { x^2cdot mu (P)ds } $ { относительно оси $mathbf { textit { Oy } } $ } ,
• $I_O =iintlimits_D { (x^2+y^2)cdot mu (P)ds } =I_x +I_y $ { относительно начала координат } .

Пластина расположена в области (R) и ее плотность в точке ( { left( { x,y }right) } ) равна ( { rho left( { x,y }right) } ).

Масса пластины

(m = largeiintlimits_Rnormalsize { rho left( { x,y }right)dA } )

Статические моменты пластины

Момент пластины относительно оси (Ox) определяется формулой

( { M_x } = largeiintlimits_Rnormalsize { yrho left( { x,y }right)dA } )

Аналогично, момент пластины относительно оси (Oy) выражается в виде

( { M_y } = largeiintlimits_Rnormalsize { xrho left( { x,y }right)dA } )

Координаты центра масс пластины

• (bar x = largefrac { { { M_y } } } { m } normalsize = largefrac { 1 } { m } normalsize largeiintlimits_Rnormalsize { xrho left( { x,y }right)dA } = largefrac { { iintlimits_R { xrho left( { x,y }right)dA } } } { { iintlimits_R { rho left( { x,y }right)dA } } } normalsize,;)
• (bar y = largefrac { { { M_x } } } { m } normalsize = largefrac { 1 } { m } normalsize largeiintlimits_Rnormalsize { yrho left( { x,y }right)dA } = largefrac { { iintlimits_R { yrho left( { x,y }right)dA } } } { { iintlimits_R { rho left( { x,y }right)dA } } } normalsize ).

Заряд пластины

(Q = largeiintlimits_Rnormalsize { sigma left( { x,y }right)dA } ),

где электрический заряд распределен по области (R) и его плотность в точке ( { left( { x,y }right) } ) равна ( { sigma left( { x,y }right) } ).

Среднее значение функции

(mu = largefrac { 1 } { S } iintlimits_Rnormalsize { fleft( { x,y }right)dA } ,;) где (S = largeiintlimits_Rnormalsize { dA } ).

Пример 1

Найти параметры неоднородной плоской пластины, ограниченной кривыми

$D:left[{ begin{array} { l } y=x^2, \ y=4; \ end{array} }right.$ если плотность $mu (x,y)=y+1$.

Решение:

$m(D)=iintlimits_D { (y+1)dxdy } =2intlimits_0^2 { dx } intlimits_ { x^2 } ^4 { (y+1)dy } =2intlimits_0^2 { left. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } =$ $ =2intlimits_0^2 { left( { 12-x^4/2-x^2 }right)dx } =2left. { left( { 12x-x^5/10-x^3/3 }right) }right|_0^2 =2left( { 24-frac { 16 } { 5 } -frac { 8 } { 3 } }right)=frac { 544 } { 15 } . $ $ x_c =frac { 1 } { m(D) } iintlimits_D { x(y+1)dx } dy=frac { 15 } { 544 } intlimits_ { -2 } ^2 { dx } intlimits_ { x^2 } ^4 { x(y+1)dy } =frac { 15 } { 544 } intlimits_ { -2 } ^2 { xleft. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } = $ $=frac { 15 } { 544 } intlimits_ { -2 } ^2 { left( { 12x-x^5/2-x^3 }right)dx } = quad =frac { 1 } { 544 } left. { left( { 6x^2-x^6/10-x^4/4 }right) }right|_ { -2 } ^2 =0$ { что и следовало ожидать, так как область и плотность симметричны относительно оси Оу). $ begin{array} { l } y_c =frac { 1 } { m(D) } iintlimits_D { y(y+1)dx } dy=frac { 15 } { 544 } intlimits_ { -2 } ^2 { dx } intlimits_ { x^2 } ^4 { y(y+1)dy } =frac { 15 } { 272 } intlimits_0^2 { left. { left( { y^3/3+y^2/2 }right) }right|_ { x^2 } ^4 dx } = \ =frac { 15 } { 272 } intlimits_0^2 { left( { 64/3+8-x^6/3-x^4/2 }right)dx } =frac { 15 } { 272 } left. { left( { 88x/3-x^7/21-x^5/10 }right) }right|_0^2 =frac { 15 } { 272 } left( { frac { 176 } { 3 } -frac { 128 } { 21 } -frac { 16 } { 5 } }right)=frac { 15 } { 272 } cdot frac { 1728 } { 35 } approx 2,72. \ end{array} $ $ I_x =iintlimits_D { y^2(y+1)dx } dy=2intlimits_0^2 { dx } intlimits_ { x^2 } ^4 { y^2(y+1)dy } =2intlimits_0^2 { left. { left( { y^4/4+y^3/3 }right) }right|_ { x^2 } ^4 dx } =2intlimits_0^2 { left( { frac { 256 } { 3 } -frac { x^8 } { 4 } -frac { x^6 } { 3 } }right)dx } = $ $ =2left. { left( { frac { 256 } { 3 } x-frac { x^9 } { 36 } -frac { x^7 } { 21 } }right) }right|_0^2 approx 300,7. $ $ I_y =iintlimits_D { x^2(y+1)dx } dy=2intlimits_0^2 { x^2dx } intlimits_ { x^2 } ^4 { (y+1)dy } =2intlimits_0^2 { x^2left. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } =2intlimits_0^2 { x^2left( { 12-frac { x^4 } { 2 } -x^2 }right)dx } = $ $ =2left. { left( { 4x^3-frac { x^7 } { 14 } -frac { x^5 } { 5 } }right) }right|_0^2 approx 32,9. quad I_O =iintlimits_D { left( { x^2+y^2 }right)(y+1)dx } dy=I_x +I_y approx 333,6. $

Пример 2

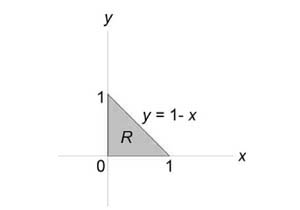
Вычислить моменты инерции треугольника, ограниченного прямыми (x + y = 1,) (x = 0,) (y = 0) и имеющего плотность $rho left( { x,y }right) = xy.$

Решение:

Найдем момент инерции пластины относительно оси (Ox:) $ { { I_x } = iintlimits_R { { y^2 } rho left( { x,y }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { { y^2 } xydy } }right]dx } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { { y^3 } dy } }right]xdx } } = { intlimits_0^1 { left[ { left. { left( { frac { { { y^4 } } } { 4 } }right) }right|_0^ { 1 – x } }right]xdx } } = \ = { frac { 1 } { 4 } intlimits_0^1 { { { left( { 1 – x }right) } ^4 } xdx } } = { frac { 1 } { 4 } intlimits_0^1 { left( { 1 – 4x + 6 { x^2 } – 4 { x^3 } + { x^4 } }right)xdx } } = \ = { frac { 1 } { 4 } intlimits_0^1 { left( { x – 4 { x^2 } + 6 { x^3 } – 4 { x^4 } + { x^5 } }right)dx } } = { frac { 1 } { 4 } left. { left( { frac { { { x^2 } } } { 2 } – frac { { 4 { x^3 } } } { 3 } + frac { { 6 { x^4 } } } { 4 } – frac { { 4 { x^5 } } } { 5 } + frac { { { x^6 } } } { 6 } }right) }right|_0^1 } = { frac { 1 } { 4 } left( { frac { 1 } { 2 } – frac { 4 } { 3 } + frac { 3 } { 2 } – frac { 4 } { 5 } + frac { 1 } { 6 } }right) } = { frac { { 49 } } { { 120 } } . } $

Аналогично вычислим момент инерции относительно оси (Oy:) $ { { I_y } = iintlimits_R { { x^2 } rho left( { x,y }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { { x^2 } xydy } }right]dx } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 – x } { ydy } }right] { x^3 } dx } } = { intlimits_0^1 { left[ { left. { left( { frac { { { y^2 } } } { 2 } }right) }right|_0^ { 1 – x } }right] { x^3 } dx } } = { frac { 1 } { 2 } intlimits_0^1 { { { left( { 1 – x }right) } ^2 } { x^3 } dx } } = \ = { frac { 1 } { 2 } intlimits_0^1 { left( { 1 – 2x + { x^2 } }right) { x^3 } dx } } = { frac { 1 } { 2 } intlimits_0^1 { left( { { x^3 } – 2 { x^4 } + { x^5 } }right)dx } } = { frac { 1 } { 2 } left. { left( { frac { { { x^4 } } } { 4 } – frac { { 2 { x^5 } } } { 5 } + frac { { { x^6 } } } { 6 } }right) }right|_0^1 } = { frac { 1 } { 2 } left( { frac { 1 } { 4 } – frac { 2 } { 5 } + frac { 1 } { 6 } }right) } = { frac { 1 } { { 120 } } . } $

Пример 3

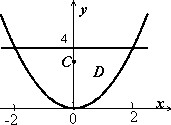
Электрический заряд распределен по площади диска ( { x^2 } + { y^2 } = 1) таким образом, что его поверхностная плотность равна $sigma left( { x,y }right) = 1 + { x^2 } + { y^2 } ;left( { text { Кл/м } ^2 }right)$ Вычислить полный заряд диска.

Решение:

В полярных координатах область, занятая диском, описывается множеством (left[{ left( { r,theta }right)|;0 le r le 1,0 le theta le 2pi }right].)

Полный заряд будет равен $ { Q = iintlimits_R { sigma left( { x,y }right)dxdy } } = { intlimits_0^ { 2pi } { left[ { intlimits_0^1 { left( { 1 + { r^2 } { { cos } ^2 } theta + { r^2 } { sin^2 } theta }right)rdr } }right]dtheta } } = { intlimits_0^ { 2pi } { dtheta } intlimits_0^1 { left( { 1 + { r^2 } }right)rdr } } = { 2pi intlimits_0^1 { left( { r + { r^3 } }right)dr } } = \ = { 2pi left. { left( { frac { { { r^2 } } } { 2 } + frac { { { r^4 } } } { 4 } }right) }right|_0^1 } = { 2pi left( { frac { 1 } { 2 } + frac { 1 } { 4 } }right) } = { frac { { 3pi } } { 2 } ;left( { text { Кл } }right). } $