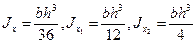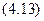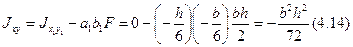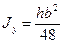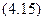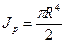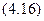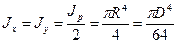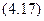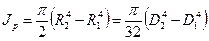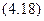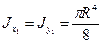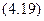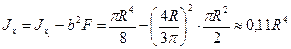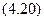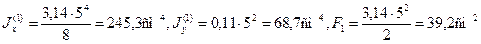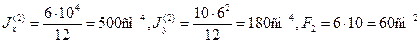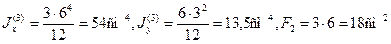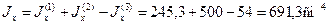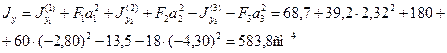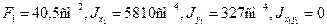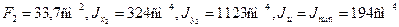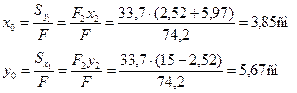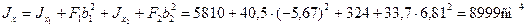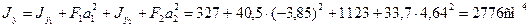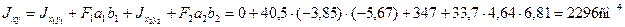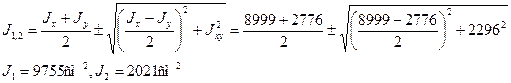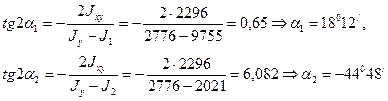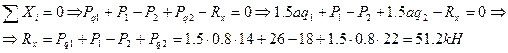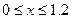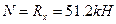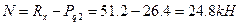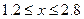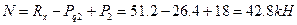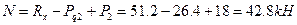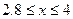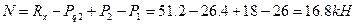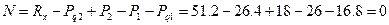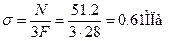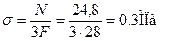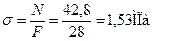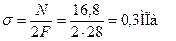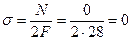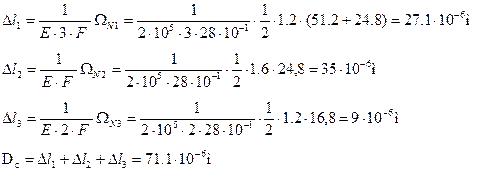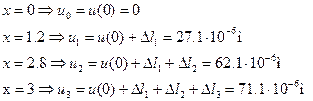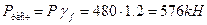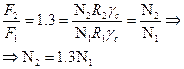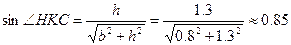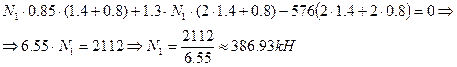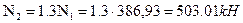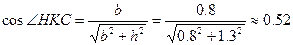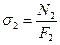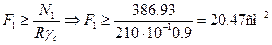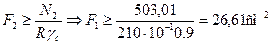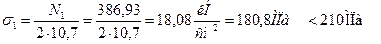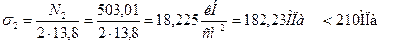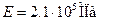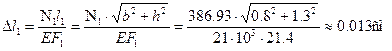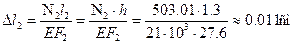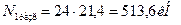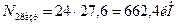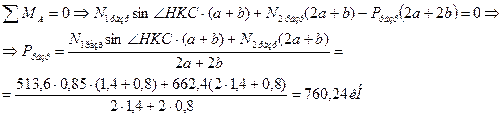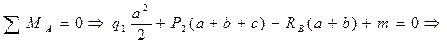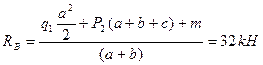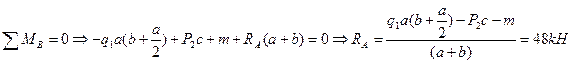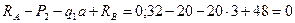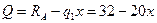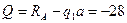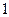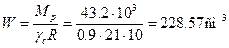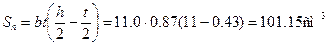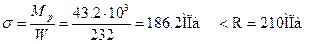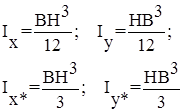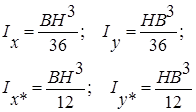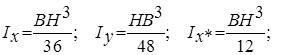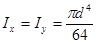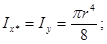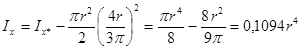Осевые моменты инерции простых сечений (фигур)
На этой странице указаны формулы для расчёта моментов инерции простых сечений (фигур). Данные формулы используются при проведении прочностных расчётов при изгибе и расчётов на жёсткость. А также для расчёта геометрических характеристик более сложных сечений.
Формулы для расчёта осевых моментов инерции
Традиционно, моменты инерции обозначаются буквой – I. Также в литературе, часто используют букву – J.
На сайте – ssopromat.ru, ты также можешь найти другую справочную информацию.
Как уже отмечалось выше, к числу простых
плоских фигур относятся три фигуры:
прямоугольник, треугольник и круг.
Простыми эти фигуры считаются потому,
что положение центра тяжести этих фигур
заранее известно. Все остальные фигуры
могут быть составлены из этих простых
фигур и считаются сложными. Вычислим
осевые моменты инерции простых фигур
относительно их центральных осей.
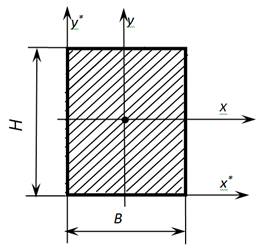
1. Прямоугольник.Рассмотрим сечение
прямоугольного профиля размерами(Рис.4.6). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянииот
центральной оси.
Рис.4.6
Вычислим момент инерции прямоугольного сечения относительно оси :
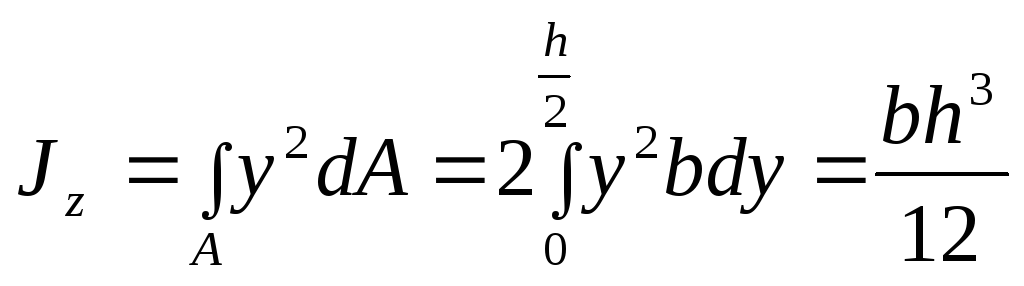
(4.10)
Момент
инерции прямоугольного сечения
относительно оси
найдем аналогично. Здесь вывод не
приводится.
.
(4.11)
Центробежный
момент инерции относительно осей
и
равен нулю, так как оси
и
являются осями симметрии, а, следовательно,
главными осями.
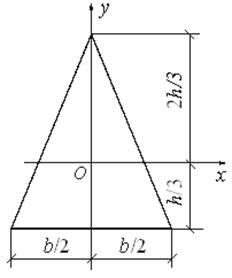
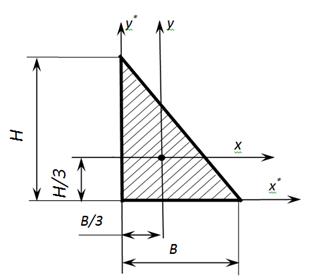
2. Равнобедренный треугольник.Рассмотрим сечение треугольного профиля
размерами(Рис.4.7). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянииот центральной оси
.
Центр тяжести треугольника находится
на расстояниот основания. Треугольник принимается
равнобедренным, так что осьсечения является осью симметрии.
Рис.4.7
Вычислим
момент инерции сечения относительно
оси :

(4.12)
Величину
определим из подобия треугольников:

откуда
.
Подставляя
выражения для
в (4.12) и интегрируя, получим:
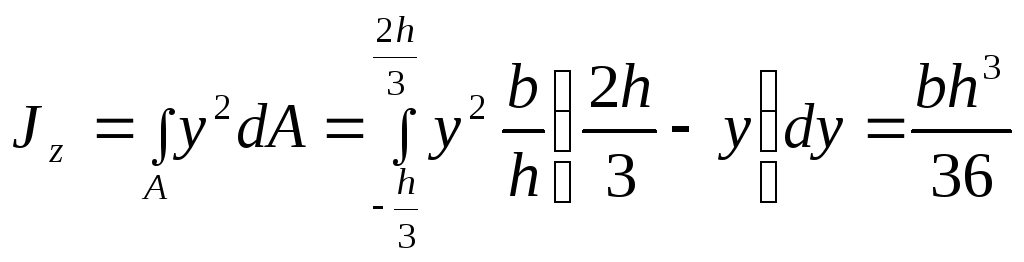
(4.13)
Момент
инерции для равнобедренного треугольника
относительно оси
находится аналогичным образом и равен:
(4.14)
Центробежный
момент инерции относительно осей
и
равен нулю, так как ось
является осью симметрии сечения.
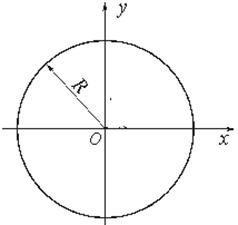
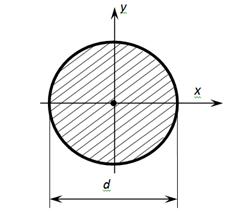
3. Круг. Рассмотрим сечение круглого
профиля диаметром(Рис.4.8).
Выделим элемент сечения двумя бесконечно
близко расположенными концентрическими
окружностями, расположенными на
расстоянииот центра тяжести круга
.
Рис.4.8
Вычислим полярный момент инерции круга,
воспользовавшись выражением (4.5):

(4.15)
Используя условие инвариантности для
суммы осевых моментов инерции относительно
двух взаимно перпендикулярных осей
(4.6) и учитывая, что для круга в силу
симметрии
,
определяем величину осевых моментов
инерции:
.
(4.16)
Откуда:
.
(4.17)
Центробежный
момент инерции относительно осей
и
равен нулю, так как оси
и
являются осями симметрии сечения.
4.4. Зависимости между моментами инерции относительно параллельных осей
При
вычислении моментов инерции для сложных
фигур следует запомнить одно правило:
значения для моментов инерции можно
складывать, если
они вычислены относительно одной и той
же оси. Для
сложных фигур чаще всего центры тяжести
отдельных простых фигур и всей фигуры
не совпадают. Не совпадают, соответственно,
и центральные оси для отдельных простых
фигур и всей фигуры. В связи с этим
существуют приемы приведения моментов
инерции к одной оси, например, центральной
оси всей фигуры. Это может быть связано
с параллельным переносом осей инерции
и дополнительными вычислениями.
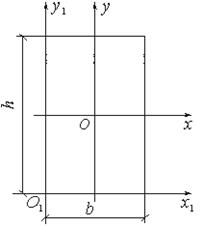
Рассмотрим
определение моментов инерции относительно
параллельных осей инерции, изображенных
на рис.4.9.
Рис.4.9
Пусть
осевые и центробежный моменты инерции
изображенной на рис.4.9. фигуры относительно
произвольно выбранных осей
и
с началом координат в точке
известны. Требуется вычислить осевые
и центробежный моменты инерции фигуры
относительно произвольных параллельных
осейи
с началом координат в точке
.
Осии
проведены на расстояниях
и
соответственно от осей
и
.
Воспользуемся
выражениями для осевых моментов инерции
(4.4) и для центробежного момента инерции
(4.7). Подставим в эти выражения вместо
текущих координат
и
элемента с бесконечно малой площадью
координатыи
в новой системе координат. Получим:
.
(4.18)
.
(4.19)
.
(4.20)
Анализируя полученные выражения,
приходим к выводу, что при вычислении
моментов инерции относительно параллельных
осей к моментам инерции, вычисленных
относительно исходных осей инерции,
следует призводить добавки в виде
дополнительных членов, которые могут
оказаться намного больше значений для
моментов инерции относительно исходных
осей. Поэтому пренебрегать этими
дополнительными членами ни в коем случае
нельзя.
Рассмотренный случай представляет
собой самый общий случай параллельного
переноса осей, когда в качестве исходных
были взяты произвольные оси инерции. В
большинстве расчетов встречаются
частные случаи определения моментов
инерции.
Первый частный случай. Исходные оси
являются центральными осями инерции
фигуры. Тогда, используя основное
свойство для статического момента
площади, можно исключить из уравнений
(4.18)(4.20) члены
уравнений, в которые входит статический
момент площади фигуры. В результате
получим:
.
(4.21)
.
(4.22)
.
(4.23)
Здесь оси
и
центральные оси
инерции.
Второй частный случай. Исходные оси
являются главными осями инерции. Тогда,
учитывая, что относительно главных осей
инерции центробежный момент инерции
равен нулю, получим:
.
(4.24)
.
(4.25)
.
(4.26)
Здесь оси
и
главные оси инерции.
Воспользуемся полученными выражениями
и рассмотрим несколько примеров
вычисления моментов инерции для плоских
фигур.
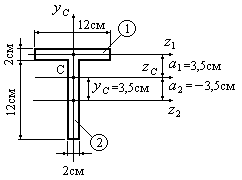
Пример 4.2.Определить осевые моменты
инерции фигуры, приведенной на рис.
4.10, относительно центральных осейи
.
Рис.4.10
Решение:
В предыдущем примере 4.1 для изображенной
на рис.4.10 фигуры было определено положение
центра тяжести С. Координата центра
тяжести откладывалась от оси
и составила
.
Вычислим расстоянияи
между осями
и
и осями
и
.
Эти расстояния составили соответственнои
.
Так как исходные осии
являются центральными осями для простых
фигур в виде прямоугольников, для
определения момента инерции фигуры
относительно осивоспользуемся выводами для первого
частного случая, в частности, формулой
(4.21).
см4.
Момент инерции относительно оси
получим путем сложения моментов инерции
простых фигур относительно этой же оси,
так как осьявляется общей центральной осью для
простых фигур и для всей фигуры.
см4.
Центробежный момент инерции относительно
осей
и
равен нулю, так как ось инерции
является главной осью (осью симметрии
фигуры).
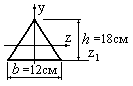
Пример
4.3. Чему равен
размер b
(в см) фигуры,
изображенной на рис. 4.11, если момент
инерции фигуры относительно оси
равен 1000 см4?
Рис.4.11
Решение:
Выразим момент инерции относительно
оси
через неизвестный размер сечения
,
воспользовавшись формулой (4.21), учитывая,
что расстояние между осямии
равно 7см:
см4.
(а)
Решая выражение (а) относительно размера
сечения
,
получим:

Пример.4.4.
Какая из фигур, изображенных на рис.4.12
, имеет больший момент инерции относительно
оси
,
если обе фигуры имеют одинаковую площадьсм2?
Рис.4.12
Решение:
1. Выразим площади фигур через их размеры
и определим:
а) диаметр сечения для круглого сечения:
см2; Откуда
см.
б) размер стороны квадрата:
;
Откудасм.
2. Вычисляем момент инерции для круглого
сечения:
см4.
3. Вычисляем момент инерции для сечения
квадратной формы:
см4.
Сравнивая полученные результаты,
приходим к выводу, что наибольшим
моментом инерции будет обладать сечение
квадратной формы по сравнению с сечение
круглой формы при одинаковой у них
площади.
Пример 4.5.Определить полярный момент
инерции (в см4) сечения прямоугольной
формы относительно его центра тяжести,
если ширина сечения
см,
высота сечениясм.
Решение:
1. Найдем моменты инерции сечения
относительно горизонтальной
и вертикальной
центральных осей инерции:
см4;
см4.
2. Определяем полярный момент инерции
сечения как сумму осевых моментов
инерции:
см4.
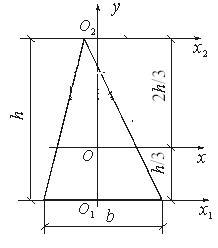
Пример
4.6. Определить
момент инерции фигуры треугольной формы
изображенной на рис.4.13, относительно
центральной оси
,
если момент инерции фигуры относительно
осиравен 2400 см4.
Рис.4.13
Решение:
Момент инерции сечения треугольной
формы относительно главной оси инерции
будет меньше по сравнению с моментом
инерции относительно осина величину
.
Поэтому присм
момент инерции сечения относительно
осинайдем следующим образом:
см4.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Моменты инерции простых сечений
Моменты инерции относительно осей Оx, Оx1, Оy, Оy1:
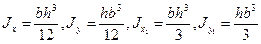
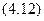
моменты инерции относительно осей Оx, О1x1 и О2x2,:
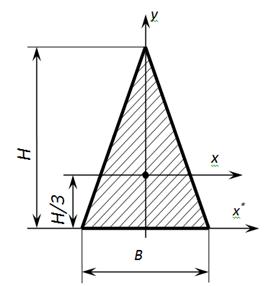
Прямоугольный и равнобедренный треугольники.
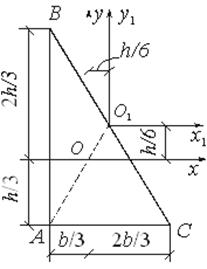
Для прямоугольного треугольника определим центробежный момент инерции Jxy относительно центральных осей Ox и Oy, параллельных катетам:
Момент инерции равнобедренного треугольника относительно оси
Круг. Полярный момент инерции круга:
Учитывая, что для круга Jx = Jy и полярный момент согласно равен сумме двух осевых моментов, получим:
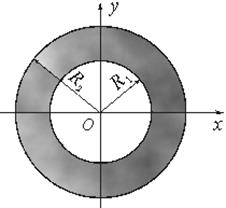
Кольцевое сечение. Моменты инерции кольца находятся как разность моментов инерции двух кругов с радиусами R2 и R1 :
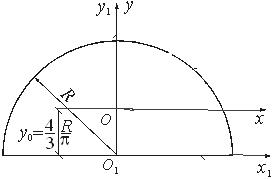
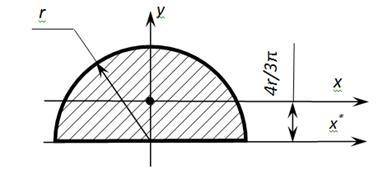
Относительно осей O1x1 и O1y1, которые являются главными осями для полукруга, осевые моменты инерции равны половине момента инерции круга:
Момент инерции относительно главной центральной оси определяется с помощью первой формулы:
Геометрические характеристики сечений прокатных профилей (двутавры, швеллеры, уголки) приведены в таблицах сортамента прокатной стали.
Моменты инерции составных сечений. При определении моментов инерции составного сечения последнее разбивают на простые фигуры, у которых известны положения центров тяжести и моменты инерции относительно собственных центральных осей. По формулам (4.6) находят координаты центра тяжести всего сечения в системе произвольно выбранных вспомогательных осей. Параллельно этим осям проводят центральные оси, относительно которых определяют осевые и центробежный моменты инерции по формулам (4.7). Моменты инерции относительно главных центральных осей определяются по формуле (4.11), а положение главных центральных осей – по формулам (4.10).
Далее рассмотрены примеры задач.
5. Примеры решения задач
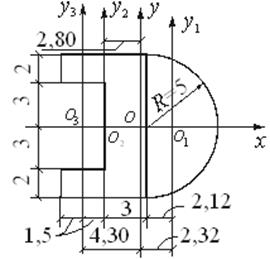
Пример 1. Определим положение центра тяжести и моменты инерции относительно главных центральных осей сечения, состоящего из полукруга и прямоугольника с вырезом. Размеры сечения на рисунке даны в сантиметрах.
Разобьем сечение на три простые фигуры: полукруг с радиусом R=5 см, прямоугольник с размерами сторон 6×10 см, прямоугольный вырез с размерами 3×6 см и определим площади и моменты инерции этих фигур относительно собственных центральных осей.
Для полукруга по формулам (2.21) и (2.22) имеем:
Положение центра тяжести О1 полукруга определяется по формуле (2.20) и равно 0,424·5 = 2,12 см (рис.2.15).
Для прямоугольника и прямоугольного выреза по формулам (2.13) получим
Площадь всего сечения равна F = 39,2 + 60 – 18 = 81,2 см 2 .
Центр тяжести О сечения лежит на горизонтальной оси симметрии. Для определения его положения выберем в качестве вспомогательной оси центральную ось прямоугольника O2y2 . Тогда получим
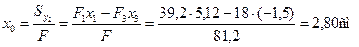
Отложим эту величину от оси О2y2 вправо и проведем ось Оy, которая вместе с осью Ох составит пару главных центральных осей всего сечения. Определим координаты центров тяжести отдельных фигур в системе координат Оxy: а1 = 2,32 см, а2 = – 2,80 см, а3 = – 4,30 см .
По формулам (2.6) найдем моменты инерции сечения относительно осей Ох и Оy:
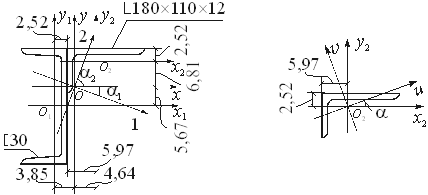
Пример 2.Для стержня несимметричного сечения, составленного из швеллера [ 30 и неравнобокого уголка L180х110х12, определим центр тяжести сечения, моменты инерции относительно главных центральных осей и положение этих осей. На рисунке размеры даны в сантиметрах.
Выпишем геометрические характеристики сечения швеллера:
Геометрические характеристики сечения неравнобокого уголка:
Величину центробежного момента инерции уголка 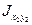
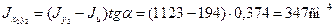
где tga = 0,374 – тангенс угла наклона главной оси u к оси Ох2 , величина которого приведена в сортаменте.
Площадь всего сечения равна F = 40,5 + 33,7 = 74,2 см 2 .
Для определения положения центра тяжести выберем в качестве вспомогательных осей оси швеллера О1x1 и О1y1. Тогда по формулам (2.5) получим
Эти величины и координаты центров тяжести швеллера и уголка в системе координат Охy показаны на рисунке и соответственно равны:
Определим по формулам (2.6) моменты инерции сечения относительно центральных осей Ох и Оy.
По формулам (2.12) и (2.11) найдем величины главных моментов инерции и углы наклона главных осей 1 и 2 к оси Ох :
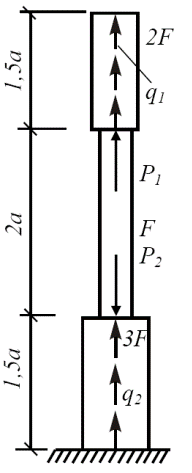
Пример 3. Для статически определимого стержня ступенчато постоянного сечения при заданных осевых нагрузках и геометрических размерах по строке требуется:
1.Определить опорную реакцию в месте закрепления стержня.
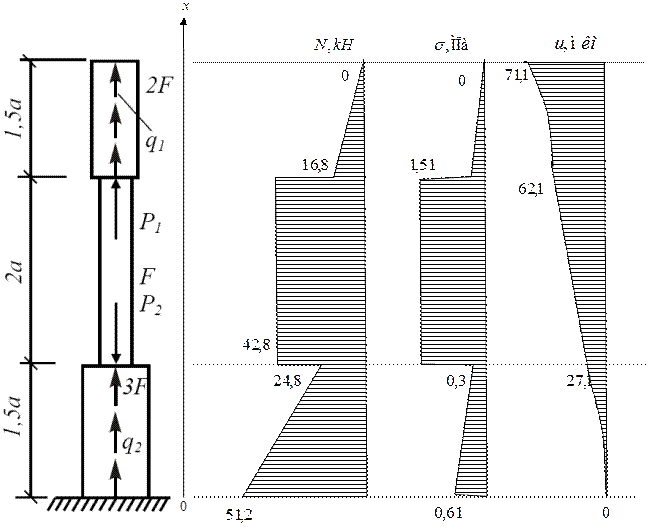
2.Вычислить значения продольных сил и нормальных напряжений в характерных сечениях и построить эпюры этих величин.
3.Найти величины абсолютных удлинений (укорочений) участков стержня и величину общего удлинения (укорочения) стержня в целом.
4.Определить значения осевых перемещений характерных сечений и построить эпюру осевых перемещений.
| a, м | F, см 2 | Р1, кН | Р2, кН | q1, кН/м | q2, кН/м | Е, МПа |
| 0,8 | 2,0·10 5 |
1. Составим уравнение равновесия:
2. Вычислим значения продольных сил:
Участок 1:
При 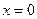
При 
Значение продольной силы линейно уменьшается
Участок 2:
При 
При 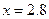
Значение продольной силы не изменяется
Участок 3:
При 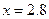
При 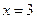
Значение продольной силы линейно уменьшается.
Найдем величины нормальных напряжений в характерных сечениях:
Участок 1:
При 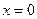
При 
Участок 2:
При 
Участок 3:
При 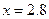
При 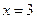
Величины абсолютных удлинений каждого их участков стержней найдем по формуле:
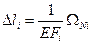
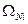
Определим величины осевых перемещений характерных сечений.
На участках 1 и 3 эпюра осевых перемещений имеет вид квадратичной параболы, на участке 2 изменяется линейно.
Пример 4. Для статически неопределимой стержневой системы, состоящей из абсолютно жесткой балки AB и поддерживающих ее стальных стержней 1 и 2 по схеме №…. при геометрических размерах, соотношениях площадей поперечных сечений стержней F2/F1 и величине нормативной нагрузки Р, указанных в строке № …. табл.2, требуется:
1.Определить расчетное значение нагрузки, приняв коэффициент надежности по нагрузке γf = 1,2.
2.Определить усилия в стержнях системы. Собственную массу элементов стержневой системы не учитывать.
3.Подобрать сечения стрежней в виде двух стальных прокатных равнобоких уголков, используя метод расчета по предельным состояниям. При подборе сечений обеспечить заданное соотношение площадей F2/F1. Расчетное сопротивление по пределу текучести стали марки ВСТ3 принять равным 210 МПа, коэффициент условий работы γс = 0,9.
4.Определить величины нормальных напряжений в поперечных сечениях стержней и проверить выполнение условий прочности.
5.Определить величины удлинений стержней, приняв Е=2,1·10 5 МПа.
6.Определить нагрузку Рт, при которой в системе возникают первые пластические деформации, считая, что материал стержней следует диаграмме Прандтля и имеет предел текучести σт = 240 МПа.
7.Определить разрушающую нагрузку Рразр, при которой система полностью исчерпывает свою несущую способность.
| a, м | b, м | h, м | F2/F1 | Р, кН |
| 1,4 | 0,8 | 1,3 | 1,3 |
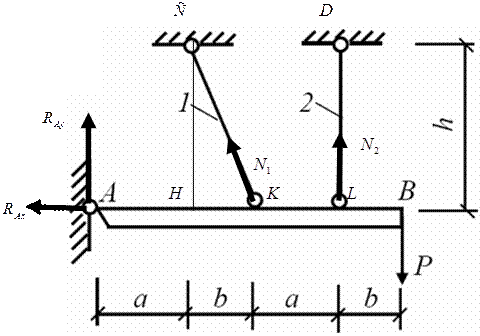
2. Определим усилия в стержнях. Система является статически неопределимой. Представим систему в деформированном виде. Рассмотрим:
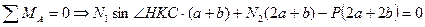
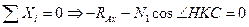
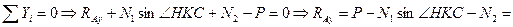
Отрицательные знаки говорят о том, что действительные направления сил противоположны указанным на чертеже.
Вычисляем напряжения в стержнях 1 и 2
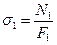
Определяем требуемые по условию прочности площади поперечных сечений
Проверим соотношение 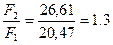
Принимаем по сортаменту сечения стержней в виде двух стальных прокатных равнобоких уголков.
Стержень 1: профиль №7, 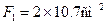
Стержень 2: профиль №10, 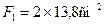
Определим удлинения стержней при
Определим нагрузку
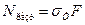
Находим из уравнения равновесия величину Рразр:
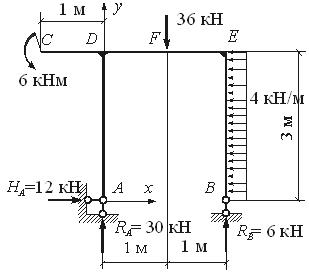
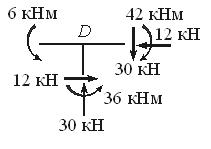
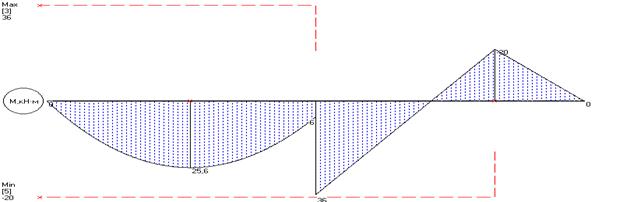
Пример 5. Для рамы с шарнирными опорами построим эпюры N,Q, и M.
Определяем величины опорных реакций.
| SX = 0 , | – 4·3 + HА = 0 , | HА = 12 кН ; |
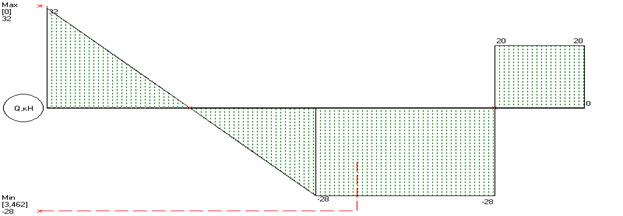
| SMА = 0 | 6 – 36·1 + 4·3·1,5 + 2RВ = 0 , | RВ = 6 кН ; |
| SMВ = 0 , | 6 + 36 + 4·3·1,5 – 2RА = 0 , | RА = 30 кН ; |
| SU = 0 (проверка) , | – 36 + 30 + 6= – 36 + 36 = 0 . |
Определяем внутренние усилия в характерных сечениях каждого участка рамы.
| Участок АD | ||
| Сечение А: | N = – RА = – 30 кН (сжатие), | Q = – HА= – 12 кН , M = 0 |
| Сечение D: | N = – 30 кН , Q = – 12 кН , | M = – 12*3 = – 36 кНм |
| (растянуты левые волокна). | ||
| Участок ВЕ | ||
| Сечение В: | N = – RА = – 6 кН , | Q = 0 , M = 0 , |
| Сечение E: | N = – 6 кН , Q = 4·3 = 12 кН , | M = – 4·3·1,5 = – 18 кНм |
| (растянуты правые волокна). | ||
| Участок CE | ||
| Сечение C: | N = 0 , Q = 0 , | M = – 6 кНм |
| (растянуты верхние волокна) . | ||
| Сечение D (слева): | N = 0 , Q = 0 , | M = – 6 кНм . |
| Сечение D (справа): | N = – HА = – 12 кН , Q = RА = 30 кН , | M = – 6 – 12·3= – 42 кНм |
| Сечение F (слева): | N = – 12 кН , Q = 30 кН , | M= –42+30·1= – 12 кНм . |
| Сечение F (справа): | N = – 12 кН , Q = 30 – 36 = – 6 кН , | M = – 12 кНм . |
| Сечение Е: | N = – 12 кН , Q = – RВ = – 6 кН , | M = – 18 кНм . |
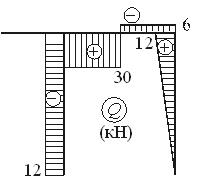
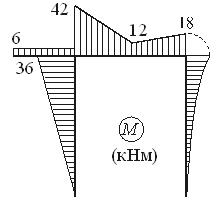
Построим эпюры N , Q , и M:
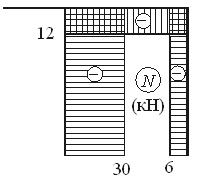
Вырежем мысленно узел D и покажем его равновесие под действием внутренних усилий в стержнях, сходящихся в узле. Нетрудно видеть, что узел находится в равновесии:
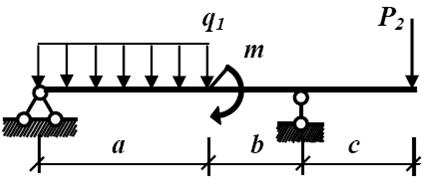
Пример 6. Рассчитать на прочность по методу предельных состояний двутавровую прокатную балку.
Материал балки сталь ВСт 3. Предел текучести σт = 240 МПа, расчетное сопротивление по пределу текучести R= 210 МПа, расчетное сопротивление при сдвиге Rs = 130 МПа. Коэффициент условий работы γс = 0,9. В табл. 2 приведены нормативные значения нагрузок. Коэффициент надежности по нагрузке γf = 1,2.
1.Определить опорные реакции;
2.Вычислить величины внутренних усилий в характерных сечениях и построить эпюры внутренних усилий.
3.Подобрать сечение балки из двутавра, используя условие прочности по первой группе предельных состояний.
1. Определим опорные реакции.
2. Проверка: 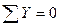
Реакции найдены правильно.
3. Построим эпюры Q и M.
Разобьем нашу балку на три участка и найдем суммы сил и моментов, действующих на каждом участке.
I участок:
II участок:
III участок: 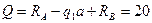
В конце балки
I участок: 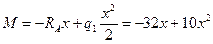
II участок: 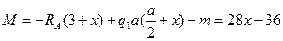
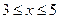
III участок: 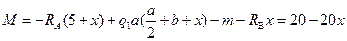
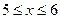
На участке 1 эпюра М имеет вид квадратичной параболы, ветви которых направлены вверх.
Построим схему конструкции и эпюры Q и M:
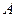
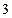
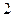
Значения М и Q в характерных сечениях балки указаны на эпюрах.
Опасным является сечение в точке с координатой 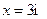
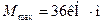
Требуемый момент сопротивления равен
По сортаменту прокатной стали принимаем двутавровый профиль № 22
h=220мм, b=110мм, d=5.4мм, t=8.7мм, Jx=2550см 4 , W=232см 3 , Sx=131см 3
Вычислим значения наибольших нормальных напряжений в опасном сечении балки:
Прочность балки обеспечена.
6. Задания для контрольной работы
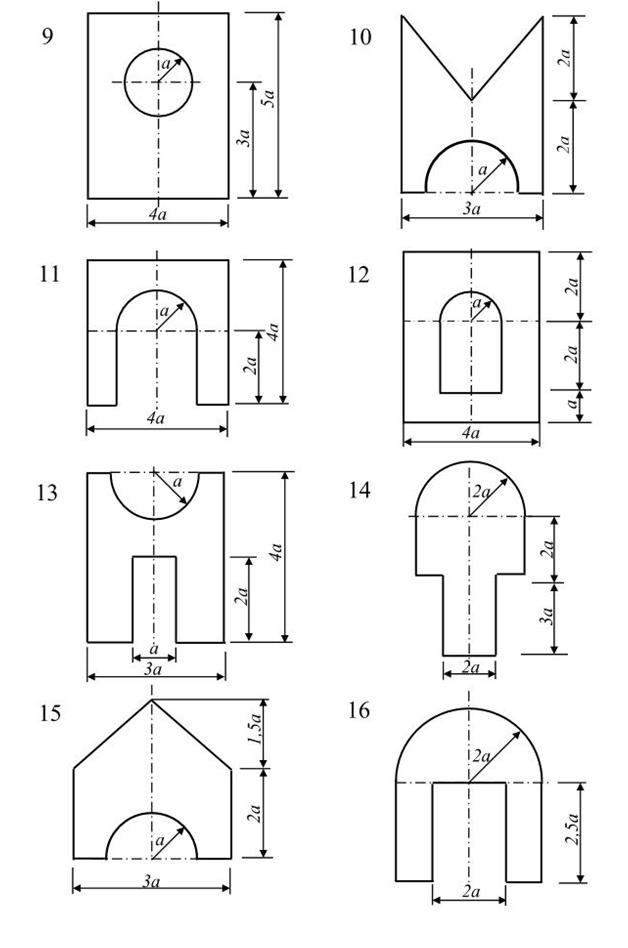
Для сечений, имеющих одну ось симметрии, по схемам №1-16 при размерах, указанных в таблице 2, требуется определить:
1) положение центра тяжести;
2) положение главных центральных осей инерции и величины главных моментов инерции.
| Первая буква фамилии студента | а, см |
| А | П |
| Б | Р |
| В | С |
| Г | Т |
| Д | У |
| Е | Ф |
| Ж | Х |
| З | Ц |
| И | Ч |
| К | Ш |
| Л | Щ |
| М | Э |
| Н | Ю |
| О | Я |
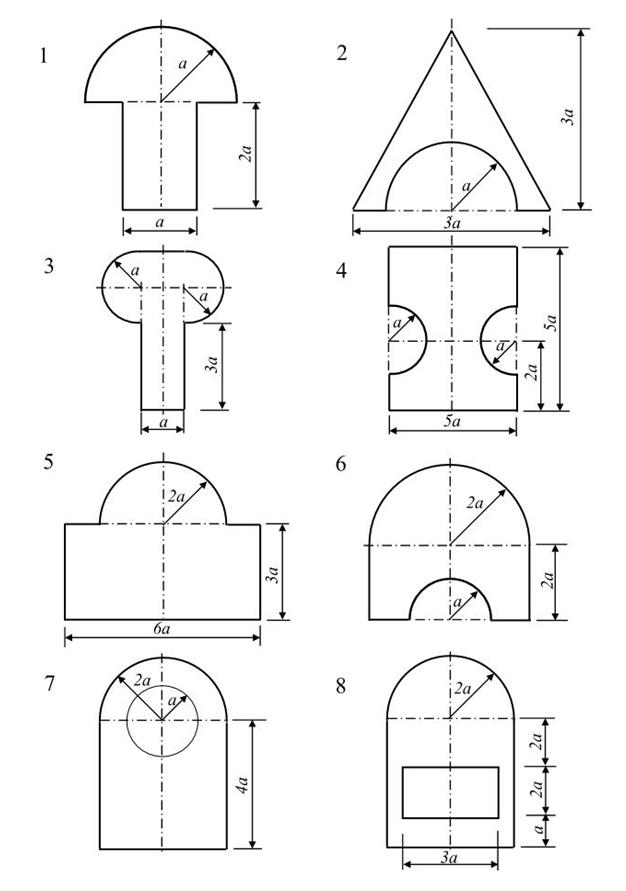
Схемы сечений стержней:
Для несимметричных сечений по схемам №1-16 при размерах, указанных в таблице 3, требуется:
1) определить положение центра тяжести;
2) вычислить осевые и центробежные моменты инерции относительно центральных осей;
3) определить положение главных центральных осей инерции и величины главных моментов инерции;
4) построить круг инерции и определить графически величины главных моментов инерции и направления главных центральных осей;
5) сравнить результаты аналитического и графического расчетов.
Момент инерции равнобедренного треугольника
Моменты инерции простых сечений
Моменты инерции относительно осей Оx, Оx1, Оy, Оy1:
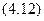
моменты инерции относительно осей Оx, О1x1 и О2x2,:
Прямоугольный и равнобедренный треугольники.
Для прямоугольного треугольника определим центробежный момент инерции Jxy относительно центральных осей Ox и Oy, параллельных катетам:
Момент инерции равнобедренного треугольника относительно оси
Круг. Полярный момент инерции круга:
Учитывая, что для круга Jx = Jy и полярный момент согласно равен сумме двух осевых моментов, получим:
Кольцевое сечение. Моменты инерции кольца находятся как разность моментов инерции двух кругов с радиусами R2 и R1 :
Относительно осей O1x1 и O1y1, которые являются главными осями для полукруга, осевые моменты инерции равны половине момента инерции круга:
Момент инерции относительно главной центральной оси определяется с помощью первой формулы:
Геометрические характеристики сечений прокатных профилей (двутавры, швеллеры, уголки) приведены в таблицах сортамента прокатной стали.
Моменты инерции составных сечений. При определении моментов инерции составного сечения последнее разбивают на простые фигуры, у которых известны положения центров тяжести и моменты инерции относительно собственных центральных осей. По формулам (4.6) находят координаты центра тяжести всего сечения в системе произвольно выбранных вспомогательных осей. Параллельно этим осям проводят центральные оси, относительно которых определяют осевые и центробежный моменты инерции по формулам (4.7). Моменты инерции относительно главных центральных осей определяются по формуле (4.11), а положение главных центральных осей – по формулам (4.10).
Далее рассмотрены примеры задач.
5. Примеры решения задач
Пример 1. Определим положение центра тяжести и моменты инерции относительно главных центральных осей сечения, состоящего из полукруга и прямоугольника с вырезом. Размеры сечения на рисунке даны в сантиметрах.
Разобьем сечение на три простые фигуры: полукруг с радиусом R=5 см, прямоугольник с размерами сторон 6×10 см, прямоугольный вырез с размерами 3×6 см и определим площади и моменты инерции этих фигур относительно собственных центральных осей.
Для полукруга по формулам (2.21) и (2.22) имеем:
Положение центра тяжести О1 полукруга определяется по формуле (2.20) и равно 0,424·5 = 2,12 см (рис.2.15).
Для прямоугольника и прямоугольного выреза по формулам (2.13) получим
Площадь всего сечения равна F = 39,2 + 60 – 18 = 81,2 см 2 .
Центр тяжести О сечения лежит на горизонтальной оси симметрии. Для определения его положения выберем в качестве вспомогательной оси центральную ось прямоугольника O2y2 . Тогда получим
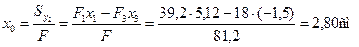
Отложим эту величину от оси О2y2 вправо и проведем ось Оy, которая вместе с осью Ох составит пару главных центральных осей всего сечения. Определим координаты центров тяжести отдельных фигур в системе координат Оxy: а1 = 2,32 см, а2 = – 2,80 см, а3 = – 4,30 см .
По формулам (2.6) найдем моменты инерции сечения относительно осей Ох и Оy:
Пример 2.Для стержня несимметричного сечения, составленного из швеллера [ 30 и неравнобокого уголка L180х110х12, определим центр тяжести сечения, моменты инерции относительно главных центральных осей и положение этих осей. На рисунке размеры даны в сантиметрах.
Выпишем геометрические характеристики сечения швеллера:
Геометрические характеристики сечения неравнобокого уголка:
Величину центробежного момента инерции уголка 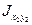
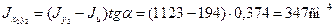
где tga = 0,374 – тангенс угла наклона главной оси u к оси Ох2 , величина которого приведена в сортаменте.
Площадь всего сечения равна F = 40,5 + 33,7 = 74,2 см 2 .
Для определения положения центра тяжести выберем в качестве вспомогательных осей оси швеллера О1x1 и О1y1. Тогда по формулам (2.5) получим
Эти величины и координаты центров тяжести швеллера и уголка в системе координат Охy показаны на рисунке и соответственно равны:
Определим по формулам (2.6) моменты инерции сечения относительно центральных осей Ох и Оy.
По формулам (2.12) и (2.11) найдем величины главных моментов инерции и углы наклона главных осей 1 и 2 к оси Ох :
Пример 3. Для статически определимого стержня ступенчато постоянного сечения при заданных осевых нагрузках и геометрических размерах по строке требуется:
1.Определить опорную реакцию в месте закрепления стержня.
2.Вычислить значения продольных сил и нормальных напряжений в характерных сечениях и построить эпюры этих величин.
3.Найти величины абсолютных удлинений (укорочений) участков стержня и величину общего удлинения (укорочения) стержня в целом.
4.Определить значения осевых перемещений характерных сечений и построить эпюру осевых перемещений.
| a, м | F, см 2 | Р1, кН | Р2, кН | q1, кН/м | q2, кН/м | Е, МПа |
| 0,8 | 2,0·10 5 |
1. Составим уравнение равновесия:
2. Вычислим значения продольных сил:
Участок 1:
При 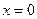
При 
Значение продольной силы линейно уменьшается
Участок 2:
При 
При 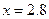
Значение продольной силы не изменяется
Участок 3:
При 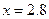
При 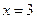
Значение продольной силы линейно уменьшается.
Найдем величины нормальных напряжений в характерных сечениях:
Участок 1:
При 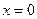
При 
Участок 2:
При 
Участок 3:
При 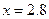
При 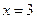
Величины абсолютных удлинений каждого их участков стержней найдем по формуле:
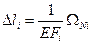
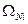
Определим величины осевых перемещений характерных сечений.
На участках 1 и 3 эпюра осевых перемещений имеет вид квадратичной параболы, на участке 2 изменяется линейно.
Пример 4. Для статически неопределимой стержневой системы, состоящей из абсолютно жесткой балки AB и поддерживающих ее стальных стержней 1 и 2 по схеме №…. при геометрических размерах, соотношениях площадей поперечных сечений стержней F2/F1 и величине нормативной нагрузки Р, указанных в строке № …. табл.2, требуется:
1.Определить расчетное значение нагрузки, приняв коэффициент надежности по нагрузке γf = 1,2.
2.Определить усилия в стержнях системы. Собственную массу элементов стержневой системы не учитывать.
3.Подобрать сечения стрежней в виде двух стальных прокатных равнобоких уголков, используя метод расчета по предельным состояниям. При подборе сечений обеспечить заданное соотношение площадей F2/F1. Расчетное сопротивление по пределу текучести стали марки ВСТ3 принять равным 210 МПа, коэффициент условий работы γс = 0,9.
4.Определить величины нормальных напряжений в поперечных сечениях стержней и проверить выполнение условий прочности.
5.Определить величины удлинений стержней, приняв Е=2,1·10 5 МПа.
6.Определить нагрузку Рт, при которой в системе возникают первые пластические деформации, считая, что материал стержней следует диаграмме Прандтля и имеет предел текучести σт = 240 МПа.
7.Определить разрушающую нагрузку Рразр, при которой система полностью исчерпывает свою несущую способность.
| a, м | b, м | h, м | F2/F1 | Р, кН |
| 1,4 | 0,8 | 1,3 | 1,3 |

2. Определим усилия в стержнях. Система является статически неопределимой. Представим систему в деформированном виде. Рассмотрим:
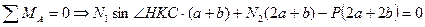
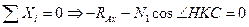
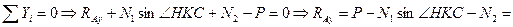
Отрицательные знаки говорят о том, что действительные направления сил противоположны указанным на чертеже.
Вычисляем напряжения в стержнях 1 и 2
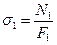
Определяем требуемые по условию прочности площади поперечных сечений
Проверим соотношение 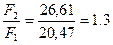
Принимаем по сортаменту сечения стержней в виде двух стальных прокатных равнобоких уголков.
Стержень 1: профиль №7, 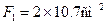
Стержень 2: профиль №10, 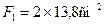
Определим удлинения стержней при
Определим нагрузку
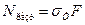
Находим из уравнения равновесия величину Рразр:
Пример 5. Для рамы с шарнирными опорами построим эпюры N,Q, и M.
Определяем величины опорных реакций.
| SX = 0 , | – 4·3 + HА = 0 , | HА = 12 кН ; |
| SMА = 0 | 6 – 36·1 + 4·3·1,5 + 2RВ = 0 , | RВ = 6 кН ; |
| SMВ = 0 , | 6 + 36 + 4·3·1,5 – 2RА = 0 , | RА = 30 кН ; |
| SU = 0 (проверка) , | – 36 + 30 + 6= – 36 + 36 = 0 . |
Определяем внутренние усилия в характерных сечениях каждого участка рамы.
| Участок АD | ||
| Сечение А: | N = – RА = – 30 кН (сжатие), | Q = – HА= – 12 кН , M = 0 |
| Сечение D: | N = – 30 кН , Q = – 12 кН , | M = – 12*3 = – 36 кНм |
| (растянуты левые волокна). | ||
| Участок ВЕ | ||
| Сечение В: | N = – RА = – 6 кН , | Q = 0 , M = 0 , |
| Сечение E: | N = – 6 кН , Q = 4·3 = 12 кН , | M = – 4·3·1,5 = – 18 кНм |
| (растянуты правые волокна). | ||
| Участок CE | ||
| Сечение C: | N = 0 , Q = 0 , | M = – 6 кНм |
| (растянуты верхние волокна) . | ||
| Сечение D (слева): | N = 0 , Q = 0 , | M = – 6 кНм . |
| Сечение D (справа): | N = – HА = – 12 кН , Q = RА = 30 кН , | M = – 6 – 12·3= – 42 кНм |
| Сечение F (слева): | N = – 12 кН , Q = 30 кН , | M= –42+30·1= – 12 кНм . |
| Сечение F (справа): | N = – 12 кН , Q = 30 – 36 = – 6 кН , | M = – 12 кНм . |
| Сечение Е: | N = – 12 кН , Q = – RВ = – 6 кН , | M = – 18 кНм . |
Построим эпюры N , Q , и M:
Вырежем мысленно узел D и покажем его равновесие под действием внутренних усилий в стержнях, сходящихся в узле. Нетрудно видеть, что узел находится в равновесии:
Пример 6. Рассчитать на прочность по методу предельных состояний двутавровую прокатную балку.
Материал балки сталь ВСт 3. Предел текучести σт = 240 МПа, расчетное сопротивление по пределу текучести R= 210 МПа, расчетное сопротивление при сдвиге Rs = 130 МПа. Коэффициент условий работы γс = 0,9. В табл. 2 приведены нормативные значения нагрузок. Коэффициент надежности по нагрузке γf = 1,2.
1.Определить опорные реакции;
2.Вычислить величины внутренних усилий в характерных сечениях и построить эпюры внутренних усилий.
3.Подобрать сечение балки из двутавра, используя условие прочности по первой группе предельных состояний.
1. Определим опорные реакции.
2. Проверка: 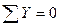
Реакции найдены правильно.
3. Построим эпюры Q и M.
Разобьем нашу балку на три участка и найдем суммы сил и моментов, действующих на каждом участке.
I участок:
II участок:
III участок: 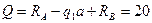
В конце балки
I участок: 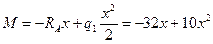
II участок: 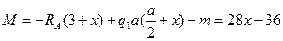
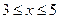
III участок: 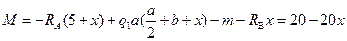
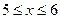
На участке 1 эпюра М имеет вид квадратичной параболы, ветви которых направлены вверх.
Построим схему конструкции и эпюры Q и M:
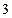
Значения М и Q в характерных сечениях балки указаны на эпюрах.
Опасным является сечение в точке с координатой 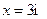
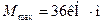
Требуемый момент сопротивления равен
По сортаменту прокатной стали принимаем двутавровый профиль № 22
h=220мм, b=110мм, d=5.4мм, t=8.7мм, Jx=2550см 4 , W=232см 3 , Sx=131см 3
Вычислим значения наибольших нормальных напряжений в опасном сечении балки:
Прочность балки обеспечена.
6. Задания для контрольной работы
Для сечений, имеющих одну ось симметрии, по схемам №1-16 при размерах, указанных в таблице 2, требуется определить:
1) положение центра тяжести;
2) положение главных центральных осей инерции и величины главных моментов инерции.
| Первая буква фамилии студента | а, см |
| А | П |
| Б | Р |
| В | С |
| Г | Т |
| Д | У |
| Е | Ф |
| Ж | Х |
| З | Ц |
| И | Ч |
| К | Ш |
| Л | Щ |
| М | Э |
| Н | Ю |
| О | Я |
Схемы сечений стержней:
Для несимметричных сечений по схемам №1-16 при размерах, указанных в таблице 3, требуется:
1) определить положение центра тяжести;
2) вычислить осевые и центробежные моменты инерции относительно центральных осей;
3) определить положение главных центральных осей инерции и величины главных моментов инерции;
4) построить круг инерции и определить графически величины главных моментов инерции и направления главных центральных осей;
5) сравнить результаты аналитического и графического расчетов.
Момент инерции сечения
Меня часто спрашивают: «…а что такое моменты инерции в сопротивлении материалов и зачем они вообще?» Об этом в сегодняшней теме
Моменты инерции сечения из простых фигур
Начнем с моментов инерции простых фигур и на их примере выясним для сложных и составных сечений.
Начать объяснение о том, что такое моменты инерции нужно с того, что спросить, а что такое площадь?
Обычная площадь квартиры, огорода сечения стержня? Зачем она и почему?
Так вот площадь это характеристика которую придумали и вывели для разных фигур, чтобы была возможность сравнивать земельные наделы. Не всегда они были прямоугольные или квадратные. А сравнить кто сколько получил в надел было нужно. Вот и вывели такую закономерность для прямоугольника, что если перемножить стороны — получим величину, которую можно будет сравнить с перемноженной высотой на основание деленное пополам для треугольника или для круга Пи умножить на эр в квадрате )). Т.е. площади простых фигур
Что касается моментов инерции в сопротивлении материалов, то тут они появились, когда стало понятно, что есть какая то геометрически измеримая величина для разных форм сечения, которая позволит сравнить сопротивляемость этих сечений изгибу.
Проще говоря бревно, которое выполняет роль балки и изгибается может иметь форму прямоугольника, квадрата или круга, а нам нужно сравнить их сопротивляемость изгибу. Вот для этих целей выводили формулу напряжений и оказалось, что в числителе оказался изгибающий момент, а в знаменателе момент инерции:
на балке изображены главные центральные оси z y
прогибы для таких балок будут разными относительно осей z и y, т.к. моменты инерции будут разные.
Вывод моментов инерции для простых фигур
Так вот ниже я приведу видео уроки, плейлист, в котором один за одним выведены моменты инерции для простых фигур, а именно для прямоугольника, треугольника и круга. А затем приводится стандартный расчет моментов инерции для более сложной фигуры, которая состоит из нескольких простых. Всегда сложную фигуру можно разбить на несколько простых. Исходя из этого расчет и ведется.
Моменты инерции измеряются в единицах длины в 4 степени, т.е. см⁴ или м⁴. Чаще всего используется см⁴, т.к. такие единицы измерения приведены в сортаменте прокатной стали.
Момент инерции, это величина, которая показывает сопротивляемость сечения изгибу. На примере линейки хорошо понятно что изгиб в одной плоскости и изгиб в другой плоскости будут сильно отличаться, хотя площадь сечения не меняется. Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.
Центральными осями называют оси, которые проходят через центр тяжести сечения
Главные оси располагаются в сечении таким образом, что центробежный момент относительно них равен нулю. Т.е. это максимальный и минимальный осевые моменты инерции
Оси, которые проходят через центр тяжести сечения и центробежный момент инерции относительно них равен нулю. При этом данные осевые моменты инерции являются экстремальными, т.е. имеют максимальное и минимальное значение. Именно относительно этих осей ведут расчет и к ним приводят нагрузки. Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.
При вычислении моментов инерции осевых, при переходе от одних осей к другим появляется центробежный момент инерции, как составляющая пары осевых моментов инерции. И только для главных осей центробежные моменты инерции равны нулю. Именно эти оси мы и отыскиваем в наших расчетах. Поэтому мы ищем величину центробежного момента инерции для не главных осей и из свойства, что главные центральные оси это такие оси, относительно которых центробежный момент инерции равен нулю, находим положение главных центральных осей.
Моменты инерции для прямоугольника
#Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.
Сопротивление материалов и Моменты инерции для прямоугольника. Понятие моментов инерции, формулы и вывод для прямоугольника. Осевые центробежный моменты инерции. для треугольника вывод моментов инерции в этом видео: https://www.youtube.com/embed/_pixohVoc-4?vq=hd720 Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2018-04-09
моменты инерции для прямоугольника для главных центральных осей равны, формула
моменты инерции для прямоугольника для осей проходящих через основные размеры равны, формула
Моменты инерции для треугольника
Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции
Сопротивление материалов и Моменты инерции для треугольника. Сопромат вывод моментов инерции для простых фигур. Моменты инерции для треугольника. Моменты инерции для осей в треугольнике, которые проходят через основные размеры. Вывод и пояснение к этой теме сопротивления материалов. для прямоугольника вывод моментов инерции в этом видео: https://www.youtube.com/watch?v=v1TE1UW_sRE&feature=youtu.be Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2018-04-09
Моменты инерции треугольника относительно произвольых осей
Момент инерции круга. Моменты инерции простых фигур. #сопромат
Вывод моментов инерции для круга. Видео урок из темы «Моменты инерции простых фигур». В видео приведен вывод момента инерции полярного, в полярной системе координат Ip Затем выведены моменты инерции осевые Iz, Iy. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14
Моменты инерции. Оси центральные и главные. Что это и где. #сопромат
Центральные оси — любая пара взаимно перпендикулярных осей, которые проходят через центр тяжести фигуры Главные оси — оси для которых центробежный момент инерции равен нулю, а осевые моменты имеют максимум и минимум. Об этом и многом другом в видео уроке по моментам инерции в сопротивлении материалов Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14
Расчет моментов инерции онлайн
При выполнении расчетов часто приходится вычислять моменты инерции сложных сечений относительно различных осей, лежащих в плоскости фигуры. Для стандартных поперечных сечений стержней моменты инерции даны в таблицах ГОСТ 8509-93, ГОСТ 8510-86, ГОСТ 57837-2017, ГОСТ 8240-97. В остальных случаях, для выполнения онлайн расчета момента инерции круга, кольца, треугольника, прямоугольного контура, нестандартных сварных швеллера, уголка и двутавра можно воспользоваться данной страницей нашего сайта.
Момент инерции треугольника
МОМЕНТ ИНЕРЦИИ ТРЕУГОЛЬНИКА
Момент инерции Ix0, м 4
Момент инерции Ix1, м 4
Момент инерции Ix2, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Момент инерции треугольника относительно центральной оси, параллельной одной из его сторон вычисляется по формуле:
Ix0 = b×h 3 / 36;
Момент инерции треугольника относительно оси, совпадающей с одной из его сторон:
Ix1 = b×h 3 / 12;
Момент инерции треугольника относительно оси, параллельной одной из его сторон и проходящей через противоположную вершину:
Ix2 = b×h 3 / 4.
Момент инерции кольца
МОМЕНТ ИНЕРЦИИ КОЛЬЦА
Момент инерции Ix, м 4
Полярный момент инерции Ip, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Момент инерции кольца относительно главной центральной оси:
Ix = π×D 4 /64 — π×d 4 /64;
Полярный момент инерции кольца:
Ip = π×D 4 /32 — π×d 4 /32.
Момент инерции прямоугольника
МОМЕНТ ИНЕРЦИИ ПРЯМОУГОЛЬНИКА
Момент инерции Ix, м 4
Момент инерции Iy, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Момент инерции прямоугольника относительно главных центральных осей:
Ix = (b×h 3 — b1×h1 3 )/12;
Iy = (h×b 3 — h1×b1 3 )/12.
Момент инерции двутавра
МОМЕНТ ИНЕРЦИИ ДВУТАВРА
Толщина полки t, мм
Толщина стенки s, мм
Момент инерции Ix, м 4
Момент инерции Iy, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Моменты инерции двутавра относительно главных центральных осей:
Ix = (B×H 3 — (B — s)×(H — 2t) 3 ) / 12;
Iy = (2t×B 3 + (H — 2t)×s 3 ) / 12.
Момент инерции уголка
МОМЕНТ ИНЕРЦИИ УГОЛКА
Момент инерции Ix, м 4
Момент инерции Iy, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Моменты инерции уголка относительно центральных осей:
Ix = (d×(H — y) 3 + B×y 3 — (B — d)×(y — d) 3 ) / 3;
Iy = (d×(B — x) 3 + H×x 3 — (H — d)×(x — d) 3 ) / 3,
где x и y — расстояния от наружных сторон уголка до центральных осей Y и X соответственно.
Момент инерции швеллера
МОМЕНТ ИНЕРЦИИ ШВЕЛЛЕРА
Толщина полки d, мм
Толщина стенки s, мм
Момент инерции Ix, м 4
Момент инерции Iy, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Моменты инерции швеллера относительно главных центральных осей:
Ix = (B×H 3 — (B — s)×(H-2d) 3 ) / 12;
Iy = (H×x 3 — (H — 2d)×(x — s) 3 + d×(B — x) 3 )/3,
где x — расстояния от наружной сторон швеллера до центральной оси Y.
Расчеты моментов инерции по умолчанию выполнены относительно центральных и главных центральных осей сечения. Моменты инерции относительно осей, параллельных главным центральным осям можно вычислить, прибавив к полученному результату произведение квадрата расстояния между соответствующими осями на площадь сечения.
Моменты инерции равнобедренного треугольника
Моменты инерции простых сечений
Моменты инерции относительно осей Оx, Оx1, Оy, Оy1:
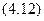
моменты инерции относительно осей Оx, О1x1 и О2x2,:
Прямоугольный и равнобедренный треугольники.
Для прямоугольного треугольника определим центробежный момент инерции Jxy относительно центральных осей Ox и Oy, параллельных катетам:
Момент инерции равнобедренного треугольника относительно оси
Круг. Полярный момент инерции круга:
Учитывая, что для круга Jx = Jy и полярный момент согласно равен сумме двух осевых моментов, получим:
Кольцевое сечение. Моменты инерции кольца находятся как разность моментов инерции двух кругов с радиусами R2 и R1 :
Относительно осей O1x1 и O1y1, которые являются главными осями для полукруга, осевые моменты инерции равны половине момента инерции круга:
Момент инерции относительно главной центральной оси определяется с помощью первой формулы:
Геометрические характеристики сечений прокатных профилей (двутавры, швеллеры, уголки) приведены в таблицах сортамента прокатной стали.
Моменты инерции составных сечений. При определении моментов инерции составного сечения последнее разбивают на простые фигуры, у которых известны положения центров тяжести и моменты инерции относительно собственных центральных осей. По формулам (4.6) находят координаты центра тяжести всего сечения в системе произвольно выбранных вспомогательных осей. Параллельно этим осям проводят центральные оси, относительно которых определяют осевые и центробежный моменты инерции по формулам (4.7). Моменты инерции относительно главных центральных осей определяются по формуле (4.11), а положение главных центральных осей – по формулам (4.10).
Далее рассмотрены примеры задач.
5. Примеры решения задач
Пример 1. Определим положение центра тяжести и моменты инерции относительно главных центральных осей сечения, состоящего из полукруга и прямоугольника с вырезом. Размеры сечения на рисунке даны в сантиметрах.
Разобьем сечение на три простые фигуры: полукруг с радиусом R=5 см, прямоугольник с размерами сторон 6×10 см, прямоугольный вырез с размерами 3×6 см и определим площади и моменты инерции этих фигур относительно собственных центральных осей.
Для полукруга по формулам (2.21) и (2.22) имеем:
Положение центра тяжести О1 полукруга определяется по формуле (2.20) и равно 0,424·5 = 2,12 см (рис.2.15).
Для прямоугольника и прямоугольного выреза по формулам (2.13) получим
Площадь всего сечения равна F = 39,2 + 60 – 18 = 81,2 см 2 .
Центр тяжести О сечения лежит на горизонтальной оси симметрии. Для определения его положения выберем в качестве вспомогательной оси центральную ось прямоугольника O2y2 . Тогда получим
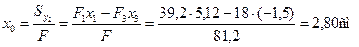
Отложим эту величину от оси О2y2 вправо и проведем ось Оy, которая вместе с осью Ох составит пару главных центральных осей всего сечения. Определим координаты центров тяжести отдельных фигур в системе координат Оxy: а1 = 2,32 см, а2 = – 2,80 см, а3 = – 4,30 см .
По формулам (2.6) найдем моменты инерции сечения относительно осей Ох и Оy:
Пример 2.Для стержня несимметричного сечения, составленного из швеллера [ 30 и неравнобокого уголка L180х110х12, определим центр тяжести сечения, моменты инерции относительно главных центральных осей и положение этих осей. На рисунке размеры даны в сантиметрах.
Выпишем геометрические характеристики сечения швеллера:
Геометрические характеристики сечения неравнобокого уголка:
Величину центробежного момента инерции уголка 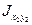
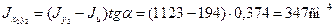
где tga = 0,374 – тангенс угла наклона главной оси u к оси Ох2 , величина которого приведена в сортаменте.
Площадь всего сечения равна F = 40,5 + 33,7 = 74,2 см 2 .
Для определения положения центра тяжести выберем в качестве вспомогательных осей оси швеллера О1x1 и О1y1. Тогда по формулам (2.5) получим
Эти величины и координаты центров тяжести швеллера и уголка в системе координат Охy показаны на рисунке и соответственно равны:
Определим по формулам (2.6) моменты инерции сечения относительно центральных осей Ох и Оy.
По формулам (2.12) и (2.11) найдем величины главных моментов инерции и углы наклона главных осей 1 и 2 к оси Ох :
Пример 3. Для статически определимого стержня ступенчато постоянного сечения при заданных осевых нагрузках и геометрических размерах по строке требуется:
1.Определить опорную реакцию в месте закрепления стержня.
2.Вычислить значения продольных сил и нормальных напряжений в характерных сечениях и построить эпюры этих величин.
3.Найти величины абсолютных удлинений (укорочений) участков стержня и величину общего удлинения (укорочения) стержня в целом.
4.Определить значения осевых перемещений характерных сечений и построить эпюру осевых перемещений.
| a, м | F, см 2 | Р1, кН | Р2, кН | q1, кН/м | q2, кН/м | Е, МПа |
| 0,8 | 2,0·10 5 |
1. Составим уравнение равновесия:
2. Вычислим значения продольных сил:
Участок 1:
При 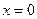
При 
Значение продольной силы линейно уменьшается
Участок 2:
При 
При 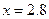
Значение продольной силы не изменяется
Участок 3:
При 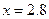
При 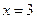
Значение продольной силы линейно уменьшается.
Найдем величины нормальных напряжений в характерных сечениях:
Участок 1:
При 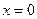
При 
Участок 2:
При 
Участок 3:
При 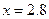
При 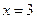
Величины абсолютных удлинений каждого их участков стержней найдем по формуле:
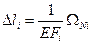
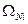
Определим величины осевых перемещений характерных сечений.
На участках 1 и 3 эпюра осевых перемещений имеет вид квадратичной параболы, на участке 2 изменяется линейно.
Пример 4. Для статически неопределимой стержневой системы, состоящей из абсолютно жесткой балки AB и поддерживающих ее стальных стержней 1 и 2 по схеме №…. при геометрических размерах, соотношениях площадей поперечных сечений стержней F2/F1 и величине нормативной нагрузки Р, указанных в строке № …. табл.2, требуется:
1.Определить расчетное значение нагрузки, приняв коэффициент надежности по нагрузке γf = 1,2.
2.Определить усилия в стержнях системы. Собственную массу элементов стержневой системы не учитывать.
3.Подобрать сечения стрежней в виде двух стальных прокатных равнобоких уголков, используя метод расчета по предельным состояниям. При подборе сечений обеспечить заданное соотношение площадей F2/F1. Расчетное сопротивление по пределу текучести стали марки ВСТ3 принять равным 210 МПа, коэффициент условий работы γс = 0,9.
4.Определить величины нормальных напряжений в поперечных сечениях стержней и проверить выполнение условий прочности.
5.Определить величины удлинений стержней, приняв Е=2,1·10 5 МПа.
6.Определить нагрузку Рт, при которой в системе возникают первые пластические деформации, считая, что материал стержней следует диаграмме Прандтля и имеет предел текучести σт = 240 МПа.
7.Определить разрушающую нагрузку Рразр, при которой система полностью исчерпывает свою несущую способность.
| a, м | b, м | h, м | F2/F1 | Р, кН |
| 1,4 | 0,8 | 1,3 | 1,3 |

2. Определим усилия в стержнях. Система является статически неопределимой. Представим систему в деформированном виде. Рассмотрим:
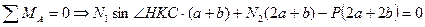
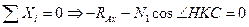
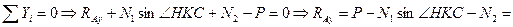
Отрицательные знаки говорят о том, что действительные направления сил противоположны указанным на чертеже.
Вычисляем напряжения в стержнях 1 и 2
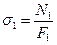
Определяем требуемые по условию прочности площади поперечных сечений
Проверим соотношение 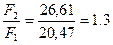
Принимаем по сортаменту сечения стержней в виде двух стальных прокатных равнобоких уголков.
Стержень 1: профиль №7, 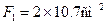
Стержень 2: профиль №10, 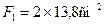
Определим удлинения стержней при
Определим нагрузку
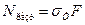
Находим из уравнения равновесия величину Рразр:
Пример 5. Для рамы с шарнирными опорами построим эпюры N,Q, и M.
Определяем величины опорных реакций.
| SX = 0 , | – 4·3 + HА = 0 , | HА = 12 кН ; |
| SMА = 0 | 6 – 36·1 + 4·3·1,5 + 2RВ = 0 , | RВ = 6 кН ; |
| SMВ = 0 , | 6 + 36 + 4·3·1,5 – 2RА = 0 , | RА = 30 кН ; |
| SU = 0 (проверка) , | – 36 + 30 + 6= – 36 + 36 = 0 . |
Определяем внутренние усилия в характерных сечениях каждого участка рамы.
| Участок АD | ||
| Сечение А: | N = – RА = – 30 кН (сжатие), | Q = – HА= – 12 кН , M = 0 |
| Сечение D: | N = – 30 кН , Q = – 12 кН , | M = – 12*3 = – 36 кНм |
| (растянуты левые волокна). | ||
| Участок ВЕ | ||
| Сечение В: | N = – RА = – 6 кН , | Q = 0 , M = 0 , |
| Сечение E: | N = – 6 кН , Q = 4·3 = 12 кН , | M = – 4·3·1,5 = – 18 кНм |
| (растянуты правые волокна). | ||
| Участок CE | ||
| Сечение C: | N = 0 , Q = 0 , | M = – 6 кНм |
| (растянуты верхние волокна) . | ||
| Сечение D (слева): | N = 0 , Q = 0 , | M = – 6 кНм . |
| Сечение D (справа): | N = – HА = – 12 кН , Q = RА = 30 кН , | M = – 6 – 12·3= – 42 кНм |
| Сечение F (слева): | N = – 12 кН , Q = 30 кН , | M= –42+30·1= – 12 кНм . |
| Сечение F (справа): | N = – 12 кН , Q = 30 – 36 = – 6 кН , | M = – 12 кНм . |
| Сечение Е: | N = – 12 кН , Q = – RВ = – 6 кН , | M = – 18 кНм . |
Построим эпюры N , Q , и M:
Вырежем мысленно узел D и покажем его равновесие под действием внутренних усилий в стержнях, сходящихся в узле. Нетрудно видеть, что узел находится в равновесии:
Пример 6. Рассчитать на прочность по методу предельных состояний двутавровую прокатную балку.
Материал балки сталь ВСт 3. Предел текучести σт = 240 МПа, расчетное сопротивление по пределу текучести R= 210 МПа, расчетное сопротивление при сдвиге Rs = 130 МПа. Коэффициент условий работы γс = 0,9. В табл. 2 приведены нормативные значения нагрузок. Коэффициент надежности по нагрузке γf = 1,2.
1.Определить опорные реакции;
2.Вычислить величины внутренних усилий в характерных сечениях и построить эпюры внутренних усилий.
3.Подобрать сечение балки из двутавра, используя условие прочности по первой группе предельных состояний.
1. Определим опорные реакции.
2. Проверка: 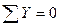
Реакции найдены правильно.
3. Построим эпюры Q и M.
Разобьем нашу балку на три участка и найдем суммы сил и моментов, действующих на каждом участке.
I участок:
II участок:
III участок: 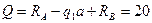
В конце балки
I участок: 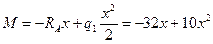
II участок: 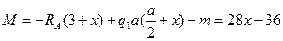
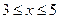
III участок: 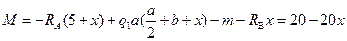
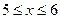
На участке 1 эпюра М имеет вид квадратичной параболы, ветви которых направлены вверх.
Построим схему конструкции и эпюры Q и M:
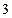
Значения М и Q в характерных сечениях балки указаны на эпюрах.
Опасным является сечение в точке с координатой 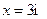
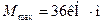
Требуемый момент сопротивления равен
По сортаменту прокатной стали принимаем двутавровый профиль № 22
h=220мм, b=110мм, d=5.4мм, t=8.7мм, Jx=2550см 4 , W=232см 3 , Sx=131см 3
Вычислим значения наибольших нормальных напряжений в опасном сечении балки:
Прочность балки обеспечена.
6. Задания для контрольной работы
Для сечений, имеющих одну ось симметрии, по схемам №1-16 при размерах, указанных в таблице 2, требуется определить:
1) положение центра тяжести;
2) положение главных центральных осей инерции и величины главных моментов инерции.
| Первая буква фамилии студента | а, см |
| А | П |
| Б | Р |
| В | С |
| Г | Т |
| Д | У |
| Е | Ф |
| Ж | Х |
| З | Ц |
| И | Ч |
| К | Ш |
| Л | Щ |
| М | Э |
| Н | Ю |
| О | Я |
Схемы сечений стержней:
Для несимметричных сечений по схемам №1-16 при размерах, указанных в таблице 3, требуется:
1) определить положение центра тяжести;
2) вычислить осевые и центробежные моменты инерции относительно центральных осей;
3) определить положение главных центральных осей инерции и величины главных моментов инерции;
4) построить круг инерции и определить графически величины главных моментов инерции и направления главных центральных осей;
5) сравнить результаты аналитического и графического расчетов.
Момент инерции сечения
Меня часто спрашивают: «…а что такое моменты инерции в сопротивлении материалов и зачем они вообще?» Об этом в сегодняшней теме
Моменты инерции сечения из простых фигур
Начнем с моментов инерции простых фигур и на их примере выясним для сложных фигур и составных сечений из стандартных профилей.
Начать объяснение о том, что такое моменты инерции нужно с того, что спросить, а что такое площадь?
Обычная площадь квартиры, огорода сечения стержня? Зачем она и почему?
Так вот площадь это характеристика которую придумали и вывели для разных фигур, чтобы была возможность сравнивать земельные наделы. Не всегда они были прямоугольные или квадратные. А сравнить кто сколько получил в надел было нужно. Вот и вывели такую закономерность для прямоугольника, что если перемножить стороны — получим величину, которую можно будет сравнить с перемноженной высотой на основание деленное пополам для треугольника или для круга Пи умножить на эр в квадрате )). Т.е. площади простых фигур
Что касается моментов инерции в сопротивлении материалов, то тут они появились, когда стало понятно, что есть какая то геометрически измеримая величина для разных форм сечения, которая позволит сравнить сопротивляемость этих сечений изгибу.
Проще говоря бревно, которое выполняет роль балки и изгибается может иметь форму прямоугольника, квадрата или круга, а нам нужно сравнить их сопротивляемость изгибу. Вот для этих целей выводили формулу напряжений и оказалось, что в числителе оказался изгибающий момент, а в знаменателе момент инерции:
на балке изображены главные центральные оси z y
прогибы для таких балок будут разными относительно осей z и y, т.к. моменты инерции будут разные.
Вывод моментов инерции для простых фигур
Так вот ниже я приведу видео уроки, плейлист, в котором один за одним выведены моменты инерции для простых фигур, а именно для прямоугольника, треугольника и круга. А затем приводится стандартный расчет моментов инерции для более сложной фигуры, которая состоит из нескольких простых. Всегда сложную фигуру можно разбить на несколько простых. Исходя из этого расчет и ведется.
Моменты инерции измеряются в единицах длины в 4 степени, т.е. см⁴ или м⁴. Чаще всего используется см⁴, т.к. такие единицы измерения приведены в сортаменте прокатной стали.
Момент инерции, это величина, которая показывает сопротивляемость сечения изгибу. На примере линейки хорошо понятно что изгиб в одной плоскости и изгиб в другой плоскости будут сильно отличаться, хотя площадь сечения не меняется. Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.
Центральными осями называют оси, которые проходят через центр тяжести сечения
Главные оси располагаются в сечении таким образом, что центробежный момент относительно них равен нулю. Т.е. это максимальный и минимальный осевые моменты инерции
Оси, которые проходят через центр тяжести сечения и центробежный момент инерции относительно них равен нулю. При этом данные осевые моменты инерции являются экстремальными, т.е. имеют максимальное и минимальное значение. Именно относительно этих осей ведут расчет и к ним приводят нагрузки. Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.
При вычислении моментов инерции осевых, при переходе от одних осей к другим появляется центробежный момент инерции, как составляющая пары осевых моментов инерции. И только для главных осей центробежные моменты инерции равны нулю. Именно эти оси мы и отыскиваем в наших расчетах. Поэтому мы ищем величину центробежного момента инерции для не главных осей и из свойства, что главные центральные оси это такие оси, относительно которых центробежный момент инерции равен нулю, находим положение главных центральных осей.
Моменты инерции для прямоугольника
#Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.
Сопротивление материалов и Моменты инерции для прямоугольника. Понятие моментов инерции, формулы и вывод для прямоугольника. Осевые центробежный моменты инерции. для треугольника вывод моментов инерции в этом видео: https://www.youtube.com/embed/_pixohVoc-4?vq=hd720 Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2018-04-09
моменты инерции для прямоугольника для главных центральных осей равны, формула
моменты инерции для прямоугольника для осей проходящих через основные размеры равны, формула
Моменты инерции для треугольника
Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции
Сопротивление материалов и Моменты инерции для треугольника. Сопромат вывод моментов инерции для простых фигур. Моменты инерции для треугольника. Моменты инерции для осей в треугольнике, которые проходят через основные размеры. Вывод и пояснение к этой теме сопротивления материалов. для прямоугольника вывод моментов инерции в этом видео: https://www.youtube.com/watch?v=v1TE1UW_sRE&feature=youtu.be Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2018-04-09
Моменты инерции треугольника относительно произвольых осей
Момент инерции круга. Моменты инерции простых фигур. #сопромат
Вывод моментов инерции для круга. Видео урок из темы «Моменты инерции простых фигур». В видео приведен вывод момента инерции полярного, в полярной системе координат Ip Затем выведены моменты инерции осевые Iz, Iy. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14
Моменты инерции. Оси центральные и главные. Что это и где. #сопромат
Центральные оси — любая пара взаимно перпендикулярных осей, которые проходят через центр тяжести фигуры Главные оси — оси для которых центробежный момент инерции равен нулю, а осевые моменты имеют максимум и минимум. Об этом и многом другом в видео уроке по моментам инерции в сопротивлении материалов Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14
Примеры расчетов моментов инерции для сечений
Ниже приводятся примеры расчетов моментов инерции относительно главных центральных осей, объяснение, что такое центробежный момент инерции и почему оси называются главными центральными для примеров:
- простейшие фигуры — прямоугольник, треугольник
- составные сечения из простейших треугольника и прямоугольника
- составные из прокатных профилей
Пример расчета моментов инерции относительно главных центральных осей для простейших фигур
Подробно объясняется как найти центробежный момент инерции, как найти осевые моменты инерции, как относительно центральных и как относительно главных осей для простых фигур.
Пример расчета моментов инерции для сечения состоящего из прямоугольника и треугольника
Сечения балок может быть составным, т.е. таким, которое складывается из нескольких фигур. В примере, в видеоуроке ниже рассказыватся как найти моменты инерции относительно главных центральных осей для такого сечения балки
Расчет моментов инерции сечения составного из стандартных прокатных профилей
В видеоуроке ниже разбирается порядок расчета моментов инерции относительно главных центральных осей для сечения составленого из трех прокатных профилей уголков
Расчет моментов инерции онлайн
При выполнении расчетов часто приходится вычислять моменты инерции сложных сечений относительно различных осей, лежащих в плоскости фигуры. Для стандартных поперечных сечений стержней моменты инерции даны в таблицах ГОСТ 8509-93, ГОСТ 8510-86, ГОСТ 57837-2017, ГОСТ 8240-97. В остальных случаях, для выполнения онлайн расчета момента инерции круга, кольца, треугольника, прямоугольного контура, нестандартных сварных швеллера, уголка и двутавра можно воспользоваться данной страницей нашего сайта.
Момент инерции треугольника
МОМЕНТ ИНЕРЦИИ ТРЕУГОЛЬНИКА
Момент инерции Ix0, м 4
Момент инерции Ix1, м 4
Момент инерции Ix2, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Момент инерции треугольника относительно центральной оси, параллельной одной из его сторон вычисляется по формуле:
Ix0 = b×h 3 / 36;
Момент инерции треугольника относительно оси, совпадающей с одной из его сторон:
Ix1 = b×h 3 / 12;
Момент инерции треугольника относительно оси, параллельной одной из его сторон и проходящей через противоположную вершину:
Ix2 = b×h 3 / 4.
Момент инерции кольца
МОМЕНТ ИНЕРЦИИ КОЛЬЦА
Момент инерции Ix, м 4
Полярный момент инерции Ip, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Момент инерции кольца относительно главной центральной оси:
Ix = π×D 4 /64 — π×d 4 /64;
Полярный момент инерции кольца:
Ip = π×D 4 /32 — π×d 4 /32.
Момент инерции прямоугольника
МОМЕНТ ИНЕРЦИИ ПРЯМОУГОЛЬНИКА
Момент инерции Ix, м 4
Момент инерции Iy, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Момент инерции прямоугольника относительно главных центральных осей:
Ix = (b×h 3 — b1×h1 3 )/12;
Iy = (h×b 3 — h1×b1 3 )/12.
Момент инерции двутавра
МОМЕНТ ИНЕРЦИИ ДВУТАВРА
Толщина полки t, мм
Толщина стенки s, мм
Момент инерции Ix, м 4
Момент инерции Iy, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Моменты инерции двутавра относительно главных центральных осей:
Ix = (B×H 3 — (B — s)×(H — 2t) 3 ) / 12;
Iy = (2t×B 3 + (H — 2t)×s 3 ) / 12.
Момент инерции уголка
МОМЕНТ ИНЕРЦИИ УГОЛКА
Момент инерции Ix, м 4
Момент инерции Iy, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Моменты инерции уголка относительно центральных осей:
Ix = (d×(H — y) 3 + B×y 3 — (B — d)×(y — d) 3 ) / 3;
Iy = (d×(B — x) 3 + H×x 3 — (H — d)×(x — d) 3 ) / 3,
где x и y — расстояния от наружных сторон уголка до центральных осей Y и X соответственно.
Момент инерции швеллера
МОМЕНТ ИНЕРЦИИ ШВЕЛЛЕРА
Толщина полки d, мм
Толщина стенки s, мм
Момент инерции Ix, м 4
Момент инерции Iy, м 4
Площадь сечения F, м 2
©Copyright Кайтек 2020
Моменты инерции швеллера относительно главных центральных осей:
Ix = (B×H 3 — (B — s)×(H-2d) 3 ) / 12;
Iy = (H×x 3 — (H — 2d)×(x — s) 3 + d×(B — x) 3 )/3,
где x — расстояния от наружной сторон швеллера до центральной оси Y.
Расчеты моментов инерции по умолчанию выполнены относительно центральных и главных центральных осей сечения. Моменты инерции относительно осей, параллельных главным центральным осям можно вычислить, прибавив к полученному результату произведение квадрата расстояния между соответствующими осями на площадь сечения.
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/moment-inertsii-ravnobedrennogo-treugolnika
http://b4.cooksy.ru/articles/momenty-inertsii-ravnobedrennogo-treugolnika
[/spoiler]
Решение задач по сопромату. Геометрические характеристики фигур
Геометрические характеристики фигур / Геометрические характеристики простых фигур: прямоугольника, квадрата, треугольника, круга, полукруга
Результат расчетов зависит не только от площади сечения, поэтому при решении задач по сопромату не обойтись без определения геометрических характеристик фигур: статических, осевых, полярного и центробежного моментов инерции. Обязательно необходимо уметь определять положение центра тяжести сечения (от положения центра тяжести зависят перечисленные геометрические характеристики). К дополнению к геометрическим характеристикам простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольников, круга, полукруга. Указаны центр тяжести и положение главных центральных осей, и определены относительно них геометрические характеристики при условии, что материал балки однородный.
Геометрические характеристики прямоугольника и квадрата
Осевые моменты инерции прямоугольника (квадрата)
Геометрические характеристики прямоугольного треугольника
Осевые моменты инерции прямоугольного треугольника
Геометрические характеристики равнобедренного треугольника
Осевые моменты инерции равнобедренного треугольника
Геометрические характеристики круга
Осевые моменты инерции круга
Геометрические характеристики полукруга
Осевые моменты инерции полукруга
Вычисление моментов инерции
Моменты инерции материальной кривой
Моментом инерции материальной точки относительно оси
называется число
, где
— масса точки, а
— ее расстояние от оси. Аналогично определяется момент инерции относительно точки.
Пусть — материальная линия, линейная плотность которой во всех точках равна единице. Тогда масса элементарного участка этой линии равна его длине
, а момент инерции
такого участка относительно оси абсцисс равен
. Интегрируя, получаем момент инерции относительно оси абсцисс всей линии:
. Так же доказывается, что
и
,
где — момент инерции относительно начала координат. Отсюда следует, в частности, что
.
Если линия задана параметрическими уравнениями
, то
Аналогичные формулы справедливы для и
Моменты инерции криволинейной трапеции
Перейдем к вычислению моментов инерции криволинейной трапеции. Будем считать, что ее поверхностная плотность равна единице. Сначала найдем момент инерции прямоугольника со сторонами и
относительно стороны
. Разобьем его на элементарные прямоугольники со сторонами
и
(см. рис. 61). Площадь (а потому и масса) каждого такого прямоугольника равна
. Значит, момент инерции элементарного прямоугольника относительно стороны
равен
, а момент инерции всего прямоугольника относительно этой стороны выражается формулой
Криволинейную трапецию разобьем на элементарные прямоугольники со сторонами и
. Момент инерции каждого из этих прямоугольников относительно оси абсцисс выражается формулой
. Интегрируя, получаем момент инерции всей криволинейной трапеции относительно оси абсцисс:
Аналогично доказывается, что момент инерции криволинейной трапеции относительно оси ординат выражается формулой
(момент инерции элементарного прямоугольника относительно оси ординат равен ).
Полярный момент инерции (т. е. момент относительно начала координат) в этом случае выражается формулой
Пример 9. Вычислить момент инерции равнобедренного треугольника относительно его основания.
Решение. Расположим оси координат так, как показано на рисунке 65.
Пусть основание треугольника , высота
. Прямая
проходит через точки
и
. Ее уравнение
, то есть
.
Ясно, что момент инерции треугольника
относительно оси
равен удвоенному моменту инерции треугольника
относительно той же оси. Значит,
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.