Как найти момент инерции в полуокружности

Занятие 21

2.7. Вычисление
моментов

Если на плоскости

масса М плотности

заполняет некоторый ограниченный
континуум

(линию, плоскую область) и

– соответствующая мера (длина дуги,
площадь) той части континуума
,
ординаты которой не превышают
,
то
–м
моментом массы М относительно

называется
число

.

Как частные случаи, получаем при
=0
массу М,

=1
статический момент,

=2
момент инерции.

Координаты центра масс однородной
плоской фигуры определяются по формуле

,

№2501.2. Найти статический момент и
момент инерции дуги полуокружности
радиуса

относительно диаметра, проходящего
через концы этой дуги.

Т.к. плотность не задана, считаем дугу
однородной с
.
Диаметр считаем горизонтальным, а центр
окружности совпадающим с началом
координат. В этом случае

.

.
Соответствующей
мерой служит длина дуги

.

С учетом выше сказанного вычисляем
статический момент

=

=
=

=
.

Момент инерции вычисляет следующий
интеграл

=

=
=
=
=

=
.

№2512. Определить координаты центра
масс области, ограниченной кривой

.

Т.к. плотность не задана, считаем область
однородной с
.

Соответствующей мерой служит площадь
области

.
=
.

Из уравнений связи декартовых и полярных
координат следует, что

,

.

Теперь легко составить интегралы,
вычисляющие моменты необходимые для
нахождения центра тяжести (особенно,
если учесть симметричность фигуры).

=

=
=

=

=
=

=

=
=

=

=
=

=
=

=
=

= 0.

=
= 0.

=

=
=

=
=

=
=

=
=

=

=
=.

В полярных координатах получаем

=

= 0,

=

=
.

Аналогично решаются №№ 2501,1, 2513.

Домашнее задание №№ 2502,1, 2511.

Соседние файлы в папке практикаинтегралы

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

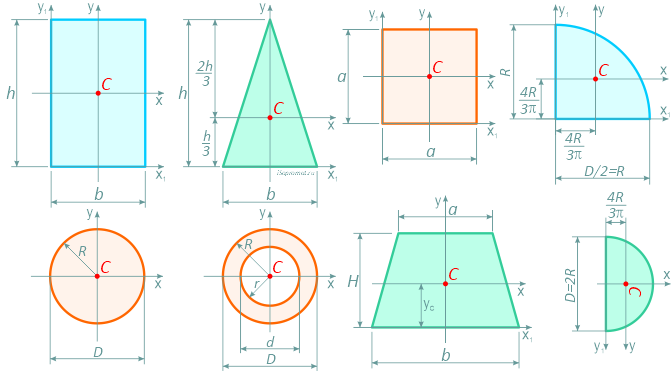
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.

Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
I_x , I_y — осевые моменты инерции сечения относительно главных осей;
I_x1 , I_y1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
I_ρ — полярный момент инерции сечения;
W_x , W_y — осевые моменты сопротивления;
W_ρ — полярный момент сопротивления

Прямоугольник

Прямоугольник высотой h и шириной b.

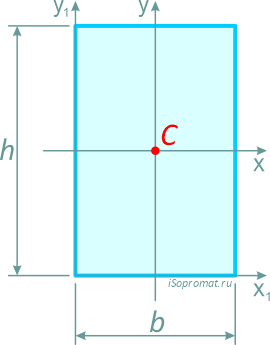
Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.

Площадь

Центральные осевые моменты инерции прямоугольника

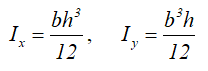
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

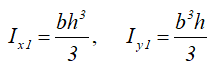
Осевые моменты сопротивления прямоугольного сечения

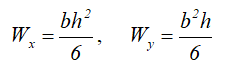
Квадрат

Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.

Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.

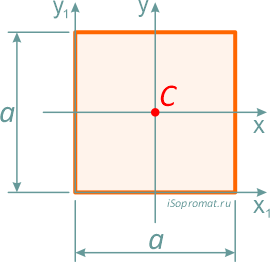
Площадь

Центральные осевые моменты инерции квадрата

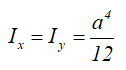
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

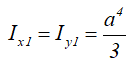
Осевой момент сопротивления квадратного сечения

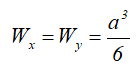
Треугольник равнобедренный

Равнобедренный треугольник высотой h и шириной основания b.

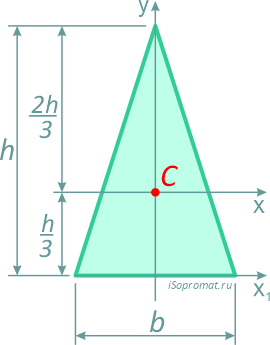
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.

Площадь

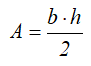
Центральные осевые моменты инерции треугольника

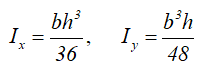
Момент инерции относительно смещенной оси x₁, проходящей через его основание

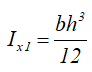
Прямоугольный треугольник

Прямоугольный треугольник высотой h и шириной основания b.

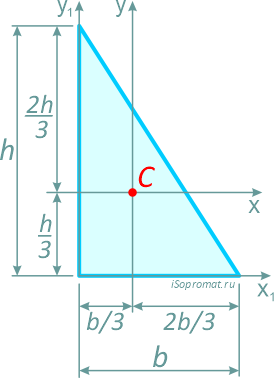
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.

Площадь

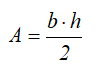
Центральные осевые моменты инерции прямоугольного треугольника

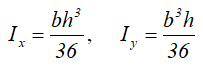
Моменты инерции относительно смещенных осей x₁ и y₁, проходящих через точку, соединяющую его катеты

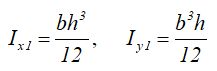
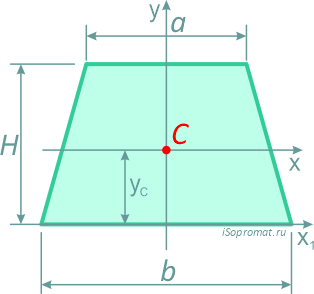
Трапеция

Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.

Площадь трапеции

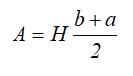
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:

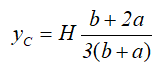
Круг

Круг диаметром D (d) или радиусом R (r)

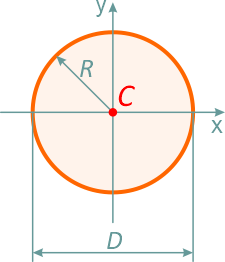
Площадь круга через его диаметр и радиус

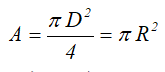
Центральные осевые и полярный моменты инерции круга

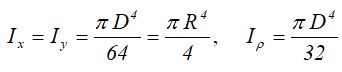
Осевые и полярный моменты сопротивления

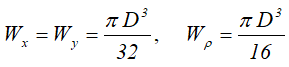
Полукруг

Половина круга диаметром D (d) или радиусом R (r)

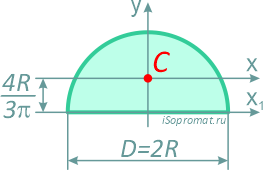
Площадь

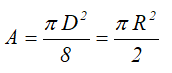
Осевые моменты инерции полукруга

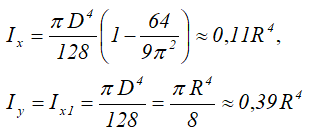
Четверть круга

Четверть круга диаметром D (d) или радиусом R (r)

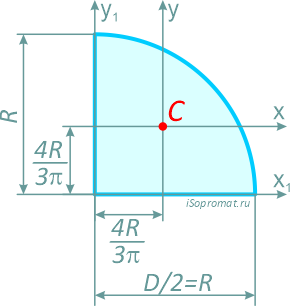
Площадь

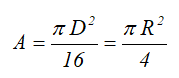
Центральные осевые моменты инерции четверти круга

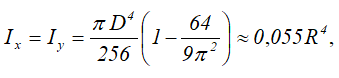
Моменты инерции относительно смещенных осей x₁ и y₁

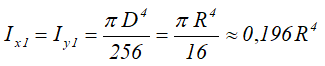
Кольцо

Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)

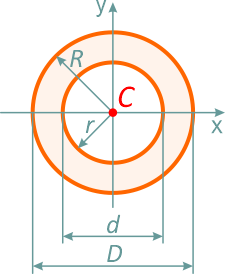
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.

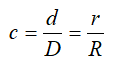
Площадь

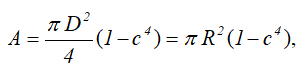
Центральные осевые и полярный моменты инерции кольца

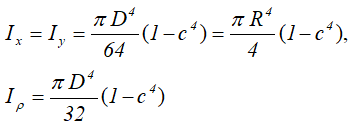
Осевые и полярный моменты сопротивления

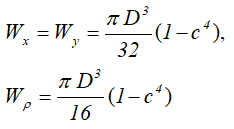
Тонкостенное сечение (труба)

Тонкостенный профиль (сечение трубы) средним радиусом R₀ и толщиной стенки трубы t при R₀>>t

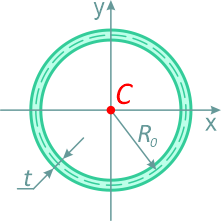
Площадь

Центральные осевые и полярный моменты инерции трубного сечения

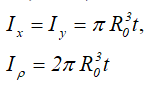
Осевые и полярный моменты сопротивления

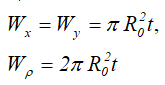
Пример определения координат центра тяжести сложной фигуры:

Другие видео

Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Содержание

• Элементы и меры полукруга
• Периметр полукруга
• Площадь полукруга
• Центроид полукруга
• Момент инерции полукруга
• Вписанный угол
• Решенные упражнения
• Упражнение 1
• Решение
• Упражнение 2.
• Решение
• Упражнение 3.
• Решение
• Упражнение 4.
• Решение
• Упражнение 5.
• Решение
• Ссылки

В полукруг это плоская фигура, ограниченная диаметром окружности и одной из двух плоских дуг окружности, определяемых указанным диаметром.

Таким образом, полукруг окаймлен полуокружность, который состоит из плоской дуги окружности и прямого сегмента, соединяющего концы плоской дуги окружности. Полукруг охватывает полукруг и все точки внутри него.

Мы можем видеть это на рисунке 1, где показан полукруг радиуса R, размер которого вдвое меньше диаметра AB. Обратите внимание, что в отличие от круга, в котором есть бесконечные диаметры, в полукруге только один диаметр.

Как мы видим на следующем изображении, полукруг – это геометрическая фигура, которая широко используется в архитектуре и дизайне:

Элементы и меры полукруга

Элементами полукруга являются:

1.- Плоская дуга окружности A⌒B

2.- Отрезок [AB]

3.- Внутренняя часть указывает на полукруг, составленный из дуги A⌒B и отрезка [AB].

Периметр полукруга

Периметр – это сумма контура дуги и прямого сегмента, поэтому:

Периметр = длина дуги A⌒B + длина сегмента [AB]

В случае полукруга радиуса R его периметр P будет задан формулой:

P = π⋅R + 2⋅R = (π + 2) ⋅R

Первый член представляет собой половину периметра окружности радиуса R, а второй – длину диаметра, который в два раза больше радиуса.

Площадь полукруга

Поскольку полукруг – это один из плоских угловых секторов, которые остаются при проведении диаметра по окружности, его площадь A будет равна половине площади круга, содержащего полукруг радиуса R:

A = (π⋅R²) / 2 = ½ π⋅R²

Центроид полукруга

Центр тяжести полукруга находится на его оси симметрии на высоте, измеренной от его диаметра, умноженного на 4 / (3π) радиуса R.

Это соответствует приблизительно 0,424⋅R, измеренному от центра полукруга и на его оси симметрии, как показано на рисунке 3.

Момент инерции полукруга

Момент инерции плоской фигуры относительно оси, например оси x, определяется как:

Интеграл от квадрата расстояния между точками, принадлежащими фигуре, до оси, дифференциал интегрирования является бесконечно малым элементом площади, взятой в положении каждой точки. 

На рисунке 4 показано определение момента инерции I_Икс полукруга радиуса R относительно оси X, проходящей через его диагональ:

Момент инерции относительно оси x определяется выражением:

я_Икс = (π⋅R⁴) / 8

А момент инерции относительно оси симметрии y равен:

Iy = (π⋅R⁴) / 8

Следует отметить, что оба момента инерции совпадают в своей формуле, но важно отметить, что они относятся к разным осям.

Вписанный угол

Угол, вписанный в полукруг, всегда равен 90 °. Независимо от того, где находится точка на дуге, угол между сторонами AB и BC фигуры всегда правильный.

Решенные упражнения

Упражнение 1

Определите периметр полукруга радиусом 10 см.

Решение

Помните, что периметр как функция радиуса определяется формулой, которую мы видели ранее:

P = (2 + π) ⋅R

P = (2 + 3,14) ⋅ 10 см = 5,14 ⋅ 10 см = 51,4 см.

Упражнение 2.

Найдите площадь полукруга радиусом 10 см.

Решение

Формула площади полукруга:

А = ½ π⋅R² = ½ π⋅ (10 см)² = 50π см² = 50 х 3,14 см² = 157 см².

Упражнение 3.

Определите высоту h центра тяжести полукруга радиусом R = 10 см, измеренную от его основания, при том же диаметре полукруга.

Решение

Центроид – это точка равновесия полукруга, и его положение находится на оси симметрии на высоте h от основания (диаметр полукруга):

h = (4⋅R) / (3π) = (4⋅10 см) / (3 x 3,14) = 4,246 см

Упражнение 4.

Найдите момент инерции полукруга относительно оси, совпадающей с его диаметром, зная, что полукруг состоит из тонкого листа. Его радиус 10 см, а масса 100 грамм.

Решение

Формула, которая дает момент инерции полукруга:

я_Икс = (π⋅R⁴) / 8

Но поскольку задача говорит нам, что это материальный полукруг, то предыдущее соотношение необходимо умножить на поверхностную плотность массы полукруга, которую мы будем обозначать σ.

я_Икс = σ (π⋅R⁴) / 8

Затем мы переходим к определению σ, которое представляет собой не что иное, как массу полукруга, деленную на его площадь.

Площадь была определена в упражнении 2, и результат составил 157 см.². Тогда поверхностная плотность этого полукруга будет:

σ = 100 грамм / 157 см² = 0,637 г / см²

Тогда момент инерции по отношению к диаметру будет рассчитываться следующим образом:

я_Икс = (0,637 г / см²) [3,1416 ⋅ (10 см)⁴] / 8

Результат:

я_Икс = 2502 г⋅см²

Упражнение 5.

Определить момент инерции полукруга радиусом 10 см из листа материала с поверхностной плотностью 0,637 г / см.² вдоль оси, проходящей через его центр тяжести и параллельной его диаметру.

Решение

Чтобы решить это упражнение, необходимо вспомнить теорему Штейнера о моментах инерции параллельных осей, которая гласит:

Момент инерции I относительно оси, находящейся на расстоянии h от центроида, равен сумме момента инерции I_c относительно оси, которая проходит через центроид и параллельна первой, плюс произведение массы на квадрат расстояния между двумя осями.

Я = Я_c+ М ч²

В нашем случае I известен как момент инерции по отношению к диаметру, который уже был вычислен в упражнении 4. Также известно расстояние h между диаметром и центроидом, которое было вычислено в упражнении 3.

Нам нужно только очистить Ic:

я_c = Я – М ч²

я_c= 2502 г⋅см² – 100 г ⋅ (4,246 см)² в результате чего момент инерции по оси, параллельной диаметру и проходящей через центроид, равен:

я_c = 699,15 г⋅см²

Ссылки

1. Александр, Д. 2013. Геометрия. 5-е. Издание. Cengage Learning.
2. Открытый справочник по математике. Полукруг. Получено с: mathopenref.com.
3. Полукруг формул Вселенной. Получено с: universaloformulas.com.
4. Формулы Вселенной. Площадь полукруга. Получено с: universaloformulas.com.
5. Википедия. Полукруг. Получено с: en.wikipedia.com.

Расчет момента инерции круглого сечения

Момент инерции сечения – это сумма произведений элементарных площадок данного сечения на квадраты их расстояний от рассматриваемой оси.

Формула расчета моментов инерции круглого сечения:

D – диаметр круга в см.

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета момента инерции круглого сечения в зависимости от размеров. С помощью этого калькулятора вы в один клик сможете рассчитать момент осевой инерции круглого сечения.

Строительный клуб

d — диаметр сечения круга в мм; y, z — центральные оси сечения.

Введите диаметр сечения d в мм:

В результате момент инерции относительно центральных осей y и z равны I_y = I _z =

Как найти момент инерции круга?

Момент инерции круга относительно центральной оси z равен моменту инерции относительно центральной оси y и рассчитывается по формуле:

l_y = l_z = Π . d 4 /64 ,

l_y — момент инерции относительно центральной оси y в мм 4 ;

l_z — момент инерции относительно центральной оси z в мм 4 ;

d — диаметр круга в мм.

5.I. Вычисление статических моментов и моментов инерции

Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 206, 207. Рассмотрите внимательно примеры, приведенные в указанных пунктах.

573. Найти статический момент полуокружности относительно диаметра.

Решение. Выберем систему координат так, чтобы центр окружности совпадал с началом координат, а диаметр, относительно которого мы ищем сгатический момент, совпадал с осью Ох. Тогда статический момент полуокружности относительно диаметра выразится следующей формулой:

В выбранной системе координат уравнение полуокружности запишется так: у —V R2—х. Тогда

574. Найти статические моменты относительно осей Ox и Oy дуги эллипса , расположен

ной в первом квадранте.

Решение. Найдем статический момент дуги эллипса относительно оси Ох. Из уравнения эллипса имеем

(мы берем перед корнем знак , так как по условию кривая расположена в первом квадранте).

Найдем статический момент дуги эллипса относительно оси Oy. Из уравнения эллипса имеем:

X = JLyW=T*-, dl = – L YbUg^ZFldy.

К, -|f VF=V? – j – /езщрг dy=

575. Найти статический момент прямоугольника с основанием а и высотой h относительно его сторон.

Решение. Выберем систему координат так, чтобы ось Ox совпадала с основанием, а начало координат — с прилегающей к основанию стороной. Тогда статический момент плоского тела относительно оси Ox будет вычисляться по формуле:

В нашем случае у = h,

Статический момент относительно оси Oy вычисляется по формуле:

576. Налти статический момент фигуры, представленной на рисунке 23 относительно стороны OD1 если известно, что OA = 3 см, AB = 5 см, BC = 5 см, OF = 8см, а дуга CD есть четвертая часть окружности радиуса CF = FD = S см.

Решение. Как видно из рисунка 23, данная фигура имеет сложную форму. Разобьем это тело на простые геометрические фигуры и применим затем теорему: статический момент фигуры относительно некоторой оси равен сумме статических моментов ее частей относительно той же оси.

Выберем систему координат, как показано на рисунке 23. Легко видеть, что данную фигуру можно рассматривать как сумму дзух трапеций OABM и MBCF и одной четвертой части круга.

Координаты точек At Bt C9 Dy F определить легко: Л (0, 3), В (4, 6), С (8, 3), £>(11, 0), F( 8, 0).

Найдем уравнения прямых AB и BCt как уравнения прямых, проходящих через две данные точки:

уравнение прямой AB:

уравнение прямой ВС:

Так как центр F окружности лежит на оси Ox и отстоит от начала координат на расстоянии OF — 8, то уравнение окружности будет

Учитывая все вышеизложенное, найдем:

577. Найти статический момент тела, ограниченного одной аркой циклоиды относительно оси Ох.

Решение. Так как параметр t для одной арки циклоиды изменяется от 0 до 2я, то

578. Найти момент инерции одной арки циклоиды

Относительно оси Ох. Решение. Как было показано в теоретическом курсе, момент инерции дуги относительно оси Ox вычисляется по формуле:

где —дифференциал дуги. Найдем дифференциал дуги:

579. Найти момент инерции дуги окружности

, лежащей в первом квадранте, относительно

Решение. Как известно, момент инерции кривой относительно оси Oy вычисляется по формуле:

Так как и, следо

Для вычисления Была использована

580. Найти момент инерциифигуры, вграниченной дугой полуокружности Относительно

Решение. Как известно из теоретического курса, момент инерции Ix плоского тела относительно оси Ojc равен:

где dS—элементарная площадь тела.

581. Найти статические моменты дуги параболы у2 = 2х (у > 0) относительно осей Ox и Oy от х = 0 до

582. Найти статический момент дуги астроиды х3 –2_ 2_

– j-y 3 = а 3 , лежащей в первом квадранте, относительно оси Oy.

583. Найти статический момент относительно оси Ox

584. Вычислить статический момент фигур, ограниченных следующими линиями:

COS X OT ТОЧКИ X —до точки

дуги косинусоиды у

а) у —- и у = Xi относительно оси Ох

б) у — X1 и у = Y х относительно оси Ох.

585. Вычислить статический момент фигуры, представленной на рисунке 24, где BC\AD, CKJ_AD, AB = 5, BC = 2, CK = KD = 3, AK = 6, относительно оси Ох.

586. Найти статический момент прямоугольного равнобедренного треугольника с катетом, равным а, относительно этого катета.

587. Найти момент инерции отрезка AB, где А (2; 3), В (5; 4), относительно обеих координатных осей.

588. Найти момент инерции треугольника ABC (рис. 25) относительно стороны Ь.

589. Найти момент инерции прямоугольника со сторонами а и b относительно обеих сторон.

590. Найти момент инерции трапеции ABCD относительно ее основания AD1 если AD=а, BC = 6, высота трапеции равна h.

591. Найти момент инерции

параболического сегмента относительно основания. Основание сегмента равно а, «стрела сегмента» равна А.

[spoiler title=”источники:”]

http://matica.org.ua/metodichki-i-knigi-po-matematike/a-z-ryvkin-i-e-s-kunitckaia-zadachnik-praktikum-po-matematicheskomu-analizu/5-i-vychislenie-staticheskikh-momentov-i-momentov-inertcii

[/spoiler]