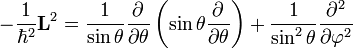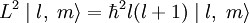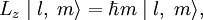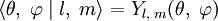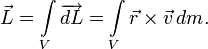Содержание:
Момент количества движения материальной точки и системы относительно центра и оси:
Момент количества движения материальной точки относительно центра является динамической характеристикой механического движения точки, выражающейся векторным произведением радиуса-вектора и количества движения материальной точки:
Момент количества движения материальной точки относительно центра
Во многих задачах динамики, например в небесной механике при изучении движения планет или комет вокруг Солнца, приходится учитывать не только количество движения данной точки, его величину и направление, но и ее положение по отношению к центру (к Солнцу).
Динамической характеристикой механического движения, учитывающей положение материальной точки (или частицы) по отношению к данному центру, является момент количества движения точки относительно данного центра.
Пусть количество движения точки M (рис. 180, а) изображается вектором
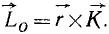
Рис. 180
Размерность момента количества движения — это размерность количества движения, умноженная на размерность длины. Таким образом, в физической системе
а в технической системе единиц момент количества движения имеет размерность первой степени относительно длины, относительно силы и относительно времени:
[L]T = L1F1T1.
Если точка M (рис. 181) движется в плоскости хОу, то момент количества движения точки M относительно начала координат удобно выражать через координаты х, у и проекции количества движения mх,mу. Величина момента количества движения равна произведению Kh, или, как видно из чертежа,
L0 = Kh — mvr sin δ = mυr sin (αK—ar).
Раскроем синус суммы:
L0 = mυr (sin αK cos ar—cos αK – sin ar).
Заменив синусы и косинусы их значениями
получим окончательно
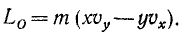
Момент количества движения материальной точки относительно оси равен проекции на эту ось момента количества движения данной материальной точки относительно какой-либо точки этой оси
Момент количества движения материальной точки относительно оси
Пусть дана какая-либо ось (рис. 182, а). Возьмем на ней произвольную точку О. Пусть момент количества движения материальной точки /И относительно точки О выражается вектором 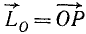
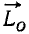
ON = OP соs 
Скалярную величину, равную проекции на данную ось момента количества движения материальной точки относительно какой-либо точки той же оси, называют моментом, количества движения материальной точки относительно оси.
Чтобы определить момент количества движения точки M относительно оси, надо спроецировать вектор количества движения 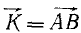
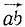
движения относительно точки О выражается удвоенной площадью треугольника OAB. Треугольник Oab есть проекция треугольника OAB, двугранный угол определяется линейным, а потому
2 пл. Δ Oab = 2 пл. Δ OAB cos 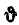
откуда в принятом масштабе
2 пл. Δ Oab OP cos 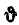
что и требовалось доказать.
Момент количества движения Lz материальной точки относительно оси Oz связан с координатами х, у этой точки и с проекциями ее количества движения mх, mу соотношением
Lz = хmу—уmх
Для определения момента количества движения материальной точки относительно координатных осей существуют удобные формулы, к выводу которых мы сейчас приступим.
Пусть х, у, z — координаты материальной точки (рис. 183), 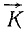
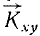
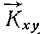
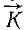
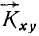
Lz = xmυy—ymυx.
Путем таких же рассуждений выведем аналогичные формулы для Lx и Ly. Обозначая точками производные от координат по времени (проекции скоростей), будем иметь:
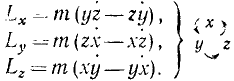
Рис. 183
Иным путем эти же формулы можно просто получить из векторного произведения (182), представив его в виде определителя:
и сравнив это равенство со следующим:
Задача №1
Материальная точка M (рис. 184) массы m движется согласно уравнениям x=r cos πt, у = r sin πt, z = r sin πt. Определить момент количества движения точки M относительно начала координат О.
Рис. 184
Решение. Определим по формуле (184) моменты количества движения точки Al относительно осей координат:
Моменты количества движения материальной точки относительно координатных осей являются проекциями на эти оси момента количества движения той же точки относительно начала координат, поэтому
Направляющие косинусы вектора момента количества движения точки M имеют следующие значения:
Ответ. Момент количества движения точки M постоянен по величине и направлению, равен но модулю mr2π
Главный момент количеств движения материальной системы относительно центра равен геометрической сумме моментов количеств движения всех точек системы относительно того же центра:
Главный момент количеств движения системы
Если дана система материальных точек и некоторый центр О, то, определив моменты количеств движения каждой материальной точки относительно этого центра, получим пучок векторов, пересекающихся в центре О. Вектор, равный геометрической сумме всех этих векторов, изображает главный момент количеств движения системы материальных точек относительно данного центра:
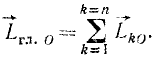
Эту же величину называют также кинетическим моментом системы материальных точек относительно данного центра. Главный момент количества движения системы относительно центра является динамической характеристикой механического движения, учитывающей положение материальной системы по отношению к данному центру.
Главный момент количеств движения материальной системы относительно оси равен алгебраической сумме моментов количеств движения всех точек системы относительно этой оси
Момент количества движения материальной частицы относительно осн — величина скалярная. Поэтому для определения главного момента количеств движения системы материальных точек относительно оси надо взять алгебраическую сумму моментов количеств движения всех точек системы относительно этой оси:
Главный момент количеств движения системы относительно оси равен проекции на эту ось главного момента количеств движения той же системы относительно какой-либо из точек оси:
Эту же величину называют также кинетическим моментом системы материальных точек относительно оси.
Для определения главного момента системы относительно координатных осей определим по (184) моменты количеств движения всех частиц системы и затем просуммируем эти выражения:
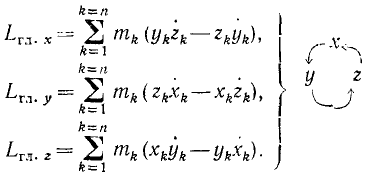
Teоpeмы о моменте количества движения
Производная по времени от момента количества движения материальной точки относительно какой-либо оси равна моменту действующей на точку силы относительно той же силы:
Теорема моментов (для материальной точки)
Пусть какая-либо точка массы т движется под действием силы. Напишем выражение момента количества движения этой точки относительно оси Ох:
Lx = m(yz-zy) (184)
Дифференцируя ио времени левую и правую части этого равенства, получим
но согласно (126′)
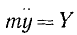
где Y и Z—проекции силы, действующей на данную точку.
Следовательно,
В правой части мы полу.чили момент силы относительно оси Ох, как это было показано (23) еще в статике (см. § 9).
Согласно этой теореме, называемой теоремой моментов, производная по времени от момента количества движения материальной точки относительно какой-либо оси равна моменту силы, действующей на эту точку, относительно той же оси. Теорема доказана для оси Ох, но совершенно аналогично можно доказать ее и для всякой другой оси:
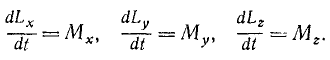
Равенства (187) справедливы для любой оси, следовательно, их можно записать и в векторной форме:
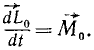
Словами это равенство читают так: производная по времени от момента количества движения материальной точки относительно какого-либо центра О равна моменту действующей на эту- точку силы относительно того же центра О.
Если точка движется в одной плоскости, то равенство (187) можно рассматривать как скалярное:
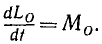
Математический маятник
Задача №2
Материальная точка M массы m подвешена на невесомой и нерастяжимой нити длины I, другой конец которой закреплен неподвижно в точке О (рис. 185). Точке M сообщили начальную скорость υ0, перпендикулярную нити, и вывели из равновесного состояния («математический маятник»). Определить движение точки при условии, что начальная скорость мала.
Рис. 185
Решение. На точку действуют собственный вес G = mg и натяжение T нити. Под действием этих сил и полученной начальной скорости математический маятник движется в вертикальной плоскости. Для решения задачи составим уравнение моментов относительно точки О.
Обозначим через φ угол отклонения маятника, тогда количество движения
К = mφl
Помножив на плечо l, получим момент количества движения:
L0 = mφl2.
Момент силы натяжения нити относительно точки О всегда равен нулю, а момент силы G
M0 = — Gl sin φ = — mgl sin φ.
Подставляя в уравнение моментов (187″) и сокращая на ml, получим
lφ =— g sin φ.
Чтобы определить движение математического маятника, надо это уравнение проинтегрировать, по оно не интегрируется в элементарных функциях и требует применения эллиптических функций, относящихся к разряду высших трансцендентных функций. Однако в нашей задаче угол φ изменяется незначительно, так как точка M до начала движения находилась в наинизшем положении, т. е. в состоянии устойчивого’ равновесия, и получила незначительную скорость. Поэтому мы можем положить
sin φ = φ.
Тогда уравнение принимает вид
Мы получили линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Для интегрирования этого уравнения составим характеристическое уравнение
Корни характеристического уравнения мнимые:
следовательно, общее решение имеет вид
где C1 и C2—постоянные интегрирования.
Определим эти постоянные по начальным данным, для чего предварительно продифференцируем по времени полученное уравнение:
и затем, подставив начальные данные 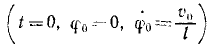
Обозначая вторую постоянную буквой α, получим
Это уравнение определяет угол поворота как функцию времени, т. е. является кинематическим уравнением качания математического маятника.
Величину
называют частотой качаний математического маятника. Она связана с периодом τм качаний математического маятника обратной зависимостью
Следовательно, период малых качаний математического маятника зависит Только от длины нити и от ускорения £ свободно падающего тела.
Ответ. Малые колебания по дуге радиуса l с периодом
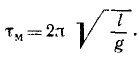
Если колебания не малые, и sinφ нельзя приравнять φ, то колебания маятника ,неизохроины, т. е. период зависит от амплитуды.
Если момент действующей на материальную точку силы относительно данной оси равен нулю, то момент количества движения точки относительно этой оси постоянен
Интеграл моментов (для материальной точки)
В случае, если момент силы, приложенной к данной материальной точке, относительно какой-либо осн, например относительно оси Oz, постоянно равен нулю, то уравнение моментов относительно этой оси имеет вид
откуда, интегрируя, получаем
m (ху—ух) = С. (189)
Мы доказали теорему, называемую законом сохранения момента количества движения материальной точки относительно оси. Сформулировать ее можно так: если момент силы, действующей на материальную точку, взятый относительно какой-либо оси, постоянно равен нулю, то момент количества движения этой точки относительно той же оси постоянен. Когда на точку действует несколько сил, то здесь (как и везде) под действующей силой мы понимаем равнодействующую.
Момент силы, не равной нулю, относительно оси может равняться нулю только в двух случаях: 1) сила параллельна оси, 2) сила пересекает ось. В обоих этих случаях имеет место закон сохранения момента количества движения относительно данной оси.
Чтобы равнялся нулю момент силы относительно данного неподвижного центра, линия действия силы должна проходить через этот центр. Следовательно, условия сохранения момента количества движения относительно данного центра следующие: 1) равнодействующая сил проходит через этот центр или 2) все силы взаимно уравновешены. В этих случаях
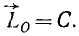
Под действием центральной силы точка описывает плоскую траекторию
Центральная сила
Пусть к точке M массы т приложена сила F, линия действия которой всегда проходит через неподвижный центр О. Такую силу называют центральной. Построим в точке О систему прямоугольных координат хОуг. Моменты силы F относительно осей координат равны нулю, следовательно, моменты количества движения точки M постоянны. Обозначим момент количества движения относительно оси Ox буквой А, относительно оси Oy—буквой В и относительно Oz— буквой С:
m (уz—zy) = А, m (zх— хz) = В, m (ху—ух) — С,
где х, у, я —координаты точки M в какое-либо мгновение, а х, у и z — проекции скорости точки в то же мгновение. Умножим первое из написанных выражений на координату х точки М, второе — на координату у, третье —на z и сложим их:
m (xyz + xyz + xyz—xyz—xyz—xyz) — Ах +By + Сz,
или
Ax+ By + Cz = 0.
Мы получили уравнение плоскости. Координаты х, у и г точки M должны удовлетворять этому уравнению, следовательно, точка M должна двигаться в этой плоскости. Таким образом, под действием центральной силы точка описывает плоскую траекторию. Например, Земля под действием притяжения к Солнцу движется в плоскости эклиптики.
«Прямая линия, соединяющая планету с Солнцем, описывает равные площади в равные промежутки времени» (Кеплер)
Интеграл площадей
Равенство (189) является первым интегралом дифференциальных уравнений движения точки для рассмотренного случая. Поэтому его называют интегралом моментов. Его называют также интегралом площадей. Чтобы пояснить это название, приведем следующую геометрическую интерпретацию.
Планета P (рис. 186) движется вокруг Солнца О, находящегося в одном из фокусов эллипса. Количество движения планеты изобразим вектором то, касательным к орбите. Момент количества движения планеты относительно оси Oz, перпендикулярной к плоскости орбиты, равен то OB, следовательно, по (189),
а так как масса т планеты постоянна, то
Пусть за время dt планета сместилась на элемент дуги ds = υdt радиус-вектор OP планеты описал сектор, заштрихованный на чертеже. Площадь этого сектора dσ равна
Отсюда видно, что площадь о, описываемая радиусом-вектором планеты, возрастает пропорционально времени t независимо от положения планеты на ее орбите. Планета движется по своей эллиптической орбите неравномерно. Чем ближе она находится к Солнцу, тем быстрее она движется по орбите, но площади, описываемые радиусом-вектором за одинаковые промежутки времени, всегда одинаковы, независимо от того, находится планета (рис. 187) в перигелии P1 (ближайшей к Солнцу точке своей орбиты), или в афелии (наиболее удаленной точке), или же где-либо в другом месте своей орбиты. На чертеже белые и заштрихованные части фигуры обозначают равные площади, соответствующие движению планеты за равные промежутки времени, а именно за 1/12 времени полного оборота планеты вокруг Солнца.
Разумеется, закон площадей справедлив не только для движения планет под действием притяжения к Солнцу. Движение каждой материальной точки под действием всякой центральной силы происходит с постоянной секторной скоростью (σ = const).
Напишем выражение интеграла площадей в декартовых координатах:
ху—ух = C1 = 2σ. (189)
Аналогичное выражение в полярных имеет вид
r2φ = C1 = 2σ. (189″)
Эту формулу можно получить из предыдущей преобразованием координат. Она полезна при решении ряда вопросов динамики.
Задача №3
Материальная точка M (искусственный спутник) движется по эллипсу (рис. 188) под действием силы притяжения к точке О (к центру Земли), находящейся в одном из фокусов эллипса. Определить скорость υ2 точки M в наиболее удаленной от фокуса О точке P2 ее траектории (в апогее), если скорость в наиболее близком положении P1 (в перигее) равна 8 км/сек, OP1 = 6500 км и OP2 = 6600 км.
Решение. Точка движется под действием центральной силы, следовательно, ее момент количества движения относительно точки О постоянен.
Если массу точки обозначим через m, то момент количества движения точки M в положении P1 получим, умножив массу на скорость и на плечо:
Lo = m∙8∙6500 = 52 ООО m κм2∙κг∙ceκ-1.
Аналогично в положении P2
Δo = m∙υ2∙6600 κм2∙κг∙ceκ-1.
Приравнивая друг другу эти два выражения постоянного момента количества движения точки, найдем ее скорость υ2.
Ответ. υ2 = 7,88 км/сек.
Задача №4
Гирька M привязана к концу нерастяжимой нити MOA (рис. 189), часть которой OA пропущена через вертикальную трубку; гирька движется вокруг оси трубки по окружности радиуса MC=R, делая no=120 об/мин. Медленно втягивая нить OA в трубку, укорачивают наружную часть нити до длины OM1 при которой гирька описывает окружность радиуса R. Сколько оборотов в минуту делает гирька по этой окружности?
Решение. Применим теорему моментов. К материальной точке (гирьке) приложены две силы: вес гирьки, направленный по вертикали вниз, и натяжение нити, направленное по нити в точку О. Первая из этих сил параллельна оси трубки, вторая пересекает эту ось; следовательно, моменты обеих приложенных к точке сил относительно оси трубки равны нулю, и согласно (189)
L1 = C.
В начале движения гирька описывала окружность радиуса R, делая n0= 120 об/мин. Обозначая массу гирьки через m, определим момент количества движения гирьки относительно оси z в начале движения:
Когда радиус уменьшился, гирька стала делать n оборотов в минуту, но момент количества движения гирьки относительно оси не изменился:
откуда n = 4n0
Ответ. n=480 об/мин.
Некоторые сведения из небесной механики
Формулы Бине позволяют решать прямые и обратные задачи динамики при движении точки под действием центральной силы
Уравнение Бине
Многие проблемы динамики содержат вопросы о движении точки под действием центральной силы. Сюда относятся задачи небесной механики о движении планет, искусственных спутников, задачи теоретической физики о движении электрона в поле ионизированного атома и многие другие задачи. Формулы Бине, к выводу которых мы сейчас приступаем, дают решение обоих основных задач динамики в случаях движения точки под действием одной центральной силы.
Под действием центральной силы точка движется в плоскости, а потому ее движение можно описать двумя дифференциальными уравнениями. Напишем эти уравнения в полярных координатах (см. стр. 272), учитывая, что проекция Fr центральной силы F на направление полярного радиуса-вектора равна модулю этой силы (с отрицательным или положительным знаком в зависимости от того, притягивает к центру или отталкивает от него центральная сила движущуюся точку), а проекция центральной силы на трансверсальное (перпендикулярное к радиальному) направление равна нулю:
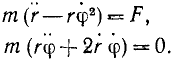
Здесь, как обычно, r —полярный радиус-вектор, φ-полярный угол, а одной и двумя точками обозначены первая и вторая производные по времени.
Второе из этих уравнений можно один раз проинтегрировать и получить первый интеграл этих уравнений. Для этого запишем второе уравнение в следующем виде:
и далее
Интегрируя
и потенцируя, получаем знакомое нам равенство
r2φ = C1 = 2σ. (189″)
Система уравнений (129) распадается на два отдельных уравнения:
Исключая φ, получаем одно уравнение
В этом уравнении произведем следующую замену, использовав равенство (189″):
и аналогичным путем:
Получаем дифференциальное уравнение относительно
Это уравнение позволяет определить центральную силу путем дифференцирования уравнения траектории r = r(φ). В небесной механике ему обычно придают другой вид, заменяя полярный радиус-вектор его обратной величиной 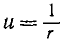
Это уравнение принадлежит Бине и его обычно называют второй формулой Бине. Первая формула Бине позволяет определить квадрат скорости точки по заданной траектории. Вывод первой формулы Бине удобнее провести тоже в полярных координатах и для этого воспользуемся известным из курса математики выражением дифференциала дуги в полярных координатах:
Деля на dt и возводя в квадрат, получим следующее выражение квадрата скорости
Напомним (см. задачу № 35 на стр. 129), что в правой части мы видим сумму квадратов радиальной и трансверсальной скоростей. Определив из равенства 189″ дифференциал времени
подставим это значение в предыдущее уравнение, тогда
Введем опять функцию 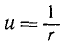
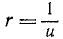
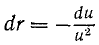
Внесем эти величины в написанное выше уравнение
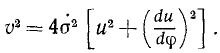
Мы получили первую формулу Бине.
Вывод закона всемирного тяготения из законов Кеплера
Задача №5
По движению планет солнечной системы определить силу, вызывающую это движение.
Решение. Планеты движутся по законам, открытым Кеплером:
1. Все планеты (и кометы) движутся по коническим сечениям, в одном из фокусов которого находится Солнце.
2. Площади, описываемые радиусом-вектором планеты относительно Солнца, пропорциональны времени.
3. Для планет (все планеты движутся по эллипсам) квадраты времен обращения относятся, как кубы больших полуосей их орбит.
Уравнение всех конических сечений в полярных координатах имеет вид:
где р— параметр, е—эксцентриситет (у гипербол е > 1, у парабол е—1, у эллипсов е < 1, у окружностей е — 0). Следовательно, для всех конических сечений имеем:
Внесем во вторую формулу Бине
Положим
и, подставив вместо и его обратную величину 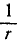
Действующая сила притягивает планету к Солнцу, так как ее проекция отрицательна, сила обратно пропорциональна квадрату расстояний; это соответствует закону тяготения. Чтобы доказать всемириость этого закона, необходимо показать, что коэффициент μ для всех планет одинаков.
Для этого воспользуемся третьим законом Кеплера:
где T1, T2…—времена обращений планет, a а1, а2…—большие полуоси их эллиптических орбит. Площадь эллипса, описываемого какой-либо 6-й планетой, равна πakbk. Обозначив σk-секторную скорость этой планеты, найдем время ее обращения, разделив площадь на секторную скорость:
Возведя в квадрат, подставим в предыдущее равенство (третий закон. Кеплера):
Но квадрат малой полуоси, деленный на большую полуось, есть параметр р эллипса, а потому
Ввиду чего предыдущее равенство принимает вид
или
Следовательно число μ постоянно и одинаково для всех планет. Оно было с большой точностью вычислено Гауссом, поэтому его называют гауссовым числом.
Положив μ-kM, где M— масса Солнца, получим равенство
выражающее закон всемирного тяготения Ньютона.
Производная по времени от суммы моментов количеств движения всех материальных точек системы относительно какой-либо оси равна сумме моментов всех внешних сил системы относительно той же оси
Теорема моментов (для системы)
Пусть движение системы материальных точек определяется дифференциальными уравнениями (130).
На всякую точку К, принадлежащую к этой системе, действуют внешние силы, равнодействующая которых 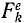
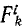
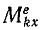
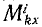
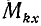
Подставим это выражение в первое из уравнений моментов (187), написанное для этой точки:
Составим такие же уравнения для всех других точек системы и просуммируем их почленно:
Согласно закону равенства действия и противодействия внутренние силы системы попарно равны и действуют по одной прямой в противоположные стороны, а потому сумма моментов всех внутренних сил системы равна нулю:
В правой части остается только первый член (первая сумма). Заменив в левой части сумму производных производной от суммы, получим окончательно уравнение моментов относительно оси Ox (и аналогично для двух других осей):
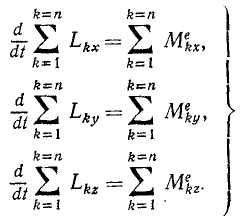
Сформулируем следующую общую теорему, называемую теоремой моментов системы материальных точек относительно оси: производная по времени от суммы моментов количеств движения всех материальных точек системы относительно какой-либо оси равна сумме моментов всех внешних сил системы относительно той же оси.
Формулировка и содержание этой теоремы очень схожи с теоремой о проекции количеств движения системы, только слова «проекция на ось» заменены здесь словами «момент относительно оси». Эта аналогия существует и между равенствами (169) и (192).
Равенствам (192) можно придать несколько иной вид, если принять во внимание, что алгебраическая сумма моментов количеств движения всех точек системы относительно какой-либо оси является главным моментом количеств движения (или кинетическим моментом) системы относительно этой оси, а алгебраическая сумма моментов всех сил относительно оси называется главным моментом системы сил относительно этой оси. Тогда
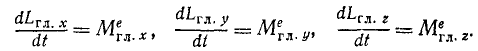
Производная по времени от кинетического момента системы относительно какой-либо оси равна главному моменту внешних сил системы относительно той же оси.
Равенства (192′) справедливы для любой оси. Следовательно, их можно записать в векторной форме:
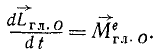
Производная по времени от вектора кинетического момента системы относительно какой-либо точки равна главному моменту внешних сил системы относительно той же точки.
Если сумма моментов всех внешних сил системы относительно какой-либо оси равна нулю, то сумма моментов количеств движения точек системы относительно этой оси постоянна
Интеграл моментов (для системы)
Если сумма моментов относительно какой-либо оси Ox всех внешних сил системы равна нулю во все время движения, то по (192)
откуда получаем интеграл моментов
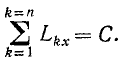
Если же (постоянно) равна нулю сумма моментов всех внешних сил системы относительно точки, то по (192″),
откуда следует, что
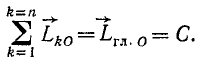
Таким образом, если сумма моментов относительно точки О всех внешних сил постоянно равняется нулю, то вектор кинетического момента системы относительно этой точки О остается постоянным во все время движения. Так как вектор Lгл.0 сохраняет свое направление в пространстве, то плоскость, перпендикулярная вектору Lгл.0, также остается неизменной. Поясним это примером.
Неизменяемая плоскость
Солнечная система может быть принята за изолированную механическую систему. Можно считать, что на точки этой системы действуют только внутренние силы и поэтому кинетический момент солнечной системы остается постоянным по величине и направлению. Зная скорость, массу и положение каждой планеты, Лаплас, принимая планеты за материальные точки, вычислил кинетический момент Lгл.0 солнечной системы и определил положение плоскости, перпендикулярной к этому вектору. Эта плоскость имеет большое значение в астрономии. Ее называют неизменяемой плоскостью Лапласа.
Только что перед этим мы показали, что Земля под действием силы притяжения к Солнцу должна двигаться в плоскости эклиптики. Но на Землю действуют также притяжения других планет солнечной системы, которыми мы пренебрегли, а потому плоскость эклиптики не может считаться неизменной. Притяжения планет друг к другу являются внутренними силами для всей солнечной системы и не влияют на положение неизменяемой плоскости Лапласа. Пуансо уточнил вычисления Лапласа. Он рассматривал каждую планету как тело, движущееся по своей орбите и вращающееся вокруг своей оси, и добавил в уравнения новые члены, вызванные вращением планет вокруг своих осей, но эти члены оказывают лишь незначительное влияние на результат.
Задача №6
Через блок, массой которого пренебрегаем, перекинута веревка; за точку А веревки ухватился человек весом Р; к точке 5 подвязан груз того же веса. Что произойдет с грузом, если человек станет подниматься по веревке со скоростью vτ относительно веревки (рис. 190,α)?
Рис. 190
Решение. Требуется по заданной относительной скорости человека определить движение груза В. Рассмотрим движение всей системы, изображенной на чертеже. На точки системы действуют три внешние силы: вес P -mg человека, вес P — mg груза и реакция в оси блока; натяжение веревки является внутренней силой в рассматриваемой системе (рис. 190,6).
Механическое движение человека передается грузу в виде механического же движения. В подобных случаях обычно бывает полезно применять теоремы о количестве движения или его моменте. В данной задаче, чтобы исключить неизвестную реакцию в оси, применим теорему о моментах для системы относительно оси вращения блока:
Внутренние силы не входят в уравнение моментов. Сумма моментов двух сил P равна нулю, так как моменты этих сил равны по величине и противоположны по знаку. Следовательно, мы имеем интеграл моментов (193)
L1x +L2x = C.
Определим моменты количеств движения точек системы. Момент количества движения человека равен произведению его массы на скорость и на плечо. Под скоростью в этих теоремах следует понимать абсолютную скорость. В условии задачи дана скорость человека относительно веревки. Чтобы получить абсолютную скорость, надо добавить к vr переносную скорость, которой является скорость веревки (среды). Направления относительной и переносной скоростей в данном случае противоположны, поэтому абсолютная скорость выразится их разностью, и момент количества движения человека относительно оси блока равен
Llx= -m(υr-υe)r.
Знак минус поставлен потому, что вектор количества движения человека направлен по ходу часов относительно оси блока.
У груза В имеется только одна скорость—скорость υe веревки. Поскольку нет относительной скорости груза, его переносная скорость одновременно является и абсолютной, и момент количества движения груза равен
L2x= + mυer.
Интеграл моментов принимает следующий вид:
—m (υr-υe) r + mυer = С.
Определим постоянную интеграции С. В начальное мгновение человек был неподвижен. Скорость веревки тоже равнялась нулю, следовательно, C=0. Решая уравнение относительно ve, находим ответ.
Ответ. Груз будет подниматься вместе с веревкой со скоростью
Закон моментов в относительном движении системы имеет тот же вид, что и в абсолютном движении, если ось моментов проходит через центр масс системы
Закон моментов при относительном движении
Во многих случаях абсолютное движение системы целесообразно рассматривать как составное, состоящее из переносного поступательного движения вместе с центром масс и относительного движения относительно осей x’Cy’z’, движущихся поступательно вместе с центром масс.
Чтобы определить это относительное движение, надо к силам, действующим на каждую материальную частицу, добавить кориолисовы силы инерции (см. § 40): поворотные и переносные.
Таким образом, чтобы получить теорему моментов для относительного движения системы, нужно в правую часть уравнений (192) добавить сумму моментов всех кориолисовых сил инерции.
Поскольку переносное движение поступательное, поворотные кориолисовы силы равны нулю. Что же касается переносных кориолисовых сил, то при переносном поступательном движении все они параллельны между собой и направлены против ускорения центра масс, а по величине каждая равна произведению массы частицы на ускорение центра масс. Равнодействующая таких сил равна произведению массы системы на ускорение центра масс, и центр параллельных сил, в котором приложена равнодействующая, совпадает с центром масс.
Но, по теореме Вариньона, момент равнодействующей силы равен сумме моментов составляющих, а следовательно, сумма моментов всех кориолисовых сил относительно осей, проходящих через центр масс, равна нулю. Поэтому теорема моментов для относительного движения системы выражается совершенно так же (192), как и для абсолютного, если переносное движение есть поступательное движение вместе с центром масс.
Кинетический момент вращающегося тела. Момент инерции
Главный момент количества движения тела относительно оси вращения равен произведению момента инерции тела относительно оси вращения на угловую скорость:
Главный момент количества движения вращающегося тела. Пусть твердое тело вращается вокруг неподвижной оси. Построим систему координатных осей xOyz, приняв ось вращения за ось Oz. Будем рассматривать это тело как состоящее из множества материальных точек. Тогда главный момент количества движения тела относительно оси Oz определится формулой (186):
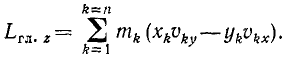
Проекции скоростей точек вращающегося тела выразим формулами Эйлера:
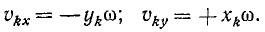
Подставляя (89) в (186) и вынося общий множитель ω за знак суммы, получим
Обозначим
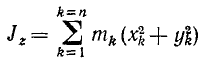
и назовем эту сумму моментом инерции твердого тела относительно оси Oz1. Тогда
Как видно из (194), момент инерции тела относительно оси равен сумме произведений массы mk каждой материальной частицы на квадрат расстояния 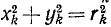
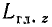
Словами равенство (195) можно выразить так: кинетический момент вращающегося тела относительно оси вращения равен произведению угловой скорости на момент инерции тела относительно той же оси.
Дифференциальным уравнением вращения тела вокруг данной неподвижной оси иг является уравнение
Дифференциальное уравнение вращения тела
Подставим выражение (195) в уравнение моментов (192):
или
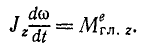
Принимая во внимание известные из кинематики соотношения, перепишем это равенство в следующей форме:
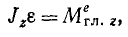
или
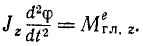
Зная моменты внешних сил, приложенных к вращающемуся твердому телу, можно найти вторую производную от угла поворота по времени. Интегрируя полученное уравнение, можно выразить угол поворота φ как функцию времени t и определить вращение тела. Конечно, при интегрировании появятся, две постоянные, которые надо определить по начальным данным, т. е. по начальным значениям φ и 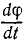
Уравнение (196) называют дифференциальным уравнением вращательного движения твердого тела вокруг неподвижной оси.
Плоское движение тела описывают: уравнениями движения центра масс и уравнением вращения вокруг центральной оси, перпендикулярной плоскости движения
Дифференциальное уравнение плоского движения тела
Если твердое тело движется в плоскости, то его движение можно рассматривать как состоящее из поступательного движения вместе с полюсом и относительного вращательного вокруг оси, проходящей через полюс перпендикулярно плоскости движения.
При относительном движении необходимо учесть кориолисовы силы. Но если за полюс принять центр масс тела, то, как было показано, момент этих сил равен нулю, а потому дифференциальные уравнения плоского движения тела имеют вид:
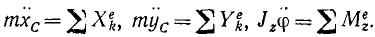
Задача №7
Шкив (рис. 191) радиуса r = 20 см и веса 3,27 кГ приводится во вращение ременной передачей. Определить натяжение T1 ведущей и T2 ведомой ветвей ремня, считая T1 = 2T2, если шкив, принимаемый за тонкий обод, вращается с угловым ускорением 1,5 сек-2, а момент сопротивления Mcoпр= – кГ . м.
Рис. 191
Решение. Задача задана в технической системе единиц. Примем при решении задачи L в см, F — в кГ и T — в сек. Составим дифференциальное уравнение вращения шкива.
На шкив действуют: момент натяжения ведущего ремия М1 = Т1r=2T2r; момент натяжения ведомого ремня M2= — T2r, момент сопротивления Mcoпp = -100 кГ . см; моменты прочих сил (вес шкива, реакции подшипников) равны нулю. Главный момент внешних сил относительно оси вращения равен алгебраической сумме составляющих моментов:
Мгл = Т2 ∙ 20 – 100.
Момент инерции шкива, принимаемого за тонкий обод, равен сумме произведений массы mk каждой частицы обода на квадрат ее расстояния 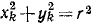
Уравнение (196) принимает вид
1,333 ∙ 1,5 = T2 ∙ 20-100,
откуда находим T2. Натяжение T1 ведущего ремня вдвое больше.
Ответ. T1 = 10,2 кГ, T2 = 5,1 кГ или в CИ T1=100h, T2 = 50 н.
Физическим маятником называют твердое тело, способное качаться относительно оси под действием собственного веса
Физический маятник
Твердое тело, закрепленное на горизонтальной или на наклонной оси так, что оно может качаться относительно этой оси под действием собственного веса, называют физическим маятником. Определим период качаний физического маятника на горизонтальной оси. Обозначим буквой φ угол, составляемый плоскостью, проведенной через ось подвеса О и центр масс C маятника с вертикальной плоскостью. Будем считать, что на фйзический маятник действуют только его вес G и реакция оси подвеса (рис. 192). Для составления дифференциального уравнения качаний физического маятника воспользуемся (196)
Jφ = — Gc sin φ.
Здесь J—момент инерции физического маятника относительно оси подвеса и с—расстояние центра масс от оси подвеса.
Рис. 192
Если угол φ достаточно мал, то, полагая sinφ≈φ, получим
т. е. дифференциальное уравнение, уже проинтегрированное нами в задаче № 126 и др. Оно описывает гармонические колебания, частота которых
а период
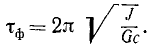
Длину l математического маятника с таким же периодом качаний, что и данный физический, называют приведенной длиной физического маятника. Чтобы определить эту длину, приравняем период τм качаний математического маятника
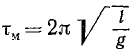
(см. стр. 320) периоду τф качаний физического маятника. Получим
Отложим от точки О (рис, 193) по прямой ОС отрезок OA, равный приведенной длине физического маятника. Точку А называют центром качания маятника, а ось, проведенную через центр качания параллельно оси подвеса маятника,—осью качания маятника. Если ось качания сделать осью подвеса, то период качаний не изменится. Это свойство использовано в «оборотном маятнике Катера» для гравиметрических измерений.
Рис. 193
Моментом инерции твердого тела относительно оси называют меру инерции этого тела при его вращательном движении вокруг данной оси, выражающуюся суммой произведений массы каждой материальной частицы тела на квадрат расстояния этой частицы от данной оси:
Момент инерции твердого тела относительно оси. Как видно из уравнений (196), угловое ускорение тела зависит не только от момента приложенных к нему внешних сил, но и от момента инерции J тела относительно оси вращения. Чем больше момент инерции тела, тем больший вращающий момент нужен, чтобы сообщить телу заданное угловое ускорение ε.
Отсюда можно сделать заключение, что момент инерции твердого тела относительно оси вращения имеет такое же значение при вращательном движении тела, какое имеет масса тела при его поступательном движении или же масса одной материальной частицы при движении этой частицы.
Следовательно, момент инерции твердого тела относительно оси есть мера инерции этого тела при вращательном движении вокруг данной оси.
Момент инерции тела относительно оси зависит только от масс частиц тела и от их распределения в теле. Исследование моментов инерции, определение центра масс и некоторые другие проблемы, связанные с распределением масс, составляют предмет геометрии масс.
Так как момент инерции является понятием геометрии масс и не зависит от вращения тела, то, очевидно, можно определять моменты инерции не только вращающихся тел относительно оси вращения, но также и тел, не вращающихся относительно любой неподвижной оси. Мы можем считать, что момент инерции неподвижного тела относительно любой оси явится мерой инерции этого тела в случае, если оно будет вращаться вокруг этой оси. Таким образом, момент инерции тела относительно оси является мерой инерции тела в его вращательном движении (реальном или воображаемом) вокруг этой оси.
Момент инерции, как и вращение, является понятием, присущим только телу. В применении к материальной точке оно теряет всякий смысл. Поэтому момента инерции материальной точки не существует.
Если даны твердое тело и координатные оси, то, разбивая мысленно это тело на n элементарных частиц, обозначая массу k-й частицы через mk, ее координаты—через xk, yk и zk (где k принимает последовательно все значения от 1 до n), мы можем написать следующие выражения момента инерции тела относительно осей координат:
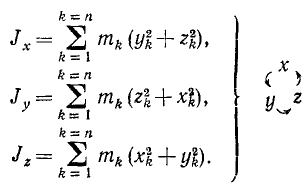
Вообще, если дано какое-либо тело и какая-либо ось и если это тело разбить мысленно,на элементарные массы m1, m2, m3, …. mn и обозначить расстояния частиц от оси соответственно rl, r2, r3, …, rn, то момент инерции тела относительно оси выразится суммой
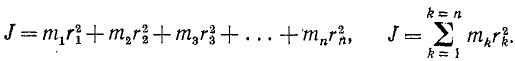
Таким образом, момент инерции тела относительно оси равен сумме произведений, полученных от умножения массы каждой частицы тела на квадрат расстояния этой частицы от оси.
Размерность момента инерции в физической системе единиц и в технической системе единиц:
[J]φ = L2M1T0, [J]t = L1F1T2.
Если тело, момент инерции которого определяют, имеет правильную геометрическую форму и масса в нем распределена непрерывно, то сумму (200) следует заменить интегралом
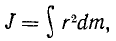
распространенным по всей массе тела.
Радиусом инерции тела относительно данной оси называют такую величину, имеющую размерность длины, на квадрат которой надо умножить массу тела, чтобы получить значение момента инерции этого тела относительно данной оси:
Радиус инерции
Только в том случае, если все частицы тела отстоят от оси на одинаковом расстоянии, r2 выходит за знак интеграла (200′) и момент инерции тела выражается произведением квадрата этого расстояния на массу тела. Такой случай можно представить себе, если предположить, что вся масса тела расположена по поверхности круглого цилиндра, построенного вокруг данной осн. В технике (например, в различных каталогах) часто вместо значения момента инерции какой-либо детали машины или какого-либо иного тела приводят так называемый радиус инерции этого тела относительно данной оси, понимая под этим радиус такого воображаемого круглого полого цилиндра, построенного вокруг данной оси, который обладает той же массой m и тем же моментом инерции J относительно этой оси, что и данное тело. Иными словами, под радиусом инерции rи тела относительно данной оси понимают такую величину, имеющую размерность длины, на квадрат которой надо умножить массу тела, чтобы получить значение момента инерции тела относительно этой оси:
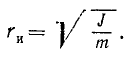
Момент инерции тела относительно какой-либо оси равен моменту инерции того же тела относительно оси, ей параллельной, но проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния между осями:
Jz = JzC + mc2 (Эйлер)
Теорема о параллельных осях
Найдем зависимость между моментами инерции одного и того же тела относительно различных осей, параллельных между собой. Пусть известен момент инерции тела относительно некоторой оси Cz, проходящей через центр масс C тела, и требуется определить момент инерции тела относительно оси Oz’, ей параллельной и отстоящей от нее на расстоянии с. Следуя Эйлеру, построим прямоугольные координатные оси с началом в центре масс С, направив ось Cy в плоскости обеих осей (рис. 194).
Рис. 194
Если координаты какой-либо материальной частицы К данного тела обозначим через xk, yk, zk, то квадрат расстояния этой частицы от оси Oz’ определится из треугольника KNL по теореме косинусов:
или
Зная квадрат расстояния каждой частицы тела от оси Oz’, мы легко определим момент инерции тела, для чего составим сумму произведений массы каждой частицы на квадрат ее расстояния от оси Oz’:
Вынесем общий множитель с за знаки второй и третьей сумм. Первый член правой части выражает момент инерции Jzc тела относительно центральной оси Cz, второй член равен произведению суммы масс всех материальных частиц (т. е. массы всего тела) на квадрат расстояния с между осями, а третий член равен нулю, так как 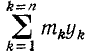
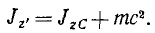
Словами равенство (202) можно прочитать так: момент инерции тела относительно оси равен моменту инерции того же тела относительно оси, проведенной через центр масс тела параллельно данной оси, сложенному с произведением массы тела на квадрат расстояния между осями.
Если надо определить момент инерции тела по известному моменту инерции того же тела относительно оси, параллельной данной, но не проходящей через центр масс, то, проведя через центр масс параллельную ось, можно для двух данных осей написать соотношения
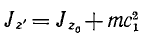
откуда непосредственно вытекает
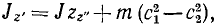
где c1 и c2—расстояния центра масс от данных осей.
Это равенство позволяет определить момент инерции тела относительно любой оси, если известен момент инерции этого тела относительно какой-либо параллельной оси и известно положение центра масс.
Если известны три момента инерции и три центробежных момента инерции тела относительно осей координат, то можно вычислить его момент инерции относительно любой оси, проходящей через начало координат: J = Jx cos2α + Jy cos2 β + Jz cos2 γ + 2Jy.z, Jz cos2 γ—2Jz.x cos β cos γ —2x.y cos a cos β
Теорема о пересекающихся осях
Пусть дано некоторое тело, оси координат xOyz и какая-либо ось OA, составляющая с осями координат углы a, β и γ. Распределение масс тела относительно координатных осей известно, и требуется определить момент инерции тела относительно оси OA.
Рассмотрим сначала одну произвольную материальную частицу К данного тела (рис. 195). Квадрат радиуса-вектора OK этой частицы равен сумме квадратов ее координат:
или
так как последняя скобка равна единице. Опустим перпендикуляр KN на ось OA. Отрезок ON является проекцией радиуса-вектора OK на ось OA:
Квадрат расстояния произвольной частицы К от оси OA определим из прямоугольного треугольника ONK:
Зная квадрат расстояния частиц тела от данной оси, мы легко определим момент инерции тела, для чего составим сумму произведений массы каждой частицы на квадрат расстояния:
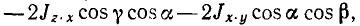
где Jx, Jy и Jz—моменты инерции тела относительно осей координат, a
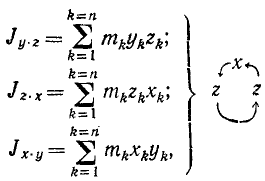
т. е. суммы произведений массы каждой частицы тела на две координаты этой частицы—центробежные моменты инерции тела или произведения инерции. Индекс справа и снизу буквы J соответствует координатам, произведения которых стоят под знаком суммы. Между индексами ставят точку, означающую произведение. Центробежные моменты инерции имеют размерность моментов инерции, но в отличие от них могут быть как положительными, так и отрицательными величинами или равняться нулю.
Рис. 195
Три взаимно перпендикулярные координатные оси, проведенные через данную точку в таких направлениях, что центробежные моменты инерции тела относительно этих осей равны нулю, называют главными осями инерции тела в этой точке
Эллипсоид инерции
Если мы будем изменять направление оси OA, то будет изменяться и момент инерции тела относительно этой оси. Зависимость момента инерции тела относительно направления оси может быть легко представлена следующим геометрическим построением. Проведем через начало координат всевозможные направления и вдоль каждого направления
отложим отрезок 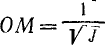
Определим геометрическое место точек М, для чего найдем их координаты:
Подставив выражения направляющих косинусов в (204) и сократив на J, получим уравнение второго порядка:
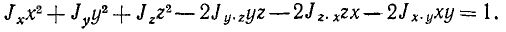
Этому уравнению удовлетворяют координаты точек М, а следовательно, геометрическое место этих точек есть поверхность второго порядка. Из всех поверхностей второго порядка только эллипсоид не имеет бесконечно удаленных точек, следовательно, концы отложенных отрезков лежат на поверхности эллипсоида. Его называют эллипсоидом инерции. Заметим, что при построении этого эллипсоида мы взяли начало координат в произвольной точке О. Следовательно, для каждого тела в каждой точке пространства можно построить свой эллипсоид инерции с центром в этой точке.Момент инерции тела относительно любой оси, проходящей через эту точку, обратно пропорционален квадрату отрезка оси, лежащей внутри эллипсоида инерции. Ясно, что наибольшей оси эллипсоида соответствует наименьший момент инерции и, наоборот, наименьшей оси эллипсоида — максимальный момент инерции. Напомним, что в эллипсоиде имеются обычно три взаимно перпендикулярные оси, называемые главными. Можно совместить координатные оси с главными осями эллипсоида инерции. Из математики известно, что уравнение эллипсоида, отнесенного к главным осям, не содержит членов с произведениями координат. Следовательно, центробежные моменты инерции относительно этих осей равны нулю. Их называют главными осями инерции в данной точке О, а моменты инерции тела относительно этих осей называют главными моментами инерции. Формула (204) принимает вид
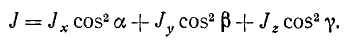
Если эллипсоид инерции построен для центра масс тела, то его называют центральным эллипсоидом инерции, а его главные оси — главными центральными осями инерции.
Радиус-вектор и все длины в эллипсоиде инерции Коши имеют размерностью величину, обратную квадратному корню из размерности момента инерции, что вносит ряд осложнений, особенно в графические построения. Значительно удобнее откладывать вдоль каждой оси, проходящей через данную точку А, не 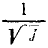
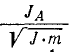
Если фигура лежит в плоскости хОу, то Jz = Jx + Jy
Теорема о плоской фигуре
Докажем еще одну теорему, называемую теоремой о плоской фигуре и полезную при решении многих задач. Материальные тела, одно из измерений которых значительно меньше двух остальных, в механике часто принимают за плоские материальные фигуры. Так возникло понятие момента инерции плоской фигуры. Пусть любая плоская фигура лежит в плоскости xOy. В таком случае координаты zk точек этой фигуры равны нулю и моменты инерции (194) относительно координатных осей:
Складывая два первых равенства, получаем третье; следовательно, для всякой плоской фигуры, лежащей в плоскости хОу,
Jz = Jx + Jy (207)
независимо от направления в этой плоскости осей Ox и Оу.
Момент инерции тела относительно начала координат равен полусумме трех моментов инерции относительно координатных осей или суммe трех моментов инерции относительно координатных плоскостей
Моменты инерции тела относительно полюса и плоскости
Наряду с моментом инерции тела относительно оси применяют понятия: момент инерции тела относительно полюса (иначе называемый моментом инерции относительно точки, или полярным моментом инерции) и момент инерции относительно плоскости, (иначе называемый моментом инерции Бине).
Эти величины не имеют самостоятельного физического смысла и служат как вспомогательные для вычисления моментов инерции относительно оси и для разработки их теории. Математически они выражаются суммами (200), в которых rk означает расстояние материальной частицы от полюса или плоскости. У полярных моментов инерции индекс справа внизу означает полюс, индекс у момента инерции относительно плоскости обычно состоит из двух букв, означающих эту плоскость, причем между буквами не ставят точки в отличие от центробежных моментов инерции (205).
В прямоугольных координатах моменты инерции тела относительно начала и координатных плоскостей выражают суммами:
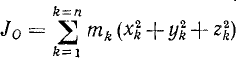
и
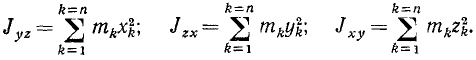
Складывая три момента инерции относительно координатных плоскостей (209), получим момент инерции относительно начала координат (208). Аналогично, складывая три момента инерции относительно координатных осей (194), получим удвоенный момент инерции относительно начала координат, следовательно:
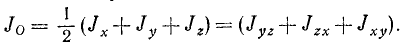
Обратим внимание на то, что равенство (210) остается справедливым независимо от направления осей координат.
Примеры вычисления моментов инерции
Задача №8
Определить момент инерции тонкого однородного прямолинейного стержня длины l относительно оси, перпендикулярной стержню в его конце. Вычисления провести с различной точностью: сосредоточив массу m стержня в двух точках, в четырех точках, в восьми точках и учитывая, что масса распределена по стержню непрерывно и равномерно.
Решение. 1) Разделим мысленно стержень на две равные части и массу каждой половины сосредоточим в ее середине (рис. 196, а). Момент инерции стержня подсчитаем по (200) как момент инерции неизменяемой системы двух материальных точек:
Рис. 196
2) Разделим мысленно стержень на четыре равные части, массу каждой части будем считать сосредоточенной в ее центре (рис. 196,6). Момент инерции стержня подсчитаем по той же формуле (200), для системы четырех материальных точек:
3) Разделим мысленно стержень на восемь частей и массу 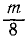
4) Чем на большее число частей мы разбивали стержень, тем меньше оказывалась масса каждой части. Разобьем стержень на бесконечно большое число бесконечно малых отрезков длины dx каждый (рис. 196, г). Чтобы подсчитать массу такого отрезка надо помножить его длину на массу единицы длины 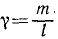
распространенный по всей массе стержня:
Ответ.
Задача №9
Вычислить момент инерции однородного тонкого круглого диска относительно оси, перпендикулярной к плоскости диска в его центре.
Решение. Если плотность диска (массу единицы его поверхности) обозначим через γ, то масса диска
откуда, дифференцируя,
Подставляем в (200′)
Ответ. Момент инерции диска относительно оси, перпендикулярной к диску в его центре, равен половине произведения массы диска на квадрат его радиуса.
Задача №10
Определить момент инерции однородного круглого цилиндра относительно его оси.
Решение. Поступая, как и в предыдущей задаче, будем иметь:
Ответ. Момент инерции цилиндра относительно его оси равен половине произведения массы цилиндра на квадрат его радиуса.
Задача №11
Определить момент инерции однородного круглого цилиндра относительно образующей.
Решение. По теореме о параллельных осях имеем
Ответ. Момент инерции цилиндра относительно образующей равен трем вторым произведения массы цилиндра на квадрат его радиуса.
Задача №12
Определить радиус инерции цилиндра относительно его оси.
Решение. Подставляя в (201) данные цилиндра, находим
Ответ. Радиус инерции цилиндра равен 0,707 его радиуса.
Задача №13
Вычислить момент инерции диска относительно диаметра.
Решение. Построим в центре диска оси координат, направив ось Oz перпендикулярно к его плоскости. Тогда, по теореме о плоской фигуре (207),
Jz = Jx + Jy
Так как моменты инерции однородного диска относительно каждого его диаметра одинаковы, то Jx = Jy.
Известно, что 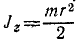
Ответ. Момент инерции диска относительно диаметра равен одной четверти произведения массы диска на квадрат его радиуса.
Задача №14
Вычислить момент инерции диска относительно касательной.
Решение. Моменты инерции диска относительно каждого из его диаметров одинаковы. Для решения задачи применим теорему о параллельных осях, выбрав диаметр, параллельный касательной:
Ответ. Момент инерции диска относительно касательной равен пяти четвертым произведения массы диска на квадрат его радиуса.
Задача №15
Вычислить момент инерции прямого тонкого стержня длины l относительно оси, перпендикулярной к стержню в его середине.
Решение. Обозначим массу единицы длины стержня у. Тогда масса стержня m=γl, дифференциал массы dm = γdl и момент инерции по (200′)
Тот же момент инерции можно получить, применив формулу (202) о моментах инерции тела относительно параллельных осей. Момент инерции стержня относительно оси, перпендикулярной к нему в его конце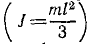
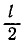
искомый момент инерции стержня относительно центральной оси
Ответ. Момент инерции тонкого стержня относительно оси, перпендикулярной к стержню в его середине, равен одной двенадцатой произведения массы стержня на квадрат его длины.
Задача №16
Определить радиус инерции тонкого стержня длины I относительно оси, перпендикулярной к стержню в его конце.
Решение. Момент инерции тонкого стержня относительно оси, перпендикулярной к стержню в его конце 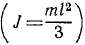
Для вычисления радиуса инерции нам остается только воспользоваться формулой (201):
Ответ. Радиус инерции тонкого стержня относительно оси, перпендикулярной к стержню в его конце, равен 0,577 его длины.
Экспериментальное определение моментов инерции
Задача №17
Для определения моментов инерции твердых тел применяют прибор (рис. 197), идея которого заключается в следующем. Горизонтальная стрелка F жестко скреплена с вертикальным цилиндром В и может вращаться вместе с ним почти без трения вокруг оси цилиндра. На цилиндре имеется винтовая резьба с большим шагом, по которой может перемещаться массивный диск А. Для определения момента инерции испытуемое тело D закрепили на цилиндре В, затем подняли диск А до наибольшей высоты и предоставили его действию силы тяжести. Опускаясь, диск повернулся по ходу часовой стрелки на некоторый угол φ, а тело D вместе с цилиндром В и стрелкой F повернулось при этом против хода часовой стрелки на угол φ1, отмеченный стрелкой F прибора. Определить момент инерции Jo тела D относительно оси CC2, если момент инерции диска равен Ja, а момент инерции стрелки F с цилиндром В равен Jβ.
Решение. Рассмотрим движение системы, состоящей из 1) диска А, 2) стрелки F, жестко соединенной с цилиндром В и представляющей с ним одно неразрывное целое, и 3) испытуемого тела D. Механическое движение диска передается другим телам системы в виде механического же движения. Тела совершают вращения вокруг оси н для решения задачи удобно воспользоваться теоремой (192) моментов системы относительно оси. На точки системы действуют только вертикальные внешние силы — веса тел и реакция в опоре С. Внешнее трение отсутствует. Трение между диском А и цилиндром В, возникающее при движении диска по винтовой резьбе, является внутренней силой и потому не входит в уравнение моментов. Моменты внешних сил относительно оси CC1 равны нулю, и мы можем написать уравнение (193)
Рис. 197
В начале движения моменты количества движения всех входящих в систему тел были равны нулю, следовательно, C1=O.
Момент количества движения вращающегося тела можно выразить через произведение момента инерции на угловую скорость тела и, раскрывая знак суммы, получим
где ω—угловая скорость диска, a ω1 — угловая скорость цилиндра. Интегрируем уравнение, принимая во внимание начальные условия:
Для конца движения к этому уравнению добавляем еще уравнение
φ1-φ = n,
где п зависит от геометрических параметров прибора.
Исключая из этих уравнений угол φ, получаем формулу
из которой можно определить момент инерции испытуемого тела, если угол φ1 найден при наблюдении за движением стрелки F.
Ответ.
Задача №18
Для определения момента инерции шатун подвесили на горизонтальную призму (рис. 198). Через ту же призму перекинули тонкую нить, на одном конце которой висел небольшой грузик, а другой натягивали рукой. Отклонив шатун и грузик из равновесного положения, заставили их свободно качаться в параллельных плоскостях. Изменяя длину нити между призмой и грузом, добились того, что период качания грузика стал в точности равен периоду качания шатуна. Определить момент инерции шатуна относительно оси подвеса, если масса шатуна т = 40,0 кг, расстояние центра тяжести шатуна от оси подвеса C = 75,0 см и длина нити Z = 107,9 см.
Рис. 198
Решение. Принимая груз на нити за математический маятник, применим для решения формулу (199) приведенной длины физического маятника
J = mcl,
или
J = 40 • 75• 107,9 = 323 700 кг• см2 = 32,37 кг• м2
При этом способе экспериментального определения моментов инерции амплитуда колебаний не ограничена, так как формула (199) справедлива для колебаний физического и математического маятников с любыми одинаковыми амплитудами.
Ответ. J = 32,37 кг• м2
Задача №19
Для измерения момента трения Mτp в подшипниках махового колеса проделали следующий опыт. Маховое колесо обмотали цепью (рис. 199), оба конца которой во все время опыта лежали на полу. К цепи в точке А при вязали гирю весом G1 и, предоставив ей опускаться с высоты h, измерили время t1 опускания. Затем опыт повторили, заменив гирю G1 гирей G2, которая опустилась с той же высоты за время t2. Вычислить момент трения в подшипниках махового колеса, считая его постоянным и не зависящим от веса гирь и цепи.
Рис. 199
Решение. Применим теорему моментов к системе, состоящей из махового колеса, цепи и груза.
Внешними силами системы являются вес махового колеса, идеальная реакция подшипников, трение в подшипниках, вес гири и той части цепи, которая не лежит на полу, так как лежащие на полу концы цепи уравновешены реакцией пола.
Главный момент внешних сил относительно оси колеса при первом эксперименте был
Кинетический момент системы относительно оси равнялся алгебраической сумме моментов количеств движения всех входящих в систему тел:
где J — момент инерции маховика; P — вес той части цепи, которая не лежит на полу, ω-угловая скорость и r — радиус махового колеса.
По теореме моментов
Разделяя переменные и интегрируя, найдем
В начальное мгновение t = 0 и ω = 0, следовательно C1=O. Выразим ω как 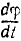
Из начальных данных определим C2=O. При опускании груза с высоты h маховое колесо повернулось за время t1 на угол φ1 = 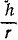
Если в этом уравнении имеются две неизвестные величины (MTp и J), то из второго опыта получим второе уравнение:
Решая оба уравнения совместно, получим ответ задачи.
Ответ.
Задача №20
C какой скоростью следовало бы пустить по экватору с запада на восток поезд, масса которого 2000 т, для того чтобы увеличить продолжительность суток на одну секунду? При этом Землю можно считать за однородный шар радиуса 6000 км и массы 5∙ IO21 т (И. В. Мещерский. Сборник зада* по теоретической механике. ГТТИ, 1932, стр. 135).
Решение. Земля вращалась вокруг своей оси, имея на поверхности (относительно) неподвижный поезд. Она совершала один оборот за 86 400 сек. По Земле с запада на восток пустили поезд с искомой относительной скоростью υr. Поезд двигался вперед, отталкиваясь силой трения и с такой же силой (по закону равенства действия и противодействия) отталкивая Землю. Механическое движение поезда передалось Земле в качестве механического же движения, угловая скорость Земли уменьшилась, и Земля стала делать один оборот за 86 401 сек. Ввиду того что переход механического движения от одного тела к другому связан с вращением, применим теорему моментов для системы, понимая под системой Землю и поезд. Примем физическую систему единиц.
Внешние силы системы (притяжение Солнца, Лупы и др.) приложены к центру Земли, и моменты внешних сил относительно земной оси равны нулю. Мы пришли к интегралу моментов (193):
Определим значения величин, входящих в это равенство. Рассмотрим механическую систему до начала движения поезда. Момент количества движения Земли относительно оси вращения равен произведению момента инерции Земли на ее угловую скорость. Землю примем за однородный шар. Момент инерции шара J=0,4mr3. Подставляя числовые значения, получим
Поезд был неподвижен относительно Земли, но он участвовал в ее движении. Скорость его υe = ωr; количество движения m2υe, момент количества движения
Находим постоянную С:
Рассмотрим теперь ту же систему после того, как поезд развил скорость vr и продолжительность суток стала 86 401 сек. Момент количества движения Земли уменьшился вследствие уменьшения угловой скорости и стал
Момент количества движения поезда увеличился, так как поезд, кроме переносной скорости (несколько уменьшившейся), получил значительную относительную скорость. Мы рассматриваем абсолютное движение точек системы и
Действие внутренних сил не изменило главного момента количества движения системы, и мы приравниваем друг другу суммы моментов количеств движения системы до начала и во время движения поезда:
Из этого уравнения первой степени определяем υr. Оказывается, что для увеличения продолжительности суток на 1 сек поезд массой 2000 т нужно было бы пустить со скоростью, в 17 миллионов раз превосходящей скорость света. Этот поезд должен был бы совершать по экватору 118 миллионов кругосветных путешествий за каждую секунду.
Ответ. υr = 5,05∙ 1012 км/ceκ.
Центр удара
Задача №21
В плоскости, проведенной через центр масс C и ось вращения тела, найти такую точку, через которую должен проходить перпепдикулярный к этой плоскости мгновенный импульс, чтобы ось вращения не испытывала удара.
Решение. Для определения этой точки, называемой центром удара, рассмотрим ударные силы, действующие на тело во время удара. Приложенный к телу ударный импульс 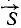
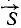
где m — масса тела, υ1 и υ2— скорости центра масс до и после удара, J — момент инерции тела относительно оси вращения, ω1 и ω2 — угловая скорость тела и l—плечо импульса S.
Рис. 200
В данном случае
Подставляя эти значения скоростей, определим импульс ударной реакции:
Эти равенства показывают, что прн
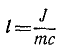
ось вращения не испытывает ударов. Полученная формула, определяющая при рассмотренных условиях центр удара, имеет большое значение при конструировании различных машин вращающиеся детали которых подвергаются ударам.
Обратим внимание на тождественность полученного равенства с (199), определяющим центр качания физического маятника, хотя, вообще говоря, центр качания и центр удара отличаются друг от друга и совпадают лишь в отдельных случаях.
Задача №22
Валы I и II вместе с насаженными на них шкивами и зубчатыми колесами (рис. 201) имеют моменты инерции, соответственно равные: J1=500 κΓ . см . сек2 и J2= 400 кГ∙cM∙ceκ2, передаточное число зубчатой передачи kl2 = 2∕3. Через сколько оборотов вал II будет делать n2 = 120 об/мин, если система приводится в движение из состояния покоя вращающим моментом Ml = 50κΓ∙м приложенным к валу l? Трением в подшипниках пренебречь.
Решение. За единицы принимаем м, кГ и сек. Тогда J1 = 5 кГ . м . сек2, J2 = 4 кГ∙M∙ceκ2, M1 = 50κΓ . м, начальные угловые скорости ω1,0=ω2,0=0, конечные угловые скорости
Задачу решим, применив дифференциальное уравнение вращения твердого тела. Сначала рассмотрим. вращение вала I вокруг оси I — I . На вал действуют вращающий момент M1=+50 и сила F сопротивления вала II, момент κoторой равен -Fr1
или
В нашем случае ωo = 0 и
Затем переходим к рассмотрению вращения вала II вокруг оси II — II. На второй вал действует сила F давления зубьев первого вала. Ее момент равен + Fr2, поэтому
Решаем оба уравнения совместно:
Под действием постоянного момента второй вал вращается равноускоренно:
За время t II вал сделал оборотов
Ответ.
Скорость конца вектора кинетического момента относительно некоторой точки равна главному моменту всех внешних сил относительно этой точки
Теорема Резаля—Гейуорда
Пусть гироскоп 2 (рис. 202, а) (волчок) имеет ось симметрии 3. Допустим, что главный момент, количеств движения волчка направлен по оси симметрии. Если бы ось была неподвижной. то такое направление кинетического момента было бы очевидным. Но основным свойством всякого гироскопа является способность быстро вращаться вокруг оси при одновременном поворачивании оси вращения. Если угловая скорость ω гироскопа вокруг его оси очень велика, а угловая скорость ωx, с которой поворачивается ось гироскопа, невелика, то с достаточной точностью можно допустить, что главный момент количеств движения гироскопа относительно точки опоры О направлен по оси симметрии и равен произведению угловой скорости на момент инерции гироскопа относительно оси симметрии:
Lo = Jω.
Построим систему координатных осей хОуz с началом в точке О (рис. 202, б) и отложим вдоль оси симметрии вектор OA=Lo в такую сторону, чтобы вращение гироскопа представлялось происходящим против хода часов, если смотреть от А к О.
Рис. 202
Проекции вектора 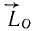
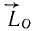
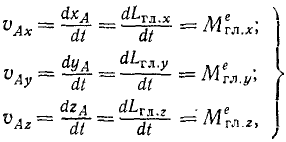
или в векторной форме
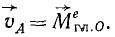
На примере гироскопа мы доказали теорему Резаля: скорость конца вектора главного момента количеств движения, взятого относительно точки О, равна главному моменту всех внешних сил системы относительно той же точки.
Прецессия оси гироскопа
Задача №23
Волчок вращается вокруг своей осн против часовой стрелки с постоянной угловой скоростью ω = 600 ceκ-1; ось OA наклонена к вертикали; нижний конец оси OA остается неподвижным; центр тяжести C волчка находится на оси OA на расстоянии ОС = 30 см от точки О; радиус инерции волчка относительно оси равен 10 см. Определить движение осн OA волчка, допуская, что при весьма большой угловой скорости ω главный момент количества движения волчка направлен по оси ОА и равен Jω.
Решение. Применим к решению данной задачи теорему Резаля. Определим главный момент внешних сил относительно точки О. Внешними силами являются вес гироскопа и реакция в точке О (рис. 202, в). Главный момент внешних сил относительно точки О направлен перпендикулярно к вертикальной плоскости, проходящей через ОС, и равен произведению веса mg на плечо СО . sin 
причем скорость υА перпендикулярна к вертикальной плоскости, содержащей в себе ось симметрии гироскопа. Так как точка А принадлежит этой оси, то движение точки А определяет движение оси гироскопа. Ось симметрии гироскопа перемещается в направлении, перпендикулярном направлению действия внешней силы (силы тяжести), и описывает коническую поверхности. Это движение оси гироскопа называют прецессией. Точка А описывает окружность радиуса Jω sin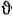
Следовательно, ось гироскопа вращается вокруг оси Oz с угловой скоростью
Ответ. Ось OA вращается вокруг вертикали против часовой стрелки, описывая круглый конус с постоянной угловой скоростью ω=0,49 сек-1.
Гироскопический эффект
Рассмотрим некоторые особенности движения гироскопа. Пусть быстровращающийся ротор установлен в кардановом подвесе (рис. 203). Он может вращаться с большой угловой скоростью ω вокруг оси OO1, в то время как эта ось вместе с рамой I может поворачиваться вокруг оси KK1 и вместе с рамой II вокруг оси NN1. Это гироскоп с тремя степенями свободы. Он имеет одну неподвижную точку C (центр масс).
Рис. 203
Если гироскоп не вращается (ω = 0), то, приложив к внутренней раме l (например, в точке О) силу F, мы сообщим раме (и вместе с нею ротору гироскопа) вращение вокруг оси KK1 в том направлении, в каком действует сила. Причем, во время действия силы (пока 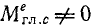
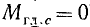
Совсем иначе подействует та же сила на гироскоп, вращающийся вокруг оси симметрии с большой угловой скоростью ω. Отложим вдоль оси OO1 вектор кинетического момента L=Jω=CA. По теореме Резаля точка А на время действия силы получит скорость, равную моменту этой силы 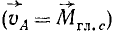
Гироскопы с двумя степенями свободы этим свойством не обладают, так как, отняв у гироскопа одну степень свободы, например, закрепив вторую раму, мы лишим ось ротора возможности перемещаться в направлении, перпендикулярном к направлению приложенной силы. От дополнительного давления гироскопа на подшипники К и K1 возникает пара сил с моментом
M = Jωω1. (213)
Этот момент носит название гироскопического момента, а его появление называют гироскопическим эффектом. Если угол tt, заключенный между осью ротора и той осью, вокруг которой она вращается, не прямой, то гироскопический момент
M = Jωω1 sin 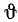
Задача №24
Определить максимальное гироскопическое давление на подшипники быстроходной турбины, установленной на корабле. Корабль подвержен килевой качке с амплитудой 9° и периодом 15 сек вокруг горизонтальной оси, перпендикулярной к оси ротора. Ротор турбины весом 3500 кГ с радиусом инерции 0,6 м делает 3000 об/мин. Расстояние между подшипниками 2 .ч.
Решение. Гироскопический момент определим по (213), так как угловые скорости взаимно перпендикулярны. Все необходимые данные имеются в условии задачи:
- момент инерции ротора
- угловая скорость ротора
Для вычисления угловой скорости ω1 оси ротора примем во внимание, что килевая качка в условии задачи задана гармонической, с угловой амплитудой 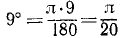
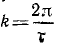
дифференцируя определим угловую скорость качки
Максимальное значение этой угловой скорости примем за ω1;
Рис. 204
Тогда по (213) гироскопический момент
Для определения давления на подшипники остается лишь поделить гироскопический момент на расстояние 2 м между подшипниками.
Ответ. 1320 кГ.
Уравновешивание вращающегося тела
Задача №25
Определить реакции в подпятнике А и в подшипнике В твердого тела (рис. 205), вращающегося вокруг неподвижной оси AB с угловой скоростью ω и с угловым ускорениемε, и найти такую ось, при вращении тела вокруг которой эти реакции не зависят от ω и ε. Заданными являются все внешние активные силы 
Рис. 205
Решение. Кроме активных сил, на тело действуют искомые реакции RA и RB. Построим оси координат, взяв начало в подпятнике, и, направив ось аппликат по оси вращения, спроецируем реакции на оси.
Представим тело как неизменяемую систему, состоящую из n частиц, и напишем уравнения (169)’ количества движения и уравнения моментов (192), учитывая, что проекции скоростей точек тела на ось вращения равны нулю (υz = Q), а последнее из уравнений (192) моментов относительно оси вращения превращается в уравнение (196):
Как видно из третьего уравнения, проекция реакции подпятника на ось вращения не зависит от cкорости и равна проекции внешних активных сил на ту же ось:
Шестое уравнение является дифференциальным уравнением вращения тела и не содержит реакций опор. Выполняя дифференцирование в четырех остальных уравнениях, получим:
Подставляя вместо akx и аkу их значения (95)
и вынося общие множители ε и ω2 за знак получим:
Из этих уравнений найдем четыре неизвестные проекции реакций. Заметим, что суммы, стоящие в левых частях первых двух из этих уравнений, являются статическими моментами:
а суммы, стоящие в левых частях двух последних уравнений
являются центробежными моментами инерции тела. Четыре полученных нами уравнения можно переписать в следующем виде:
Чтобы реакции в опорах вращающегося тела не зависели от ω и ε (или, что то же, от скоростей его точек), необходимо и достаточно выполнение следующих условий:
Вращающееся тело, реакции в опорах которого не зависят от скоростей точек тела, называют полностью уравновешенным телом.
Если выполнены два первых условия, т. е. ось вращения проходит через центр масс («центральная ось»), то тело называют статически уравновешенным.
Если выполнены два последних условия, то вращающееся тело называют динамически уравновешенным, а ось — главной осью инерции
Ответ. Для полной уравновешенности вращающегося тела необходимой достаточно, чтобы оно вращалось вокруг центральной и главной оси инерции.
Кинетическая энергия материальной точки, системы и твердого тела
Кинетической энергией называют меру механического движения, выражающуюся половиной суммы произведений массы каждой частицы материальной системы на квадрат ее скорости:
Кинетическая энергия
Ознакомившись в двух предыдущих главах с одной из мер механического движения, перейдем теперь к другой мере—кинетической энергии, которая наряду с количеством движения существует во всяком движущемся материальном теле. Кинетическая энергия каждой материальной точки выражается половиной произведения массы точки на квадрат ее скорости:
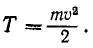
Чтобы получить кинетическую энергию системы, надо взять сумму кинетических энергий всех ее точек. Сумму надо брать, конечно, арифметическую, потому что, как видно из (214), кинетическая энергия есть величина скалярная и всегда положительная:
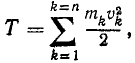
или
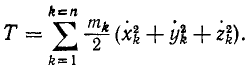
Размерность кинетической энергии в физической системе единиц
в технической системе единиц
Обе меры механического движения (количество движения и кинетическая энергия), как это уже было сказано в гл. XIII, не противоречат одна другой, но каждая из них является мерой для определенного круга явлений. Количество движения характеризует способность механического движения передаваться от одних материальных частиц другим в виде механического же движения, а кинетическая энергия характеризует способность механического движения превращаться в эквивалентное количество другого движения (в потенциальную энергию, в теплоту и пр.).
Так, например, во время удара движущегося биллиардного шара по неподвижному шару часть механического движения перешла от ударяющего шара к ударяемому и ударяемый получил некоторую скорость. Мерой этого переданного механического движения является количество движения. От удара количество движения системы двух шаров не изменилось, потому что внутренняя сила не изменяет количества движения в системе. Вместе с тем часть механического движения шара во время удара перешла в другие виды движения (в звук, теплоту), и мерой этого движения является кинетическая энергия. Часть кинетической энергии ударяющего шара была потеряна системой, перешла в другие виды движения, кинетическая энергия системы от удара уменьшилась.
Отсюда не следует делать вывод, что уравнения проекций количеств движения (169) и уравнения моментов количеств движения (192), а также уравнение кинетической энергии (230), которое будет доказано в этой главе, не имеют всеобщего применения, а законны лишь в отдельных частных случаях. Они выведены математически вполне строго из дифференциальных уравнений движения и носят название семи всеобщих уравнений движения. В зависимости от условий задачи приходится решать, каким из этих уравнений удобнее воспользоваться. При этом полезно иметь в виду, что если проекции силы являются функциями времени, то часто бывает возможно проинтегрировать уравнения (169). Уравнение кинетической энергии дает интеграл в тех случаях, когда силы являются функциями расстояния. Этим часто определяется выбор того или другого уравнения для решения задачи.
Выяснив физический смысл и математическое выражение кинетической энергии, резюмируем все сказанное о ней: кинетической энергией называется мера механического движения, характеризующая его способность превращаться в эквивалентное количество другого вида движения и выражающаяся половиной суммы произведений массы каждой материальной частицы механической системы на квадрат ее скорости.
В случаях движения неизменяемой механической системы (твердого тела) выражению (215) можно придать вид, более удобный для вычисления.
Кинетическая энергия поступательно движущегося тела, как и кинетическая энергия материальной точки, выражаются половиной произведения массы на квадрат скорости:
Кинетическая энергия поступательно движущегося тела
Скорости всех частив поступательно движущегося тела между собой равны (80), поэтому если твердое тело совершает поступательное движение, то в формуле (215) кинетической энергии квадрат скорости как общий множитель выходит за знак суммы:
где k= 1, 2, 3, …, п.
Сумма масс всех частиц тела равна массе m всего тела и
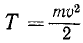
Таким образом, кинетическая энергия поступательно движущегося тела, как и кинетическая энергия материальной точки, равна половине произведения массы тела на квадрат скорости любой из его частиц.
Кинетическая энергия вращающегося тела равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости:
Кинетическая энергия вращающегося тела. Скорости частиц вращающегося твердого тела пропорциональны угловой скорости тела и расстояниям частиц от оси вращения:
υk = ωrk. (90)
Возводя это равенство в квадрат и подставляя в (215), получим
Вынося общий множитель 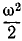
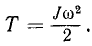
Таким образом, кинетическая энергия вращающегося тела равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости.
Эта формула применима не только в случае вращения тела вокруг неподвижной оси, но и вокруг мгновенной оси. В случае плоского движения момент инерции фигуры или тела в формуле (216) надо подсчитывать относительно оси, проходящей через мгновенный центр скоростей, перпендикулярно плоскости движения, тогда
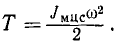
Кинетическая энергия твердого тела равна кинетической энергии его центра масс, в котором предполагается сосредоточенной масса всего тела, плюс кинетическая энергия тела в его вращательном движении вокруг оси, проходящей через центр масс тела:
Формула Кёнига
Выведем формулу для определения кинетической энергии твердого тела, совершающего плоское движение. Для определения проекций скорости были выведены формулы
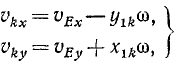
где x1k и y1k — координаты каждой точки тела относительно системы координатных осей, параллельных неподвижным осям, но имеющих начало в произвольной точке Е, принятой за полюс.
Возводя эти равенства в квадрат и складывая, найдем квадрат полной скорости любой точки тела:
Подставляя затем в (215), найдем
Разобьем эту сумму на четыре части и вынесем за знаки 
Здесь
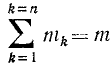
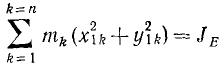
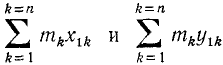
Если за полюс принять центр масс C тела, то последние два члена обращаются в нуль (x1,С = 0, y1,С = 0) и кинетическая энергия получает простое выражение
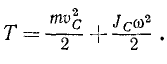
Эта формула доказана нами для плоского движения твердого тела. Она имеет большое применение в различных областях механики и, в частности, в теории механизмов и машин, где плоское движение встречается очень часто. Но формула (217) остается справедливой при всяком движении твердого тела. Словами ее можно прочитать так: кинетическая энергия твердого тела равна кинетической энергии материальной точки, обладающей массой всего тела и скоростью центра масс, плюс кинетическая энергия тела в его вращательном движении вокруг оси, проходящей через центр масс.
При разложении движения в кинематике мы могли принимать за полюс любую точку тела. При определении кинетической энергии по формуле (217) мы обязаны принимать за полюс только центр масс тела, иначе появятся члены, содержащие статические моменты масс.
Задача №26
Определить кинетическую энергию диска массы m = 10 кг и радиуса ∙ R = 0,5 м, катящегося со скоростью υС= 2 м/сек по прямолинейному рельсу без скольжения.
Решение. Задачу решим пока двумя различными способами (система единиц физическая).
1-й способ. Мгновенный центр скоростей находится в точке касания (рис. 206, а). Угловая скорость диска
Момент инерции диска относительно оси, проходящей через мгновенный центр скоростей перпендикулярно диску, определим по теореме о параллельных осях:
Кинетическую энергию диска определим по (216′):
Рис. 206
2-й способ. Кинетическую энергию определяем по формуле (217) Кёнига (рис. 206, б):
Теорема Коши
Однако существуют и некоторые другие определенные точки, которыми в формуле (217) можно заменить центр масс С. Найдем эти точки.
В общем случае движения тела скорости его частиц можно рассматривать (см. § 35) как состоящие из двух взаимно перпендикулярных скоростей: переносной скорости ve, направленной по мгновенной винтовой оси, и относительной, вращательной вокруг этой оси (рис. 207, а). Квадрат скорости какой-либо точки К, отстоящей на расстоянии rk от мгновенной винтовой оси:
Подставим это выражение в (215):
Момент инерции тела относительно мгновенной винтовой оси обозначим через JE, тогда
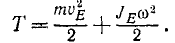
Проведем через центр масс C ось параллельно мгновенной винтовой оси. Если расстояние между этими осями равно cl, то, выразив JE по (202), получим
Но 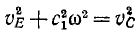
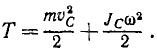
Проведем через какую-либо точку А третью ось AA (рис. 207, б) параллельно двум предыдущим, обозначим через JА момент инерции
Рис. 207
тела относительно этой оси, через с2—расстояние ее от центральной оси, а через с3—от мгновенной винтовой оси. Согласно (203)
подставим в (217′):
В случае, если плоскость, проведенная через эту ось AA и мгновенную винтовую ось, составляет с плоскостью, проведенной через эту ось AA и центр масс C тела, прямой угол (α = 90O), то по пифагоровой теореме 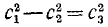
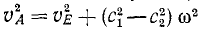
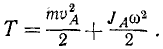
Если же α≠90o, то это равенство не выполняется.
Для определения кинетической энергии твердого тела этим способом надо провести через центр масс тела ось, параллельную мгновенной винтовой оси (рис. 207, в). Приняв обе оси за диаметрально противоположные образующие, построить на них поверхность прямого круглого цилиндра. Во всякое мгновение кинетическая энергия тела равна половине произведения массы тела на квадрат скорости любой из точек этой цилиндрической поверхности, сложенной с половиной произведения момента инерции тела относительно образующей, проходящей через эту точку, на квадрат угловой скорости тела.
Задача №27
Решить задачу № 26, применив теорему Коши.
Решение. Мгновенная винтовая ось существует в общем случае движения тела. При плоском движении она превращается в мгновенную ось вращения, проходящую через мгновенный центр скоростей перпендикулярно плоскости движения. Построенная на мгновенной винтовой оси цилиндрическая поверхность, о которой говорится в теореме Коши, в пересечении с плоскостью движения фигуры образует окружность, у которой мгновенный центр скоростей и центр масс фигуры являются диаметрально противоположными точками (см. рис. 206, в).
Возьмем на этой окружности какую-либо точку А. Ее скорость
Момент инерции диска относительно оси, перпендикулярной к его плоскости в точке А, определим по (202):
Полная кинетическая энергия диска
Если взять какую-либо точку, не лежащую на окружности, нанесенной на чертеже пунктиром (см. рис. 206, в), то полусумма произведений массы диска на квадрат скорости этой точки и момента инерции диска относительно проходящей через эту точку оси на квадрат угловой скорости диска не будет равна кинетической энергии’диска. Так, например, для точки В
Ответ. Кинетическая энергия диска T-=30κг∙м2∕ceκ2.
Задача №28
Определить кинетическую энергию эллипсографа.
Решение. Механическая система состоит из четырех тел: кривошипа, линейки и двух ползунов. Чтобы определить кинетическую энергию этих тел, найдем сначала скорости.
Эллипсограф является плоским механизмом: все звенья его совершают плоские движения. Угловая скорость кривошипа дана. Скорость пальца равна ωl. Эта же точка принадлежит и линейке эллипсографа. Известны направления скоростей трех точек линейки. Перпендикуляры, восставленные в этих точках к направлениям их скоростей, пересекаются в мгновенном центре скоростей Eмсц (рис. 208). Определяем угловую скорость линейки вокруг мгновенного центра скоростей. Для этого делим линейную скорость пальца на его расстояние от мгновенного центра скоростей:
Рис. 208
Следовательно, угловая скорость линейки вокруг мгновенного центра скоростей равна угловой скорости кривошипа вокруг оси О. Для определения кинетической энергии линейки нам надо знать угловую скорость линейки вокруг оси, проходящей перпендикулярно к плоскости движения в центре масс. Напомним, что угловая скорость не зависит от выбора полюса, а потому искомая угловая скорость равна найденной угловой скорости относительно мгновенного центра скоростей.
Чтобы определить скорости точек А и В линейки, надо умножить угловую скорость линейки на расстояние этих точек от мгновенного центра скоростей. Если обозначим через φ угол поворота кривошипа, то
Кинетическую энергию кривошипа определим по формуле (216) как энергию вращающегося тела:
Кинетическую энергию линейки определим по формуле (217) Кёнига:
Кинетическую энергию поступательно движущихся ползунов определим по (215):
Кинетическая энергия механизма равна арифметической сумме кинетических энергий его звеньев:
Ответ.
Задача №29
Определить кинетическую энергию планетарного механизма (рис. 209). Рукоятка O1O3 массы mи длины 4r вращается с угловой скоростью ω вокруг неподвижной оси O1, проходящей через центр неподвижного зубчатого колеса I. На рукоятке свободно насажены два зубчатых колеса радиуса r и массы m каждый.
Рис. 209
Решение. Система состоит из рукоятки и двух зубчатых колес (II и III), Кинетическая энергия системы равна сумме кинетических энергий этих тел. Кинетическую энергию рукоятки определим по (216), приняв рукоятку за однородный стержень:
Кинетическую энергию среднего колеса определим по формуле (217) Кёнига, считая зубчатое колесо круглым диском. Скорость центра O2 диска II
потому что эта точка принадлежит и рукоятке, вращающейся вокруг O1. Мгновенный центр скоростей этого диска находится в точке касания его с неподвижным зубчатым колесом l. Угловую скорость среднего диска найдем, поделив υO2 на расстояние от O2 до мгновенного центра скоростей:
Тогда
Эту же величину можно определить по (216′), считая, что колесо вращается вокруг мгновенного центра скоростей; в таком случае момент инерции колеса относительно осн вращения надо подсчитать по теореме о параллельных осях 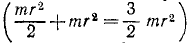
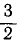
Чтобы определить угловую скорость крайнего колеса, найдем скорость точки касания его со средним колесом. Скорости точек среднего колеса определим как вращательные вокруг мгновенного центра скоростей. Таким образом, точка касания обоих подвижных колес движется со скоростью ω22r = 4ωr, равной скорости O, откуда угловая скорость крайнего колеса ωз=0, следовательно, крайнее колесо совершает поступательное движение.
Кинетическая энергия крайнего зубчатого колеса
Кинетическая энергия всего механизма равна сумме кинетических энергий его звеньев
Ответ.
- Мощность и работа силы
- Потенциальная энергия
- Обобщенные координаты системы
- Сложение двух сил
- Касательное и нормальное ускорения точки
- Основные законы динамики
- Колебания материальной точки
- Количество движения
Момент количества движения точки.
В некоторых задачах в качестве динамической
характеристики движущейся точки вместо
самого количества движения рассматривают
его момент относительно какого-либо
центра или оси. Эти моменты определяются
также как и моменты силы.
М
количеством движенияматериальной
точкиотносительно
некоторого центра О называется вектор,
определяемый равенством
Момент количества движения точки
называют также кинетическим моментом.
Момент количества движенияотносительно какой-либо оси,
проходящий через центр О, равен проекции
вектора количества движенияна эту ось
.
Если количество движения
задано своими проекциями
на оси координат и даны координаты
точки
в пространстве, то момент количества
движенияотносительно начала координат вычисляется
следующим образом:
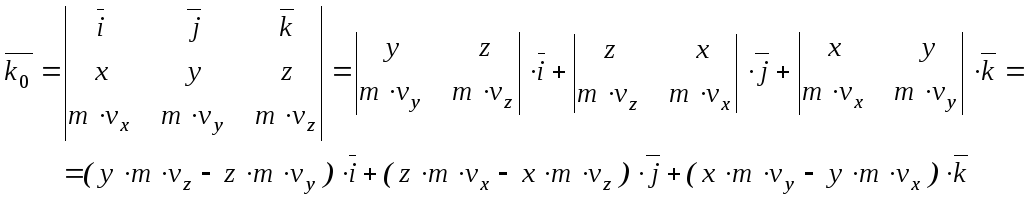
момента количества движенияна
оси координат равны:
Единицей измерения количества движения
в СИ является –
.
Теорема об изменении момента количества движения точки.
Теорема.Производная по времени
от момента количества движения точки,
взятого относительно какого-нибудь
центра, равна моменту действующей на
точку силы относительно того же центра.
Доказательство: Продифференцируем
момент количества движения по времени
,
,
следовательно,
(*)
что и требовалось доказать.
Теорема.Производная по времени
от момента количества движения точки,
взятого относительно какой-либо оси,
равна моменту действующей на точку силы
относительно той же оси.
Для доказательства достаточно
спроектировать векторное уравнение
(*) на эту ось. Для оси
это
будет выглядеть так:
Следствия из теорем:
1. Если момент силы относительно точки
равен нулю, то момент количества движения
относительно этой точки величина
постоянная.
,
2. Если момент силы относительно оси
равен нулю, то момент количества движения
относительно этой оси величина постоянная.
,
Приложение общих теорем к динамике твердого тела
Количеством движениясистемы
материальных точекназывается векторная сумма количеств
движений отдельных точек системы.
Единицей измерения количества движения
в СИ является –
Количество движения системы можно
выразить через массу системы и скорость
центра масс.
Теорема об изменении количества движения системы.
Эта теорема существует в трех различных
формах.
Теорема.Производная по времени
от количества движения системы равна
векторной сумме всех внешних сил,
действующих на систему.
,
(6.1)
Доказательство: Теорема об изменении
количества движения для
точки
имеет вид:
,
Сложим все
уравнений и получим:
,
что и требовалось доказать.
В проекциях на оси координат это
утверждение выглядит так:
,
,
.
Теорема.(в дифференциальной
форме).Дифференциал от количества
движения системы равен сумме элементарных
импульсов всех внешних сил, действующих
на систему.
Умножим левую и правую части уравнения
(6.1) на
и
получим
,
(6.2)
В проекциях на оси координат это
утверждение выглядит так:
,
,
.
Теорема (в интегральной форме).Изменение количества движения системы
за какой-либо промежуток времени равно
векторной сумме элементарных импульсов
всех внешних сил, действующих на систему
за этот же промежуток времени.
Интегрируя обе части уравнения (**) по
времени в пределах от нуля до
получаем:
В проекциях на оси координат это
утверждение выглядит так:
,
,
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Момент импульса | |
|---|---|
 |
|
| Размерность | L2MT−1 |
| Единицы измерения | |
| СИ | м2·кг/с |
| СГС | см2·г/с |
| Примечания | |
| псевдовектор |
Моме́нт и́мпульса (момент импульса относительно точки, также: кинетический момент, угловой момент, орбитальный момент, момент количества движения) — физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение[1].
Для одной материальной точки момент импульса равен векторному произведению радиус-вектора точки на её импульс, для системы точек — сумме таких произведений. Стандартное обозначение: 

Момент импульса замкнутой системы сохраняется. Он является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения. При наличии внешних сил производная момента импульса по времени равна моменту сил (относительно того же начала O).
Основное использование понятия момента импульса относится к задачам, связанным с реальным вращением (особенно при наличии центральной или осевой симметрии; тогда О обычно выбирается в центре или на оси). Но величина 
В случае вращения твёрдого тела вокруг фиксированной оси часто используется не сам момент импульса, а его проекция 
Понятие момента импульса было изначально введено в классической механике, но имеет обобщения в квантовой механике и электродинамике.
Момент импульса в классической механике[править | править код]
Связь между силой F, моментом силы τ, импульсом 
Определение[править | править код]
Момент импульса 
,
где 

Из определения момента импульса следует его аддитивность: для системы, состоящей из нескольких материальных точек, выполняется
.
Количество частиц может быть бесконечным, например в случае твёрдого тела с распределённой массой.
Так как момент импульса задаётся векторным произведением, он является псевдовектором, перпендикулярным обоим векторам 

Момент импульса можно вычислить относительно любого начала отсчета O (получающиеся при этом разные значения 
Выбор точки O иногда связан с характером задачи. Так, при рассмотрении орбитального движения планеты вокруг Солнца за начало отсчёта естественно взять Солнце, а при анализе её же собственного вращения — центр этой планеты. Естественно, получатся два разных момента импульса: 

Вычисление в общем случае[править | править код]
Если имеется материальная точка массой 



.
Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки 

.
На практике 
.
Если считать, что 
Случай фиксированной оси[править | править код]
Важным случаем использования понятия «момент импульса» является движение вокруг неизменной оси. В такой ситуации часто рассматривают не сам момент импульса (псевдовектор), а его проекцию на ось как псевдоскаляр, знак которого зависит от направления вращения:
.
Параллельность-перпендикулярность (




.
Если при этом все точки тела движутся по окружностям (вращаются) с одинаковой угловой скоростью 


или
.
Величину 

Для абсолютно твёрдого тела, величина последнего интеграла называется моментом инерции относительно оси вращения и обозначается 


Сохранение момента импульса[править | править код]
Закон сохранения момента импульса: суммарный момент импульса относительно любой неподвижной точки для замкнутой системы остается постоянным со временем.
Производная момента импульса по времени есть момент силы:
,
Таким образом, требование замкнутости системы может быть ослаблено до требования равенства нулю главного (суммарного по всем частицам 
,
где 
По теореме Нётер закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол 




С учётом 


Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:
где 



Смежные понятия[править | править код]
При рассмотрении задач, связанных с вращением, фигурируют понятия, частично упоминавшиеся выше:
- момент импульса относительно оси (термин состоит из четырёх слов) — проекция момента импульса на ось;
- момент инерции твёрдого тела (см. также моменты инерции некоторых тел);
- момент силы (он же: крутящий момент, вращательный момент, вертящий момент);
- импульс момента силы
(единица измерения — Н·м·с) — мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении).
Несмотря на созвучность с «моментом импульса», эти понятия не синонимичны термину «момент импульса» и несут самостоятельный смысл.
Момент импульса в электродинамике[править | править код]
При описании движения заряженной частицы в электромагнитном поле канонический импульс 

где 



где 
Момент импульса в квантовой механике[править | править код]
Оператор момента[править | править код]
В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определёнными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на 


Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновый момент импульса всегда кратен 


В классическом определении момент импульса зависит от 6 переменных 





Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:
,
где 

,
где 
,
где 
и даже более важные подстановки с гамильтонианом частицы без заряда и спина:
.
Симметрия вращения[править | править код]
Операторы момента импульса обычно встречаются при решении задач сферической симметрии в сферических координатах. Тогда момент импульса в пространственном отображении:
Когда находят собственные значения этого оператора, получают следующее:
где 


— сферические функции.
Примечания[править | править код]
- ↑ Pivarski, Jim Spin. Symmetry Magazine (март 2013). Дата обращения: 28 апреля 2014. Архивировано 15 апреля 2014 года.
- ↑ [Информация с сайта Нобелевского комитета (англ.). Дата обращения: 3 ноября 2017. Архивировано 18 мая 2008 года. Информация с сайта Нобелевского комитета (англ.)]
Литература[править | править код]
- Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. — М.: Мир, 1984. — Т. 1. — 302 с.
- Блохинцев Д. И. Основы квантовой механики. — М.: Наука, 1976. — 664 с.
- Боум А. Квантовая механика: основы и приложения. — М.: Мир, 1990. — 720 с.
- Варшалович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория углового момента. — Л.: Наука, 1975. — 441 с.
- Зар Р. Теория углового момента. О пространственных эффектах в физике и химии. — М.: Мир, 1993. — 352 с.
Теорема об изменении момента количества движения
Момент количества движения
Так как количество движения — вектор, имеющий определенную линию действия (и даже определенную точку приложения), то можно находить момент этого вектора относительно точки и оси так же, как определяли соответствующие моменты силы.
Сначала о моменте количества движения материальной точки.
Ее момент количества движения 
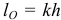
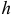
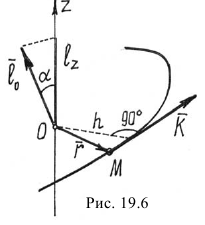
Момент количества движения 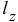
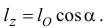
То есть момент количества движения материальной точки относительно оси равен проекции вектора момента количества движения относительно какой-либо точки 
Для движущейся материальной системы вводится понятие главного момента количеств движения относительно центра 
Вводится и понятие главного момента количеств движения относительно оси как алгебраической суммы моментов количеств движения точек системы относительно этой оси
Зависимость между ними аналогична зависимости между соответствующими главными моментами сил
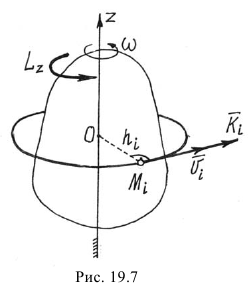
Главный момент количеств движения относительно оси равен проекции вектора главного момента относительно точки, расположенной на оси, на эту ось. Для твердого тела как материальной системы при некоторых движениях главный момент относительно оси определяется довольно просто.
Так, если тело вращается вокруг неподвижной оси 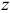
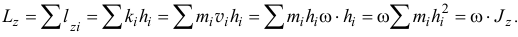
To есть равен произведению момента инерции тела относительно оси вращения на угловую скорость
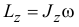
и направлен он по направлению вращения тела.
Если однородное тело имеет плоскость симметрии, перпендикулярную оси вращения, то вектор количества движения тела 
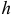
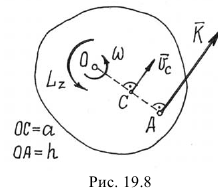
На рис. 19.8 показано сечение тела этой плоскостью симметрии и положение вектора количества движения 
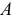
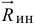
Можно найти главный момент количеств движения тела и при плоскопараллельном движении относительно центральной оси 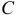
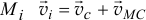
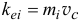
Главный момент количеств движения точек тела относительно оси 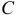
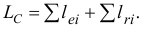
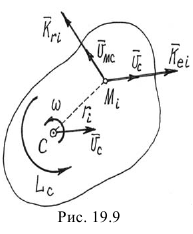
Но первая сумма равна нулю, так как по теореме Вариньона эта сумма моментов векторов 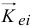
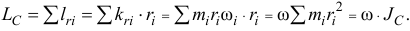
Значит, главный момент количеств движения точек тела при плоскопараллельном движении относительно центральной оси 
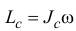
и имеет направление, совпадающее с направлением вращения, с направлением угловой скорости.
Аналогичный результат получается и для главного момента количеств движения относительно оси 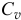
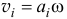
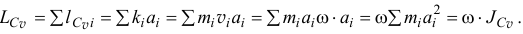
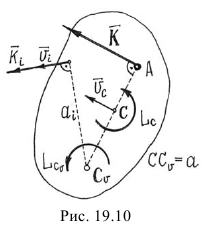
Итак
где 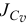
При плоскопараллельном движении также можно найти положение вектора количества движения 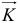
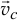
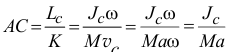
и от мгновенного центра скоростей
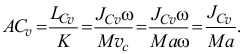
Очень похоже на результат, полученный при вращении тела вокруг неподвижной оси. Но разница в том, что здесь положение точки 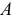
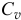
Теорема о моменте количества движения
Рассмотрим движение материальной системы под действием внешних 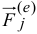
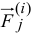
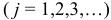
Определим момент количеств движения каждой точки этой системы относительно некоторого неподвижного центра 
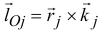
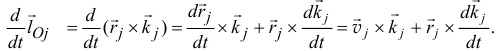
Первый член равен нулю, так как векторы 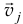
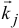
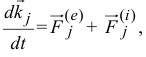
то второй член
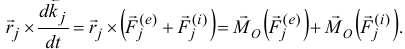
Поэтому
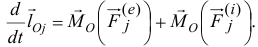
Сложим правые и левые части этих равенств, составленных для всех точек системы:
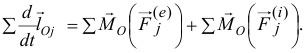
Вторая сумма в правой части равна нулю, так как главный момент внутренних сил относительно любой точки равен нулю. Оставшуюся часть равенства перепишем так:
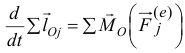
или
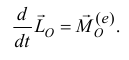
Производная но времени главного момента количеств движения материальной системы относительно неподвижной точки 
Оказывается, точно так же формулируется эта теорема и относительно центра масс произвольно движущейся материальной системы. Действительно, рассмотрим движение системы как сумму двух движений: переносного — поступательного движения системы осей вместе с центром масс и относительного — относительно этих осей.
В разд. XIII, §3 мы установили, что движение точек, а значит, и всей материальной системы относительно движущейся системы координатных осей можно определять так же, как относительно неподвижных, если учесть переносные и кориолисовы силы инерции.
Значит, таким способом можно записать и теорему о моменте количества движения относительно движущегося центра масс
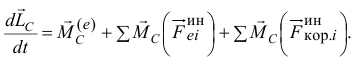
Но сумма моментов кориолисовых сил инерции равна нулю, так как при переносном поступательном движении эти силы отсутствуют. И первая сумма, сумма моментов переносных сил инерции, тоже равна нулю. Потому что по теореме Вариньона она равна моменту равнодействующей 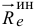
Поэтому теорема об изменении количества движения относительно центра масс 
Спроектировав векторные уравнения (19.17) и (19.18) на какую-нибудь ось, проходящую через точку 
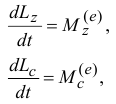
где 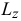
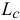
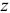

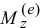
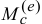
К теореме о моменте количества движения следует сделать очень важные и полезные замечания. Если внешние силы на систему не действуют или действуют, но сумма моментов их относительно неподвижной точки 

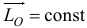
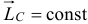
То же самое можно сказать и о моментах относительно осей: если главный момент внешних сил относительно какой-нибудь оси 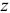
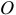

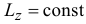
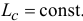
Например, на фигуриста, вращающегося на льду (рис. 19.11) вокруг оси 
Моменты их относительно оси 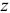
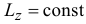
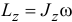
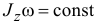
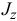
Еще пример. Вертолет, неподвижно висящий в воздухе (рис. 19.12). Лопасти винта вращаются с угловой скоростью 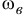
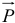
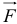

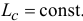
Если изменится скорость вращения винта 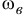
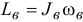
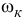
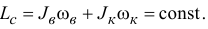
Значит, если винт увеличит угловую скорость, корпус начнет вращаться, но в противоположном направлении; уменьшит — корпус начнет вращаться в том же направлении. Чтобы не произошло этого нежелательного явления, у некоторых типов вертолетов предусмотрен еще один винт на хвосте, вращающийся в вертикальной плоскости и создающий горизонтальную внешнюю силу. Эта сила и будет ликвидировать вращение корпуса изменением момента 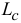
Несколько примеров на решение задач с помощью этой теоремы.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.
Момент импульса замкнутой системы сохраняется.
Содержание
- 1 Момент импульса в классической механике
- 1.1 Определение
- 1.2 Вычисление момента
- 1.3 Сохранение углового момента
- 2 Момент импульса в электродинамике
- 3 Момент импульса в квантовой механике
- 3.1 Оператор момента
- 3.2 Симметрия вращения
- 4 Вычисление момента импульса
- 5 Литература
Момент импульса в классической механике
Связь между импульсом 
Определение
Момент импульса 
где 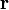
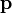
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.
Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение:
Вычисление момента
Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам 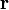
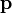
где 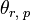
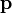
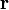
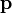
Запишем 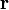
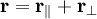
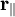
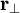
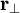
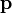
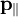
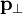
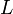
Для систем, совершающих вращение вокруг одной из осей симметрии (вообще говоря, вокруг так называемых главных осей инерции), справедливо соотношение
где 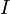
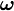
В общем случае вектор момента связан с вектором угловой скорости линейным оператором момента инерции:
Сохранение углового момента
| Симметрия в физике | ||
|---|---|---|
| Преобразо- вания |
Инвариант- ность |
Закон сохранения |
| ↕ трансляции времени | Консервативность | …энергии |
| ↔ изотропия времени | Изотропия времени | …энтропии в обратимых процессах |
| ↔ трансляции пространства | Однородность | …импульса |
| ○ Вращения | Изотропия | …момента импульса |
| × Группа Лоренца | Относительность Лоренц-инвариантность |
инвариантность интервала (и др. скаляров пространства-времени) |
Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.
В замкнутых системах момент импульса постоянен. Производная момента импульса по времени есть момент силы:
Таким образом, требование системы быть «замкнутой», означает равенство нулю главного (суммарного) момента внешних сил:
где 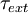
Математически закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол 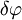
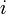
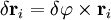
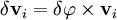
С учетом 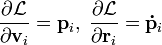
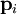
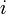
Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:
где, 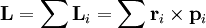
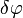
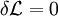
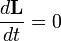
На орбитах момент импульса распределяется между собственным вращением планеты и момента импульса ее орбитального движения:
Момент импульса в электродинамике
При описании движения заряженной частицы в электромагнитном поле, канонический импульс 
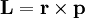
где 

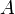
где 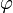
Момент импульса в квантовой механике
Оператор момента
В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определенными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на 
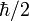
В классическом определении момент импульса зависит от 6 переменных 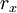
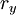
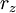
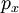
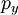
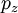
Математически, момент импульса в квантовой механике определяется как количество движения — не количественно, а как оператор физической величины:
где 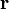
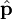
где 
и даже более важные подстановки с гамильтонианом частицы без заряда и спина:
Симметрия вращения
Операторы момента импульса обычно встречаются при решении задач сферической симметрии в сферических координатах. Тогда момент импульса в пространственном отображении:
Когда находят собственные значения этого оператора, получают следующее:
где
— сферические гармоники.
Вычисление момента импульса
Если имеется материальная точка массой 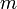
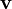
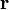
где 
Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки и векторно просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:
Литература
- Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. Том 1. М.: Мир, 1984. 302с.
- Блохинцев Д. И. Основы квантовой механики. 5-ое изд. Наука, 1976. — 664 с.
- Боум А. Квантовая механика: основы и приложения. М.: Мир, 1990. — 720c.
- Варшалович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория углового момента. Л.: Наука, 1975.
Wikimedia Foundation.
2010.
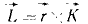
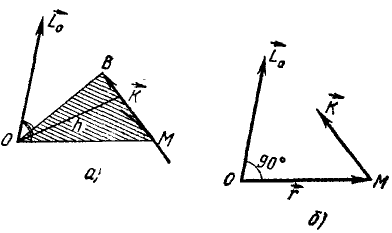
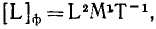
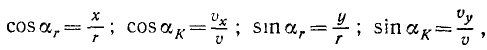
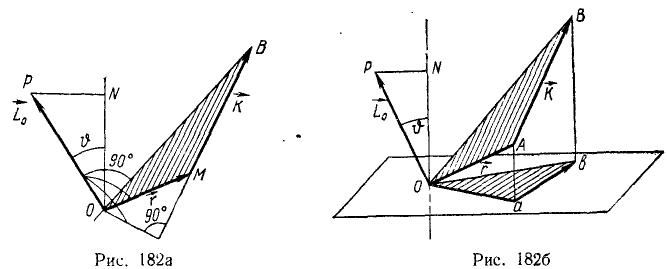
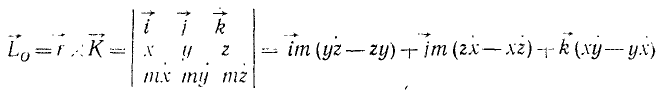
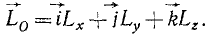
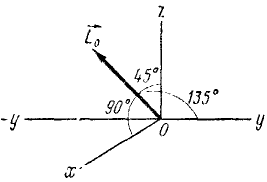
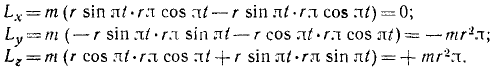
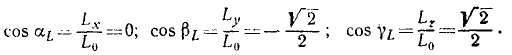
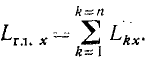
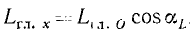
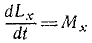
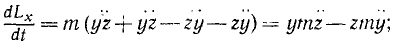
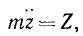
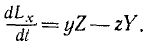
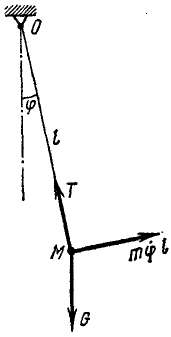
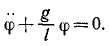
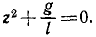
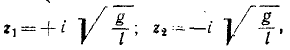
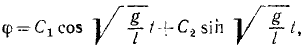
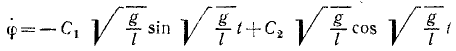
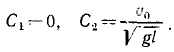
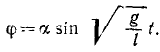
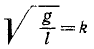
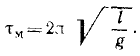
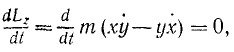
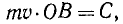
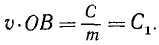
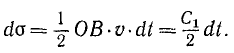
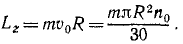
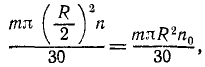
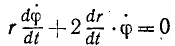
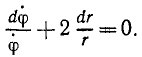
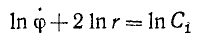
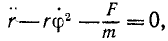
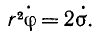
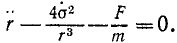
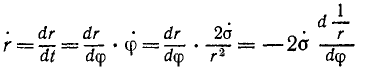
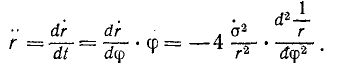
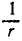
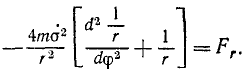
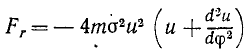
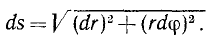
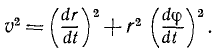
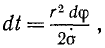
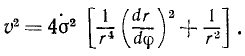
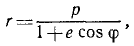
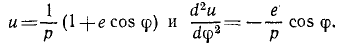
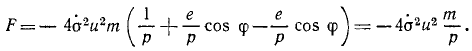
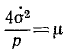
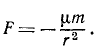
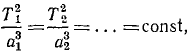
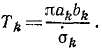
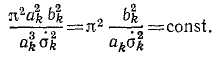
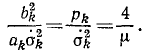
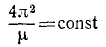
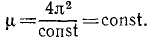
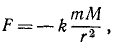
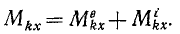
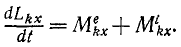
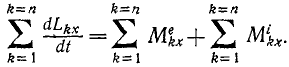
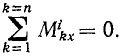
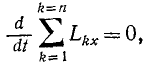
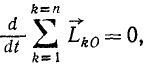
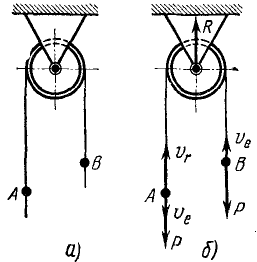
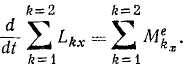
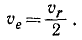
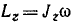
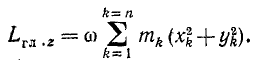
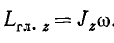
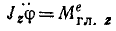
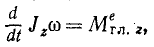
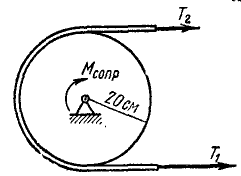
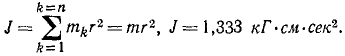
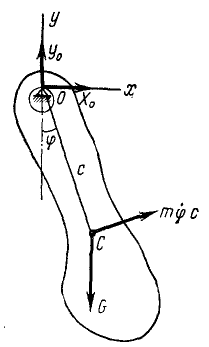
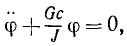
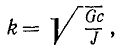
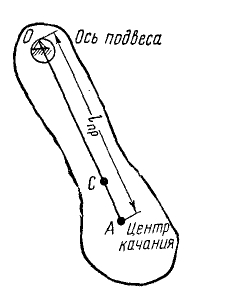
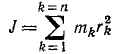
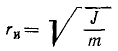
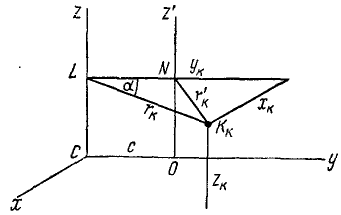
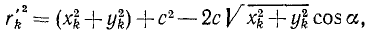
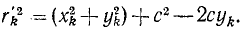
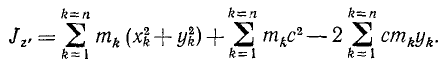
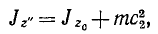
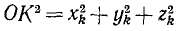
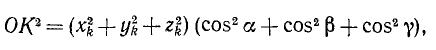
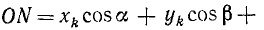
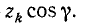
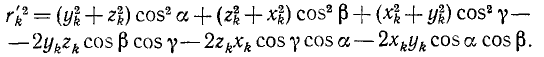
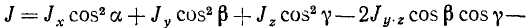
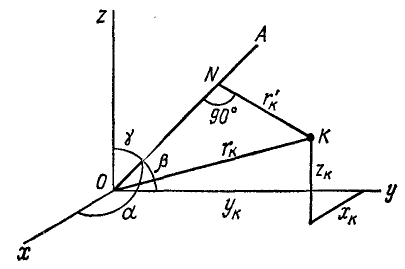
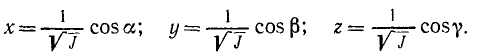
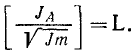
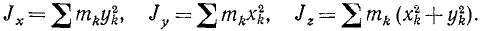
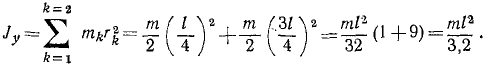
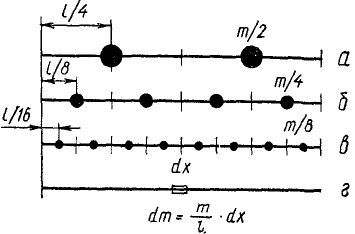
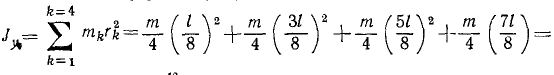
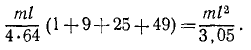
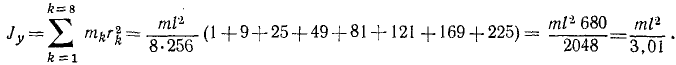
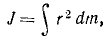
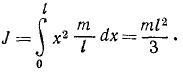
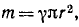
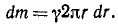
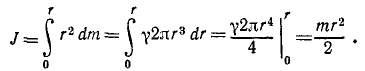
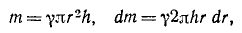
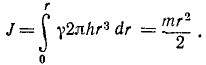
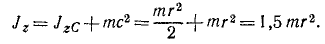
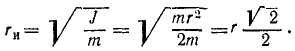
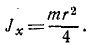
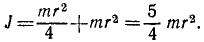
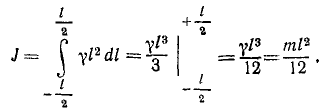
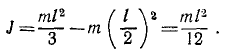
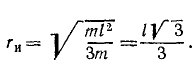
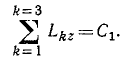
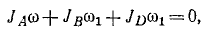
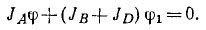
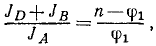
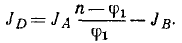
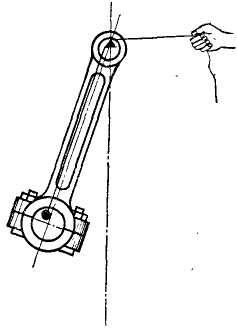
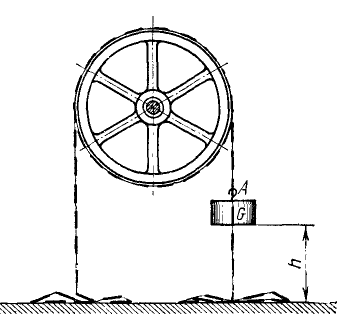
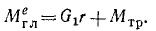
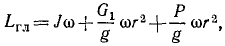
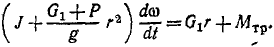
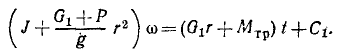
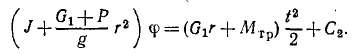
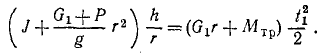
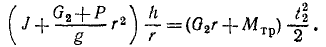
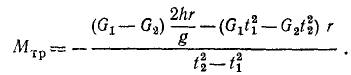
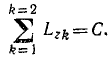
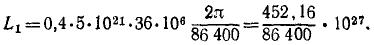
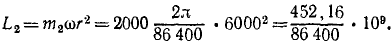
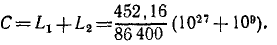
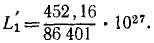
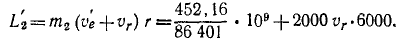
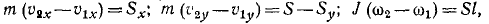
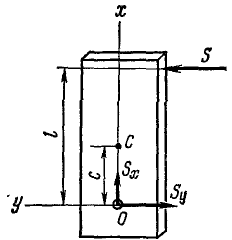
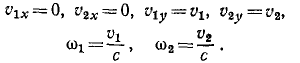
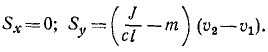
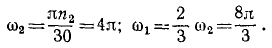
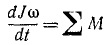
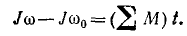
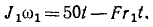
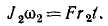
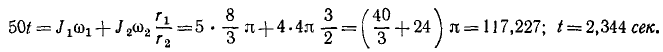
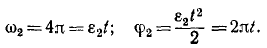
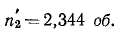
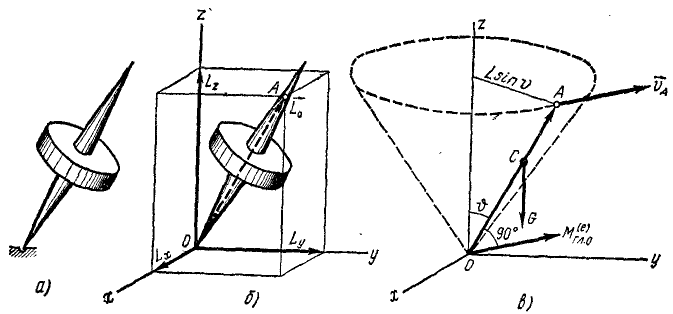
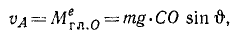
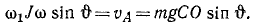
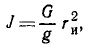
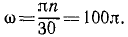
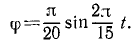
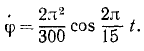
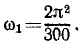
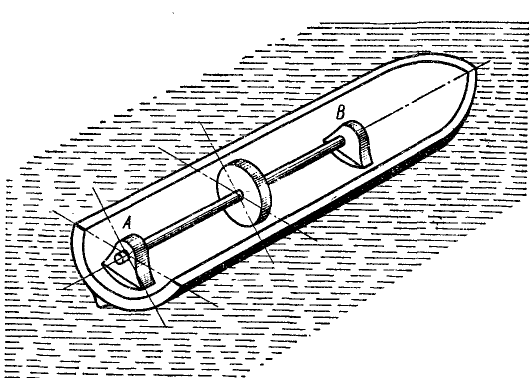
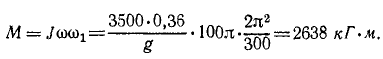
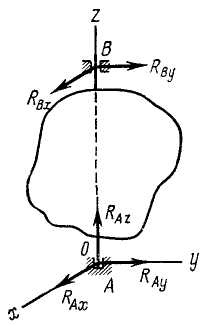
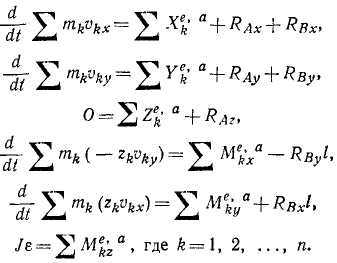
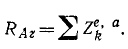
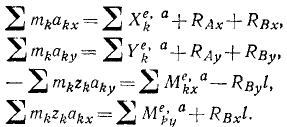
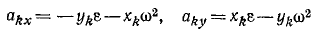
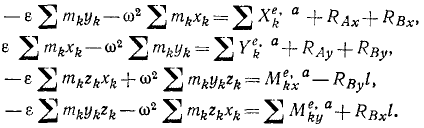
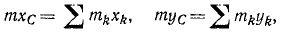
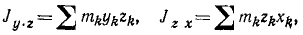
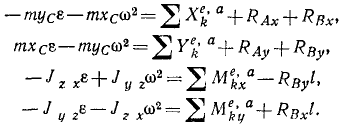
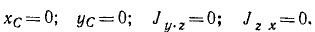
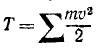

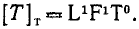
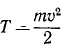
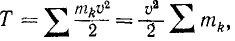
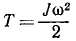
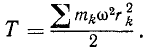
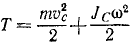
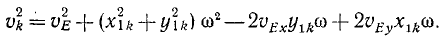
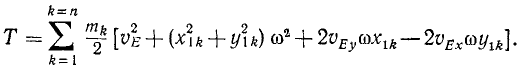
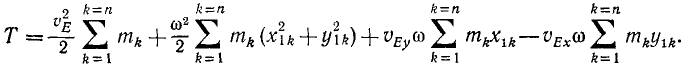
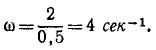
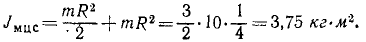
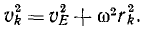
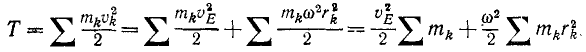
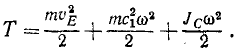
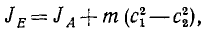
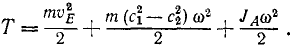
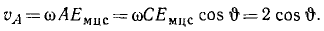
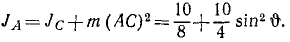
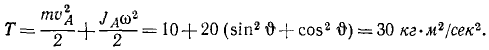
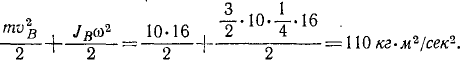
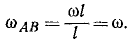
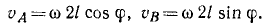
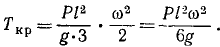
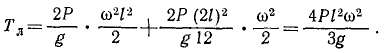
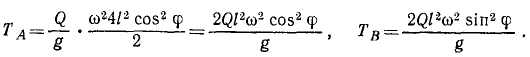
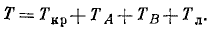
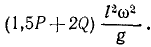
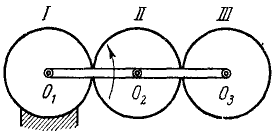
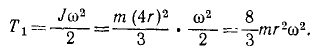
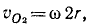
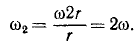
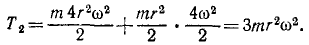
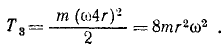
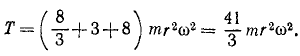





















![[L_i,; L_j ] = i hbar varepsilon_{ijk} L_k, quadleft[L_i,; mathbf{L}^2 right] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc71cd271eeabf833358dbaf02930a174d88e1f0)
![left[L_i,; H right] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbcc5ef1a6821f34a74fdf4ab2b1767ad83a639d)





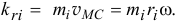

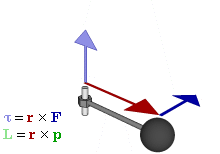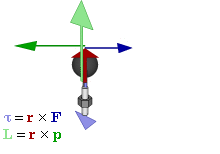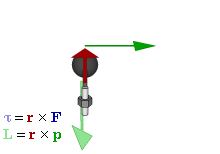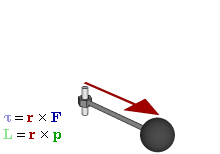

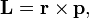
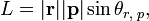
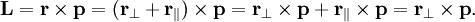
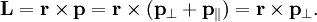
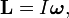
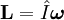
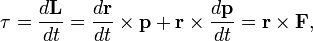
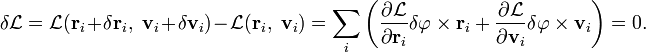
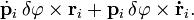
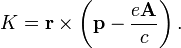
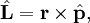
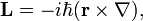
![[L_i,; L_j ] = i hbar varepsilon_{ijk} L_k, quadleft[L_i,; mathbf{L}^2 right] = 0](https://dic.academic.ru/pictures/wiki/files/97/afcc4aada5ef2cf78f75e84f8f86cb24.png)
![left[L_i,; H right] = 0](https://dic.academic.ru/pictures/wiki/files/54/64436c517ce6a1dc36baf3faa8685e3f.png)