Определение величины момента M создаваемого равномерно распределенной нагрузкой q в произвольной точке балки.
Вопрос: Как определить момент в заданной точке балки, возникающий от распределенной нагрузки?
Ответ: При расчетах балок, в сопромате часто возникает задача определить изгибающий момент в сечениях балки вызванный действием равномерно распределенной нагрузки q.
В этом случае, как правило, удобнее пользоваться понятием равнодействующей силы Rq, которой можно заменить распределенную нагрузку.
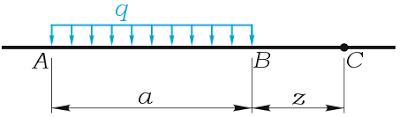
Рассмотрим пример нахождения момента в произвольной точке C от равномерно распределенной между точками A и B нагрузки интенсивностью q.
Для определения момента нагрузки необходимо знать ее длину a и расстояние z от любого ее края до рассматриваемой точки.
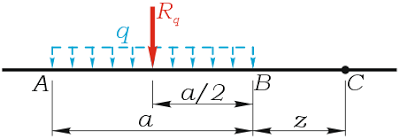
Заменим распределенную нагрузку ее равнодействующей Rq, которая для равномерного случая распределения будет располагаться ровно посередине нагрузки, при этом ее величина определяется как произведение интенсивности q нагрузки на ее длину a
Rq=qa
Как известно момент силы определяется произведением силы на плечо
M=Fl
В данном случае силой в вышеуказанном выражении является равнодействующая Rq.
Плечом этой силы является расстояние от точки C до равнодействующей нагрузки
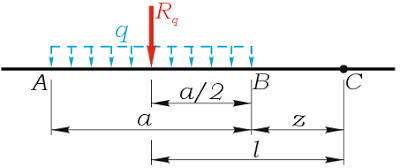
l=a/2+z
Таким образом, момент нагрузки равен произведению интенсивности q нагрузки на ее длину a и на расстояние от ее середины до рассматриваемой точки a/2+z
MС=Rql=qa(a/2+z)
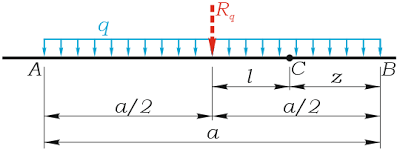
Для случая, когда точка лежит в пределах действия нагрузки, аналогично:
MС= Rql=qa(a/2-z)
Примечания:
- В случае действия неравномерно распределенной нагрузки ее интенсивность задается функцией.
- Для нагрузки, распределенной по площади (объему) при вычислении равнодействующей вместо длины надо подставлять площадь (объем) ее действия.
- Момент части распределенной нагрузки определяется аналогично.
Примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:


Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
3.1. Расчетная
схема. Определение расчетных нагрузок
и усилий на главную балку.
А=6м
А=6м
M=3103,35
Определяем
нормативную нагрузку на балку:
где g =
(26+0,864+0,486/1)*6,0*1,02=167,7 кН/м ;
Определяем расчетную
нагрузку на балку:
;
где n1
– коэффициент перегрузки для собственной
массы настила;
n2
– коэффициент перегрузки для временной
нагрузки;
«1,02» – коэффициент
учитывающий собственный вес гл. балки;
Определяем расчетный
изгибающий момент в середине пролета:
Поперечная сила
на опоре:
Главную балку
рассчитываем с учетом развития
пластических деформаций. По формуле
определяем требуемый момент сопротивления
балки.
где tf– толщина пояса;
b – ширина поясных
листов;
hw– высота стенки;
tw– толщина стенки;
h – высота главной
балки;
3.2. Определение
высоты главной балки.
Высота главной
балки определяется экономическими
соображениями.
Ее выбирают из 3
условий:
а) Определяем
строительную(максимальную) высоту балки
исходя из максимально возможной заданной
высоты перекрытия и его конструкции:
hmax= hстр– hбалки нас– tнаст–;
где hбалки нас– высота балки настила равная 36 см;
tнаст–
толщина настила, равная 12 см;
- величина равная 15-20 мм; принимаем 20 мм;
hстр–
строительная высота перекрытия, равная
250 см;
hmax= 250 – 36 – 12 – 2 = 200 см;
+8,000м
б) Определяем
оптимальную высоту балки hопт,
это высота при которой суммарный вес
поясов и стенки будет наименьшим.
;
где Wтр–
требуемый момент сопротивления; см3;
w– гибкость стенки, определяется как
отношение hw/tw
и задается
по нормам в пределах
w=
120-150;
;
в) Определяем
минимальную высоту балки hmin. Она
обеспечивает необходимую жесткость
при полном использовании несущей
способности материала. Вычисляется по
следующей формуле:
;
где Ry–
расчетное сопротивление стали; кН/см2;
E – модуль
упругости; кН/см2;
gн–
нормативная нагрузка, действующая на
главную балку; кН/м;
gp– расчетная
нагрузка, действующая на главную балку;
кН/м;
– допустимый относительный прогиб
главной балки;
;
;
Закономерности
изменения высоты балки показывают, что
наиболее целесообразно принимать высоту
балки близкой к hопт, определенной
из экономических соображений, и не
меньшей hmin, установленной из
условия допустимого прогиба балки.
Естественно, что во всех случаях принятая
высота балки в сумме с толщиной настила
не должна превышать заданную строительную
высоту перекрытия. Т.е. принимаем h = 160
см =1600 мм.
3.3. Подбор сечения
главной балки.
а) Определяем
толщину стенки главной балки tст.
Она определяется из трех условий:
1) из опыта
проектирования:
;
2) из условия
прочности на срез:
;
где Qmax–
максимальная поперечная сила главной
балки; кН;
h – высота главной
балки; см;
Rs– расчетное сопротивление стали срезу,
кН/см2; (Rs=
0,58Ry);
;
3) из условия местной
устойчивости стенки:
;
где R – расчетное
сопротивление стали; кН/см2;
E – модуль
упругости; кН/см2;
h – высота главной
балки; см;
;
Принимаем толщину
стенки tст= 12 мм.
При этом гибкость
стенки:
;
где hст–
высота стенки и определяется:
Принимаем толщину
полки: tп= 25 мм.
;
Полученная стнезначительно отличается от ранее
принятого.
Размеры горизонтальных
поясных листов находим исходя из
необходимой несущей способности балки.
Для этого вычисляем требуемый момент
инерции сечения балки:
;
где Wтр–
требуемый момент сопротивления главной
балки, см3;
Находим момент
инерции стенки балки, принимая толщину
поясов tf=25 мм;
;
Момент инерции,
приходящийся на поясные листы:
;
где Iтр–
требуемый момент инерции сечения балки,
см4;
Iw– момент инерции стенки балки, см4;
Момент инерции
поясных листов балки относительно ее
нейтральной оси:
If= 2Аf(h0/2)2,
где Аf– площадь
сечения пояса. Моментом инерции поясов
относительно их собственной оси ввиду
его малости пренебрегаем.
Отсюда получаем
требуемую площадь сечения поясов балки:
;
где If– момент инерции поясных листов, см3;
;
б) Определяем
ширину поясных листов:
;

где Аfтр– требуемая площадь сечения поясов
балки, см2;
tf– толщина поясных листов, см;
;
Учитывая универсальные
размеры, принимаем bf= 23 см =230 мм.
Т.е. принимаем
пояса размером 230х25 мм из широкополосной
универсальной горячекатаной стали ГОСТ
82-72*
Уточняем принятый
ранее коэффициент учета пластической
работы c исходя из следующего:
По приложению 5
(Е.И. Беленя) принимаем с=1,12 что практически
соответствует с=1,1.
в) Проверяем
принятую ширину (свес) поясов, исходя
из местной их устойчивости:
;
где bf– ширина свеса поясов, определяется
как
;
tw– толщина стенки, см;
E – модуль
упругости, кН/см2;
Ry– расчетное сопротивление стали, кН/см2;
;
– условие выполняется
г) Подобранное
сечение балки проверяем на прочность.
Для этого определяем момент инерции Ixи момент сопротивления балки Wx:
Ix= Iw+ If;
где Iw– момент инерции стенки балки, см4;
If– момент инерции, приходящийся на
поясные листы, см4;
;
Ix=
372387,5+713179,69 = 1085567 см4;
Момент сопротивления
балки Wx:
Наибольшее
нормальное напряжение в балке:
=< R = 34,5 кН/см2;
где Mmax–
максимальный момент главной балки,
кН.м;
Wx– момент
сопротивления главной балки, см3;
– условие выполняется
В результате
подобранное сечение балки имеет размеры:
b=230
tw=12
3.4. Изменение
сечения главной балки по длине.
Сечение главной
балки по длине изменяют в целях экономии
металла. Место изменения сечения
принимаем на расстоянии 1/6 пролета от
опоры. Сечение изменяем уменьшением
ширины поясов. Для растянутого пояса
Rсв= 0,85.R – расчетное
сопротивление металла стыковых сварных
соединений.
x1=2,33
м
x1=2,33
м
А=14 м
Mmax=5103,35
кН.м
Место изменения
сечения принимаем равным:
;
Определяем расчетный
момент и перевязывающую силу в сечении
1-1:
;
;
где gp–
расчетная нагрузка на главную балку,
кН/м;
l – длина балки,
м;
Определяем требуемый
момент сопротивления W1измененного
сечения исходя из прочности сварного
стыкового шва, работающего на растяжение:
;
где Rf– расчетное сопротивление металла
стыковых сварных соединений;
Rf= 0,85.Ry;
Момент инерции
измененного сечения:
;
где W1тр– требуемый момент сопротивления
измененного сечения, см3;
h – высота главной
балки, м;
Определяем требуемый
момент инерции поясов:
;
где I1тр– момент инерции измененного сечения,
см4;
Iw– момент инерции стенки главной балки,
см4;
Определяем требуемую
площадь полки измененного сечения:

где If1– требуемый момент инерции поясов, см4;
h0– высота
балки между центрами тяжести поясных
листов, м;
;

Принимаем b1= 130мм.
Т.о. принимаем
размеры измененного сечения из
широкополосной универсальной горячекатаной
стали 130 x 25 мм. Принятый пояс удовлетворяет
рекомендациям:
; 23
см > 11,5 см;
; 13
см 14 см;
Определяем
геометрические характеристики измененного
сечения, т.е. определяем момент инерции
и момент сопротивления уменьшенного
сечения:
;
где Iw– момент инерции стенки главной балки,
см4;
b1– ширина
измененного сечения, см;
tf– толщина пояса, см;
;
где Ix1–
момент инерции измененного сечения,
см4;
h – высота главной
балки, см;
Определяем
статический момент пояса Sf1:
;
где А1–
площадь измененного сечения, см2;
;
Определяем
статический момент полусечения
относительно нейтральной оси:
;
где Sf1– статический момент пояса, см3;
–
статический момент полусечения стенки
балки, см3;

;
Наибольшее
нормальное напряжение в уменьшенном
сечении балки:
σmax=M1/Wx1=283195/9693.6=29.2<
Rсв= 34,5.0,85 = 29,325 кН/см2;
где M1–
расчетный момент в сечении 1-1, кН.см;
Wx1– момент
сопротивления измененного сечения,
см3;
Rсв–
расчетное сопротивление металла стыковых
сварных соединений.
Измененное сечение
балки удовлетворяет проверки прочности
и не должно иметь недонапряжение больше
5%.
<
5 %
Проверим прочность,
устойчивость и прогиб сварной балки:
1) проверяем
прочность в месте изменения сечения по
приведенным напряжениям на грани
соединения стенки с полкой в точке Б.
(балки настила
опирать нельзя)
<=
1,15.R;
где прив– приведенные напряжения в сечении
1-1;
Б– нормальные напряжения в сечении 1-1;
Б– касательные напряжения в сечении
1-1;
;
где M1–
расчетный момент в сечении 1-1, кН.см;
Wx1– момент
сопротивления измененного сечения,
см3;
hw– высота стенки главной балки, см;
h – высота главной
балки, см;
;
где Q1–
поперечная сила в сечении 1-1, кН;
Sf1– статический момент пояса в сечении
1-1, см3;
Ix1– момент
инерции в сечении 1-1, см4;
tw– толщина стенки главной балки, см;
<= 1,15.R = 1,15.34,5 = 39,68 кН/см2;
Т.о. прочность
балки обеспечена.
2) Проверяем
прочность опорного сечения на срез:
;
где Qmax–
максимальная поперечная сила главной
балки, кН;
Smax–
статический момент полусечения
относительно нейтральной оси;
Ix1– момент
инерции в сечении 1-1, см4;
tw– толщина стенки главной балки, см;
Rs– расчетное сопротивление стали срезу,
кН/м2;;
- коэффициент условия работы балки;
< Rср. = 0,58.34,5=20 кН/см2;
3) Проверяем
максимальные нормальные напряжения в
поясах в середине балки:
;
где Mmax–
максимальный изгибающий момент главной
балки, кН.м;
Wтр–
требуемый момент сопротивления главной
балки, см3;
Ry– расчетное сопротивление стали, кН/см2;
;
4) Проверяем
прочность стенки на местное давление
балок настила:
l0
;
где F – опорная
реакция балки настила;
gpнастила– расчетная нагрузка настила;
B – шаг колонн в
поперечном направлении (или длина балки
настила);
lef– длина передачи нагрузки на стенку
балки, см;
;
bб.н.– длина участка передачи местной
нагрузки на балку, см;
tf– толщина пояса балки, см;
=2
Отсюда следует:
;
Т.о. прочность
принятого уменьшенного сечения главной
балки обеспечена.
3.5. Проверка
обеспеченности общей устойчивости
балки.
Проверка общей
устойчивости балки не производится,
так как главная балка закреплена балками
настила.
3.6. Проверка
местной устойчивости сжатого пояса и
стенки главной балки.
1. Проверка
устойчивости сжатого пояса производится
в месте максимальных нормальных
напряжений в нем – в середине пролета
балки, где возможны пластические
деформации.
Данная проверка
производится по следующим формулам:
;
где h0–
расстояние между осями поясных листов,
см;
tw– толщина стенки балки, см;
Ry– расчетное сопротивление стали, кН/см2;

– модуль упругости.
в=23
bf=21,8
tw=1.2
– удовлетворяет условию.
;
где bf– ширина свеса балки, определяется как
bf= bп– tw= 23 –
1,2 = 21,8 см;
tf– толщина полки балки, см;
;
;
Т.о. проверка
показала, что местная устойчивость
пояса обеспечена.
2. Проверяем
устойчивость стенки.
Первоначально
определяем необходимость постановки
ребер жесткости:
;
где –
условная гибкость стенки;
hw– высота стенки главной балки, см;
tw– толщина стенки главной балки, см;
E – модуль упругости;
Ry– расчетное сопротивление стали.
;
т.е. вертикальные
ребра жесткости необходимы.
Кроме того, в зоне
учета пластических деформаций необходима
постановка ребер жесткости под каждой
балкой настила, так как местные напряжения
в стенке в этой зоне недопустимы.
Определяем длину
зоны использования пластических
деформаций в стенке:
;
где L– пролет балки, см;
h – высота главной
балки, см;
hw– высота стенки балки, см;
с1–
коэффициент, учитывающий развитие
пластических деформаций.
;
Принимаем
одностороннее расположение ребер
жесткости, так как закрепление главных
балок происходит над колонной. Определяем
толщину и ширину ребра:
,
принимаем bр= 115 мм = 11,5 см;
,
принимаем tр= 9 мм;
Расчет
=
5,3 > 3,2 показал, что необходима проверка
устойчивости стенки:
а) Проверяем
устойчивость стенки в области действия
больших касательных напряжений – вблизи
от опоры балки т.к. а>hw
(2>1,55), то х1=1,55/2=0,775.
;
;
где Mx–
изгибающий момент в сечении на заданном
расстоянии, кН.м;
Qx– поперечная
сила в заданном сечении, кН;
gp– расчетная
нагрузка, действующая на главную балку,
кН/м;
l – пролет балки,
м;
;
;
Определяем
нормальные напряжения и касательные
напряжения:
;
;
где Wтр–
требуемый момент сопротивления главной
балки, см3;
tст– толщина
стенки балки, см;
;
;
Ранее мы вычислили
местные напряжения в стенке под балками
настила:
loc= 9,46 кН/см2;
Определяем
критические напряжения:

где Rs– расчетное сопротивление стали срезу,
кН/см; Rs= 0,85.R;
– условная гибкость
стенки, определяется как:
;
a – меньшая
сторона отсека, а = 155 см;
tw– толщина стенки балки, см;
- величина, равная отношению большей
стороны отсека к меньшей;
;
где b – большая
сторона отсека;
;
Определяем степень
упругого защемления стенки в поясах :
;
где - коэффициент, который принимается
равным= 0,8 (в
соответствии с таблицей 22 СНиПа
II-23-81*);
bnи tn– ширина и толщина сжатого пояса балки,
см;
По
таб. 24 СНиП П-23-81* в зависимости от а/hст
и δ определяем σloc/σ:
Расчетное значение
>0,6;
а/hcn>0,8;
поэтомукропределяем по формуле
Определяем cr:

где c2–
коэффициент, который принимается равным
c2= 49,7 (в соответствии с таблицей
7.7 Е.И. Беленя);
Определяем cr
loc– критическое
напряжение потери устойчивости от
действия местных напряжений, по следующей
формуле:

где с1–
коэффициент, определяемый по таблице
7.5. Е.И. Беленя (с1=22,7)
Rs– расчетное сопротивление стали срезу,
кН/см; Rs= 0,85.Ry;
– условная гибкость
стенки, определяется как:
;
где b – шаг ребер
жесткости;
tw– толщина стенки балки, см;
Следовательно
;
Теперь все найденные
значения подставляем в следующую
формулу:

Проверка показала,
что устойчивость стенки обеспечена в
I-ом отсеке.
б) Проверяем
устойчивость стенки балки в месте
изменения сечения балки.
Определяем среднее
значение M и Q на расстоянии x2=
2,33 м от опоры:
;
;
Определяем
нормальные напряжения в стенке балки:
;
Определяем
касательные напряжения:
;
Местные напряжения:
loc= 9,46 кН/см2;
;
Критические
нормальные напряжения равны: cr= 61,27 кН/см2;
Критическое
напряжение потери устойчивости от
действия местных напряжений: cr.loc.= 16,84 кН/см2;
Следовательно:

Проверка показала,
что устойчивость стенки обеспечена.
в) Проверяем
устойчивость стенки в середине пролета
в области больших нормальных напряжений.
Определяем среднее
значение M и Q в на расстоянии x3=
14/2 м = 7 м от опоры:
;
;
Определяем
нормальные напряжения в стенке балки:
;
Определяем степень
упругого защемления стенки:
δ=β*b/hст*(tп/tст)3=0,8*34/155*(2,5/1,2)3=1,59;
Т.к.
а/hст=100/155=0,65<0,8 ,то
σсr=(ccr*Ry)/λ2ст;
ccr
из таб. 7.4 Е.И. Беленя ссr=32,7;
σсr=(ccr*Ry)/λ2ст=(32,7*34,5)/5,292=40,3кН/см2;
Вычисляем
местные критические напряжения:
σм.cr=(c1*Ry)/λa2=(19,5*34,5)/3,42=58,2кН/см2;
λа=а/tст*√Ry/E=100/1,2*√34,5/2,06*104=3,4;
с1 из таб.
7.5 Е.И. Беленя , с1=19,5.
Следовательно:
;
Проверка показала,
что устойчивость стенки обеспечена.
3.7. Проверка
прочности поясных швов.
Существуют 2 способа
выполнения поясных швов: односторонние
и двухсторонние. СНиП рекомендует
выполнять односторонние швы при условии:
1) Сечение балки
подобрано без учета пластических
деформаций, т.е. loc= 0;
2) В местах приложения
сосредоточенных нагрузок установлены
ребра жесткости со стороны, противоположной
поясному шву;
3) В сварных балках,
работающих без учета пластических
деформаций, при хорошей обеспеченности
местной устойчивости стенки, когда
значения левой части формул:


где = 1.
В данном случае
loc0, следовательно
применение односторонних поясных швов
не допускается. Т.о. принимаем двусторонние
поясные швы.
Расчет двухсторонних
поясных швов выполняется с учетом
местных напряжений мпод балками настила, по формуле:
;
где Rwf– расчетное сопротивление металла
стыковых сварных соединений растяжению,
сжатию, изгибу по пределу текучести;
wf-коэффициент условий работы сварного
соединения угловыми швами при расчете
по металлу шва;
с– коэффициент условий работы;
T – горизонтальная
составляющая на сварные швы или сдвигающая
сила;
V – вертикальная
составляющая на сварные швы;
Сдвигающая сила
стремиться срезать поясные швы, а потому
сопротивление этих швов срезу должно
быть не меньше силы T. Расчетное усилие
на единицу длины шва от максимальной
поперечной силы определяется:
;
где Qmax–
максимальная поперечная сила главной
балки, кН;
Sf– статический момент пояса относительно
нейтральной оси сечения балки, см3;
Ix– момент
инерции сечения балки, см4;
;
Напряжение в стенке
в зоне сварного шва от местных напряжений
на единицу длины определяется:
;
где F – опорные
реакции балок настила, кН;
lef– длина передачи нагрузки на стенку
балки, см;
;
Следовательно:
;
Принимаем
автоматическую сварку и накладываем
сварные швы сварной проволокой марки
Св-08А.
Rwf= 18 кН/см2 ;Rwz=0,45*Rup=0,45*47=21,15кН/см2(по таб. 3 и 51 СНиП П.23-81*);
Принимаем минимальный
допустимый катет шва в зависимости от
максимальной толщины соединяемых
элементов kf= 7 мм
(по таблице 38* СНиП ΙΙ.23-81*).
f= 1,1;βz=1,15-коэффициенты
проплавления.
Получаем следующее
выражение проверки прочности сварного
шва:
βf*Rwz=1,1*18=19,8кН/см2;
βz*Rwz=1,15*21,15=24,3кН/см2.
;
;
Т.о. принимаем kш= 7 мм.
3.8. Расчетное
конструирование.
Так как вначале
расчетов была принята балочная клетка
нормального типа, то сопряжение балок
со стальными колоннами осуществляется
путем их опирания сверху. Конец балки
в месте опирания балок на колонны
укрупняют опорными ребрами, считая при
этом, что вся опорная реакция передается
с балки на опору через эти ребра жесткости.
Ребра жесткости для передачи опорной
реакции надежно прикрепляют к стенке
сварными швами, а торец строгают для
непосредственной передачи опорного
давления на стальную колонну. Опорное
ребро крепится к стенке с помощью
полуавтоматической сварки в углекислом
газе, сварочной проволокой Св-08А. Размер
выступающей части опорного ребра
принимаем 20 мм. из условий работы ребра
на смятие.
Определяем требуемую
площадь опорного ребра:
;
где Fop– опорная реакция балки, Fop= Qmax= 1458,1 кН;
Rp– расчетное сопротивление смятию
торцевой поверхности,;
Rp
= Run
/ n
= 47/1,025=45,8 кН/см2;
Run- по таблице 51* СНиП II-23-81*.
;
Из эстетических
соображений принимаем ширину ребра bрравную ширине поясов в зоне крепления
опорного ребра:
bp= 130 мм;
;

Принимаем ts= 2,5мм. Т.о. принимаем ребро из широкополосной
универсальной горячекатаной стали
130×25 мм. Аp= bp.ts= 13*2,5=32,5см2> Атрp=31,84
см2. Проверяем опорную стойку
балки на устойчивость относительно оси
X. Ширина участка стенки включенной в
работу опорной стойки:
;
где tw– толщина стенки главной балки, см;
Определяем площадь
опорной части Аs:
;
Определяем момент
инерции опорной части, относительно
оси X:
;
где ts– толщина опорного ребра, см;
bр– ширина
опорного ребра, см;
bw– ширина стенки, включенной в работу
опорной стойки, см;
tw– толщина стенки балки, см;
;
– радиус инерции;
Определяем гибкость
стенки x:
;
По значениям xи Ry(по таблице 72
СНиПа II-23-81*) с помощью интерполяции
находимx–
коэффициент продольного изгиба;
x= 0,809
Определяем
устойчивость опорной части относительно
оси X:
;
Опорную часть
балки проверяем на устойчивость из
условия:
Также должно
выполняться условие:
Подбираем размер
катета сварных швов крепления опорного
ребра к стенке для полуавтоматической
сварки проволоки Св-08А.
Определяем параметры
сварки:
f– коэффициент сварного соединения
угловыми швами при расчете по металлу
шва;f= 0,9;
z– коэффициент сварного соединения
угловыми швами при расчете по металлу
границы сплавления;z=1,05;
Rwf– расчетное сопротивление угловых
сварных швов срезу (условному) по металлу
шва. Rwf= 180 МПа;
Rwz– расчетное сопротивление угловых
сварных швов при расчете по границе
сплавления;Rwz=0,45*47=211,5
МПа;
Произведения
Расчетным сечением
является сечение по металлу шва.
где Fop– опорная реакция балки, кН; Fop= Qmax;
“2 .85” –
предельно допустимая длина шва, см;
Т.о. катет сварного
шва принимаем равным 8 мм.
Проверяем длину
расчетной части шва:
lw=85*bf*kf=85*0.9*0.8=61см<155см.
3.9. Конструирование
и расчет укрупнительного стыка главной
балки (стык на высокопрочных болтах).
Для соединения
металлических конструкций помимо сварки
применяют болты. Запроектируем стык
главной балки, т.к. она состоит из 2-х
составных балок, на высокопрочных
болтах. Все параметры берутся из расчета
главной балки.
Запроектируем и
выберем диаметр высокопрочных болтов.
Принимаем d=24 мм из стали 40Х «селект»,
имеющей нормативное сопротивление
стали болтов, принимаемое равным
временному сопротивлению впо ГОСТ на болты Rbun= 110 кН/см2. Стык делаем в середине
пролета балки, где Mmax=5103,35 кН.м.
Определяем несущую
способность одного болта, считая, что
разность между номинальными диаметрами
болта и отверстия превышает 1 мм и b= 0,85:
;
где Rbh– расчетное сопротивление болтов
(высокопрочных) растяжению, кН/см2;
;
Аn– площадь сечения нетто, определяется
по табл. 62* (СНиП П-23-81*)
b– коэффициент условий работы болтового
соединения;b= 0,85;
h– коэффициент надежности, определяется
по табл. 36* СНиП ΙΙ-23-81*,
h= 1,12;
- коэффициент трения, определяется по
табл. 36* СНиП ΙΙ-23-81*,
= 0,42;
к=2-две
плоскости трения.
;
1. Стык поясов
главной балки:
Стык поясов
перекрываем накладками сечением 230 x 14
мм и 2-мя 105 x 14 мм, общая площадь сечения:
Определяем
площадь нижнего сечения балки с учетом
ослабления его двумя отверстиями под
болты:
Определяем
усилие в поясе:
Mp=(Mmax*Ip)/Ix
Ip-момент
инерции поясных листов;
Ix-момент
инерции сечения балки;
Mp=(Mmax*Ip)/Ix=(5103,35*713179,69)/10855667=3352,72кН*м;
Растягивающая
сила действующая на соединение:
Количество болтов
рассчитываем по формуле:
Следовательно
количество болтов принимаем равное 14
шт.
2. Стык стенок
главной балки:
Стык стенки
перекрываем 2-мя вертикальными накладками
размером 210х1500х8 мм.
Определяем момент
Mf, действующий на
стенку:
;
где Mmax–
максимальный изгибающий момент главной
балки, кН.м;
Iw– момент инерции стенки балки, см4;
Ix– момент
инерции сечения балки, см4;
Принимаем расстояние
между крайними по высоте рядами болтов
на 120-180 мм меньше высоты стенки:
;
Находим коэффициент
стыка :
;
где Q– расчетное двигающее усилие воспринимаемое
болтом,
Mw– момент приходящийся на стенку, кН.м;
amax–
расстояние между крайними по высоте
рядами болтов, см;
m – число
вертикальных рядов на полунакладке.
;
По таблице 7.9 (Е.И.
Беленя) находим количество рядов болтов
по вертикали
k = 12 шт., с шагом
130 мм.
Проверяем стык
стенки по формуле:
;
где
Прочность стыка
стенки обеспечена.
Как определить крутящий момент в балке

При расчете сборных или монолитных железобетонных балок (ригелей) всегда нужно внимательно относиться к крутящему моменту. Очень часто расчет на кручение требует увеличить сечение или армирование балки. Сечение балки при кручении эффективней увеличивать в ширину (увеличение балки по высоте дает малый эффект), оптимально при кручении уходить от прямоугольного сечения к квадратному.
В каких ситуациях в балке возникает крутящий момент?
1) Если на балку опирается перекрытие только с одной стороны – оно своим весом пытается крутить балку в сторону пролета перекрытия.
2) Если на балку опирается перекрытие с двух сторон, но пролет этих перекрытий разный – тогда нагрузка от перекрытия с большим пролетом перевешивает в свою сторону и крутит балку.
3) Если на балку опирается перекрытие равных пролетов, но нагрузки на этих перекрытиях отличаются (разное назначение помещений, наличие оборудования на перекрытии и т.п.) – тогда балка также прокручивается в сторону большей нагрузки.
4) Если вдоль балки действует вертикальная нагрузка (например, от веса перегородки), сбитая в сторону от оси балки.
Рассмотрим определение крутящего момента на примерах.
Пример 1. Монолитное балочное перекрытие. Необходимо определить крутящий момент в крайней балке. Суммарная нагрузка от веса монолитного перекрытия и всех нагрузок на нем равна: qн = 675 кг/м² (нормативная) и qр =775 кг/м² (расчетная).
Расчет ведется на 1 погонный метр балки.
В монолитном перекрытии связь перекрытия с балками жесткая. При такой схеме расчетный пролет перекрытия равен пролету плиты в свету между балками L₀ = 2,8 м, а нагрузка от плиты на балку передается в месте примыкания балки к перекрытию.
Найдем нагрузку на 1 п.м балки от половины пролета плиты 2,8/2 = 1,4 м:
Рн = 675∙1,4 = 945 кг/м;
Рр = 775∙1,4 = 1085 кг/м.
Крутящий момент в балке рассчитывается умножением вертикальной нагрузки на эксцентриситет – расстояние от оси приложения этой нагрузки до оси, проходящей через центр тяжести балки. В нашем случае эксцентриситет равен половине ширины балки, т.е. 100 мм = 0,1 м.
Итак, определяем крутящий момент в балке (на 1 п.м балки):
Мн = 945∙0,1 = 94,5 кг∙м/м;
Мр = 1085∙0,1 = 108,5 кг∙м/м.
Пример 2. Сборное перекрытие опирается на балку с двух сторон. С одной стороны пролет перекрытия 6 м и есть пригруз в виде перегородки, опирающейся параллельно балке; с другой стороны пролет перекрытия 3,6 м. Нагрузка от перегородки 0,65 т/м, расстояние от оси балки до перегородки 1,5 м. Нагрузка от собственного веса перекрытия 0,3 т/м². Нагрузка на перекрытии: постоянная 0,1 т/м²; временная 0,3 т/м². Ширина балки 0,3 м. Глубина опирания плит перекрытия на балку 0,14 м.
Расчет ведется на 1 п.м балки.
Определим расчетный пролет каждого перекрытия и найдем точку приложения нагрузки от перекрытия на балку.
Плита опирается на балку на 140 мм. Нагрузка от плиты на этой площади распределена не равномерно, а по треугольнику. Максимально плита давит со стороны пролета (с края балки), а к краю плиты нагрузка сходит к нулю. Чтобы привести эту распределенную нагрузку к сосредоточенной, нужно принять ось приложения этой сосредоточенной нагрузки – в центре тяжести треугольника, на расстоянии 1/3 от края балки. У нас получается, что расстояние от края балки до сосредоточенной нагрузки 140/3 = 47 мм, а расстояние от этой нагрузки до оси, проходящей через центр тяжести балки 150 – 47 = 103 мм. Расстояние между сосредоточенными нагрузками равно расчетному пролету плиты L₀, который для наших плит будет равен:
– для плиты 6 м: L₀ = 6000 – 2∙103 = 5794 мм;
– для плиты 3,6 м: L₀ = 3600 – 2∙103 = 3394 мм.
Построим эпюры поперечных сил для наших плит.
Равномерно-распределенная нагрузка на 1 погонный метр плиты равна:
– нормативная qн = 1∙(0,3 + 0,1 + 0,3) = 0,7 т/м;
– расчетная qр = 1∙(1,1∙0,3 + 1,1∙0,1 + 1,2∙0,3) = 0,8 т/м.
Сосредоточенная нагрузка от перегородки на плите Nн = 0,65 т/м (нормативная) и Nр = 1,1∙0,65 = 0,72 т/м (расчетная) находится на расстоянии 1500 мм от оси балки и на расстоянии 1500 – 103 = 1397 мм от принятой нами точки опоры плиты, через которую проходит ось передачи вертикальной нагрузки на балку.
Схема для нормативных нагрузок будет следующая (так как плиты опираются шарнирно, то каждую из них нужно посчитать по отдельной схеме):
Левая плита разбита на два участка: 1-2 и 2-3, правая плита представляет собой один участок 4-5.
В правой плите мы сразу можем найти значения поперечной силы:
Q = 0,5∙qL₀ = 0,5∙0,65∙3,394 = 1,1 т.
Построим эпюру для правой плиты:
Значение поперечной силы на опоре (в точке 4) равно искомой нагрузке, которую плита передает на балку: Р4 = 1,1 т (направлена вниз).
Теперь разберемся с эпюрой для левой плиты. Так как помимо распределенной нагрузки у нас есть сосредоточенная сила, у нас будет несколько больше операций.
Для удобства расчета левой плиты заменим равномерно распределенную нагрузку q равнодействующей силой N:
N1-2 = 0.65∙4,397 = 2,86 т;
N2-3 = 0,65∙1,397 = 0,91 т.
Зная, что в шарнирно-опирающейся плите моменты на опоре равны нулю, составим уравнение равновесия, чтобы найти реакции на опоре.
ΣМ1 = 0:
2,86∙2,199 + 0,65∙4,397 + 0,91∙5,096 – R3∙5,794 = 0, откуда найдем реакцию:
R3 = -13.78/5,794 = 2,38 т.
ΣМ3 = 0:
0,91∙0,698 + 0,65∙1,397 + 2,86∙3,595 – R1∙5,794 = 0, откуда найдем реакцию:
R1 = 11,82/5,794 = 2,04 т.
Строить эпюру поперечных сил в плите для определения крутящего момента в балке нам не нужно, т.к. найденная нами реакция на опоре R3 равна максимальной поперечной силе и равна нагрузке, передаваемой плитой на балку: Р3 = 2,38 т (направлена вниз).
Теперь у нас есть все исходные данные для определения крутящего момента.
Определим нормативный крутящий момент путем умножения сил на плечо. Принимаем силу, вращающую балку против часовой стрелки со знаком «+», а по часовой – со знаком “-“:
Мн = 2,38∙0,103 – 1,1∙0,103 = 0,13 т∙м/м – нормативный крутящий момент, приходящийся на 1 п.м балки.
Расчетный крутящий момент находится точно так же.
Пример 3. Вдоль балки расположена перегородка, которая сбита относительно оси балки на 150 мм. Перекрытие опирается на балку с двух сторон, пролеты перекрытия и нагрузки – одинаковые. Толщина перегородки 0,12 м, материал кирпич (1,8 т/м³), высота 3 м.
Расчет ведем на 1 погонный метр балки.
Определим вертикальную нагрузку от перегородки:
0,12∙3∙1,8 = 0,65 т/м – нормативная нагрузка;
1,1∙0,65 = 0,72 т/м – расчетная нагрузка.
Определим крутящий момент в балке путем умножения силы на плечо:
Мн = 0,65∙0,15 = 0,1 т∙м/м;
Мр = 0,72∙0,15 = 0,11 т∙м/м.
Определение опорных реакций
1. Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.
ΣFx=0:
HA + P1*cos(30)=0
ΣMA=0:
Найдем сумму моментов относительно шарнирно-неподвижной опоры в точке A:
– q1*4*(4/2) – P1*sin(30)*8 + RB*12 + M1=0
ΣMB=0:
Найдем сумму моментов относительно шарнирно-подвижной опоры в точке B:
– RA*12 + q1*4*(12 – 4/2) + P1*sin(30)*4 + M1=0
2. Вычислим реакцию шарнирно-подвижной опоры в точке B:
RB=( q1*4*(4/2) + P1*sin(30)*8 – M1) / 12=( 6*4*(4/2) + 20*0.50008 – 42) / 12=7.17 (кН)
3. Вычислим реакцию шарнирно-неподвижной опоры в точке A:
RA=( q1*4*(12 – 4/2) + P1*sin(30)*4 + M1) / 12=( 6*4*(12 – 4/2) + 20*sin(30)*4 + 42) / 12=26.83 (кН)
4. Решаем полученную систему уравнений, находим неизвестные:
HA=- P1*cos(30)=- 20*0.8660=-17.32 (кН)
5. Выполним проверку решения, подставляя найденные значения в уравнение равновесия относительно оси Oy:
ΣFy=0:
RA – q1*4 – P1*sin(30) + RB=26.83*1 – 6*4 – 20*0.5000 + 7.17*1=0
Построение эпюр
Рассмотрим первый участок 0 ≤ x1 <
4
Продольная сила N:
N(x1)=HA
Значения N на краях участка:
N1(0)=17.32=17.32 (кН)
N1(4)=17.32=17.32 (кН)
Поперечная сила Q:
Q(x1)=+ RA – q1*(x1 – 0)
Значения Q на краях участка:
Q1(0)=+ 26.83 – 6*(0 – 0)=26.83 (кН)
Q1(4)=+ 26.83 – 6*(4 – 0)=2.83 (кН)
Изгибающий момент M:
M(x1)=+ RA*(x1) – q1*(x1)2/2
Значения M на краях участка:
M1(0)=+ 26.83*(0) – 6*(0 – 0)2/2=0 (кН*м)
M1(4)=+ 26.83*(4) – 6*(4 – 0)2/2=59.33 (кН*м)
Рассмотрим второй участок 4 ≤ x2 <
8
Продольная сила N:
N(x2)=HA
Значения N на краях участка:
N2(4)=17.32=17.32 (кН)
N2(8)=17.32=17.32 (кН)
Поперечная сила Q:
Q(x2)=+ RA – q1*(4 – 0)
Значения Q на краях участка:
Q2(4)=+ 26.83 – 6*(4 – 0)=2.83 (кН)
Q2(8)=+ 26.83 – 6*(4 – 0)=2.83 (кН)
Изгибающий момент M:
M(x2)=+ RA*(x2) – q1*(4 – 0)*[(x2 – 4) + (4 – 0)/2]
Значения M на краях участка:
M2(4)=+ 26.83*(4) – 6*4*(0 + 2)=59.33 (кН*м)
M2(8)=+ 26.83*(8) – 6*4*(4 + 2)=70.67 (кН*м)
Рассмотрим третий участок 8 ≤ x3 <
12
Продольная сила N:
N(x3)=HA – P1*cos(30)
Значения N на краях участка:
N3(8)=17.32 – 20*0.8660=0 (кН)
N3(12)=17.32 – 20*0.8660=0 (кН)
Поперечная сила Q:
Q(x3)=+ RA – q1*(4 – 0) – P1*sin(30)
Значения Q на краях участка:
Q3(8)=+ 26.83 – 6*(4 – 0) – 20*0.50=-7.17 (кН)
Q3(12)=+ 26.83 – 6*(4 – 0) – 20*0.50=-7.17 (кН)
Изгибающий момент M:
M(x3)=+ RA*(x3) – q1*(4 – 0)*[(x3 – 4) + (4 – 0)/2] – P1*(x3 – 8)*sin(30)
Значения M на краях участка:
M3(8)=+ 26.83*(8) – 6*4*(4 + 2) – 20*(8 – 8)*0.5000=70.67 (кН*м)
M3(12)=+ 26.83*(12) – 6*4*(8 + 2) – 20*(12 – 8)*0.5000=42 (кН*м)