Как найти момент реакции связи

Как найти момент реакции связи

Связями называют тела, ограничивающие свободу перемещения рассматриваемого тела.

Реакции связей — это усилия, с которыми связи действуют на данное тело.

Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными.

Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.

Виды связей и их реакции

Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными.

Рассмотрим реакции связей основных типов, встречающихся при решении задач: гладкой поверхности, ребра, гибкой нити, стержня, шарнирных опор и заделок, а также примеры замены связей их реакциями.

Реакции гладкой поверхности и ребра

Ниже приведены примеры замены связей гладкой поверхности и ребра их реакциями.
На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.
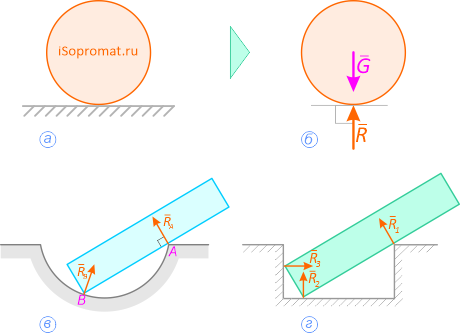
Реакции связей поверхности и ребра

а – тело весом G на гладкой поверхности;
б – действие поверхности заменено реакцией – силой R;
в – в точке А связь «опорная точка» или ребро;
г – реакции направлены перпендикулярно
опираемой или опирающейся плоскостям

Рисунок 1.1

Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1).

Реакции связей нити и стержня

Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль самого троса (нити, цепи, стержня) (рисунок 1.2).
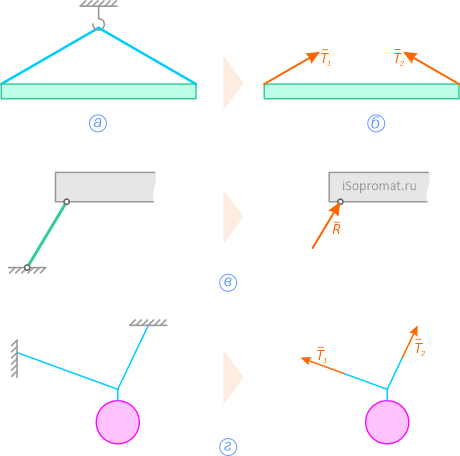
Реакции нитей и стержней

а – балка висит на двух тросах;
б – действие тросов заменено силами Т1 и Т2;
в – связь «идеальный стержень»;
г – связь «идеальная нить»

Рисунок 1.2

Реакции связей шарнирных опор

Шарнирные опоры допускают вращение относительно шарнира, поэтому в них не возникает вращающий момент.

Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3,а или 1.3,б). Она может быть заменена либо силой R с углом α (рисунок 1.3,в), либо двумя силами, например, XA и YA (рисунок 1.3,г).

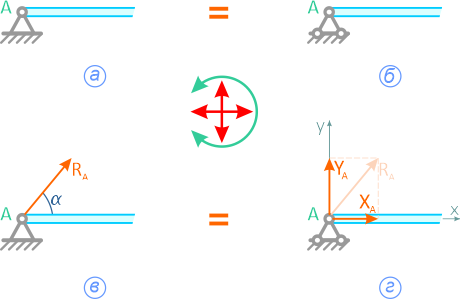
Проекции реакции связи

Рисунок 1.3

Всегда можно перейти от R и α к XA и YA (и наоборот):

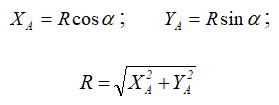
Составляющие проекции реакции связи

Шарнирно-подвижная опора (рисунок 1.4,а, б, в) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное.

Реакция R может быть направлена только по нормали к опорной поверхности (рисунок 1.4, г).
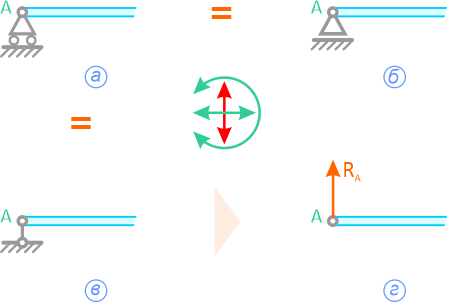
Реакции связей шарнирных опор

Рисунок 1.4

В следующем примере, связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), а их действие заменено силами XA, YA и RB.

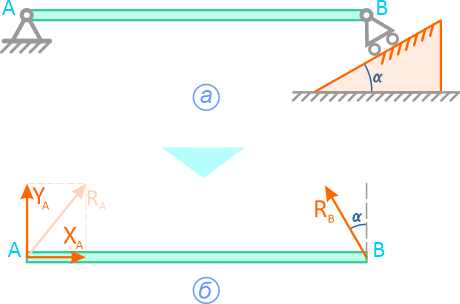
Замена шарнирных опор связями

Рисунок 1.5

Подробнее про связи и реакции связей смотрите в нашем видео:

Другие видео

Реакции связи в заделках

Все виды заделок исключают поворот, поэтому в них всегда возникает связь «момент».

Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросив втулку – получаем действие на стержень силы RD и момента MD.

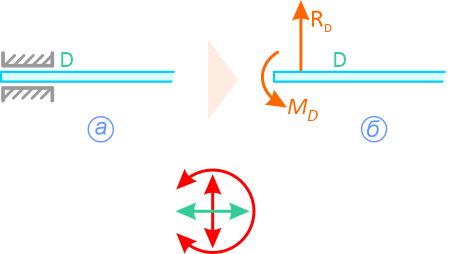
Связи в скользящей заделке

Рисунок 1.6

На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет только момент MC (рисунок 1.7, б).

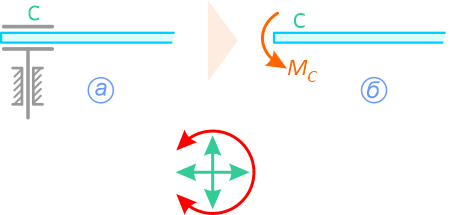
Связи бискользящей заделки

Рисунок 1.7

Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила RA с углом α (или XA и YA) и момент ΜA (рисунок 1.8).

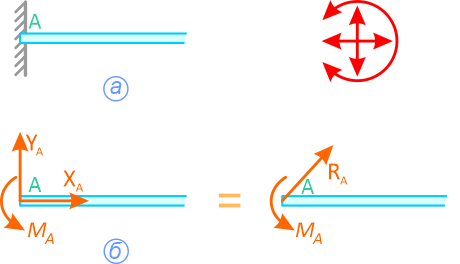
Реакции связей в заделке

Рисунок 1.8

Реакции пространственных связей

Трехмерная шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменяется системой сил (рисунок 1.9, б) XA, YA и ZA, т.е. силой, неизвестной по величине и направлению.

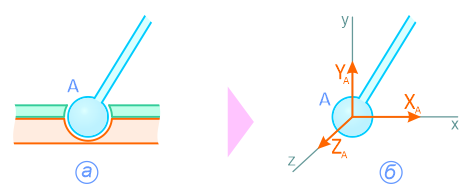
Реакции связей трехмерного шарнира

Рисунок 1.9

На рисунке 1.10, а показан вал с колесом, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами XA, YA, ZA и XB, ZB (рисунок 1.10, б).

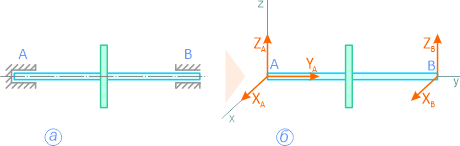
Реакции связей в подшипниках вала

Рисунок 1.10

На следующих рисунках показаны примеры замены различных типов связей их реакциями.

Примеры замены связей их реакциями

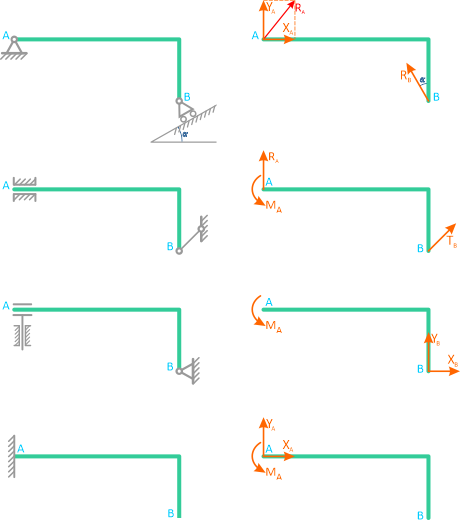
Рисунок 1.11

Трехмерная система удерживаемая в равновесии тремя типами связей: скользящей заделкой, шарнирно неподвижной опорой и тросом.
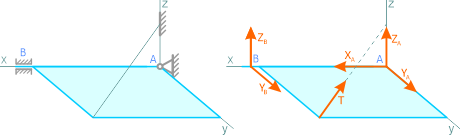
Связи трехмерной системы

Рисунок 1.12

В общем случае пространственного нагружения, в глухой заделке может возникать до шести реакций связей: три силы и три момента.
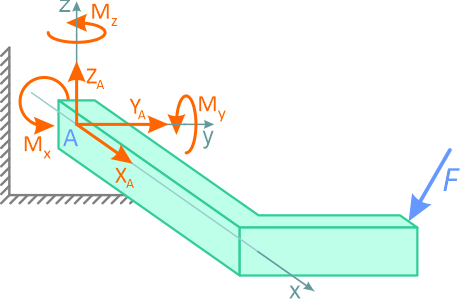
Общий случай - 6 реакций связей

Рисунок 1.13

Величина и истинное направление сил реакций связей определяются из уравнений равновесия рассматриваемой системы.
Для плоской системы сил составляется 3 уравнения
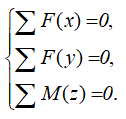
Уравнения равновесия плоской системы сил
Для пространственной системы — до шести уравнений статики.
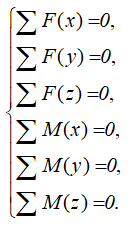
Уравнения равновесия пространственной системы сил
Из которых выражаются и рассчитываются искомые реакции.

Пример определения сил реакций связей

Задача
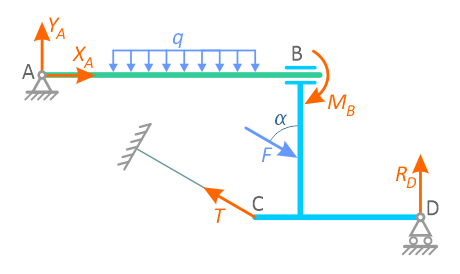
Жесткая рама закреплена в точке A шарнирной связью, а в точке B удерживается в состоянии статического равновесия опорой на катках, с упором в наклонную плоскость под углом 30°.
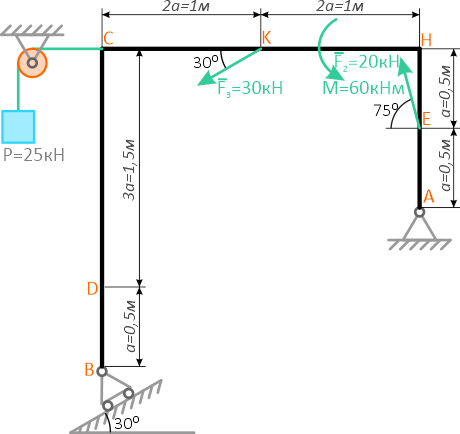
Схема для определения реакций связей
В точке C к раме привязан трос, перекинутый через блок и несущий на конце груз весом P=25кН.
На раму действует пара сил с моментом M=60кНм и две силы F2 и F3 приложенные в точках K и E и расположенные под углами 30° и 75° к горизонтальной оси.

Требуется определить реакции связей в точках A и B, вызываемые заданными действующими нагрузками.
При расчетах, принять размер a=0,5м.

Решение
Рассмотрим равновесие рамной пластины.
Проведем координатные оси x-y и изобразим действующие на пластину внешние нагрузки: силы F, пару сил с моментом M, натяжение троса T (по модулю T=P) и реакции связей XA, YA, RB.
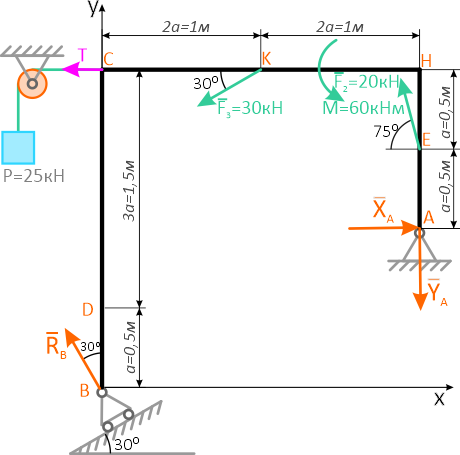
Направление сил реакций связей жесткой рамы
Реакцию неподвижной шарнирной опоры A изображаем двумя составляющими её связями. Реакция на катке направлена перпендикулярно опорной плоскости.
Для полученной плоской системы сил составим три уравнения равновесия системы.

При вычислении моментов сил F относительно точки A воспользуемся теоремой Вариньона, т.е. разложим силы на составляющие Fx=Fcosα и Fy=Fsinα и учтём что mA(F)=mA(Fx)+mA(Fy).

Запишем уравнения сумм проекций сил на оси x и y, а также суммы моментов относительно любой точки системы, например, точки A.

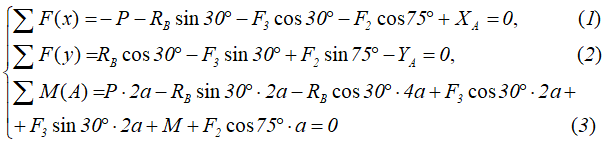
Решая полученную систему уравнений, определяем неизвестные реакции связей катка и шарнирно-неподвижной опоры.

Из уравнения (3) находим реакцию катка
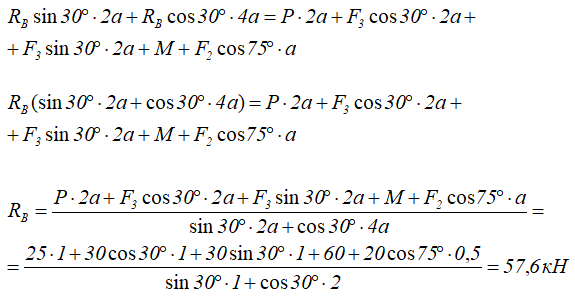
Реакция катка
Из уравнения (1) горизонтальную реакцию в точке A

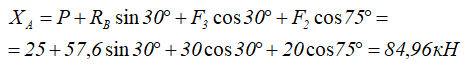
Из уравнения (2) — вертикальную.

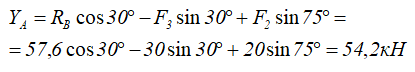
Положительные значения найденных реакций говорят о том, что направление связей было выбрано, верно.

Проверку можно выполнить, составив уравнение суммы моментов, в котором будут записаны все искомые реакции, например, относительно точки D:
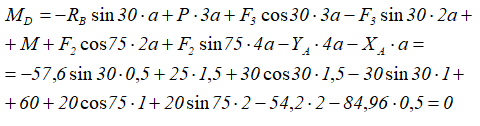
Проверка реакций связей
Ноль, полученный в ответе, означает правильность составления и решения уравнений

Ответ: Получены следующие значения сил реакций связей: в катке RB=57,6кН, в шарнирной опоре XA=84,96кН и YA=54,2кН.

Другие примеры решения задач >
Проекция силы на ось >

Источник

1. Гладкая (без
трения) опорная поверхность.
Такая связь препятствует движению тела
в одном направлении. Реакция
гладкой поверхности направлены всегда
по общей нормали к поверхности тела и
поверхности связи в их точке касания
(рис. 6).

Рис. 6

Рис.
7

2. Гибкая связь.
Реакции гибких связей всегда направлены
вдоль самих связей к точке их подвеса
(рис. 7).

3. Неподвижный
цилиндрический шарнир (неподвижная
шарнирная опора).
Тело может только вращаться вокруг оси
шарнира, перпендикулярной плоскости
рисунка (рис. 8).

Рис. 8

Реакция RA
проходит через ось шарнира и может иметь
любое направление в плоскости. При
решении задач целесообразно заменить
ее составляющими RAX
и RAY.

4. Подвижная
шарнирная опора. Реакция
такой опоры направлена по нормали к
опорной поверхности (рис. 9).

Рис. 9

5. Стержень.
Стержень
– прямолинейный невесомый элемент с
двумя шарнирами на концах. При отсутствии
нагрузки по его длине реакция стержня
направлена вдоль его оси (рис. 10).


Рис.10


Рис.11

6. Шаровой шарнир
(рис. 11). Этот
вид связи закрепляет какую-нибудь точку
тела так, что она не может совершать
линейных перемещений в пространстве,
при решении задач целесообразно заменить
эту силу ее составляющими RAX,
RAY,
RAZ.

7. Жесткая
заделка (неподвижное защемление). Такая
связь не допускает не только линейных
перемещений, но и поворота тела (рис.
12).

Рис. 12

Со стороны связи
на тело действует реакция RA
и момент MA
(момент реакции заделки или реактивный
момент). При решении задач рекомендуется
силу
заменить ее составляющимиRAX
и MA.

Равновесие
несвободных тел изучается в статике на
основании аксиомы связей:

-всякое несвободное
тело можно рассматривать как свободное,
если отбросить связи и заменить их
действие соответствующими реакциями.

Например, элемент,
для которого связями являются
шарнирно-неподвижная опора А
и стержень ВС
(рис. 13,а), можно рассматривать как
свободное тело, находящееся в равновесии
под действием заданных сил и реакций
связей RAX,
RAY
и RB
(рис. 13,б). Значения этих реакций
определяются из условий равновесия.

а)
б)

Рис. 13

1.4. Плоская система сходящихся сил

Система си, линии
действия которых пересекаются в одной
точке, называется системой сходящихся
сил (рис. 14,а.)

а)
б) в)

Рис. 14

Продолжив линии
действия заданных сил до пересечения,
перенесем точки приложения сил в точку
пересечения (рис. 14,б).

Используя
последовательно правило параллелограмма,
получим:

;
.

В общем случае
(для n
сил):
.

Таким образом,
система сходящихся сил приводится к
равнодействующей, равной их векторной
сумме и проходящей через точку их
пересечения.

Равнодействующую
можно определить графически с помощью
векторного (силового многоугольника
(рис. 14,в). Для этого последовательно в
выбранном масштабе откладываются
векторы заданных сил. Равнодействующей
системы сил является вектор, соединяющий
начало первого вектора с концом
последнего.

Равнодействующую
можно также определить аналитическим
способом. Проекция силы на ось (рис.
15,а) определяется произведением модуля
силы на косинус угла между направлением
силы и направлением оси.

На рис. 15,б показан
многоугольник сил. Из рисунка видно,
что

,

где ;
,
…., .

а)
б)

Рис. 15

Аналогичные
соотношения можно записать и для оси
Y.

Т.е. проекция
равнодействующей на какую-либо ось
равна сумме проекций составляющих сил
на ту же ось:

,
(4)

Равнодействующая
определяется так:

(5)

где
,– единичные векторы – орты.

Модуль равнодействующей
равен

(6)

Направление вектора
равнодействующей определяется с помощью
направляющих косинусов – косинусов
углов между равнодействующей и осями
x,
y:

,
(7)

Источник

Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.

Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.

В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.

Что такое реакция опоры?

Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

Схема, демонстрирующая схему балки (стержня) и опоры

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Возникшие реакции в опорах балки под нагрузкой

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.

Виды связей и их реакции

Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.

 В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.

Жёсткая заделка

Схема жёсткой заделки

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Реакции жёсткой заделки

Шарнирно-подвижная и шарнирно-неподвижная опора

В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

Схема шарнирно-подвижной и шарнирно-неподвижной опоры

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Реакции в шарнирно-подвижной и шарнирно-неподвижной опоре

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.

Что такое момент силы?

Также необходимо разобраться с понятием момент силы.

Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.

Проиллюстрирую написанное:

Схема для нахождения момента силы
На изображении показано, как определить момент силы F, относительно точки O.

Правило знаков для моментов

Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:

  • если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
  • если она стремится повернуть ПО часовой стрелке, то момент отрицательный.
Правило знаков для моментов

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.

Определение реакций для двухопорной балки

Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Расчётная схема балки, загруженная распределённой нагрузкой

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Указание координатных осей для схемы балки

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.

В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Обозначение векторов

Условия равновесия системы

Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Условия равновесия

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.

Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.

Уравнения равновесия

Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Расчётная схема для определения реакций

Уравнение проекций

Запишем первое уравнение — уравнение проекций для оси x.

В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:

Тогда HA будет равна:

Поздравляю, первая реакция найдена!

Уравнения моментов

А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.

Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.

Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:

Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций

Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.

Составим дополнительное уравнение проекций для оси y и подставим все численные значения:

Как видишь, реакции опор найдены правильно.

Определение реакций опор для балки с распределенной нагрузкой

Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Схема балки, загруженная распределённой нагрузкой

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Сворачивание распределённой нагрузки до сосредоточенной силы

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:

Обозначение реакций в опорах и координатных осей
Условия равновесия для балки

Расчёт реакций для консольной балки

Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Консольная балка, загруженная распределённой нагрузкой и силой под определённым углом

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:

Раскладывание сил на составляющие и силовой треугольник

Покажем реакции в заделке и выполним расчёт:

Обозначение реакций, сил и координатных осей для консольной балки

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:

Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.

В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.

У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.

Если получили отрицательное значение, нужно отразить это на схеме:

Изменение направления реактивного момента

С учётом изменений на схеме реакция будет равна:

Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:

Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:

Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.

Реакции опор для плоской рамы

Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Расчётная схема плоской рамы

Проводим ряд действий с расчетной схемой рамы:

  • заменяем опоры на реакции;
  • сворачиваем распределенную нагрузку до сосредоточенной силы;
  • вводим систему координат x и y.
Обозначение реакций, сворачивание распределённой нагрузки и введение осей координат

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

Изменение направления опорной реакции

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!

Источник

    Теоретическая механика в университете

  • Статика твердого тела. Решение примеров
    • Основные понятия и законы статики
    • Связи и их реакции
    • Момент силы относительно точки
    • Момент силы относительно оси
    • Момент пары сил
    • Преобразование сходящейся системы сил
    • Преобразование произвольной системы сил
    • Условия равновесия систем сил
    • Равновесие произвольной системы сил
  • Кинематика. Решение примеров
    • Основные понятия кинематики
    • Способы задания движения точки
    • Определение кинематических характеристик точки
    • Ускорение точки
    • Кинематика твердого тела
    • Плоско-параллельное движение твердого тела
    • Сложное движение точки
  • Динамика. Решение примеров
    • Основные понятия динамики
    • Аксиомы динамики
    • Дифференциальные уравнения динамики
    • Общие теоремы динамики
    • Принцип Даламбера
  • Примеры решения задач

Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.

Теоретическая механика является наукой, в которой изучаются перемещения тел с течением времени (механические движения). Она служит базой других разделов механики (теория упругости, сопротивление материалов, теория пластичности, теория механизмов и машин, гидроаэродинамика) и многих технических дисциплин.

Механическое движение — это изменение с течением времени взаимного положения в пространстве материальных тел.

Механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.

Статика твердого тела

Статика — это раздел теоретической механики, в котором рассматриваются задачи на равновесие твердых тел и преобразования одной системы сил в другую, ей эквивалентную.

    Основные понятия и законы статики

  • Абсолютно твердое тело (твердое тело, тело) – это материальное тело, расстояние между любыми точками в котором не изменяется.
  • Материальная точка – это тело, размерами которого по условиям задачи можно пренебречь.
  • Свободное тело – это тело, на перемещение которого не наложено никаких ограничений.
  • Несвободное (связанное) тело – это тело, на перемещение которого наложены ограничения.
  • Связи – это тела, препятствующие перемещению рассматриваемого объекта (тела или системы тел).
  • Реакция связи — это сила, характеризующая действие связи на твердое тело. Если считать силу, с которой твердое тело действует на связь, действием, то реакция связи является противодействием. При этом сила — действие приложена к связи, а реакция связи приложена к твердому телу.
  • Механическая система – это совокупность взаимосвязанных между собой тел или материальных точек.
  • Твердое тело можно рассматривать как механическую систему, положения и расстояние между точками которой не изменяются.
  • Сила – это векторная величина, характеризующая механическое действие одного материального тела на другое.
    Сила как вектор характеризуется точкой приложения, направлением действия и абсолютным значением. Единица измерения модуля силы – Ньютон.
  • Линия действия силы – это прямая, вдоль которой направлен вектор силы.
  • Сосредоточенная сила – сила, приложенная в одной точке.
  • Распределенные силы (распределенная нагрузка) – это силы, действующие на все точки объема, поверхности или длины тела.
    Распределенная нагрузка задается силой, действующей на единицу объема (поверхности, длины).
    Размерность распределенной нагрузки – Н/м3 (Н/м2, Н/м).
  • Внешняя сила – это сила, действующая со стороны тела, не принадлежащего рассматриваемой механической системе.
  • Внутренняя сила – это сила, действующая на материальную точку механической системы со стороны другой материальной точки, принадлежащей рассматриваемой системе.
  • Система сил – это совокупность сил, действующих на механическую систему.
  • Плоская система сил – это система сил, линии действия которых лежат в одной плоскости.
  • Пространственная система сил – это система сил, линии действия которых не лежат в одной плоскости.
  • Система сходящихся сил – это система сил, линии действия которых пересекаются в одной точке.
  • Произвольная система сил – это система сил, линии действия которых не пересекаются в одной точке.
  • Эквивалентные системы сил – это такие системы сил, замена которых одна на другую не изменяет механического состояния тела.
    Принятое обозначение: (vec{F_1},~vec{F_2},~...,~vec{F_n}){doubleleftright}(vec{P_1},~vec{P_2},~...,~vec{P_m}).
  • Равновесие – это состояние, при котором тело при действии сил остается неподвижным или движется равномерно прямолинейно.
  • Уравновешенная система сил – это система сил, которая будучи приложена к свободному твердому телу не изменяет его механического состояния (не выводит из равновесия).
    (vec{F_1},~vec{F_2},~...,~vec{F_n}){doubleleftright}0.
  • Равнодействующая сила – это сила, действие которой на тело эквивалентно действию системы сил.
    vec{R}{doubleleftright}(vec{F_1},~vec{F_2},~...,~vec{F_n}).
  • Момент силы – это величина, характеризующая вращающую способность силы.
  • Пара сил – это система двух параллельных равных по модулю противоположно направленных сил.
    Принятое обозначение: (vec{F},~vec{F{prime}}).
    Под действием пары сил тело будет совершать вращательное движение.
  • Проекция силы на ось – это отрезок, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой оси.
    Проекция положительна, если направление отрезка совпадает с положительным направлением оси.
  • Проекция силы на плоскость – это вектор на плоскости, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой плоскости.
  • Закон 1 (закон инерции). Изолированная материальная точка находится в покое либо движется равномерно и прямолинейно.
    Равномерное и прямолинейное движение материальной точки является движением по инерции. Под состоянием равновесия материальной точки и твердого тела понимают не только состояние покоя, но и движение по инерции. Для твердого тела существуют различные виды движения по инерции, например равномерное вращение твердого тела вокруг неподвижной оси.
  • Закон 2. Твердое тело находится в равновесии под действием двух сил только в том случае, если эти силы равны по модулю и направлены в противоположные стороны по общей линии действия.
    Эти две силы называются уравновешивающимися.
    Вообще силы называются уравновешивающимися, если твердое тело, к которому приложены эти силы, находится в покое.
  • Закон 3. Не нарушая состояния (слово «состояние» здесь означает состояние движения или покоя) твердого тела, можно добавлять и отбрасывать уравновешивающиеся силы.
    Следствие. Не нарушая состояния твердого тела, силу можно переносить по ее линии действия в любую точку тела.
    Две системы сил называются эквивалентными, если одну из них можно заменить другой, не нарушая состояния твердого тела.
  • Закон 4. Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке, равна по модулю диагонали параллелограмма, построенного на этих силах, и направлена вдоль этой
    диагонали.
    По модулю равнодействующая равна:
    R=sqrt{{F_1}^2+{F_2}^2+2*{F_1}*{F_2}*cos(hat{{F_1},{F_2}})}
  • Закон 5 (закон равенства действия и противодействия). Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены в противоположные стороны по одной прямой.
    Следует иметь в виду, что действие — сила, приложенная к телу Б, и противодействие — сила, приложенная к телу А, не уравновешиваются, так как они приложены к разным телам.
  • Закон 6 (закон отвердевания). Равновесие нетвердого тела не нарушается при его затвердевании.
    Не следует при этом забывать, что условия равновесия, являющиеся необходимыми и достаточными для твердого тела, являются необходимыми, но недостаточными для соответствующего нетвердого тела.
  • Закон 7 (закон освобождаемости от связей). Несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив действие связей соответствующими реакциями связей.
    Связи и их реакции

  • Гладкая поверхность ограничивает перемещение по нормали к поверхности опоры. Реакция направлена перпендикулярно поверхности.
  • Шарнирная подвижная опора ограничивает перемещение тела по нормали к опорной плоскости. Реакция направлена по нормали к поверхности опоры.
  • Шарнирная неподвижная опора противодействует любому перемещению в плоскости, перпендикулярной оси вращения.
  • Шарнирный невесомый стержень противодействует перемещению тела вдоль линии стержня. Реакция будет направлена вдоль линии стержня.
  • Глухая заделка противодействует любому перемещению и вращению в плоскости. Ее действие можно заменить силой, представленной в виде двух составляющих и парой сил с моментом.
    Момент силы относительно оси

  • Момент силы относительно оси — это момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
    Момент считается положительным, если с положительного конца оси поворот, который сила стремится совершить, виден происходящим против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.
    {M_z}(vec{F})={M_0}(vec{F_{xy}})={F_{xy}}h
  • Чтобы найти момент силы относительно оси, нужно:
    1) Провести плоскость перпендикулярную оси z.
    2) Спроецировать силу vec{F} на эту плоскость и вычислить величину проекции F_{xy}.
    3) Провести плечо h из точки пересечения оси с плоскостью на линию действия проекции силы F_{xy} и вычислить его длину.
    4) Найти произведение этого плеча и проекции силы с соответствующим знаком.
  • Свойства момента силы относительно оси.
    Момент силы относительно оси равен нулю, если:
    1) F_{xy}=0, то есть сила vec{F} параллельна оси.
    2) h=0, то есть линия действия силы пересекает ось.
    Момент пары сил

  • Момент пары сил равен произведению одной силы на кратчайшее расстояние между линиями действия сил пары, которое называется плечом пары (пара сил оказывает на тело вращающее действие)
    M(vec{F},vec{F})=Fh,
    где: vec{F},vec{F} — силы, составляющие пару;
    h — плечо пары.
    Момент пары считают положительным, если силы стремятся вращать плечо против хода часовой стрелки.
  • Свойства пары сил.
    1) Сумма проекций сил пары на любую ось равна нулю.
    2) Не изменяя момента пары можно одновременно соответственно изменять значение сил и плечо пары.
    3) Пару можно переносить в плоскости ее действия при этом действие пары на тело не изменится.

Кинематика

Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.

    Основные понятия кинематики

  • Закон движения точки (тела) – это зависимость положения точки (тела) в пространстве от времени.
  • Траектория точки – это геометрическое место положений точки в пространстве при ее движении.
  • Скорость точки (тела) – это характеристика изменения во времени положения точки (тела) в пространстве.
  • Ускорение точки (тела) – это характеристика изменения во времени скорости точки (тела).
    Способы задания движения точки

  • Задать движение точки — значит задать изменение ее положения по отношению к выбранной системе отсчета. Существуют три основные системы отсчета: векторная, координатная, естественная.
  • В векторной системе положение точки относительно начала отсчета задается радиус-вектором.
    Закон движения: overline{r}=overline{r}(t).
  • В системе координат OXYZ положение точки задается тремя координатами X, Y, Z.
    Закон движения: x = x(t), y = y(t); z = z(t).
  • В естественной системе отсчета положение точки задается расстоянием S от начала отсчета до этой точки вдоль траектории.
    Закон движения: overline{s}=overline{s}(t).
    Движение точки, при естественном способе задания движения, определено если известны:
    1) Траектория движения.
    2) Начало и направление отсчета дуговой координаты.
    3) Уравнение движения.
    При естественном способе задания движения, в отличии от других способов, используются подвижные координатные оси, движущиеся вместе с точкой по траектории. Такими осями являются:
    Касательная (τ) – направлена в сторону возрастания дуговой координаты по касательной к траектории.
    Главная нормаль (n) – направлена в сторону вогнутости кривой.
    Бинормаль (b) – направлена перпендикулярно к осям τ, n.
    Кинематика твердого тела

  • В кинематике твердых тел решаются две основные задачи:
    1) задание движения и определение кинематических характеристик тела в целом;
    2) определение кинематических характеристик точек тела.
  • Поступательное движение твердого тела
    Поступательное движение — это движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению.
    Теорема: при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения.
    Вывод: поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки.
  • Вращательное движение твердого тела вокруг неподвижной оси
    Вращательное движение твердого тела вокруг неподвижной оси — это движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.
    Положение тела определяется углом поворота varphi. Единица измерения угла – радиан. (Радиан — центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2π радиана.)
    Закон вращательного движения тела вокруг неподвижной оси varphi=varphi(t).
    Угловую скорость и угловое ускорение тела определим методом дифференцирования:
    omega={d{varphi}}/{dt} — угловая скорость, рад/с;
    varepsilon={d{omega}}/{dt} — угловое ускорение, рад/с².
    Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точку М, то точка М будет описывать вокруг точки С окружность радиуса R. За время dt происходит элементарный поворот на угол d{varphi}, при этом точка М совершит перемещение вдоль траектории на расстояние ds=R*{d{varphi}}.
    Модуль линейной скорости:
    V={ds}/{dt}=R*{{d{varphi}}/{dt}}=R*{omega}.
    Ускорение точки М при известной траектории определяется по его составляющим overline{a}=overline{a_{tau}}+overline{a_n}:
    a=sqrt{{a_{tau}}^2+{a_n}^2},
    где overline{a_{tau}}={dV}/{dt};~overline{a_n}={V^2}/R.
    В итоге, получаем формулы
    тангенциальное ускорение: a_{tau}={dR*{omega}}/{dt}=R*{varepsilon};
    нормальное ускорение: a_n={(R*{omega})^2}/R=R*{omega}^2.

Динамика

Динамика — это раздел теоретической механики, в котором изучаются механические движении материальных тел в зависимости от причин, их вызывающих.

    Основные понятия динамики

  • Инерционность — это свойство материальных тел сохранять состояние покоя или равномерного прямолинейного движения, пока внешние силы не изменят этого состояния.
  • Масса — это количественная мера инерционности тела. Единица измерения массы — килограмм (кг).
  • Материальная точка — это тело, обладающее массой, размерами которого при решении данной задачи пренебрегают.
  • Центр масс механической системы — геометрическая точка, координаты которой определяются формулами:
    X_C={{Sigma}m_k*x_k}/m;~Y_C={{Sigma}m_k*y_k}/m;~Z_C={{Sigma}m_k*z_k}/m;
    где mk, xk, yk, zk — масса и координаты k-той точки механической системы, m — масса системы.
    В однородном поле тяжести положение центра масс совпадает с положением центра тяжести.
  • Момент инерции материального тела относительно оси – это количественная мера инертности при вращательном движении.
    Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси:
    J_Z=m*r^2.
    Момент инерции системы (тела) относительно оси равен арифметической сумме моментов инерции всех точек:
    J_Z={Sigma}m_k*{r_k}^2
  • Сила инерции материальной точки — это векторная величина, равная по модулю произведению массы точки на модуль ускорения и направленная противоположно вектору ускорения: {vec{F^u}}={-m}vec{a}
  • Сила инерции материального тела — это векторная величина, равная по модулю произведению массы тела на модуль ускорения центра масс тела и направленная противоположно вектору ускорения центра масс: {vec{F^u}}={-m}vec{a_c},
    где a_c — ускорение центра масс тела.
  • Элементарный импульс силы — это векторная величина d{vec{S}}, равная произведению вектора силы vec{F}на бесконечно малый промежуток времени dt:
    d{vec{S}}=vec{F}*dt.
    Полный импульс силы за Δt равен интегралу от элементарных импульсов:
    d{vec{S}}=int{0}{t}{vec{F}*dt}.
  • Элементарная работа силы — это скалярная величина dA, равная скалярному произведению вектора силы vec{F} на бесконечно малое перемещение d{vec{s}}.
    Скалярное произведение векторов равно произведению их модулей на косинус угла между направлениями векторов:
    dA=F*ds*cos{alpha},
    где α — угол между направлениями векторов перемещения и силы.
  • Работа силы vec{F} на конечном перемещении точки её приложения равна интегралу от элементарной работы, взятому по перемещению:
    A=int{0}{s}{F*cos{alpha}*ds}.
    Единица измерения работы — Джоуль (1 Дж = 1 Н·м).
  • Количество движения материальной точки — это векторная величина vec{q}, равная произведению массы m на её скорость vec{V}:
    vec{q}=m*{vec{V}}.
  • Количество движения механической системы равно векторной сумме количества движения её точек.
    vec{Q}={Sigma}m_k*{vec{V_k}} или
    vec{Q}=m*{vec{V_C}},
    где m — масса механической системы, vec{V_C} — вектор скорости центра масс системы.
  • Кинетическая энергия материальной точки — это скалярная величина Т, равная половине произведения массы точки на квадрат её скорости:
    T={m*v^2}/2.
  • Кинетическая энергия механической системы равна сумме кинетических энергий всех её точек:
    T={Sigma}T_k.
    Принцип Даламбера

  • Формулировка принципа Даламбера: если в любой момент времени к действующим на точку силам присоединить силы инерции, то полученная система сил будет уравновешенной:
    {Sigma}vec{F_k}+{Sigma}vec{{F_k}^u}=0.
  • Для механической системы:
    delim{}{matrix{2}{5}{{{Sigma}vec{F_k}} {+} {{Sigma}vec{{F_k}^u}} {=} {0~} {{Sigma}vec{M}(vec{F_k})} {+} {{Sigma}vec{M}(vec{{F_k}^u})} {=} {0~}}}{rbrace}.

Примеры решения задач

Решение примеров по теме: «Статика твердого тела»

Пример 1. Условия равновесия

Рисунок к примеру 1. Задача на уравнения равновесия
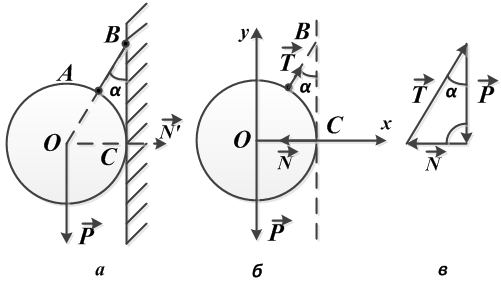
Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.

Дано: P = 10 Н; α = 45°
Найти: N, T — ?

Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.

Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).

Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).

При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).

В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:
N=P*tg{alpha};~T=P/{cos{alpha}}

После подстановки в формулы числовых значений, получим:
N=10*tg{45^{circ}}=10*1=10~H;~T=10/{cos{45^{circ}}}=10/{0,707}=14,142~H.

Ответ: N=10~H;~T=14,142~H.

Решение примеров по теме: «Кинематика»

Пример 2. Уравнение траектории точки

Дано:
Движение точки задано уравнениями x=2sint;~y=4cos{2t};
(x, у — в сантиметрах, t — в секундах).
Найти: уравнение траектории точки в координатной форме.

Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем sint=x/2 и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:
y=4cos{2t}=4({cos}^2{t}-{sin}^2{t})=4(1-2{sin}^2{t})=4(1-2{{x^2}/4})=4-2{x^2}.

Опуская промежуточные выражения, получаем уравнение траектории:
y=4-2x^2.

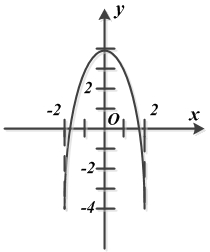Рисунок к примеру 2. Уравнение траектории движения точкиУравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0, 4). Траекторией служит кусок этой параболы, заключенный между точками с координатами (-2, -4) и (2, -4).

Ответ: y=4-2x^2.

Решение примеров по теме: «Динамика»

Пример 3. Основной закон динамики точки

Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.

Дано: m = 10 кг; a = 0,5 м/с2.
Найти: F — ?

Решение.
Согласно основному закону динамики: F=m*a.

Подставив значения в формулу, получим:
F=m*a=10*0,5=5~ H

Ответ: сила, сообщающая массе, равной 10 кг,
ускорение 0,5 м/с2, равна 5 Н.

В помощь студенту
    Формулы, правила, законы, теоремы, уравнения, примеры решения задач

  • Теоретические основы электротехники
  • Электрические машины
  • Высшая математика

Список литературы:
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах.
Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие.

Источник

Макеты страниц

Выше отмечалось, что основная задача механики голономных систем становится определенной для класса идеальных связей. Действительно, пусть на систему из точек наложено голономных идеальных связей. Число проекций виртуальных перемещений точек на координатные оси или, иначе говоря, число вариаций координат точек равно Так как вариации координат подчинены уравнениям (24.6), то вариаций являются зависимыми, а вариаций независимыми. Зависимые вариации могут быть единственным образом выражены через независимые, поскольку детерминант из коэффициентов при зависимых вариациях в системе (24.6), по предположению, отличен от нуля (в противном случае среди связей будут такие, которые являются следствием остальных). Учтем далее, что кроме требования голономности связей выполняется требование их идеальности (см. (24.7)). В этом условии зависимых вариаций с помощью (24.6) можно выразить через независимых вариаций. После такой подстановки (для того, чтобы удовлетворить требованию идеальности) следует приравнять нулю коэффициенты при независимых вариациях. Тем самым можно получить соотношений между реакциями связей и радиусами-векторами точек. Таким образом, основная задача динамики несвободной системы с голономными идеальными связями является определенной, поскольку число уравнений и число неизвестных функций в этом случае совпадают.

Рассмотренное сейчас непосредственное исключение зависимых вариаций координат можно в общем случае провести методом неопределенных множителей Лагранжа. Изложим существо этого метода. В силу идеальности и голономности связей из условий (24.7) и (24.6) имеем

Умножая каждое из последних соотношений на соответствующий неопределенный скалярный множитель и складывая все полученные результаты с условием идеальности, придем к соотношению

котором вариаций координат являются зависимыми, а независимыми. Подберем множителей так, чтобы коэффициенты при зависимых вариациях в (25.2) обратились в нуль. Этот подбор можно провести единственным образом, так как детерминант из коэффициентов при зависимых вариациях в системе (24.6) отличен от нуля (по предположению о связях). С другой стороны, коэффициенты при независимых вариациях в (25.2) должны равняться нулю в силу условия идеальности.

Итак, коэффициенты при всех , должны быть приравнены нулю. В результате приходим к заключению, что между реакциями идеальных голономных связей и функциями определяющими уравнения связей, имеют место соотношения

Соотношения (25.3) являются необходимым условием обращения в нуль виртуальной работы реакций связей, т. е. необходимым условием идеальности голономных связей. Можно непосредственно убедиться и в достаточности этого условия.

Проиллюстрируем исключение зависимых вариаций координат на примере точки, движущейся по гладкой окружности, наклоненной под углом а к горизонту. Эта кривая представляет собой пересечение сферы и наклонной плоскости. Следовательно, на точку наложены две голономные связи (см. (24.4))

(начало координат помещено в центр сферы, ось направлена по вертикали вверх, а плоскость проходит через центр сферы и ось и наклонена к оси под углом а). Так как кривая гладкая, то условие идеальности (24.7) выполняется:

Виртуальное перемещение точки подчинено системе двух уравнений (см.

поэтому одна из вариаций координат, например является независимой. Выразим зависимые вариации через независимую что можно осуществить, поскольку соответствующий детерминант отличен от нуля:

Используя полученные выражения

и исключая из условия идеальности зависимые вариации, найдем

Отсюда видно, что между проекциями реакции связей и радиуса-вектора точки имеет место соотношение

Это же соотношение можно получить методом неопределенных множителей. Действительно, умножая уравнения для вариаций координат на соответственно и складывая результаты умножения с условием идеальности связей, находим (см. (25.2))

Затем подберем множители так, чтобы коэффициенты этого уравнения при зависимых вариациях и обратились в нуль; тогда

Указанный подбор множителей можно осуществить единственным способом, так как два последних соотношения являются системой, которую можно разрешить относительно и поскольку соответствующий детерминант отличен от нуля:

(этот детерминант равен детерминанту, использованному выше).

После указанного подбора и следует приравнять нулю коэффициент при независимой вариации т. е. положить

В результате придем к соотношению (см. (25.3))

которое в декартовых координатах имеет вид

Исключая отсюда найдем ранее полученное соотношение между проекциями векторов

Итак, реакции идеальных голономных связей являются линейными формами относительно градиентов функций определяющих уравнения связей (24.4). Подставляя (25.3) в (23.6), получим уравнения движения механической системы с голономными идеальными связями, т. е. уравнения Лагранжа с реакциями связей или уравнения Лагранжа первого рода,

Здесь силы являются заданными функциями Неизвестными в этих уравнениях являются все радиусы-векторы точек и множители Лагранжа Число уравнений и число неизвестных функций совпадают и равны

Подчеркнем, что реакции связей определяются в результате решения уравнений (25.4) и, следовательно, зависят от заданных сил, поэтому заданные силы часто называют активными силами, а реакции связей — пассивными. Такая зависимость одних сил от других появляется в результате упрощения представлений о реальном взаимодействии тел: само наложение связей на систему представляет собой по существу такое упрощение (например, в задаче о сферическом маятнике мы пренебрегаем упругими свойствами нити подвеса и тем самым налагаем связь).

При применении уравнений Лагранжа возникает также вопрос о выполнении условия идеальности связей. Выше мы видели, что это требование связано с определенными физическими допущениями, которые не всегда выполняются, например наличие сил трения на голономных связях делает их неидеальными. Однако всегда можно выделить нормальные составляющие реакций, которые будут удовлетворять условию идеальности (24.7); тогда остальные составляющие реакций должны быть заданы как функции положений, скоростей точек и времени.

Законы изменения импульса, кинетического момента и энергии системы при наличии связей могут быть получены из уравнений Лагранжа (25.4) так же, как аналогичные законы для

свободных систем были получены из уравнений Ньютона (3.5) с помощью закона (3.6). В самом деле, учитывая, что по отношению к исследуемой системе связи могут быть как внутренними, так и внешними, найдем

где — сумма реакций внутренних и внешних связей на -тую точку; сумма реакций внешних связей; — сумма моментов реакций внешних связей. По сравнению с законами (9.15), (10.5) и (11.18) здесь появились дополнительные члены: сумма внешних реакций и их моменты, а также мощность как внутренних, так и внешних реакций.

Мощность реакций можно представить и в другом виде, используя идеальность и голономность связей. Действительно имея в виду (25.3) и (24.5), получим

Это выражение позволяет записать уравнение (25.7) в виде

Законы сохранения импульса и момента при наличии связей должны быть сформулированы в соответствии с (9.16) и (10.6), только к требованиям на заданные внешние силы добавятся аналогичные требования к реакциям внешних связей. Что касается закона сохранения энергии при наличии связей, то он имеет место при условиях (11.19) и стационарности идеальных голономных связей, когда

Во многих случаях применение законов сохранения упрощает решение задач о движении несвободных систем. В свою очередь законы сохранения могут быть связаны с симметрией заданных силовых полей и связей. Поэтому выбор координат целесообразно осуществлять с учетом этой симметрии.

Рассмотрим некоторые примеры на составление и решение уравнений Лагранжа с реакциями связей.

Пример 25.1. Точка на колеблющейся горизонтальной плоскости.

Точка массы движется по колеблющейся горизонтальной гладкой плоскости. Найти положение точки и реакцию связи как функции времени, если плоскость колеблется в направлении, перпендикулярном плоскости, с амплитудой а и частотой , а напряженность поля тяжести равна

Выберем систему координат так, как это показано на рис. 23.2, а, т. е. направим ось коллинеарно вектору тогда систему уравнений (25.4) можно записать в виде

Здесь учтено, что плоскость является гладкой, поскольку составляющие реакции приравнены нулю.

Из первых двух уравнений движения находим

а из третьего уравнения движения и уравнения связи получим, что

Проекции импульса точки на оси сохраняются, так как проекции заданной силы и реакции связи на эти оси равны нулю; кроме того, сохраняется проекция момента импульса точки на ось поскольку проекции момента заданной силы и момента реакции на эту ось равны нулю. Что касается энергии, то она изменяется со временем согласно уравнению.

Обратим внимание на то, что если частота колебаний плоскости достаточно мала Если же то – будет отрицательной на интервалах времени

где — целые неотрицательные числа. Это

связано с тем, что на указанных интервалах времени компонента ускорения точки отрицательна и достигает большой величины.

Пример 25.2. Точка на расширяющейся цилиндрической поверхности.

Точка массы движется в поле тяжести по расширяющейся гладкой цилиндрической поверхности с вертикальной осью. Найти закон движения: точки, если напряженность поля тяжести равна а радиус цилиндра увеличивается с постоянной скоростью ро-Учитывая симметрию связи, местим ось с осью цилиндра, а ось Ох (или Оу) направим произвольно (рис. 25.1). Из тех же соображений симметрии будем использовать цилиндрические координаты. Тогда, разлагая обе части уравнения (25.4) по ортам пр, получим

Рис. 25.1

Здесь учтено, что реакция перпендикулярна к цилиндрической поверхности и, следовательно, только отлична от нуля.

Используя второе из уравнений движения, найдем первый интеграл

который по существу представляет собой интеграл площадей. Отсюда

Интегрируя это уравнение, найдем

а интегрируя третье уравнение движения, получим

Наконец, подставляя функции в первое из уравнений движения, найдем реакцию связи

Полная энергия точки Е не сохраняется вследствие нестационарности связи.

Пример 25.3. Точка на пересечении сферы и движущейся плоскости.

Точка массы движется по пересечению неподвижной гладкой сферы радиуса а и гладкой горизонтальной плоскости, движущейся в вертикальном направлении по закону Найти закон движения точки и реакции связей для

Рис. 25.2

Учитывая симметрию связей, поместим начало координат в центр сферы, а ось направим коллинеарно вектору (рис. 25.2). Тогда систему (25.4) с уравнениями связей можно записать в виде

Замечая, что момент импульса точки относительно оси постоянен и что от цилиндрической координаты уравнения связей не зависят, спроектируем обе части уравнения Лагранжа на цилиндрические орты. В результате получим следующую систему уравнений:

Из уравнений связей и второго уравнения движения найдем функции :

(здесь учтено, что в начальный момент времени

Интегрируя получим угол как функцию времени:

Множители и определим из первого и третьего уравнений движения:

Отсюда с помощью соотношений

находим реакции связей

1

Оглавление

  • ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
  • ЧАСТЬ I. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
  • Глава I. ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ МЕХАНИКИ
  • § 1. Понятия о материальной точке, о пространстве и времени
  • § 2. Понятия о силе и массе
  • § 3. Понятие об инерциальной системе отсчета и законы Ньютона. Принцип относительности Галилея
  • § 4. Решение уравнений движения и начальные условия
  • Глава II. ЗАКОНЫ ИЗМЕНЕНИЯ И СОХРАНЕНИЯ ИМПУЛЬСА, КИНЕТИЧЕСКОГО МОМЕНТА И ЭНЕРГИИ
  • § 5. Законы изменения и сохранения импульса и момента импульса материальной точки
  • § 6. Законы изменения и сохранения энергии материальной точки
  • § 7. Движение в центрально-симметричном поле
  • § 8. Движение под действием силы, обратно пропорциональной квадрату расстояния до центра силы. Законы Кеплера
  • § 9. Движение центра масс; законы изменения и сохранения импульса системы
  • § 10. Законы изменения и сохранения кинетического момента системы
  • § 11. Законы изменения и сохранения энергии системы
  • Глава III. ЗАДАЧА ДВУХ ТЕЛ И ТЕОРИЯ РАССЕЯНИЯ ЧАСТИЦ
  • § 12. Задача двух тел
  • § 13. Упругое рассеяние частиц
  • § 14. Поперечные сечения рассеяния
  • § 15. Распад частиц
  • Глава IV. ДВИЖЕНИЕ ОТНОСИТЕЛЬНО НЕИНЕРЦИАЛЬНЫХ СИСТЕМ ОТСЧЕТА
  • § 16. Положение системы отсчета (твердого тела)
  • § 17. Поступательное движение и изменение ориентации системы отсчета (твердого тела)
  • § 18. Общий случай движения системы отсчета (твердого тела)
  • § 19. Положение, скорость и ускорение материальной точки относительно разных систем отсчета
  • § 20. Уравнение движения материальной точки относительно неинерциальной системы отсчета; силы инерции
  • § 21. Законы изменения кинетического момента и кинетической энергии относительно поступательно движущейся системы центра масс
  • § 22. Законы изменения и сохранения импульса, кинетического момента и энергии относительно произвольных неинерциальных систем отсчета
  • Глава V. УРАВНЕНИЯ ЛАГРАНЖА
  • § 23. Основная задача динамики несвободной системы и понятие о связях
  • § 24. Действительные, возможные и виртуальные перемещения; идеальные связи
  • § 25. Уравнения Лагранжа с реакциями связей; законы изменения импульса, кинетического момента и энергии для систем со связями
  • § 26. Уравнения Лагранжа в независимых координатах и общее уравнение механики; циклические координаты и симметрия силового поля и связей
  • § 27. Структура уравнений движения в независимых координатах и функция Лагранжа
  • § 28. Законы сохранения обобщенного импульса и обобщенной энергии
  • § 29. Ковариантность уравнений Лагранжа в независимых координатах
  • Глава VI. ЛИНЕЙНЫЕ КОЛЕБАНИЯ
  • § 30. Собственные одномерные колебания
  • § 31. Положение устойчивого равновесия
  • § 32. Собственные и главные колебания системы под действием потенциальных сил
  • § 33. Собственные колебания системы под действием потенциальных, гироскопических и диссипативных сил
  • § 34. Вынужденные колебания
  • Глава VII. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
  • § 35. Собственные колебания и метод Крылова — Боголюбова
  • § 36. Вынужденные колебания и резонанс
  • Глава VIII. ДИНАМИКА ТВЕРДОГО ТЕЛА
  • § 37. Уравнения движения твердого тела
  • § 38. Тензор инерции
  • § 39. Плоскопараллельное движение твердого тела
  • § 40. Движение твердого тела с одной неподвижной точкой. Уравнения Эйлера
  • § 41. Линейные неголономные связи
  • Глава IX. УРАВНЕНИЯ ГАМИЛЬТОНА
  • § 42. Канонические уравнения
  • § 43. Фазовое пространство и теорема Лиувилля
  • § 44. Скобки Пуассона
  • § 45. Уравнение Гамильтона — Якоби
  • § 46. Метод разделения переменных
  • § 47. Движение материальной точки и волновой процесс
  • § 48. Интегральный инвариант Пуанкаре — Картана
  • § 49. Канонические преобразования
  • § 50. Переменные «действие — угол» и адиабатические инварианты
  • § 51. Уравнения движения и интегральные вариационные принципы
  • ЧАСТЬ II. ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД
  • § 52. Физически бесконечно малая частица
  • § 53. Деформация малой частицы
  • § 54. Законы сохранения массы, изменения импульса и кинетического момента
  • § 55. Уравнение изменения кинетической энергии. Законы термодинамики
  • Глава XI. ИДЕАЛЬНАЯ ЖИДКОСТЬ
  • § 56. Уравнения движения идеальной жидкости
  • § 57. Основные теоремы динамики идеальной жидкости
  • § 58. Потоки импульса и энергии
  • § 59. Несжимаемая жидкость
  • § 60. Звуковые волны
  • § 61. Ударные волны
  • § 62. Магнитогидродинамика идеальной жидкости
  • Глава XII. ВЯЗКАЯ ЖИДКОСТЬ
  • § 63. Тензор напряжений и уравнения движения
  • § 64. Уравнение Навье—Стокса
  • § 65. Малые колебания
  • § 66. Магнитогидродинамика вязкой жидкости
  • ПРИЛОЖЕНИЕ К ГЛАВЕ XII
  • Глава XIII. ИДЕАЛЬНО УПРУГОЕ ТЕЛО
  • § 67. Закон Гука и уравнения изменения импульса
  • § 68. Равновесие изотропных тел
  • § 69. Упругие волны
  • ПРИЛОЖЕНИЕ К ГЛАВЕ XIII
  • ЛИТЕРАТУРА
Источник

Добавить комментарий