Статика — раздел механики, изучающий условия равновесия тел.
Виды равновесия
Устойчивое равновесие |
|
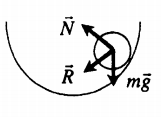 |
Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (Ep min). |
Неустойчивое равновесие |
|
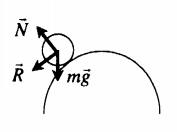 |
Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (Ep max). |
Безразличное равновесие |
|
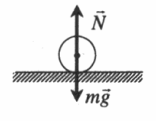 |
При выведении тела из положения безразличного равновесия дополнительных сил не возникает. |
Момент силы
Определение
Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:
M = Fd
M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).
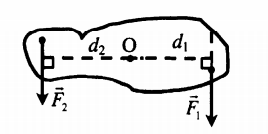
Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?
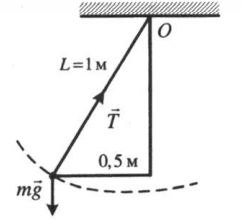
Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:
M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)
Момент силы может быть положительным и отрицательным.
Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:
M1 = F1d1
Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:
M2 = F2d2
Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
∑Mi=0
Иначе правило моментов можно сформулировать так:
Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.
∑Mпо час. стр.=∑Mпр. час. стр.
Условия равновесия тел
| Тело не участвует в поступательном движении: |
∑→Fi=0; →vo=0 |
| Тело не участвует во вращательном движении: |
∑Mi=0; ω0=0 |
| Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении) |
∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0 |
Простые механизмы
Определение
Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.
Наклонная плоскость |
|
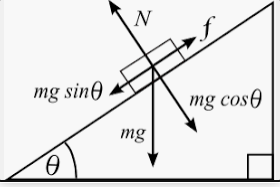 |
Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsinθ<mg |
Рычаг |
|
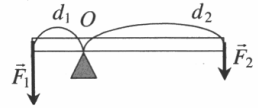 |
Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2=d2d1 |
Неподвижный блок |
|
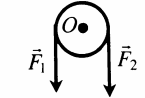 |
Изменяет направление действия силы. Модули и плечи сил при этом равны: F1 = F2 M1 = M2 |
Подвижный блок |
|
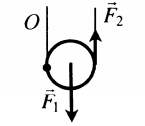 |
Дает выигрыш в силе в 2 раза:
d1 = R d2 = 2R F1 = 2F2 |
Клин |
|
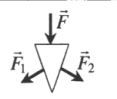 |
Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2 |
Золотое правило механики
При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.
Задание EF22660
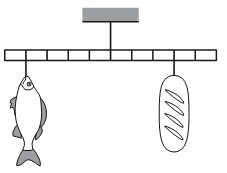 Мальчик взвесил рыбу на самодельных весах с коромыслом из лёгкой рейки (см. рисунок). В качестве гири он использовал батон хлеба массой 0,8 кг. Определите массу рыбы.
Мальчик взвесил рыбу на самодельных весах с коромыслом из лёгкой рейки (см. рисунок). В качестве гири он использовал батон хлеба массой 0,8 кг. Определите массу рыбы.
Алгоритм решения
1.Записать исходные данные.
2.Записать правило моментов и выполнить решение в общем виде.
3.Подставить известные данные и вычислить искомую величину.
Решение
Известна лишь масса батона: m1 = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:
d1 = 0,3
d2 = 0,4
Запишем правило моментов:
F1 d1 = F2 d2
Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:
m1gd1 = m2gd2
m1d1 = m2d2
Отсюда масса рыбы равна:
m2=m1d1d2=0,8·0,30,4=0,6 (кг)
Ответ: 0,6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18706
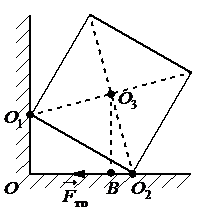 Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения Fтр относительно оси, проходящей через точку О3 перпендикулярно плоскости чертежа, равно…
Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения Fтр относительно оси, проходящей через точку О3 перпендикулярно плоскости чертежа, равно…
Ответ:
а) 0
б) О2О3
в) О2В
г) О3В
Алгоритм решения
- Сформулировать определение плеча силы.
- Найти плечо силы трения и аргументировать ответ.
Решение
Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О3В.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 9.6k
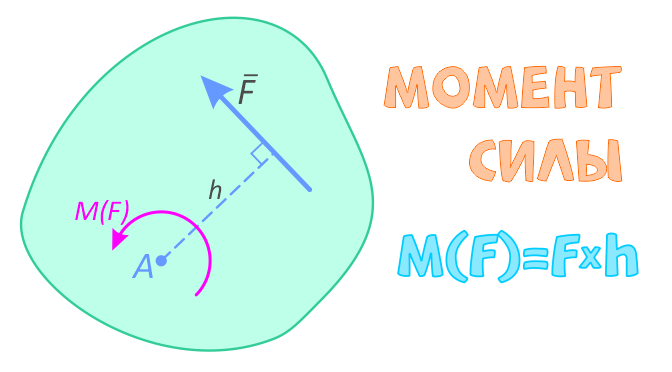

Моментом силы называют вращательное усилие создаваемое вектором силы относительно твердого тела, оси или точки.
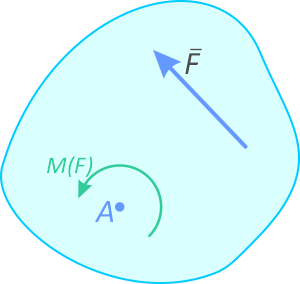
Обозначение: M, m или M(F).
Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]
Аналогом момента силы является момент пары сил.
Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.
Определение
Момент определяется как произведение силы F на плечо h:
M(F)=F×h
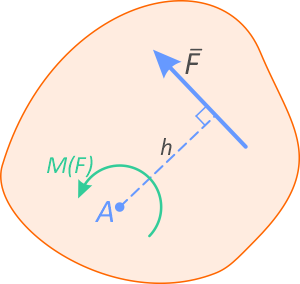
Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.
Наш короткий видеоурок про момент силы с примерами:
Другие видео
Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки вращения создает момент M=7×0,35=2,45 кНм.
Пример момента силы
Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.
Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.
Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.
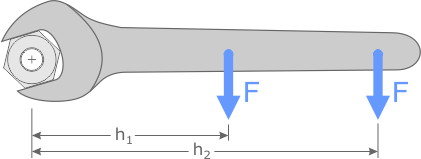
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h2>h1).
Плечом при этом служит расстояние от центра гайки до точки приложения силы.
Плечо момента силы
Рассмотрим порядок определения плеча h момента:
Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.

Покажем линию действия силы F (штриховая линия)
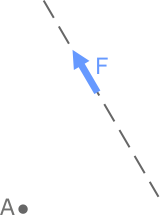
Проведем из точки A перпендикуляр h к линии действия силы
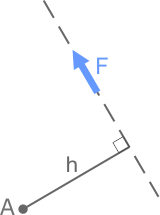
Длина отрезка h есть плечо момента силы F относительно точки A.
Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).
Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.
Примеры расчета момента силы
Сила расположена перпендикулярно оси стержня
Если сила F приложена перпендикулярно к оси бруса и известно расстояние между точками A и B.

То момент силы F относительно точки A:
МA=F×AB
Сила расположена под углом к оси стержня
В случае, если сила F приложена под углом α к оси балки

Момент силы относительно точки B:
MB=F×cosα×AB
Известно расстояние от точки до линии действия силы
Если известно расстояние от точки где определяется момент до линии действия силы (плечо h)
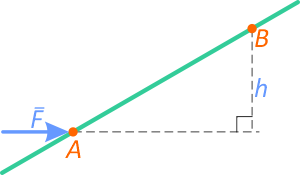
Момент силы относительно точки B:
MB=F×h
См. также:
- Примеры решения задач >
- Момент силы относительно точки
- Момент силы относительно оси
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Содержание:
- Момент силы
- Момент силы относительно точки (центра)
- Момент силы относительно оси
- Зависимость между моментом силы относительно точки и оси, проходящей через эту точку
- Моменты силы относительно координатных осей
- Теорема Вариньона для пространственной системы сходящихся сил (Теорема о моменте равнодействующей силы)
Момент силы (момент силы относительно точки; также: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — эо векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Момент силы
Система сходящихся сил, которая будет рассмотрена в главе 2, является особой среди
систем сил. Только в этой системе линии действия сил имеют одну точку пересечения. Поэтому для ее изучения достаточно основных понятий статики, рассмотренных в разделе 1. Для изучения других систем сил необходимо ознакомиться с понятиями момента силы и пары сил.
Понятие о моменте силы – одно из основных понятий механики, которое широко используется и в теоретических исследованиях и при практических расчетах. К понятию момента силы человечество пришло, рассматривая равновесие и движение тел, имеющих точку или ось вращения (в частности блоков и рычагов, которые использовались в практике еще до нашей эры).
Например, на неподвижный блок (рис. 3.1) действует сила  , вращающей его вокруг горизонтальной оси О. Стержень АВ (рис. 3.2), который имеет неподвижную шарнирную опору A, будет вращаться вокруг оси шарнира под действием собственной силы тяжести
, вращающей его вокруг горизонтальной оси О. Стержень АВ (рис. 3.2), который имеет неподвижную шарнирную опору A, будет вращаться вокруг оси шарнира под действием собственной силы тяжести  В обоих примерах сила обуславливает вращательное движение тела. По мере вращательного действия силы на тело является момент силы.
В обоих примерах сила обуславливает вращательное движение тела. По мере вращательного действия силы на тело является момент силы.


Момент силы относительно точки (центра)
Заданная сила  , изображена вектором
, изображена вектором  , приложенная к некоторому телу в точке А. Определим момент силы
, приложенная к некоторому телу в точке А. Определим момент силы  относительно точки О (рис. 3.3). Векторным моментом силы относительно точки О называется вектор, приложенный в точке О, равный векторному произведению радиуса вектора точки приложения силы на вектор силы:
относительно точки О (рис. 3.3). Векторным моментом силы относительно точки О называется вектор, приложенный в точке О, равный векторному произведению радиуса вектора точки приложения силы на вектор силы:

где  – радиус-вектор точки приложения силы относительно точки О.
– радиус-вектор точки приложения силы относительно точки О.
Определим величину (модуль) и направление вектора  . Согласно понятиям и свойствам векторного произведения двух векторов, величина (Модуль) момента силы
. Согласно понятиям и свойствам векторного произведения двух векторов, величина (Модуль) момента силы  относительно точки О равна:
относительно точки О равна:

Обозначим  . Поскольку
. Поскольку 
 Тогда:
Тогда:

где  (рис. 3.3) – высота
(рис. 3.3) – высота  опущенная из вершины В (с точки О) на сторону АВ этого треугольника, совпадает с линией действия силы. Короткое расстояние от точки О до линии действия силы называется плечом силы относительно этой точки. Из этого следует, что модуль (величина) момента силы относительно точки равна произведению величины силы на ее плечо относительно этой точки.
опущенная из вершины В (с точки О) на сторону АВ этого треугольника, совпадает с линией действия силы. Короткое расстояние от точки О до линии действия силы называется плечом силы относительно этой точки. Из этого следует, что модуль (величина) момента силы относительно точки равна произведению величины силы на ее плечо относительно этой точки.

Вектор  направляется по правилу векторного произведения: векторный момент силы относительно точки (Центра) является перпендикулярным к плоскости, в которой размещены сила и точка (центр) так, чтобы с его конца было видно попытки силы возвращать тело вокруг точки (Центра) против хода часовой стрелки.
направляется по правилу векторного произведения: векторный момент силы относительно точки (Центра) является перпендикулярным к плоскости, в которой размещены сила и точка (центр) так, чтобы с его конца было видно попытки силы возвращать тело вокруг точки (Центра) против хода часовой стрелки.
Заметим, что  . Поэтому:
. Поэтому:

Модуль момента силы относительно точки равен удвоенной площади треугольника, вершинами которого является точка и начало и конец вектора 
Если линия действия силы проходит через точку (центр), то h = 0, и из формулы (3.2) видно, что момент силы относительно этой точки будет равняться нулю.
Момент силы относительно точки не изменяется при переносе силы вдоль ее линии действия, поскольку неизменным остается плечо силы относительно точки (рис. 3.4).

Если на тело действует плоская система сил, то векторы моментов всех сил системы относительно некоторого центра, что лежит в плоскости действия сил, будут перпендикулярны этой плоскости, а следовательно, параллельные и их можно считать скалярными величинами, которые отличаются только величиной и знаками.
В этом случае целесообразно ввести понятие алгебраического момента силы относительно точки (центра), равный взятом со знаком «+» или «-» произведения модуля силы на плечо относительно этой точки (центра)

Будем считать момент положительным, если сила пытается вращать тело вокруг точки (центра) против хода часовой стрелки (рис. 3.5, а), и отрицательным – если по ходу часовой стрелки (рис. 3.5, б). Единицы момента силы: 

Момент силы относительно оси
Изучая пространственные системы сил, будем использовать понятие момента силы относительно оси.
Моментом силы относительно оси называется величина, равная алгебраическому моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Пусть к телу в некоторой точке А приложена сила  (Рис. 3.6). определим момент силы
(Рис. 3.6). определим момент силы  относительно произвольной оси
относительно произвольной оси  . Проведем плоскость П, перпендикулярную оси
. Проведем плоскость П, перпендикулярную оси  .
.
Точку пересечения плоскости П с осью  обозначим А. Спроектируем силу
обозначим А. Спроектируем силу  на плоскость П и получим силу
на плоскость П и получим силу 

Согласно определению 
Таким образом, чтобы определить момент силы относительно оси, необходимо:
– спроектировать эту силу на плоскость, перпендикулярную оси;
– найти точку пересечения оси с этой перпендикулярной плоскостью;
– определить алгебраический момент полученной проекции относительно точки пересечения оси с плоскостью.
Из формулы (3.5) следует, что момент силы относительно оси равен нулю, если:
1) сила параллельна оси, тогда 
2) линия действия силы пересекает ось, тогда 
Эти два условия эквивалентны одному условию: момент силы относительно оси равен нулю, когда сила и ось лежат в одной плоскости. поскольку момент силы относительно оси  , то согласно принятому правилу знаков моментов следует, что момент силы относительно оси положительный, если, смотря с конца оси, видим, что проекция этой силы на плоскость, перпендикулярную оси, пытается вращать тело вокруг оси против часовой стрелки (рис. 3.7, а). если вращение происходит в направлении хода часовой стрелки, то момент силы относительно оси будет отрицательным (рис. 3.7, б). Можно доказать, что момент силы относительно оси не зависит от выбора точки О на этой оси.
, то согласно принятому правилу знаков моментов следует, что момент силы относительно оси положительный, если, смотря с конца оси, видим, что проекция этой силы на плоскость, перпендикулярную оси, пытается вращать тело вокруг оси против часовой стрелки (рис. 3.7, а). если вращение происходит в направлении хода часовой стрелки, то момент силы относительно оси будет отрицательным (рис. 3.7, б). Можно доказать, что момент силы относительно оси не зависит от выбора точки О на этой оси.

Зависимость между моментом силы относительно точки и оси, проходящей через эту точку
Теорема 3.1. Проекция векторного момента силы относительно точки на ось, проходящей через эту точку, равен моменту силы относительно этой оси.
Доказательство. Сила  приложена в точке А пространства. Выберем произвольную точку О и проведем оси
приложена в точке А пространства. Выберем произвольную точку О и проведем оси  (рис. 3.8). Определим момент силы
(рис. 3.8). Определим момент силы  относительно оси
относительно оси  и относительно точки О на ней.
и относительно точки О на ней.
Известно, что 

где 
Из курса элементарной геометрии известно, что 
где  – угол между плоскостями этих треугольников, а следовательно, и угол между перпендикулярами к этим плоскостей.
– угол между плоскостями этих треугольников, а следовательно, и угол между перпендикулярами к этим плоскостей.
Поскольку вектор  перпендикулярный плоскости
перпендикулярный плоскости , а ось
, а ось  перпендикулярна к
перпендикулярна к 

Учитывая равенства (3.6), (3.7), получим 
Знак  полностью определяется знаком
полностью определяется знаком  .
.
Поскольку

что и требовалось доказать.
Моменты силы относительно координатных осей
Пусть на тело действует сила  приложенная в точке А (рис. 3.9). выберем произвольную точку О и из нее проведем оси декартовой системы координат.
приложенная в точке А (рис. 3.9). выберем произвольную точку О и из нее проведем оси декартовой системы координат.
Определим момент силы  относительно этих осей. Для этого запишем выражение для момента силы
относительно этих осей. Для этого запишем выражение для момента силы  относительно точки О.
относительно точки О.

Согласно (3.1), где
где  – радиус-вектор точки А относительно точки О.
– радиус-вектор точки А относительно точки О.
Вектор силы  и радиусвектор
и радиусвектор  через проекции на оси координат выражаются:
через проекции на оси координат выражаются:

где  – координаты точки А;
– координаты точки А;  – орты выбранной системы координат.
– орты выбранной системы координат.
Тогда векторное произведение  можно записать в виде определителя:
можно записать в виде определителя:

Раскрывая этот определитель, получим

Представим векторный момент  через его проекции на оси координат:
через его проекции на оси координат:

Сравнивая правые части равенств (3.9) и (3.10), получим:

Поскольку точка О принадлежит осями  , то из формул (3.11), учитывая зависимость (3.8), получим выражения:
, то из формул (3.11), учитывая зависимость (3.8), получим выражения:

Теорема Вариньона для пространственной системы сходящихся сил (Теорема о моменте равнодействующей силы)
Теорема 3.2. Момент равнодействующей пространственной системы сходящихся сил
относительно некоторого центра (точки) равна векторной сумме моментов составляющих сил относительно того же центра (точки).
Доказательство. На тело действует пространственная система сходящихся сил  линии действия которых пересекаются в точке В (Рис. 3.10, а). заменим
линии действия которых пересекаются в точке В (Рис. 3.10, а). заменим
данную систему сил эквивалентной системой, все силы которой приложенные в точке В
(Рис. 3.10, б). Равнодействующую системы, прилагаемую в той же точке В, обозначим  . Найдем момент равнодействующей
. Найдем момент равнодействующей  относительно точки (центра) О. Согласно формуле (3.1),
относительно точки (центра) О. Согласно формуле (3.1),  где
где  – радиус-вектор точки приложения всех сил системы и равнодействующей относительно центра О.
– радиус-вектор точки приложения всех сил системы и равнодействующей относительно центра О.

Известно, что  . Тогда
. Тогда 
Итак, получили равенство 
Теорема доказана.
Уравнение (3.13) является математическим записи теоремы Вариньона для пространственной системы сходящихся сил.
В случае плоской системы сходящихся сил теорема Вариньона запишется так:

Итак, момент равнодействующей плоской системы сходящихся сил относительно некоторого центра (точки), лежащий в плоскости действия сил, равна алгебраической сумме моментов составляющих сил относительно этого самого центра (точки).
Рассмотрим пример на применение теоремы Вариньона.
Задача. На согнутый под прямым углом стержень АВС действуют силы  и
и  как показано на рис. 3.11. Найти моменты этих сил относительно точки А, если
как показано на рис. 3.11. Найти моменты этих сил относительно точки А, если 

Решение.

Для определения момента силы  относительно точки используем теорему Вариньона.
относительно точки используем теорему Вариньона.
Разложим силу  на две составляющие: горизонтальную
на две составляющие: горизонтальную  и вертикальную
и вертикальную  . Величины этих составляющих
. Величины этих составляющих 
 Тогда, согласно теоремой 3.2, получим:
Тогда, согласно теоремой 3.2, получим:

Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Словосочетания «момент силы» и «вращательный момент» — это синонимы. Можно употреблять любой из них.
Сила может заставлять тело двигаться:
- поступательно,
- или вращательно.
В этой статье будем рассматривать вращательное движение.
Рекомендую также ознакомиться со статьей о видах механического движения (откроется в новой вкладке).
Что такое линия действия силы
Линия действия – это прямая линия, на которой лежит вектор.
Провести эту линию легко. Приложить линейку к вектору и пунктиром провести прямую, продолжив ее в обе стороны от вектора.

Рис. 1. Линия (пунктир), на которой лежит вектор, называется линией действия вектора
Что такое плечо силы и как его нарисовать
Предположим, нужно с помощью ключа закрутить гайку (см. рис. 2).

Рис. 2. Красная точка, вокруг которой вращается ключ — это центр гайки
Винт, на который накручена гайка – это ось вращения. Ключ может вращаться вокруг красной точки. Для упрощения назовем ее кратко: «точка вращения».
Примечание:
Ось вращения проходит перпендикулярно плоскости рисунка через красную точку. Используем вместо оси вращения термин «точка вращения» для простоты.
Рассмотрим следующий рисунок (см. рис. 3)

Рис. 3. Плечо силы – это перпендикуляр ( l ). Он соединяет линию действия силы с точкой вращения
На рисунке 3 черная стрелка – это вектор силы, которая вращает ключ. Пунктир – линия действия силы. Из красной точки к линии действия силы проведен перпендикуляр. Этот перпендикуляр, обозначенный ( l ), называется плечом силы.
Перпендикуляр к линии действия легко провести с помощью прямоугольного треугольника (см. рис. 4):

Рис. 4. Один катет приложим к линии действия силы, вдоль второго проведем перпендикуляр к точке вращения
Плечо силы проводят так:
- взять прямоугольный треугольник;
- приложить один из катетов к линии действия;
- провести перпендикуляр к точке вращения, используя второй катет;
Момент силы, формула
Момент силы (вращательный момент) можно вычислить, когда известны сила и ее плечо.
Перемножим силу на плечо силы, получим момент силы.
[ large boxed { M = F cdot l } ]
( M left( H cdot text{м} right) ) – момент силы (вращательный момент);
( F left( H right) ) – сила, которая вращает тело;
( l left( text{м} right) ) – плечо этой силы;
Примечание:
Отрезок, не перпендикулярный силе, плечом силы не является. Сила и ее плечо всегда перпендикулярны!
Еще одна формула для момента силы
Вращательный момент можно рассчитать еще одним способом.
Для этого вместо плеча силы нужно использовать:
- величину ( d ) и
- угол ( gamma ) между силой и этим расстоянием.
Величина ( d ) – это расстояние между двумя точками:
- точкой, к которой приложена сила
- и точкой, вокруг которой происходит вращение.

Рис. 5. Момент силы можно рассчитать, зная: — силу; — расстояние между точками приложения силы и вращения; — угол между силой и этим расстоянием
На рисунке 5: черная стрелка – это вектор вращающей силы ( vec{ F } ); красная линия – это расстояние ( d ) между точкой приложения силы и точкой вращения.
[ large boxed { M = F cdot d cdot sin(gamma) } ]
Этой формулой во многих случаях пользоваться удобнее, чем формулой, содержащей ( l ) плечо силы.
Когда момент силы обращается в ноль
Рассмотрим внимательнее формулу для момента силы.
[ M = F cdot d cdot sin(gamma) ]
В правой части формулы находятся три множителя: ( F ) , (d) и ( sin(gamma) )
Если любой из трех множителей будет равен нулю, то правая часть уравнения обратится в ноль.
Левая часть уравнения, при этом, также, обратится в ноль. Потому, что между левой и правой частями записан знак равенства.
Кратко: Вращательный момент будет нулевым в любом из таких случаев:
- ( F = 0) – когда вращающая сила отсутствует;
- (d = 0 ) – когда сила приложена к точке вращения;
- ( sin(gamma) = 0 ) – когда сила ( F ) и величина (d ) лежат на одной прямой. В таком случает, угол между величинами ( F ) и (d ) равен нулю;
Действительно: ( sin(0) = 0 ), такое будет, когда ( F || d )
Эти три случая изображены на рисунке 6.

Рис. 6. Сверху вниз представлены три случая, в которых вращательный момент обращается в ноль
На рисунке 6: черная стрелка – это вектор силы, красная линия – это расстояние между точкой приложения силы и точкой вращения.
Сверху вниз представлены три случая для нулевого вращательного момента.
- В верхней части рисунка сила отсутствует;
- Средняя часть рисунка соответствует случаю, когда сила (черная стрелка) приложена к точке, вокруг которой тело может вращаться;
- Внизу — сила ( F ) параллельна величине (d ) — расстоянию между точкой приложения силы и точкой вращения.
4. Статика и механические колебания
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Момент силы, механическое равновесие тела
При одновременном действии на одно тело нескольких сил тело движется с ускорением.
Линия действия силы — прямая, проходящая через вектор силы. Если силы действуют параллельно друг другу, то точки приложения результирующей силы нет.
Момент силы относительно оси вращения — это произведение силы на плечо. [vec{M}=vec{F}vec{l}]
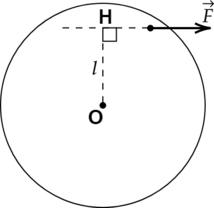
Плечо силы — это расстояние от оси вращения до линия действия силы. В качестве примера на рисунке изображён некий диск, к которому приложена сила (vec{F}). Ось вращения перпендикулярна плоскости чертежа и проходит через точку O. Плечом силы является величина (l = OH), где (displaystyle H) — основание перпендикуляра, опущенного из точки O на линию действия силы.
Момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.
Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил равна нулю.
Условия равновесия тела:
1) Силы уравновешены вдоль любой оси.
2) Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону.
Также условия равновесия тела можно сформулировать следующим образом:
1) Равна нулю векторная сумма всех сил, приложенных к телу.
2) Равна нулю алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной.
Центр тяжести тела — центр параллельных сил тяжести элементарных частей этого тела.
1) Если однородное тело имеет ось симметрии, то центр тяжести находится на этой оси.
2) Если однородное тело имеет плоскость симметрии, то центр тяжести находится в этой плоскости.
3) Если однородное тело имеет центр симметрии, то центр тяжести находится в этой точке.
Виды равновесия
Равновесие называется устойчивым, если после небольших внешних воздействий тело возвращается в исходное состояние равновесия.
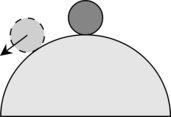
Равновесие называется неустойчивым, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия.
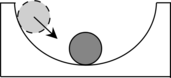
Равновесие называется безразличным, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил равна нулю.
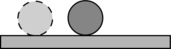
Сила, приложенная к рычагу слева равна 300 Н. Какой длины должно быть ее плечо, чтобы рычаг находился в равновесии, если момент силы, действующей на него справа, равен 90 Н(cdot)м? (Ответ дайте в сантиметрах.)
Пусть (M_1) – момент силы, приложенной к рычагу справа, а (M_2) – слева. Чтобы рычаг находился в равновесии, моменты сил, действующих на него слева и справа, должны быть равны: [M_1 = M_2] В то же время момент силы (M_2) по определению равен произведению силы на ее плечо: [M_2 = Fcdot{l},] где (F) – величина силы, приложенной слева; (l) – длина плеча слева. Исходя из этого получаем, что: [M_1 = Fcdot{l}] Отсюда выразим (l): [l = frac{M_1}{F}] [l = frac{90text{ Н}cdot{text{м}}}{300text{ Н}} = 0,3text{ м} = 30text{ см }]
Ответ: 30
Тело массой 1 кг подвешено к правому плечу невесомого рычага (см. рисунок). К какому делению левого плеча рычага нужно подвесить груз массой 3,5 кг для достижения равновесия?

Пусть масса правого груза (m_1), а левого – (m_2).
Обозначим длину одного деления за (l). Тогда, исходя из рисунка, длина правого плеча равна (l_1 = 7l), а длина левого плеча равна (l_2 = nl), где (n) – количество делений.
Чтобы рычаг достиг равновесия, моменты сил, действующих на него справа и слева, должны быть равны: (M_1 = M_2).
В то же время моменты сил (M_1) и (M_2) по определению равны произведению силы на ее плечо: [M_1 = F_1l_1] [M_2 = F_2l_2] Отсюда получаем: (F_1l_1 = F_2l_2)
Выразим длину левого плеча рычага: (displaystyle{l_2 = frac{F_1l_1}{F_2}})
На оба груза действует единственная сила – сила тяжести, поэтому: [F_1 = m_1g] [F_2 = m_2g] С учетом этого: [l_2 = displaystyle{frac{m_1gcdot{l_1}}{m_2g}} = frac{m_1l_1}{m_2}] [displaystyle{l_2 = frac{1text{ кг}cdot{7l}}{3,5text{ кг}} = 2l}Rightarrow nl = 2l Rightarrow n = 2]
Ответ: 2
Две вершины однородного железного куба объемом (V = 512) см(^3) опираются на две точки горизонтальной и вертикальной поверхностей, как показано на рисунке. Чему равно плечо силы реакции опоры относительно оси, перпендикулярной плоскости чертежа и проходящей через точку (O_3)? (O_2C = sqrt{7}) см (Ответ дайте в метрах.)
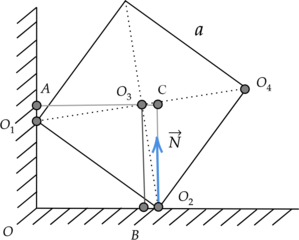
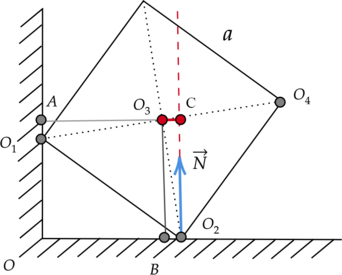
Плечо – это кратчайшее расстояние между осью вращения и линией действия силы. Мысленно продолжим линию действия силы реакции опоры (N) и перпендикуляром соединим ее с прямой, проходящей через точку (O_3). Получаем, что плечом этой силы является отрезок (O_3C).
Воспользуемся геометрией, чтобы найти отрезок (O_3C).
Рассмотрим треугольник (Delta O_1O_2O_4) с прямым углом (O_2): [O_1O_4^2 = O_1O_2^2 + O_4O_2^2] [O_1O_2 = O_2O_4 = a] [displaystyle{O_1O_4 = sqrt{2a^2} = asqrt{2}}] Далее найдем отрезок (O_2O_3): [displaystyle{O_2O_3 = frac{1}{2}O_1O_4} = frac{asqrt{2}}{2}] Рассмотрим треугольник (Delta O_3O_2C) с прямым углом (C): [O_3O_2^2 = O_3C^2 + O_2C^2] [displaystyle{O_3C = {sqrt{O_3O_2^2 – O_2C^2 }}}] [displaystyle{O_3C = {sqrt{left(frac{asqrt{2}}{2}right)^2 – O_2C^2 }}}] Зная объем куба, можно найти его сторону (a): [V = a^3 Rightarrow a = sqrt[3]{V} = sqrt[3]{512text{ см}^3} = 8 text{ см }] Тогда: [displaystyle{O_3C = {sqrt{left(frac{8text{ см}cdotsqrt{2}}{2}right)^2 – (sqrt{7}text{ см})^2 }} = 5 text{ см} = 0,05text{ м }}]
Ответ: 0,05
Две вершины однородного медного куба опираются на две точки горизонтальной и вертикальной поверхностей, как показано на рисунке. Чему равен момент силы трения относительно оси, проходящей через точку (O_1) перпендикулярно плоскости рисунка, если масса куба равна 0,7 кг? (OO_2 = 0,4) м (Ответ дайте в Н(cdot)м)
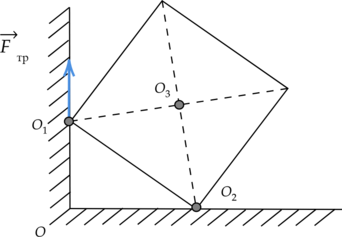
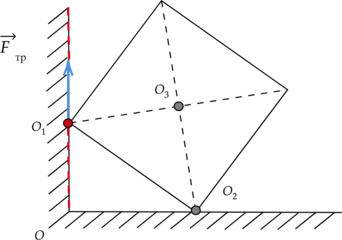
Момент силы трения (M) равен произведению модуля силы трения (F_text{тр}) на ее плечо (l): [M = F_text{тр}cdot{l}] Прямая (OO_1) – линия действия силы трения. По рисунку видно, что длина плеча силы трения (l) относительно точки (O_1) равна нулю (так как ось вращения, проходящая через точку (O_1), перпендикулярна линии действия силы трения).
Следовательно, и момент силы трения (M) так же равен нулю: [M = F_text{тр}cdot{0}text{ м} = 0text{ Н}cdot{text{м }}]
Ответ: 0
Две вершины однородного деревянного куба со стороной (a = 5sqrt{2}) м опираются на две точки горизонтальной и вертикальной поверхностей, как показано на рисунке. Чему равен момент силы тяжести относительно оси, перпендикулярной плоскости чертежа и проходящей через точку (A)? (AO_1 = 3) м (Ответ дайте в МН(cdot)м и округлите до десятых.) 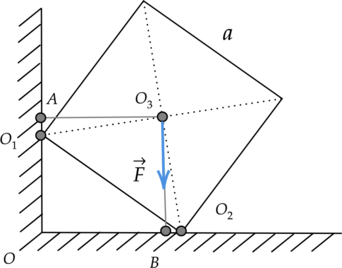
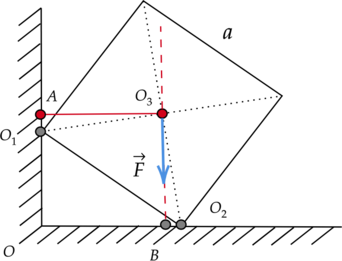
Момент силы тяжести M равен произведению модуля силы тяжести (F) на ее плечо (l): [M = Fcdot{l}] Плечо – это кратчайшее расстояние между осью вращения и линией действия силы. Мысленно продолжим линию действия силы тяжести (F) и перпендикуляром соединим ее с прямой, проходящей через точку (A). Получаем, что плечом силы тяжести является отрезок (AO_3).
Воспользуемся геометрией, чтобы найти отрезок (AO_3).
Рассмотрим треугольник (Delta O_1O_2O_3) с прямым углом (O_3): [O_1O_2^2 = O_1O_3^2 + O_2O_3^2] [O_1O_3 = O_2O_3] [O_1O_2^2 = 2O_1O_3^2] [displaystyle{O_1O_3 = frac{O_1O_2}{sqrt{2}}}] [displaystyle{O_1O_3 = frac{5sqrt{2}}{sqrt{2}}} = 5text{ м }] Рассмотрим треугольник (Delta O_1AO_3) с прямым углом A: [O_1O_3^2 = AO_3^2 + AO_1^2] [AO_3 = sqrt{O_1O_3^2 – AO_1^2}] [AO_3 = sqrt{(5text{ м})^2 – (3text{ м})^2} = 4text{ м }] Сила тяжести равна произведению массы куба (m) на ускорение свободного падения (g): [F = mg] Подставим это значение в исходную формулу: [M = mgcdot{AO_3}] Зная плотность и объем куба, можно найти его массу: [displaystyle{rho =frac{m}{V}},text{ где }V = a^3] [m = rho V = rho a^3] Подставим это значение в предыдущую формулу и найдем искомую величину: [M = rho a^3gcdot{AO_3}] [displaystyle{M = 400text{ }frac{text{кг}}{text{м}^3}cdot{(5sqrt{2}text{ м})}^3cdot{10frac{text{м}}{text{с}^2}}cdot{4}text{ м} approx 5,7text{ М,Н$cdot$м }}]
Ответ: 5,7
На прут массой 1 кг со стороны вертикальной поверхности действует сила трения, равная 3 Н. Найдите момент силы реакции опоры, действующей на него со стороны горизонтальной поверхности, относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, если (AB = 6,5) м, а (AC = 9,7) м. (Ответ дайте в Н(cdot)м и округлите до целого числа.) 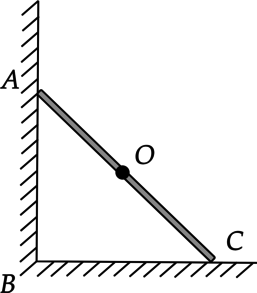
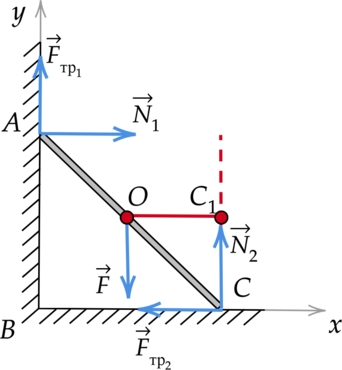
Момент действующей на горизонтальную стенку силы реакции опоры относительно оси, перпендикулярной плоскости рисунка и проходящей через точку (O), равен: [M = N_2l,] где (l) – плечо силы. Мысленно продолжим линию действия силы рекции опоры (N_2) и перпендикуляром соединим ее с прямой, проходящей через точку (O). Получаем, что плечом силы (N_2) является отрезок (OC_1), равный: [displaystyle{OC_1 = frac{BC}{2}} = frac{sqrt{AC^2 – AB^2}}{2}] [OC_1 = frac{sqrt{9,7text{ м}^2 – 6,5text{ м}^2}}{2} = 3,6text{ м }] Чтобы найти неизвестную величину (N_2), укажем все силы, действующие на прут, и запишем второй закон Ньютона с учетом того, что тело находится в равновесии: [vec{F}_{text{тр}1} + vec{N}_1 + vec{F} + vec{N}_2 + vec{F}_{text{тр}2} = 0] Введем оси (OX) и (OY), спроецируем на них все силы. [OX: N_1 – F_{text{тр}2} = 0] [OY: F_{text{тр}1} + N_2 – F = 0] Выразим силу реакции опоры (N_2), действующую на горизонтальную стенку: [N_2 = F – F_{text{тр}1}] Сила тяжести (F) по определению равна: (F = mg), поэтому: [N_2 = mg – F_{text{тр}1}] [N_2 = 1text{ кг}cdot{10text{ }frac{text{м}}{text{c}}^2} – 3text{ H} = 7text{ H }] Подставим найденные значения в начальную формулу: [M = 7{text{ Н}cdot{3,6}text{ м}} = 25,2text{ Н}cdot{text{м}}approx{25}text{ Н}cdot{text{м }}]
Ответ: 25
Группа школьников проводила лабораторную работу, исследуя основные условия равновесия легкого рычага, плечи сил которого равны (l_1) и (l_2). К рычагу с двух сторон ребята подвесили грузы массой (m_1) и (m_2).
Результаты эксперимента были занесены в следующую таблицу:
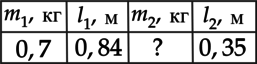
Чему равна масса груза (m_2), если рычаг находился в равновесии? (Ответ дайте в килограммах и округлите до десятых.)
Так как рычаг находился в равновесии, то моменты сил, действующих на него справа и слева, должны быть равны: (M_1 = M_2).
В то же время моменты сил (M_1) и (M_2) по определению равны произведению силы на ее плечо: [M_1 = F_1l_1] [M_2 = F_2l_2] Отсюда получаем: (F_1l_1 = F_2l_2)
На оба груза действует единственная сила – сила тяжести, поэтому: [F_1 = m_1g] [F_2 = m_2g] С учетом этого: (M_1 = m_1gcdot{l_1}) и (M_2 = m_2gcdot{l_2}). Приравняв (M_1) и (M_2), получаем, что: [m_1gcdot{l_1} = m_2gcdot{l_2}] [m_1l_1 = m_2l_2] Выразим массу второго груза (m_2): [displaystyle{m_2 = frac{m_1l_1}{l_2}}] [displaystyle{m_2 = frac{0,7text{ кг}cdot{0,84text{ м}}}{0,35text{ м}}} approx 1,7text{ кг }]
Ответ: 1,7

УСТАЛ? Просто отдохни
