Как найти момент силы шара - Сайт, где вы сможете решить свои вопросы

Момент силы это векторная величина, понятие момента силы используется, в основном, в области задач статики и задач, связанных с вращением деталей (рычагов и др.) в технической механике.

Что такое вращательное движение тела Момент силы Момент инерции

Движение, при котором все точки тела описывают окружности, лежащие в параллельных плоскостях, с центрами, расположенными на одной неподвижной прямой, называется вращательным движением тела.

Прямая О’О» (рис. 2, а) называется осью вращения. Угловая скорость для всех точек вращающегося тела одинакова, линейные скорости различны: чем дальше расположена точка от центра вращения, тем больше ее линейная скорость.

Для того чтобы вызвать вращение тела, к нему надо приложить силу F, которая:

Действует в плоскости Р, перпендикулярной оси вращения.
Не проходит через эту ось.
Направлена под прямым углом к радиусу r, проведенному от оси вращения О’О» к точке приложения силы. При этом действие силы тем значительнее, чем дальше расположена точка ее приложения от оси вращения.

Это учитывается с помощью величины, называемой вращающим моментом или просто моментом силы.

Момент силы

Движение тела называется вращательным, если все его точки движутся по окружностям, центры которых расположены на одной прямой, называемой осью вращения.

Колеса всевозможных машин и механизмов могут вращаться вокруг неподвижной оси; пропеллер самолета, колодезный «журавль», дверь на петлях, откидная крышка школьной парты представляют собой примеры того же случая.

Если вначале тело покоится, то, чтобы вызвать вращение, необходимо подействовать на тело с некоторой силой. Однако не всякая приложенная сила вызовет вращение тела.

Силы, одинаковые по величине, но различные по направлению или приложенные в разных точках, могут вызвать весьма различные эффекты.

Оказывается, сила момента сейчас, действующая на тело, закрепленное на оси, только тогда может вызвать его вращение, когда направление силы не проходит через ось.

Сила, направленная параллельно оси вращения, также не вызывает вращение тела, а только стремится изогнуть ось.

От чего зависит действие силы

Вращающее действие силы зависит не только от ее величины, но и от расстояния между осью вращения и прямой, по которой действует сила.

Кратчайшее расстояние от оси вращения до прямой, по которой действует сила, называется плечом силы.

На рис. плечо силы обозначено буквой l. Величина, характеризующая вращающее действие силы, называется моментом силы и обозначается буквой М.Момент силы измеряется произведением силы на плечо (момент силы формула):

М =Ft.

Момент силы — векторная величина. Направление вектора М определяется поступательным движением буравчика, расположенного вдоль оси вращения, если направление вращения его головки совпадает с направлением действующей силы.

В СИ за единицу момента силы принимается момент силы в один ньютон, имеющий плечо в один метр

1 Н • 1 м = 1 Нм.

Чтобы отличить моменты сил, создающих вращение в противоположные стороны, условились считать моменты сил, вращающих тело против часовой стрелки, положительными, а моменты сил, вращающих тело по часовой стрелке,— отрицательными.

Момент силы, направленной вдоль прямой, проходящей через ось вращения, равен нулю (так как l = 0).

Чтобы получить нужный момент при наименьшем усилии, надо стараться приложить силу как можно дальше от оси вращения, увеличивая тем самым плечо силы и соответственно уменьшая величину силы.

Не случайно дверная ручка закреплена на наибольшем расстоянии от оси вращения

Момент силы относительно центра вращения

Момент силы М относительно центра вращения в общем случае называют векторную величину, численно равную произведению силы F на длину d перпендикуляра, опущенного из центра вращения на направление силы, который называют плечом силы (рис. 2, б) (в нашем случае плечом силы F является радиус r, проведенный из центра вращения О к точке приложения силы — рис. 2, а).

Вектор М момента силы приложен к центру О окружности и направлен вдоль оси вращения в направлении, определяемом по «правилу буравчика».

Если под действием момента силы тело по отношению к наблюдателю вращается по часовой стрелке (рис. 2, а), то момент считается положительным, в противном случае — отрицательным.

Если на теле действует несколько моментов сил, то они складываются алгебраически (т. е. с учетом знака момента).

Для того чтобы тело, имеющее ось вращения, находилось в равновесии, алгебраическая сумма моментов, действующих на него, должна равняться нулю.

Инерция вращающегося тела

Аналогично тому как действие силы при вращательном движении зависит от плеча силы, так и инерция вращающегося тела зависит от расположения его массы относительно оси вращения.

Чем дальше от оси вращения расположена масса тела, тем больше ее инерция. Это можно продемонстрировать с помощью прибора, показанного на рис. 3. На стойке П укреплен блок Б с четырьмя стержнями, по которым могут передвигаться грузы М.

На блок намотана нить, на конце которой подвешена гиря Г. Натяжение нити создает на оси блока вращающий момент, постоянный по величине, под действием которого блок со стержнями приводится во вращение.

Ускорение блока можно определить путем наблюдения времени, в течение которого гиря Г опускается на определенное расстояние, отмечаемое по шкале Ш. Это ускорение зависит от инерции блока.

Если грузы М расположены близко от оси вращения, блок имеет небольшую инерцию и гиря опускается очень быстро. Если передвинуть грузы к краям стержней в положение М’, то инерция блока увеличится и гиря будет опускаться заметно медленнее.

Как увеличить инерцию

Для того чтобы учитывать инерцию при вращательном движении тела, пользуются величиной, называемой моментом инерции.

Момент инерции j для тела достаточно малой массы m относительно оси, находящейся на расстоянии r от центра масс тела (рис. 4), численно равняется произведению этой массы на квадрат расстояния:

j = mr².

Напомним, что центром масс (или центром тяжести) тела называют точку, в которой может быть приложена равнодействующая силы тяжести всех отдельных частей тела.

Для тел сплошных, однородных, правильной геометрической формы центр масс совпадает с геометрическим центром.

Центр масс тела человека находится в сагиттальной плоскости несколько впереди второго крестцового позвонка.

Вычисление момента инерции

Для вычисления момента инерции какого-либо тела его разделяют на множество достаточно малых по массе элементов, для каждого из них вычисляют момент инерции j относительно заданной оси вращения и затем последние суммируют.

Момент инерции в системе СИ измеряется в кг•м², в СГС — г•см². Моменты инерции однородных тел правильной геометрической формы могут быть вычислены по известным формулам.

Например, для однородного цилиндра относительно продольной оси: J = (1/2) тr², где т — масса иr — радиус цилиндра.

Для однородного шара с массой т и радиусом r момент инерции относительно оси, проходящей через центр шара:

J = (2/5) mr².

Для тел неоднородных или сложной геометрической формы момент инерции обычно определяется опытным путем.

Если вращательное движение тела происходит равноускоренно, то оно характеризуется угловым и линейным ускорениями.

Угловое ускорение ε измеряется отношением изменения ∆ω угловой скорости за достаточно малый промежуток времени ∆t к этому промежутку:

ε = ∆ω/∆t

Единицы измерения

Единицей измерения углового ускорения является рад/сек² или 1/сек².

Линейное ускорение а какой-либо точки тела равняется произведению углового ускорения ε на расстояние r точки от оси вращения:

а = εr = (∆ω/∆t)r.

Единица измерения в системе СГС — см/сек², в системе СИ — м/сек²При равноускоренном вращательном движении угловое ускорение ε прямо пропорционально приложенному моменту силы М и обратно пропорционально моменту инерции J тела:

ε = M/J, откуда М = εJ = J (∆ω/∆t).

Эта зависимость выражает второй закон Ньютона применительно к вращательному движению и называется основным уравнением вращательного движения.

Определим кинетическую энергию Е_к тела достаточно малой массы m, вращающегося равномерно с угловой скоростью ω вокруг неподвижной оси, находящейся на расстоянии г от центра масс тела. По общему правилу:

Eк = (mυ²)/2 = (mω²r²)/2 = j(ω²/2)

Для вычисления кинетической энергии Е_к вращающегося тела с массой М его надо разделить на множество достаточно малых по массе элементов, вычислить для каждого из них кинетическую энергию Е_к и затем суммировать:

Eк = Е’к1 + Е’к2 + … = j1(ω²/2) + j(ω²/2) + … = ω²/2(j₁ + j₂ + …) = J(ω²/2)

Кинетическая энергия тела, вращающегося вокруг неподвижной оси, равняется половине произведения момента инерции тела на квадрат его угловой скорости.

Статья на тему Момент силы

Источник

Определение

Статика — раздел механики, изучающий условия равновесия тел.

Виды равновесия

Устойчивое равновесие
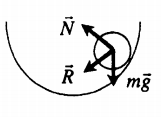	Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (E_{p min}).
Неустойчивое равновесие
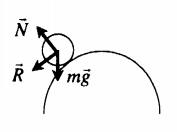	Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (E_{p max}).
Безразличное равновесие
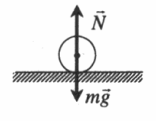	При выведении тела из положения безразличного равновесия дополнительных сил не возникает.

Момент силы

Определение

Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:

M = Fd

M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).

Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.

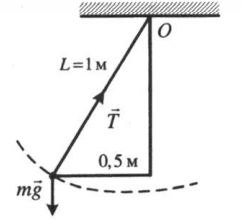
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?

Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:

M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)

Момент силы может быть положительным и отрицательным.

Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:

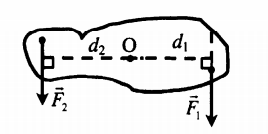
M₁ = F₁d₁

Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:

M₂ = F₂d₂

Правило моментов

Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

∑Mi=0

Иначе правило моментов можно сформулировать так:

Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.

∑Mпо час. стр.=∑Mпр. час. стр.

Условия равновесия тел

Тело не участвует в поступательном движении:	∑→Fi=0; →vo=0
Тело не участвует во вращательном движении:	∑Mi=0; ω0=0
Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении)	∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0

Простые механизмы

Определение

Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.

Наклонная плоскость
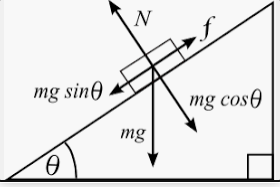	Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsinθ<mg
Рычаг
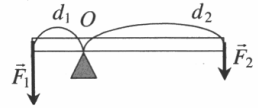	Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2=d2d1
Неподвижный блок
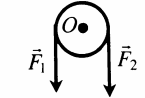	Изменяет направление действия силы. Модули и плечи сил при этом равны: F₁= F₂ M₁ = M₂
Подвижный блок
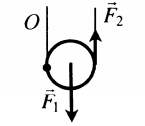	Дает выигрыш в силе в 2 раза: d₁ = R d₂= 2R F₁= 2F₂
Клин
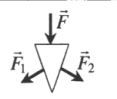	Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2

Золотое правило механики

При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.

Задание EF22660

Мальчик взвесил рыбу на самодельных весах с коромыслом из лёгкой рейки (см. рисунок). В качестве гири он использовал батон хлеба массой 0,8 кг. Определите массу рыбы.

Алгоритм решения

1.Записать исходные данные.

2.Записать правило моментов и выполнить решение в общем виде.

3.Подставить известные данные и вычислить искомую величину.

Решение

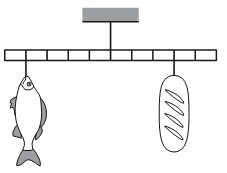
Известна лишь масса батона: m₁ = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:

d₁ = 0,3

d₂ = 0,4

Запишем правило моментов:

F₁ d₁ = F₂ d₂

Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:

m₁gd₁ = m₂gd₂

m₁d₁ = m₂d₂

Отсюда масса рыбы равна:

m2=m1d1d2=0,8·0,30,4=0,6 (кг)

Ответ: 0,6

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18706

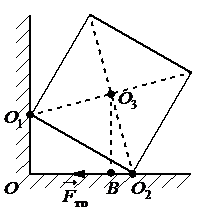
Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения F_тр относительно оси, проходящей через точку О₃ перпендикулярно плоскости чертежа, равно…

Ответ:

а) 0

б) О₂О₃

в) О₂В

г) О₃В

Алгоритм решения

Сформулировать определение плеча силы.
Найти плечо силы трения и аргументировать ответ.

Решение

Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О₃В.

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 9.6k

Источник

Рис. 6.3

Сплошной
однородный шар можно представить как
сумму бесконечно тонких сферических
слоев с массами dm
= mdV/V
(рис. 6.3). Объем сферического слоя dV
представим в виде: dV
= 4r²dr,
где r
– радиус сферического слоя. Объем шара
V
= 4/3R³,
где R – радиус шара. Если шар полый, то
момент инерции сферического слоя
относительно его центра масс (точка С)^I_c^{= mR}²^{,

но}
^,где
из-за симметрии I_x= I_y= I_z.
^{Момент

инерции сферического слоя относительно

диаметра}
^.

Тогда момент
инерции шара

6.5.1. Примеры моментов инерции некоторых тел

4. Тонкое кольцо
радиусом R

и шириной d.

однородного состава
относительно оси

3. Полый цилиндр
с внутренним r
и внешним R
радиусами

2. Тонкое кольцо

радиуса
R

1. Сплошной

цилиндр
радиуса R

5.
Тонкий параллелепипед

6.6. Работа, совершаемая
телом

при
вращательном движении

Если
произвольная м. т. вращается по окружности
и на нее действует сила

(рис.
6.4), то при повороте на некоторый угол
совершается элементарная работа

Рис. 6.4

А
= F
ds,
где ds
= r
d.

Тогда
А
= (r
F)
d
= M
d.
(6.8)

Полученное
выражение остается справедливым и
случае системы м.т. (твердых тел),
совершающих вращательное движение
относительно оси Z
при 
= сonst.
В этом случае момент внутренних сил
равен нулю и работа не совершается. Для
нахождения полной работы необходимо
вычислить интеграл:

,
(6.9)

где

= ₂
_1.

Если
действующая сила является потенциальной,
то А = 
dWp ,

где
dWp 
бесконечно малое изменение потенциальной
энергии тела при повороте на малый угол
dj,
т. е.

dWp
= 
M_zd
или M_z

=
dWp/d
.

6.7. Кинетическая энергия тела, совершающего

вращательное
движение

Кинетическая
энергия м. т. W_k
= mv²
/ 2 . Тогда для системы м. т. или тела
.
Используя связь линейной скорости с
угловой в видеv_i
= r_i,
получим
.
(6.10)

Замечание:
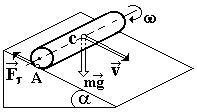
При плоском движении тел (например,
цилиндр скатывается по наклонной
плоскости, рис. 6.5) полная скорость

,
(6.11)

где
С 
центр инерции.

Полная кинетическая
энергия тела равна сумме кинетической
энергии поступательного движения его
центра масс (центра инерции) и кинетической
энергии вращательного движения тела
относительно точки С, т. е.

.
(6.12)

Замечание:
При скатывании тела (без проскальзывания)
на него действует сила трения покоя
(рис. 6.5).

Рис. 6.5

Несмотря на
наличие диссипативной силы (сила трения
покоя) можно применять законы сохранения,
так как сила трения покоя приложена к
точкам (А) тела, которые лежат на мгновенной
оси вращения. Скорость таких точек равна
нулю. Поэтому сила трения сцепления
работы не совершает и не влияет на
величину полной кинетической энергии.Роль
силы трения сцепления заключается в
том, чтобы привести тело во вращательное
движение для обеспечения чистого
качения. При этом работа силы тяжести
приводит к увеличению кинетической
энергии как поступательного, так и
вращательного движений.

Источник

Момент инерции
${displaystyle J=int limits _{(m)}r^{2}mathrm {d} m}$
Размерность	L²M
Единицы измерения
СИ	кг·м²
СГС	г·см²

Моме́нт ине́рции — тензорная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле. Момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества, которое, формально, может представлять собой не обязательно ось вращения (т.е. прямую), но и точку или плоскость. В последних случаях говорят о моменте инерции относительно точки или плоскости, а возникать такие величины могут в формальных вычислениях, например, при расчете тензора инерции.

Единица измерения в Международной системе единиц (СИ): кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.

Осевой момент инерции[править | править код]

Осевые моменты инерции некоторых тел

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси^[1]:

${displaystyle J_{a}=sum _{i=1}^{n}m_{i}r_{i}^{2},}$

где:

m_i — масса i-й точки,
r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

${displaystyle J_{a}=int limits _{(m)}r^{2}dm=int limits _{(V)}rho r^{2}dV,}$

где:

dm = ρ dV — масса малого элемента объёма тела dV,

ρ — плотность,

r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

${displaystyle J_{a}=rho int limits _{(V)}r^{2}dV.}$

Теорема Гюйгенса — Штейнера[править | править код]

Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями^[1]:

${displaystyle J=J_{c}+md^{2},}$

где m — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

${displaystyle J=J_{c}+md^{2}={frac {1}{12}}ml^{2}+mleft({frac {l}{2}}right)^{2}={frac {1}{3}}ml^{2}.}$

Осевые моменты инерции некоторых тел[править | править код]

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения

Описание	Положение оси a	Момент инерции J_a
Материальная точка массы m	На расстоянии r от точки, неподвижная	$mr^{2}$
Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра	$mr^{2}$
Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра	${frac {1}{2}}mr^{2}$
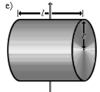
Полый толстостенный цилиндр массы m с внешним радиусом r₂ и внутренним радиусом r₁	Ось цилиндра	$m{frac {r_{2}^{2}+r_{1}^{2}}{2}}$ ^{[Комм 1]}
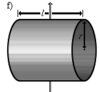
Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна образующей цилиндра и проходит через его центр масс	${1 over 4}mcdot r^{2}+{1 over 12}mcdot l^{2}$
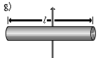
Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс	${1 over 2}mcdot r^{2}+{1 over 12}mcdot l^{2}$
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс	${frac {1}{12}}ml^{2}$
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец	${frac {1}{3}}ml^{2}$
Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы	${frac {2}{3}}mr^{2}$
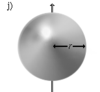
Шар радиуса r и массы m	Ось проходит через центр шара	${frac {2}{5}}mr^{2}$
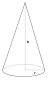
Конус радиуса r и массы m	Ось конуса	${frac {3}{10}}mr^{2}$
Равнобедренный треугольник с высотой h, основанием a и массой m	Ось перпендикулярна плоскости треугольника и проходит через вершину (при высоте)	${frac {1}{24}}m(a^{2}+12h^{2})$
Правильный треугольник со стороной a и массой m	Ось перпендикулярна плоскости треугольника и проходит через центр масс	${frac {1}{12}}ma^{2}$
Квадрат со стороной a и массой m	Ось перпендикулярна плоскости квадрата и проходит через центр масс	${frac {1}{6}}ma^{2}$
Прямоугольник со сторонами a и b и массой m	Ось перпендикулярна плоскости прямоугольника и проходит через центр масс	${frac {1}{12}}m(a^{2}+b^{2})$
Правильный n-угольник радиуса r и массой m	Ось перпендикулярна плоскости и проходит через центр масс	${displaystyle {frac {mr^{2}}{6}}left[1+2cos(pi /n)^{2}right]}$
Тор (полый) с радиусом направляющей окружности R, радиусом образующей окружности r и массой m	Ось перпендикулярна плоскости направляющей окружности тора и проходит через центр масс	${displaystyle I=mleft({frac {3}{4}},r^{2}+R^{2}right)}$

Вывод формул[править | править код]

Тонкостенный цилиндр (кольцо, обруч)

Вывод формулы

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

${displaystyle J=sum dJ_{i}=sum R_{i}^{2}dm.qquad (1).}$

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

$J=sum R^{2}dm=R^{2}sum dm=mR^{2}.$

Толстостенный цилиндр (кольцо, обруч)

Вывод формулы

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

$dm=rho dV=rho cdot 2pi rhdr;qquad dJ=r^{2}dm=2pi rho hr^{3}dr.$

Момент инерции толстого кольца найдём как интеграл

$J=int _{R_{1}}^{R}dJ=2pi rho hint _{R_{1}}^{R}r^{3}dr=$

${displaystyle =2pi rho hleft.{frac {r^{4}}{4}}right|_{R_{1}}^{R}={frac {1}{2}}pi rho hleft(R^{4}-R_{1}^{4}right)={frac {1}{2}}pi rho hleft(R^{2}-R_{1}^{2}right)left(R^{2}+R_{1}^{2}right).}$

Поскольку объём и масса кольца равны

$V=pi left(R^{2}-R_{1}^{2}right)h;qquad m=rho V=pi rho left(R^{2}-R_{1}^{2}right)h,$

получаем окончательную формулу для момента инерции кольца

$J={frac {1}{2}}mleft(R^{2}+R_{1}^{2}right).$

Однородный диск (сплошной цилиндр)

Вывод формулы

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

$J={frac {1}{2}}mR^{2}.$

Сплошной конус

Вывод формулы

Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен

$r={frac {Rh}{H}},$

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска.
Масса и момент инерции такого диска составят

$dm=rho dV=rho cdot pi r^{2}dh;$

$dJ={frac {1}{2}}r^{2}dm={frac {1}{2}}pi rho r^{4}dh={frac {1}{2}}pi rho left({frac {Rh}{H}}right)^{4}dh;$

Интегрируя, получим

${begin{aligned}J=int _{0}^{H}dJ={frac {1}{2}}pi rho left({frac {R}{H}}right)^{4}int _{0}^{H}h^{4}dh={frac {1}{2}}pi rho left({frac {R}{H}}right)^{4}left.{frac {h^{5}}{5}}right|_{0}^{H}=={frac {1}{10}}pi rho R^{4}H=left(rho cdot {frac {1}{3}}pi R^{2}Hright){frac {3}{10}}R^{2}={frac {3}{10}}mR^{2}.end{aligned}}$

Сплошной однородный шар

Вывод формулы

Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

$r={sqrt {R^{2}-h^{2}}}.$

Масса и момент инерции такого диска составят

$dm=rho dV=rho cdot pi r^{2}dh;$

$dJ={frac {1}{2}}r^{2}dm={frac {1}{2}}pi rho r^{4}dh={frac {1}{2}}pi rho left(R^{2}-h^{2}right)^{2}dh={frac {1}{2}}pi rho left(R^{4}-2R^{2}h^{2}+h^{4}right)dh.$

Момент инерции шара найдём интегрированием:

${begin{aligned}J&=int _{-R}^{R}dJ=2int _{0}^{R}dJ=pi rho int _{0}^{R}left(R^{4}-2R^{2}h^{2}+h^{4}right)dh=\&=pi rho left.left(R^{4}h-{frac {2}{3}}R^{2}h^{3}+{frac {1}{5}}h^{5}right)right|_{0}^{R}=pi rho left(R^{5}-{frac {2}{3}}R^{5}+{frac {1}{5}}R^{5}right)={frac {8}{15}}pi rho R^{5}=\&=left({frac {4}{3}}pi R^{3}rho right)cdot {frac {2}{5}}R^{2}={frac {2}{5}}mR^{2}.end{aligned}}$

Тонкостенная сфера

Вывод формулы

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

$J_{0}={frac {2}{5}}MR^{2}={frac {8}{15}}pi rho R^{5}.$

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

${displaystyle {begin{aligned}J&={frac {dJ_{0}}{dR}}dR={frac {d}{dR}}left({frac {8}{15}}pi rho R^{5}right)dR=\&={frac {8}{3}}pi rho R^{4}dR=left(rho cdot 4pi R^{2}dRright){frac {2}{3}}R^{2}={frac {2}{3}}mR^{2}.end{aligned}}}$

Тонкий стержень (ось проходит через центр)

Вывод формулы

Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

$dm={frac {mdr}{l}};qquad dJ=r^{2}dm={frac {mr^{2}dr}{l}}.$

Интегрируя, получим

$J=int _{-l/2}^{l/2}dJ=2int _{0}^{l/2}dJ={frac {2m}{l}}int _{0}^{l/2}r^{2}dr={frac {2m}{l}}left.{frac {r^{3}}{3}}right|_{0}^{l/2}={frac {2m}{l}}{frac {l^{3}}{24}}={frac {1}{12}}ml^{2}.$

Тонкий стержень (ось проходит через конец)

Вывод формулы

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние ^l⁄₂. По теореме Штейнера новый момент инерции будет равен

$J=J_{0}+mr^{2}=J_{0}+mleft({frac {l}{2}}right)^{2}={frac {1}{12}}ml^{2}+{frac {1}{4}}ml^{2}={frac {1}{3}}ml^{2}.$

Безразмерные моменты инерции планет и их спутников^[2]^[3]^[4]

Безразмерные моменты инерции планет и спутников[править | править код]

Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr²). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра^[5]^[6].

Центробежный момент инерции[править | править код]

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины^[1]^[7]:

${displaystyle J_{xy}=int limits _{(m)}xydm=int limits _{(V)}xyrho dV,}$

${displaystyle J_{xz}=int limits _{(m)}xzdm=int limits _{(V)}xzrho dV,}$

${displaystyle J_{yz}=int limits _{(m)}yzdm=int limits _{(V)}yzrho dV,}$

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции J_xy и J_xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела^[7].

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции^[7].

Геометрические моменты инерции[править | править код]

Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой^[8]:

${displaystyle J_{Va}=int limits _{(V)}r^{2}dV,}$

где, как и ранее r — расстояние от элемента dV до оси a.

Размерность J_Va — длина в пятой степени ( $mathrm {dim} J_{Va}=mathrm {L^{5}}$ ), соответственно единица измерения СИ — м⁵.

Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой^[8]:

${displaystyle J_{Sa}=int limits _{(S)}r^{2}dS,}$

где интегрирование выполняется по поверхности S, а dS — элемент этой поверхности.

Размерность J_Sa — длина в четвёртой степени ( $mathrm {dim} J_{Sa}=mathrm {L^{4}}$ ), соответственно единица измерения СИ — м⁴. В строительных расчетах, литературе и сортаментах металлопроката часто указывается в см⁴.

Через геометрический момент инерции площади выражается момент сопротивления сечения:

${displaystyle W={frac {J_{Sa}}{r_{max}}}.}$

Здесь r_max — максимальное расстояние от поверхности до оси.

Геометрические моменты инерции площади некоторых фигур
Прямоугольника высотой и шириной :	$J_{y}={frac {bh^{3}}{12}}$ $J_{z}={frac {hb^{3}}{12}}$
Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно	$J_{z}={frac {BH^{3}}{12}}-{frac {bh^{3}}{12}}={frac {1}{12}}(BH^{3}-bh^{3})$ $J_{y}={frac {HB^{3}}{12}}-{frac {hb^{3}}{12}}={frac {1}{12}}(HB^{3}-hb^{3})$
Круга диаметром	$J_{y}=J_{z}={frac {pi d^{4}}{64}}$

Геометрические моменты инерции площади некоторых фигур

Прямоугольника высотой

и шириной

$J_{y}={frac {bh^{3}}{12}}$

$J_{z}={frac {hb^{3}}{12}}$

Прямоугольного коробчатого сечения высотой и шириной по внешним контурам

, а по внутренним

соответственно

$J_{z}={frac {BH^{3}}{12}}-{frac {bh^{3}}{12}}={frac {1}{12}}(BH^{3}-bh^{3})$

$J_{y}={frac {HB^{3}}{12}}-{frac {hb^{3}}{12}}={frac {1}{12}}(HB^{3}-hb^{3})$

Круга диаметром

$J_{y}=J_{z}={frac {pi d^{4}}{64}}$

Момент инерции относительно плоскости[править | править код]

Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости^[9].

Если через произвольную точку провести координатные оси x,y,z , то моменты инерции относительно координатных плоскостей xOy , yOz и zOx будут выражаться формулами:

${displaystyle J_{xOy}=sum _{i=1}^{n}m_{i}z_{i}^{2} ,}$

${displaystyle J_{yOz}=sum _{i=1}^{n}m_{i}x_{i}^{2} ,}$

${displaystyle J_{zOx}=sum _{i=1}^{n}m_{i}y_{i}^{2} .}$

В случае сплошного тела суммирование заменяется интегрированием.

Центральный момент инерции[править | править код]

Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) ${displaystyle J_{O}}$ — это величина, определяемая выражением^[9]:

${displaystyle J_{a}=int limits _{(m)}r^{2}dm=int limits _{(V)}rho r^{2}dV,}$

где:

Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей^[9]:

${displaystyle J_{O}={frac {1}{2}}left(J_{x}+J_{y}+J_{z}right),}$

${displaystyle J_{O}=J_{xOy}+J_{yOz}+J_{xOz}.}$

Тензор инерции и эллипсоид инерции[править | править код]

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором ${displaystyle {vec {s}}=leftVert s_{x},s_{y},s_{z}rightVert ^{T},leftvert {vec {s}}rightvert =1}$ , можно представить в виде квадратичной (билинейной) формы:

${displaystyle I_{s}={vec {s}}^{T}cdot {hat {J}}cdot {vec {s}},qquad }$

(1)

где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:

${displaystyle {hat {J}}=leftVert {begin{array}{ccc}J_{xx}&-J_{xy}&-J_{xz}\-J_{yx}&J_{yy}&-J_{yz}\-J_{zx}&-J_{zy}&J_{zz}end{array}}rightVert ,}$

${displaystyle J_{xy}=J_{yx},quad J_{xz}=J_{zx},quad J_{zy}=J_{yz},quad }$

${displaystyle J_{xx}=int limits _{(m)}(y^{2}+z^{2})dm,quad J_{yy}=int limits _{(m)}(x^{2}+z^{2})dm,quad J_{zz}=int limits _{(m)}(x^{2}+y^{2})dm.}$

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :

${displaystyle {hat {J}}_{d}={hat {Q}}^{T}cdot {hat {J}}cdot {hat {Q}},}$

${displaystyle {hat {J}}_{d}=leftVert {begin{array}{ccc}J_{X}&0&0\0&J_{Y}&0\0&0&J_{Z}end{array}}rightVert ,}$

где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины ${displaystyle J_{X},J_{Y},J_{Z}}$ — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

${displaystyle I_{s}=J_{X}cdot s_{x}^{2}+J_{Y}cdot s_{y}^{2}+J_{Z}cdot s_{z}^{2},}$

откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на ${displaystyle I_{s}}$

${displaystyle left({s_{x} over {sqrt {I_{s}}}}right)^{2}cdot J_{X}+left({s_{y} over {sqrt {I_{s}}}}right)^{2}cdot J_{Y}+left({s_{z} over {sqrt {I_{s}}}}right)^{2}cdot J_{Z}=1}$

и произведя замены:

${displaystyle xi ={s_{x} over {sqrt {I_{s}}}},eta ={s_{y} over {sqrt {I_{s}}}},zeta ={s_{z} over {sqrt {I_{s}}}},}$

получаем канонический вид уравнения эллипсоида в координатах :

${displaystyle xi ^{2}cdot J_{X}+eta ^{2}cdot J_{Y}+zeta ^{2}cdot J_{Z}=1.}$

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

${displaystyle r^{2}=xi ^{2}+eta ^{2}+zeta ^{2}=left({s_{x} over {sqrt {I_{s}}}}right)^{2}+left({s_{y} over {sqrt {I_{s}}}}right)^{2}+left({s_{z} over {sqrt {I_{s}}}}right)^{2}={1 over I_{s}}.}$

См. также[править | править код]

Кинематика твёрдого тела
Метод главных компонент
Сопротивление материалов
Теорема Штейнера
Теорема Кёнига (механика)
Механические приложения тройного интеграла
Механические приложения двойного интеграла
Полярный момент инерции
Список моментов инерции
Момент силы
Момент импульса

Комментарии[править | править код]

↑ При получении этой формулы путём вычитания момента инерции сплошного цилиндра радиусом r₁ из цилиндра радиусом r₂ необходимо обратить внимание, что их массы при этом не будут одинаковыми или равны m. При этом должно выполняться условие ${displaystyle m_{2}-m_{1}=m}$ . Из формулы для массы соответствующего цилиндра можно определить, что в этом случае ${displaystyle m_{1}=m{frac {r_{1}^{2}}{r_{2}^{2}-r_{1}^{2}}}}$ и ${displaystyle m_{2}=m{frac {r_{2}^{2}}{r_{2}^{2}-r_{1}^{2}}}}$ . В правильности использования знака «+» в этой формуле также можно убедиться, если сравнить моменты инерции полого толстостенного и сплошного цилиндров с одинаковыми массами. Действительно, у первого из этих цилиндров масса в среднем сосредоточена дальше от оси, чем у второго, поэтому и момент инерции этого цилиндра должен быть больше, чем у сплошного. Именно такое соотношение моментов инерции и обеспечивает знак «+». С другой стороны, в пределе при стремлении r₁ к r₂ формула для полого толстостенного цилиндра должна приобрести тот же вид, что и формула для полого тонкостенного цилиндра. Очевидно, что такой переход происходит только при использовании формулы со знаком «+».

Примечания[править | править код]

↑ ¹ ² ³ Тарг С. М. Момент инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 206—207. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
↑ Planetary Fact Sheet. Дата обращения: 31 августа 2010. Архивировано 14 марта 2016 года.
↑ Showman, Adam P.; Malhotra, Renu. The Galilean Satellites (англ.) // Science. — 1999. — Vol. 286, no. 5437. — P. 77—84. — doi:10.1126/science.286.5437.77. — PMID 10506564.
↑ Margot, Jean-Luc; et al. Mercury’s moment of inertia from spin and gravity data (англ.) // Journal of Geophysical Research (англ.) (рус. : journal. — 2012. — Vol. 117. — doi:10.1029/2012JE004161.
↑ Галкин И.Н. Внеземная сейсмология. — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X.
↑ Пантелеев В. Л. Физика Земли и планет. Гл. 3.4 — Гравитационное поле планеты. Дата обращения: 31 августа 2010. Архивировано 3 октября 2013 года.
↑ ¹ ² ³ Тарг С. М. Краткий курс теоретической механики. — М.: «Высшая школа», 1995. — С. 269—271. — 416 с. — ISBN 5-06-003117-9.
↑ ¹ ² Бухгольц Н. Н. Основной курс теоретической механики. — 4-е изд. — М.: «Наука», 1966. — Т. 2. — С. 131.
↑ ¹ ² ³ Яблонский А. А. Динамика // Курс теоретической механики. — 3-е изд. — М.: «Высшая школа», 1966. — Т. II. — С. 102—103. — 411 с.

Литература[править | править код]

Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Архивная копия от 7 января 2014 на Wayback Machine Издательство Физического факультета МГУ, 1997.
Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с.
Беляев Н. М. Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.

Ссылки[править | править код]

Определение момента инерции тел простой формы.

Источник

<img fetchpriority="high" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" title="Момент силы" src="https://znaesh-kak.com/wp-content/uploads/2021/09/1-1.jpg" alt="Момент силы" width="400" height="209" />

Что такое вращательное движение тела Момент силы Момент инерции

Момент силы

От чего зависит действие силы

Момент силы относительно центра вращения

Инерция вращающегося тела

Как увеличить инерцию

Единицы измерения

Виды равновесия

Устойчивое равновесие

Неустойчивое равновесие

Безразличное равновесие

Момент силы

Правило моментов

Условия равновесия тел

Простые механизмы

Наклонная плоскость

Рычаг

Неподвижный блок

Подвижный блок

Клин

6.5.1. Примеры моментов инерции некоторых тел

6.7. Кинетическая энергия тела, совершающего

Осевой момент инерции[править | править код]

Теорема Гюйгенса — Штейнера[править | править код]

Осевые моменты инерции некоторых тел[править | править код]

Вывод формул[править | править код]

Безразмерные моменты инерции планет и спутников[править | править код]

Центробежный момент инерции[править | править код]

Геометрические моменты инерции[править | править код]

Момент инерции относительно плоскости[править | править код]

Центральный момент инерции[править | править код]

Тензор инерции и эллипсоид инерции[править | править код]

См. также[править | править код]

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Вам также может понравиться

Как найти свой интерес к чему либо

Как лучше найти квартиру для съема

Как найти друга в мире танков

Добавить комментарий Отменить ответ