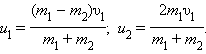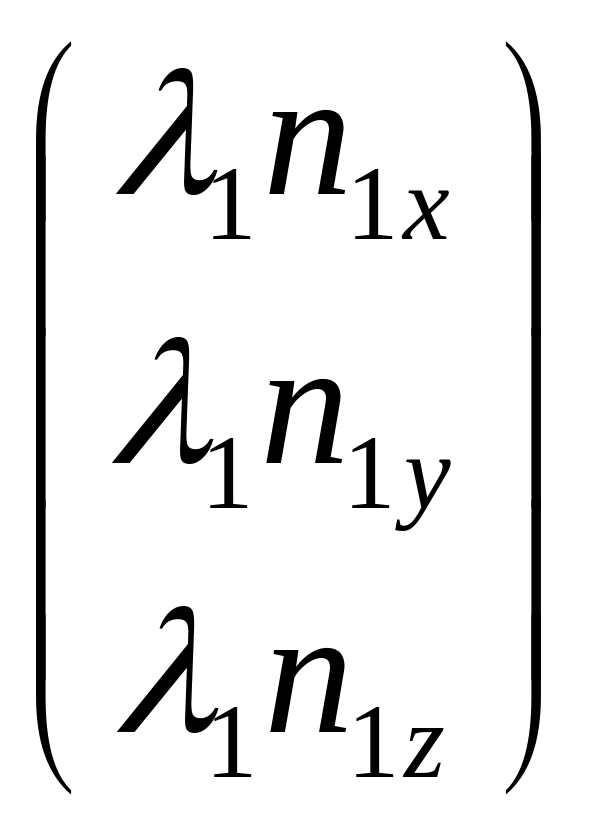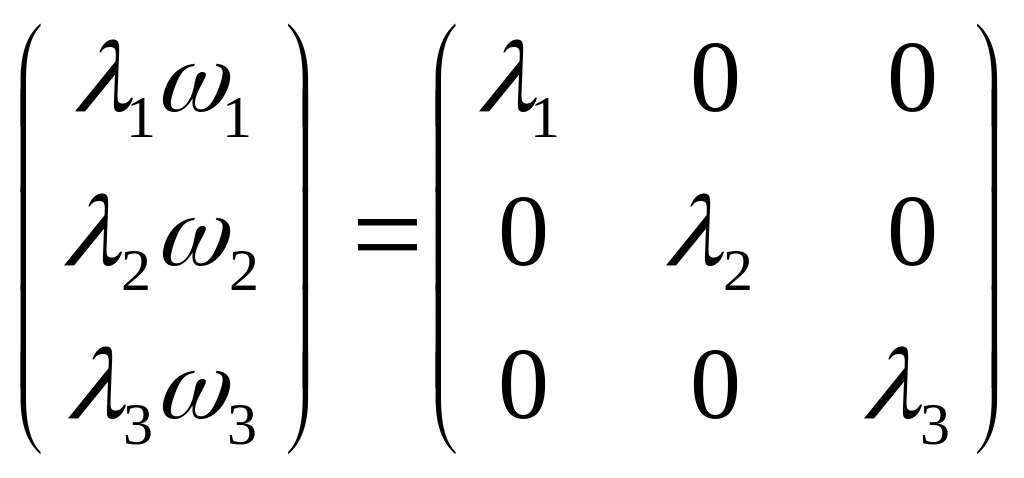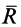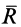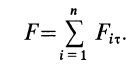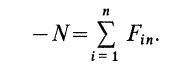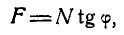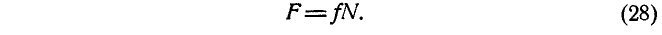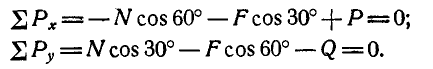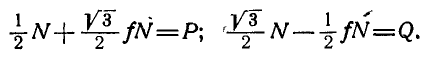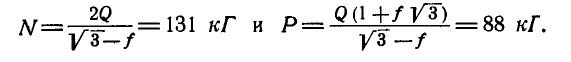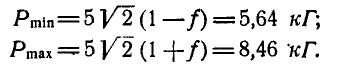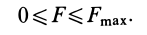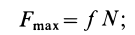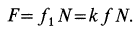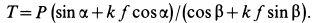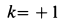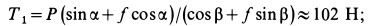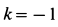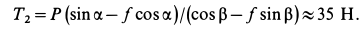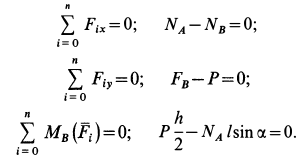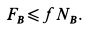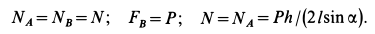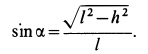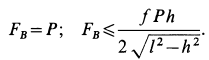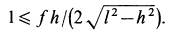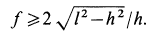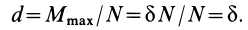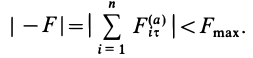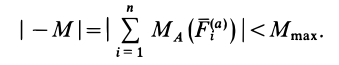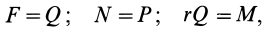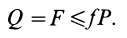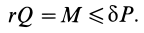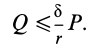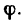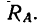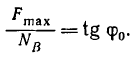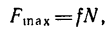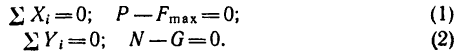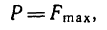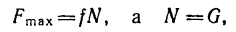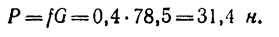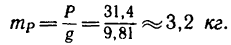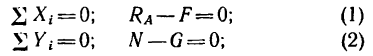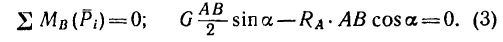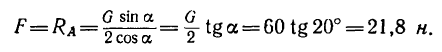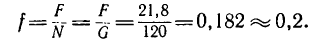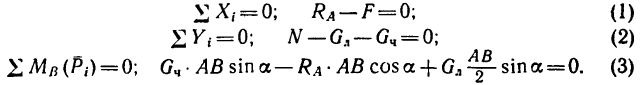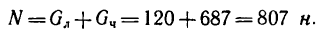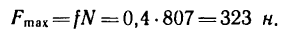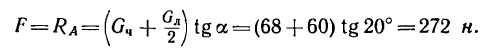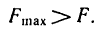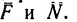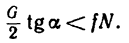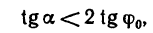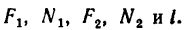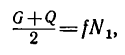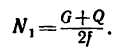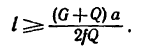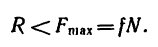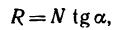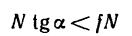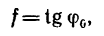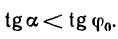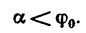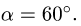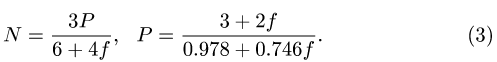Когда решают любые задачи по физике, в которых имеются движущиеся объекты, то всегда говорят о силах трения. Их либо учитывают, либо ими пренебрегают, но факт их присутствия ни у кого не вызывает сомнения. В данной статье рассмотрим, что такое момент сил трения, а также приведем проблемы, для устранения которых воспользуемся полученными знаниями.
Сила трения и ее природа
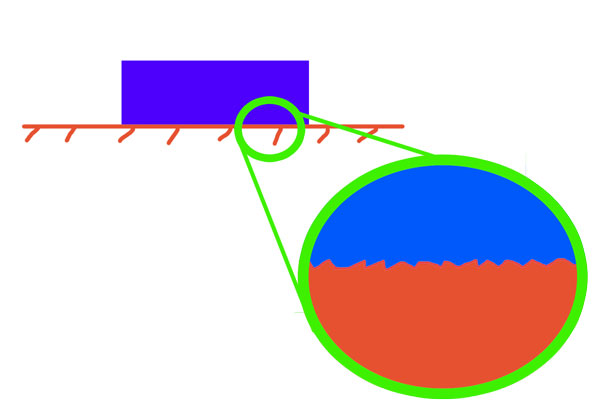
Каждый понимает, что если одно тело движется по поверхности другого совершенно любым способом (скользит, катится), то всегда существует некоторая сила, которая препятствует этому перемещению. Она называется динамической силой трения. Причина ее возникновения связана с тем фактом, что любые тела имеют микроскопические шероховатости на своих поверхностях. Когда соприкасаются два объекта, то их шероховатости начинают взаимодействовать друг с другом. Это взаимодействие носит как механический характер (пик попадает во впадину), так и происходит на уровне атомов (дипольные притяжения, ван-дер-ваальсовые и другие).
Когда соприкасаемые тела находятся в покое, то, чтобы привести их в движение относительно друг друга, необходимо приложить усилие, которое больше такового для поддержания скольжения этих тел друг по другу с постоянной скоростью. Поэтому помимо динамической также рассматривают статическую силу трения.
Свойства силы трения и формулы для ее вычисления
В школьном курсе физики говорится, что впервые законы трения изложил французский физик Гийом Амонтон в XVII веке. На самом деле это явление стал изучать еще в конце XV века Леонардо да Винчи, рассматривая движущийся предмет по гладкой поверхности.
Свойства трения могут быть кратко изложены следующим образом:
- сила трения всегда действует против направления перемещения тела;
- ее величина прямо пропорциональна реакции опоры;
- она не зависит от площади контакта;
- она не зависит от скорости перемещения (для небольших скоростей).
Эти особенности рассматриваемого явления позволяют ввести следующую математическую формулу для силы трения:
F = μ*N, где N – реакция опоры, μ – коэффициент пропорциональности.
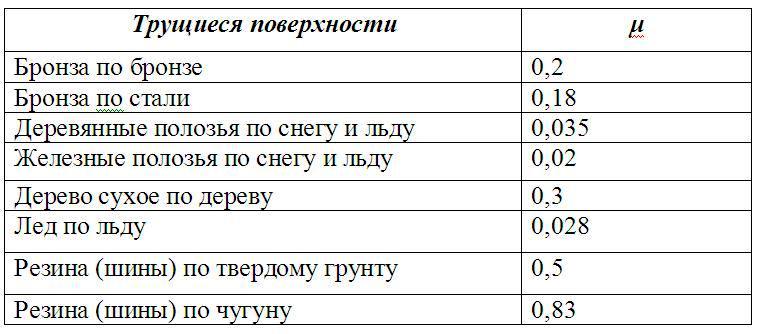
Значение коэффициента μ зависит исключительно от свойств поверхностей, которые трутся друг о друга. Таблица значений для некоторых поверхностей приведена ниже.
Для трения покоя формула используется та же самая, что приведена выше, однако значения коэффициентов μ для тех же поверхностей будут совершенно иные (они больше по величине, чем для скольжения).
Особый случай представляет трение качения, когда одно тело катится (не скользит) по поверхности другого. Для силы в этом случае применяют формулу:
F = f*N/R.
Здесь R – радиус колеса, f- коэффициент качения, который согласно формуле имеет размерность длины, что его отличает от безразмерного μ.
Момент силы
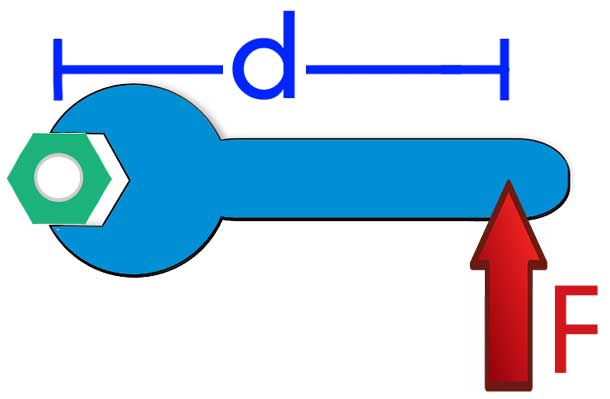
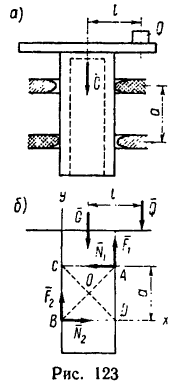
Перед тем как отвечать на вопрос, как определить момент сил трения, необходимо рассмотреть само физическое понятие. Под моментом силы M понимают физическую величину, которая определяется как произведение плеча на значение силы F, приложенной к нему. Ниже приведен рисунок.
Здесь мы видим, что приложение F к плечу d, которое равно длине гаечного ключа, создает крутящий момент, приводящий к откручиванию зеленой гайки.
Таким образом, для момента силы справедлива формула:
M = d*F.
Заметим, что природа силы F не имеет никакого значения: она может быть электрической, гравитационной или вызванной трением. То есть определение момента силы трения будет тем же самым, что приведено в начале пункта, и записанная формула для M остается справедливой.
Когда появляется момент сил, вызванный трением?
Эта ситуация возникает, когда выполняются три главных условия:
- Во-первых, должна иметь место вращающаяся система вокруг некоторой оси. Например, это может быть колесо, движущееся по асфальту, или крутящаяся на оси горизонтально расположенная музыкальная пластинка патефона.
- Во-вторых, должно существовать трение между вращающейся системой и некоторой средой. В примерах выше: на колесо действует трение качения при его взаимодействии с поверхностью асфальта; если положить музыкальную пластинку на стол и раскрутить ее, то она будет испытывать трение скольжения о поверхность стола.
- В-третьих, возникающая сила трения должна действовать не на ось вращения, а на крутящиеся элементы системы. Если сила имеет центральный характер, то есть действует на ось, то плечо равно нулю, поэтому она не будет создавать момента.
Как найти момент силы трения?
Чтобы решить эту задачу, необходимо сначала определить, на какие вращающиеся элементы действует сила трения. Затем следует найти расстояние от этих элементов до оси вращения и определить, чему равна сила трения, действующая на каждый элемент. После этого необходимо выполнить умножение расстояний ri на соответствующие величины Fi и сложить полученные результаты. В итоге суммарный момент сил трения вращения вычисляется по формуле:
M = ∑nri*Fi.
Здесь n – количество сил трения, возникающих в системе вращения.
Любопытно отметить, что хотя M – это величина векторная, поэтому при сложении моментов в скалярной форме следует учитывать ее направление. Трение всегда действует против направления вращения, поэтому каждый момент Mi=ri*Fi будет иметь один и тот же знак.
Далее решим две задачи, где используем рассмотренные формулы.
Вращение диска болгарки
Известно, что когда диск болгарки радиусом 5 см режет металл, то он вращается с постоянной скоростью. Необходимо определить, какой момент сил создает электромотор прибора, если сила трения о металл диска равна 0,5 кН.
Поскольку диск вращается с постоянной скоростью, то сумма всех моментов сил, которые на него действуют, равна нулю. В данном случае мы имеем всего 2 момента: от электромотора и от силы трения. Поскольку они действуют в разных направлениях, то можно записать формулу:
M1 – M2 = 0 => M1 = M2.
Поскольку трение действует только в точке соприкосновения диска болгарки с металлом, то есть на расстоянии r от оси вращения, то ее момент силы равен:
M2 = r*F=5*10-2*500 = 25 Н*м.
Поскольку электромотор создает такой же по модулю момент, получаем ответ: 25 Н*м.
Качение деревянного диска
Имеется диск из дерева, его радиус r равен 0,5 метра. Этот диск начинают катить по деревянной поверхности. Необходимо рассчитать, какое расстояние способен он преодолеть, если начальная скорость вращения его ω составляла 5 рад/с.
Кинетическая энергия вращающегося тела равна:
E = I*ω2/2.
Здесь I – момент инерции. Сила трения качения будет приводить к замедлению движения диска. Работу, совершаемую ей, можно вычислить по следующей формуле:
A = M*θ.
Здесь θ – угол в радианах, на который сможет повернуться диск в процессе своего движения. Тело будет катиться до тех пор, пока вся его кинетическая энергия не расходуется на работу трения, то есть можно приравнять выписанные формулы:
I*ω2/2 = M*θ.
Момент инерции диска I равен m*r2/2. Чтобы вычислить момент M силы трения F, следует заметить, что она действует вдоль края диска в точке его соприкосновения с деревянной поверхностью, то есть M = r*F. В свою очередь F = f*mg/r (сила реакции опоры N равна весу диска mg). Подставляя все эти формулы в последнее равенство, получим:
m*r2*ω2/4 = r*f*mg/r*θ => θ=r2*ω2/(4*f*g).
Поскольку пройденное диском расстояние L связано с углом θ выражением L=r*θ, то получаем конечное равенство:
L=r3*ω2/(4*f*g).
Значение f можно посмотреть в таблице для коэффициентов трения качения. Для пары дерево-дерево он равен 1,5*10-3 м. Подставляем все величины, получаем:
L=0,53*52/(4*1,5*10-3*9,81) ≈ 53,1 м.
Для подтверждения правильности полученной конечной формулы можно проверить, что получаются единицы измерения длины.
Когда решают любые задачи по физике, в которых имеются движущиеся объекты, то всегда говорят о силах трения. Их либо учитывают, либо ими пренебрегают, но факт их присутствия ни у кого не вызывает сомнения. В данной статье рассмотрим, что такое момент сил трения, а также приведем проблемы, для устранения которых воспользуемся полученными знаниями.
Сила трения и ее природа
Каждый понимает, что если одно тело движется по поверхности другого совершенно любым способом (скользит, катится), то всегда существует некоторая сила, которая препятствует этому перемещению. Она называется динамической силой трения. Причина ее возникновения связана с тем фактом, что любые тела имеют микроскопические шероховатости на своих поверхностях. Когда соприкасаются два объекта, то их шероховатости начинают взаимодействовать друг с другом. Это взаимодействие носит как механический характер (пик попадает во впадину), так и происходит на уровне атомов (дипольные притяжения, ван-дер-ваальсовые и другие).
При решении уравнений вращательного или колебательного (осциллирующего) движения необходимо знать…
Когда соприкасаемые тела находятся в покое, то, чтобы привести их в движение относительно друг друга, необходимо приложить усилие, которое больше такового для поддержания скольжения этих тел друг по другу с постоянной скоростью. Поэтому помимо динамической также рассматривают статическую силу трения.
Свойства силы трения и формулы для ее вычисления
В школьном курсе физики говорится, что впервые законы трения изложил французский физик Гийом Амонтон в XVII веке. На самом деле это явление стал изучать еще в конце XV века Леонардо да Винчи, рассматривая движущийся предмет по гладкой поверхности.
Свойства трения могут быть кратко изложены следующим образом:
- сила трения всегда действует против направления перемещения тела;
- ее величина прямо пропорциональна реакции опоры;
- она не зависит от площади контакта;
- она не зависит от скорости перемещения (для небольших скоростей).
Эти особенности рассматриваемого явления позволяют ввести следующую математическую формулу для силы трения:
Типичными задачами раздела физики “Статика” являются проблемы равновесия тел. В этом…
F = μ*N, где N – реакция опоры, μ – коэффициент пропорциональности.
Значение коэффициента μ зависит исключительно от свойств поверхностей, которые трутся друг о друга. Таблица значений для некоторых поверхностей приведена ниже.
Для трения покоя формула используется та же самая, что приведена выше, однако значения коэффициентов μ для тех же поверхностей будут совершенно иные (они больше по величине, чем для скольжения).
Особый случай представляет трение качения, когда одно тело катится (не скользит) по поверхности другого. Для силы в этом случае применяют формулу:
F = f*N/R.
Здесь R – радиус колеса, f- коэффициент качения, который согласно формуле имеет размерность длины, что его отличает от безразмерного μ.
Момент силы
Перед тем как отвечать на вопрос, как определить момент сил трения, необходимо рассмотреть само физическое понятие. Под моментом силы M понимают физическую величину, которая определяется как произведение плеча на значение силы F, приложенной к нему. Ниже приведен рисунок.
Здесь мы видим, что приложение F к плечу d, которое равно длине гаечного ключа, создает крутящий момент, приводящий к откручиванию зеленой гайки.
Таким образом, для момента силы справедлива формула:
M = d*F.
Заметим, что природа силы F не имеет никакого значения: она может быть электрической, гравитационной или вызванной трением. То есть определение момента силы трения будет тем же самым, что приведено в начале пункта, и записанная формула для M остается справедливой.
Чтобы привести какое-либо тело во вращательное движение, необходимо к нему приложить момент силы. В…
Когда появляется момент сил, вызванный трением
Эта ситуация возникает, когда выполняются три главных условия:
- Во-первых, должна иметь место вращающаяся система вокруг некоторой оси. Например, это может быть колесо, движущееся по асфальту, или крутящаяся на оси горизонтально расположенная музыкальная пластинка патефона.
- Во-вторых, должно существовать трение между вращающейся системой и некоторой средой. В примерах выше: на колесо действует трение качения при его взаимодействии с поверхностью асфальта; если положить музыкальную пластинку на стол и раскрутить ее, то она будет испытывать трение скольжения о поверхность стола.
- В-третьих, возникающая сила трения должна действовать не на ось вращения, а на крутящиеся элементы системы. Если сила имеет центральный характер, то есть действует на ось, то плечо равно нулю, поэтому она не будет создавать момента.
Как найти момент силы трения?
Чтобы решить эту задачу, необходимо сначала определить, на какие вращающиеся элементы действует сила трения. Затем следует найти расстояние от этих элементов до оси вращения и определить, чему равна сила трения, действующая на каждый элемент. После этого необходимо выполнить умножение расстояний ri на соответствующие величины Fi и сложить полученные результаты. В итоге суммарный момент сил трения вращения вычисляется по формуле:
M = ∑nri*Fi.
Здесь n – количество сил трения, возникающих в системе вращения.
Любопытно отметить, что хотя M – это величина векторная, поэтому при сложении моментов в скалярной форме следует учитывать ее направление. Трение всегда действует против направления вращения, поэтому каждый момент Mi=ri*Fi будет иметь один и тот же знак.
Далее решим две задачи, где используем рассмотренные формулы.
Вращение диска болгарки
Известно, что когда диск болгарки радиусом 5 см режет металл, то он вращается с постоянной скоростью. Необходимо определить, какой момент сил создает электромотор прибора, если сила трения о металл диска равна 0,5 кН.
Поскольку диск вращается с постоянной скоростью, то сумма всех моментов сил, которые на него действуют, равна нулю. В данном случае мы имеем всего 2 момента: от электромотора и от силы трения. Поскольку они действуют в разных направлениях, то можно записать формулу:
M1 – M2 = 0 => M1 = M2.
Поскольку трение действует только в точке соприкосновения диска болгарки с металлом, то есть на расстоянии r от оси вращения, то ее момент силы равен:
M2 = r*F= 10-2*500 = 25 Н*м.
Поскольку электромотор создает такой же по модулю момент, получаем ответ: 25 Н*м.
Качение деревянного диска
Имеется диск из дерева, его радиус r равен 0,5 метра. Этот диск начинают катить по деревянной поверхности. Необходимо рассчитать, какое расстояние способен он преодолеть, если начальная скорость вращения его ω составляла 5 рад/с.
Кинетическая энергия вращающегося тела равна:
E = I*ω2/2.
Здесь I – момент инерции. Сила трения качения будет приводить к замедлению движения диска. Работу, совершаемую ей, можно вычислить по следующей формуле:
A = M*θ.
Здесь θ – угол в радианах, на который сможет повернуться диск в процессе своего движения. Тело будет катиться до тех пор, пока вся его кинетическая энергия не расходуется на работу трения, то есть можно приравнять выписанные формулы:
I*ω2/2 = M*θ.
Момент инерции диска I равен m*r2/2. Чтобы вычислить момент M силы трения F, следует заметить, что она действует вдоль края диска в точке его соприкосновения с деревянной поверхностью, то есть M = r*F. В свою очередь F = f*mg/r (сила реакции опоры N равна весу диска mg). Подставляя все эти формулы в последнее равенство, получим:
m*r2*ω2/4 = r*f*mg/r*θ => θ=r2*ω2/( f*g).
Поскольку пройденное диском расстояние L связано с углом θ выражением L=r*θ, то получаем конечное равенство:
L=r3*ω2/( f*g).
Значение f можно посмотреть в таблице для коэффициентов трения качения. Для пары дерево-дерево он равен 1, 10-3 м. Подставляем все величины, получаем:
L=0,53*52/( 1, 10-3*9,81) ≈ 53,1 м.
Для подтверждения правильности полученной конечной формулы можно проверить, что получаются единицы измерения длины.
Опыт №3:
|
m |
h1 |
h2 |
t |
M |
I |
Опыт №1:
h2ср=
tср=
Момент сил трения:
M=
Момент инерции:
I=
Опыт №2:
h2ср=
tср=
Момент сил трения:
M=
Момент инерции:
I=
Опыт №3:
h2ср=
tср=
Момент сил трения:
M=
Момент инерции:
I=
Найдем момент инерции диска теоретически:
I=
Rвнутр=
I=
Получилось расхождение значений, измерения при опыте
были сделаны неточно.
Контрольные вопросы:
1)Что называется моментом инерции материальной точки?
От чего зависит момент инерции тела?
Величина I равна сумме произведений масс mi всех материальных точек, образующих механическую систему, на квадрат
их расстояний pi от
данной оси, называется моментом инерции системы.
2)Что называется моментом силы относительно точки,
неподвижной оси? Как определить его направление, и в каких единицах измеряется.
Моментом силы относительно точки называется величина
равная векторному произведению радиус-вектора точки, проведенного из этой точки
на силу.M=[rk],[Н*м].
3)Определение угловой скорости и углового ускорения.
Как направлен вектор угловой скорости?
Угловая скорость – кинематическая величина, характеризующая
направление ее быстроту вращения тела. Угловая скорость направлена по оси
вращения и связана с направлением вращения по правилу правого винта.
Угловое ускорение – это вектор, характеризующий
быстроту изменения угловой скорости тела.
4)Связь между угловыми и векторными величинами.
V=R*W; ar=E*R; an=R*W2=W*V
5)Вывести уравнение основного закона динамики
вращательного движения.
, где l –
момент импульса вращающегося тела относительно оси вращения.
6)Какая сила сообщает вращательный момент маятнику.
Это сила тяжести, так как при подъеме тела на
высоту h под действием силы тяжести тело возвращается в
исходное положение и тем самым заставляет маятник вращаться.
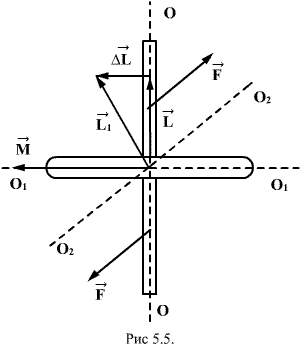
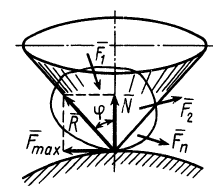
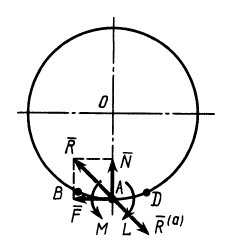
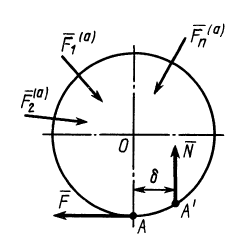
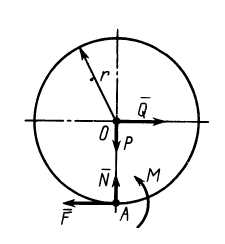
Момент сил трения качения
Определим для подвижного цилиндра
момент, тормозящий вращательное движение
тела. Рассматривая данный момент
относительно оси вращающегося колеса
(например, колеса автомобиля), находим,
что он равен произведению тормозного
усилия на оси на радиус колеса.
Относительно точки контакта движущегося
тела с землей момент будет равен
произведению внешней силы, уравновешивающей
силу трения, на радиус колеса (рис.
2):
.
С другой стороны, момент трения равен
моменту прижимающей силы
на
плечо, длина которого равна коэффициенту
трения качения f:
где
-
—
момент силы трения в [Н] · [м]; -
R — радиус тела качения;
-
P — внешняя сила;
-
Ft — сила трения качения;
-
f — коэффициент трения качения в
[м].
Коэффициент трения качения
Из выписанного выше уравнения следует,
что коэффициент трения качения может
быть определен как отношение момента
трения качения Mt к прижимной
силе N:
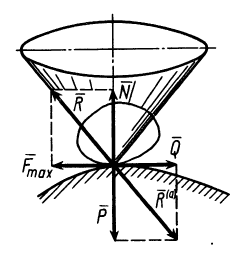
Графическая интерпретация коэффициента
трения качения f дана на рис. 3
и 4.
Коэффициент трения качения имеет
следующие физические интерпретации:
-
Если тело находится в покое и внешняя
сила отсутствует, то реакция опоры
лежит на той же линии, что и прижимающая
сила. Когда тело катится, то из условия
равновесия следует, что нормальная
составляющая реакции опоры параллельна
и противонаправлена прижимающей силе,
но не лежит с ней на одной линии.
Коэффициент трения качения равен
расстоянию между прямыми, вдоль которых
действуют прижимающая сила и нормальная
составляющая реакции опоры (рис. 4).
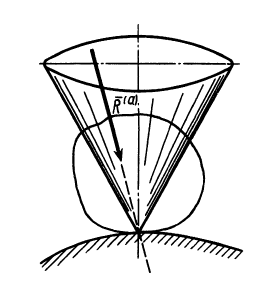
-
Движение катящегося тела без
проскальзывания можно рассматривать
как поворот вокруг мгновенной оси
вращения (на рис. 4 — точка
приложения вектора
),
которая для абсолютно твёрдых тел
совпадает с основанием перпендикуляра,
опущенного из центра круга на опору.
Для случая реальных (деформирующихся
под нагрузкой) материалов мгновенный
центр вращения смещён в направлении
качения тела, а величина смещения равна
значению коэффициента трения качения.
Билет 16.
Система материальных точек. Внутренние
и внешние силы. Закон сохранения импульса
изолированной системы.
В любой системе частиц имеется одна
замечательная точка, называемая центром
масс, которая обладает рядом интересных
и важных свойств. Ее положение относительно
начала данной системы координат
характеризуется радиус-вектором
,
определяемым как
(2.10)
где
–
масса и радиус-вектор
-й
частицы,
–
масса всей системы,
–
полное число частиц в системе. Если
взять производную по времени от обеих
частей уравнения и умножить обе части
на
,
то получится:
Или
,
где
–
скорость движения центра масс системы.
Таким образом, импульс системы материальных
точек равен произведению массы системы
на скорость ее центра масс:
.
(2.11)
Отсюда следует, что центр масс системы
материальных точек движется как
материальная точка, масса которой равна
суммарной массе всей системы, а действующая
сила – геометрической сумме всех внешних
сил, действующих на все точки системы. Этот
результат называется теоремой о движении
центра масс системы материальных точек.
Уравнение (2.11) по форме совпадает с
основным уравнением динамики материальной
точки и является его обобщением на
систему материальных точек: ускорение
системы как целого прямо пропорционально
результирующей всех внешних сил и
обратно пропорционально суммарной
массе системы.
Если система замкнута, то
и
уравнение (2.11) переходит в
,
следовательно,
.
Таким образом, центр масс замкнутой
системы движется прямолинейно и
равномерно или покоится.
Внутренние силы – это силы взаимодействия
между частицами системы тел.
Внешние силы – это силы, обусловленные
действием других тел, не входящих в
систему.
По способу приложения они могут быть
сосредоточенными и распределенными.
Сосредоточенные внешние силы действуют
на тело через очень маленькие площадки
и с достаточной степенью точности могут
считаться приложенными в точке. По
характеру действия внешние силы делятся
на постоянные и переменные.
Импульс системы может изменяться под
действием только внешних сил. Импульс
замкнутой системы частиц остается
постоянным. Закон сохранения импульса
изолированной системы:
Изолированная система – система,
состоящая из некоторого количества
тел, изолированных от всех остальных
тел и образующих механическую систему,
т.е. на эти тела не действуют внешние
силы, и сами эти тела взаимодействуют
друг с другом.
При этом импульсы отдельных частиц или
частей замкнутой системы могут меняться
со временем. Однако эти изменения всегда
происходят так, что приращение импульса
одной части системы равно убыли импульса
оставшейся части системы.
Внутренние силы – силы, с которыми
взаимодействуют тела, составляющие
механическую систему.
– сила, действующая со стороны тела
на
,
– антисимметричная матрица
Импульс изолированной системы сохраняется.
Импульсы системы тела – постоянны, если
внешние силы отсутствуют.
Билет 17.
Работа силы. Связь работы и энергии.
Мощность. Закон сохранения механической
энергии. Превращение энергии из одного
вида в другой. Примеры. Кинетическая
энергия поступательного движения.
Потенциальная энергия упругого
деформированного тела.
Работа силы.



,
Мощность
– величина, характеризующая скорость
совершения работы, называется. Мощность
численно равна отношению
к
промежутку времени
за
который она совершается.
или
в общем случае
,
Подставляя
значение
получим
Частный случай мощности при вращательном
движении:
M — момент силы,
—
угловая скорость, n — частота вращения
(число оборотов в минуту, об/мин).
Если тела, составляющие замкнутую
механическую систему, взаимодействуют
между собой только посредством сил
тяготения и упругости, то работа этих
сил равна изменению потенциальной
энергии тел, взятому с
противоположным знаком:
|
A = –(Eр2 – Eр1). |
По теореме о кинетической энергии эта
работа равна изменению кинетической
энергии тел:
|
|
Следовательно
|
|
|
Сумма кинетической и потенциальной
энергии тел, составляющих замкнутую
систему и взаимодействующих между собой
посредством сил тяготения и сил упругости,
остается неизменной.
Это утверждение выражает закон
сохранения энергии в механических
процессах. Он является следствием
законов Ньютона. Сумму E = Ek + Ep называют полной
механической энергией. Закон сохранения
механической энергии выполняется только
тогда, когда тела в замкнутой системе
взаимодействуют между собой консервативными
силами, то есть силами, для которых можно
ввести понятие потенциальной энергии.
Рассмотрим
случай, когда материальная точка движется
из точки 1 в точку 2 под действием
приложенных к ней сил (рис.4.4.)

Причем
силы, действующие на материальную точку,
могут иметь разную природу, т.е. могут
быть консервативными и неконсервативными.
Уравнение движения в этом случае
запишется в виде
(4.6)
где
Перепишем
(4.6) в виде
(4.7)
Умножим
скалярно уравнение (4.7) на
и
проинтегрируем от точки1 до точки 2,
получим:
(4.8)
Учитываем
то, что
,
и интеграл в правой части выражения
(4.8) представляет собой работу всех сил,
на участке 1-2, можно записать:
(4.9)
Величина
(4.10)
называется
кинетической энергией материальной
точки. Таким образом, кинетическая
энергия материальной точки – это
энергия, которой обладает эта точка
вследствие своего движения.
Из
полученного выражения (4.9) следует, что
работа всех сил, действующих на
материальную точку на участке траектории
1-2 равна изменению ее кинетической
энергии на этом участке.
Физическая величина, равная половине
произведения коэффициента жесткости
на квадрат абсолютной деформации,
называется потенциальной энергией
упруго деформированного тела:

Билет 18.
Потенциальная энергия в однородном
поле силы тяжести.
Потенциальная
энергия – это энергия, обусловленная
взаимным расположением тел и характером
их взаимодействия. При соответствующих
условиях возможно изменение потенциальной
энергии, за счет чего совершается
работа. Для поднятия тела массой m на
высоту
необходимо
совершить работу против сил тяготения
Р:
,
знак
минус перед интегралом, т.к. сила Р
направлена в сторону противоположную
изменению h.
Проинтегрируем
это выражение:
Эта
энергия пойдет на увеличение энергии
замкнутой системы тело – Земля т.е.
численно равна
Считая
поверхности Земли
,
получим
Эта
энергия
системы
тело – Земля и является потенциальной
энергией тела, поднятого на высоту h:
Билет 19.
Абсолютно
упругий и абсолютно неупругий удары
(столкновения) Превращение энергии в
процессе столкновения. Законы сохранения
импульса и энергии. Связь между скоростями
соударяющихся тел до и после удара.
Убыль механической энергии в неупругом
ударе.
Ударом (или столкновением)
принято называть кратковременное
взаимодействие тел, в результате которого
их скорости испытывают значительные
изменения
Абсолютно неупругим ударом называют
такое ударное взаимодействие, при
котором тела соединяются (слипаются)
друг с другом и движутся дальше как одно
тело.
При абсолютно неупругом ударе механическая
энергия не сохраняется. Она частично
или полностью переходит во внутреннюю
энергию тел (нагревание).
Примером абсолютно неупругого удара
может служить попадание пули (или
снаряда) в баллистический маятник.
Маятник представляет собой ящик с песком
массой M, подвешенный на веревках.
Пуля массой m, летящая горизонтально
со скоростью
попадает
в ящик и застревает в нем. По отклонению
маятника можно определить скорость
пули.
Обозначим скорость ящика с застрявшей
в нем пулей через
.Тогда
по закону сохранения импульса
|
|
При застревании пули в песке произошла
потеря механической энергии:
|
|
Отношение M / (M + m) – доля
кинетической энергии пули, перешедшая
во внутреннюю энергию системы:
|
|
Эта формула применима не только к
баллистическому маятнику, но и к любому
неупругому соударению двух тел с разными
массами.
При m << M
почти
вся кинетическая энергия пули переходит
во внутреннюю энергию. При m = M
–
во внутреннюю энергию переходит половина
первоначальной кинетической энергии.
Наконец, при неупругом соударении
движущегося тела большой массы с
неподвижным телом малой массы (m >> М)
отношение
Дальнейшее движение маятника можно
рассчитать с помощью закона сохранения
механической энергии:
|
|
где h – максимальная высота подъема
маятника. Из этих соотношений следует:
|
|
Абсолютно упругим ударом называется
столкновение, при котором сохраняется
механическая энергия системы тел.
Во многих случаях столкновения атомов,
молекул и элементарных частиц подчиняются
законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с
законом сохранения импульса выполняется
закон сохранения механической энергии.
Простым примером абсолютно упругого
столкновения может быть центральный
удар двух бильярдных шаров, один из
которых до столкновения находился в
состоянии покоя (рис. 1.21.2).
Центральным ударом шаров называют
соударение, при котором скорости шаров
до и после удара направлены по линии
центров.
В общем случае массы m1 и m2 соударяющихся
шаров могут быть неодинаковыми. По
закону сохранения механической энергии
|
|
Здесь υ1 – скорость первого
шара до столкновения, скорость второго
шара υ2 = 0, u1 и u2 –
скорости шаров после столкновения.
Закон сохранения импульса для проекций
скоростей на координатную ось, направленную
по скорости движения первого шара до
удара, записывается в виде:
|
m1υ1 = m1u1 + m2u2. |
Мы получили систему из двух уравнений.
Эту систему можно решить и найти
неизвестные скорости u1 и u2 шаров
после столкновения:
|
|
В частном случае, когда оба шара имеют
одинаковые массы (m1 = m2),
первый шар после соударения останавливается
(u1 = 0), а второй движется со
скоростью u2 = υ1,
т. е. шары обмениваются скоростями
(и, следовательно, импульсами).
Если бы до соударения второй шар также
имел ненулевую скорость (υ2 ≠ 0),
то эту задачу можно было бы легко свести
к предыдущей с помощью перехода в новую
систему отсчета, которая движется
равномерно и прямолинейно со
скоростьюυ2 относительно
«неподвижной» системы. В этой системе
второй шар до соударения покоится, а
первый по закону сложения скоростей
имеет скорость υ1‘ = υ1 – υ2.
Определив по приведенным выше формулам
скорости u1 и u2 шаров
после соударения в новой системе, нужно
сделать обратный переход к «неподвижной»
системе.
Таким образом, пользуясь законами
сохранения механической энергии и
импульса, можно определить скорости
шаров после столкновения, если известны
их скорости до столкновения.
Центральный (лобовой) удар очень редко
реализуется на практике, особенно если
речь идет о столкновениях атомов или
молекул. При нецентральном упругом
соударении скорости частиц (шаров) до
и после столкновения не направлены по
одной прямой.
Частным случаем нецентрального упругого
удара может служить соударение двух
бильярдных шаров одинаковой массы, один
из которых до соударения был неподвижен,
а скорость второго была направлена не
по линии центров шаров (рис. 1.21.3).
После нецентрального соударения
шары разлетаются под некоторым углом
друг к другу. Для определения
скоростей
и
после
удара нужно знать положение линии
центров в момент удара или прицельное
расстояние d (рис. 1.21.3), т. е.
расстояние между двумя линиями,
проведенными через центры шаров
параллельно вектору скорости
налетающего
шара. Если массы шаров одинаковы, то
векторы скоростей
и
шаров
после упругого соударения всегда
направлены перпендикулярно друг к
другу. Это легко показать, применяя
законы сохранения импульса и энергии.
При m1 = m2 = m эти
законы принимают вид:
|
|
Первое из этих равенств означает, что
векторы скоростей
,
и
образуют
треугольник (диаграмма импульсов), а
второе – что для этого треугольника
справедлива теорема Пифагора, т. е.
он прямоугольный. Угол между
катетами
и
равен 90°.
Билет 20.
Понятие абсолютно твердого тела.
Поступательное, вращательное и
плоско-параллельное движение твердого
тела. Связь между угловой и линейной
скоростями твердого тела.
Твердое тело (абсолютно твердое тело)
– это тело, которое ни при каких условиях
не может деформироваться; в абсолютно
твердом теле при всех условиях расстояние
между точками остается постоянным.
Поступательное движение твердого тела
– движение, при котором линия, соединяющая
любые две точки тела, сохраняет неизменное
направление в пространстве. При
поступательном движении любая линия
переносится параллельно самой себе,
т.е. смещение всех точек тела одинаково.
Поэтому при поступательном движении
все точки твердого тела обладают
одинаковыми линейными скоростями и
одинаковыми линейными ускорениями.
Вращательное движение – движение, при
котором траекторией всех точек являются
концентрические окружности с центрами
на одной прямой, называемой осью вращения.
Концентрические окружности – окружности,
у которых один центр.При вращательно
движении все точки данного тела обладают
одинаковыми угловыми скоростями и
одинаковыми угловыми ускорениями.
Линейные скорости вращающегося тела
одинаковы: чем дальше от оси вращения
отстоит точка, тем большей линейной
скоростью она обладает.
Плоскопараллельное движение – движение,
при котором любая точка твердого тела
во время движения остается в одной из
параллельных плоскостей.
Связь между линейной и угловой скоростями:
Билет 21.
Центр инерции твердого тела. Связь
координат и масс твердого тела в системе
координат, связанной с центром масс
(лемма о центре масс). Координаты центра
инерции. Закон движение центра инерции
твердого тела.
Если укрепить тело в центре тяжести, то
оно будет находиться в равновесии при
любом положении тела, т.е. сумма моментов
сил тяжести всех частиц тела относительно
любой горизонтальной оси, проходящей
через центр тяжести, будет равна нулю.

– лемма о центре масс
Если повернуть тело относительное оси
на
по
часовой стрелке, то ось
займет положение
,
и плечом силы тяжести относительно
будет являться
,
т.е

– саму произведения центра масс тела на
его радиус-вектор.

,
(
– скорость движения системы отсчета
относительно другой.)
а)
(масса
всей системы на скорость центра масс)
б)

ex – external – внешний
in – internal – внутренний
Центр инерции твердого тела движется
так, как если бы к нему были приложены
все внешние силы и масса, всего тела
была бы сосредоточена в центре масс.
Билет 22.
Момент силы. Закон динамики вращения
тела вокруг неподвижной оси (уравнение
вращательного движения). Момент инерции.
,
,
=0
– уравнение вращательного движения
– момент инерции
Момент инерции зависит не только от
величины массы тела, но и от распределения
масс относительно оси.
Уравнение вращательного движения
является аналогом II-го
закона Ньютона. Что бы вызвать
поступательное движение точки, нужно
приложить силу; чтобы получить вращательное
движение тела, необходимо приложить
момент силы. Так же как сила вызывает
линейное ускорение, так и момент силы
вызывает появление углового ускорения.
Коэффициентами в этих уравнениях
является масса и момент инерции. Значит,
масса является мерой инерции для
поступательного движения, а момент
инерции является мерой инерции для
вращательного движения.
Билет 23.
Момент импульса. Уравнение моментов
(относительно оси). Закон сохранения
момента импульса.
– момент импульса точки относительно
оси
– момент импульса тела относительно оси
– уравнение моментов (относительно оси)
Если
Закон сохранения момента импульса:
Момент импульса твердого тела остается
постоянным, если суммарный момент
внешних сил равен нулю.
Билет 24.
Момент импульса и момент силы
относительно точки. Уравнение моментов
(относительно точки).
Связь моментов относительно точки и
моментов относительно оси:
Момент силы, относительно оси есть
проекция момента силы относительно
точки на эту ось; при этом полюс должен
лежать на оси вращения. Такая же связь
существует между моментом относительно
точки и моментом относительно оси.
Получим уравнение моментов относительно
точки в случае плоского движения.
на
слева

{левая часть}=
– уравнение моментов относительно точки.
Билет 25.
Кинетическая энергия вращающегося
тела. Работа по повороту вращающегося
тела.
Кинетическая энергия тела, движущегося
произвольным образом, равна сумме
кинетических энергий всех n материальных
точек па которые это тело можно разбить:
.
Если тело вращается вокруг неподвижной
оси с угловой скоростью
, то
линейная скорость i-ой точки равна
,
где
,
– расстояние от этой точки до оси вращения.
Следовательно.
,
где
–
момент инерции тела относительно оси
вращения. В общем случае движение
твердого тела можно представить в виде
суммы двух движений – поступательного
со скоростью, равной скорости
центра
инерции тела, и вращения с угловой
скоростью
вокруг
мгновенной оси, проходящей через центр
инерции. При этом выражение для
кинетической энергии тела преобразуется
к виду
,
где
–
момент инерции тела относительно
мгновенной оси вращения, проходящей
через центр инерции.
Работа по повороту твердого тела.

Рассмотрим действие внешней силы
,
приложенной к точке массой
.
За время
элементарная
масса
проходит
путь
Работа
силы
на
этом пути определяется проекцией силы
на направление перемещения, которая
очевидно, равна тангенциальной
составляющей
силы.
Но
равна
модулю момента
силы
относительно
оси вращения. Работа
,
и будет положительна, если
имеет
такое же направление, как и
отрицательное,
если направление векторов
и
противоположны.
С учетом, что
Работа всех сил, приложенных к телу
Полная работа

1.
2.
– дуга
Билет 26.
Аналогия между поступательным движением
материальной точки и вращательным
движением твердого тела.
|
Поступательное относительно точки |
Вращательное движение твердого тела |
|
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5.m |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
Билет 27.
Момент инерции. Вычисление моментов
инерции тел ( на примере моментов инерции
цилиндра, кольца, тонкого кольца, стержня
и шара)
Чтобы найти момент инерции тела, надо
просуммировать момент инерции всех
материальных точек, составляющих данное
тело
В
общем случае, если тело сплошное, оно
представляет собой совокупность
множества точек с бесконечно малыми
массами
,
и моменты инерции тела определяется
интегралом
где
–
расстояние от элемента
до
оси вращения.
Распределение массы в пределах тела
можно охарактеризовать с помощью
плотности
где
m – масса однородного тела, V – его объем.
Для тела с неравномерно распределенной
массой это выражение дает среднюю
плотность.
.
Плотность в данной точке в этом случае
определяется следующим образом
и тогда
Пределы интегрирования зависят от формы
и размеров тела Интегрирование уравнения
(5.5) наиболее просто осуществить для тех
случаев, когда ось вращения проходит
через центр тяжести тела. Рассмотрим
результаты интегрирования для простейших
(геометрически правильных) форм твердого
тела, масса которого равномерно
распределена по объему.

Момент инерции полого цилиндра с тонкими
стенками, радиуса R.
Для полого цилиндра с тонкими стенками
Сплошной однородный диск. Ось вращения
является осью диска радиуса
.
и массы m с плотностью
Высота
диска h. Внутри диска на расстоянии
вырежем пустотелый цилиндр с толщиной
стенки
и
массой
.
Для него
Весь диск можно разбить на бесконечное
множество цилиндров, а затем просуммировать:
Момент инерции шара относительно оси,
проходящей через центр тяжести.
Момент инерции стержня длиной L и
массой m относительно оси, проходящей:
а) через центр стержня –
б) через начало стержня –

Билет 28.
Момент инерции. Теорема Гюйгенса-Штейнера.
Теорема Гюйгенса-Штейнера. Момент
инерции тела относительно произвольной
оси равен сумме момента инерции тела
относительно оси, проходящей через
центр масс и параллельной данной оси,
плюс произведение массы тела на квадрат
расстояния между осями:
—
известный момент инерции относительно
известной оси,
—
искомый момент инерции,
—
масса тела,
—
расстояние между осями (известной и
относительно которой необходимо найти
момент инерции)
Чтобы найти момент инерции тела, надо
просуммировать момент инерции всех
материальных точек, составляющих данное
тело
В
общем случае, если тело сплошное, оно
представляет собой совокупность
множества точек с бесконечно малыми
массами
,
и моменты инерции тела определяется
интегралом
где
–
расстояние от элемента
до
оси вращения.
Распределение массы в пределах тела
можно охарактеризовать с помощью
плотности
где
m – масса однородного тела, V – его объем.
Для тела с неравномерно распределенной
массой это выражение дает среднюю
плотность.
.
Плотность в данной точке в этом случае
определяется следующим образом
и тогда
Пределы интегрирования зависят от формы
и размеров тела Интегрирование уравнения
наиболее просто осуществить для тех
случаев, когда ось вращения проходит
через центр тяжести тела.
Билет 29.
Момент импульса относительно точки.
Связь между импульсом относительно
точки и угловой скорость вращения
твердого тела. Тензор инерции.
Моментом импульса материальной точки
относительно неподвижной точки О
называется физическая величина,
определяемая векторным произведением:
∆
=
=
Тензор инерции
Тензором называют упорядоченную
совокупность чисел, называемых
компонентами тензора и зависящих от
выбора системы координат.
Размерность тензора называется
рангом.(количество индексов у
компонентов)оэтому вектор является
тензором первого ранга, а матрица
второго.
симметричная
Покажем, что элементами главной диагонали
являются моменты инерции относительно
координатных осей.
расстояние
от А до осин
момент
инерции относительно Оz
Билет 30.
Теорема о главных осях. Диагонализация
тензора инерции. Главные моменты инерции
твердого тела.
Для любого тела и любой точки О существует
3 взаимно перпендикулярных направления,
при вращении вокруг которых вектор
момента импульса сонаправлен с вектором
угловой скорости.
Такие направления называются главными
осями и для них
, λ-скаляр
1)
Система линейных однородных уравнений
=0
=
=
Расписывая систему уравнений
и домнажая уравнение этой системы на
компоненты вектора
, после сложения получим:

Диагонализации тензора инерции.
Базис системы координат:
–
единичные вектора вдоль главных
направлений

-главные
моменты инерции
Если
,
то имеется бесконечное количество
главных осей, лежащих в плоскости
нормальной к
.
Билет 31.
Связь момента инерции твердого тела
относительно произвольной оси, проходящей
через центр масс, с тензором инерции
относительно системы координат, связанных
с центром масс.
–
момент импульса относительно центра
масс
-проекция
на ось
(момент
импульса относительно оси)
Билет 32.
Гироскопы. Гироскоп под действием сил
(приближенная теория). Прецессия
гироскопа. Гироскопические силы.
Нутации.
Гироскопом называют любое быстро
вращающееся симметричное тело, ось
которого может менять свое направление
в пространстве.
При
закреплении в кардановом подвесе
гироскоп можно рассматривать как
симмитричное твердое тело, закрепленное
в центре масс. Ось гироскопа может занять
любое положение в пространстве.
Свойства гироскопа (2 основных):
-
Устойчивость положения оси гироскопа
относительно малых воздействий; -
Безынертность воздействия
моментов внешних сил (момент силы
создает не ускорение, а скорость
вращения оси гироскопа).
,
,
если N мал, то
Свободным называется гироскоп, к которому
приложен внешний момент сил. Свободный
гироскоп не изменят направления своей
оси, если ось вращения совпадает с
геометрической осью гироскопа (т.е. не
прецессирует).
Прецессией называется вращение оси
гироскопа в горизонтальной плоскости
под действием момента внешней силы.
Нутацией называется вращающая ось
гироскопа в вертикальной плоскости
(«нырки» при вращении).
Гироскопические
силы – силы, зависящие от
скоростей и обладающие тем свойством,
что сумма их работ (или мощностей) при
любом перемещении системы, на которую
действуют эти силы, равна нулю. Если
–
гироскопические силы, то для них
или
где
–
радиусы-векторы точек приложения
сил,
–
скорости этих точек. Хотя гироскопические
силы, как зависящие от скоростей, не
являются потенциальными, но на систему,
на которую кроме потенциальных сил
действуют ещё и гироскопические, тоже
распространяется закон сохранения
механической энергии.
Примерами гироскопических сил
являются сила
Кориолиса
материальной
точки с массой m,
движущейся со скоростью
по
отношению к подвижной (неинерциальной)
системе отсчёта (
–
угловая скорость этой системы отсчёта),
и сила Лоренца
,
действующая на заряженную частицу
с зарядом е,
движущуюся со скоростью v в
магнитном поле (B –
магнитная индукция, с – скорость
света). Каждая из этих сил
направлена перпендикулярно скорости,
поэтому их работа или мощность при любом
перемещении точки (частицы) равна нулю.
,
,
Билет 33.
Законы Кеплера. Закон всемирного
тяготения. Опыт Кавендиша.
Первый закон Кеплера (закон эллипсов)
Каждая планета Солнечной
системы обращается
по эллипсу,
в одном из фокусов которого находится Солнце.
Форма эллипса и степень его сходства с
окружностью характеризуется отношением
,
где c — расстояние от центра эллипса
до его фокуса (половина межфокусного
расстояния), a — большая
полуось.
Величина e называется эксцентриситетом эллипса.
При c = 0 и e = 0 эллипс
превращается в окружность.
Второй закон Кеплера (закон площадей)
Каждая планета движется в плоскости,
проходящей через центр Солнца, причём
за равные промежутки времени радиус-вектор,
соединяющий Солнце и планету, описывает
равные площади. Применительное к нашей
Солнечной системе, с этим законом связаны
два понятия: перигелий —
ближайшая к Солнцу точка орбиты,
и афелий —
наиболее удалённая точка орбиты. Таким
образом, из второго закона Кеплера
следует, что планета движется вокруг
Солнца неравномерно, имея в перигелии
большую линейную скорость, чем в афелии.
Каждый год в начале января Земля, проходя
через перигелий, движется быстрее,
поэтому видимое перемещение Солнца
по эклиптике к
востоку также происходит быстрее, чем
в среднем за год. В начале июля Земля,
проходя афелий, движется медленнее,
поэтому и перемещение Солнца по эклиптике
замедляется. Закон площадей указывает,
что сила, управляющая орбитальным
движением планет, направлена к Солнцу.
Доказательство второго закона Кеплера. По
определению угловой
момент
точечной
частицы с массой m и
скоростью
записывается
в виде:
.где
—
радиус-вектор частицы а
—
импульс частицы. Площадь, заметаемая
радиус-вектором
за
время dt из геометрических соображений
равна
,
где θ представляет собой угол
между направлениями
и
.
По определению
В результате мы имеем
.Продифференцируем
обе части уравнения по времени
поскольку
векторное произведение параллельных
векторов равно нулю. Заметим, что F всегда
параллелен r, поскольку сила радиальная,
и p всегда параллелен v по
определению. Таким образом можно
утверждать, что
,
а следовательно и пропорциональная ей
скорость заметания площади
—
константа.
Квадраты периодов обращения планет
вокруг Солнца относятся как кубы больших
полуосей орбит
планет. Справедливо не только для
планет, но и для их спутников.
,
где T1 и T2 — периоды
обращения двух планет вокруг Солнца,
а a1 и a2 — длины
больших полуосей их орбит.
Ньютон установил,
что гравитационное
притяжение планеты
определенной массы зависит только от
расстояния до неё, а не от других свойств,
таких, как состав или температура. Он
показал также, что третий закон Кеплера
не совсем точен — в действительности
в него входит и масса планеты:
,
где M — масса Солнца, а m1 и m2 —
массы планет.
Поскольку движение и масса оказались
связаны, эту комбинацию гармонического
закона Кеплера и закона тяготения
Ньютона используют для определения
массы планет и спутников, если известны
их орбиты и орбитальные периоды.
Космическая
скорость (первая v1, вторая v2, третья v3 и четвёртая v4) —
это минимальная скорость, при которой
какое-либо тело в свободном движении с
поверхности небесного тела сможет:
-
v1 —
стать спутником небесного
тела (то есть способность
вращаться по орбите вокруг НТ и не
падать на поверхность НТ). -
v2 —
преодолеть гравитационное
притяжение небесного
тела. -
v3 —
покинуть звёздную
систему, преодолев
притяжение звезды. -
v4 —
покинуть галактику.
Закон всемирного тяготения. Сила
гравитационного притяжения между двумя
материальными точками массы m1 и m2,
разделёнными расстоянием R,
пропорциональна обеим массам и обратно
пропорциональна квадрату расстояния
между ними — то есть
:
Здесь G — гравитационная
постоянная, равная
м³/(кг
с²).
Опыт Кавендиша. Установка представляет
собой деревянное коромысло с прикреплёнными
к его концам небольшими свинцовыми
шарами диаметром 5 см и массой 775 г.
Оно подвешено на нити из посеребрённой
меди длиной 1 м. К шарам подносят шары
большего размера диаметром 20 см и
массой 49,5 кг, сделанные также из
свинца. В результате действия гравитационных
сил коромысло закручивается на некий
угол. Жёсткость нити была такой, что
коромысло делало одно колебание за 15
минут. Угол поворота коромысла определялся
с помощью луча света, пущенного на
зеркальце на коромысле, и отражённого
в микроскоп. Зная упругие свойства нити,
а также угол поворота коромысла, можно
вычислить гравитационную
постоянную. Для предотвращения
конвекционных потоков установка была
заключена в ветрозащитную камеру. Угол
отклонения измерялся при помощи
телескопа. Заподозрив в качестве причины
закручивания нити магнитное взаимодейстивие
железного стержня и свинцовых шаров,
Кавендиш заменил стержень медным,
получив те же результаты.
Г.
Кавендиш получил значение G=6,754×10−11
Билет 10 . Кинетическая энергия вращающегося
тела. Работа по повороту твердого тела.
Кинетическая энергия тела, движущегося
произвольным образом, равна сумме
кинетических энергий всех n материальных
точек па которые это тело можно разбить:
.
Если тело вращается вокруг неподвижной
оси с угловой скоростью
, то
линейная скорость i-ой точки равна
,
где
,
– расстояние от этой точки до оси вращения.
Следовательно.
,
где
–
момент инерции тела относительно оси
вращения. В общем случае движение
твердого тела можно представить в виде
суммы двух движений – поступательного
со скоростью, равной скорости
центра
инерции тела, и вращения с угловой
скоростью
вокруг
мгновенной оси, проходящей через центр
инерции. При этом выражение для
кинетической энергии тела преобразуется
к виду
,
где
–
момент инерции тела относительно
мгновенной оси вращения, проходящей
через центр инерции.
Работа по повороту твердого тела.
Рассмотрим действие внешней силы
,
приложенной к точке массой
.
За время
элементарная
масса
проходит
путь
Работа
силы
на
этом пути определяется проекцией силы
на направление перемещения, которая
очевидно, равна тангенциальной
составляющей
силы.
Но
равна
модулю момента
силы
относительно
оси вращения. Работа
,
и будет положительна, если
имеет
такое же направление, как и
отрицательное,
если направление векторов
и
противоположны.
С учетом, что
Работа всех сил, приложенных к телу
Полная работа
Билет 34.
Гармонические колебания. Колебания
математического маятника и груза на
пружине. Уравнения колебаний и их
решения. Изменение смещения, скорости,
ускорения и энергии в процессе колебаний.
Функция
называется периодической, если для
любого
выполняется
соответствие
,
где t – период функции.
В периодическом явлении (процессе)
изменение какой-либо величины повторяется
в том же виде через определенное время,
называемым периодом колебаний.
Гармонические колебания представляют
собой периодический процесс, в котором
изменения наблюдаемой величины происходит
по закону синуса или косинуса.
,
где
– амплитуда (максимальное смещение);
– круговая (циклическая) частота
;
– начальная фаза;
– смещение из положения равновесия.
,
Математическим маятником называется
небольшое тело, подвешенное на нити,
при условии, что нить является невесомой
и нерастяжимой, а тело можно считать
материальной точкой.
,
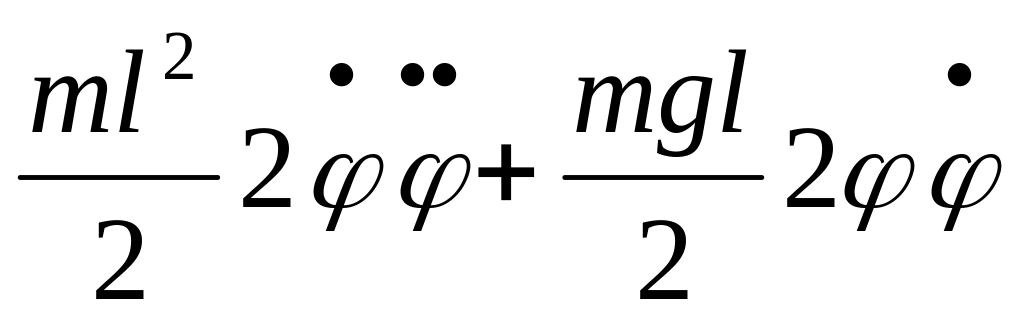
–
уравнение колебаний,
–
уравнение гармонического осциллятора

,
2)





При уменьшении угла положение
приближается к положению оси
и поэтому, ввиду малости угла, проекции
возвращающей силы на эти направления
становятся одинаковы.
длина
дуги =

Билет 35.
Физический маятник. Уравнение колебаний
и его решение. Приведенная длина
физического маятника.
Физический маятник – достаточно тяжелое
тело, которое может совершать колебания
вокруг горизонта оси, проходящей выше
центра тяжести.
– возвращающий момент

Приведенной длинной физического маятника
называют длину математического маятника,
который совершает колебания с той же
частотой, что и физический.
– приведенная длина
Ц
ентр
качения физического маятника – точка,
расположенная на расстоянии приведенной
длины от точки подвеса до линии,
соединяющей точку подвеса и центр
тяжести.
– центр тяжести
Билет 36.
Физический маятник. Обратимость точки
подвеса и центра качаний.
Физическим маятником называется
достаточно тяжелое тело, которое может
совершать колебания вокруг горизонтальной
оси, проходящей выше центра тяжести.
Центром качаний физического маятника
называется точка, расположенная на
расстоянии приведенной длины от точки
подвеса по линии, соединяющей точку
подвеса и центр тяжести.
Теорема об обратимости точки подвеса
и центра качания.
Если ось вращения поместить в центр
качаний, то маятник будет совершать
колебания с той же частотой (т.е. новый
центр качаний будет совпадать со старой
точкой подвеса)
Докажем, что
(1)
=>
(2)
(2)=>(1)
Билет 37.
Затухающие собственные колебания.
Уравнение колебаний и его решение.
Зависимость амплитуды колебаний от
времени. Условный период затухающих
колебаний. Коэффициент затухания и
логарифмический декремент затухания.
Собственными колебаниями называются
колебания системы, выведенной из
положения равновесия и предоставленной
самой себе.
Затухающими называются колебания, у
которых амплитуда уменьшается с течением
времени.
Пружинный маятник:
, h-коэф. силы трения
Решение:
-коэффициент
затухания
-время
релаксации, это время за которое амплитуда
колебаний уменьшается в е раз.
,
Декремент
логарифмический
декремент затухания
=>
Билет 38.
Вынужденные колебания. Резонанс.
Амплитудно-частотная и фазо-частотная
характеристики. Резонансная частота
Вынужденными называются колебания,
которые происходят под действием внешней
периодической силы.
,
где
–
возвращающая сила,
–
сила трения,
–
периодическая сила
,
β=
–
коэффициент затухания
Следовательно, коэффициент
затухания β есть физическая
величина, обратная времени, в
течение которого амплитуда уменьшается
в е раз.
Время релаксации τ – время, в
течение которого амплитуда А уменьшается
в e раз.
Предположим, что возникающее под
действием силы установившиеся вынужденные
колебания системы также являются
гармоническими:
(7.22)
причем их циклическая частота равна
циклической частоте ω вынуждающей силы.

Явление резкого
возрастания амплитуды вынужденных
колебаний при приближении вынуждающей
частоты ω к частоте собственных колебаний
системы
называется
резонансом.

Для того, чтобы
полученное уравнение было справедливо
для всех времен, необходимо, чтобы
коэффициенты при
и
были тождественно равны 0.

–
резонансная частота. p обозначает
то значение циклической частоты ω
вынуждающей силы, при котором
С увеличением коэффициента затухания
ω явление резонанса проявляется все
слабее, и, наконец при
исчезает
совсем.
Резонансом называется резкое увеличение
амплитуды вынужденных колебаний при
приближении частоты вынуждающей силы
и частоте собственных колебаний системы.
–
вынуждающая сила.
Явление резонанса используется для
усиления колебаний, например,
электромагнитных. Однако при конструировании
различных машин и сооружений необходимо
учитывать даже самую небольшую
периодическую силу с тем, чтобы
предотвратить нежелательные последствия
резонанса.
X(t)=В cos
(Ѡt+ϕ)
ϕ-разность фаз между
колебаниями силы F и
смещением F(t)
При низких частотах колебания смещений
x(t) происходят
в фазе с колебаниями вынужденные силы,
при резонансе отстают на пи пополам.
При высоких частотах протекают в
противофазе с колебаниями вынужденные
силы.
Билет 39.
Колебания связанных систем. Собственная,
парциальная и нормальные частоты.
Синфазные и антифазные колебания.
Биения. Теоретический анализ биений.
Если между колебательными системами
имеется связь, через которую они
воздействуют друг на друга – связанная
система.
Системы с одной степенью свободы, на
которые можно расчленить связанную
систему, называются парциальными.
Частота парциальных колебаний будет
больше собственной частоты, т.к.
возвращающая к положению равновесия
сила состоит из двух слагаемых:
составляющая силы тяжести и упругой
силы деформированной пружины.
Биениями называются колебания с
амплитудой, меняющейся по периодическому
закону.
Амплитуда гармонических колебаний
постоянна, поэтому биения не являются
гармоническими колебаниями. Биения в
системе возникают при сложении 2-х
гармонических колебаний одинакового
направления, которые мало отличаются
друг от друга по частоте. Биения
возникают от того, что один из двух
сигналов постоянно отстаёт от другого
по фазе и
в те моменты, когда колебания происходят
синфазно, суммарный сигнал оказывается
усилен, а в те моменты, когда два сигнала
оказываются в противофазе, они взаимно
гасят друг друга. Эти моменты периодически
сменяют друг друга по мере того как
нарастает отставание. Биения звука можно
слышать при настройке струнного
музыкального инструмента по камертону.
Если частота струны незначительно
отличается от частоты камертона, то
слышно, что звук пульсирует — это и
есть биения. Струну нужно подтягивать
или ослаблять так, чтобы частота биений
уменьшалась. При совпадении высоты
звука с эталонным биения полностью
исчезают. Биения звука также можно
услышать при игре на музыкальных
инструментах, например пианино или
гитаре, когда различной высоты звуки
создают интервалы и многозвучия.
(аккорды).
Гармонические колебания, возникающие
в связанной системе, называются
нормальными колебаниями, а соответствующие
частоты называются нормальными частотами.
Система с двумя степенями свободы
обладает двумя начальными колебаниями:
синфазными и антифазными. Биения в
связанной системе возникают как результат
сложениями нормальных частот.
Частота синфазных колебаний ѠС
равна частоте собственных колебаний
Ѡ0 ,т.к. при синфазных колебаниях
связь не деформируется. Частота антифазных
колебаний ѠА больше частоты
синфазных колебаний, т.к. пружина,
связывающая маятник, деформируется
Частота биений ѠБ=ѠА-ѠС
Синфазность –
совпадение по фазе двух или нескольких
периодических колебаний.
Опираясь на более общее понятие
когерентности, С. можно определить как
частный случай когерентности, при
котором разность фаз
колебаний постоянна и
равна нулю [на рис. 1 см.синфазные гармонические
колебания, описываемые функциями
вида
где
A1,2 – амплитуды,
–
круговая (циклическая) частота, Т –
период колебаний,
–
начальная фаза; эти колебания синфазные,
если , где п = 0, 1, 2, …; на рис.
2- синфазные
колебания
взаимно перпендикулярных векторов
напряжённостей электрических и магнитных
полей].

Рис. 1.
Примеры синфазных колебаний: 1) колебания
всех точек стоячей
волны; они происходят с
различными отклонениями от нулевого
положения, но в одинаковой фазе (в то
время как в бегущей
волне, наоборот, колебания
всех точек происходят е одинаковыми
отклонениями, но в различных фазах);
Антифазные – это колебания маятников,
происходящие в противофазе с большей
из нормальных частот ω2.
Нормальные колебания
– собственные
(свободные) гармонические колебания
линейных систем с постоянными параметрами,
в которых отсутствуют как потери энергии,
так и приток ее извне. Каждое нормальное
колебание характеризуется определенным
значением частоты, с которой колеблются
все элементы системы, и формой –
распределением амплитуд и фаз. Число
степени свободы —
это совокупность независимых координат
перемещения и/или вращения, полностью
определяющая движение и/или положение
тела или системы тел нормальных
колебаний равно числу колебательных
степеней свободы системы.
Билет 40.
Преобразования Галилея. Принцип
относительности Галилея. Инварианты
преобразований Галилея. Специальный
принцип относительности. Постулаты
специальной теории относительности.
Преобразования Лоренца (без вывода).
Инварианты преобразований Лоренца.
Преобразования Галилея —
преобразования координат и времени при
переходе от одной инерциальной
системы отсчета (ИСО) к
другой.
Принцип относительности Галилея:
Во всех инерциальных системах отсчета
законы Ньютона имеют одинаковую форму;
инерциальные или галилеевы системы
равноправны с точки зрения ньютоновской
динамики.
–
преобразования Галилея
,
Инвариантами при некоторых
преобразованиях называются величины,
не меняющиеся при этих преобразованиях.
Инварианты преобразований Галилея.
-
Расстояние между двумя
точками; -
Относительная скорость
(относительно друг друга) ; -
Так как силы зависят от
относительного расположения тел или
от их относительных скоростей, то силы
являются инвариантами; -
Поскольку, потенциальная
энергия зависит только от расстояния
между телами, то она инвариант; -
Второй закон Ньютона
является инвариантом, сила и ускорение
являются инвариантами, поэтому масса
– инвариант.
Импульс и кинетическая
энергия не являются инвариантами.
Специальный принцип относительности:
Все инерциальные системы равноправны
(не только относительно ньютовской
динамики, а относительно все законов
природы, в частности законов
электромагнетизма)
Постулат о постоянстве
скорости света:
Скорость света в пустоте
не зависит от движения источника.
Преобразования Лоренца:

Билет 44.
Продольные и поперечные волны. Волновое
уравнение. Интерференция волн. Эффект
Доплера.
Продольными называются волны, в которых
частицы среды совершают колебания вдоль
направления распространения волны
(пример: звуковая волна)
Поперечными называются волны, в которых
частицы среды движутся поперек направления
распространения волны (например: волна
вдоль натянутой струны).
Волновой поверхностью (волновым фронтом)
называется поверхность равной фазой.
В зависимости от типа волнового фронта
различают сферические и плоские волны.
Пример сферической волны: звуковая
волна в однородной изотропной среде,
распространяющейся во всех направлениях
одинаково; волновым фронтом является
сфера с центром в источнике колебаний.
Пример плоской волны: волны,
распространяющиеся вдоль оси трубы от
колеблющегося поршня, волны сгущений
и раздражений; волновым фронтом является
плоскость, перпендикулярная оси трубы.
Волновое уравнение
1) Адиабатический процесс (Q=0)
Уравнение адиабаты
,
– коэффициент Пуассона, показатель
адиабаты
2)
,
,
3)
–
скорость света в среде
,
– равновесная плотность,
– изменение
Содержание:
Трение:
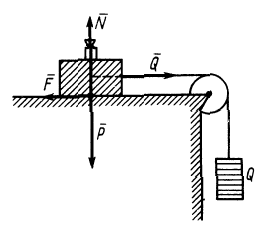
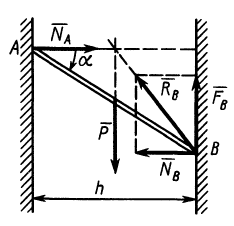
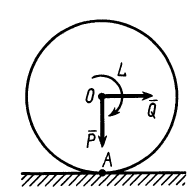
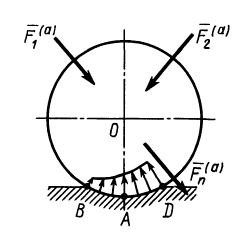
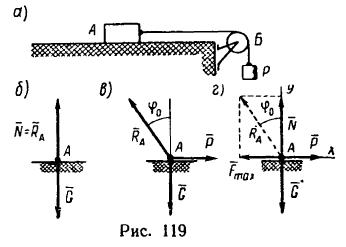
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей соприкосновения возникает сила трения скольжения.
Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, то кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает пара сил, препятствующая качению катка. Возникновение силы трения, препятствующей скольжению, иногда называют трением первого рода, а возникновение пары сил, препятствующей качению,— трением второго рода.
Трение скольжения
Пусть на тело действует плоская система активных сил и тело находится в равновесии, соприкасаясь с поверхностью другого тела, являющегося связью для рассматриваемого тела. Если поверхности соприкасающихся тел абсолютно гладкие и тела абсолютно твердые, то реакция поверхности связи направлена по нормали к общей касательной в точке соприкосновения и направление реакции в этом случае не зависит от действующих на тело активных сил. От активных сил зависит только числовое значение силы реакции. В действительности абсолютно гладких поверхностей и абсолютно твердых тел не бывает. Все поверхности тел в той или иной степени шероховаты и все тела деформируемы. В связи с этим и сила реакции
Если силу реакции
В теоретической механике обычно рассматривается только сухое трение между поверхностями тел, т. е. такое трение, когда между ними нет смазывающего вещества. Для сухого трения надо различать трение скольжения при покое или равновесии тела и трение скольжения при движении одного тела по поверхности другого с некоторой относительной скоростью.
При покое сила трения зависит только от активных сил. При выбранном направлении касательной в точке соприкосновения поверхностей тел сила трения вычисляется по формуле
Аналогично, при выбранном направлении нормали нормальная реакция выражается через заданные силы
В 1781 г. Кулон установил основные приближенные законы для сухого трения скольжения. В дальнейшем законы Кулона многократно проверялись другими исследователями. Но эти законы подтверждались в случае, когда поверхности тел не вдавливались друг в друга и шероховатость была не очень велика.
Законы Кулона можно установить на приборе, схема которого дана рис. 59. На этом приборе изменяя вес гири, можно изменять нормальное давление 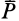
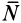
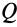
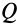
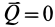
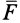
Если силу 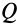
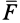
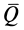
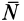
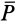
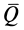
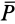
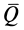
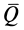
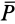
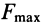
Рис. 59
Трение скольжения:
При решении многих технических вопросов приходится принимать в расчет силы трения. Остановимся на рассмотрении сил трения 1-го рода (скольжения).
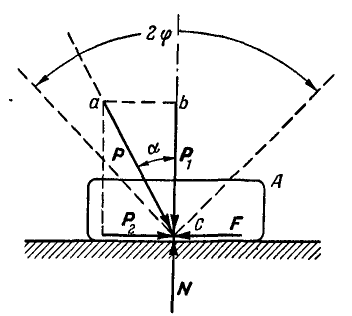
Рис. 31.
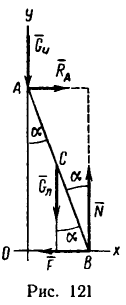
Пусть на тело А (рис. 31), лежащее на горизонтальной негладкой плоскости, действует сила Р под углом а к вертикали. Раскладывая силу Р на две составляющие 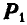
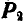
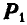
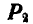
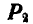
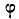

где 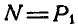
Угол 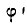
Формула (28) выражает первый закон трения, который формулируется так:
Первый закон трения
1. Сила трения прямо пропорциональна нормальному давлению или реакции связи и направлена в сторону, противоположную относительному перемещению трущихся тел.
Этот закон был установлен опытным путем. Амонтоном-Кулоном и другими исследователями были установлены еще следующие законы:
2. Коэффициент трения зависит от материала и состояния трущихся поверхностей.
3. Коэффициент трения в покое больше коэффициента трения в движении.
4. Коэффициент трения не зависит от величины трущихся поверхностей (можно считать правильным лишь в первом приближении).
5. Коэффициент трения зависит от скорости движения трущихся поверхностей и с увеличением этой скорости уменьшается, приближаясь к некоторой предельной величине.
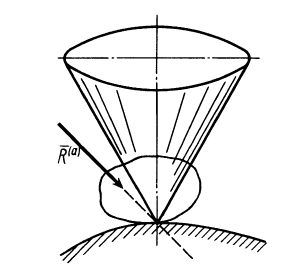
Обращаясь к рисунку 31, замечаем, что тело А находится в равновесии, если сила Р проходит внутри конуса с углом при вершине С, равным двойному углу трения 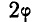
Когда тело А находится еще в покое (рис. 31), то по мере увеличения угла 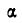
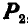
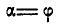
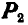
Рис. 32.
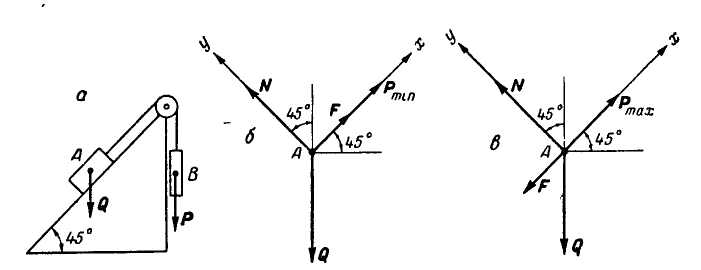
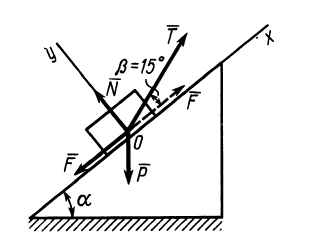
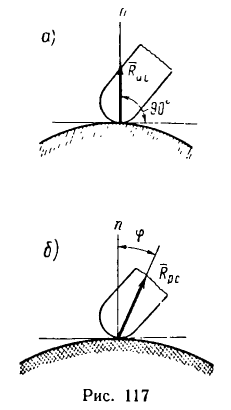
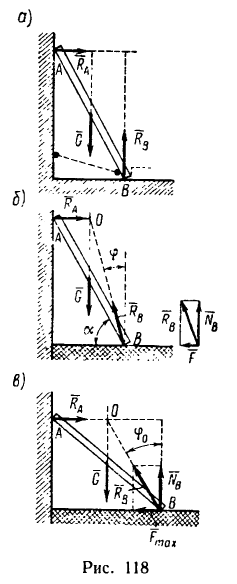
Задача №1
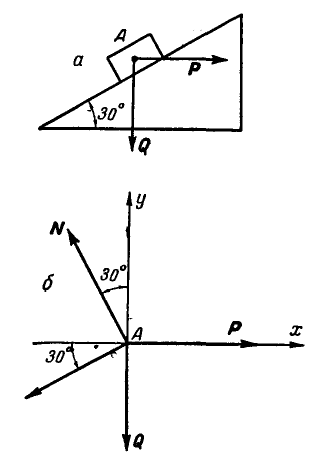
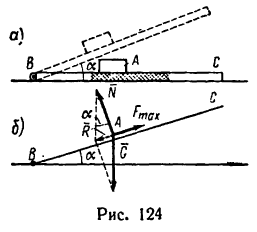
Тело А весом Q=100кГ лежит на шероховатой наклонной плоскости (рис. 32,а). Какую наименьшую горизонтальную силу Р ладо приложить к телу, чтобы оно начало двигаться, если коэффициент трения тела о плоскость f=0,2.
Решение. Рассмотрим равновесие тела А. Помимо горизонтальной силы Р на тело действует сила Q, нормальная реакция N плоскости и сила трения F, направленная параллельно плоскости в обратную сторону движения тела (рис. 32,6).
Составляя уравнения равновесия (27), имеем:
В двух уравнениях имеются три неизвестные величины: Р, N и F. Для получения третьего уравнения по формуле (28) имеем > зависимость: 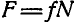
Выражая в уравнениях равновесия F через N, получим:
Оторда находим:
Задача №2
Определить наибольший и наименьший груз Р, при котором груз Q = 10 кГ не будет двигаться (рис» 33, а). Коэффициент трения груза Q о плоскость f=0,2.
Рис. 33.
Указание: при наименьшем грузе 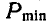
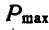
Составляя для каждого из случаев (рис. 33, б и 33, в) по два уравнения равновесия и принимая во внимание формулу (28), получим:
32
Законы Кулона
1. Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного или реального скольжения тела под действием приложенных сил. Сила трения при покое зависит от активных сил и ее модуль заключен между нулем и максимальным значением, которое достигается в момент выхода тела из положения равновесия, т. е.
2. Максимальная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того, чтобы сдвинуть, например, кирпич, надо приложить одну и ту же силу независимо от того, какой гранью он положен на поверхность, широкой или узкой.
3. Максимальная сила трения скольжения пропорциональна нормальному давлению (нормальной реакции), т. е.
где безразмерный коэффициент 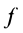
4. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, т. е. от величины и характера шероховатости, влажности, температуры и других условий. Коэффициент трения скольжения в зависимости от различных условий устанавливается экспериментально. Так, коэффициент трения для кирпича по бетону равен 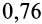
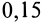
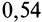
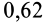
Опыты показывают, что при скольжении одного тела по поверхности другого с некоторой относительной скоростью возникает сила трения скольжения, равная максимальной, только при этом коэффициент трения скольжения незначительно изменяется в зависимости от скорости скольжения. Для большинства материалов он уменьшается с увеличением скорости скольжения, но для некоторых материалов, наоборот, увеличивается (трение кожи о металл).
В приближенных технических расчетах обычно считают, что коэффициент трения скольжения не зависит от относительной скорости скольжения.
В отличие от сухого трения трение при наличии смазывающего слоя между поверхностями определяется распределением относительной скорости скольжения в этом слое. В этом случае трение происходит не между поверхностями тел, а между слоями смазывающего вещества. Теория трения в смазывающем слое жидкости рассматривается в гидродинамике.
Угол и конус трения
Многие задачи на равновесие тела на шероховатой поверхности, т. е. при наличии силы трения, удобно решать геометрически. Для этой цели введем понятия угла и конуса трения.
Пусть твердое тело под действием активных сил находится на шероховатой поверхности в предельном состоянии равновесия, т. е. таком состоянии, когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции (рис. 60). В этом случае полная реакция шероховатой поверхности 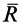
Этот наибольший угол 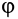
Угол трения 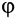
Но по третьему закону Кулона,
следовательно,
т. е. тангенс угла трения равен коэффициенту трения.
Рис. 60
Конусом трения называют конус, описанный полной реакцией, построенной на максимальной силе трения, вокруг направления нормальной реакции. Его можно получить изменяя активные силы так, чтобы тело на шероховатой поверхности находилось в предельных положениях равновесия, стремясь выйти из равновесия по всем возможным направлениям, лежащим в общей касательной плоскости соприкасающихся поверхностей.
Если коэффициент трения во всех направлениях одинаков, то конус трения круговой. Если не одинаков, то конус трения не круговой, например в случае, когда свойства соприкасающихся поверхностей различны (вследствие определенного направления волокон или в зависимости от направления обработки поверхности тел, если обработка происходит на строгальном станке и т. п.).
Равновесие тела на шероховатой поверхности
При равновесии сил, действующих на твердое тело, находящееся в равновесии на шероховатой поверхности, возникает дополнительно неизвестная сила реакции шероховатой поверхности— сила трения. В случае предельного равновесия сила трения достигает своего максимального значения и по формуле (1) выражается через нормальную реакцию. В общем случае равновесия сила трения находится между нулем и ее максимальным значением. Поэтому соответствующие условия равновесия, в которые входит сила трения после замены ее максимальным значением, становятся неравенствами. После этого неизвестные находят путем совместного решения уравнений и неравенств. Для всех неизвестных или для их части получают решения в виде неравенств.
Некоторые задачи на равновесие с учетом сил трения удобно решать геометрически с помощью конуса трения.
Можно сформулировать условия равновесия тела на шероховатой поверхности используя конус трения. Если активные силы, действующие на тело, приводятся к равнодействующей силе 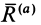
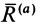
Очевидно, при изменении равнодействующей активных сил тело находится в равновесии до тех пор, пока составляющая 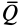
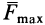
Рис. 61
Рис. 62
Предельным положением равновесия тела является случай, когда сила 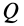
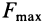
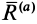
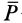
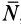
Тело нельзя вывести из равновесия любой по модулю активной силой, если ее линия действия проходит внутри конуса трения.
Если линия действия равнодействующей активных сил не проходит внутри конуса трения или по его образующей, то тело на шероховатой поверхности не может находиться в равновесии (рис. 63).
Рис. 63
Рис. 64
Пример 1.
Тело, сила тяжести которого 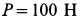
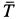
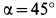
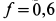
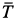
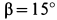
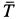
Решение. К телу приложены силы 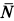
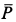
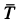
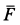
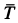
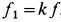
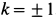
Составляем условия равновесия в виде суммы проекций сил на координатные оси для обоих предельных случаев. Имеем
По закону Кулона,
Решая эти уравнения относительно 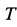
Отсюда при
при
Таким образом, сила 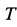
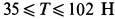
Пример 2.
Однородный тяжелый стержень 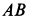
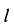
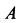
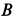
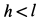
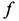
Рис. 65
Решение. Рассмотрим случай, когда точка 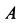
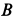
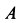
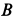
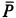
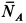
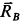
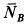
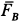
Составим условия равновесия плоской системы сил:
К этим условиям следует добавить неравенство для силы трения
Из уравнений равновесия находим
Из геометрических условий задачи имеем
Итак, для силы трения 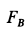
Исключая из них силу трения 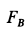
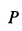
Искомое условие для коэффициента трения 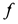
Трение качения
Если рассматриваемое тело имеет форму катка и под действием приложенных активных сил может катиться по поверхности другого тела, то из-за деформации поверхностей этих тел в месте соприкосновения могут возникнуть силы реакции, препятствующие не только скольжению, но и качению. Примерами таких катков являются различные колеса, как, например, у электровозов, вагонов, автомашин, шарики и ролики в шариковых и роликовых подшипниках и т. п.
Пусть цилиндрический каток находится на горизонтальной плоскости под действием активных сил. Соприкосновение катка с плоскостью из-за деформации фактически происходит не вдоль одной образующей, как в случае абсолютно твердых тел, а по некоторой площадке. Если активные силы приложены симметрично относительно среднего сечения катка, т. е. вызывают одинаковые деформации вдоль всей его образующей, то можно изучать только одно среднее сечение катка. Этот случай рассмотрен ниже.
Активные силы, действующие на катки в виде колес (рис. 66), кроме силы тяжести 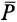
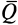
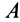
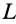
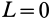
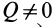
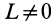
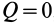
Если активные силы, действующие на колесо, привести к точке 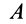
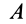
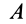
Рис. 66
Рис. 67
Рис. 68
Соприкосновение среднего сечения колеса с неподвижной плоскостью из-за деформации колеса и плоскости происходит по некоторой линии 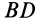
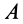
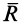
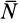
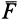
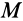
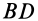
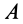
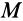
Приведем активные силы 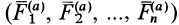
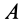
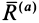
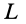
При равновесии катка, т. е. когда каток не катится и не скользит по плоскости, активные силы уравновешиваются силами реакций связи и, следовательно,
Изменив активные силы, приложенные к катку так, чтобы увеличивался момент 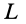
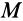
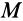
Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению:
1. Наибольший момент пары сил, препятствующей качению, в довольно широких пределах не зависит от радиуса катка.
2. Предельное значение момента 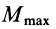
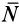
Коэффициент пропорциональности 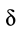
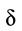
3. Коэффициент трения качения 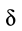
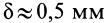
Законы трения качения, как и законы трения скольжения, справедливы для не очень больших нормальных давлений и не слишком легко деформирующихся материалов катка и плоскости.
Эти законы позволяют не рассматривать деформации катка и плоскости, считая их абсолютно твердыми телами, касающимися в одной точке. В этой точке соприкосновения в среднем сечении катка кроме нормальной реакции и силы трения надо приложить еще и пару сил, препятствующую качению.
Коэффициент трения качения равен длине 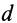
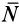
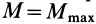
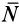
В предельном случае равновесия катка 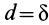
Для того чтобы каток не скользил, необходимо выполнение условия
Для заданных активных сил соответственно
Для того чтобы каток не катился, должно выполняться условие
Для активных сил оно имеет вид
Рис. 69
Рис. 70
Для примера рассмотрим случай ведомого колеса, к которому кроме силы тяжести 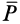
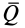
Если каток находится в равновесии, то из условий равновесия плоской системы сил, приложенных к катку, получаем
где за моментную точку взята точка 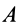
В случае отсутствия скольжения по формуле (4) с учетом условий равновесия
Аналогично, при отсутствии качения по формуле (5) имеем
Таким образом, при отсутствии скольжения сила 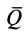
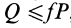
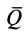
Если 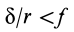
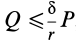
Если 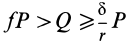
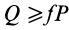
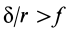
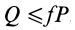
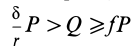
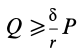
В том случае, если 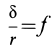
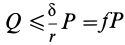
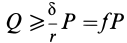
Обычно 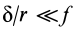
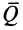
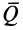
С точки зрения затраты энергии выгодно заменять скольжение качением. Этим объясняется преимущество шариковых и роликовых подшипников по сравнению с подшипниками скольжения, если даже в них трение и не уменьшается введением смазывающего вещества.
Аналогично трению качения можно рассмотреть и явление возникновения так называемого трения верчения, т.е. случая, когда активные силы стремятся вращать тело, например в форме шара, вокруг нормали к общей касательной поверхности соприкосновения.
В этом случае возникает пара сил, препятствующая верчению, причем наибольший ее момент, возникающий в момент начала верчения, также прямо пропорционален нормальной реакции. Коэффициент пропорциональности, т. е. коэффициент трения верчения, обычно значительно меньше коэффициента трения качения.
Равновесие с учетом сил трения
Задачи, приведенные в этом параграфе, отличаются от предыдущих тем, что в них рассматривается равновесие тел, имеющих, кроме идеальных, еще и реальные связи, т. е. связи с трением.
При свободном опирании тела на поверхность идеальной связи реакция такой связи 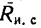
Если же тело опирается на поверхность реальной связи (в отличие от идеальных связей реальные связи условимся отмечать двойной штриховкой), то ее реакция 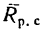
Поясним это общее положение следующим примером.
Наклонный брус (рис. 118, а), вес которого G, опирается в двух
точках А и В соответственно на вертикальную и горизонтальную поверхности идеальных связей. Этот брус не может находиться в равновесии, потому что три силы —вес бруса G и реакции 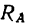
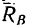
Чтобы брус, показанный на рис. 118, а, находился в равновесии, необходимо наложить еще одну связь, например, удержать брус шнуром или упереть в выступ на горизонтальной плоскости (обе возможные связи показаны пунктиром).
Теперь представим, что в точке В брус опирается не на идеально гладкую, а на шероховатую (реальную) поверхность (рис 118, б). В этом случае брус может находиться в равновесии без дополнительной связи (шнура или упорной планки). Значит три силы — вес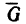
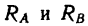
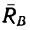
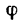
Если реакцию 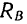
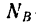
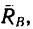
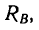
При увеличении угла а, характеризующего наклон бруса относительно горизонтальной поверхности, угол 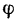
Если же уменьшать угол а, то угол ф, характеризующий отклонение реакции 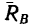
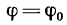
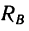
У гол 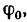
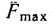
Для случая предельного равновесия между силой трения и углом трения имеем такую зависимость;
Постоянное для данной пары соприкасающихся тел значение 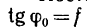
Таким образом,
При решении задач необходимо учитывать, что сила трения направлена всегда в сторону, противоположную той, при которой точка может скользить по идеальной поверхности.
Если в число реакций связей, обеспечивающих равновесие тела, входит сила трения, то такое состояние равновесия называется самоторможением. Во всех приведенных ниже задачах рассмотрены различные случаи самоторможения (равновесия при наличии силы трения) и условия, при которых возможно самоторможение.
Задача №3
Тело А массой 8 кг поставлено на шероховатую горизонтальную поверхность стола. К телу привязана нить, перекинутая через блок Б (рис. 119, а). Какой груз Р можно подвязать к концу нити, свешивающейся с блока, чтобы не нарушить равновесия тела А? Коэффициент трения f = 0,4. Трением на блоке пренебречь.
Решение.
1. Если масса тела А m = 8 кг, то его вес
2. Пренебрегая размерами тела, будем считать, что все силы приложены к точке А.
3. Когда тело поставлено на горизонтальную поверхность, то на него действуют только две силы: вес 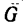
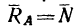
4. Если же приложить некоторую силу 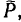
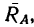
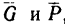
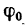
5. Разложив реакцию 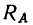
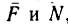
Спроектировав эту систему сил на оси хну, получим два уравнения равновесия:
Решаем полученную систему уравнений:
но
поэтому
Таким образом, равновесие тела А сохраняется при условии, что к концу нити, перекинутой через блок, подвешен груз, не превышающий по весу 31,4 н.
При этом масса груза Р
Задача №4
При каком минимальном коэффициенте трения между полом и лестницей последняя может находиться в равновесии, опираясь верхним концом о гладкую стену, как показано на рис. 120, а? Вес лестницы G = 120 н.
Решение.
1. На лестницу действует только одна нагрузка — ее собственный вес, приложенный в точке С посредине длины лестницы АВ.
2. Вес лестницы уравновешен реакцией 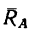
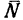
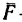
3. Составим три уравнения равновесия:
4. Из уравнений (1) и (3)
А так как N = G [из уравнения (2)[, то минимальный коэффициент трения, обеспечивающий равновесие лестницы.
Таким образом, при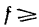
Задача №5
В месте соприкосновения пола и лестницы в предыдущей задаче коэффициент трения f= 0,4. Сможет ли человек, масса которого 70 кг, подняться по лестнице до самого верха и чтобы лестница при этом не скользила по полу?
Решение.
1. К силам 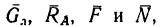
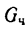
2. Вес человека
3. Человек сможет подняться до самого верха лестницы лишь в том случае, если горизонтальная составляющая реакции пола (сила 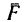
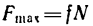
4. Составим уравнения равновесия:
5. Из уравнения (2)
Максимальная сила трения, которая может возникнуть в данном случае
Из уравнений (1) и (3) находим силу F—горизонтальную составляющую реакции пола, которая может обеспечить равновесие лестницы с человеком, стоящим наверху:
Таким образом,
Следовательно, человек сможет подняться по лестнице до самого верха.
- Заказать решение задач по теоретической механике
Задача №6
При каких значениях угла а, образуемого с гладкой вертикальной стеной, лестница, опирающаяся нижним концом о шероховатый горизонтальный пол, будет находиться в равновесии, если, кроме собственного веса, она ничем не нагружена и известно, что коэффициент трения при соприкосновении лестницы с полом f?
Решение.
1. Для решения этой задачи воспользуемся рис. 120, б, так как на лестницу действуют те же четыре силы: вес лестницы 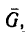
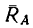
2. Лестница не выйдет из состояния равновесия (не начнет скользить) до тех пор, пока
т. е. пока горизонтальная составляющая реакции пола остается меньше максимальной силы трения, возникающей при опирании лестницы о пол в данном случае.
3. Из уравнений (1) и (3), составленных при решении задачи 90-15, найдено, что
Сопоставляем уравнения (а) и (б):
А так как в данном случае G =N, то лестница находится равновесии до тех пор, пока выполняется неравенство
или
где 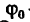
Следовательно, лестница находится в равновесии до тех пор, пока тангенс угла, образуемого лестницей с вертикальной гладкой стеной, остается меньше удвоенного коэффициента трения между лестницей и полом. Например, при f=0,4
и неравенство (в) соблюдается при значениях углов
Следовательно, при f=0,4 лестница не будет скользить по полу при любом значении угла a от 0 до 38°40′.
Следующую задачу рекомендуется решить самостоятельно.
Задача №7
При каких значениях угла a однородная лестница, опирающаяся на шероховатые стену и пол (рис. 122), будет находиться в равновесии? Коэффициенты трения при опирании лестницы о стену и о пол считать одинаковыми и равными f.
Ответ.
Указание. В данной задаче в системе сил, действующих на лестницу, образуется пять неизвестных: четыре реакции и угол а. Поэтому при решении задачи нужно к трем уравнениям равновесия добавить еще два уравнения, выражающих зависимость сил трения от нормального давления.
Задача №8
Цилиндр с горизонтальной площадкой наверху (рис. 123, а), находясь в двух кольцевых направляющих, скользит вниз, так как между поверхностью цилиндра и поверхностями направляющих имеется незначительный зазор. Вес цилиндра 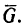
Решение.
1. На цилиндр в состоянии равновесия действуют две нагрузки: вес 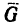
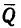
2. Груз Q, помещенный на горизонтальную площадку, прижимает цилиндр к верхнему направляющему кольцу в точке А, а к нижнему — в точке В. Благодаря зазору в точках С и D цилиндр не касается направляющих колец. В точках А и В возникают две реакции, которые заменим их составляющими 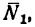
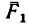
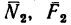
3. Образовалось пять неизвестных величин:
Если спроектировать все силы на ось х, то получим
откуда
Так как и
и
также, имея в виду равенство (1а), находим что
Скоректировав все силы на ось у, получим четвертое уравнение:
откуда с учетом (За)
Приняв за центр моментов точку О, лежащую на оси цилиндра и на середине расстояния а, составим пятое уравнение — уравнение моментов, в котором d- диаметр цилиндра (d = CA = BD):
Имея в виду равенства (1а) и (За), уравнение (5) можно упростить так:
откуда
Если теперь в уравнение (2) подставить значение 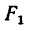
откуда
И теперь выражение (5а) принимает окончательный вид:
При значениях /, удовлетворяющих полученному неравенству, цилиндр не скользит вниз.
Задача №9
Тело А поставлено на негладкую пластину ВС, которую можно поворачивать около шарнира В. Коэффициент трения f между телом А и пластиной ВС известен. Определить, при каких значениях угла а (рис. 124, а) тело А будет оставаться на пластине в покое? Решение.
1. Представим, что пластина ВС наклонена к горизонту на некоторый угол а (рис. 124, б).
При этом положении пластины на тело А действуют три силы: его собственный вес 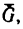
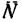
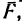
2. Тело А будет находиться в покое до тех пор, пока равнодействующая сил 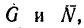
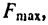
но
поэтому
или
Следовательно, пока тангенс угла наклона пластины к горизонту меньше коэффициента трения, тело А остается в покое.
Это положение выражает так называемое условие самоторможения тела по наклонной плоскости.
3. Учитывая, что
где 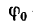
Так как углы 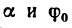
Тело А находится в покое на наклонной плоскости до тех пор, пока угол наклона плоскости меньше угла трения.
Следующую задачу рекомендуется решить самостоятельно.
Равновесие при наличии трения
Постановка Задачи. Конструкция состоит из двух шарнирно соединенных между собой тел. Одна из опор конструкции представляет собой одностороннюю связь и допускает проскальзывание с трением. Коэффициент трения, размеры конструкции и часть внешних нагрузок заданы. Найти пределы изменения одной из внешних нагрузок, действующей на конструкцию в условии равновесия.
План решения:
1. Задаем направление возможного движения подвижной опоры, скользящей с трением. Прикладываем к этой опоре силу трения, направляя ее в сторону противоположную возможному движению. Предельное значение силы трения связываем с величиной нормальной реакции опоры N по формуле Кулона 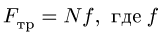
2. Решаем задачу о равновесии системы тел. Для этого разбиваем систему на две отдельные части, для которых составляем и решаем уравнения равновесия. Из решения определяем предельное значение нагрузки д.чя заданного направления скольжения опоры.
3. Меняем направление возможного движения системы и направление предельной силы трения. Предыдущий пункт плана выполняем заново и определяем другое предельное значение нагрузки. Два найденных значения нагрузки определяют ту область ее изменения, при которой конструкция находится в равновесии.
Задача №10
Конструкция состоит из двух частей, шарнирно соединенных в точке С (рис. 52). Опора В представляет собой одностороннюю связь и допускает проскальзывание с коэффициентом трения 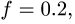
Размеры даны в метрах. Найти продолы изменения нагрузки Р, действующей под углом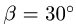
Решение
1. Задаем направление возможного движения подвижной опоры, скользящей с трением Предполагая возможное движение ползуна В влево, силу трения 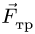
где 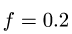
2. Решаем задачу о равновесии системы тел. Для этого систему разбиваем по шарниру С на две отдельные части — АС и СВ. Реакции шарнира С 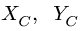
Действие ползуна заменяем нормальной реакцией N, направленной вниз, так как ползун по условию задачи является односторонней связью, и силой трения 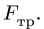
Уравнения (2) вместе с законом Кулона (1) образуют замкнутую систему трех линейных уравнений с тремя неизвестными 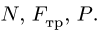
При 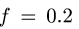
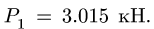
3. Меняем направление возможного движения системы и направление предельной силы трения. Пусть ползун В движется вправо. Силу 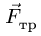
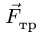
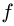
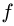
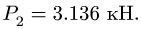
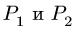
Чтобы убедиться, что равновесие соответствует значениям нагрузки между этими числами, определим Р при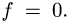
Из выражения (3) для N также следует, что при 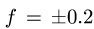
где
Этим нагрузкам соответствуют следующие значения нормальной реакции:
Замечание. Неравенство 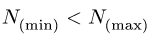
Трение качения
Постановка задачи. Система состоит из двух цилиндров, соединенных стержнем. Цилиндры могут кататься без проскальзывания, один цилиндр без сопротивления, другой — с трением качения. В каких пределах меняется внешний момент, приложенный к одному из цилиндров, в условии равновесия системы?
Трение качения происходит за счет деформации цилиндра и опорной поверхности в месте контакта. В результате реакция опоры смещается в сторону возможного движения на половину длины площадки контакта и создает момент сопротивления. Плечо этого момента принимают за коэффициент трения качения. Таким образом, 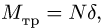
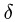
в теле мала, а глубиной продавливания цилиндра в поверхность (или величиной смятия цилиндра) пренебрегают. Коэффициент трения качения зависит не только от свойств материала цилиндра и поверхности, но и от радиуса цилиндра.
План решения:
1. Задаем направление возможного движения при достижении условия предельного равновесия. К катящемуся телу (цилиндру, колесу) прикладываем момент трения качения, направляя его в сторону, противоположную возможному движению. Не забываем про силу сцепления в точке контакта, направленную вдоль плоскости.
2. Решаем задачу о равновесии системы тел. Используем метод разбиения системы на отдельные тела. Внешние и внутренние связи заменяем их реакциями. Составляем и решаем уравнения равновесия. Оси координат для уравнения проекций для цилиндрических тел выбираем вдоль нормальной реакции, а уравнение моментов составляем относительно точки касания. Из решения системы уравнений равновесия определяем условие предельного равновесия.
3. Меняем направление возможного движения системы и направление момента трения качения. Решаем задачу заново, определяем второе условие предельного равновесия.
Задача №11
Система состоит из двух цилиндров весом 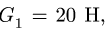
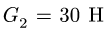
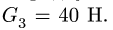
Коэффициент трения качения 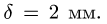
Решение
1. Задаем направление возможного движения при достижении условия предельного равновесия. Пусть за счет достаточно большой, по сравнению с моментом М, силы F произойдет движение системы влево. Тогда момент трения качения, приложенный к цилиндру 2, будет направлен по часовой стрелке (рис. 57). Его величину находим по формуле
2. Решаем задачу о равновесии системы двух цилиндров и стержня. Разбиваем систему на три тела (рис. 56, 57, 58). Внешние связи заменяем реакциями
Реакции 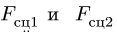
При составлении системы семи уравнений с неизвестными 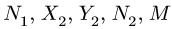
Составляем уравнения равновесия для цилиндра 1 (рис. 56):
Уравнения равновесия цилиндра 2 (рис. 57) имеют вид
3.2.Трения качения
Уравнения равновесия стержня АВ (рис. 58) имеют вид
Из решения системы уравнений (1-3) определяем
Радиус и коэффициент трения качения переводим в метры R = 0.5 м, 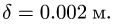
Убеждаемся, что 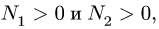
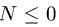
3. Меняем направление возможного движения системы. Пусть за счет действия момента М произойдет движение системы вправо. Момент трения качения направим против часовой стрелки (рис. 59). Составляя уравнения равновесия для новой системы сил, заметим, что отличие от прежней системы проявляется только в знаке 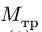
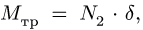
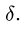
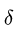
Точно так же находим нормальные реакции опор: 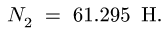
цилиндру 1, изменяется в пределах (в Нм)
- Пространственная система сил
- Центр тяжести
- Кинематика точки
- Плоское движение твердого тела
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Плоская система сил