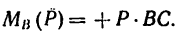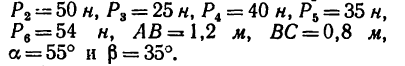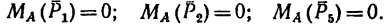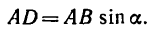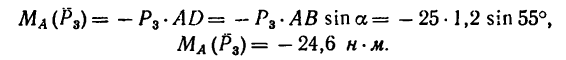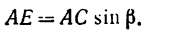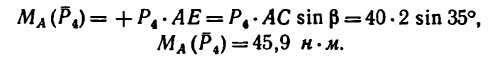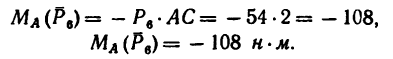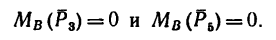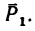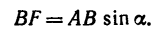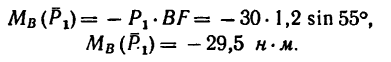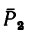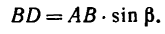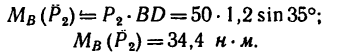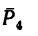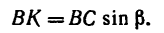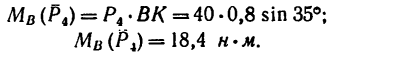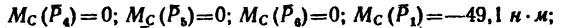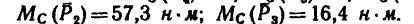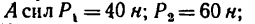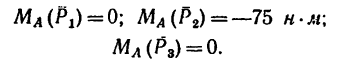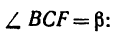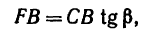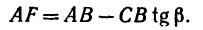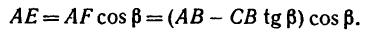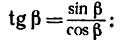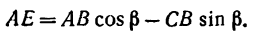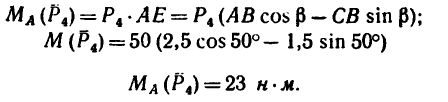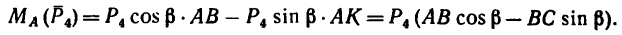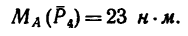Содержание:
Моменты силы относительно точки и оси:
Для рассмотрения различных систем сил необходимо ввести понятия алгебраического и векторного моментов силы относительно точки и момента силы относительно оси. Введем эти характеристики действия силы на твердое тело и рассмотрим их свойства.
Алгебраический момент силы относительно точки
При рассмотрении плоской системы сил, приложенных к твердому телу, используется понятие алгебраического момента силы относительно точки.
Рис. 19
Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки (рис. 19), взятое со знаком плюс или минус.
Плечом 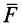

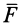
Обозначим 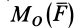
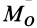
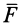

Если сила стремится вращать тело вокруг моментной точки (точки, относительно которой вычисляют алгебраический момент силы) против часовой стрелки, то берем знак плюс, если по часовой стрелке — знак минус.
Алгебраический момент силы представляет собой произведение силы на длину (в 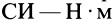
Из определения алгебраического момента силы относительно точки следует, что он не зависит от переноса силы вдоль ее линии действия. Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через моментную точку. Сумма алгебраических моментов относительно точки двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой, равна нулю. Численно алгебраический момент относительно точки равен удвоенной площади треугольника, построенного на силе 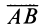
Векторный момент силы относительно точки
При рассмотрении пространственной системы сил, приложенных к твердому телу, применяется понятие векторного момента силы относительно точки.
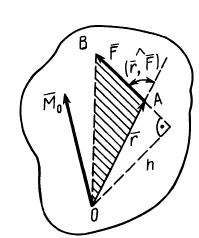
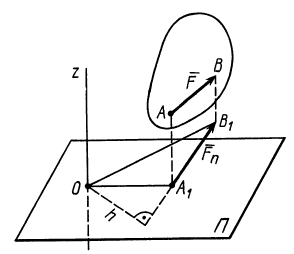
Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть стремление силы вращать тело против движения часовой стрелки (рис. 20).
Плечом 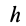

Рис. 20
Условимся векторный момент силы 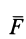


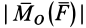
Как и для алгебраического момента, векторный момент силы относительно точки равен удвоенной площади треугольника, построенного на силе и моментной точке:
Справедлива формула
где 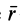

Чтобы убедиться в справедливости формулы (3), достаточно показать, что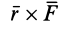

Как показано на рис. 20, 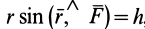
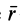
что совпадает с векторным моментом силы относительно точки 
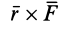
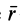
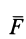
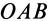

Направление 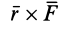

Векторный момент силы относительно точки не изменяется от переноса силы вдоль ее линии действия. Он станет равным
нулю, если линия действия силы пройдет через моментную точку.
Рис. 21
Если сила 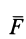
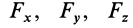
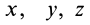
где 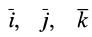
Используя формулу (4), можно выделить проекции 
Модуль векторного момента 
В формулах (6) числовую величину 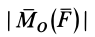
Момент силы относительно оси
Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью (рис. 22). Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси (проекция силы на плоскость является вектором), стремится вращать тело вокруг положительного направления оси против часовой стрелки, и отрицательным, если она стремится вращать тело по часовой стрелке. Момент силы, например, относительно оси 
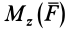
Рис. 22
По определению,
где 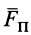
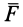





Из определения момента силы относительно оси следует, что введенный выше алгебраический момент силы относительно точки можно считать моментом силы относительно оси, проходящей через эту точку, перпендикулярно плоскости, в которой лежат сила и моментная точка. Момент силы относительно оси можно выразить через площадь треугольника, построенного на проекции силы 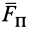

Из формулы (8) можно получить следующие важные свойства момента силы относительно оси:
- Момент силы относительно оси равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси.
- Момент силы относительно оси равен нулю, если линия действия силы пересекает эту ось. В этом случае линия действия проекции силы на плоскость, перпендикулярную оси, проходит через точку пересечения оси с плоскостью и, следовательно, равно нулю плечо силы
относительно точки
.
В обоих этих случаях ось и сила лежат в одной плоскости. Объединяя их, можно сказать, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
Связь момента силы относительно оси с векторным моментом силы относительно точки на оси
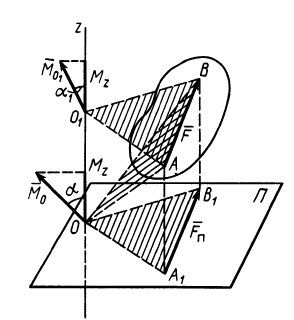
Используя формулу (8), имеем (рис. 23)
Векторный момент силы 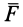



Векторный момент 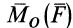
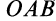
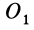
причем векторный момент 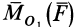
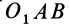
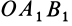
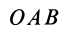
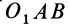

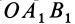

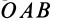
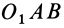
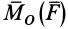
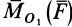
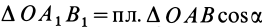
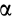
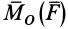

причем знак 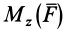
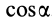
Аналогично,
т. е.
где 

Формулы (11) и (12) отражают искомую связь между моментом силы относительно оси и векторными моментами силы относительно точек, лежащих на этой оси: момент силы относительно оси равен проекции на эту ось векторного момента силы относительно любой точки на оси.
Эту зависимость между моментом силы относительно оси и векторным моментом силы относительно точки на оси можно принять за определение момента силы относительно оси.
Рис. 23
Формулы для моментов силы относительно осей координат
Используя связь момента силы относительно оси с векторным моментом силы относительно точки на оси, можно получить формулы для вычисления моментов относительно осей координат, если даны проекции силы на оси координат и координаты точки приложения силы. Для оси 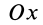
Согласно (5),
следовательно,
Аналогично, для осей 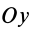
Окончательно
По формулам (13) можно вычислить моменты силы относительно прямоугольных осей координат.
По этим формулам получаются необходимые знаки для 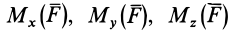
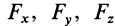
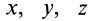
При решении задач момент силы относительно какой-либо оси часто получают, используя его определение, т. е. проецируя силу на плоскость, перпендикулярную оси, и вычисляя затем алгебраический момент этой проекции относительно точки пересечения оси с этой плоскостью.
Момент пары сил. Сложение пар сил. Равновесие пар сил
При изучении теоретической механики необходимо совершенно отчетливо уяснить, что в статике рассматриваются два простейших элемента: сила и пара сил. Любые две силы, кроме сил, образующих пару, всегда можно заменить одной —сложить их (найти равнодействующую). Пара сил нс поддается дальнейшему упрощению, она не имеет равнодействующей и является простейшим элементом.
Действие пары сил на тело характеризуется ее моментом — произведением одной из сил пары на ее плечо (на кратчайшее расстояние между линиями действия сил, образующих пару).
Единицей момента пары сил в Международной системе служит 1 нм (ньютон-метр = 1 н-1ж), а в системе МКГСС (технической)— 1 кГ-м.
Несколько пар сил, действующих на тело в одной плоскости, можно заменить одной парой сил (равнодействующей парой), момент которой равен алгебраической сумме моментов данных пар:
При равновесии пар сил
Если пары сил действуют в одной плоскости, то при решении задач достаточно рассматривать моменты пар как алгебраические величины. Причем знак момента определяется в зависимости от направления вращающего действия пары сил.
Дальнейшее изложение основано на правиле, т. е. считается момент положительным, если пара сил действует против хода часовой стрелки, если же пара сил действует на тело но ходу часовой стрелки, то момент считается отрицательным.
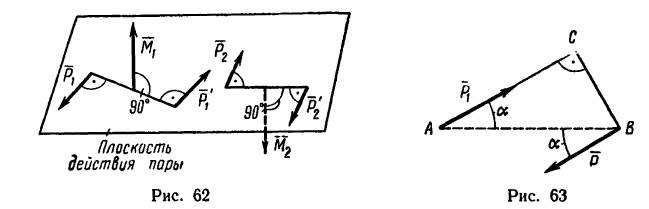
В том случае когда пары сил действуют на тело будучи расположенными в различных плоскостях, гораздо удобнее рассматривать пару сил как вектор, направленный перпендикулярно
к плоскости действия пары сил (рис. 62). Направление вектора в зависимости от направления вращательного действия пары определяется по направлению движения винта с правой нарезкой.
Задача 1.
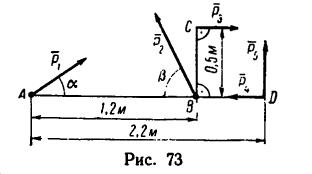
Определить момент пары сил (рис. 63), если 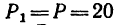
Решение.
1. При определении момента пары сил нужно прежде всего правильно определить плечо пары. При этом необходимо различать следующие понятия: плечо пары сил и расстояние между точками приложения сил нары.
Так как в механике твердого тела сила—скользящий вектор, то действие силы не изменяется при переносе точки ее приложения вдоль линии ее действия. Значит расстояние между точками приложения сил, образующих пару, можно изменять неограниченно. Но плечо пары при этом переносе остается неизменным.
В частном случае расстояние между точками приложения сил, образующих пару, может быть равно плечу.
Чтобы определить плечо данной пары из точки приложения одной из сил, например из точки В, восставим перпендикуляр ВС к линии действия другой силы. Расстояние ВС и есть плечо данной пары сил. Расстояние между точками приложения сил, образующих пару, АВ=0,5 м.
Легко видеть, что
2. Найдем момент пары сил:
Задача 2.
Как изменится момент пары сил 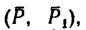
повернуть силы 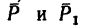
1. Найдем момент пары при заданном положении ее сил (рис. 64, а).
Из точки В восставим перпендикуляр ВС к линиям действия сил 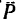
Момент пары при заданном положении сил
2. Повернем силы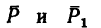
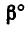
3. Сравнивая полученные результаты, видим, что после поворота сил момент пары увеличивается на 20—14,5 = 5,85 н-м.
4. Легко заметить, что силы 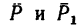
Момент пары сил изменяет свой знак.
Задача 3.
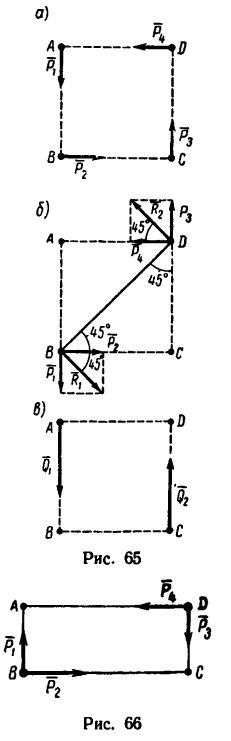
К точкам А, С и В, D, образующим вершины квадрата со стороной 0,5 м (рис. 65, а), приложены равные по модулю силы (Р = 12н) таким образом, что они образуют две пары сил
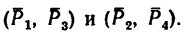
Решение 1.
Плечи у обеих пар сил равны стороне квадрата поэтому
Решение 2.
1. Перенесем силы 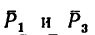
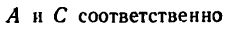
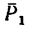
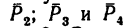
2. Сложим попарно эти силы у каждой из точек В и D. В обоих случаях
3. Силы R, модули которых теперь известны, направлены перпендикулярно к диагонали BD квадрата. Значит эта диагональ является плечом вновь образовавшейся пары сил 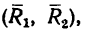
4. Найдем момент пары
и, следовательно,
Эту пару в соответствии со вторым решением можно представить в виде пары 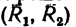
Но можно равнодействующую пару представить и в любом другом виде, например в виде сил Q = 24 и, приложенных к двум любым вершинам квадрата ABCD (рис. 65, в)
- Заказать решение задач по теоретической механике
Задача 4.
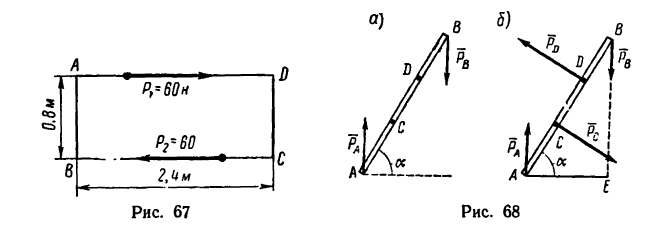
На прямоугольник ABCD (рис. 67) вдоль его длинных сторон действует пара сил 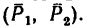
Решение.
1. Момент данной пары сил
необходимо уравновесить парой, момент которой обозначим Л1м. Тогда, согласно условию равновесия,
Откуда
2. Обозначив силы, образующие искомую пару 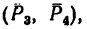
Отсюда
•Значит к прямоугольнику необходимо приложить пару сил с положительным (направленным против хода часовой стрелки) моментом, равным 48 н м. Силы, образующие эту пару, равняются
20 н каждая и одна из них должна действовать вдоль стороны АВ от А к В, вторая — вдоль стороны CD от С к D.
Задача 5.
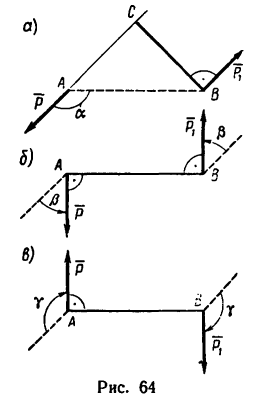
Прямолинейный стержень АВ должен находиться в равновесии в положении, показанном на рис. 68, а (угол а = 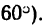
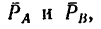
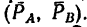
Решение.
1. Пару сил можно уравновесить только парой сил. Поэтому в точках С и D к стержню необходимо приложить две равные силы так, чтобы они образовали пару сил с моментом, равным моменту пары 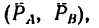
Так как пара 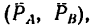
2. Применяем условие равновесия:
Или, подставив значения моментов,
где
Отсюда
Следовательно, в точках С и D необходимо приложить силы 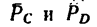
Момент силы относительно точки
Момент силы относительно точки при решении задач по статике, а затем и по динамике имеет не менее важное значение, чем проекции сил. Поэтому нужно уметь определять эту величину безошибочно. Обычно его числовое значение находят неправильно из-за ошибок, допускаемых при определении плеча.
Чтобы не допускать ошибок при определении моментов сил относительно точки, рекомендуется придерживаться следующего порядка:
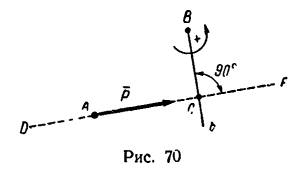
- Прежде всего нужно научиться «видеть» силу, момент которой определяем, и центр моментов – точку, относительно которой определяем момент (рис. 70 – сила
и центр моментов – точка В).
- Затем из центра момента проводим прямую ВЬ перпендикулярно к линии действия силы DF. Длина перпендикуляра ВС от центра момента до линии действия силы и есть плечо.
- Потом находим знак момента. При этом если сила стремится повернуть плечо вокруг центра момента против хода часовой стрелки, то считаем момент положительным; если по ходу часовой стрелки, то отрицательным (тоже правило, что и при определении знака момента пары сил).
- Находим числовое значение момента силы относительно точки, умножив модуль силы на плечо.
По рис. 70
В частном случае момент силы может равняться нулю. Это происходит тогда, когда центр моментов лежит на линии действия силы, при этом плечо равняется нулю. По рис. 70 момент силы 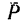
Задача 6.
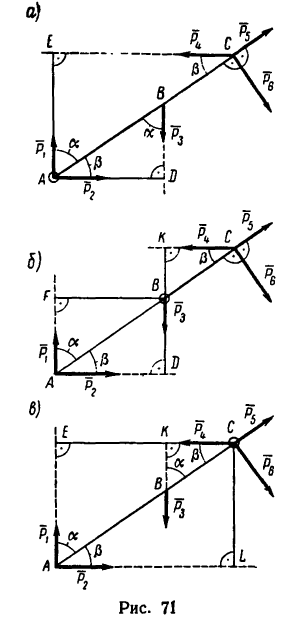
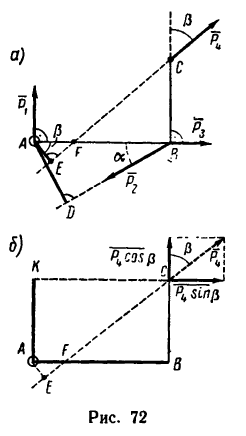
Определить моменты шести заданных сил (рис. 71) относительно точек А, В и С, если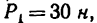
Решение 1 — определение моментов гнести заданных сил относительно точки А (рис. 71, а).
1. Центр моментов в точке А. Через точку А проходят линии действия трех сил 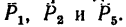
2. Находим момент силы 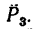
силы 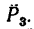
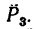
3. Величина момента отрицательная (сила 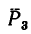
4. Находим момент силы 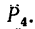
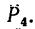
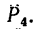
Величина момента положительная (плечо АЕ поворачивается около точки А силой 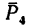
5. Находим момент силы 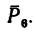
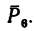
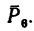
Решение 2 — определение моментов сил относительно точки В (рис. 71, б).
1. Центр моментов в точке В.
2. Через точку В проходят линии действия двух сил: 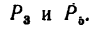
3. Находим момент силы 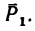
Величина момента отрицательная:
4. Находим момент силы 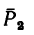
Момент отрицательный:
5. Находим момент силы 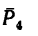
Величина момента положительная:
6. Находим момент силы 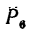
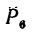
Решение 3 — определение моментов сил относительно точки С (рис. 71, в) рекомендуется выполнить самостоятельно.
Ответ.
В задаче силы расположены так, что либо их плечи определяются очень просто – как катеты прямоугольных треугольников, в которых даны гипотенузы, либо плечи заданы в условии задачи (ВС и АС).
Но иногда некоторые силы заданной системы оказываются расположенными относительно выбранного центра моментов так, что определить длину плеча трудно и требуется, например, предварительно вычислить длины еще одного-двух отрезков. В таких случаях целесообразно силу разложить на две составляющие и применить для определения ее момента теорему Вариньона.
Задача 7.
Определить моменты относительно точки 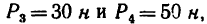

Решение.
1. Относительно точки А моменты сил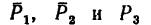
2. Находим момент силы 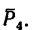
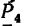
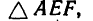
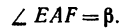
AF = AB – FB.
Величину FB находим из 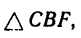
следовательно,
И теперь можем определить плечо АЕ:
Раскрываем скобки и заменяем
Момент положительный, следовательно:
Вариант 2-й. Чтобы избежать определения плеча АЕ, которое в данном случае находится после предварительного вычисления двух отрезков (FB и AF), необходимо момент силы 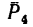
Разложим силу 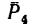
Модуль первой составляющей 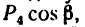
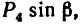
Применяя теорему Вариньона, получаем
Как видно, получено точно такое же значение момента, что и в первом варианте решения:
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Плоская система сил
- Аксиомы и теоремы статики
- Система сходящихся сил
- Плоское движение тела
- Принцип виртуальных перемещений
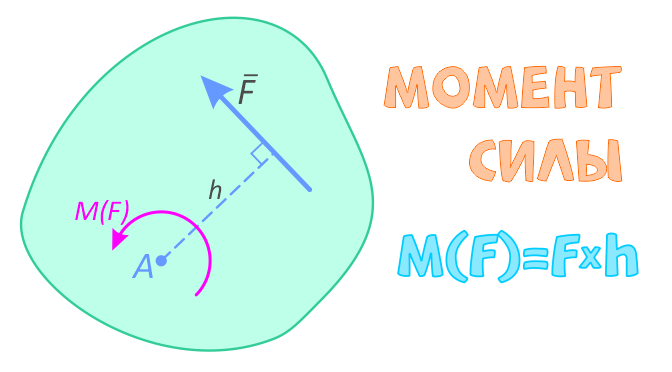
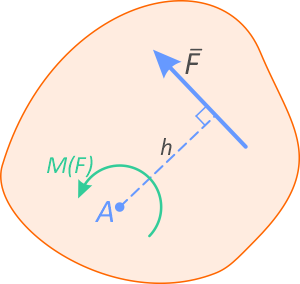
Моментом силы называют вращательное усилие создаваемое вектором силы относительно твердого тела, оси или точки.
Обозначение: M, m или M(F).
Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]
Аналогом момента силы является момент пары сил.
Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.
Определение
Момент определяется как произведение силы F на плечо h:
M(F)=F×h
Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.
Наш короткий видеоурок про момент силы с примерами:
Другие видео
Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки вращения создает момент M=7×0,35=2,45 кНм.
Пример момента силы
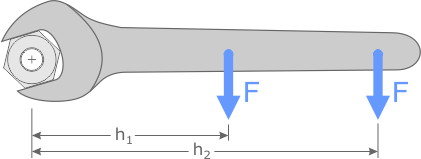
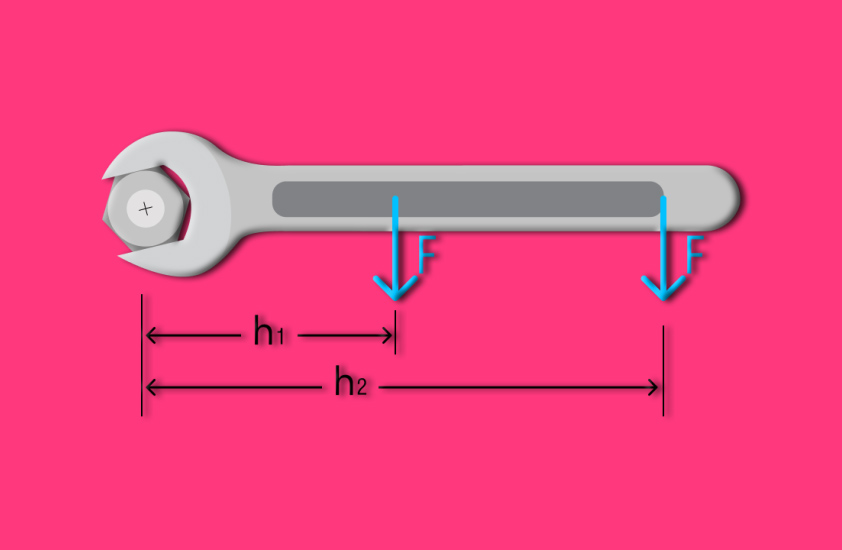
Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.
Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.
Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h2>h1).
Плечом при этом служит расстояние от центра гайки до точки приложения силы.
Плечо момента силы
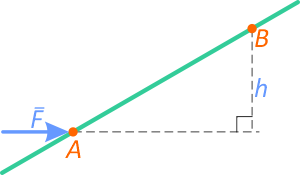
Рассмотрим порядок определения плеча h момента:
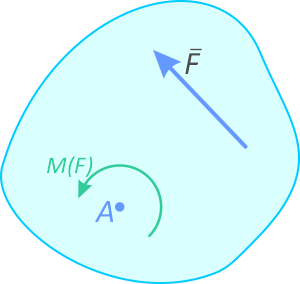
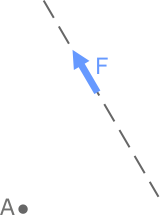
Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.
Покажем линию действия силы F (штриховая линия)
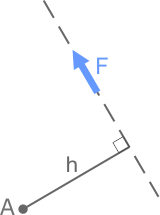
Проведем из точки A перпендикуляр h к линии действия силы
Длина отрезка h есть плечо момента силы F относительно точки A.
Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).
Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.
Примеры расчета момента силы
Сила расположена перпендикулярно оси стержня
Если сила F приложена перпендикулярно к оси бруса и известно расстояние между точками A и B.
То момент силы F относительно точки A:
МA=F×AB
Сила расположена под углом к оси стержня
В случае, если сила F приложена под углом α к оси балки
Момент силы относительно точки B:
MB=F×cosα×AB
Известно расстояние от точки до линии действия силы
Если известно расстояние от точки где определяется момент до линии действия силы (плечо h)
Момент силы относительно точки B:
MB=F×h
См. также:
- Примеры решения задач >
- Момент силы относительно точки
- Момент силы относительно оси
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Момент силы — онлайн калькулятор. Как найти и в чем измеряется момент силы, формулы
Момент силы — это векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение. По другому можно сказать, что момент силы – это произведение силы на плечо этой силы.
В данном обзоре приведен онлайн калькулятор момента силы, теоретические основы и формулы расчета момента силы.
Калькулятор момента силы
Для расчета момента силы (M) необходимо ввести в калькуляторе значения силы (F) и радиус-вектор (r). Также имеется возможность определять силу по известному моменту силы и радиус-вектору, и соответственно радиус-вектор по известной силе и моменту силы. Определившись с неизвестной величиной, введя известные значения и нажав кнопку «Вычислить», вы получите нужный результат.
Момент силы — определения и формулы
При вращательном движении линейные кинематические характеристики (пройденный путь s, линейная скорость υ, тангенциальное ускорение aτ) пропорциональны соответствующим угловым характеристикам. При этом коэффициентом пропорциональности является радиус вращения r. В качестве силовой характеристики вращательного движения вводится понятие момента силы. Следует отличать моменты силы относительно оси и относительно точки.
Момент силы относительно точки O
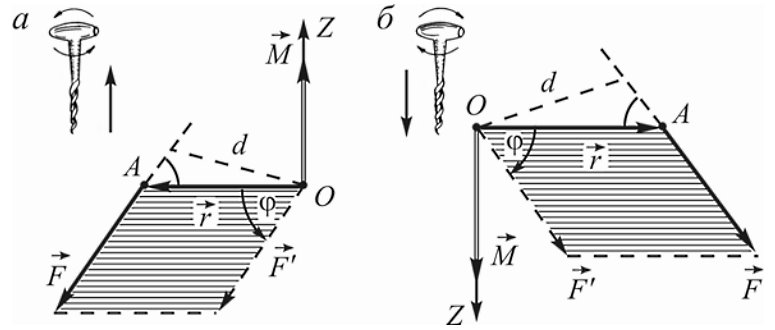
Моментом силы относительно точки O называется векторное произведение M→ = [r→, F→], где r→ — радиус-вектор, проведенный из этой точки к точке приложения силы. Вектор M→ перпендикулярен плоскости, в которой лежат векторы r→ и F→, и численно равен площади параллелограмма, сторонами которого являются данные векторы M = rFsinφ.
 |
|
| Направление вектора M→ определяется по правилу векторного произведения: если совместить точки приложения векторов r→ и F→, то кратчайший поворот от радиус-вектора r→ к силе F→′ будет происходить против часовой стрелки, если смотреть с вершины вектора M→. |
Иногда удобнее смотреть вслед вектору M→, тогда кратчайший поворот от радиус-вектора r→ к силе F→′ будет происходить по часовой стрелке. На практике удобно определять направление вектора M→ по правилу правого винта: если вращать головку винта в направлении действия силы, то его поступательное движение покажет направление момента силы M→. |
Момент силы равен нулю, если равна нулю сила или линия действия силы проходит через точку O.
 |
|
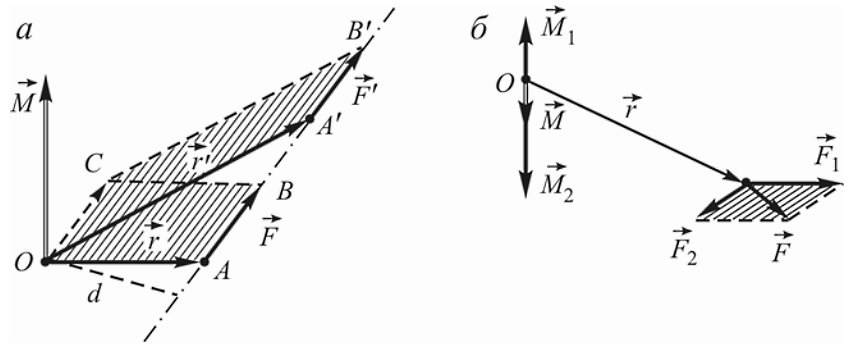
| Момент силы M→ не изменяется, если вектор F→ (точку приложения силы) переносить вдоль линии действия. Наглядно видно, что площади параллелограммов OABC и OA′B′C равны, поскольку они имеют общее основание OC и высоту d. | Геометрическая сумма моментов нескольких сил, действующих на материальную точку A относительно некоторой точки O, равна моменту суммы этих сил относительно той же точки M→ = [r→, F→] = [r→,(F→1+F→2 +…)] = [r→,F→1]+[r→,F→2]+… |
Момент силы относительно некоторой оси
Моментом силы относительно некоторой оси называют проекцию Mz на данную ось вектора момента этой силы M→ относительно любой точки, лежащей на оси.
Величина Mz не зависит от выбора точки O‘ на оси, поскольку момент силы M при переносе точки приложения силы вдоль линии ее действия не изменяется. Момент силы относительно точки O численно равен моменту этой силы относительно оси OZ, перпендикулярной плоскости, в которой лежат векторы r→ и F→ (а значит и точка O).
Плечо силы — это кратчайшее расстояние между осью и линией действия силы d = r sinφ. В таком случае момент силы относительно этой оси может быть определен как произведение силы и плеча M = Fd. Такое определение момента силы дается в элементарной физике. При этом положительными считаются те моменты сил, которые вызывают вращение по часовой стрелке, а отрицательными — вызывающие вращение против часовой стрелки.
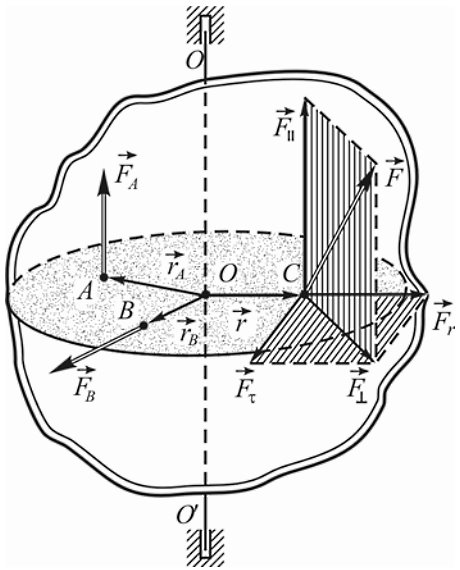
Рассмотрим действие сил на тело, способное вращаться вокруг неподвижной оси OO′:
Сила F→a, параллельная оси, может только деформировать эту ось. Не вызовет вращения и сила F→b, лежащая в плоскости, перпендикулярной оси вращения, если линия, вдоль которой она действует, проходит через эту ось, то есть совпадает по направлению с радиус-вектором r→b, проведенным в точку ее приложения B.
Вызвать вращение тела вокруг неподвижной оси может только сила или ее составляющая, которая лежит в плоскости, перпендикулярной данной оси, и не совпадает по направлению с радиус-вектором, проведенным в этой плоскости к точке ее приложения. Силу, образующую произвольный угол с осью вращения, можно спроецировать на перпендикулярную плоскость, а затем разложить на тангенциальную F→τ и радиальную F→r составляющие. Именно тангенциальная составляющая силы создает момент относительно оси M = F→τr и является причиной тангенциального ускорения точки тела, к которой она приложена, то есть вызывает изменение модуля линейной скорости этой точки при вращательном движении.
Как найти момент сопротивления квадратного сечения относительно его центральных осей?
Момент сопротивления квадратного сечения относительно центральных осей z и y одинаковый и его можно рассчитать по формуле:
Wy = Wz = a3 /6 где
Wy — момент сопротивления относительно центральной оси y в мм3 ;
Wz — момент сопротивления относительно центральной оси y в мм3 ;
а — длина стороны квадрата в мм;
Момент инерции квадратного сечения (формула и расчет)
Радиус инерции квадратного сечения (формула и расчет)
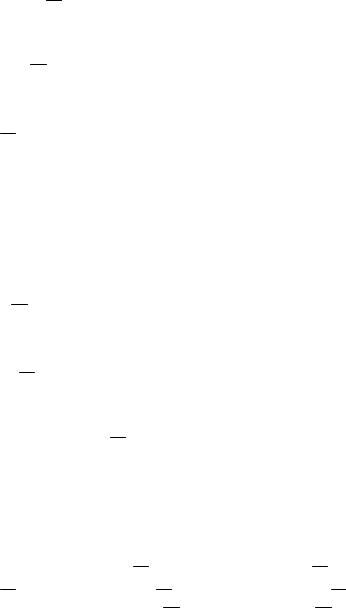
29
Пример 4.1
Определить моменты сил Р1 = 10 кН, Р2 = 20 кН, Р3 = 30 кН, приложенных в вершинах квадрата АВСО (рис. 4. 3, а), относительно точки О, при стороне квадрата а = 0,2 м.
Решение:
1) Определяем момент силы Р1 = 10 кН относительно точки О.
Мо (Р1) = – Р1 . а = -10 . 0,2 = -2 кНм
2) Определяем момент силы Р2 = 20 кН относительно точки О.
Мо (Р2) = Р2 . ОВ = 20 . а√2 = 5,66 кНм
3) Определяем момент силы Р3 = 30 кН относительно точки О.
Мо (Р3) = – Р3 . ОД = -30 . а Соs 30° = -5,20 кНм
Пример 4.2
Определить моменты сил Р1 = 10 кН, Р2 = 15 кН, Р3 = 30 кН, приложенных в вершинах А и В прямоугольного равнобедренного треугольника (рис. 4. 3, б), относительно точки О, при а = 0,3 м.
Решение:
Определяем момент силы Р1 = 10 кН относительно точки О.
Мо (Р1) = Р1 . ОС = 10 . а Sin 45° = 2,12 кНм Определяем момент силы Р2 = 15 кН относительно точки О.
Мо (Р2) = Р2 . ОД = 15 . а Sin 60° = 3,9 кНм Определяем момент силы Р3 = 30 кН относительно точки О.
Мо (Р3) = Р3 . 0 = 0
Пример 4.3
Определить моменты сил Р1 = 15 кН, Р2 = 20 кН, Р3 = 40 кН, приложенных в вершинах А, В, С прямоугольника (рис. 4. 3, в) и треугольников (рис. 4. 3, г, д, е), относительно точки О, при а = 0,6 м самостоятельно.
Результаты решения:
Рис. 3в Мо (Р1) = 9 кНм, Мо (Р2) = -10,39 кНм, Мо (Р3) = -33,94 кНм Рис. 3г Мо (Р1) = -4,5 кНм, Мо (Р2) = -20,78 кНм, Мо (Р3) = 20,78кНм Рис. 3д Мо (Р1) = -7,79 кНм, Мо (Р2) = -12 кНм, Мо (Р3) = 20,78 кНм Рис. 3е Мо (Р1) = -7,79 кНм, Мо (Р2) = -18 кНм, Мо (Р3) = -24 кНм
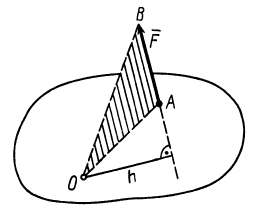
Момент силы относительно точки в пространстве определяется вектором, приложенным в этой точке, модуль которого равен произведению модуля силы на плечо.

30
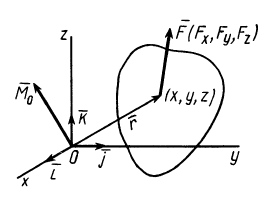
Этот вектор перпендикулярен к плоскости, проведенной через моментную точку и линию действия силы и направлен так, чтобы вращение плоскости (если смотреть с конца вектора) происходило против хода часовой стрелки (рис. 4.4). Если из моментной точки О в точку приложения силы провести радиус – вектор r (рис. 4.4), то вектор момента силы можно выразить векторным произведением.
|
Мо (Р) = |
r |
* |
р |
(4.3) |
Модуль момента силы
Мо (Р) = r . р Sin α = Р . d
5. ТЕОРИЯ ПАР СИЛ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
5. 1. Пара сил. Момент пары сил на плоскости
Парой сил называется совокупность двух параллельных сил (линии действия которых не совпадают), равных по модулю и направленных в противоположные стороны.
Плоскость, в которой действуют силы, называется плоскостью действия пары.
Кратчайшее расстояние d между линиями действия сил, составляющих пару, называется плечом пары.
Если пару сил приложить к телу, находящемуся в покое, то оно будет совершать вращательное движение.
Пару сил нельзя уравновесить силой, так как она не имеет равнодействующей. Уравновесить пару можно только с помощью другой пары.
Вращательное действие пары на твердое тело характеризуют моментом пары.
Момент пары сил на плоскости – это скалярная величина, равная произведению одной из сил на плечо пары со знаком плюс или минус
Мо (Р1, Р1′) = ± Р1 . d
Если вращение плоскости действия пары происходит против хода часовой стрелки, то момент пары считаем положительным, если по ходу часовой стрелки – отрицательным.
Выразим моменты пар сил на плоскости (рис. 5. 1, а):
Мо (Р1, Р1′) = Р1 . d1 Мо (Р2, Р2′) = – Р2 . d2
Поскольку пару сил характеризуют только моментом и в расчетах нужен лишь момент пары сил, то обычно для обозначения пары сил пользуются дуговой стрелкой в плоскости действия пары, которая показывает направление вращения пары и модуль момента М = М (Р1, Р1′) (рис. 5. 1, б). Численно момент пары можно определить как удвоенную площадь треугольника ОАВ,
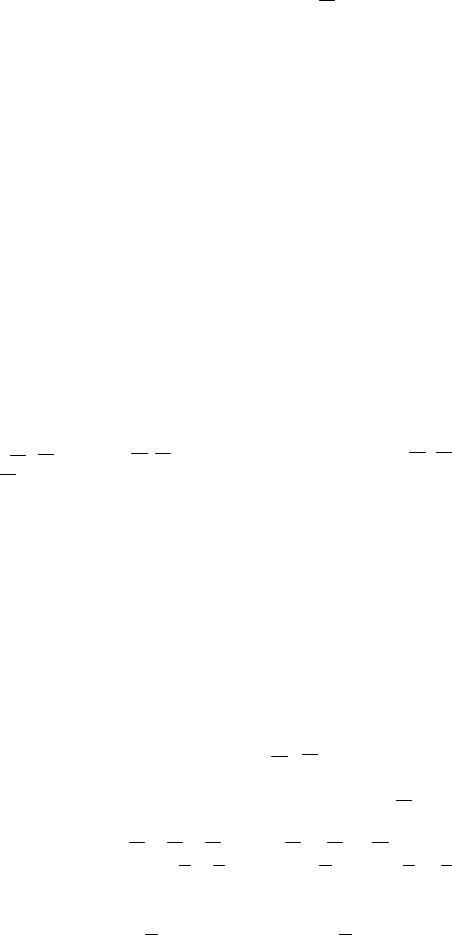
31
основанием которого является одна из сил Р1, а вершиной О – точка приложения другой силы Р1′ (рис. 5. 1, б).
5. 2. Момент пары сил в пространстве. Эквивалентные пары
Пару сил характеризуют:
–плоскость действия;
–величина момента пары;
–направление вращения.
Момент пары в пространстве зависит от расположения плоскости действия и от направления, в котором пара стремится вращать тело, т.е. является векторной величиной.
Вектор, определяющий момент пары, называют вектор-моментом. Вектормомент пары равен по модулю произведению силы пары на ее плечо и направлен перпендикулярно к плоскости действия пары таким образом, чтобы вращение плоскости происходило против хода часовой стрелки, если смотреть с конца вектора (рис. 5. 2).
Эквивалентными называются пары, оказывающие на твердое тело одинаковое действие, т.е. вектор-моменты которых геометрически равны. Пары сил, расположенные в одной плоскости эквивалентны, если их моменты численно равны и совпадают по направлению вращения (рис. 5. 3).
Пара (Р1, Р1′) и пара (Р2, Р2′) эквивалентны, так как М (Р1, Р1′) = 20 кНм иМ (Р2, Р2′) = 20 кНм, а направление вращения одинаково (против хода часовой стрелки).
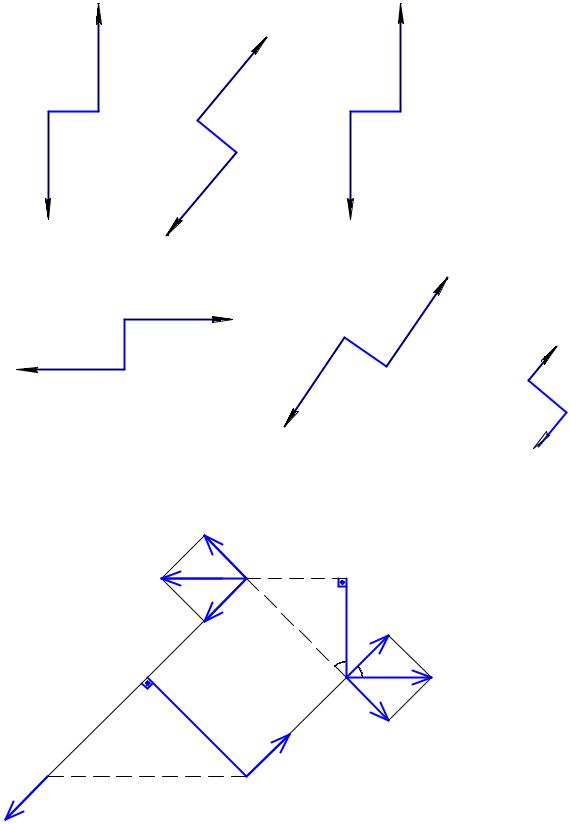
Определить эквивалентные пары на рис. 5. 4 самостоятельно.
Ответ. Первая и третья пары эквивалентны. Четвертая и шестая пары эквивалентны.
5. 3. Теоремы об эквивалентности пар
Теорема 1
Всякую пару сил, не изменяя ее действия на твердое тело, можно заменить другой парой, расположенной в той же плоскости, имеющей одинаковое с заданной парой направление вращения и равный по модулю момент.
Доказательство
Пусть на тело действуют пара сил (Р1, Р1′) в точках А и В (рис.5.5). Перенесем эти силы в точки Д и С, лежащие на их линиях действия. Приложим в точках С и Д две взаимно уравновешенные силы Т1 = – Т1′. Найдем равнодействующие:
R1 = Р1 + Т1, R1′ = Р1′ + Т1′
Получим новую пару сил (R1 , R1′). У пар (Р1, Р1′) и (R1 , R1′) одинаковое направление вращения.
Покажем, что обе пары имеют одинаковый по величине момент. M (Р1, Р1′) = Р1 . d1 M (R1, R1′) = R1 . d2
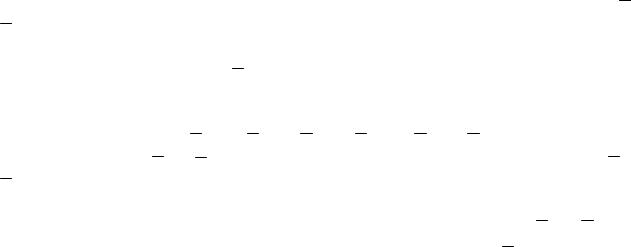
32
|
Р1 |
||
|
R1 = ———– |
d2 = d1 Cos α |
|
|
Cos α |
||
|
Р1 |
. d1. |
|
|
M (R1, R1′) = ———- |
d1 Cos α = Р1 |
Cos α
Таким образом, эти пары эквивалентны.
Следствия:
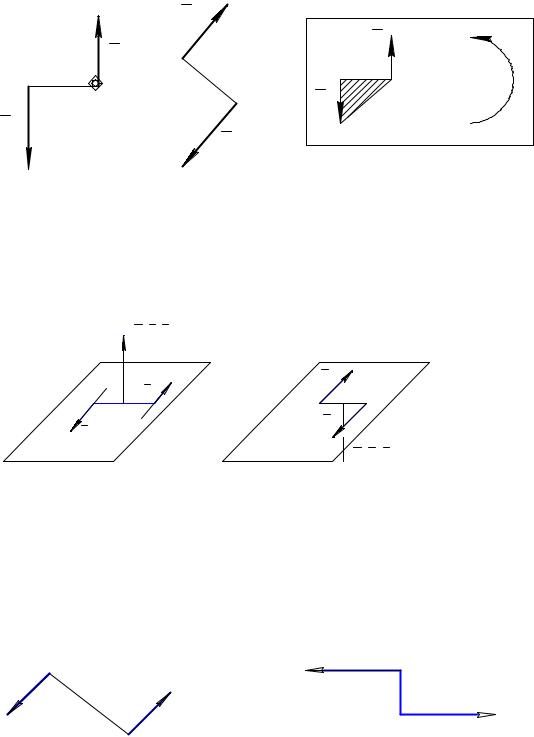
1.Действие пары сил на тело не изменится, если не изменяя момента пары переместить ее или повернуть в любое положение в плоскости действия
(рис.5.6).
2.Действие пары на тело не изменится, если не изменяя момента пары изменить силы пары и ее плечо. Во сколько раз уменьшаем силу, во столько раз увеличиваем плечо, и наоборот (рис. 5. 7).
Теорема
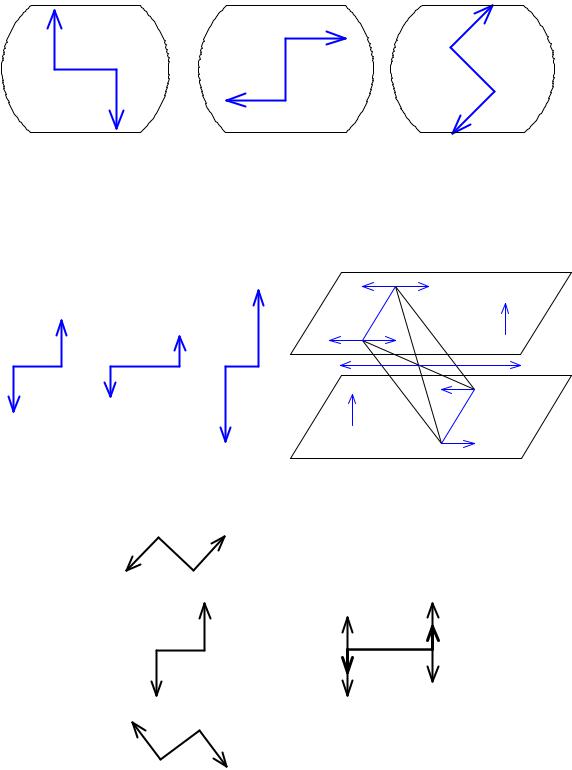
Действие пары сил на твердое тело не изменится, если пару сил перенести из данной плоскости в любую другую параллельную плоскость.
Доказательство
Рассмотрим твердое тело, на которое в плоскости I действует пара сил (Р1, Р1′). В произвольной плоскости II, параллельной плоскости I, проведем отрезок СД, параллельный и равный отрезку АВ (рис. 5. 8). В точках С и Д приложим уравновешенные силы Р2 = – Р2′ и Р3 = – Р3′. Модули этих сил выберем равными модулям сил заданной пары
Р1 = Р1′ = Р2 = Р2′ = Р3 = Р3′
Сложив силы Р′1 и Р3′, а также Р1 и Р2, найдем их равнодействующие R1 и R1′, которые приложены в точке пересечения диагоналей параллелограмма АВСД, равны по модулю и противоположно направлены.
Силы R1 и R1′ образуют уравновешенную систему сил, т.е. R1 + R1′ = 0, поэтому их можно устранить. Оставшаяся пара сил (Р2′, Р3) эквивалентна заданной, но расположена в параллельной плоскости.
Следствие
Вектор-момент пары является свободным вектором, т.е. его точку приложения можно переносить в любую точку тела, не изменяя модуль и направление.
33
|
б. |
||
|
P’ |
||
|
2 |
M |
|
|
d |
P’1 |
|
|
А |
d |
|
|
2 |
1 О |
|
|
P1 |
В |
|
|
P |
||
|
2 |
Рис. 5.1
M (P1,P’1)
P2
P’1
P1 P’2
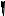
Рис.5.2
|
P1 |
=2H |
P2 =5Н |
||||||||
|
d=10м |
d=4м |
|||||||||
|
P’1 |
=2H |
|||||||||
|
P’2 |
=5Н |
|||||||||
Рис. 5.3
1.
P1=6H
d=4м
P’1=6H
4.
P’4 =6Н
A
_
P1‘
34
2. 3.
P2 =12Н
d=2м
P’2 =12Н
5.
P4 =6Н
d=3м P5 =6H
P3 =3Н
d=8м
P’3 =3Н
d =3м
d=9м
P’6 =2Н
|
Рис.5.4 |
||||
|
_ |
||||
|
_ |
T1‘ |
|||
|
R1‘ |
_ C |
_ |
||
|
d2 |
||||
|
P1‘ |
1 |
|||
|
a |
P |
|||
|
a |
_ |
|||
|
D |
R1 |
|||
|
d1 |
_ |
|||
|
_ |
T1 |
|||
|
B |
P1 |
Рис. 5.5
_
P1
d
_
P1‘
P1=4H
P2=2H
4м 8м
P2‘=2H
P1‘=4H
Рис. 5.7
_
P1 d1
d2
_
P2
35
_
P1
d
_
P1‘
Рис.5.6
P3=8H
_
P2
2м _
R’
P3‘=8H
_
P1‘
_
P1
d
_
P1‘
|
_ |
_ |
II |
|
|
P3‘ |
|||
|
M |
|||
|
O |
_ |
||
|
_ |
R |
||
|
B |
I |
||
|
P1 |
d _
A P1‘
Рис. 5.8
|
_ |
_ |
|||
|
_ |
Q2‘ |
|||
|
Q3 |
||||
|
P2‘ |
_ |
|||
|
A _1 |
d |
Q1‘ |
||
|
B_ |
||||
|
Q |
Q3‘ |
|||
|
_ |
||||
|
Q2 |
_
P3‘
Рис.5.9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

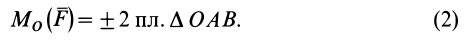
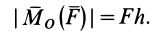
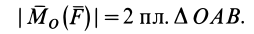

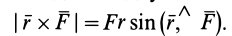
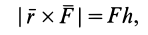
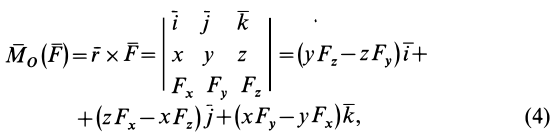
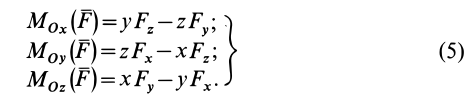
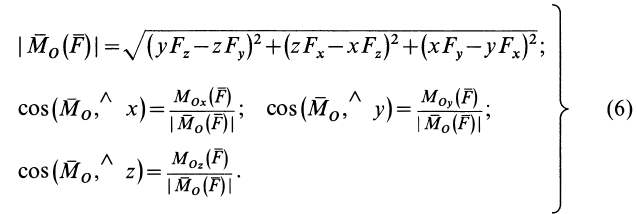
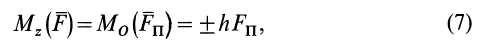
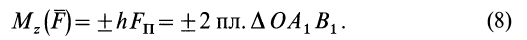
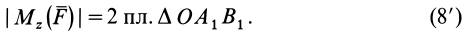
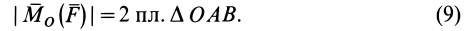
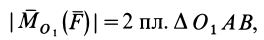
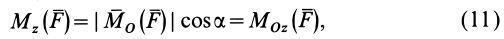
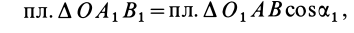
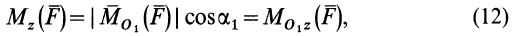
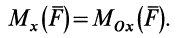
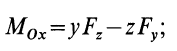
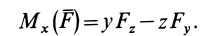
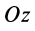
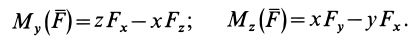
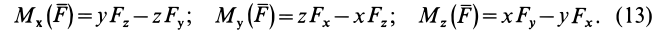
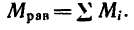
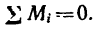
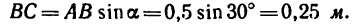
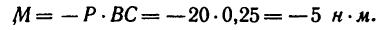
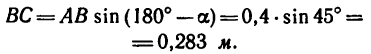
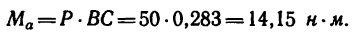
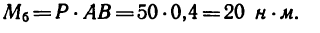
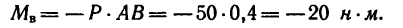
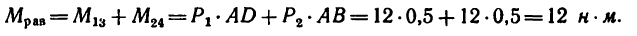
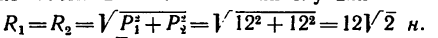
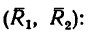
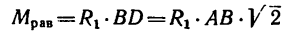
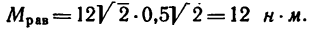
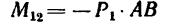
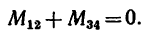
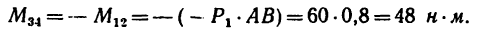
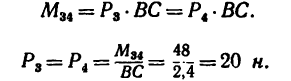
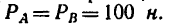
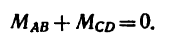
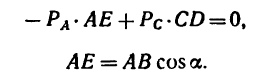
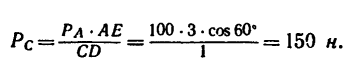
 и центр моментов – точка В).
и центр моментов – точка В).