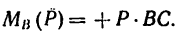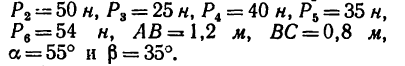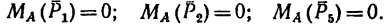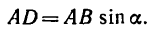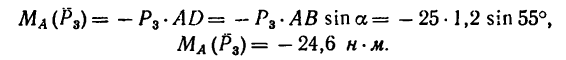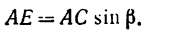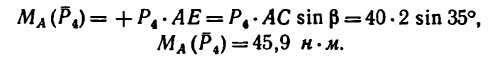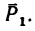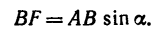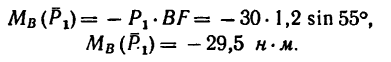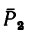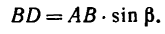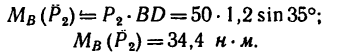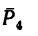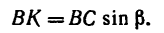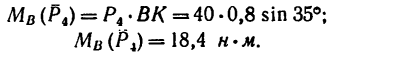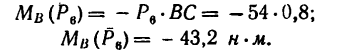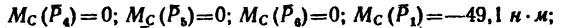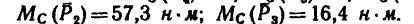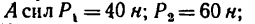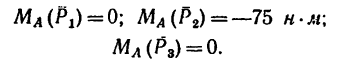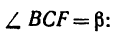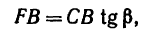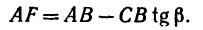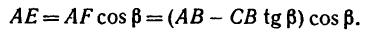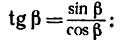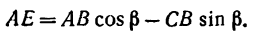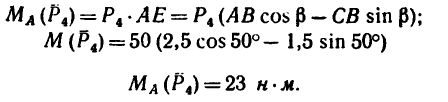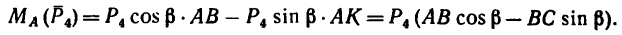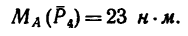Статика — раздел механики, изучающий условия равновесия тел.
Виды равновесия
Устойчивое равновесие |
|
 |
Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (Ep min). |
Неустойчивое равновесие |
|
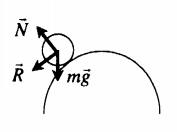 |
Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (Ep max). |
Безразличное равновесие |
|
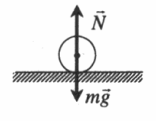 |
При выведении тела из положения безразличного равновесия дополнительных сил не возникает. |
Момент силы
Определение
Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:
M = Fd
M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).
Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.
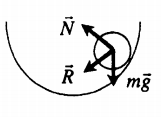
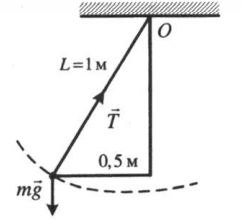
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?
Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:
M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)
Момент силы может быть положительным и отрицательным.
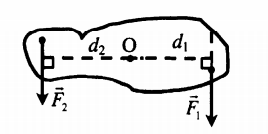
Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:
M1 = F1d1
Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:
M2 = F2d2
Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
∑Mi=0
Иначе правило моментов можно сформулировать так:
Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.
∑Mпо час. стр.=∑Mпр. час. стр.
Условия равновесия тел
| Тело не участвует в поступательном движении: |
∑→Fi=0; →vo=0 |
| Тело не участвует во вращательном движении: |
∑Mi=0; ω0=0 |
| Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении) |
∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0 |
Простые механизмы
Определение
Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.
Наклонная плоскость |
|
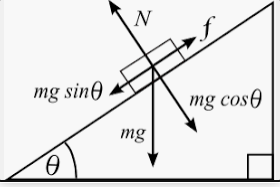 |
Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsinθ<mg |
Рычаг |
|
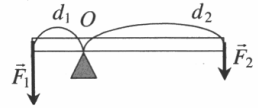 |
Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2=d2d1 |
Неподвижный блок |
|
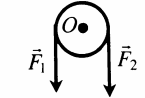 |
Изменяет направление действия силы. Модули и плечи сил при этом равны: F1 = F2 M1 = M2 |
Подвижный блок |
|
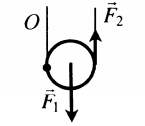 |
Дает выигрыш в силе в 2 раза:
d1 = R d2 = 2R F1 = 2F2 |
Клин |
|
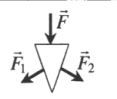 |
Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2 |
Золотое правило механики
При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.
Задание EF22660
Алгоритм решения
1.Записать исходные данные.
2.Записать правило моментов и выполнить решение в общем виде.
3.Подставить известные данные и вычислить искомую величину.
Решение
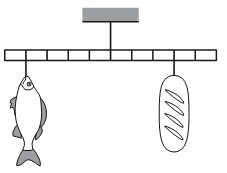
Известна лишь масса батона: m1 = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:
d1 = 0,3
d2 = 0,4
Запишем правило моментов:
F1 d1 = F2 d2
Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:
m1gd1 = m2gd2
m1d1 = m2d2
Отсюда масса рыбы равна:
m2=m1d1d2=0,8·0,30,4=0,6 (кг)
Ответ: 0,6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18706
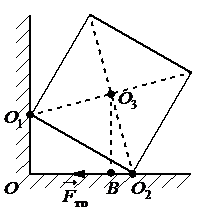
Ответ:
а) 0
б) О2О3
в) О2В
г) О3В
Алгоритм решения
- Сформулировать определение плеча силы.
- Найти плечо силы трения и аргументировать ответ.
Решение
Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О3В.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 9.7k
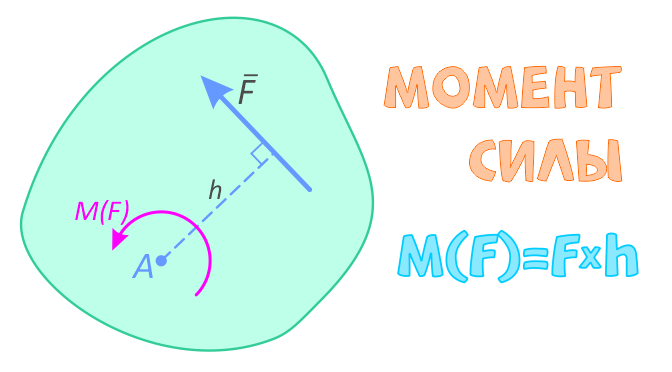
Моментом силы называют вращательное усилие создаваемое вектором силы относительно твердого тела, оси или точки.
Обозначение: M, m или M(F).
Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]
Аналогом момента силы является момент пары сил.
Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.
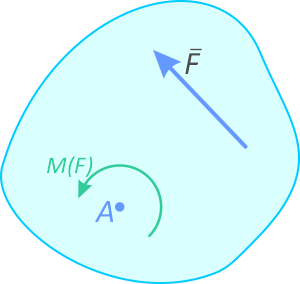
Определение
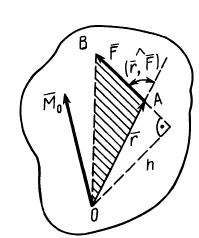
Момент определяется как произведение силы F на плечо h:
M(F)=F×h
Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.
Наш короткий видеоурок про момент силы с примерами:
Другие видео
Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки вращения создает момент M=7×0,35=2,45 кНм.
Пример момента силы
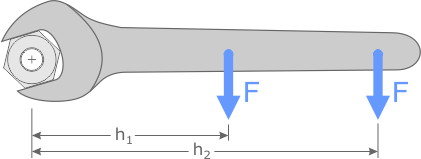
Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.
Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.
Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h2>h1).
Плечом при этом служит расстояние от центра гайки до точки приложения силы.
Плечо момента силы
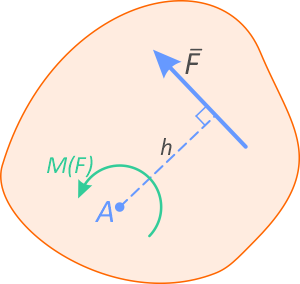
Рассмотрим порядок определения плеча h момента:
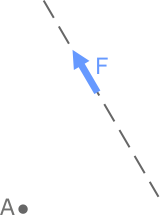
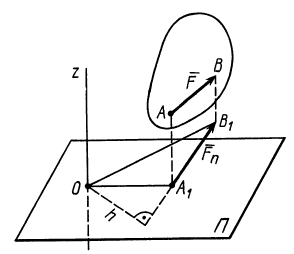
Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.
Покажем линию действия силы F (штриховая линия)
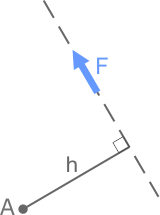
Проведем из точки A перпендикуляр h к линии действия силы
Длина отрезка h есть плечо момента силы F относительно точки A.
Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).
Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.
Примеры расчета момента силы
Сила расположена перпендикулярно оси стержня
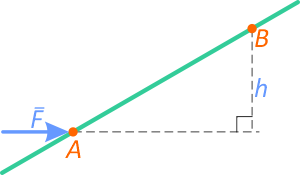
Если сила F приложена перпендикулярно к оси бруса и известно расстояние между точками A и B.
То момент силы F относительно точки A:
МA=F×AB
Сила расположена под углом к оси стержня
В случае, если сила F приложена под углом α к оси балки
Момент силы относительно точки B:
MB=F×cosα×AB
Известно расстояние от точки до линии действия силы
Если известно расстояние от точки где определяется момент до линии действия силы (плечо h)
Момент силы относительно точки B:
MB=F×h
См. также:
- Примеры решения задач >
- Момент силы относительно точки
- Момент силы относительно оси
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
| Момент силы | |
|---|---|
![vec{M}=left[vec{r}timesvec{F}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb353a429aeedc00390e7ccd563692a29a4607c0) |
|
| Размерность | L2MT−2 |
| Единицы измерения | |
| СИ | Н·м |
| СГС | Дина-сантиметр |
| Примечания | |
| Псевдовектор |
Моме́нт си́лы (момент силы относительно точки) — векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение. Определяется как векторное произведение радиус-вектора точки приложения силы 

Момент силы обозначается символом 

Единица измерения в СИ: Н⋅м. Величина момента силы зависит от выбора начала отсчёта радиус-векторов O.
Понятие момента силы используется, в основном, в области задач статики и задач, связанных с вращением деталей (рычагов и др.) в технической механике. Особенно важен случай вращения твёрдого тела вокруг фиксированной оси — тогда O выбирают на этой оси, а вместо самого момента рассматривают его проекцию на ось 
Наличие момента силы влечёт изменение момента импульса тела 


Определение, общие сведения[править | править код]
В физике момент силы играет роль вращающего воздействия на тело.
Видеоурок: вращающий момент
В простейшем случае, если сила 


.
Например, сила в 3 ньютона, приложенная на расстоянии 2 м от оси, создаёт такой же момент, что и сила в 1 ньютон с плечом 6 м.
Если действуют две силы, говорят о моменте пары сил (такая формулировка восходит к трудам Архимеда). При этом равновесие достигается в ситуации 
Для случаев более сложных движений и более сложных объектов определение момента как произведения 
Момент силы иногда называют вращающим или крутящим моментом. «Вращающий» момент понимается в технике как внешнее усилие, прикладываемое к объекту, а «крутящий» — как внутреннее, возникающее в самом объекте под действием приложенных нагрузок (этим понятием оперируют в сопромате).
Момент силы относительно точки[править | править код]
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
В общем случае момент силы 
,
где 



Начало отсчета радиус-векторов O может быть любым. Обычно O выбирают в чем-либо выделенной точке: в месте закрепления подвеса, в центре масс, на оси вращения и т.д.. Если одновременно анализируется момент импульса тела 


Если не оговорено иное, то «момент силы» — это момент силы относительно точки (O), а не некоей оси.
В случае нескольких приложенных сосредоточенных сил их моменты векторно суммируются:
,
где 



.
Если 
Момент силы относительно оси[править | править код]
Моментом силы относительно оси называется алгебраическое значение проекции момента 
,
где 
,
где через 

В отличие от момента силы 

Для краткости символ параллельности и знак могут опускаться, а 

Единицы измерения[править | править код]
Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
Формально, размерность 
Некоторые примеры[править | править код]
Формула момента рычага[править | править код]
Момент, действующий на рычаг
Момент силы, действующей на рычаг, равен
или, если записать момент силы относительно оси,
,
где 



Статическое равновесие[править | править код]
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма моментов всех сил вокруг любой точки.
Для двумерного случая с горизонтальными и вертикальными силами требование сводится к тому, чтобы нулевыми были сумма сил в двух измерениях: 

Движение твёрдого тела[править | править код]
Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если 
где 
Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:
Связь с другими величинами[править | править код]
С моментом импульса[править | править код]
Момент силы — производная момента импульса 
,
Аналогичную формулу можно записать для моментов относительно оси:
.
Если момент силы 

С мощностью[править | править код]
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу и развивает мощность 

.
В системе СИ мощность 

С механической работой[править | править код]
Если под действием момента силы 

.
Для поворота, скажем, рычага вокруг фиксированной оси на угол 
.
В системе СИ работа 
Размерность работы (и энергии) совпадает с размерностью момента силы («ньютон-метр» и джоуль — это одни и те же единицы). Момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию 
Измерение момента силы[править | править код]
Измерение момента силы осуществляется с помощью специальных приборов — торсиометров. Принцип их действия обычно основан на измерении угла закручивания упругого вала, передающего крутящий момент, либо на измерении деформации некоторого упругого рычага. Измерения деформации и угла закручивания производится различными датчиками деформации — тензометрическими, магнитоупругими, а также измерителями малых перемещений — оптическими, ёмкостными, индуктивными, ультразвуковыми, механическими.
Существуют специальные динамометрические ключи для измерения крутящего момента затягивания резьбовых соединений и регулируемые и нерегулируемые ограничители крутящего момента, так называемые «трещотки», применяемые в гаечных ключах, шуруповёртах, винтовых микрометрах и др.
Из истории понятия[править | править код]
Для того чтобы понять, откуда появилось понятие момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы 

Пусть под действием силы конец рычага смещается на бесконечно малый отрезок 









Следовательно, бесконечно малая работа 




Теперь попытаемся выразить модуль вектора 




Так как для бесконечно малого перемещения рычага 




Для проекции вектора силы 




Теперь запишем бесконечно малую работу через новые равенства: 

Видно, что произведение 





Теперь полная работа записывается просто: 

См. также[править | править код]
- Момент инерции
- Момент импульса
- Теорема Вариньона
Как известно, вся классическая механика делится на кинематику, динамику и статику. Про кинематику и динамику мы уже писали, а сегодня расскажем про статику и займемся решением задач.
Не забывайте подписаться на наш телеграм-канал и получать полезную рассылку каждый день.
Задачи на статику и равновесие тел
Мы не будем решать страшные задачи по теормеху, сопротивлению материалов или предмету Тут Моя Могила Теория Машин и Механизмов (ТММ). Разберем несколько примеров, связанных с равновесием и простейшими механизмами.
Именно на базе статики строится знаменитый сопромат, столь нелюбимый технарями.
Задача №1. Момент силы
Условие
На рычаг в состоянии равновесия действуют две силы. Момент первой равен 20 Н*м. Модуль второй силы равен 5 Н. Найдите плечо второй силы.
Решение
Запишем условие равновесия рычага:
Отсюда:
Ответ: 4м.
Задача №2. Статика
Условие
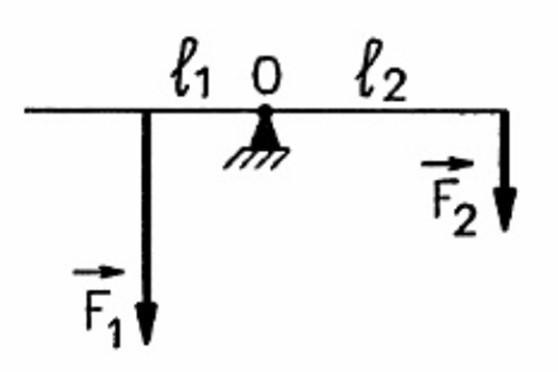
На концах рычага действуют силы с модулями 20 и 120 Н соответственно. Рычаг находится в равновесии. Найдите длину рычага, если расстояние от точки опоры до большей силы равно 2 см.
Решение
Запишем равенство моментов:
Ответ: 14 см.
В этой задаче мы не переводили размерности в систему СИ.
Задача №3. Расчет силы
Условие
Рабочий на стройке поднимает плиту с помощью рычага. Большее плечо равно 2,4м, меньшее – 0,8м. Какую силу прикладывает рабочий к большему плечу рычага, если масса плиты равна 120 кг?
Решение
Обозначим большее плечо через d1. К нему рабочий прикладывает искомую силу F1. Вторая сила, приложенная к меньшему плечу, равна весу плиты.
Ответ: 400 Н.
Задача№4. Подвижный блок
Условие
Какую силу нужно приложить, чтобы поднять груз весом 1000 Н с помощью подвижного блока? Какую работу совершит эта сила при подъеме груза на 1 метр?
Подвижный блок позволяет выиграть в усилии в два раза.
Решение
Найдем силу и работу:
Ответ: 500 Н, 1000 Дж.
Задача №5. Нахождение плеча рычага
Условие
На плечи рычага действуют силы 300 Н и 20 Н. Меньшее плечо равно 5см. Найдите большее плечо рычага.
Решение
Условие равновесия рычага можно записать так:
Ответ: 75 см.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Вопросы и ответы по статике
Вопрос 1. Что нужно, чтобы тело находилось в равновесии, каково условие равновесия тел?
Ответ. Из законов Ньютона известно, что тело движется равномерно или покоится, если равнодействующая всех сил, приложенных к нему, равна нулю. Это и есть условие равновесия.
Это условие справедливо только для тела, которое может двигаться поступательно, но не может вращаться вокруг некоторой оси.
Вопрос 2. Каково условие равновесия для вращающихся тел?
Ответ. Если тело имеет неподвижную ось вращения, то оно находится в равновесии, если алгебраическая сумма моментов всех сил, приложенных к телу относительно этой оси, равна нулю.
Вопрос 3. Что такое момент силы?
Ответ. Момент силы — скалярная физическая величина, равная произведению модуля силы F на плечо силы d.
Вопрос 4. Что такое плечо силы?
Ответ. Плечо силы — это длина перпендикуляра, проведенного от оси вращения к линии действия силы.
Вопрос 5. Материальные тела в статике считаются упругими, или абсолютно твердыми?
Ответ. Абсолютно твердыми. Деформации и изменение размеров тела под действием сил не принимаются во внимание при решении задач, если иное не оговорено в условии.
Вопрос 6. Что такое рычаг в механике?
Ответ. Рычаг — простейший механизм. Рычагом может быть любое тело, которое может вращаться вокруг неподвижной опоры или подвеса. Используется для создания большего усилия на меньшем плече за счет меньшего усилия на длинном плече.
Статика: определение
Статика — раздел теоретической механики, изучающий основы равновесия тел.
Нужна помощь в решении более сложных заданий? Не знаете, как решать задачи по теоретической механике? Обращайтесь в профессиональный студенческий сервис.
Содержание:
Моменты силы относительно точки и оси:
Для рассмотрения различных систем сил необходимо ввести понятия алгебраического и векторного моментов силы относительно точки и момента силы относительно оси. Введем эти характеристики действия силы на твердое тело и рассмотрим их свойства.
Алгебраический момент силы относительно точки
При рассмотрении плоской системы сил, приложенных к твердому телу, используется понятие алгебраического момента силы относительно точки.
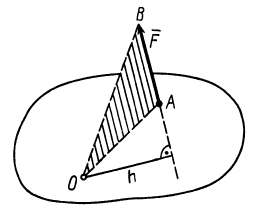
Рис. 19
Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки (рис. 19), взятое со знаком плюс или минус.
Плечом 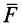

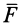
Обозначим 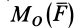
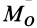
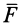

Если сила стремится вращать тело вокруг моментной точки (точки, относительно которой вычисляют алгебраический момент силы) против часовой стрелки, то берем знак плюс, если по часовой стрелке — знак минус.
Алгебраический момент силы представляет собой произведение силы на длину (в 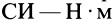
Из определения алгебраического момента силы относительно точки следует, что он не зависит от переноса силы вдоль ее линии действия. Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через моментную точку. Сумма алгебраических моментов относительно точки двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой, равна нулю. Численно алгебраический момент относительно точки равен удвоенной площади треугольника, построенного на силе 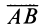
Векторный момент силы относительно точки
При рассмотрении пространственной системы сил, приложенных к твердому телу, применяется понятие векторного момента силы относительно точки.
Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть стремление силы вращать тело против движения часовой стрелки (рис. 20).
Плечом 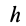

Рис. 20
Условимся векторный момент силы 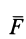


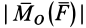
Как и для алгебраического момента, векторный момент силы относительно точки равен удвоенной площади треугольника, построенного на силе и моментной точке:
Справедлива формула
где 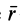

Чтобы убедиться в справедливости формулы (3), достаточно показать, что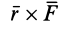

Как показано на рис. 20, 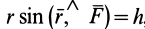
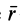
что совпадает с векторным моментом силы относительно точки 
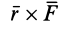
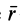
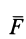
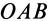

Направление 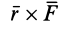

Векторный момент силы относительно точки не изменяется от переноса силы вдоль ее линии действия. Он станет равным
нулю, если линия действия силы пройдет через моментную точку.
Рис. 21
Если сила 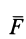
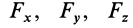
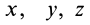
где 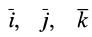
Используя формулу (4), можно выделить проекции 
Модуль векторного момента 
В формулах (6) числовую величину 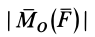
Момент силы относительно оси
Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью (рис. 22). Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси (проекция силы на плоскость является вектором), стремится вращать тело вокруг положительного направления оси против часовой стрелки, и отрицательным, если она стремится вращать тело по часовой стрелке. Момент силы, например, относительно оси 
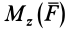
Рис. 22
По определению,
где 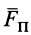
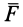





Из определения момента силы относительно оси следует, что введенный выше алгебраический момент силы относительно точки можно считать моментом силы относительно оси, проходящей через эту точку, перпендикулярно плоскости, в которой лежат сила и моментная точка. Момент силы относительно оси можно выразить через площадь треугольника, построенного на проекции силы 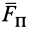

Из формулы (8) можно получить следующие важные свойства момента силы относительно оси:
- Момент силы относительно оси равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси.
- Момент силы относительно оси равен нулю, если линия действия силы пересекает эту ось. В этом случае линия действия проекции силы на плоскость, перпендикулярную оси, проходит через точку пересечения оси с плоскостью и, следовательно, равно нулю плечо силы
относительно точки
.
В обоих этих случаях ось и сила лежат в одной плоскости. Объединяя их, можно сказать, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
Связь момента силы относительно оси с векторным моментом силы относительно точки на оси
Используя формулу (8), имеем (рис. 23)
Векторный момент силы 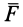



Векторный момент 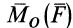
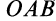
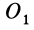
причем векторный момент 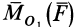
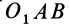
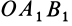
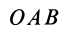
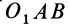

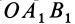

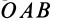
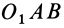
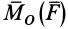
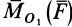
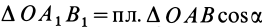
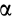
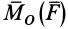

причем знак 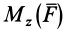
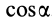
Аналогично,
т. е.
где 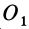

Формулы (11) и (12) отражают искомую связь между моментом силы относительно оси и векторными моментами силы относительно точек, лежащих на этой оси: момент силы относительно оси равен проекции на эту ось векторного момента силы относительно любой точки на оси.
Эту зависимость между моментом силы относительно оси и векторным моментом силы относительно точки на оси можно принять за определение момента силы относительно оси.
Рис. 23
Формулы для моментов силы относительно осей координат
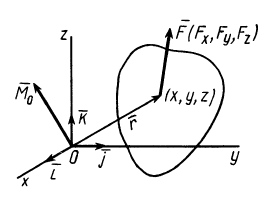
Используя связь момента силы относительно оси с векторным моментом силы относительно точки на оси, можно получить формулы для вычисления моментов относительно осей координат, если даны проекции силы на оси координат и координаты точки приложения силы. Для оси 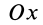
Согласно (5),
следовательно,
Аналогично, для осей 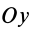
Окончательно
По формулам (13) можно вычислить моменты силы относительно прямоугольных осей координат.
По этим формулам получаются необходимые знаки для 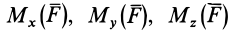
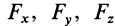
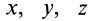
При решении задач момент силы относительно какой-либо оси часто получают, используя его определение, т. е. проецируя силу на плоскость, перпендикулярную оси, и вычисляя затем алгебраический момент этой проекции относительно точки пересечения оси с этой плоскостью.
Момент пары сил. Сложение пар сил. Равновесие пар сил
При изучении теоретической механики необходимо совершенно отчетливо уяснить, что в статике рассматриваются два простейших элемента: сила и пара сил. Любые две силы, кроме сил, образующих пару, всегда можно заменить одной —сложить их (найти равнодействующую). Пара сил нс поддается дальнейшему упрощению, она не имеет равнодействующей и является простейшим элементом.
Действие пары сил на тело характеризуется ее моментом — произведением одной из сил пары на ее плечо (на кратчайшее расстояние между линиями действия сил, образующих пару).
Единицей момента пары сил в Международной системе служит 1 нм (ньютон-метр = 1 н-1ж), а в системе МКГСС (технической)— 1 кГ-м.
Несколько пар сил, действующих на тело в одной плоскости, можно заменить одной парой сил (равнодействующей парой), момент которой равен алгебраической сумме моментов данных пар:
При равновесии пар сил
Если пары сил действуют в одной плоскости, то при решении задач достаточно рассматривать моменты пар как алгебраические величины. Причем знак момента определяется в зависимости от направления вращающего действия пары сил.
Дальнейшее изложение основано на правиле, т. е. считается момент положительным, если пара сил действует против хода часовой стрелки, если же пара сил действует на тело но ходу часовой стрелки, то момент считается отрицательным.
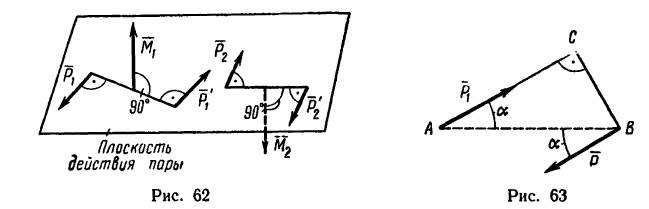
В том случае когда пары сил действуют на тело будучи расположенными в различных плоскостях, гораздо удобнее рассматривать пару сил как вектор, направленный перпендикулярно
к плоскости действия пары сил (рис. 62). Направление вектора в зависимости от направления вращательного действия пары определяется по направлению движения винта с правой нарезкой.
Задача 1.
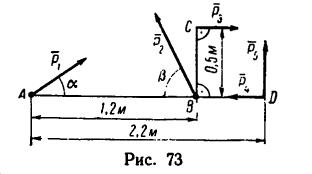
Определить момент пары сил (рис. 63), если 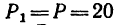
Решение.
1. При определении момента пары сил нужно прежде всего правильно определить плечо пары. При этом необходимо различать следующие понятия: плечо пары сил и расстояние между точками приложения сил нары.
Так как в механике твердого тела сила—скользящий вектор, то действие силы не изменяется при переносе точки ее приложения вдоль линии ее действия. Значит расстояние между точками приложения сил, образующих пару, можно изменять неограниченно. Но плечо пары при этом переносе остается неизменным.
В частном случае расстояние между точками приложения сил, образующих пару, может быть равно плечу.
Чтобы определить плечо данной пары из точки приложения одной из сил, например из точки В, восставим перпендикуляр ВС к линии действия другой силы. Расстояние ВС и есть плечо данной пары сил. Расстояние между точками приложения сил, образующих пару, АВ=0,5 м.
Легко видеть, что
2. Найдем момент пары сил:
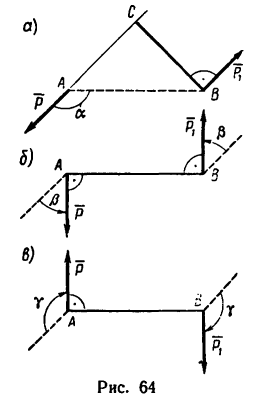
Задача 2.
Как изменится момент пары сил 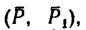
повернуть силы 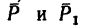
1. Найдем момент пары при заданном положении ее сил (рис. 64, а).
Из точки В восставим перпендикуляр ВС к линиям действия сил 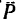
Момент пары при заданном положении сил
2. Повернем силы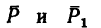
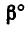
3. Сравнивая полученные результаты, видим, что после поворота сил момент пары увеличивается на 20—14,5 = 5,85 н-м.
4. Легко заметить, что силы 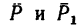
Момент пары сил изменяет свой знак.
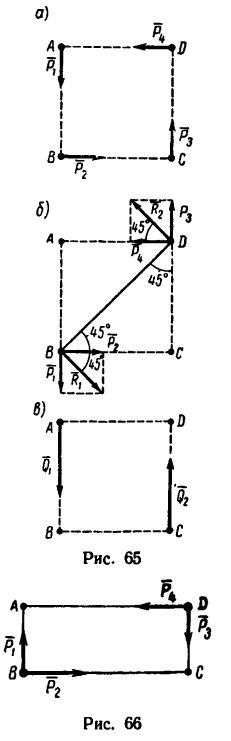
Задача 3.
К точкам А, С и В, D, образующим вершины квадрата со стороной 0,5 м (рис. 65, а), приложены равные по модулю силы (Р = 12н) таким образом, что они образуют две пары сил
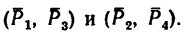
Решение 1.
Плечи у обеих пар сил равны стороне квадрата поэтому
Решение 2.
1. Перенесем силы 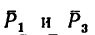
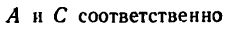
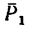
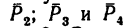
2. Сложим попарно эти силы у каждой из точек В и D. В обоих случаях
3. Силы R, модули которых теперь известны, направлены перпендикулярно к диагонали BD квадрата. Значит эта диагональ является плечом вновь образовавшейся пары сил 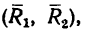
4. Найдем момент пары
и, следовательно,
Эту пару в соответствии со вторым решением можно представить в виде пары 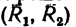
Но можно равнодействующую пару представить и в любом другом виде, например в виде сил Q = 24 и, приложенных к двум любым вершинам квадрата ABCD (рис. 65, в)
- Заказать решение задач по теоретической механике
Задача 4.
На прямоугольник ABCD (рис. 67) вдоль его длинных сторон действует пара сил 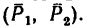
Решение.
1. Момент данной пары сил
необходимо уравновесить парой, момент которой обозначим Л1м. Тогда, согласно условию равновесия,
Откуда
2. Обозначив силы, образующие искомую пару 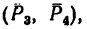
Отсюда
•Значит к прямоугольнику необходимо приложить пару сил с положительным (направленным против хода часовой стрелки) моментом, равным 48 н м. Силы, образующие эту пару, равняются
20 н каждая и одна из них должна действовать вдоль стороны АВ от А к В, вторая — вдоль стороны CD от С к D.
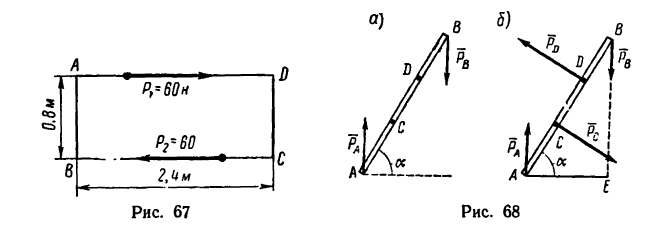
Задача 5.
Прямолинейный стержень АВ должен находиться в равновесии в положении, показанном на рис. 68, а (угол а = 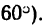
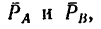
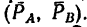
Решение.
1. Пару сил можно уравновесить только парой сил. Поэтому в точках С и D к стержню необходимо приложить две равные силы так, чтобы они образовали пару сил с моментом, равным моменту пары 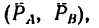
Так как пара 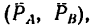
2. Применяем условие равновесия:
Или, подставив значения моментов,
где
Отсюда
Следовательно, в точках С и D необходимо приложить силы 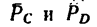
Момент силы относительно точки
Момент силы относительно точки при решении задач по статике, а затем и по динамике имеет не менее важное значение, чем проекции сил. Поэтому нужно уметь определять эту величину безошибочно. Обычно его числовое значение находят неправильно из-за ошибок, допускаемых при определении плеча.
Чтобы не допускать ошибок при определении моментов сил относительно точки, рекомендуется придерживаться следующего порядка:
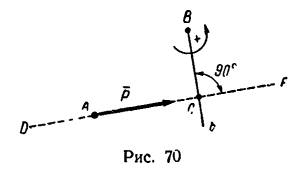
- Прежде всего нужно научиться «видеть» силу, момент которой определяем, и центр моментов – точку, относительно которой определяем момент (рис. 70 – сила
и центр моментов – точка В).
- Затем из центра момента проводим прямую ВЬ перпендикулярно к линии действия силы DF. Длина перпендикуляра ВС от центра момента до линии действия силы и есть плечо.
- Потом находим знак момента. При этом если сила стремится повернуть плечо вокруг центра момента против хода часовой стрелки, то считаем момент положительным; если по ходу часовой стрелки, то отрицательным (тоже правило, что и при определении знака момента пары сил).
- Находим числовое значение момента силы относительно точки, умножив модуль силы на плечо.
По рис. 70
В частном случае момент силы может равняться нулю. Это происходит тогда, когда центр моментов лежит на линии действия силы, при этом плечо равняется нулю. По рис. 70 момент силы 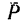
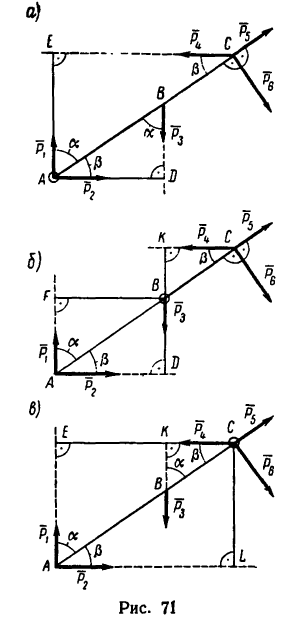
Задача 6.
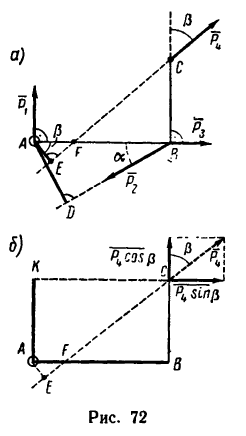
Определить моменты шести заданных сил (рис. 71) относительно точек А, В и С, если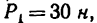
Решение 1 — определение моментов гнести заданных сил относительно точки А (рис. 71, а).
1. Центр моментов в точке А. Через точку А проходят линии действия трех сил 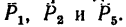
2. Находим момент силы 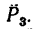
силы 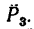
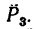
3. Величина момента отрицательная (сила 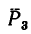
4. Находим момент силы 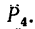
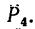
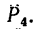
Величина момента положительная (плечо АЕ поворачивается около точки А силой 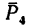
5. Находим момент силы 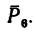
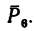
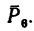
Решение 2 — определение моментов сил относительно точки В (рис. 71, б).
1. Центр моментов в точке В.
2. Через точку В проходят линии действия двух сил: 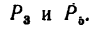
3. Находим момент силы 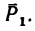
Величина момента отрицательная:
4. Находим момент силы 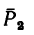
Момент отрицательный:
5. Находим момент силы 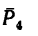
Величина момента положительная:
6. Находим момент силы 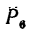
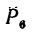
Решение 3 — определение моментов сил относительно точки С (рис. 71, в) рекомендуется выполнить самостоятельно.
Ответ.
В задаче силы расположены так, что либо их плечи определяются очень просто – как катеты прямоугольных треугольников, в которых даны гипотенузы, либо плечи заданы в условии задачи (ВС и АС).
Но иногда некоторые силы заданной системы оказываются расположенными относительно выбранного центра моментов так, что определить длину плеча трудно и требуется, например, предварительно вычислить длины еще одного-двух отрезков. В таких случаях целесообразно силу разложить на две составляющие и применить для определения ее момента теорему Вариньона.
Задача 7.
Определить моменты относительно точки 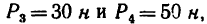

Решение.
1. Относительно точки А моменты сил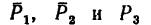
2. Находим момент силы 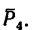
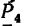
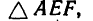
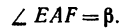
AF = AB – FB.
Величину FB находим из 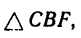
следовательно,
И теперь можем определить плечо АЕ:
Раскрываем скобки и заменяем
Момент положительный, следовательно:
Вариант 2-й. Чтобы избежать определения плеча АЕ, которое в данном случае находится после предварительного вычисления двух отрезков (FB и AF), необходимо момент силы 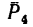
Разложим силу 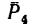
Модуль первой составляющей 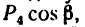
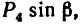
Применяя теорему Вариньона, получаем
Как видно, получено точно такое же значение момента, что и в первом варианте решения:
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Плоская система сил
- Аксиомы и теоремы статики
- Система сходящихся сил
- Плоское движение тела
- Принцип виртуальных перемещений






![{displaystyle {vec {M}}=sum _{i}left[{vec {r}}_{i}times {vec {F}}_{i}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b7fe1a3cdb4607b6f4ba588d40385667fac01df)
![{displaystyle {vec {M}}=int limits _{V}left[{vec {r}}times {frac {d{vec {F}}}{dV}}right]dV}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bd127004c78eb2ab9f734f69002b3e6f5dbba22)





![{displaystyle {vec {L_{o}}}=I_{c},{vec {omega }}+[M({vec {r_{o}}}-{vec {r_{c}}}),{vec {v_{c}}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecacc6649ed8fc84a6acadbafed8c4a1b6aea97d)

![{displaystyle {vec {M_{c}}}=I_{c}{frac {d{vec {omega }}}{dt}}+[{vec {w}},I_{c}{vec {w}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f99dacfe48211745407ecd9854ebc44b9465e417)






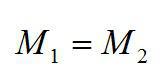
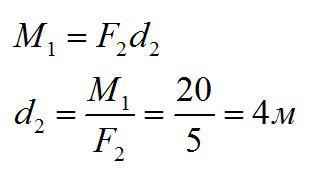
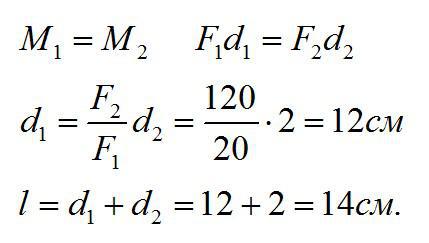
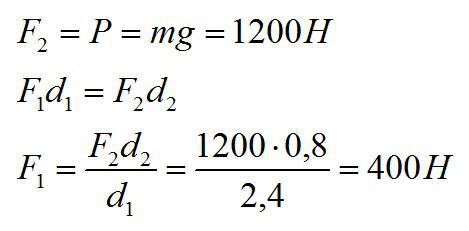
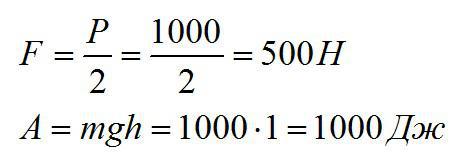
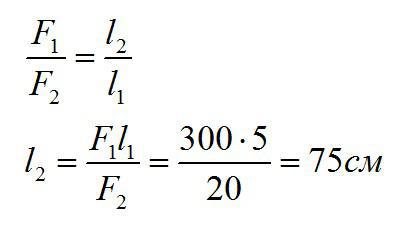

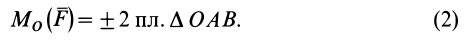
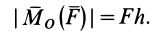
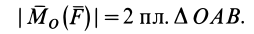

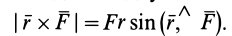
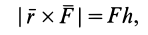
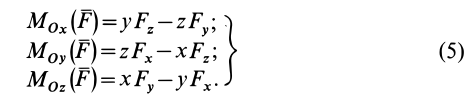
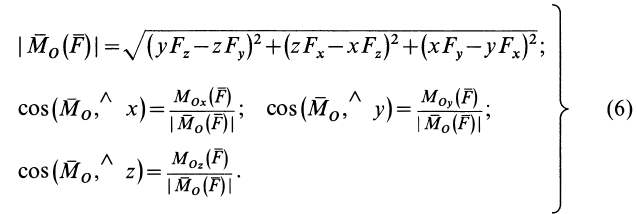
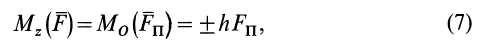
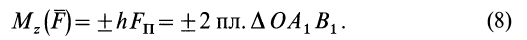
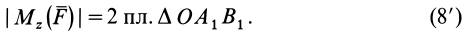
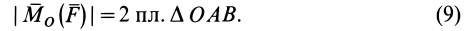
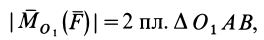
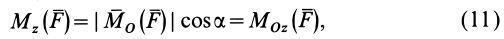
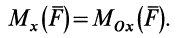
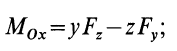
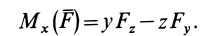
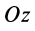
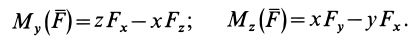
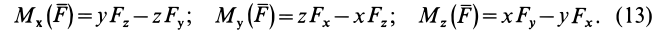
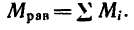
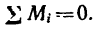
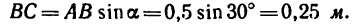
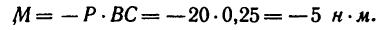
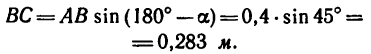
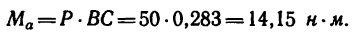
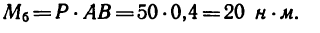
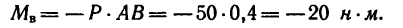
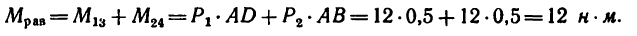
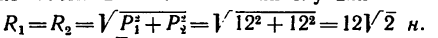
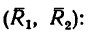
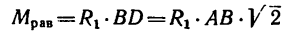
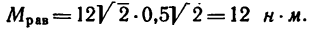
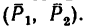
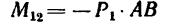
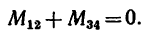
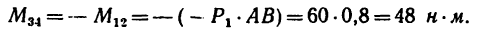
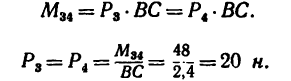
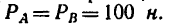
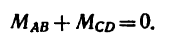
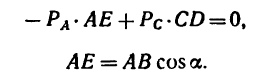
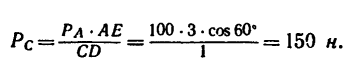
 и центр моментов – точка В).
и центр моментов – точка В).