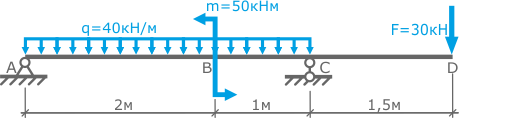
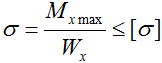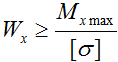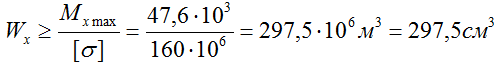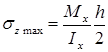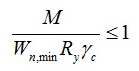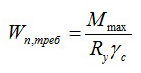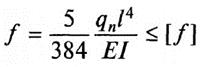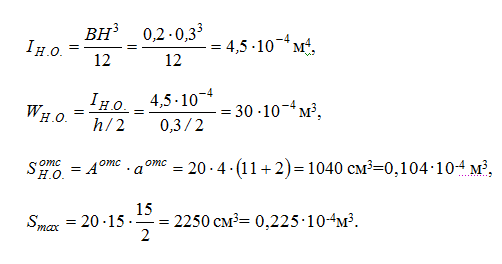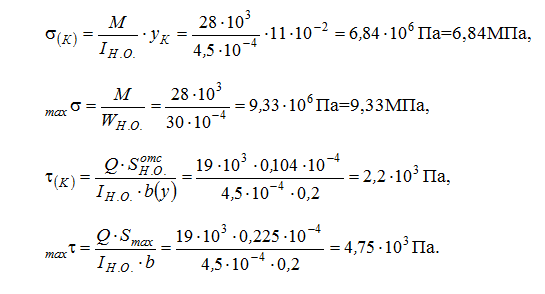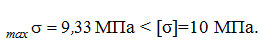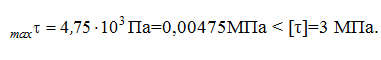Пример решения задачи по расчету минимального момента сопротивления Wx сечения стальной балки, обеспечивающего её прочность.
Задача
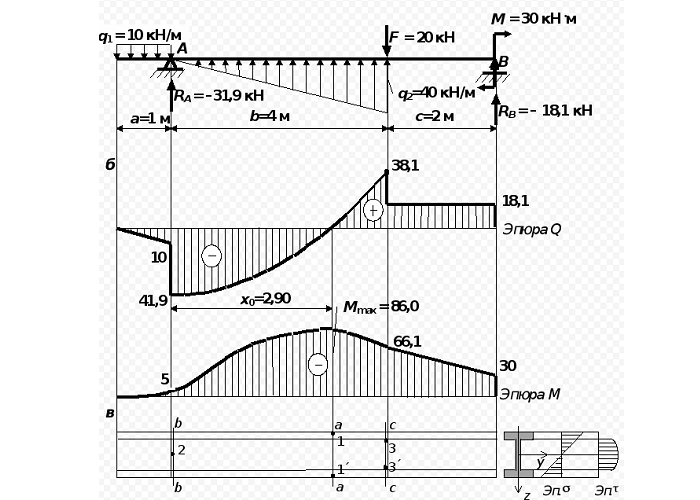
Для заданной стальной балки требуется определить минимальный момент сопротивления сечения Wx для последующего подбора двутавра и расчета размеров других сечений балки по условию прочности.
Допустимые напряжения [σ]=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
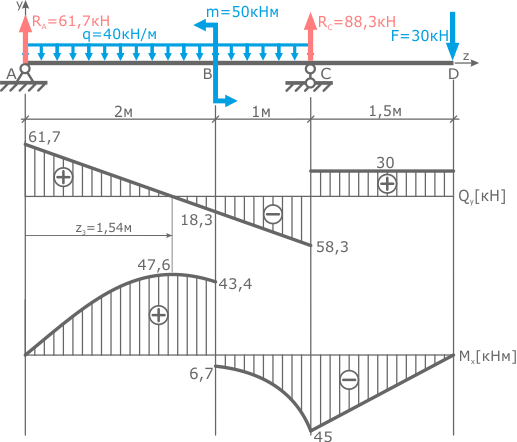
Предыдущие пункты решения задачи:
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов.
Прежде чем приступать к расчету размеров сечений балки обеспечивающих ее прочность, определим минимально необходимую величину момента сопротивления сечения Wx.
Момент сопротивления сечений зависит от их формы, размеров и расположения.
Его минимально необходимая величина рассчитывается из условия прочности по нормальным напряжениям при изгибе:
откуда получаем
По построенной эпюре Mx видно, что максимальная величина изгибающего момента составляет 47,6 кНм, поэтому
Таким образом, какую бы форму не имело сечение балки, для обеспечения ее прочности момент сопротивления сечения в данном случае должен иметь величину не менее 297,5 см3.
Теперь можно перейти к определению размеров поперечного сечения балки:
- Расчет диаметра круглого сечения >
- Расчет размеров прямоугольного сечения >
- Подбор номера двутавра >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
где
m =0,9 – коэффициент снижения нормативных
расчетных сопротивлений RН
при тяжелом режиме работы;
RН
= 29 кH /см2
– расчетное сопротивление стали
10ХСНД;
2
– понижение расчетных сопротивлений с
учетом влияния на прочность верхнего
пояса горизонтальных нагрузок, кH/см2.
3.6 Подбор сечения и проверка прочности балки
3.6.1
Подбор сечения балки
Определение
высоты балки по условию жесткости [1,
с. 62, формула (3.10) и с. 319, приложение 4; 2,
с. 174, табл. 4-36]:

где
l=1200см
– пролет балки;
R=
29 кН/см2
– расчетное сопротивление стали;
МН
=338194
кН см –
нормативный момент в сечении 5;
МР
=468737
кН см – расчетный момент в сечении 5.
Определение
высоты балки по оптимальности веса
[1, с. 62, формула (3.11); 3, с.113-114].
Задаемся
гибкостью стенки по таблицам [1, с. 63,
табл. 3.1]:
Wн=Мр/mR-2.

Определение
высоты балки из условия экономичности
Принимаем
высоту балки по большему значению,
округляя последнюю цифру до 5 или 0,
принимаем, h
= 130 см, высота стенки hст
= 166 см, оставляем по 2 см на полки.
Определение
толщины стенки:
–
по прочности на опоре от действия
касательных напряжений [1, с.63, формула
(3.13)]:

где
QН=1207кН
– перерезывающая нормативная сила;
RСР
= 17 кН/см2
– расчетное сопротивление среза для
стали 10ХСНД.
–
по прочности от местного давления
под колесом крана [4, с. 74, формула
(3.50)]:
где
Р1
–
расчетное давление колеса крана с учетом
коэффициента перегрузки
n
= 1,2;
P1
= Рнn=340*1,2=408
(кН);
n1
=1,3– коэффициент при тяжелом режиме и
гибком подвесе;
IР
= 4924 см4
– момент
инерции кранового рельса, для КР 120;
RН
= 29 кН/см2
– расчетное сопротивление стали 10 ХСНД.
Принимаем
толщину стенки ст
=1см из
сортового проката.
Определение
сечений поясов балки [1,
с. 63, формула (3.14); 3, с. 144, §4]:

но
Fn
= n
bn,
где bn
30n;
Fn
302n,
откуда

Принимаем
широкополосную сталь по ГОСТ 82-70 [2,
с.39],
сечением 14х450 мм – для полок, для стенки
-16х760 мм.
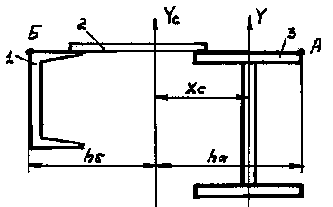
Рисунок
3.4
–Эскиз подкрановой балки двутаврового
сечения.
Подбор
сечений тормозной балки [1, с. 69-72, с.
114-118]
Рисунок
3.5
– Сечение тормозной и подкрановой балки
Поле
тормозной балки выполняем из швеллера
№24, параметры которого: F1
= 30,6 см2;
Zо1
= 2,42 см; I1
=208 см4.
Лист 1050х6 мм рифлёный.
Определение
геометрических характеристик тормозной
балки.
Положение
центра тяжести сечения тормозной балки
относительно оси Y-Y:
где
F1
=30,6 см2–
площадь элемента 1 (швеллера);
F2
=105*0,6=63(см2)–
площадь элемента 2 (листа);
F3
=45*1,4=63(см2)–
площадь элемента 3 (верхнего пояса);
X1
=70-2,4=67,6(см)– расстояние от центра тяжести
элемента 1 до оси Y-Y;
Х2
=52,5+24=76,5(см)- расстояние от центра тяжести
элемента 2 до оси Y-Y.
Момент
инерции сечения относительно оси УС.

где
Хс1
=89,4 см – расстояние от центра тяжести
элемента 1 до оси YС;
Хс2
=33,3 см – Расстояние от центра тяжести
элемента 2 до оси YС.
Моменты
сопротивления изгибу для крайних волокон
в точках а и в (см. рис. 2.7):

(3.16)

(3.17)
где
hА,
hВ
– расстояние от центра тяжести сечения
до точек А и В.
3.6.2
Определение геометрических характеристик
сечения балки

где
h ст=166
см – высота стенки балки.



(3.21)
Определим
процент содержания металла сечения в
поясах балки:

поясах содержится более 30% обшей массы
сечения.
3.6.3
Проверка прочности балки по нормальным
и касательным напряжениям
В
точке “а” верхнего пояса

–
в нижнем поясе
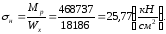
Касательные
напряжения в стенке под опорой


для стали 10ХСНД.
значит


но при этом:

что допустимо.
3.6.4
Проверка жесткости балки от вертикальных
нормативных нагрузок

где
к = 1,1 – коэффициент динамичности;
n
= 1,2 – коэффициент перегрузки.
Абсолютный
прогиб балки

Е
= 2,1 104,
кН/см2
– модуль упругости стали.
Относительный
прогиб

2.6.6 Проверка
прочности стенки при местном давлении
колеса крана
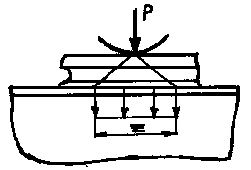
Рисунок
3.6
– Схема передачи давления от колеса
крана на лист стенки.

где

= 1,3;
Р1
=456 кН –
расчетное давление колеса крана.
Z
– линейная зона передачи давления.
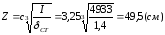
(3.29)
IР
=4923
см4
– момент инерции рельса КР120,
In
– момент инерции пояса балки, In
=

C
= 3,25 для сварных балок.
2.6.7
Проверка общей устойчивости балки
При

и
общая устойчивость обеспечена, но
действительное значение составляет:
больше
допускаемого, поэтому требуется:
-устройство
тормозной площадки;
-дополнительное закрепление
верхнего пояса от изгиба в горизонтальной
плоскости.
Общую устойчивость
обеспечиваем установкой тормозной
площадки и стержневых связей с колонной.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
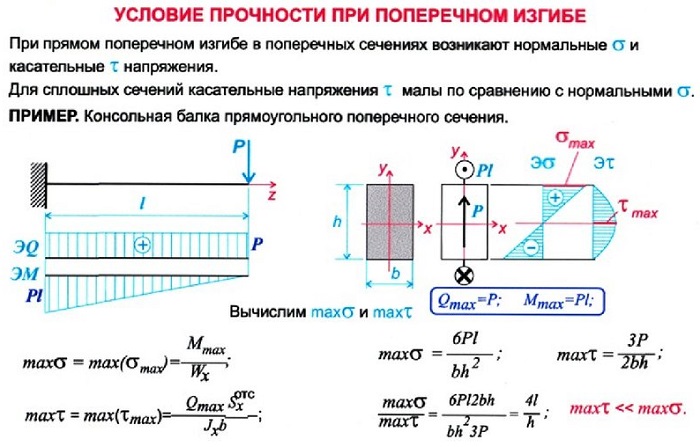
Осевой момент сопротивления при изгибе
Формула осевого момента сопротивления при изгибе выводится просто. Когда поперечное сечение балки симметрично относительно нейтральной оси, нормальные напряжения в наиболее удаленных точках (при 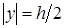
Геометрическую характеристику поперечного сечения балки, равную 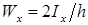
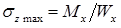
формула осевого момент сопротивления при изгибе для прямоугольного поперечного сечения: 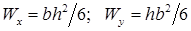
формула осевого момент сопротивления при изгибе для круглого поперечного сечения: 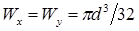
При строительстве деревянных домов, каркасных построек, деревянных надстроек над капитальными зданиями (мансарда, второй этаж) применяются почти всегда только деревянные балки перекрытий. Это связано как с необходимостью максимально близких физико-технических характеристик всех строительных материалов, так и с соображениями прочности – нет смысла на относительно легкие деревянные или каркасные стены монтировать тяжелые элементы перекрытий.
В современном строительстве используются деревянные балки трех видов:
- цельное или тесаное бревно – сравнительно редко, в основном при создании бревенчатых домов;
- цельный или срощенный брус – наиболее частый вариант, используется обычно именно цельный брус;
- клееные балки с сечением в виде прямоугольника, уголка, тавра или двутавра.
Соответственно, при расчете нагрузочной способности перекрытий, шага балок перекрытия и их сечения необходимо учитывать особенности выбранного материала и знать его характеристики.
Технические условия для деревянных балок перекрытия изложены в ГОСТ 4981-87. Этот документ предусматривает несколько видов балок:
- БЦ0 – балка из цельной древесины без черепных брусков;
- БЦ1 – то же, с одним черепным бруском;
- БЦ2 – то же с двумя черепными брусками;
- БК0 – балка из клееной древесины без черепных брусков;
- БК1 – то же, с одним черепным бруском;
- БК2 – то же с двумя черепными брусками.
Обратите внимание, что ГОСТ рассматривает балки из бруса с прямоугольным сечением, бревно-кругляк рассчитывается по отдельным нормативам.
По иллюстрациям хорошо видно – фактически ГОСТ рассматривает только балки с прямоугольным сечением, уголок и тавр, двутавр в документе не упоминается. Соответственно, и данные о размерах таких изделий, точнее, требования к размерам есть только для этих типов изделий (таблица 1).
Прочностные характеристики для расчетов берутся из СНиП II-25-80 для изделий из цельной древесины, ГОСТ 19414-90 для срощенного бруса и ГОСТ 20850-84 для клееного бруса.
Обычно принимают следующие расчетные сопротивления для древесины сортов 1…3 по таблице 2.
Если вместо хвойной древесины (сосна, ель) используются другие породы дерева, принимают данные из таблицы 3.
Площадь сечения, моменты инерции и сопротивления определяются по формулам из таблицы ниже (для квадратного и прямоугольного бруса).
Есть также уже готовый набор значений для типовых размеров бруса с квадратным сечением.
Таким образом, подставляя в стандартные расчетные формулы данные из таблиц 1…5, можно получить необходимые данные для деревянных балок с прямоугольным или квадратным профилем. Для более сложных сечений расчет вести сложнее, и если для балок типов БЦ и БК данные в ГОСТах есть, то для деревянного двутавра исходную информацию найти трудно – как минимум потому, что каждый производитель изготавливает двутавровые балки по собственным техническим условиям.
Фактически для расчета балки сложного сечения необходимо принимать формулы для вычисления момента инерции и сопротивления по таблице 7.
Полученные из таблиц данные используют для расчета прогиба балки (момент инерции) и для расчета несущей способности (момент сопротивления).
Таким образом, на основании приведенных данных и формул можно определить необходимую площадь сечения балки с простым или сложным профилем, а также ее прогиб. Если выбранное сечение удовлетворяет условиям прочности и обеспечивает прогиб менее допустимой величины, балка полностью подходит для строительства.
Расчет балки на прогиб нужно проводить практически для любой конструкции, чтобы проверить ее надежность и прочность. Под влиянием внешних, внутренних факторов, природных явлений балка подвержена деформации.
Балку сравнивают со стержнем, закрепленным на опорах. Чем больше опор, тем сложнее провести расчет самостоятельно. Основная нагрузка считается путем сложения сил, перпендикулярно направленных к сечению.
Данный расчет – основы сопромата, помогает определить наивысшую деформацию. Значения показателей должны входить в рамки допустимых величин.
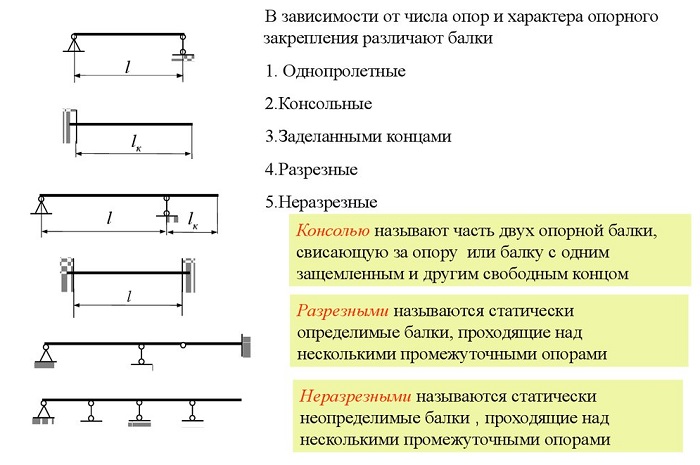
Виды балок
При возведении зданий используется балки разных конфигураций, размеров, профиля, характера сечения. Их изготавливают из металла и дерева. Для любого вида используемого материала нужен индивидуальный расчёт изгиба.
Виды балок:
-
Деревянные – их используют в основном при строительстве индивидуальных построек. Они применяются при возведении полов, потолков, несущих перекрытий. Дерево – капризный материал и подвержено деформации. Для определения максимального изгиба, существенны такие параметры: используемый профиль, размер, нагрузка, характер поперечного сечения.
-
Металлические – такие балки изготавливают из сплава металлов и сечение у них сложное. Поэтому особое внимание уделяется жесткости, а также прочности соединений. Балки из металла применяются в возведении многоэтажек, сооружений, требующих высокой прочности.
Прочность и жесткость балки
При проектировании следует учесть изгиб балок, чтобы конструкция была надежная, качественная, прочная и практичная.
На эти параметры влияют следующие факторы:
-
величина наружных нагрузок, их положение;
-
параметры, характер, нахождение поперечного сечения;
-
продольные величины;
-
материал;
-
число опор, метод их закрепления.
Выделяют 2 метода исчисления: простой – применяется увеличительный коэффициент, и точный – дополнительно включает пограничные подсчеты.
Построение эпюр балки
Эпюра распределения величины нагрузки на объект:
Расчет на жесткость
Алгоритм исчисления:
В формуле обозначены:
-
M – max момент, возникающий в брусе;
-
Wn,min – момент сопротивления сечения (табличный показатель);
-
Ry – сопротивление на изгиб (расчётный показатель);
-
γc – показатель условий труда (табличный показатель).
Такой расчет не трудоемок, но для более верного значения требуется следующее:
-
рабочий план объекта;
-
определение характеристик балки, характер сечения;
-
определение max нагрузки, воздействующей на брус;
-
оценка точки max прогиба;
-
проверка прочности max изгибающего момента.
Расчет моментов инерции и сопротивления сечения
Алгоритм исчисления:
Где:
-
J – момент инерции сечения;
-
W – момент сопротивления.
Для определения данных параметров необходимо учитывать сечение по грани разреза. Если момент инерции возрастает, величина жесткости также возрастает.
Нахождение максимальной нагрузки и прогиба
Формула для вычисления:
Здесь обозначены:
-
q – нагрузка равномерно-распределенная;
-
E – гибкость (табличный показатель);
-
l – длина;
-
I – момент инерции сечения.
Нагрузки учитываются статические и периодические.
Расчет на прогиб и его особенности
Он необходим для всех перекрытий при высоких эксплуатационных нагрузках.
При применении соответствующих коэффициентов, придерживаются следующего:
-
балка, держащаяся на одной жесткой и одной шарнирной опоре, подвергающаяся воздействию сосредоточенной нагрузки;
-
балка, держащаяся на жесткой и шарнирной опоре, подвергающаяся воздействию распределенной нагрузки;
-
нагрузка консольного типа;
-
воздействие комплексной нагрузки.
Пример расчет балки на прогиб
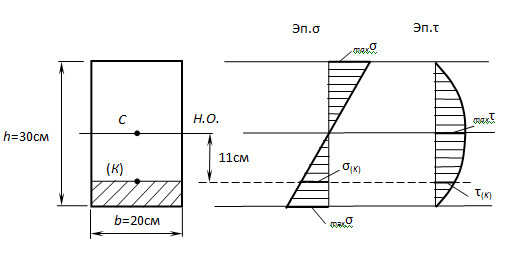
Рассмотрим задачу из курса сопромата.
Дано: балка четырехугольного сечения 20 на 30 см; поперечная сила Q = 19 кН; изгибающий момент М = 28 кНм.
Необходимо рассчитать напряжение: нормальное и в пределе К, отдаленной на 11 см от оси, узнать прочность бруса из дерева, при [σ] = 10 МПа, [τ] = 3 МПа.
Решение.
Чтобы узнать σ(К), τ(К), σmax, τmax
определяем значение осевого момента инерции общего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсеченного ряда и статического момента середины сечения Smax:
Из этого следует:
Определение прочности по нормальному напряжению:
Определение прочности по касательному напряжению:
Задача решена.
При проектировании конструкций важно соблюдать все физико-механические вычисления на прочность. Удобно и качественно произвести расчеты может онлайн, что существенно сократит временные сроки.
Калькулятор выполняет подробный подсчет на основе формул, эпюр усилий, подбирает номер сечения металлической балки из прокатных профильных, двутавровых материалов, а также из металлических труб.