В большинстве ЭМС
электродвигатель приводит в действие
производственный механизм через систему
передач, элементы которой могут
осуществлять как вращательные так и
поступательные движения, с момент
сопротивления приложенный к
производственному механизму.
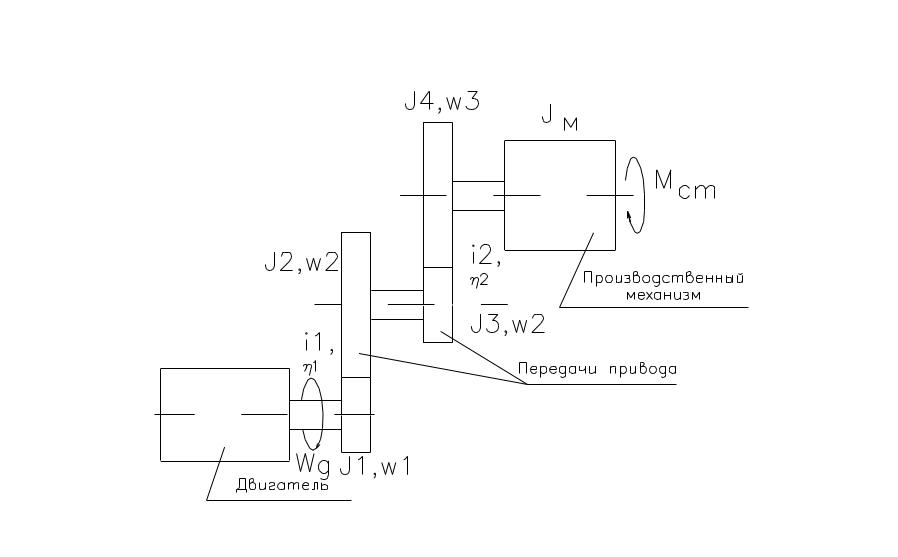
Рис.1
В процессе
приведения необходимо определить такой
момент Мс,
который приложен к валу двигателя
оказывает на систему такое же действие
как и момент Мсм,
приложенный к производственному
механизму этот момент и называется
приведенным.
Приведение моментов
сопротивления выполняется на основании
уравнения энергетического баланса:
мощность, передаваемая всем элементам
системы, с учетом КПД, остается неизменной.
![]()
,
где
![]()
–
КПД всего механизма
![]()
![]()
![]()
Приведение Сил сопротивления к валу электродвигателя.
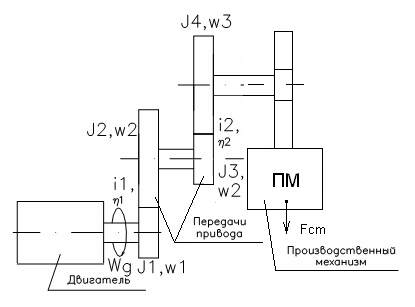
Рис. 2
![]()
![]()
Для приведения
вращательного движения в поступательное
уравнение записывается в виде:
![]()
![]()
Fc
– приведенная сила
Uд
– скорость выходного элемента двигателя
Приведение моментов инерции и масс к валу двигателя.
Привеление моментов
инерции к валу двигателя осуществляется
на том основании, что
![]()
запас
кинематической энергии, отнесенный к
одной оси, остается неизменным.
Ii
– момент инерции передач системы
Im
– момент инерции производственного
механизма
Целью приведения
является нахождении такого момента
инерции, который будучи соединенным с
валом двигателя, оказывает на системы
такое же действие как и различные
элементы системы вращающиеся с различной
скоростью.

– для поступательного
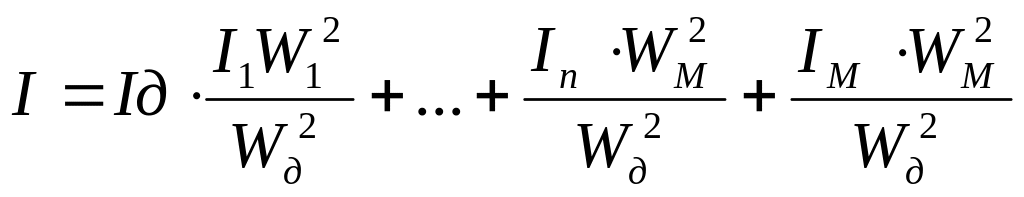
![]()
Если часть элементов
системы вращается с одинаковыми
скоростями, то эти элементы объедены в
группы. Так для рис.1 приведен момент
инерции
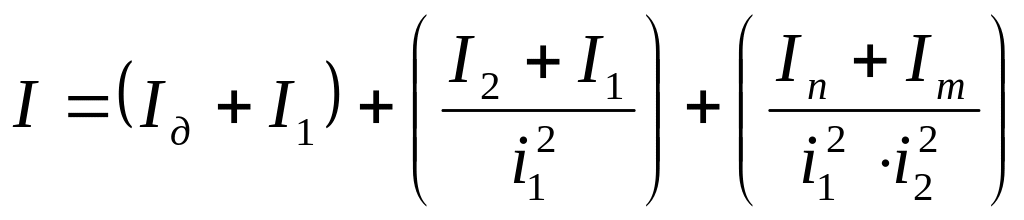
Если часть элементов
системы совершает поступательные
перемещения, то доп.
![]()
Если производственный
механизм совершает поступательный
перемещения, то
![]()
Если двигатель
совершает поступательные перемещения,
а производственный механизм вращается,
то находится приведенная масса
![]()
m
– приведенная масса
mg
– масса подвижных частей двигателя
5. Моделирование динамики разомкнутой системы
Динамика
электродвигателя постоянного тока
полностью описывается системой двух
уравнений, первое из которых является
основным уравнением двигателей
постоянного тока и описывает переходные
процессы в электрических цепях
электродвигателя, а второе уравнение
описывает механическую систему
электродвигателя и построено на основании
второго закона Ньютона для вращательного
движения.
![]()
(1)
![]()
(2)
где U- напряжение,
приложенное к якорной цепи; E-э.д.с.
двигателя;![]()
-активное сопротивление, ток и индуктивность
якорной цепи;
![]()
–
активный момент двигателя и момент
сопротивления, приведенный к валу
двигателя;
![]()
-круговая
частота вращения якоря двигателя, J
– момент инерции всех элементов системы,
приведенный к валу электродвигателя.
Э.д.с. двигателя
пропорциональна частоте вращения
,
(3)
где c![]()
–
конструктивный коэффициент двигателя,
Ф- магнитный поток возбуждения, n- частота
вращения в об/мин, c- коэффициент
пропорциональности.
Активный момент
двигателя пропорционален току якоря
![]()
, (4)
где
![]()
–
конструктивный коэффициент.
Коэффициент
пропорциональности c
может быть определен из формулы
![]()
![]()
где
![]()
-номинальная
круговая частота вращения,
![]()
–
частота вращения в об/мин,
![]()
–
номинальное напряжение ,
![]()
-номинальный
ток якоря.
Иногда в таблицах
справочных данных отсутствует одно из
значений
![]()
либо
![]()
,
тогда недостающую величину можно оценить
из следующих соображений:
![]()
;
![]()
;
![]()
;
![]()
.
Индуктивность
якорной цепи может быть приближенно
определена по формуле
![]()
где
![]()
–
коэффициент, равный 0,6 для двигателей
без компенсационной обмотки и равный
0,25 для двигателей с компенсационной
обмоткой, p- число пар полюсов двигателя.
Напишем
уравнения (1) и (2) таким образом, чтобы
производные тока и скорости находились
в левой части
![]()
;
![]()
или
![]()
;
![]()
.
Моделирование
динамики электродвигателя с приведенными
нагрузками осуществляется по алгоритму,
представленному на рис.2 , где n
– счетчик циклов, z
– количество циклов, через которое
осуществляется печать,
![]()
– предполагаемое время переходного
процесса.
Р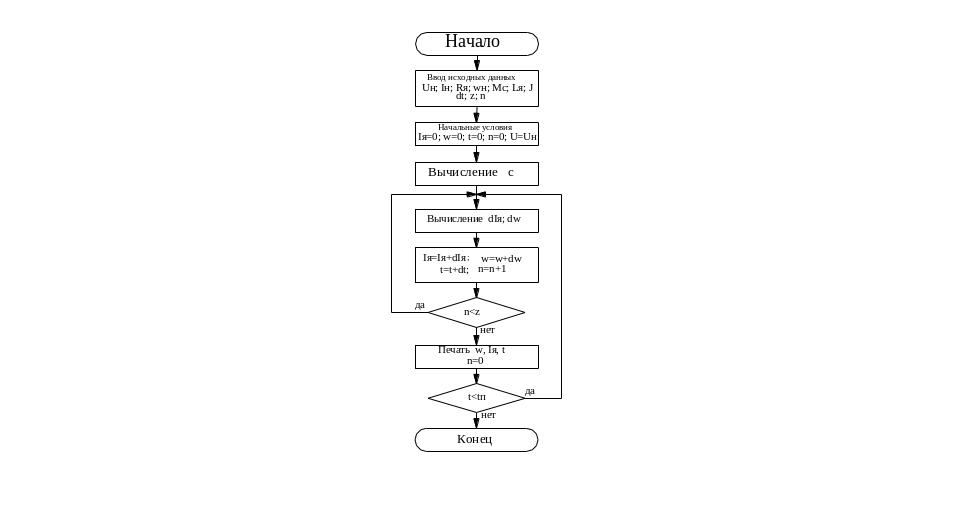
ис.2
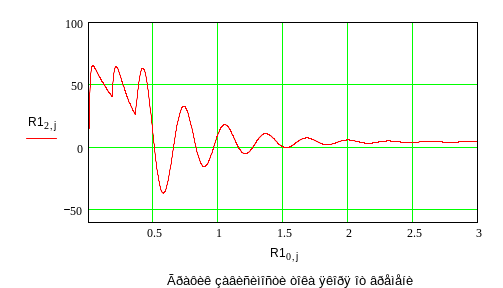
На основании
моделирования необходимо построить
две характеристики: механическую и
регулировочную.
Механическая
характеристика
![]()
строится по двум точкам при некоторых
значениях момента сопротивления.
Для построения
регулировочной характеристики
![]()
необходимо задать 6…8 значений напряжения
(влево и вправо от номинального значения)
и определить значения установившейся
частоты вращения.
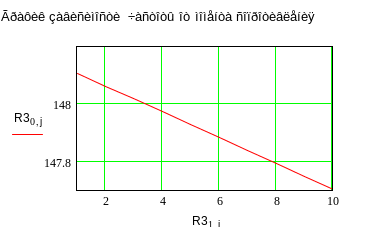
По регулировочной
характеристике определяют значения
минимальной
![]()
и максимальной
![]()
частот вращения и соответствующие им
напряжения
![]()
и
![]()
.


Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Приведение статических моментов сопротивления к валу электродвигателя
Процесс приведения будем рассматривать на примере кинематической схемы механизма подъема крана.
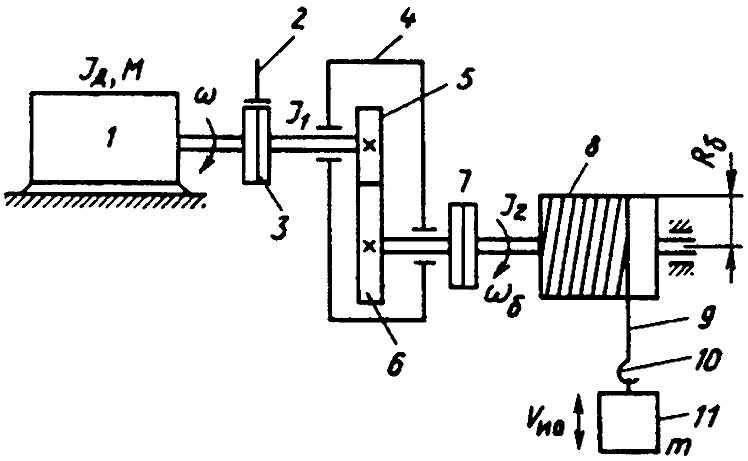
Кинематическая схема механизма подъема крана.
Для того чтобы перемещать груз с массой m со скоростью vио к нему должна быть приложена механическая мощность Pио, равная произведению усилия, развиваемого при подъеме и скорости.
Pио = Fио·vио = m·g·vио
Во всех частях электропривода существуют потери, которые учитываются с помощью КПД. В нашей кинематической схеме суммарный КПД равен произведению КПД барабана на КПД редуктора.
η = ηб·ηр
В соответствии с законом сохранения энергии, необходимый момент, развиваемый двигателем должен обеспечивать необходимую мощность для перемещения груза.
Mс·ω = m·g·vио / η
Поделив обе части уравнения на ω, получим:
Mс = (mg / η)·(vиоgρ / η)
Mс – момент сопротивления производственного механизма, приведен к валу двигателя от сил, совершающих поступательное движение.
vио/ω = ρ – радиус приведения.
Для того чтобы привести к валу двигателя моменты, действующие при вращательном движении рабочего органа, используем:
Mс·ω = Mио·ωб / η
Mс = Mио·(ωб / ω) / η
I = ω/ωб – передаточное число.
Mс = Mио / (η·i)
Чтобы привести к валу двигателя статические моменты, действующие в электродвигателе, не нужно знать тип передачи и количество ступеней передачи, а достаточно знать отношение скоростей на входе в привод и на его выходе – скорость вращения барабана.
Приведенный к валу двигателя статический момент исполнительного органа производственного механизма называется моментом сопротивления и обозначается Mс.
Определение приведенного момента инерции электропривода
В отличие от определения статического момента, для приведения динамического момента необходимо знать параметры механической передачи и тип передачи. Принцип приведения основан на том, что величина суммарного запаса кинетической энергии всех движущихся частей электропривода, приведенных к валу двигателя, остается неизменной.
J(ω2/2) = Jд(ω2/2) + J5(ω2/2) + J6(ωб2/2) + Jб(ωб2/2) + m(v2/2)
J(ω2/2) = (Jд + J5)(ω2/2) + (J6 + Jб)(ωб2/2) + m(v2/2)
Jд + J5 = J1
J6 + Jб = J2
J1 – момент инерции всех элементов привода, вращающихся со скоростью ω.
J2 – момент инерции всех частей привода, совершающих вращательное движение со скоростью ωб.
J(ω2/2) = J1(ω2/2) + J2(ωб2/2) + m(v2/2)
J = J1 + J2(ωб/ω)2 + m(v/ω)2
J = J1 + J2/i2 + mρ2
Для приведения суммарного момента инерции к валу двигателя нужно знать моменты инерции всех вращающихся элементов электрического привода и отношение скоростей между скоростью вращения двигателя и скоростью вращения элемента привода. Если они вращаются с разными скоростями, то момент инерции нужно разделить на передаточное число в квадрате, а момент инерции от массы всех частей электропривода, совершающих поступательное движение, для приведения умножить на квадрат радиуса приведения.
Момент – сопротивление – двигатель
Cтраница 1
Момент сопротивления двигателя в основном зависит от вязкости масла, трения деталей кривошипно-шатунного и распределительного механизмо В и степени сжатия. При понижении температуры вязкость масла сильно возрастает, а следовательно, увеличивается момент сопротивления, что понижает обороты коленчатого вала и затрудняет пуск двигателя. Момент сопротивления двигателя Мсопр зависит от рабочего объема цилиндров 1 / л, выражаемого в литрах, и составляет 3 – 4 5 кгм на 1 л рабочего объема.
[1]
Момент сопротивления двигателя изменяется в широких пределах и имеет резко-переменный характер.
[3]
Момент сопротивления двигателя снижают применением зимних марок моторных масел и подогревом двигателя, а повышение пусковых качеств батареи – хранением ее в теплом помещении в период стоянки автомобиля на улице при низких температурах.
[4]
При этих условиях моменты сопротивления двигателя и механизма будут равны и агрегат будет работать с постоянной скоростью при скольжении SH.
[5]
Часто при расчетах моментами сопротивления двигателя и редуктора пренебрегают и учитывают только приведенный момент рабочего механизма. Как правило, нагрузочный момент является случайной величиной. Точное его определение возможно лишь при статистической обработке результатов измерений на реальном объекте.
[7]
С и ниже) момент сопротивления двигателя возрастает настолько, что стартер уже не обеспечивает запуска. Одним увеличением мощности стартера разрешить проблему зимнего запуска нельзя, так как из-за крутого протекания кривых Мдв f ( n), где п – число оборотов коленчатого вала, значительное увеличение мощности стартера дает малый эффект; кроме того, принудительное вращение коленчатого вала при застывшем масле ( например, заводка буксиром) можег вызвать поломку валика масляного насоса и повредить другие детали.
[8]
Для пуска необходимо, чтобы момент сопротивления двигателя был меньше крутящего момента, создаваемого давлением газов на поршни при первых вспышках. Между тем, прц понижении температуры вязкость масла, а следовательно и момент сопротивления, возрастают и пуск двигателя затрудняется. Поэтому существует некоторое предельное значение вязкости масла, при котором пуск еще возможен. Величина момента сопротивления двигателя при этой предельной вязкости масла и является расчетным моментом сопротивления при определении мощности стартера.
[9]
Характеристики стартера ( а) и диаграмма работы стартера на двигателе ( б): MQS – момент сопротивления двигателя; М – вращающий момент стартера, приведенный к валу ДВС.
[10]
Как изменяются основные параметры стартера ( сила тока, момент, частота вращения, мощность, напряжение) при увеличении момента сопротивления двигателя пуску.
[11]
Мд – момент вращения двигателя; Jn, Mcn – моменты инерции и сопротивления в расчетном интервале Аап, приведенные к оси двигателя и включающие инерцию и момент сопротивления двигателя.
[13]
Для того чтобы двигатель начал работать самостоятельно, стартер должен сообщить его коленчатому валу определенную начальную ( пусковую) частоту вращения. При этом стартер должен преодолевать момент сопротивления двигателя, являющийся суммой нескольких составляющих.
[14]
Одним из источников периодических возмущений является резко переменная нагрузка на некоторых промышленных предприятиях; в частности, такую нагрузку несут двигатели прокатных станов. Для введения в расчет резко переменной нагрузки используется соответствующая многоэлементная модель, моменты сопротивления двигателей задаются как функции времени.
[15]
Страницы:
1
2
