Как найти момент трения маятника обербека

Определение момента сил трения в подшипнике маятника Обербека

Постановка
задачи.
На шкив маятника Обербека радиусом r
намотана нить, к концу которой привязан
груз массой m₁.
Груз опускается с высоты h.
Определить момент сил трения в подшипнике
маятника Обербека при его вращении,
если известны время ₁
движения груза m₁,
момент инерции маятника Обербека I₁;
после изменения момента инерции до
величины I₂
время движения груза m₁
оказывается равным ₂.
Изменение момента инерции маятника
Обербека производится перемещением
грузов равной массы m
вдоль стержней установки (рис. 9.1).

Указания
к решению. Момент
инерции маятника с грузами равен
I=I₀+I_гр,
где I₀–
момент инерции маятника без грузов:
I_гр–
момент инерции грузов, закрепленных на
стержнях. Считаем, что размеры грузов
массой m
малы по сравнению с их расстоянием до
оси вращения (грузы считаем “точечными”),
тогда

I=I₀+4mR².
(9.17)

Здесь
R
– расстояние от центров масс грузов до
оси вращения. Изменяя положение грузов
на стержнях, можно изменить момент
инерции маятника Обербека

.
(9.18)

Запишем
уравнения (9.1) и (9.2) для двух опытов, в
которых моменты инерции маятника
Обербека равны I₁
и I₂,
а время движения груза m₁
равно ₁
и ₂
соответственно. При этом получим систему
уравнений

I₁₁=T₁r–M_тр,

m₁a₁=m₁g–T₁,

I₂₂=T₂r-M_тр,
(9.19)

m₁a₂=m₁g-T₂.

Эта
система дополняется кинетическими
уравнениями движения груза m₁:

,
(9.20)

причем
a₁=₁r,
a₂=₂r.

Решая
систему уравнений (9.19), (9.20) с учетом
соотношения (9.18), определим момент сил
трения в подшипнике:

.
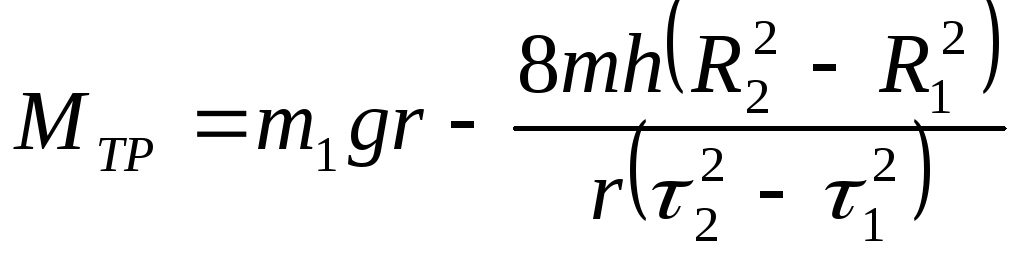(9.21)

Определение отношения моментов сил, действующих на маятник Обербека при его движении, для случаев, когда нить намотана на шкивы радиусами r1 и r2

Постановка
задачи. На
шкив маятника Обербека радиусом r₁
намотана нить, к концу которого привязан
груз массой m₁.
Груз опускается с высоты h
за время ₁.
Момент инерции маятника Обербека I,
масса груза m₁
известны, время движения груза ₁
измеряется в опыте. Аналогичные измерения
производятся для случая, когда нить
намотана на шкив радиусом r₂.

Указания
к решению.
Момент инерции маятника с заданными
расстояниями грузов m
до оси вращения определяем из (9.17).
Используя (9.1), (9.2) и (9.3), а также соотношения
между линейным ускорением груза а
и угловым ускорением маятника Обербека
а=r,
находим

.
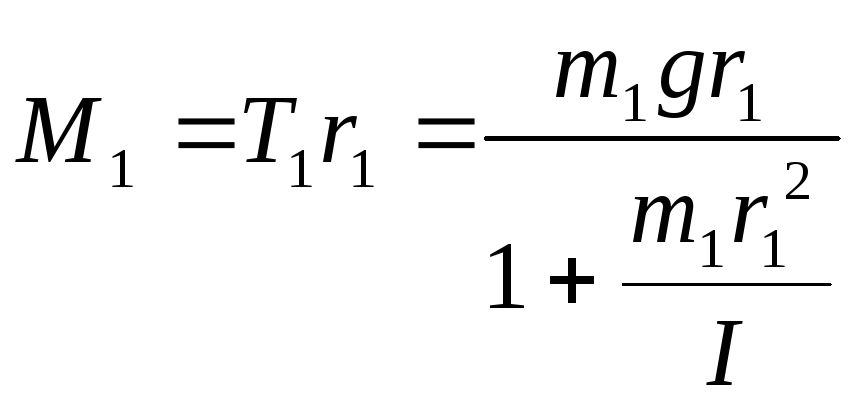(9.22)

Аналогично
для радиуса шкива r₂:

.
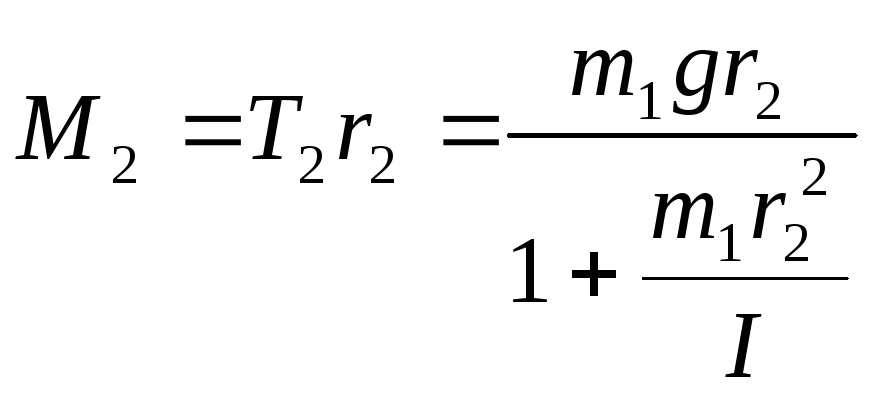(9.23)

Из
(9.22) и (9.23) получаем

.
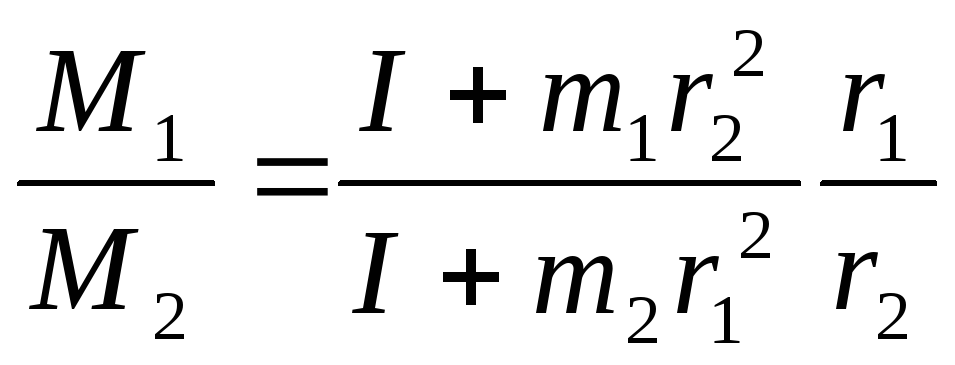(2.24)

Это
теоретическое соотношение проверяем
экспериментально: из (9.2) и (9.3) получаем

.

Отсюда

.
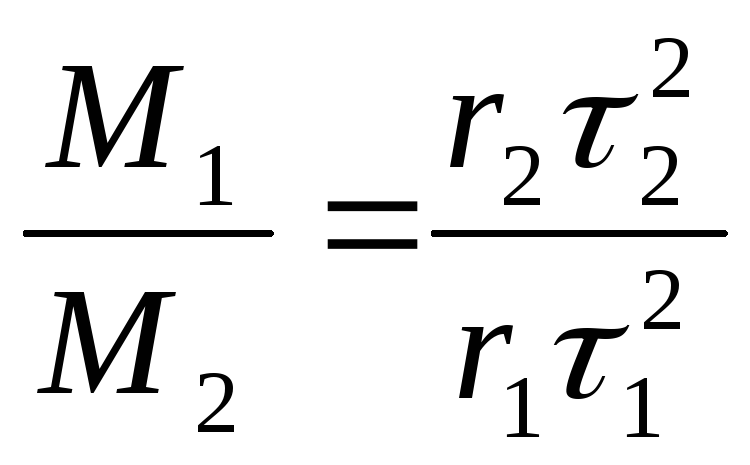(9.25)

Проверка формулы для периода колебаний физического маятника на установке “Маятник Обербека”

Постановка
задачи. Маятника
Обербека (как это показывает его название)
дает возможность исследовать колебания
массивного тела относительно неподвижной
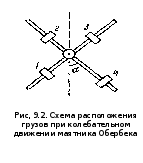
горизонтальной оси. Сместим один из
грузов m
дальше от оси вращения (рис.9.2). Тогда
маятник, отклоненный от положения
равновесия, будет совершать колебания.
Определяя период колебания с помощью
секундомера, можно проверить формулу
для периода колебаний физического
маятника.

Указания к
решению. Запишем уравнение вращательного
движения для маятника Обербека (рис.9.2).
Если маятник отклонить от положения
равновесия на малый угол
(sin),то

.
(9.26)

Здесь
M_jz–
алгебраическое значение момента силы
тяжести, действующего на систему со
стороны груза m_j.
Для j=1,2,3
значения R₁=R₂=R₃=R,
для j=4
имеем R₄>R.
Согласно принятому правилу, положительными
считаем моменты сил, вращающих тел
против часовой стрелки. Отсюда

I=M₁+M₂–M₃–M₄.

Учитывая,
что
,
получим

I=M₂–M₄.
(9.27)

Подставляя
в (9.27) значения

I=I₀+3mR²+mR₄²;

;

=
mgR₂
sin

mgR ;

=
mgR₄
sin

mgR₄
;

получим
дифференциальное уравнение малых
колебаний маятника Обербека

.

Вводя
общепринятое уравнение

,
(9.28)

где
₀-циклическая
частота колебаний

,
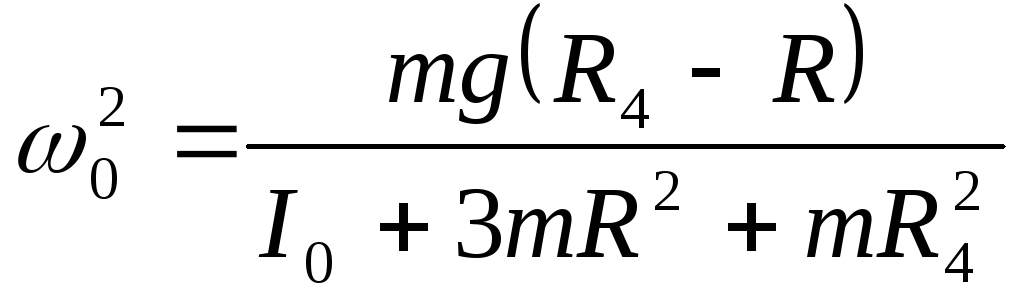(9.29)

убедимся
подстановкой, что решение уравнения
(9.28) имеет вид

.

Здесь
₀–максимальный
угол отклонения; ₀–
начальная фаза колебаний. Из условия
периодичности для функции cos(₀t+)
находим период колебаний физического
маятника

.
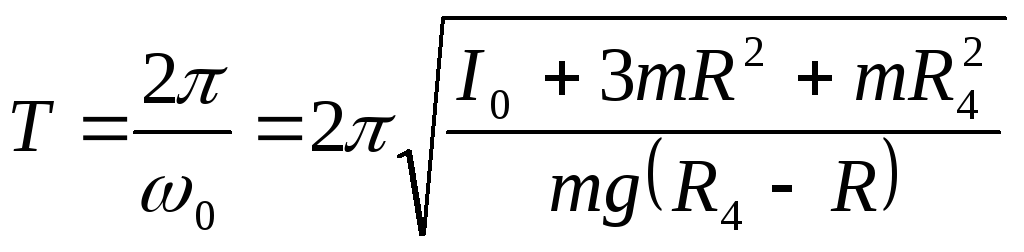(9.30)

Полученный
результат сравнивается с экспериментальным

.

Здесь

– время десяти полных колебаний маятника
Обербека.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Маятник Обербека состоит из шкива и стержней, укрепленных на одной неподвижной
горизонтальной оси, проходящей через центр симметрии системы. Относительно этой оси маятник может вращаться. На стержни насажены одинаковые
по массе грузы , которые
могут перемещаться и закрепляться в нужном положении. Передвижение грузов приводит к изменению момента инерции маятника. К шкиву
крепится гибкая нить, к свободному концу которой подвешивается груз массой . При поступательном движении груза момент силы натяжения приводит маятник во вращение.

I. Теоретическое введение.

Основной закон динамики твердого тела, вращающегося вокруг неподвижной оси, имеет вид:

(1),

где – алгебраическая сумма моментов сил, действующих на тело относительно оси вращения,

– момент инерции тела относительно той же оси,

– угловое ускорение.

Маятник Обербека вращается под действием момента силы натяжения нити (–сила натяжения,
– плечо этой силы, равное
радиусу шкива) и моменты силы трения .

Момент инерции маятника равен ,где – момент инерции системы без грузов (для
каждого маятника известен), – расстояние от
центра тяжести грузов до
оси вращения,
– число грузов , равное 3 или 4.

Уравнение (1) перепишем в виде:

(2)

Груз под действием силы натяжения нити и силы тяжести поступательного движения вниз. Пренебрегая растяжением нити, запишем II закон Ньютона в проекции на ось OY:

,

отсюда

(3)

Ускорение можно
найти из опыта. Нить наматывается на шкив, грузу предоставляется
возможность из состояния покоя пройти
расстояние , равное длине
нити. Одновременно измеряется время движения
груза. Из формулы кинематики рассчитывается ускорение:

(4)

Если нить перемещается по шкиву без проскальзывания, то тангенциальное ускорение
точек на поверхности шкива совпадает с ускорением .

Поэтому угловое ускорение маятника равно

(5)

Момент силы трения определим из закона сохранения энергии

Груз опускается
до нижней точки и затем поднимается на меньшую
высоту .
Убыль потенциальной энергии равна работе силы трения.

(6),

где –
изменение угла поворота шкива.

Перепишем (6):

, отсюда .

Обозначим

(7)

Тогда

(8)

Подставив (3), (5), (8) в (2), получим

(9),

II. Приложение.

Динамика вращательного движения

Краткие теоретические сведения

1. Момент инерции материальной точки

,

где – масса точки;

– расстояние до
оси вращения.

2. Моменты инерции тел правильной
   геометрической формы относительно оси,
   проходящей через центр:

В таблице –
радиус тел, – длина
стержня (ось перпендикулярна стержню)

3. Теорема Штейнера

Момент инерции тела относительно
произвольной оси равен

, где

– момент инерции
этого тела относительно оси, проходящей через
центр тяжести тела параллельно заданной оси;

– расстояние
между осями;

– масса тела.

4. Кинетическая энергия тела, вращающегося
   вокруг неподвижной оси:

, где

– момент инерции;

– угловая
скорость.

5. Момент силы, действующей в плоскости,
   перпендикулярной оси вращения

, где

– сила,

– плечо силы
(кратчайшее расстояние от оси вращения до линии
действия силы).

6. Момент импульса твердого тела

.

III. Практическая часть.

Порядок выполнения работы.
Выберите груз . Установите грузы на маятнике в
одно из двух возможных положений. Проведите
эксперимент, замерив при этом время опускания
груза и
расстояние недохода груза до первоначального
положения. Результаты занесите в протокол
испытаний и рассчитайте остальные величины.
Изменяя положение грузов и массу груза проведите
остальные опыты

Внимание!!! Перед выполнением работы посмотрите указания по выполнению лабораторных работ.

Для измерения времени опускания груза применяется секундомер.

Назначение кнопок секундомера показано на рисунке.

Часто задаваемые вопросы.

1. Как выбрать груз ? Для того чтобы выбрать груз
надо навести указатель мыши на него и нажать
левую кнопку мыши.

2. Как изменить положение грузов на маятнике Положение грузов на маятнике меняется путем нажатия левой кнопки мыши на маятнике.

Изучение законов движения на маятнике Обербека

Изучение законов движения на маятнике Обербека

Цель работы: Изучение динамики вращательного движения, оценка влияния трения на точность результатов проведенных измерений.

Оборудование: лабораторная установка (маятник Обербека), набор грузиков, линейка.

Теоретическое введение

Маятник Обербека представляет собой крестовину, состоящую из 4 стержней, прикрепленных ко втулке с осью (см. рис.1).

На стержни надеваются одинаковые грузы массой m1, которые могут быть закреплены на различных расстояниях от оси вращения. Два легких шкива с различными радиусами r1, и r2, насажены на ось вращения маятника. На один из шкивов наматывается нить, к свободному концу которой прикрепляется груз массой m. Под действием груза нить разматывается и приводит маятник в равноускоренное вращательное движение. Положение груза m отмечается по шкале с делениями. Вся эта система может свободно вращаться вокруг горизонтальной оси. Момент инерции системы можно менять, передвигая грузы m1 вдоль стержней.

Вращение твердого тела постоянной массы вокруг неподвижной оси описывается уравнением моментов:

(1)

Здесь М – момент сил, действующих на тело, I – момент инерции тела, ω — угловая скорость.

Уравнение (1) является прямым следствием второго закона Ньютона, поэтому экспериментальная проверка его является в то же время проверкой основных положений механики. Проверку основного закона динамики для вращающихся тел можно осуществить следующим образом. Оставляя неизменным момент инерции вращающейся части установки (I = const), будем изменять вращающий момент М (изменяя вес груза m). Угловое ускорение при этом будет прямо пропорционально М [см. формулу (1)]. Если же оставить постоянным вращающий момент (M = const) и изменять момент инерции вращающейся системы путем передвижения грузов m1 по стержням крестовины, то угловое ускорение должно быть обратно пропорционально моменту инерции системы. В данной работе для проверки основного закона динамики применены оба указанных метода. Момент сил создается грузом m, привязанным к нити, которая навита на один из шкивов. Если момент сил трения Мтр приложенный к оси маятника, мал по сравнению с моментом М силы натяжения нити (см. рис. 1), то проверка уравнения (1) не представляет труда. Действительно, измеряя время t, в течение которого груз m из состояния покоя опустится на расстояние h, можно легко найти ускорения груза:

(2)

которое связано с угловым ускорением dω/dt соотношением:

(3)

где r – радиус шкива. Если через Т обозначить силу натяжения нити, то

(4)

Силу Т моно найти из уравнения движения груза:

(5)

Легко видеть, что система записанных выше уравнений (1)-(5) полностью решает поставленную задачу. Момент сил трения Мтр обычно оказывается довольно велик и способен существенно исказить результаты опыта.

Уменьшить относительную роль момента сил трения при данной конфигурации установки можно было бы увеличивая массу m. Однако здесь приходится принимать во внимание два обстоятельства:

Увеличение массы m ведет к увеличению давления маятника на ось, что свою очередь вызывает возрастание сил трения. С увеличением m уменьшается время падения t и снижается точность измерения времени.

В дальнейшем вместо (1) мы будем пользоваться более точным уравнением:

(6)

С использованием формул (2)-(6) получаем выражение для момента инерции маятника:

(7)

ВЫПОЛНЕНИЕ РАБОТЫ: В данной работе проводится доказательство того положения, что при постоянном моменте сил, действующем на вращающееся тело, угловое ускорение его dω/dt обратно пропорционально моменту инерции тела I.

ПРИНАДЛЕЖНОСТИ: Маятник Обербека, набор разновесов, секундомер, масштабная линейка, штангенциркуль.

ОПИСАНИЕ ПРИБОРА: Маятник Обербека схематически изображен на рис.1. Основные параметры прибора следующие: радиус шкива г1 = 9,0 мм, радиус шкива r = 17,1 мм, масса одного из стержней крестовины mст = 94 г, длина одного из стержней крестовины lст = 46 см, масса груза m1 = 142 г, высота груза m1 Н = 2,5 см, внешний радиус груза m1 ρ = 1,6 см, вес чашечки Pчаш = (25,75±0,05) г.

В каждом случае установки грузов m на одном из расстояний R от оси маятника необходимо проверять, находятся ли маятник в безразличном равновесии. Прежде, чем начинать эксперимент, рекомендуется несколько раз привести маятник во вращение, каждый раз давая ему возможность остановиться. На основании этого сделайте вывод о том, находится ли маятник в безразличном равновесии. Увеличивая нагрузку на нить путем добавления на чашечку различных грузов из набора разновесов, найдите минимальное значение массы m0, при котором маятник начинает вращаться. Оцените величину момента сил трения как произведения m, на радиус шкива. Установите грузы m1 в ближнее к оси положение. Положите на чашечку некоторый груз m>m0. С помощью секундомера измерьте время падения груза с заданной высоты h до касания с полом. Повторите опыт не менее пяти раз. Старайтесь при этом выдерживать определенную высоту h и измерять время падения t как можно точнее. Измерьте расстояние R от оси вращения до центра груза m. Результаты измерений занесите в таблицу.

Уравнение поступательного движения для грузов маятника обербека

Справедливость основного уравнения динамики вращательного движения можно проверить на маятнике Обербека, схема которого изображена на рисунке 2.3.

Маятник Обербека состоит из четырех стержней 1, укрепленных на втулке под прямым углом друг к другу. На стержнях закрепляются грузы 2, которые могут быть закреплены на разных расстояниях R от оси вращения. На ось насажен диск 3 радиусом r. Гиря 4, приводящая маятник во вращение, прикреплена к концу нити, которая перекинута через блок 5 и наматывается на диск 3. На основную гирю 4 могут надеваться от одного до четырех дополнительных грузов 6.

Вращение маятника происходит под действием момента М силы натяжения нити и противоположно направленного момента сил трения М_тр. Таким образом, согласно равенству (2.6) уравнение движения маятника имеет вид

(2.7)

. (2.8)

Из равенства (2.8) видно, что если сила трения постоянна (не зависит от скорости), то зависимость величины М от ε является линейной функцией вида . При этом J играет роль углового коэффициента k. Таким образом, экспериментальное исследование взаимосвязи между моментом силы натяжения М и угловым ускорением ε позволяет найти момент инерции маятника J.

Движение гири 4 происходит под действием силы тяжести (где m – масса гири) и силы натяжения нити F. Согласно второму закону Ньютона, уравнение движения гири имеет вид

, (2.9)

где а – ускорение гири, которое можно найти зная время t ее опускания и пройденный путь h. Используя известное уравнение равноускоренного движения, имеем

. (2.10)

Из равенств (2.9) и (2.10) получаем выражение для определения момента сила натяжения

. (2.11)

Учитывая соотношение , связывающее угловое и линейное ускорения для точек окружности диска, из формулы (2.10) находим

. (2.12)

Формулы (2.11) и (2.12) позволяют найти по экспериментальным данным момент силы натяжения М и угловое ускорение ε. Тогда, проведя опыты с гирями различной массы m, можно исследовать зависимость М от ε и построить соответствующий график.

Таким образом, определение момента инерции маятника сводится к определению углового коэффициента найденной из опыта функции коэффициента М (ε), а определение момента силы трения М_тр – к экстраполяции найденной зависимости на ε = 0.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: “Что-то тут концом пахнет”. 8526 – | 8113 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Изучение законов движения на маятнике Обербека

Цель работы: Изучение динамики вращательного движения, оценка влияния трения на точность результатов проведенных измерений.

Оборудование: лабораторная установка (маятник Обербека), набор грузиков, линейка.

Теоретическое введение

Маятник Обербека представляет собой крестовину, состоящую из 4 стержней, прикрепленных ко втулке с осью (см. рис.1).

На стержни надеваются одинаковые грузы массой m1, которые могут быть закреплены на различных расстояниях от оси вращения. Два легких шкива с различными радиусами r1, и r2, насажены на ось вращения маятника. На один из шкивов наматывается нить, к свободному концу которой прикрепляется груз массой m. Под действием груза нить разматывается и приводит маятник в равноускоренное вращательное движение. Положение груза m отмечается по шкале с делениями. Вся эта система может свободно вращаться вокруг горизонтальной оси. Момент инерции системы можно менять, передвигая грузы m1 вдоль стержней.

Вращение твердого тела постоянной массы вокруг неподвижной оси описывается уравнением моментов:

(1)

Здесь М – момент сил, действующих на тело, I – момент инерции тела, ω — угловая скорость.

Уравнение (1) является прямым следствием второго закона Ньютона, поэтому экспериментальная проверка его является в то же время проверкой основных положений механики. Проверку основного закона динамики для вращающихся тел можно осуществить следующим образом. Оставляя неизменным момент инерции вращающейся части установки (I = const), будем изменять вращающий момент М (изменяя вес груза m). Угловое ускорение при этом будет прямо пропорционально М [см. формулу (1)]. Если же оставить постоянным вращающий момент (M = const) и изменять момент инерции вращающейся системы путем передвижения грузов m1 по стержням крестовины, то угловое ускорение должно быть обратно пропорционально моменту инерции системы. В данной работе для проверки основного закона динамики применены оба указанных метода. Момент сил создается грузом m, привязанным к нити, которая навита на один из шкивов. Если момент сил трения Мтр приложенный к оси маятника, мал по сравнению с моментом М силы натяжения нити (см. рис. 1), то проверка уравнения (1) не представляет труда. Действительно, измеряя время t, в течение которого груз m из состояния покоя опустится на расстояние h, можно легко найти ускорения груза:

(2)

которое связано с угловым ускорением dω/dt соотношением:

(3)

где r – радиус шкива. Если через Т обозначить силу натяжения нити, то

(4)

Силу Т моно найти из уравнения движения груза:

(5)

Легко видеть, что система записанных выше уравнений (1)-(5) полностью решает поставленную задачу. Момент сил трения Мтр обычно оказывается довольно велик и способен существенно исказить результаты опыта.

Уменьшить относительную роль момента сил трения при данной конфигурации установки можно было бы увеличивая массу m. Однако здесь приходится принимать во внимание два обстоятельства:

Увеличение массы m ведет к увеличению давления маятника на ось, что свою очередь вызывает возрастание сил трения. С увеличением m уменьшается время падения t и снижается точность измерения времени.

В дальнейшем вместо (1) мы будем пользоваться более точным уравнением:

(6)

С использованием формул (2)-(6) получаем выражение для момента инерции маятника:

(7)

ВЫПОЛНЕНИЕ РАБОТЫ: В данной работе проводится доказательство того положения, что при постоянном моменте сил, действующем на вращающееся тело, угловое ускорение его dω/dt обратно пропорционально моменту инерции тела I.

ПРИНАДЛЕЖНОСТИ: Маятник Обербека, набор разновесов, секундомер, масштабная линейка, штангенциркуль.

ОПИСАНИЕ ПРИБОРА: Маятник Обербека схематически изображен на рис.1. Основные параметры прибора следующие: радиус шкива г1 = 9,0 мм, радиус шкива r = 17,1 мм, масса одного из стержней крестовины mст = 94 г, длина одного из стержней крестовины lст = 46 см, масса груза m1 = 142 г, высота груза m1 Н = 2,5 см, внешний радиус груза m1 ρ = 1,6 см, вес чашечки Pчаш = (25,75±0,05) г.

В каждом случае установки грузов m на одном из расстояний R от оси маятника необходимо проверять, находятся ли маятник в безразличном равновесии. Прежде, чем начинать эксперимент, рекомендуется несколько раз привести маятник во вращение, каждый раз давая ему возможность остановиться. На основании этого сделайте вывод о том, находится ли маятник в безразличном равновесии. Увеличивая нагрузку на нить путем добавления на чашечку различных грузов из набора разновесов, найдите минимальное значение массы m0, при котором маятник начинает вращаться. Оцените величину момента сил трения как произведения m, на радиус шкива. Установите грузы m1 в ближнее к оси положение. Положите на чашечку некоторый груз m>m0. С помощью секундомера измерьте время падения груза с заданной высоты h до касания с полом. Повторите опыт не менее пяти раз. Старайтесь при этом выдерживать определенную высоту h и измерять время падения t как можно точнее. Измерьте расстояние R от оси вращения до центра груза m. Результаты измерений занесите в таблицу.

Лабораторная работа №4

Изучение законов вращательного движения при помощи маятника Обербека.

Выполнил: Курдюков Е.А.

Проверил: Пшеницин В. И.

1. Цель работы: анализ основного уравнения вращательного движения.

2. Основные понятия и закономерности:

Основное уравнение вращательного движения тела относительно неподвижной оси вращения имеет вид:

Где М – сумма проекций на ось вращения моментов всех внешних сил, действующих на тело, ω – его угловая скорость, J – момент инерции тела относительно данной оси. Для однородного твердого тела момент инерции представляет собой постоянную величину. Поэтому уравнение можно записать в виде:

Момент инерции J играет во вращательном движении ту же роль, что и масса m тела в его поступательном движении, момент инерции отражает инертность тела в его вращательном движении. Чем больше J тем труднее заставить вращающееся тело изменить угловую скорость ω.

3. Идея метода измерений и суть предлагаемой методики:

Основное уравнение вращательного движения удобно исследовать с помощью маятника Обербека.

На нити подвешивается груз массы m, натягивающий нить. Если натяжение нити равно Т, то момент сил, действующий на маятник, равен:

Величина Т определяется следующим образом. При вращении маятника, груз начинает опускаться с ускорением а. Уравнение движения опускающегося груза выглядит следующим образом:

Соответственно, момент внешних сил, приложенных к маятнику, равен:

Ускорение а можно вычислить, измерив время τ падения груза с известной высоты h. Падение груза является равноускоренным, поэтому для движения груза справедливо уравнение:

4. Таблицы экспериментальных данных и результаты расчетов.

h	R	m	T	a	ε	M
100		54,2	8.4	0.028	0.93	0.015
100		100.2	5.7	0.061	2.03	0.03
100		146.2	4.5	0.098	3.26	0.04
100		54,2	21.3	0.004	0.25	0.008
100		100.2	11.5	0.015	0.93	0.015
100		146.2	8.9	0.025	1.56	0.02

Расчет плотности материала в СИ:

Вопросы к лабораторной работе:

1.Сформулируйте основной закон динамики вращательного движения.

Ответ: произведение момента инерции тела на его угловое ускорение равно суммарному моменту внешних сил, действующих на тело. Моменты сил и инерции берутся относительно оси, вокруг которой происходит вращение.

2.дайте определение момента силы, приложенной к телу и момента импульса вращающегося тела. Как направлены векторы этих величин по отношению к оси вращения тела?

Ответ: момент силы – векторная физическая величина, равная произведению радиус-вектора проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения.

Лабораторные работы по физике

ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА

Цель работы: 1) изучение кинематических и динамических характеристик вращательного движения;

2) экспериментальное определение момента инерции крестовины маятника Обербека и момента сил трения;

3) проверка справедливости закона сохранения (превращения) энергии механической системы.

Схема экспериментальной установки

1 – ось вращения;

Основным элементом маятника Обербека (рис. 1) является крестовина, способная свободно вращаться вокруг неподвижной горизонтальной оси 1. Крестовина состоит из четырех стержней 2 с грузами-насадками 3, расположенными симметрично относительно оси вращения. С крестовиной жестко скреплен шкив 4 радиусом R. На шкив намотана нить 5, перекинутая через легкий блок 6. К свободному концу нити привязан груз 7, массу которого m можно изменять в процессе опытов. Для измерения высоты h расположения груза над полом служит линейка 8, а для измерения времени его падения – секундомер 9.

Если поднятый на высоту h груз отпустить, то он начнет падать с ускорением , которое определяется вторым законом Ньютона. На груз действуют две силы: сила тяжести и сила натяжения нити (сопротивлением воздуха в данном случае можно пренебречь). Уравнение основного закона динамики:

в проекциях на направление движения груза имеет вид:

Пренебрегая массами нити 5 и блока 6, можно считать, что нить действует на поверхность шкива касательной силой , равной по модулю силе : | | = | | = Fн . Касательная сила создает вращающий момент , по модулю равный произведению модуля силы на ее плечо, т.е. на радиус шкива R: Мн = Fн R. С учетом (1) вращающий момент силы натяжения нити равен

Под действием момента крестовина начинает вращаться с угловым ускорением . При этом на оси вращения возникают, хотя и незначительные, силы трения. Эти силы создают тормозящий момент , направленный противоположно угловому ускорению. С учетом направления моментов сил натяжения и трения алгебраическая запись уравнения основного закона динамики вращательного движения имеет вид

J e = Мн – Мтр , (3)

где J – момент инерции крестовины маятника Обербека относительно оси вращения.

Известно, что момент инерции зависит только от распределения массы тела относительно оси. Для крестовины маятника величина J определяется в основном положением грузов-насадок 3 на стержнях 2. Если их положение в ходе опытов не изменяется, то и момент инерции остается постоянным. Момент сил трения также можно считать практически неизменным. Поэтому зависимость углового ускорения e от момента силы натяжения Мн , согласно уравнению (3), имеет линейный характер. Определив опытным путем значения e при различных Мн и обработав соответствующим образом полученную экспериментальную зависимость e (Мн), с помощью этого уравнения можно найти неизвестные величины J и Мтр . Рассмотрим теперь методику измерения углового ускорения e и момента силы натяжения Мн .

Так как нить 5 практически нерастяжима, все ее точки, включая точки на поверхности шкива, движутся с одинаковым ускорением , равным по модулю ускорению падающего груза : | | = | | = a. Груз падает с высоты h равноускоренно; при этом за время t он проходит путь

Измерив высоту h и время падения груза t, можем найти ускорение

Если известны масса груза т и радиус шкива R, то по формуле (2) можно рассчитать момент силы натяжения нити Мн .

Угловое ускорение вращения шкива, а следовательно, и крестовины и тангенциальное (касательное) ускорение точек на поверхности шкива связаны известным соотношением

Таким образом, зная массу груза т, радиус шкива R и высоту h, с которой падает груз, а также измерив время его падения t, можно экспериментально определить величины e и Мн .

Рассмотрим теперь превращение энергии в вышеописанном опыте. Поднятый на высоту h груз обладает потенциальной энергией

кинетическая энергия системы «груз + крестовина» при этом равна нулю. В момент падения груза на пол его потенциальная энергия обращается в ноль, но за счет ее уменьшения груз приобретает кинетическую энергию

а крестовина – кинетическую энергию вращения

где v – скорость груза в момент падения; w – угловая скорость вращения крестовины к этому моменту.

Итак, начальное значение полной механической энергии рассматриваемой системы равно W0 = Wp , а конечное W = Wk1 + Wk2 . Изменение энергии:

Как известно, изменение полной механической энергии консервативной системы равно нулю, а при наличии неконсервативных сил – их работе. В данной системе действуют неконсервативные силы трения, работа которых равна

где j – угол поворота крестовины за время падения груза. Знак « – » отражает тот факт, что работа сил трения и сопротивления всегда отрицательна (угол между направлениями силы и перемещения равен 180 ° ). Итак, закон сохранения (превращения) энергии в данном случае можно записать как

С учетом соотношений (6)-(9) уравнение (10) примет вид:

Для экспериментальной проверки справедливости уравнения (11) необходимо знать все входящие в него величины. К ним относятся, во-первых, заранее известные ускорение свободного падения g, масса груза т и высота h; во-вторых, определяемые путем обработки экспериментальной зависимости момент инерции крестовины J и момент сил трения Мтр ; в-третьих, кинематические характеристики системы v, w и j . Остановимся на определении последних.

Скорость груза в момент его падения на пол найдем исходя из закономерностей равноускоренного движения:

Такую же по величине скорость имеют и точки на поверхности шкива. Используя связь между линейной и угловой скоростями, получим

Так как линейное расстояние, пройденное точками на поверхности шкива, равно перемещению груза за тот же промежуток времени, угол j (в радианах) может быть рассчитан как

Порядок измерений и обработки результатов

1. Запишите радиус шкива R , выразив его в метрах, в тетрадь (R=17мм).

2. Занесите во второй столбец таблицы 1 значение массы груза т (в кг).

3. Вращая крестовину, намотайте нить на шкив так, чтобы нижняя поверхность груза 7 оказалась на заданной высоте h над полом, запишите значение высоты в тетрадь (значение h задает преподаватель или спишите с экрана монитора).

4. Отпустив крестовину, одновременно включите секундомер, а в момент касания грузом пола – выключите. Запишите время падения в третий столбец таблицы 1.

5. Повторите пп. 3 и 4 с тем же грузом еще два раза. Рассчитайте и занесите в таблицу среднее из трех значений времени t.

6. Увеличивая массу груза согласно рекомендациям, выполните пп. 2-5 еще пять раз.

7. Для каждого из шести проделанных опытов рассчитайте ускорение а по формуле (4), подставляя в нее среднее из трех измеренных значений времени падения t. Величину а (с точностью не менее чем до трех значащих цифр) запишите в четвертый столбец таблицы 1.

8. По формулам (2) и (5) вычислите значения момента силы натяжения нити Мн и углового ускорения e . Результаты занесите в соответствующие столбцы табл. 1.

9. Руководствуясь правилами [1], постройте график зависимости углового ускорения от момента силы натяжения (в данной работе необходимо, чтобы начало координат совпадало с нулевыми значениями откладываемых величин e и Мн). Нанесите на график экспериментально полученные точки.

10. Одним из описанных ниже способов* обработайте линейную экспериментальную зависимость e (Мн) и найдите значения момента инерции крестовины J и момента сил трения Мтр. Запишите эти значения в тетрадь.

11. Для одного из проделанных опытов рассчитайте по формулам (12)-(14) скорость груза v, угловую скорость вращения w и угол поворота j крестовины маятника Обербека в момент падения груза на пол.

12. Вычислите значения левой и правой частей уравнения закона сохранения энергии (11). Сравнив эти значения между собой, сделайте выводы.

Обработка зависимости e (Мн)

Угловое ускорение крестовины e и момент силы натяжения нити Мн связаны уравнением основного закона динамики вращательного движения (3). Зависимость e (Мн) можно представить в виде

где . Таким образом, определив коэффициенты линейной зависимости (15) K и b, легко найти момент инерции J и момент сил трения Мтр :

Обработку экспериментальной зависимости e (Мн) можно провести либо графически, либо методом наименьших квадратов.

Графический способ. По экспериментальным точкам проведите сглаживающую прямую. Из уравнения (3) следует, что угловое ускорение e обращается в нуль при Мн = Мтр . Таким образом, момент сил трения Мтр определяется (с учетом масштаба!) отрезком, отсекаемым проведенной прямой на оси абсцисс (рис. 2).

Величина K в уравнении (15) представляет собой угловой коэффициент прямой, т.е. тангенс угла ее наклона к оси абсцисс. Согласно (16), момент инерции J есть величина, обратная K, – значит, его можно найти как котангенс этого угла. Выбрав на сглаживающей прямой две достаточно удаленные друг от друга точки, рассчитайте значение J как отношение отрезков

причем величины отрезков D Мн и D e должны быть взяты с учетом масштаба графика и выражены в соответствующих единицах измерения: D Мн – в Н × м, а D e – в рад/с2 или в с – 2. Только в этом случае результат будет правильным, и момент инерции будет иметь размерность кг × м2.

Метод наименьших квадратов. (Подробно этот метод рассмотрен в [1]). Изучив данный материал, заполните два последних столбца табл. 1. Найдите суммы значений величин в последних четырех столбцах и занесите их в строку « S = ». Вычислите коэффициенты K и b зависимости (15); результаты расчетов запишите в тетрадь. Для определения момента инерции крестовины J и момента сил трения Мтр воспользуйтесь соотношениями (16). На графике зависимости e (Мн) проведите прямую по двум точкам, координаты которых рассчитайте по найденным значениям коэффициентов. Убедитесь в правильности проведенных расчетов (прямая должна «наилучшим» образом пройти через экспериментальные точки).

Какие величины характеризуют вращательное движение?

Что характеризует момент инерции твердого тела относительно оси вращения? Как он рассчитывается?

Сформулируйте и докажите теорему Штейнера.

Как изменится кинетика опускания гири, если грузы на крестовине передвинуть ближе (дальше) к оси вращения.

Дайте определение момента силы. Какие моменты сил действуют на крестовину маятника Обербека в этой работе.

Запишите математически и сформулируйте главный закон динамики вращательного движения.

Покажите, что в пренебрежении трением, расчетная формула для момента инерции маятника Обербека будет иметь вид:
.

Запишите и поясните закон сохранения (превращения) механической энергии в этой работе.

[spoiler title=”источники:”]

http://games-on-pc.ru/info/uravnenie-postupatelnogo-dvizhenija-dlja-gruzov/

http://rtb-t.ru/experement/induktixno41.htm

[/spoiler]