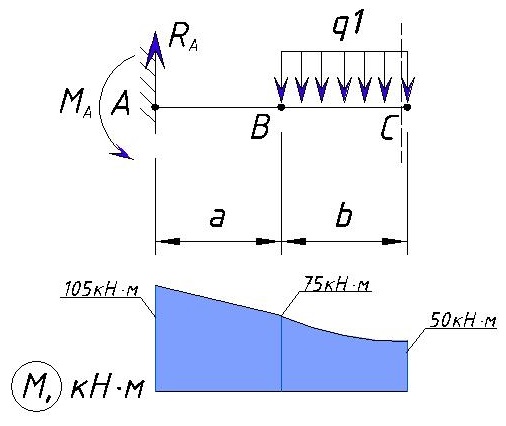
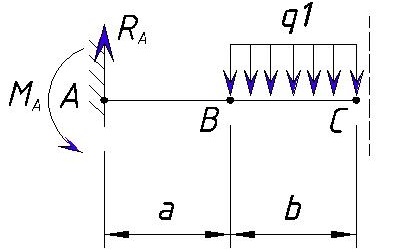
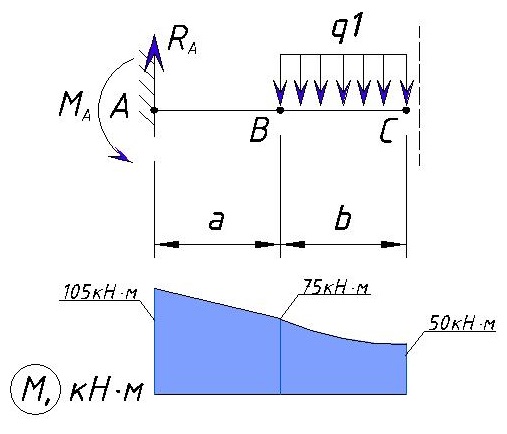
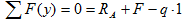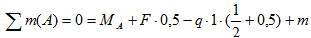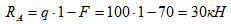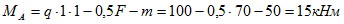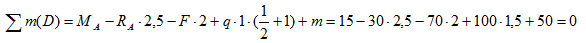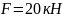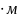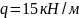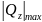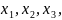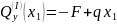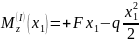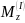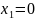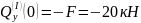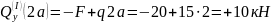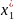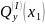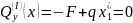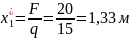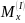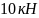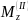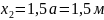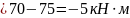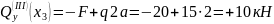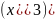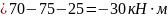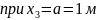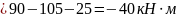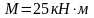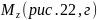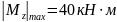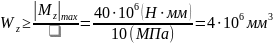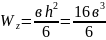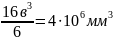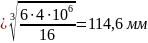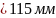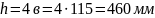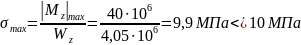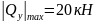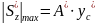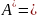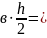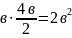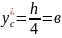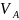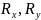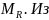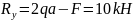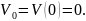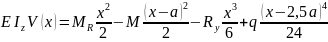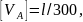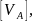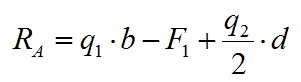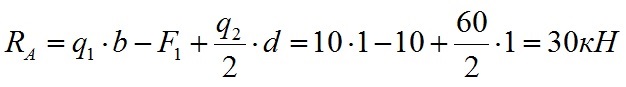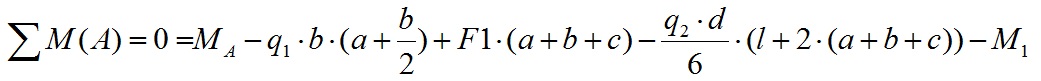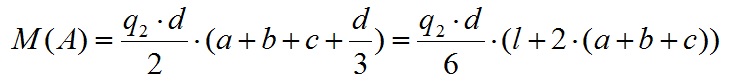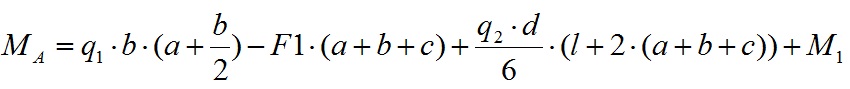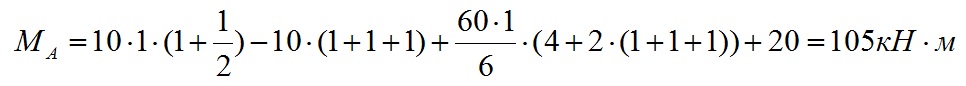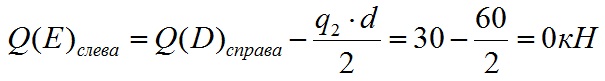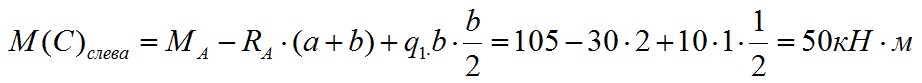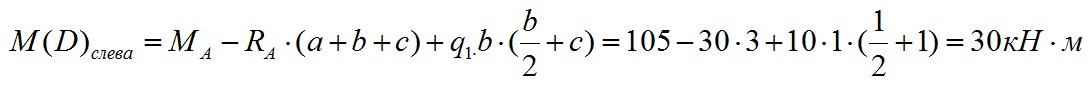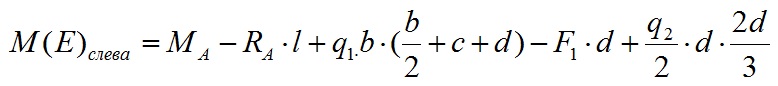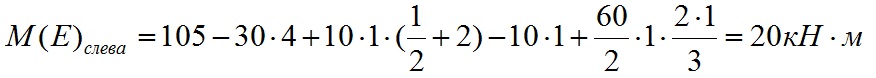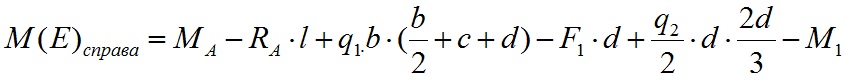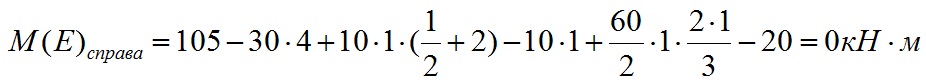Пример решения задачи по расчету реакций опоры стальной консольной балки, нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.
Задача
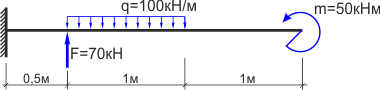
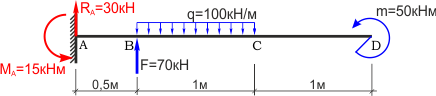
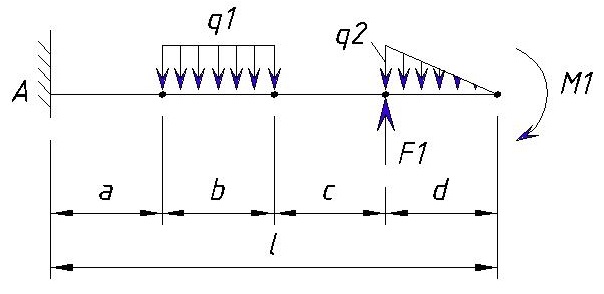
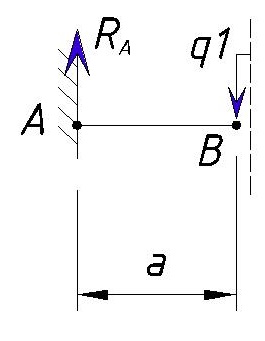
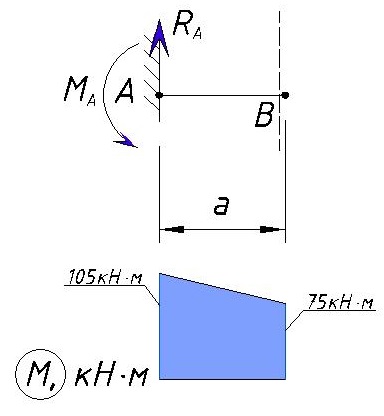
Консольная балка, нагружена сосредоточенными силой F и моментом m, а также равномерно распределенной нагрузкой q. Определить величину и направление опорных реакций в заделке.
Другие примеры решений >
Помощь с решением задач >
Пример решения
В данном случае имеет место случай плоского поперечного изгиба, поэтому реакции, очевидно, также будут располагаться исключительно в плоскости чертежа.
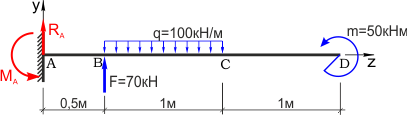
Для удобства обозначим характерные сечения балки точками A, B, C и D и установим систему координат с началом в т. A
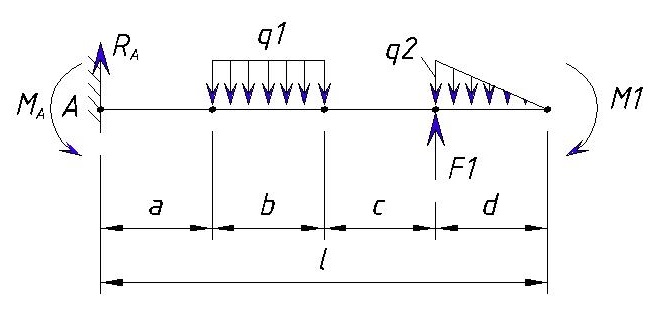
Как известно заделка препятствует одновременно перемещению и вращению балки, поэтому в защемлении возникнут сила R и момент M.
Подробнее о реакциях в заделках смотрите в нашем видео:
Другие видео
Не зная истинного направления, направим их произвольно, например: реакцию R направим вверх, а опорный момент M против хода часовой стрелки
Для определения неизвестных усилий запишем уравнения равновесия системы (уравнения статики):
Правила знаков для сил и моментов.
из первого уравнения определяем опорную силу
из второго — момент в заделке
Положительный знак найденных реакций показывает, что произвольно выбранное их направление оказалось правильным.
В качестве проверки полученных данных запишем уравнение суммы моментов относительно любой другой точки балки, например точки D:
Ноль говорит о том, что опорные реакции определены верно.
Расчет реакций опор простой двухопорной балки >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.
В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.
Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.
Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.
Поперечные силы и изгибающие моменты
При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (Mизг).


Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.
Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.
Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!
Обозначения поперечных сил и изгибающих моментов
Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.
Например, если выбрать следующие обозначения для координатных осей:

То, поперечная сила, будет обозначаться, как Qy (параллельна оси y), а изгибающий момент, как Mx (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Qy, Mz или Qz, Mx. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – Mизг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.
Расчётная схема балки
Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.
К примеру, балка может иметь прямоугольное поперечное сечение:

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.
Правила знаков для поперечных сил и изгибающих моментов
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).
Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и Мизг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).
Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.
Правило знаков для поперечных сил
Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:
Правило знаков для изгибающих моментов
Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.
На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;

• нижние волокна, то нужно учесть его с «плюсом».

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.
Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:
Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:


Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:
Как построить эпюры поперечных сил и изгибающих моментов ?
В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.
Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉
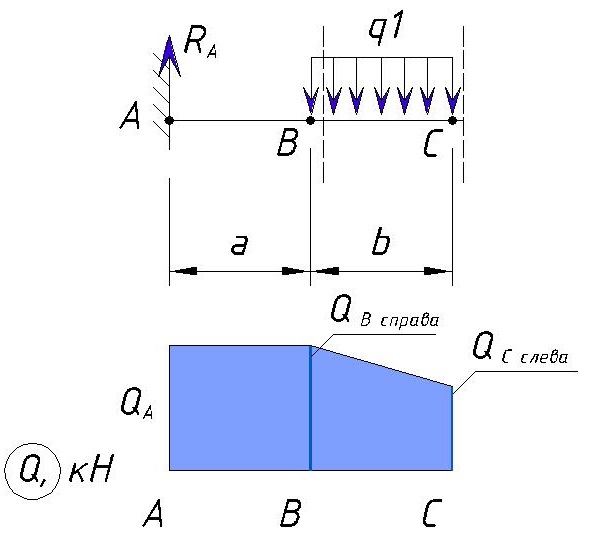
Построение эпюр для консольной балки
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Будем рассчитывать балку справа налево.
Рассмотрим первый участок
Обозначим некоторое сечение 1-1 на расстоянии x1, от свободного торца балки, при этом x1 будет находиться в диапазоне: 0 ≤ x1 ≤ 4м.

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.
Поперечные силы на первом участке
Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:
Как видишь, поперечная сила будет постоянна на первом участке:
Уже можем отразить это на эпюре поперечных сил:

Изгибающие моменты на первом участке
Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:
Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Расчёт второго участка
Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x2 от начала участка (0 ≤ x2 ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке
Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:
Теперь можем показать окончательную эпюру поперечных сил:

Изгибающие моменты на втором участке
Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:
Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Проверка построенных эпюр
Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.
Определение реакций в жёсткой заделке
Первым делом, нам потребуется определить реакции в заделке:

Расчёт эпюр поперечных сил и изгибающих моментов
Рассчитываем все участки теперь слева направо:

Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.
Эпюра моментов со стороны растянутых или сжатых волокон
По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.
Причем сама эпюра была построенна со стороны растянутых волокон:

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.
Учёт распределённой нагрузки
Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.
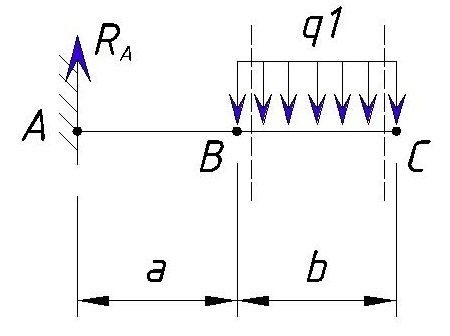
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Определение поперечной силы и изгибающего момента в сечении A
Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.
После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Тогда поперечная сила QA будет равна:
Изгибающий момент Mизг, A будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов
Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Уравнение для поперечных сил будет следующее:
Рассчитаем значения на эпюре поперечных сил:


Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:


На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.
Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

Построение эпюр для двухопорной балки
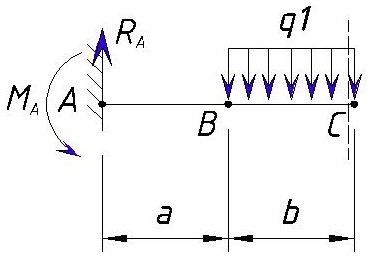
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

Определим реакции опор:

Рассчитываем первый участок:
Строим эпюры на первом участке:

Определение экстремума на эпюре моментов
Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.
Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:
Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Расчет эпюр на остальных участках
Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:
Определение экстремума:


Оценка правильности построенных эпюр поперечных сил и изгибающих моментов
И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.
Вот несколько признаков, правильно построенных эпюр:
- На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
- На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
- Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
- Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.
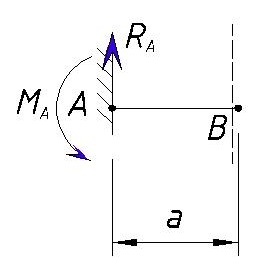
Для деревянной
консольной балки, расчетная схема
которой дана на рис. 22, а, требуется:
-
подобрать из
условия прочности по допускаемым
напряжениям размерыи в
прямоугольного поперечного сечения
(рис. 18,б), принявв,
а =1 м, допускаемое
напряжение для дерева на растяжение
=
10 МПа,
а допускаемое напряжение при сдвиге
[τ]= 5 МПа.
-
проверить жесткость
спроектированной балки, считая
допускаемое значение прогиба сечения
А равным 1/300 её длины, а E=1∙104
МПа.
Расчетные значения
нагрузок:
,
М=25 кН
,
.
Решение
1.
Определение
вида расчета
По условию задачи
требуется подобрать размеры поперечного
сечения балки, т.е. требуется выполнить
проектный расчет. Из условия прочности
по нормальным напряжениям проектный
расчет выполняется по соотношению
.
Поскольку значение
допускаемого напряжения
задано,
то для выполнения расчета следует
знать
.
Для проверки
прочности по касательным напряжениям
необходимо знать
.
Для определения
и
строим эпюры
и
.
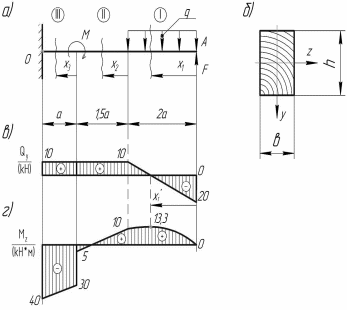
Рис.
22. Расчетная
схема балки (а), сечение балки (б),
эпюры
поперечных сил (в) и изгибающих моментов
(г)
2.
Построение
эпюр
и
а)
Определяем
реакции
опор
Обычно
построение эпюр
и
начинают с определения реакций опор. В
данной задаче балка консольная, поэтому
нет необходимости определять реакции
опор, так как эпюры
и
можно
построить, двигаясь от свободного конца
к заделке и рассматривая отсеченную
правую часть, на которую не наложены
связи.
б)
Разбиваем
балку на участки
Используя
правило, изложенное в разделе 2.1, разбиваем
балку на три участка.
в)
Записываем
аналитические выражения
и
по участкам
Рассекая
балку на каждом из участков произвольным
сечением, координаты которых обозначены
и
рассматривая каждый раз отсеченную
правую часть балки, записываем выражения
и
по участкам
Участок I:
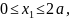
;
.
Анализируя
полученные выражения, приходим к выводу,
что поперечная сила
изменяется по линейной зависимости, а
изгибающий момент – квадратичная
функция координаты
.
Определим значения
и
в граничных сечениях I
участка:
при
;
;
при
;
.
Так как поперечная
сила
на первом участке, меняя знак в одном
из сечений (обозначим его координату
)
, обращается в нуль (см. рис. 22,в), то в
соответствии со следствием 3 из
дифференциальных зависимостей (1.3)
изгибающий момент в этом сечении будет
иметь локальный экстремум. Приравнивая
выражение
нулю, определим координату
этого сечения:
,
отсюда
.
Подставляя значение
в выражение
,
находим экстремальное значение
на первом участке. Это будет локальный
максимум
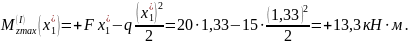
Переходим к
рассмотрению участка II.
Участок
II:
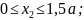
Рассматривая
отсеченную правую часть, получим
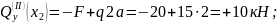
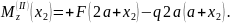
Таким образом,
поперечная сила во всех сечениях второго
участка постоянна и равна +
,
а изгибающий момент – линейная функция
координаты
.
Для построения эпюры
на втором участке определим значения
в граничных сечениях этого участка.
При
;
при
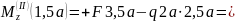
.
Участок
III:
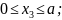
Рассматривая
по-прежнему отсеченную правую часть,
получим:
;
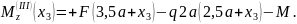
Как и на участке
II,
поперечная сила на участке III
постоянна во всех его поперечных сечениях
(т.к. не зависит от координаты
),
а изгибающий момент – линейная
функция координаты
.
Для построения эпюры
на участке III
определим значения изгибающего момента
в граничных сечениях этого участка.
При
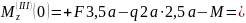
;

.
г) Строим
эпюры
и
,
располагая их строго под схемой балки
(рис. 22, в, г).
Для построения
эпюры
проводим нулевую линию эпюры параллельно
оси балки. Положительные значения
откладываем выше нулевой линии, а
отрицательные – ниже (рис. 22, в).
Для построения
эпюры
проводим нулевую линию параллельно оси
балки. Положительные значения
откладываем выше нулевой линии, а
отрицательные – ниже (рис. 22, г).
д) Проводим
проверку правильности построения эпюр
и
При
анализе правильности построения эпюр
с учетом следствий из дифференциальных
зависимостей между Мz,
Qy
и q
(3.3) отмечаем:
– на участках,
где отсутствует q
(участки
II
и III),
поперечная сила Qy–
постоянна, а изгибающий момент
изменяется по линейному закону;
– на участке,
где имеется равномерно распределенная
нагрузка интенсивностью q,
поперечная сила Qy
изменяется по линейному закону, а
изгибающий момент
– по закону квадратной параболы, с
выпуклостью направленной навстречу
действия q;
– на эпюре
Qy
имеются скачки в сечениях, где приложены
сосредоточенная сила F=20
кН и опорная реакция заделки;
– на эпюре Мz
имеются скачки там, где приложены внешний
сосредоточенный момент
и
реактивный момент заделки.
Все
это позволяет сделать вывод, что эпюры
построены правильно и могут быть
использованы при дальнейшем решении
задачи.
3.
Подбор размеров поперечного сечения
Из эпюры
следует, что
,
следовательно,
.
Осевой момент
сопротивления для прямоугольного
сечения при заданном соотношении сторон
(
в)
определяется по формуле
.
Приравнивая
найдем размер в:
;
в
.
Округляя
в большую сторону, примем
в
,
.
Проверим
прочность подобранного сечения по
нормальным напряжениям:
.
.
Прочность по
нормальным напряжениям обеспечена.
Недонапряжение в 1% объясняется округлением
размера сечения в
в большую сторону.
4.
Проверка
прочности по касательным напряжениям
Поскольку балка
изготовлена из дерева, то проверка
прочности по касательным напряжениям
является обязательной.
Для проверки
прочности по касательным напряжениям
используем условие (3.13):
.
Из
эпюры поперечных сил (см.рис. 22, в)
следует, что
.
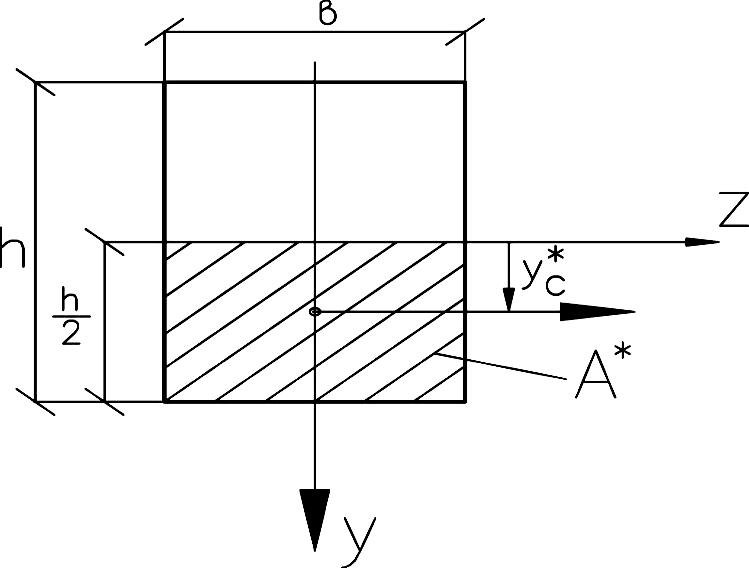
Для прямоугольного
сечения
с учетом соотношения
в
получим
в.
Наибольшие
касательные напряжения для прямоугольного
сечения возникают в точках, лежащих на
главной и центральной оси
,
так как
для половины сечения максимален, а в(y)
= в = Const
(рис.
23).
|
Рис. |
.
|
Таким
образом,
,
а максимальные касательные напряжения
.
Приходим к
выводу, что прочность по касательным
напряжениям обеспечена с большим
запасом.
Окончательно
принимаем следующие размеры поперечного
сечения:
в
;
h=
46 см.
5. Проверка
выполнения условия жесткости
Согласно
условию задачи, для данной балки условие
жесткости имеет вид:
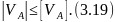
Для определения
воспользуемся методом начальных
параметров
1. Выбираем
систему координат.
Начало координат помещаем в заделку,
ось x
направляем слева направо, ось y
– вниз (рис. 24).
Рис. 24
Отбрасывая
заделку, заменим ее реакциями
и реактивным моментом
уравнений статики определим реакции
связей:
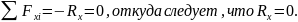
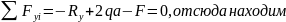
.
.
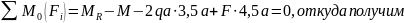
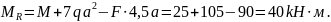
Проверим
правильность определения реакций:

Следовательно,
реакции найдены верно.
2. Составление
универсального уравнения упругой линии
балки. Запишем
выражение изгибающего момента для
произвольного сечения участка балки,
наиболее удаленного от начала
координат:
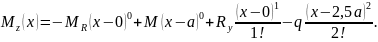
Тогда универсальное
уравнение упругой линии балки будет
иметь вид
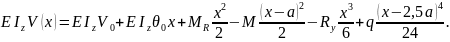
3. Определение
начальных параметров.
Для определения начальных параметров
воспользуемся граничными условиями в
заделке, где прогиб и угол поворота
равны нулю, т.е.
Таким
образом, универсальное уравнение упругой
линии балки приводится к виду
.
4.
Вычисление
прогиба сечения А.
Для этого сечения x
=4,5 a
=4,5 м.
Подставляя
в уравнение упругой линии получим:
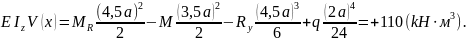
Для подобранного
прямоугольного поперечного сечения
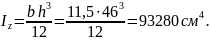
Тогда прогиб
сечения А
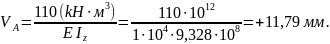
Знак «+» говорит
о том, что сечение А перемещается по
направлению оси y,
т.е. вниз.
5) Проверка
выполнения условия жесткости. По
условию
где l
– длина
балки. Так как l
= 4,5 a
= 4,5 м, то
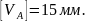
Сравнение
показывает, что VA<
следовательно, условие жесткости
выполняется, что позволяет окончательно
принять размеры сечения, полученные из
условия прочности, т.е. принимаем
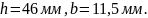
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
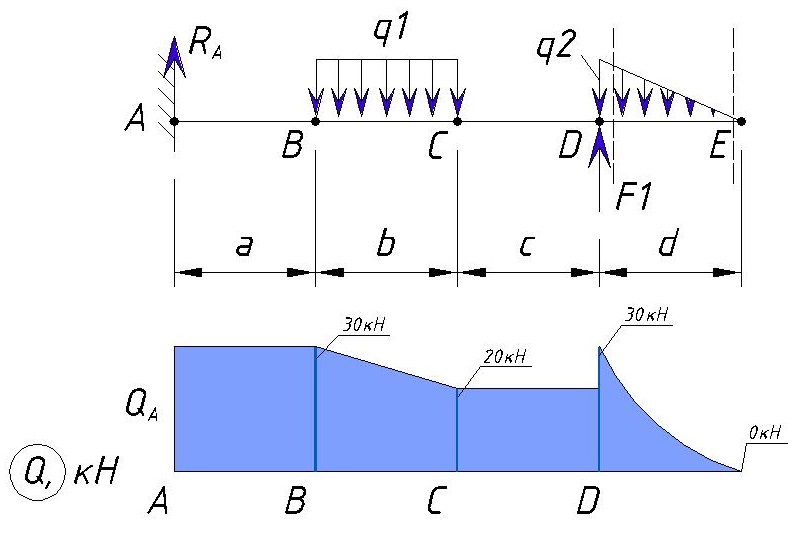
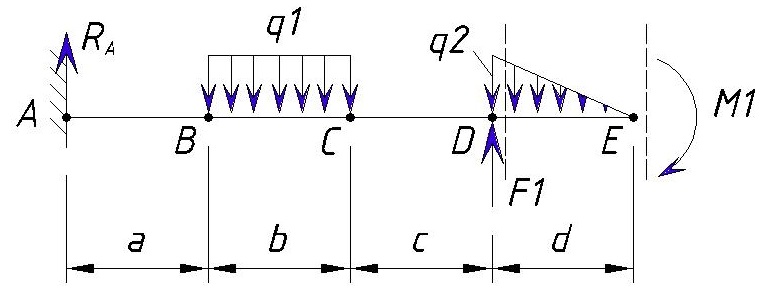
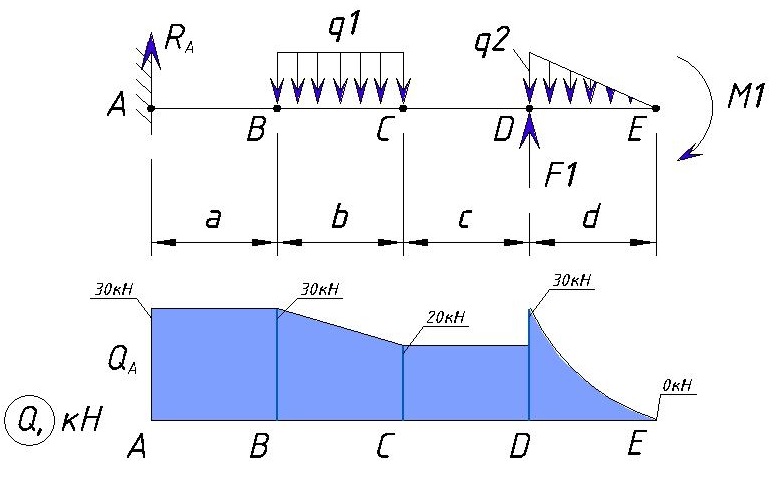
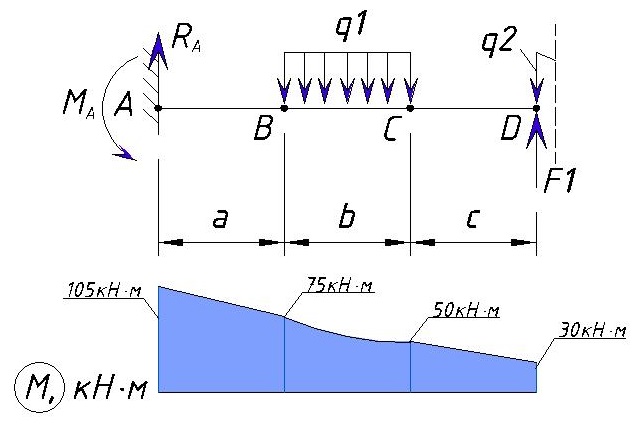
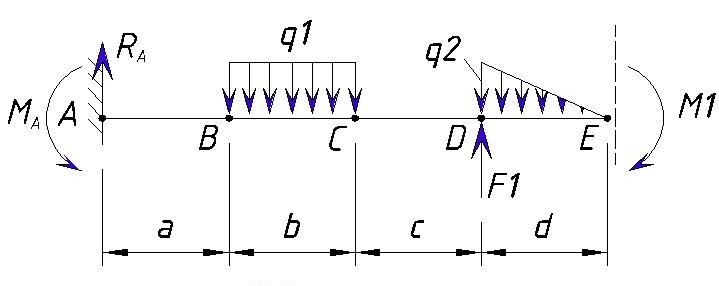
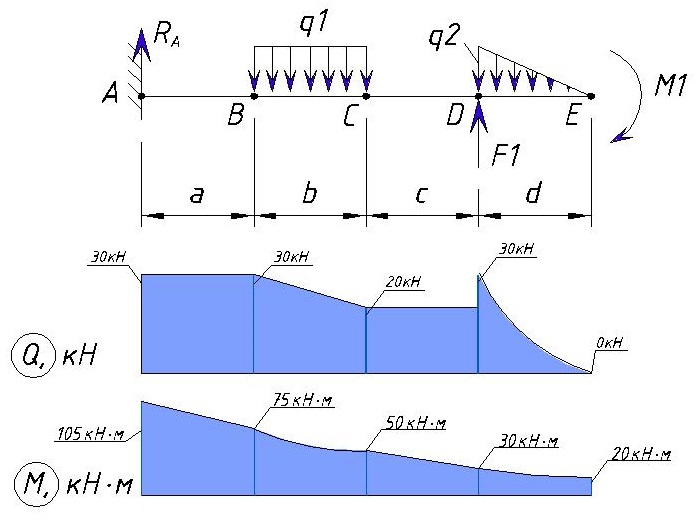
Мы уже рассматривали типовые эпюры консольной балки, теперь расскажем про построение эпюры консольной балки если на нее воздействуют сразу несколько нагрузок.
Чтобы легче было понять материал разберемся на примере:
Значения нагрузок:
q1=10 кН/м
q2=60 кН/м
F1=10 кН
M1=20 кН·м
Расстояния между точками равны т,е. a=b=c=d=1м
Опорные реакции
Построение эпюр, как правило, начинают с определения опорных реакций.
Определяем поперечную силу и изгибающий момент в точке А.
Для начала зададим направление опорных реакций
Т.к. система не подвижна, то сумма сил должна равняться нулю.
Нагрузки, направленные вверх, принимаются со знаком плюс.
Нагрузки, направленные вниз, принимаем со знаком минус.
Направление Ra мы приняли вверх. Если в процессе решения уравнение значение Ra будет отрицательным, значит она направлена в другую сторону.
В уравнении уравновешивающих сил вдоль оси Y изгибающий момент M1 не присутствует. Да и в консольной балке момент, приложенный на любом участке балки, не влияет на поперечные силы. Только если будет как минимум еще одна опора момент повлияет на опорную реакцию и, соответственно, на поперечные силы, но в данном уравнении его все равно не будет.
Из этого уравнения вычисляем значение опорной реакции Ra:
Подставляем значения нагрузок и вычисляем значение опорной реакции Ra:
Мы вычислили значение опорной реакции Ra. Значение положительное, значит направление нагрузки мы назначили правильно.
Далее составляем уравнение равновесия изгибающих моментов вокруг точки A. Если система неподвижна, сумма моментов вокруг любой точки равна нулю.
Уравнение равновесия моментов вокруг точки A для нашего примера будет выглядеть следующим образом:
Значение момента от действия силы вокруг определенной точки равно произведению этой силы на расстояние от заданной точки до центра приложения нагрузки. Чтобы было понятно какой изгибающий момент создает каждый вид нагрузки, давайте рассмотрим их по отдельности.
Изгибающий момент M1 влияет на опорный момент вне зависимости от того где он приложен, т.е. не важно приложен он в середине балки или на конце на опорный момент он будет влиять одинаково.
Сосредоточенная сила F1 создает изгибающий момент равный произведению его значения на плечо (расстояние от рассматриваемой точки до точки приложения силы). Т.е. чем больше плечо, тем больший изгибающий момент создает сила F1.
Равномерно-распределенная сила q1 создает момент, равный произведению этой нагрузки на длину приложения этой нагрузки и на плечо (расстояние от рассматриваемой точки до центра равномерно-распределенной нагрузки). Т.е. мы можем представить распределенную нагрузку как сосредоточенную в центре этой нагрузки и умножить это значение на плечо.
Переменная нагрузка сила q2 создает момент, равный произведению половины произведения этой нагрузки на длину приложения и на плечо (расстояние от рассматриваемой точки, до центра приложения нагрузки, который расположен на расстоянии 1/3 от общей длины приложения этой нагрузки, ближе к максимальному значению). В данном примере это выглядит так:
Из этого уравнения мы можем вычислить значение опорного момента Ma:
Подставляем значения и вычисляем значение опорного момента в точке A:
Мы вычислили значение опорного момента Ma. Значение опорного момента Ma положительное, поэтому направление действия момента задано правильно.
Назначение контрольных точек
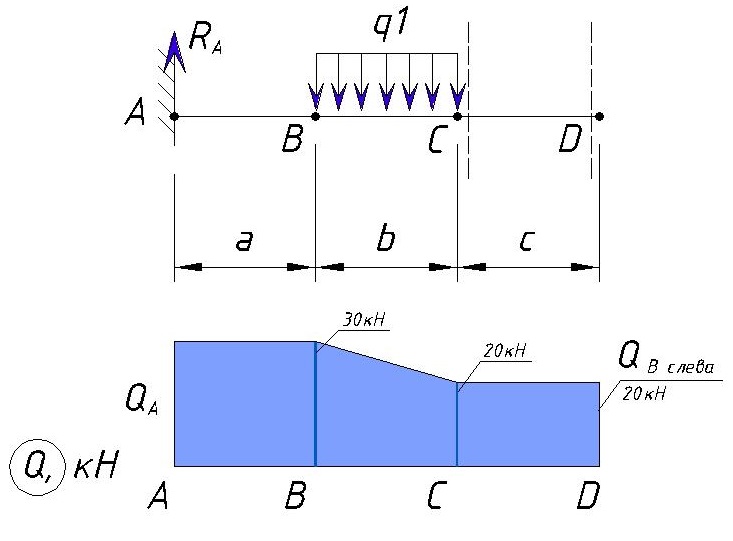
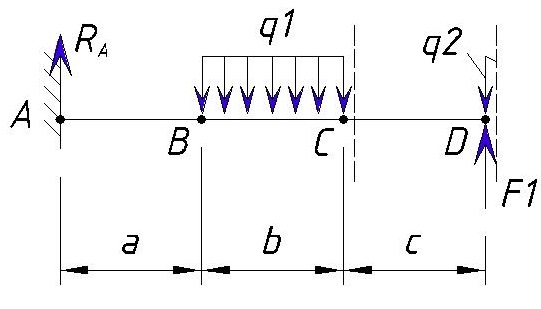
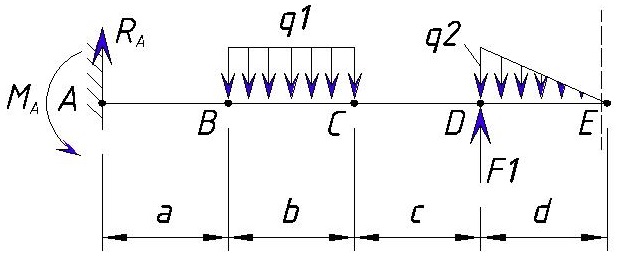
Для начала определяем контрольные точки на балке. 2-е точки естественно будут начало и конец балки, а промежуточные точки будут места приложения нагрузок (в случае равномерно-распределенной или переменной нагрузки точками будут начало и коней приложения нагрузки). Рассмотрим на примере разделение консольной балки на участки:
Точку заделки мы обозначили буквой «А».
Далее ближайшая точка «В» — это место приложения начала равномерно-распределенной нагрузки q1. Расстояние между точкой «А» и «B» равно a.
Далее следующая точка «С» — это конец приложения равномерно-распределенной нагрузки q1. Расстояние между точкой «B» и «C» равно b.
Следующая точка «D» — это начало приложения переменной нагрузки q1 и точка приложения силы F1. Расстояние между точкой «C» и «D» равно c.
Следующая точка «E» — это конец приложения переменной нагрузки q1, точка приложения изгибающего момента M1 и конец балки. Расстояние между точкой «D» и «E» равно d.
Построение эпюры Q (поперечной силы)
Разбиваем балку на участки между контрольными точками, т.е. участок AB (между точками A и B), участок BC (между участками B и C) и т.д.
В нашем примере у нас есть 4 участка: AB, BC, CD,DE.
Эпюру поперечных сил Q мы можем строить перемещаясь от точки А до точки E, рассчитывая значения в каждой точке, либо наоборот от точки E до точки A. В данном примере мы будем следовать от точки A, до точки E.
На каждом участке мы определяем значения и строим эпюру. По горизонтальной оси будут откладываться координаты, по вертикали откладываются значения (вверх от консольной балки откладываются положительные значения, вниз откладываются отрицательные значения).
Далее необходимо соединить эти точки линиями. Все точки, кроме точек между началом и концом переменной нагрузки, соединяются по прямой линии. Переменная нагрузка от начала, до конца соединяется изогнутой линией, напоминающей гиперболу, изогнутой вниз если нагрузка возрастает к месту заделки (если заделка слева) и изогнутой вверх если нагрузка к месту заделки спадает.
Правило знаков для построения эпюры Q
Если внешняя нагрузка, приложенная к рассматриваемой части, стремится повернуть сечение на заданном участке по часовой стрелке, то значение будет положительным и откладывается вверх.
Если внешняя нагрузка стремится повернуть сечение на заданном участке против часовой стрелки, то значение будет отрицательным и откладывается вниз.
Точка, вокруг которой поворачивают заданный участок не обязательно точка закрепления. Это точка, которую мы задаем на заданном участке в направлении к которой мы строим эпюру: если мы строим эпюру слева направо (как в данном примере), то это самая правая точка на заданном участке, если строим эпюру справа налево, то это самая левая точка на заданном участке.
Определяем напряжения Q на участке AB.
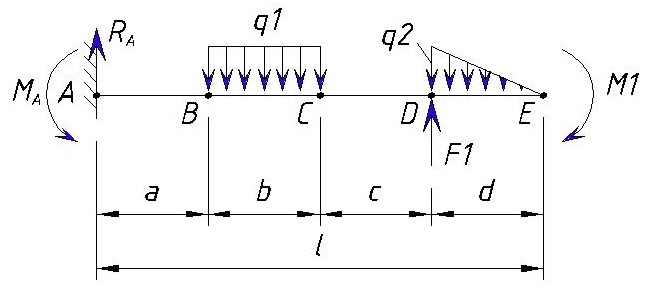
Рассмотрим участок AB. При рассмотрении участка AB мы как бы отбрасываем все остальные участки и не учитываем их на данном этапе. Кроме этого вначале мы не учитываем силы, приложенные в точке B.
Значение поперечной силы в точке А равно значению опорной реакции Ra, которое мы вычислили ранее. Не забываем про правило знаков — если сила стремится повернуть рассматриваемый участок по часовой стрелке, то значение принимается со знаком плюс, если против часовой, то со знаком минус. Мы как-бы откидываем закрепление балки в точке А, заменив ее силой Ra, и закрепляем в точке B. Сила Ra стремится повернуть участок вокруг точки B по часовой стрелке, поэтому Ra принимается со знаком плюс.
С правилом знаков поначалу возникают некоторые проблемы. Точка, вокруг которой мы мысленно вращаем данный участок, это не точка закрепления балки, а точка на участке, который мы в данный момент рассматриваем. Если мы строим эпюру слева направо (как в данной примере), это это будет самая правая точка, на рассматриваемом участке. Если строим эпюру справа налево, то это будет самая левая точка, на рассматриваемом участке.
Далее мы рассматриваем участок от точки А, до точки B, но при этом не учитываем нагрузки, которые приложены в самой точке B.
Пунктирной линией на рисунке обозначен участок, который мы рассматриваем.
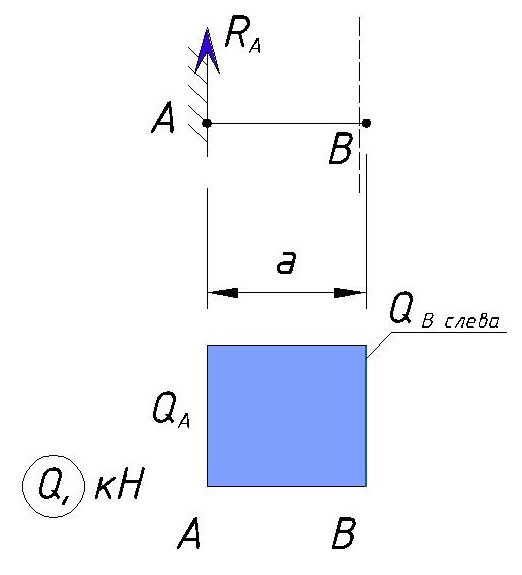
На данном участке нет поперечных сил, кроме Ra, поэтому
Т.е. мы пока не учитываем силы, которые справа от этой точки и сила которая приложена именно в этой точке. Естественно силы, приложенные правее правее точки B влияют на значение поперечных сил на данном участке и они сейчас выражены в опорной реакции Ra. Как уже ранее выяснили сила Ra стремится повернуть сечение по часовой стрелке, поэтому Ra принимается со знаком «плюс» и откладывается вверх от оси.
Т.к. значение поперечной силы не изменилось, то эпюра Q на данном участке будет выглядеть как прямоугольник:
По вертикали мы откладываем значение поперечной силы, по горизонтали координаты балки.
Далее мы рассматриваем участок AB с учетом точки B, но принимаем участок не много правее точки B (на рисунке участок отсечен пунктирной линией)
В точке B начинается равномерно-распределенная нагрузка q1, но мы рассматриваем участок правее точки как бы равный нулю, т.е. нагрузка q1 приложена в точке B, но еще имеет нулевую длину приложения нагрузки, поэтому она не изменяет значение поперечной силы в точке B.
Тут мы опять действуем согласно правилу знаков: точка, вокруг которой мы вращаем участок, находится не много правее точки B. Сила Ra стремится повернуть данный участок по часовой стрелке, поэтому она принимается со знаком «плюс». Чтобы было проще при построении эпюры слева направо сила, направленная вверх всегда будет со знаком «плюс», а сила направленная вниз будет со знаком «минус».
Эпюра Q на данном участке получается следующая:
Определяем напряжения Q на участке BС.
Далее мы рассматриваем участок от точки B до точки C.
Пунктирными линиями я указал рассматриваемый участок.
Значение поперечной силы в точке B справа мы уже вычислили ранее — это Q(B справа)=Ra=30 кН (именно значение, что справа).
На участке от точки B до точки C действует сила q1. По правилу знаков данная нагрузка стремится повернуть участок BC вокруг точки C против часовой стрелки, поэтому оно учитывается со знаком минус. Значение Q слева от точки C равно:
Строим эпюру поперечных сил на данном участке
Далее рассматриваем участок BC, с точкой несколько правее точки C
В точке C справа ничего не изменилось, поэтому
Эпюра Q на участке от A до C будет выглядеть следующим образом:
Определяем напряжения Q на участке СD.
Рассмотрим участок от точки C до точки D. Вначале рассматриваем участок левее точки D.
На данном участке нет поперечных сил, поэтому поперечная сила Q на данном участке не изменяется:
Эпюра на данном участке выглядит следующим образом:
Далее рассмотрим участок с учетом сил, действующих в точке D
В точке D действует сосредоточенная сила F1 и начинает действовать переменная сила q2. Переменная сила q2 не влияет на поперечную силу в точке D т.к. она еще имеет нулевую длину приложения (правее этой точки она будет влиять, но это будет рассмотрено на участке DE). А сила F1 создает скачок поперечной нагрузки. Т.к. сила F1 стремится повернуть участок CD вокруг точки D по часовой стрелке сила F1 учитывается со знаком плюс (сила F1 вообще не может повернуть сечение вокруг точки D т.к. она приложена именно к этой точке, но тут точку вращения мы принимаем не много правее точки D т.к. это значение будет правее точки D).
Строим эпюру Q с учетом силы F1
На эпюре мы видим скачок поперечной силы.
Определяем напряжения Q на участке DE.
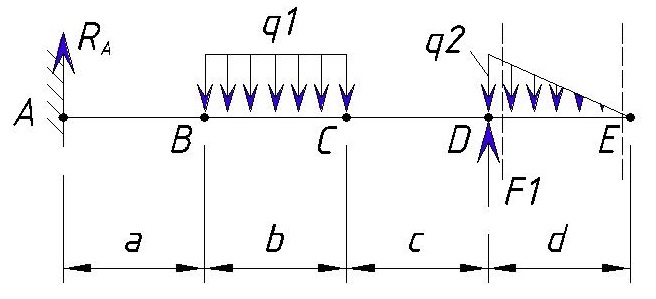
Рассмотрим участок от точки D до точки E (слева)
На участке от точки D до точки E приложена переменная нагрузка q2.
Определим значение Q в левее точки E. Сила q2 стремится повернуть сечение DE вокруг точки E против часовой стрелки, поэтому принимается со знаком минус. Значение поперечной силы в точке E слева равно:
Эпюра на этом участке будет выглядеть как изогнутая линия т.к. переменная нагрузка с увеличением длины уменьшает свое влияние на поперечную силу и сводится к нулю в конце участка
Далее рассматриваем участок DE с участком правее точки E
В точке E действует изгибающий момент M1, но он не влияет на поперечную силу, поэтому
Эпюра Q
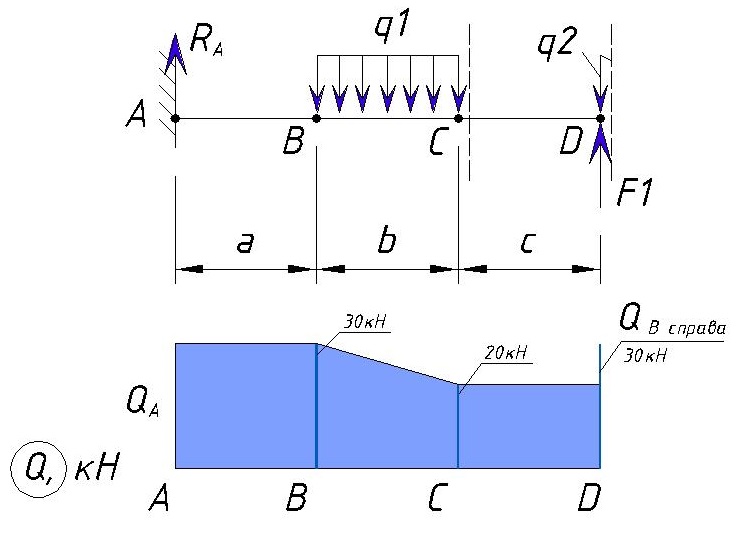
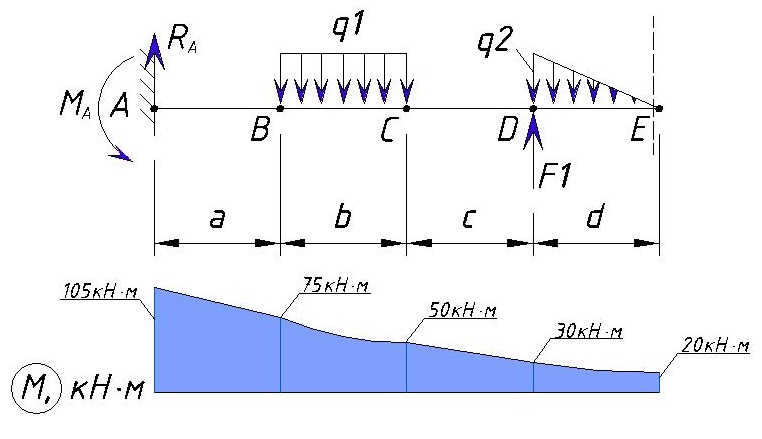
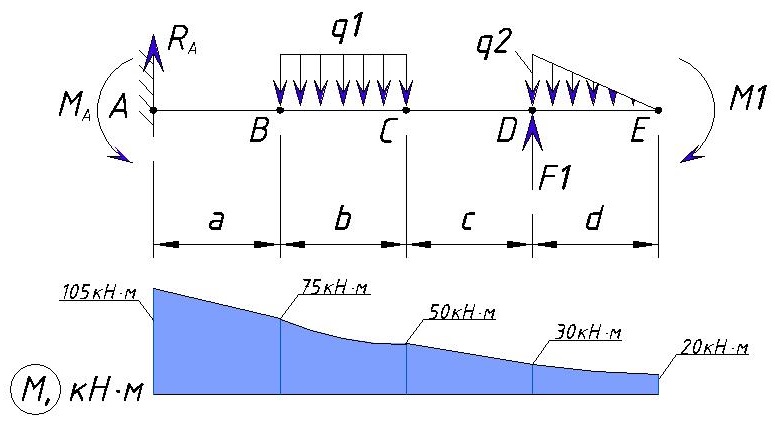
В итоге эпюра поперечной силы Q для данного примера выглядит следующим образом:
Как видим максимальная поперечная нагрузка, в данном примере, находится на участке от точки А до точки В, а также в точке D и равна Ra=30кН.
Вообще не во всех случаях обязательно рассматривать участок левее и правее заданной точки — только если в точке приложена сосредоточенная сила F эпюра Q осуществляет скачок, во всех остальных случаях Q(слева)=Q(справа). Я просто показал принцип построения эпюры.
В консольной балке напряжения Q в конце балки должны быть равны нулю. Конечно если на конце приложена сила F будет скачок напряжения, но Q(справа) будет равна нулю.
Построение эпюры M (изгибающий момент)
Для построения эпюры М мы используем те же контрольные точки и те же участки, что мы использовали при построении эпюры Q.
Последовательно передвигаясь от точки А к концу балки мы вычисляем значения моментов в контрольных точках и соединяем их в график который и будет указывать изгибающий момент в любой точке балки.
Изгибающий момент вычисляется произведением силы или центра приложения силы на плечо.
Для сосредоточенной силы мы умножаем значение нагрузки на расстояние до рассматриваемой точки. На графике эпюра M от действия сосредоточенной силы имеет прямую линию.
Чтобы определить изгибающий момент от действия равномерно-распределенной нагрузки определяем расстояние до середины рассматриваемого участка равномерно-распределенной нагрузки, умножаем на длину рассматриваемого участка и на величину нагрузки. На графике эпюра М от действия равномерно-распределенной нагрузки напоминает изогнутую линию, гиперболу.
Для переменной нагрузки изгибающий момент определяем следующим образом: определяется центр приложения нагрузки (длина приложения нагрузки делится в соотношении 1/3-2/3, центр приложения нагрузки находится ближе к максимальной нагрузке), определяем длину от этой точки до рассматриваемой, умножаем на длину приложения нагрузки, и умножаем на половину от приложенной нагрузки (q).На графике эпюра М от действия переменной нагрузки также как и для равномерно-распределенной напоминает изогнутую линию, но с большим изгибом.
Приложенный момент в точке просто суммируется с вычисляемым изгибающим моментом от других нагрузок. В точке где приложен момент эпюра совершает скачок. Значение момента не умножается на расстояние, а остается неизменным по всей длине.
Правило знаков для построения эпюры M
Тут есть 2-а метода: метод которым пользуются строители и метод, которым пользуются машиностроители.
У строителей изгибающий момент считается положительным, если внешняя нагрузка приводит к растяжению верхних волокон и график откладываем вверх. Если внешняя нагрузка приводит к растяжению нижних волокон, то изгибающий момент считается отрицательным и график откладывается вверх. Т.е. график всегда откладывается в сторону растянутых волокон.
У машиностроителей все наоборот — положительное значение откладывается в сторону сжатых волокон.
Ни в том, ни в другом случае ошибки нет, просто разные методы и итоговые значения будут одинаковыми, только знаки противоположными.
Не могу с уверенностью сказать почему у строителей изгибающий момент направлен в сторону растянутых волокон. Возможно из-за того, что при данном рассмотрении эпюра моментов во многих случаях повторяет изгиб балки.
Мы будем рассматривать метод, которым пользуются строители.
Определяем напряжение M на участке AB
Также как и при определении эпюры Q, эпюру М также строим по тем же участкам.
Значение изгибающего момента в точке равно значению опорного момента Ma, который мы вычислили ранее.
Также как и при построении эпюры Q мы рассматриваем участок с точкой левее точки B и правее этой точки, но если при построении эпюры Q мы не учитывали изгибающие моменты, то при построении эпюры изгибающих моментов мы должны учитывать и изгибающие моменты, и поперечные силы.
Изгибающий момент Ma стремится повернуть сечение вокруг точки B против часовой стрелки, а опорная реакция Ra по часовой стрелке. Теперь обратимся к правилу знаков. Изгибающий момент Ma стремится растянуть верхние волокна и сжать нижние, поэтому мы его учитываем со знаком плюс (читаем правило знаков для эпюры M). Опорная реакция Ra напротив стремится сжать верхние волокна и растянуть нижние, поэтому принимается со знаком минус. Напоминаю, что мы вращаем участок вокруг точки B, заделка в точке A заменена опорными реакциями Ra и Ma, т.е. если мы вместо заделки приложим эти силы, то система будет неподвижна.
Изгибающий момент в точке B слева будет равен:
На участке между точками A и B изгибающий момент изменяется прямолинейно т.к. на этом участке только реакция Ra изменяет значение, поэтому эпюра M на данном участке будет выглядеть так:
Теперь рассмотрим участок до точки B справа
Тут добавляется равномерно распределенная нагрузка q1, но длина ее приложения еще равна нулю, поэтому она не влияет на изгибающий момент в точке B справа. Изгибающий момент справа от точки B буден равен значению слева от точки B.
Эпюра M выглядит следующим образом:
Определяем напряжение M на участке BС
Рассмотрим участок BC взяв участок без учета нагрузок в точке C (ну или как мы приняли левее точки C).
При вычислении изгибающего момента в точке C мы рассматриваем участок от точки A до С. Изгибающий момент в точке B вычисленный ранее является только значением в точке B и на точку C уже не влияет т.к. значение изгибающего момента изменяется в зависимости от плеча (расстояние от точки приложения нагрузки до рассматриваемой точки).
Изгибающий момент в точке С формируется из следующих составных:
1) Изгибающий момент Ma — опорная реакция в точке A. Значение изгибающего момента на изменяется от расстояния. Также как и для точки B значение изгибающего момента принимаем со знаком плюс т.к. он растягивает верхние волокна в точке C.
2) Опорная реакция Ra. Значение изгибающего момента в точке C напрямую зависит от плеча приложения нагрузки, поэтому в точке C опорная реакция Ra создает изгибающий момент в 2-а раза больше чем в точке B. Опорная реакция также сжимает верхние волокна, поэтому принимается со знаком минус.
3) Равномерно-распределенная нагрузка q1 создает изгибающий момент в точке C равный произведению этой нагрузки на длину ее приложения и на расстояние до центра ее приложения. По правилу знаков нагрузка q1 растягивает верхние волокна и принимается со знаком плюс.
Значение изгибающего момента в точки С слева равно:
На участке действия равномерно-распределенной нагрузки эпюра M имеет изогнутую форму. Изгиб направлен в сторону действия нагрузки. Эпюра на участке от A до C имеет следующий вид:
Теперь рассмотрим участок правее точки C
В принципе тут ничего не изменяется, новых нагрузок не появляется, расстояние (плечо) тоже остается тоже, поэтому эпюра с учетом этого участка выглядит также
Определяем напряжение M на участке СD
Также рассматриваем участок слева от точки D
Изгибающий момент в точке D формируется из следующих составных:
1) Изгибающий момент Ma — опорная реакция в точке A. Значение изгибающего момента на изменяется от расстояния. Также как и для точки B значение изгибающего момента принимаем со знаком плюс т.к. он растягивает верхние волокна в точке D.
2) Опорная реакция Ra. Значение изгибающего момента в точке Dнапрямую зависит от плеча приложения нагрузки, поэтому в точке D опорная реакция Ra создает изгибающий момент в 3-и раза больше чем в точке B. Опорная реакция также сжимает верхние волокна, поэтому принимается со знаком минус.
3) Равномерно-распределенная нагрузка q1 создает изгибающий момент в точке D равный произведению этой нагрузки на длину ее приложения и на расстояние до центра ее приложения. По правилу знаков нагрузка q1 растягивает верхние волокна и принимается со знаком плюс.
Значение изгибающего момента в точки D слева равно:
На участке CD нет никаких нагрузок, поэтому изменение напряжения M прямолинейно
Рассмотрим точку D справа
В точке D начинается приложение переменной нагрузки q2 и приложена сосредоточенная сила F1, но плечо приложения нагрузки еще равно нулю, поэтому значение изгибающего момента M в точке D справа не изменяется и равно значению слева от точки D.
Определяем напряжение M на участке DE
Рассматриваем участок слева от точки E
Изгибающий момент в точке E слева формируется из следующих составных:
1) Изгибающий момент Ma — опорная реакция в точке A. Значение изгибающего момента на изменяется от расстояния. Также как и для точки B значение изгибающего момента принимаем со знаком плюс т.к. он растягивает верхние волокна в точке E.
2) Опорная реакция Ra. Значение изгибающего момента в точке E напрямую зависит от плеча приложения нагрузки, поэтому в точке E опорная реакция Ra создает изгибающий момент в 4-ре раза больше чем в точке B. Опорная реакция также сжимает верхние волокна, поэтому принимается со знаком минус.
3) Равномерно-распределенная нагрузка q1 создает изгибающий момент в точке E равный произведению этой нагрузки на длину ее приложения и на расстояние до центра ее приложения. По правилу знаков нагрузка q1 растягивает верхние волокна и принимается со знаком плюс.
4) Сосредоточенная сила F1 создает изгибающий момент, равный произведению силы на плечо. Т.к. действие силы стремится сжать верхние волокна (напоминаю мы рассматриваем действие силы вокруг точки E), то изгибающий момент принимаем со знаком минус.
5) Переменная нагрузка q2 создает изгибающий момент, равный произведению половины от максимальной силы, на длину приложения и на расстояние от центра сил (точка находится примерно 1/3 участка приложения сил ближе к максимальной нагрузке) до рассматриваемой точки
Значение изгибающего момента в точки E слева равно:
На участке DE изменение изгибающего момента не равномерно т.к. на этом участке имеется переменная нагрузка, эпюра имеет изогнутый вид
Теперь рассмотрим точку E с учетом приложенной к нему нагрузок (точка E справа)
Тут добавляется момент M1. Действие изгибающего момента M1 стремится сжать верхние волокна поэтому мы принимаем его со знаком минус.
Значение изгибающего момента справа от точки E равно:
Действие изгибающего момента создает скачок в точке E. В итоге мы получаем такую эпюру изгибающих моментов для данного примера:
Значение изгибающего момента для консольной балки всегда равно нулю на свободном конце. Только если в конце балки приложен момент он будет отличатся на графике и будет равен значению этого момента, но изгибающий момент для E справа все равно будет равен нулю.
Также как и для эпюры Q не всегда обязательно рассматривать значения справа и слева от рассматриваемой точки. Только для точки в которой приложен изгибающий момент нужно рассматривать отдельно с учетом этого момента и без т.к. изгибающий момент создает скачок на эпюре моментов.
Эпюра Q и M
Покажем эпюры Q и M вместе чтобы увидеть где будут максимальные нагрузки
Надеюсь моя статья поможет в освоении азов сопротивления материалов.
Также ознакомитесь со статьей «Типовые эпюры консольной балки»
перейти к содержанию
Ваш гид по программному обеспечению SkyCiv – учебные пособия, практические руководства и технические статьи
-
Домой
-
Учебники
-
Beam Tutorials
- Полное руководство по консольной балке | Прогибы и моменты
Полное руководство по консольной балке | Прогибы и моменты
Список содержания
- Что такое Консольный Луч?
- Уравнения консольной балки и расчеты вручную
- прогиб
- Изгибающий момент
- Стрессы
- Реакции
- Конструкция консольной балки
- Программное обеспечение для консольных балок
Определение консольной балки: Что такое Консольный Луч?
Консольная балка представляет собой конструктивный элемент, который простирается горизонтально и поддерживается только на одном конце.. Неподдерживаемый конец известен как кантилевер., и выходит за пределы точки опоры. Консольные балки часто используются в строительстве для поддержки балконов., крыши, и другие навесы. Их также можно использовать в мостах и других сооружениях, чтобы расширить настил над водным путем или другим препятствием..
Консольные балки — это элементы, которые поддерживаются только с одной стороны. – обычно с фиксированной опорой. Для того чтобы структура была статичной, опора должна быть закреплена так, чтобы она была способна воспринимать все силы и моменты во всех направлениях. Консольный луч обычно моделируется так, с левым концом, являющимся опорой, и правым концом, являющимся консольным концом:

Консольные уравнения луча
Существует ряд уравнений для расчета усилий и прогибов консольной балки.. Их можно упростить до простой формулы консольной балки., на основании следующих:
Прогибы консольной балки
Взято из нашего формула и уравнение прогиба балки страница. Уравнения консольной балки можно рассчитать по следующей формуле, где:
- W = нагрузка
- L = длина члена
- E = модуль Юнга
- Я = Момент инерции луча
Моменты консольной балки
Так как же рассчитать максимальную силу изгибающего момента консольной балки?? Вы можете сделать это, используя тот же метод, который показан в нашем как рассчитать изгибающий момент в балке статья. тем не мение, есть короткие уравнения, которые вы можете использовать. Например, уравнение для изгибающего момента в любой точке x вдоль консольной балки имеет вид:
(M_x = -Px)
где:
(M_x ) = изгибающий момент в точке x
(п ) = нагрузка, приложенная к концу кантилевера
(Икс ) = расстояние от фиксированного конца (опорная точка) до точки интереса по длине луча.
Для распределенной нагрузки, уравнение изменится на:
(М_х = – ∫wx) по длине (от х1 до х2)
где: w = распределенная нагрузка x1 и x2 – пределы интегрирования.
Это уравнение справедливо для простой консольной балки с точечной или равномерно распределенной нагрузкой, приложенной к свободному концу балки.. Следует учитывать, что консольная балка может иметь сложные нагрузочные и граничные условия., такие как многоточечные нагрузки, переменная распределенная нагрузка, или даже наклонные нагрузки, в этих случаях приведенное выше уравнение может быть недействительным, и может потребоваться более сложный подход, здесь пригодится FEA.
Консольный пучковый стресс
Как рассчитать напряжение в консольной балке? Консольное напряжение рассчитывается по изгибающей силе и зависит от поперечного сечения балки.. Например, если член совсем маленький, не так много площади поперечного сечения, по которой сила распределяется по, поэтому стресс будет довольно высоким. Напряжение балки кантилевера можно рассчитать с помощью нашего учебника по как рассчитать напряжение пучка или используя Программное обеспечение SkyCiv Beam – который покажет напряжения вашего луча.
Полезно отметить, что консольные балки обычно приводят к натяжению верхних волокон балки.. Это означает, что в случае бетонной консольной балки, первичная растяжимая арматура обычно требуется вдоль верхней поверхности. Это отличается от обычной бетонной балки, поддерживаемой с обоих концов., где первичная растяжимая арматура обычно располагается вдоль нижней поверхности балки.
Силы реакции консольной балки
Консоли отклоняются больше, чем большинство типов балок, поскольку они поддерживаются только с одного конца.. Это означает, что меньше поддержки для передачи нагрузки. Прогиб консольной балки можно рассчитать несколькими способами, включая использование упрощенных уравнений пучка кантилевера или калькуляторов пучка кантилевера и программного обеспечения (больше информации об обоих ниже). Уравнение реакции на неподвижной опоре консольной балки просто задается выражением:
Программное обеспечение для консольных балок
Программное обеспечение для анализа лучей SkyCiv позволяет пользователям легко и точно анализировать консольные балочные конструкции. Вы можете получить упрощенный анализ вашего балочного элемента, включая реакции, сдвигающая сила, изгибающий момент, отклонение, подчеркивает, и неопределенные лучи за считанные секунды. Применяйте любую комбинацию нагрузок и выполняйте полный расчет в соответствии с американскими стандартами., Европейская, австралиец, Канадские стандарты, назвать несколько!
Если вы хотите сначала попробовать, Бесплатный онлайн калькулятор луча отличный способ начать, или просто зарегистрируйтесь бесплатно сегодня!
да
Нет