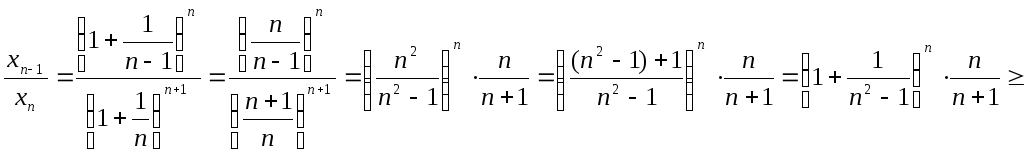Как найти монотонность последовательности

Содержание:

• Основные понятия и определения
• Примеры исследования последовательностей на монотонность
• Нестрогая монотонность

Основные понятия и определения

Можно дать еще одно альтернативное определение возрастающей последовательности.

Примеры исследования последовательностей на монотонность

Нестрогая монотонность

Последовательность $left{x_{n}right}$ является неубывающей
или нестрого возрастающей (невозрастающей или нестрого убывающей), если
для $forall n in N$, $x_{n} leq x_{n+1}left(x_{n} geq x_{n+1}right)$

Последовательность $left{x_{n}right}$ называется монотонной,
если она убывающая или возрастающая.

Если все элементы последовательности $left{x_{n}right}$ равны одному
и тому же числу, то последовательность называется постоянной.

Читать дальше: предел числовой последовательности.

Для начала вспомним, что называют последовательностью и дадим ей определение:

В качестве примера для иллюстрации данной темы можно привести арифметическую прогрессию $a, a + d, a+2d, …,a+(n-1)d,…$,в ней каждому элементу соответствует номер $1, 2, 3,…n$, являющийся целым и неотрицательным числом. Другой пример последовательности — геометрическая прогрессия, её элементы представлены ниже:
$a, aq, aq^2,…,aq^{n-1},…$.

Что такое монотонность последовательности

Монотонной называют последовательность, которая на всём своём промежутке всё время увеличивается или уменьшается.

Также существует монотонно неубывающая разновидность, её можно описать неравенством $x_1$ ≤ $x_2$ ≤ $… x_i …$ ≤ $x_n$ ≤ $x_{n+1}$ ≤ $…$.

Последовательность является монотонно убывающей, если соблюдается условие $x_1 > x_2 >… x_i…> x_n > x_{n+1} >…$. Используем альтернативную формулировку: если $n’$ > $n$, то $x_{n’}$

«Определение монотонности последовательности» 👇

Для того чтобы понять, является ли функция монотонно убывающей или возрастающей, необходимо:

1. Записать, чему равны $y_n$ и $y_{n+1}$.
2. Найти разность между $y_{n+1}$ и $y_n$.
3. Рассмотреть знак полученного на втором этапе выражения, если он отрицательный — последовательность убывающая, а если положительный – возрастающая.

Теорема Вейерштрасса о монотонных последовательностях

Для возрастающей последовательности:

Аналогичным образом звучит теорема для убывающей разновидности:

План урока:

Понятие числовой последовательности

Способы задания последовательностей

Возрастающие и убывающие последовательности

Ограниченные и неограниченные последовательности

Последовательности в жизни

Понятие числовой последовательности

Попытаемся записать в ряд все четные числа, начиная с двойки:

2, 4, 6, 8, 10, 12

Ясно, что запись можно продолжать бесконечно. Мы получили некоторый ряд чисел, в данном случае бесконечный. Любой такой ряд называется бесконечной числовой последовательностью

Приведем примеры бесконечных числовых послед-тей:

Заметим, что числа в послед-ти могут повторяться. Так, известно, что число π – это бесконечная десятичная дробь 3,1415926… Выписывая в ряд эти цифры, можно получить послед-ть, в которой будут повторяющиеся числа:

3, 1, 4, 1, 5, 9, 2, 6

Числа, входящие в состав послед-ти, называют членами послед-ти. Всегда можно указать, какое число является первым членом послед-ти, какое – вторым и т. д. Для их обозначения используются буквы с индексами. Например, есть послед-ть четных чисел 2, 4, 6, 8… Выпишем первые ее члены, обозначая их буквой а:

Получается, что каждому натуральному числу n соответствует какой-то единственный член послед-ти, который обозначается как а_n. То есть послед-ть задает некое правило, с помощью которого для каждого числа n можно вычислить число a_n. Отсюда можно сформулировать более сложное определение бесконечной числовой послед-ти – это функция, областью определения которой является множество натуральных чисел.

Способы задания последовательностей

Чтобы задать послед-ть, необходимо указать способ, с помощью которого можно вычислить любой ее член. Проще всего это сделать, записав формулу, в которой в качестве переменной использует номер члена послед-ти n.Такая формула называется формулой n-ого члена последовательности.

Пример. Послед-ть задается формулой а_n = 3n. Выпишите первые пять членов этой послед-ти.

Решение. Чтобы найти первый член послед-ти, то есть а₁, просто подставим в формулу единицу:

Аналогично можно вычислить и следующие четыре члена послед-ти:

Итак, послед-ть имеет вид:

3, 6, 9, 12, 15…

Ответ: 3, 6, 9, 12, 15

Пример:Запишите формулу n-ого члена для послед-ти

1, 3, 5, 7, 9…

состоящей из положительных нечетных чисел.

Решение. Каждое нечетное число можно представить в виде 2n– 1. Тогда получаем:

Получаются как раз члены послед-ти, указанной в условии. Поэтому формула n-ого члена будет выглядеть как а_n = 2n– 1.

Ответ: а_n = 2n– 1.

Стоит обратить внимание, что для вычисления n-ого члена послед-ти НЕ нужно вычислять все предшествующие члены.

Пример. Запишите 38-й член послед-ти, заданной формулой а_n = 2n² + 1.

Решение. Подставим n = 38 в формулу и получим:

Ответ: 1445

Теперь рассмотрим послед-ть, в которой первые два числа равны единице, а каждый следующий член равен сумме двух предыдущих. Она называется последовательностью Фибоначчи и начинается так:

1, 1, 2, 3, 5, 8, 13, 21…

Действительно, по условию, первые два члена – это единица:

а каждый следующий равен сумме предыдущих:

Формулу n-ого члена записать для послед-ти Фибоначчи очень сложно (хотя и возможно). Вместо этого здесь удобнее использовать рекуррентный способ задания последовательности. Записываются первые несколько членов послед-ти, а после дается формула (ее называют рекуррентной), которая позволяет вычислить следующие члены по предыдущим:

При использовании рекуррентного способа для вычисления n-ого члена обычно необходимо вычислить все предыдущие члены послед-ти.

Пример. Найдите пятый член послед-ти, заданной рекуррентной формулой а_n= 3•а_n–1– 1, если а₁ = 2.

Решение. Будем последовательно вычислять все члены послед-ти, вплоть до пятого:

Ответ: 5

Надо понимать, что одну и ту же послед-ть можно задать по-разному. Так, послед-ть четных чисел можно задать формулой n-ого члена а_n = 2n, так и рекуррентной формулой а_n = a_n–1 + 2, если а₁ = 1.

Пример. Дана послед-ть, заданная формулой а_n = n². Задайте ее рекуррентным способом.

Решение. Сначала вычислим первый член послед-ти:

Чтобы записать рекуррентную формулу, попытаемся найти разницу между членами, имеющими номера n и (n– 1):

Итак, получили равенство

Перенесем в нем слагаемое (– a_{n– 1}) вправо и получим рекуррентную формулу:

Наконец, некоторые послед-тине получается задать ни формулой n-ого члена, ни рекуррентным способом. Их можно только описать. Таковой является, например, послед-ть простых чисел:

2, 3, 5, 7, 11…

Мы не будем это доказывать, однако не существует такой формулы, которая позволяла бы вычислить n-ое простое число либо по самому числу n, либо по предыдущим простым числам. Действительно, для построения такой послед-ти используют особый алгоритм, известный как решето Эратосфена. Если бы существовала формула n-ого члена, то потребность в использовании решета Эратосфена отпала бы.

Возрастающие и убывающие последовательности

Рассмотрим послед-ть, заданную формулой а_n = 5n:

5, 10, 15, 20, 25…

Очевидно, что каждый следующий член больше предыдущего. Это значит, что мы имеем дело с возрастающей последовательностью.

Теперь изучим послед-ть, заданной рекурсивным способом:

Выглядеть он будет так:

50, 48, 46, 44, 42…

Ясно, что каждый следующий член послед-ти меньше предыдущего. Такой ряд чисел называется убывающей последовательностью.

Убывающие и возрастающие послед-ти называют также монотонными последовательностями.

Для того, чтобы определить характер послед-ти, достаточно найти разность членов а_nи а_n+1. Если получается положительное выражение, то послед-ть возрастает, а если выражение отрицательно, то послед-ть убывает. Если получилось выражение, которое может иметь различный знак, то послед-ть вовсе не является монотонной.

Пример. Послед-ть задана формулой a_n = n/(n + 1). Является ли она убывающей либо возрастающей?

Решение. Запишем выражения для вычисления n-ого и (n+ 1)-ого члена послед-ти:

Осталось найти их разницу:

При натуральных значениях n полученная разница является положительным числом. Это значит, что каждый следующий член больше предыдущего, то есть послед-ть является возрастающей.

Ответ: возрастающая.

Пример. Исследуйте на монотонность послед-ть, заданную формулой

Решение. Если выписать первые члены послед-ти, может показаться, что она – убывающая:

-7, -12, -15, -16…

Но это не так. Запишем выражения для n-ого и (n + 1)-ого члена послед-ти:

Теперь найдем их разность:

Получили выражение (2n– 7), которое может быть как отрицательным, так и положительным (при n≥ 4). Это значит, что послед-ть немонотонна. В этом можно убедиться, вычислив четвертый и пятый член послед-ти:

Получаем, что у₅>у₄, поэтому послед-ть не является убывающей

Ответ: послед-ть немонотонна.

 Ограниченные и неограниченные последовательности

Изучим послед-ть, заданную с помощью формулы b_n = 1/n. Её первые члены будут выглядеть так:

Очевидно, что она является убывающей, ведь каждая следующая дробь меньше предыдущей. Вместе с тем все члены послед-ти являются положительными числами. Это значит, что для каждого n выполняется неравенство b_n> 0. То есть последовательность ограничена числом 0. В математике такие послед-ти называют ограниченными снизу.

Существует и послед-ти, ограниченные сверху. Это такие послед-ти, каждый член которых меньше какого-то постоянного числа.

В качестве примера можно привести послед-ть, заданную формулой с_n = 1 – 1/n. Каждый следующий ее член все ближе к единице, но ни один из них не достигает ее. Покажем, как строго доказать это. Для этого используют метод рассуждений «от противного».

Предположим, что послед-ть с_n = 1 – 1/n не ограничена числом 1 сверху. Тогда существует такой ее член с_n, для которого выполняется условие

Попытаемся найти номер этого члена:

Полученное нер-во выполняется только для отрицательных n. Но n – это натуральное, то есть положительное число. Это говорит о том, что не существует такого натурального n, для которого справедливо нер-во 0 ≥ 1/n. Значит, и не существует такого с_n, для которого верно нер-во с_n ≥ 1. Из этого следует, что послед-ть ограничена сверху числом 1.

Пример. Докажите, что послед-ть m_n = n² – 6n + 4 ограничена снизу числом (– 6).

Решение. Предположим, что на самом деле послед-ть не ограничена снизу числом (– 6). Тогда хотя бы для одного ее члена будет выполняться нер-во

Найдем номер этого члена:

Получили неравенство второй степени. Для его решения следует найти корни квадратного трехчлена. Начнем с вычисления дискриминанта:

Дискриминант отрицательный, а ветви параболы смотрят вверх. Поэтому схематично парабола относительно оси Ох будет располагаться так:

Видно, что нер-во решений не имеет. Значит, не существует такого номера n, для которого верно условие m_n ≤ – 6. Следовательно, послед-ть ограничена снизу числом (– 6).

Если послед-ть ограничена одновременно и снизу, и сверху, то ее называют просто ограниченной послед-тью.

Примером ограниченной последовательности является b_n = 1/n. С одной стороны, она ограничена нулем снизу. С другой стороны, она ограничена сверху числом 2, так как первый ее член равен единице, а вся послед-ть – убывающая.

Примером неограниченной последовательности является v_n = 5n, ведь ее невозможно ограничить сверху.

Примером ограниченной последовательности является b_n = 1/n. С одной стороны, она ограничена нулем снизу. С другой стороны, она ограничена сверху числом 2, так как первый ее член равен единице, а вся послед-ть – убывающая.

Примером неограниченной последовательности является v_n = 5n, ведь ее невозможно ограничить сверху.

1, 3, 5, 7, 9…

Начнем вычислять сумму первых n членов двумя способами: просто складывая и используя формулу S_n= n². Посмотрим, будут ли получаться одинаковые результаты.

Видно, что формула работает. Однако, сколько бы раз мы не проверяли ее, это не будет служить строгим доказательством ее справедливости. Возможно, что она будет работать для первого миллиона члена послед-ти, а для 1000001-ого даст ошибку. Поэтому поступим иначе. Предположим, что фор-ла S_n= n² верна хотя бы для одного значения n, равного k:

Докажем, что тогда она будет верна и для следующего числа k + 1. То есть нужно доказать равенство

Ясно, что сумму (k + 1) членов послед-ти можно получить, прибавив к сумме k членов (то есть к S_k )ещё одно слагаемое a_n+1, то есть справедлива запись:

При этом мы предположили, что верно равенство

а число a_n+1 можно посчитать по формуле n-ого члена:

Тогда можно записать

Получили формулу сокращенного умножения – квадрат суммы. Его можно «свернуть»:

Итак, если для формула S_k= k² верна для k = 1 (а в этом мы убедились в самом начале), то она верна и для k = 2. Но если она верна для k = 2, то она верна и для k = 3 и т.д. Получаем цепочку утверждений, каждое из которых подтверждает истинность формулы для конкретного натурального числа k, а все вместе они подтверждают ее истинность для всех натуральных чисел. Таким образом, нам удалось доказать справедливость формулы S_n= n².

Сформулируем принцип математической индукции:

То есть сначала надо доказать, что утверждение выполняется при n = 1. Это действие называют шагом индукции. Далее предполагают, что утверждение верно при n = k, и из этого выводят, что оно верно и для n =k + 1.

Пример. Докажите с помощью математической индукции, что сумма квадратов первых n натуральных чисел вычисляется по формуле:

Решение. Докажем базис индукции, то есть то, что утверждение верно при n = 1. Действительно, подставив единицу в формулу, получим:

Получили один и тот же результат. Базис индукции доказан.

Теперь предположим, что формула верна для произвольного n = k:

Тогда сумма (k + 1) квадратов может быть найдена по формуле

Подставим в нее выражение для S_k и получим:

С другой стороны, нам надо доказать, что величина S_k+1определяется по формуле

Приравняем выражения (1) и (2) и покажем, что они тождественно равны:

Умножим обе части на 6 и получим:

Получили одинаковые выражения в обоих частях рав-ва, поэтому оно является верным при любом значении k. Значит, мы смогли доказать шаг индукции, и следовательно, всё исходное утверждение.

Пример. Докажите, что любую сумму, большую 7 копеек, можно оплатить, используя только два типа монет: по 3 и 5 копеек.

Это утверждение, очевидно, верно сумм в 8, 9 и 10 копеек:

Добавив к этим суммам ещё одну трехкопеечную монету, мы сможем получить выражения для следующих трех чисел:

С помощью ещё одной монетки в три копейки можно уплатить следующие 3 суммы:

Ясно, что продолжая подобные рассуждения, можно для любого натурального числа записать эквивалентную ему сумму пятерок и троек, что доказывает утверждение из условия.

Последовательности в жизни

Порою, изучая математические объекты, люди задумываются – а какое отношение все эти формулы имеют к реальной жизни? Встречаются ли последовательности в природе и обществе, или они являются лишь плодом фантазии математиков?

На самом деле последовательности имеют большое практическое приложение. Так, Фибоначчи сформулировал свою последовательность тогда, когда изучал скорость размножения кроликов. Если каждая пара кроликов рожает в месяц ещё одну пару, а через месяц и старая, и новая пара рожает ещё кроликов, то их численность будет расти также, как и последовательность Фибоначчи! Аналогично протекают процессы роста популяций других животных.

Большое значение последовательности имеют в программировании. Дело в том, что порою программам нужно получить некоторое случайное число, чтобы имитировать случайные события. Однако по ряду причин компьютеру тяжело сгенерировать истинно случайное число, поэтому часто используют генераторы псевдослучайных чисел. Это особые алгоритмы, порождающие последовательности чисел, которые кажутся случайными, хотя таковыми на самом деле не являются.

Встречаются последовательности и в астрономии. В частности, расстояние от планет до Солнца примерно можно рассчитать с помощью особой последовательности Тициуса-Боде. Последние исследования показывают, что и расположение планет в других планетных системах хорошо описывается этой последовательностью.

Определение 1. Последовательностьназываетсяубывающей (невозрастающей),
если для всехвыполняется неравенство.

Определение 2. Последовательностьназываетсявозрастающей (неубывающей),
если для всехвыполняется неравенство.

Определение 3. Убывающие, невозрастающие,
возрастающие и неубывающие последовательности
называютсямонотонными
последовательностями, убывающие
и возрастающие последовательности
называют такжестрого монотонными
последовательностями.

Очевидно, что неубывающая последовательность
ограничена снизу, невозрастающая
последовательность ограничена сверху.
Поэтому всякая монотонная последовательность
заведомо ограничена с одной стороны.

Пример 1. Последовательностьвозрастает,не
убывает,убывает,не возрастает,– немонотонная последовательность.

Для монотонных последовательностей
важную роль играет следующая

Теорема 1. Если неубывающая
(невозрастающая) последовательность
ограничена сверху (снизу), то она сходится.

Доказательство. Пусть последовательностьне убывает и ограничена сверху, т.е.и множествоограничено сверху. По теореме 1 § 2
существует.
Докажем, что.

Возьмем
произвольно. Посколькуа – точная
верхняя граница, существует номерN
такой, что.
Так как последовательность неубывающая,
то для всехимеем,
т.е.,
поэтомудля всех,
а это и означает, что.

Для невозрастающей последовательности,
ограниченной снизу, доказательство
проводится аналогично (студенты могут
доказать это утверждение дома
самостоятельно). Теорема доказана.

Замечание. Теорему 1 можно сформулировать
иначе.

Теорема 2. Для того чтобы монотонная
последовательность сходилась, необходимо
и достаточно, чтобы она была ограничена.

Достаточность установлена в теореме
1, необходимость – в теореме 2 § 5.

Условие монотонности не является
необходимым для сходимости
последовательности, так как сходящаяся
последовательность не обязательно
монотонна. Например, последовательность

не монотонная, однако сходится к нулю.

Следствие. Если последовательностьвозрастает (убывает) и ограничена сверху
(снизу), то().

Действительно, по теореме 1
().

Определение 4. Еслиипри,
то последовательностьназываетсястягивающейся системой
вложенных отрезков.

Теорема 3 (принцип вложенных отрезков).
У всякой стягивающейся системы вложенных
отрезков существует, и притом единственная,
точкас, принадлежащая всем отрезкам
этой системы.

Доказательство. Докажем, что точкас существует. Поскольку,
тои, следовательно, последовательностьне убывает, а последовательностьне возрастает. При этомиограничены, так как.
Тогда по теореме 1 существуюти,
но так как,
то=.
Найденная точкас принадлежит всем
отрезкам системы, так как по следствию
теоремы 1,,
т.е.для всех значенийn.

Покажем теперь, что точка с –
единственная. Предположим, что таких
точек две:с иdи пусть для определенности.
Тогда отрезок
принадлежит всем отрезкам,
т.е.для всехn, что
невозможно, так каки, значит, начиная с некоторого номера,.
Теорема доказана.

Отметим, что здесь существенно то, что
рассматриваются замкнутые промежутки,
т.е. отрезки. Если рассмотреть систему
стягивающихся интервалов, то принцип,
вообще говоря, неверен. Например,
интервалы
,
очевидно, стягиваются в точку,
однако точкане принадлежит ни одному интервалу этой
системы.

Рассмотрим теперь примеры сходящихся
монотонных последовательностей.

1) Число е.

Рассмотрим теперь последовательность
.
Как она себя ведет? Основание

степени
,
поэтому?
С другой стороны,,
а,
поэтому?
Или предел не существует?

Чтобы ответить на эти вопросы, рассмотрим
вспомогательную последовательность
.
Докажем, что она убывает и ограничена
снизу. При этом нам будет нужна

Лемма. Если,
то для всех натуральных значенийnимеем

(неравенство Бернулли).

Доказательство. Воспользуемся
методом математической индукции.

Если
,
то,
т.е. неравенство верно.

Предположим, что оно верно для
и докажем его справедливость для+1.

Верно
.
Умножим это неравенство на:

.

Таким образом,
.
Значит, согласно принципу математической
индукции, неравенство Бернулли верно
для всех натуральных значенийn.
Лемма доказана.

Покажем, что последовательность
убывает. Имеем

‌‌‌׀неравенство
Бернулли׀

,а это и означает, что
последовательностьубывает.

Ограниченность снизу следует из
неравенства
‌‌‌׀неравенство
Бернулли׀для всех натуральных значенийn.

По теореме 1 существует
,
который обозначают буквойе. Поэтому.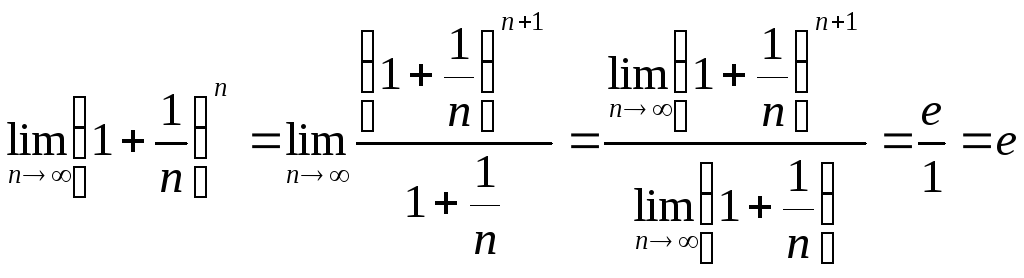

Число еиррационально и трансцендентно,е= 2,718281828… . Оно является, как
известно, основанием натуральных
логарифмов.

Замечания. 1) Неравенство Бернулли
можно использовать для доказательства
того, чтопри.
Действительно, если,
то.
Тогда, по неравенству Бернулли,при.
Отсюда приимеем,
то естьпри.

2) В рассмотренном выше примере основание
степени
стремится к 1, а показатель степениn– к,
то есть имеет место неопределенность
вида.
Неопределенность такого вида, как мы
показали, раскрывается с помощью
замечательного предела.

2)
(*)

Докажем, что эта последовательность
сходится. Для этого покажем, что она
ограничена снизу и не возрастает. При
этом воспользуемся неравенством
для всех,
которое является следствием неравенства.

Имеем
см.
неравенство выше,
т.е. последовательность ограничена
снизу числом.

Далее,
так
как,
т.е. последовательность не возрастает.

По теореме 1 существует
,
который обозначимх. Переходя в
равенстве (*) к пределу при,
получим

,
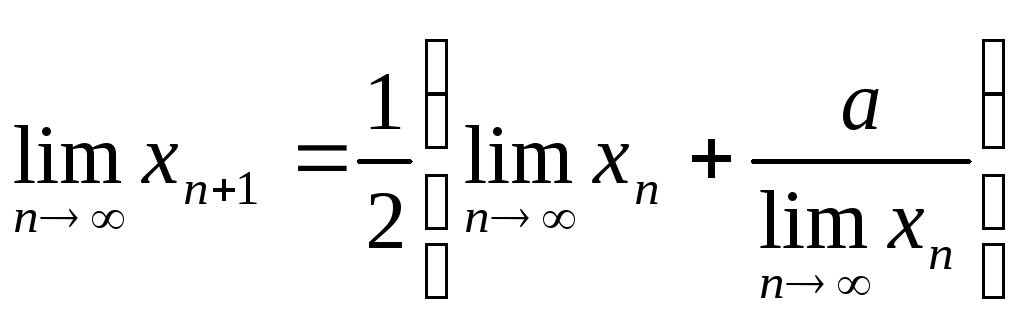
т.е.,
откуда(берем знак «плюс», так как все члены
последовательности положительны).

Последовательность (*) применяется при
вычислении
приближенно. Заберут любое положительное число.
Например, найдем.
Пусть.
Тогда,.
Таким образом,.

3)
.

Имеем
.
Посколькупри,
существует номерN,
такой, что для всехвыполняется неравенство.
Таким образом, последовательность,
начиная с некоторого номераN,
убывает и ограничена снизу, так какдля всех значенийn.
Значит, по теореме 1 существует.
Поскольку,
имеем.

Итак,
.

4)
,
справа –n корней.

Методом математической индукции покажем,
что
для всех значенийn.
Имеем.
Пусть.
Тогда,
отсюда получаем утверждение по принципу
математической индукции. Используя
этот факт, находим,
т.е. последовательностьвозрастает и ограничена сверху. Поэтому
существует,
так как.

Таким образом,
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей.

Определения[править | править код]

Пусть имеется множество , на котором введено отношение порядка.

Последовательность элементов множества называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.

— неубывающая

Последовательность элементов множества называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.

— невозрастающая

Последовательность элементов множества называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий.

— возрастающая

Последовательность элементов множества называется убывающей, если каждый элемент этой последовательности превышает следующий за ним.

— убывающая

Последовательность называется монотонной, если она является неубывающей, либо невозрастающей.^[1]

Последовательность называется строго монотонной, если она является возрастающей, либо убывающей.

Очевидно, что строго монотонная последовательность является монотонной.

Иногда используется вариант терминологии, в котором термин «возрастающая последовательность» рассматривается в качестве синонима термина «неубывающая последовательность», а термин «убывающая последовательность» — в качестве синонима термина «невозрастающая последовательность». В таком случае возрастающие и убывающие последовательности из вышеприведённого определения называются «строго возрастающими» и «строго убывающими», соответственно.

Промежутки монотонности[править | править код]

Может оказаться, что вышеуказанные условия выполняются не для всех номеров , а лишь для номеров из некоторого диапазона

(здесь допускается обращение правой границы в бесконечность). В этом случае последовательность называется монотонной на промежутке , а сам диапазон называется промежутком монотонности последовательности.

Примеры[править | править код]

• Последовательность натуральных чисел.

• Последовательность Фибоначчи.

• Геометрическая прогрессия с основанием .

• Последовательность, сходящаяся к числу e.

Свойства[править | править код]

• Ограниченность.
  • Всякая неубывающая последовательность ограничена снизу.
  • Всякая невозрастающая последовательность ограничена сверху.
  • Всякая монотонная последовательность ограничена по крайней мере с одной стороны.

• Монотонная последовательность сходится тогда и только тогда, когда она ограничена с обеих сторон.(Теорема Вейерштрасса об ограниченных монотонных последовательностях)
  • Сходящаяся неубывающая последовательность ограничена сверху своим пределом.
  • Сходящаяся невозрастающая последовательность ограничена снизу своим пределом.

Примечания[править | править код]

1. ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 68 — 105. — 672 с. — ISBN 5-482-00445-7.

См. также[править | править код]

• Монотонная функция