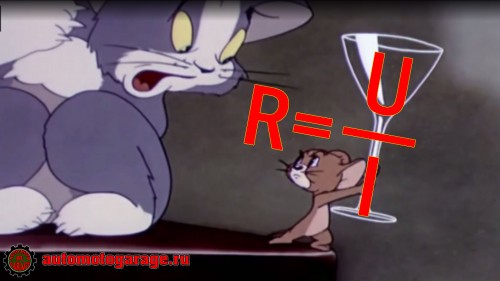Как найти мощность через закон ома

Электрическая мощность и закон Ома

Для анализа и расчета параметров нагревателей, как правило, мы используем различные методы, в частности закон Ома. Этот закон используется в основном для определения неизвестных величин, таких как напряжение, ток, сопротивление и мощность, которые связаны с одним или несколькими элементами электронной схемы. Закон Ома – основной закон теории электрических цепей, который определяет линейную зависимость между напряжением, током и сопротивлением. В данной статье мы постараемся  подробно рассказать о законе Ома и его практическом применении.

Закон Ома

Закон Ома – это основной, главный и важный закон теории электрических цепей, который исследует взаимосвязь между напряжением, током и сопротивлением. В нем говорится, что при постоянной температуре ток, протекающий по цепи, прямо пропорционален напряжению или разности потенциалов в этой цепи.

В алгебраической форме, V∝ I

V = IR

Где

I – ток, протекающий по цепи, измеряется в амперах.

V — напряжение, приложенное к цепи, измеряется в вольтах.

А R — это константа пропорциональности, называемая сопротивлением, которое измеряется в омах.

Это сопротивление также указывается в килоомах, мегаомах и т. д.

Следовательно, закон Ома гласит, что ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению в этой цепи. Закон Ома можно применить как к отдельным частям, так и ко всей цепи.

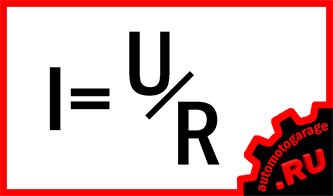
Математически ток, I = V/R

Напряжение, V = IR

Сопротивление, R = V/I

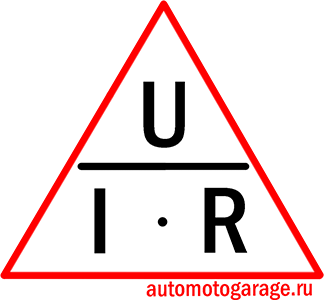
Треугольник закона Ома

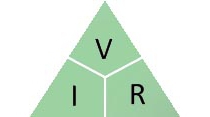
Ниже показано, что отношение между различными величинами в законе Ома называется треугольником закона Ома. Это простой метод описания, а также простой для запоминания соотношения между напряжением, током и сопротивлением.

На приведенном выше рисунке показан треугольник закона Ома, где отдельные термины, такие как напряжение, ток и сопротивление, и их формулы представлены из основного уравнения закона Ома. На приведенном выше рисунке один параметр вычисляется из оставшихся двух параметров. Таким образом, можно сделать вывод, что при высоком сопротивлении ток будет низким, а ток будет высоким, когда сопротивление низкое, при любом приложенном напряжении.

Электрическая мощность

Электрическая мощность дает скорость, с которой энергия передается по цепи. Электрическая мощность измеряется в ваттах. Эта мощность потребляется, когда напряжение вызывает протекание тока в цепи.

Следовательно, электрическая мощность есть произведение напряжения и силы тока.

Математически P = VI

По закону Ома V = IR и I = V/R

Подставляя в уравнение мощности

P = I² R

P = V²/ R

Следовательно, электрическая мощность, P =VI или I ² R или V ² / R

Это три основные формулы для нахождения электрической мощности в цепи. Таким образом, мощность может быть рассчитана, когда известна любая из двух величин.

Треугольник мощности

Подобно треугольнику закона Ома, на рисунке ниже показан треугольник мощности, чтобы показать соотношение между мощностью, напряжением и током. Уравнения отдельных параметров легко запоминаются по этому рисунку. Округлите и скройте параметр, который необходимо измерить, а положение оставшихся двух параметров дает уравнение для поиска скрытого или округленного параметра, как показано на рисунке ниже.

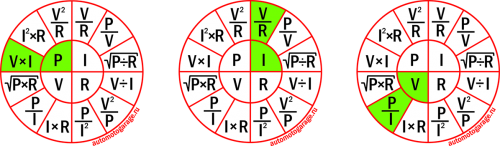
Круговая диаграмма закона Ома

В дополнение к двум вышеупомянутым концепциям существует еще один метод определения параметров схемы с использованием закона Ома, который представляет собой круговую диаграмму закона Ома. Используя круговую диаграмму закона Ома, можно легко запомнить все уравнения для нахождения напряжения, тока, сопротивления и мощности, которые необходимы для упрощения электрических цепей, которые могут быть простыми или сложными.

На приведенном выше рисунке показана круговая диаграмма, которая показывает взаимосвязь между мощностью, напряжением, током и сопротивлением. Эта диаграмма разделена на четыре блока для мощности, напряжения, сопротивления и тока. Каждый блок состоит из трех формул с двумя известными значениями для каждой формулы. Из диаграммы для нахождения каждого параметра в цепи мы можем использовать любую из трех доступных формул.

Графическое представление закона Ома

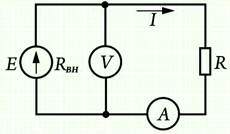
Для лучшего понимания этой концепции ниже приведена экспериментальная установка, в которой регулируемый источник напряжения с шестью ячейками (по 2 В каждая) подключен к нагрузочному резистору через переключатель выбора напряжения. Измерительные приборы, такие как вольтметр и амперметр, также подключены к цепи для измерения напряжения и тока в цепи.

Регулируемый источник напряжения с нагрузочным резистором

Сначала подключите резистор 10 Ом и установите переключатель в положение «1». Тогда амперметр показывает 0,2 А, а вольтметр показывает 2 В, потому что I = V/R, т. е. I = 2/10 = 0,2 А. Затем измените положение селекторного переключателя на вторую ячейку, чтобы подать 4 В на нагрузку и запишите показания амперметра. По мере того, как селектор будет постепенно изменяться от первого положения к последнему, мы получим текущие значения, такие как 0,2, 0,4, 0,6, 0,8, 1, 1,2 для значений напряжения 2, 4, 6, 8, 10 и 12 соответственно.

Точно так же поместите резистор 20 Ом вместо резистора 10 Ом и выполните ту же процедуру, что и выше. Мы получим значения тока 0,1, 0,2, 0,3, 0,4, 0,5, 0,6 для значений напряжения 2, 4, 6, 8, 10 и 12В соответственно. Постройте график этих значений, как показано ниже.

Графическое представление закона Ома

На приведенном выше графике для данного напряжения ток меньше, когда сопротивление больше. Рассмотрим случай приложенного напряжения 12 В, когда значение тока составляет 1,2 А при сопротивлении 10 Ом и 0,6 Ом при сопротивлении 20 Ом. Точно так же при одном и том же токе напряжение тем больше, чем больше сопротивление. Из приведенных выше результатов следует, что отношение напряжения к току постоянно, когда сопротивление постоянно. Следовательно, зависимость между напряжением и током является линейной, и наклон этой линейной кривой становится тем круче, чем больше сопротивление.

Пример применения закона Ома

Рассмотрим приведенную ниже схему, в которой батарея на 6 В подключена к нагрузке 6 Ом. Амперметр и вольтметры подключены к цепи для измерения тока и напряжения практически. Но используя закон Ома мы можем найти силу тока и мощность следующим образом.

Из закона Ома

V = IR

I = V/R

I = 6/6

I = 1 А

Мощность, P = VI

P = 6×1

P = 6 Вт

Но практически амперметр не показывает точное значение из-за внутреннего сопротивления батареи. Включив внутреннее сопротивление батареи (предположим, что батарея имеет внутреннее сопротивление 1 Ом), текущее значение рассчитывается следующим образом.

Общее сопротивление цепи 6+1=7 Ом.

Ток, I = V/R

I = 6/7

I = 0,85 Ампер

Цепь фар в автомобиле

На приведенном ниже рисунке показана схема фар легкового автомобиля без схемы управления. С применением закона Ома мы можем узнать ток, протекающий через каждую лампу. Как правило, каждая лампочка подключается параллельно к аккумулятору, что позволяет другим элементам светиться, даже если какой-то из них поврежден. К этим параллельным лампам подводится батарея 12 В, где лампы имеют сопротивление 2,4 каждая (считается в данном случае).

Общее сопротивление цепи равно R = R1x R2/(R1 + R2), так как они соединены параллельно.

R = 5,76/4,8 = 1,2

Тогда ток, протекающий по цепи, равен I = V/R.

I = 12/1,2

I = 10А.

Ток, протекающий через отдельную лампу, равен I1 = I2 = 5 А (из-за одинаковых сопротивлений).

Закон Ома для цепей переменного тока

В общем, закон Ома можно применить и к цепям переменного тока . Если нагрузка индуктивная или емкостная, то также учитывается реактивное сопротивление нагрузки. Следовательно, с некоторыми изменениями закона Ома, учитывающими влияние реактивного сопротивления, его можно применять к цепям переменного тока. Из-за индуктивности и емкости в переменном токе будет значительный фазовый угол между напряжением и током. А также сопротивление переменному току называется импедансом и обозначается как Z.

Таким образом, закон Ома для цепей переменного тока задается как

E = IZ

I = E/Z

Z = E/I

Где E – напряжение в цепи переменного тока,

I – текущий ток,

Z — импеданс.

Все параметры в приведенном выше уравнении представлены в комплексной форме, которая включает фазовый угол. Подобно круговой диаграмме цепи постоянного тока, круговая диаграмма закона Ома для цепи переменного тока приведена ниже.

Пример закона Ома (цепи переменного тока)

Рассмотрим приведенную ниже схему, в которой нагрузка переменного тока (сочетание резистивной и индуктивной) подключена к источнику переменного тока 10 В, 60 Гц. Нагрузка имеет сопротивление 5 Ом и индуктивность 10 мГн.

Тогда значение импеданса нагрузки Z = R + jX _L

Z = 5 + j (2∏ × f × L)

Z = 5+ j (2×3,14×60×10×10-3)

Z = 5 + j3,76 Ом или 6,26 Ом при фазовом угле -37,016

Ток, протекающий по цепи, равен

I = V/Z = 10/(5+ j3,76) = 1,597 А при фазовом угле -37,016

Для расчета параметров сети для подключения нагревателей вы можете воспользоваться данными в данной статье основными формулами, или же просто позвоните нашим специалистам компании Термоэлемент по телефону и получите полную бесплатную консультацию и помощь с выбором нужных параметров нагревателей для вашей задачи по нагреву.

Начнём с терминологии.
Электрический ток – это направленное движение заряженных частиц, при котором происходит перенос заряда из одной области
электрической цепи в другую.
Силой электрического тока (I) является величина, которая численно равна количеству заряда Δq, протекающего через заданное поперечное
сечение проводника S за единицу времени Δt: I = Δq/Δt.
Напряжение электрического тока между точками A и B электрической цепи – физическая величина, значение которой равно работе эффективного
электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.
Омическое (активное) сопротивление – это сопротивление цепи постоянному току, вызывающее безвозвратные потери энергии
постоянного тока.
Теперь можно переходить к закону Ома.

Закон Ома был установлен экспериментальным путём в 1826 году немецким физиком Георгом Омом и назван в его честь.

По большому счёту, Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях,
определяющих зависимость между электрическими величинами, такими как: напряжение, сопротивление и сила тока исключительно
для проводников, обладающих постоянным сопротивлением.
При расчёте напряжений и токов в нелинейных цепях, к примеру, таких, которые содержат полупроводниковые или электровакуумные приборы,
этот закон в простейшем виде уже использоваться не может.

Тем не менее, закон Ома был и остаётся основным законом электротехники, устанавливающим связь силы
электрического тока с сопротивлением и напряжением.

Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо
пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника
и записана в следующем виде:

I=U/R,

где
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеря- емая в вольтах [В];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные от этой формулы приобретают такой же незамысловатый вид:

R=U/I и U=R×I.

Зная любые два из трёх приведённых параметров можно произвести и расчёт величины мощности,
рассеиваемой на резисторе.

Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам,
также являющимся производными от основной формулы закона Ома:

P_(Вт) = U_(В)×I_(А) = I²_(А)×R_(Ом) =
U²_(В)/R_(Ом)

Формулы, описывающие закон Ома, настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной
крупной статьи на страницах уважающего себя сайта.

Не заслуживают, так не заслуживают. Деревянные счёты Вам в помощь, уважаемые дамы и рыцари!

Считайте, учитывайте размерность, не стирайте из памяти, что:

Единицы измерения напряжения: 1В=1000мВ=1000000мкВ;
Единицы измерения силы тока:1А=1000мА=1000000мкА;
Единицы измерения сопротивления:1Ом=0.001кОм=0.000001МОм;
Единицы измерения мощности:1Вт=1000мВт=100000мкВт.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатый калькулятор, позволяющий в онлайн
режиме проверить расчёты, связанные со знанием формул закона Ома.

ОНЛАЙН КАЛЬКУЛЯТОР ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА

Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.

Напряжение U
Сопротивление R
Сила тока I
Мощность Р

Все наши расчёты проводились при условии, что значение внешнего сопротивления
R значительно превышает внутреннее
сопротивление источника напряжения r_внутр.
Если это условие не соблюдается, то под величиной R следует
принять сумму внешнего и внутреннего сопротивлений:
R = R_внешн + r_внутр ,
после чего закон приобретает солидное название – закон Ома для полной цепи:
I=U/(R+r) .

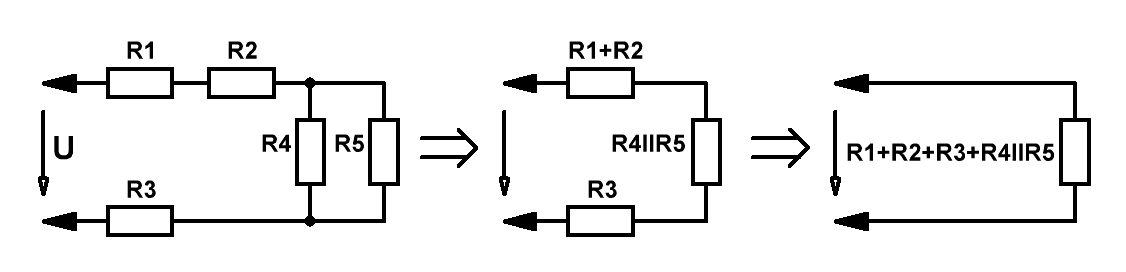
Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду:

Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов
определяются исходя из формулы:

1/R_ll = 1/R₄+1/R₅.
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице
ссылка на страницу.

Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше,
остаётся в силе.

Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока – под значением U следует
понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
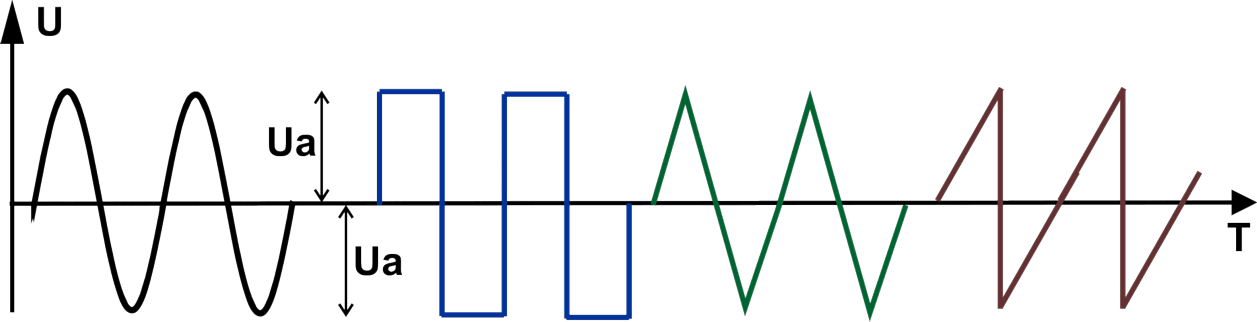
Приведём диаграммы для нескольких различных форм сигнала.

Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2),
сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов – это максимальное значение, которого достигает
амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитываем действующее значение напряжение интересующей нас формы:

Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.

С этим разобрались!

Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости
в цепи переменного тока.
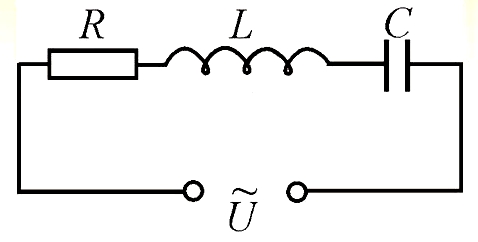
В общем случае смотреться это будет так:

А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z,
состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих
трёх элементов обойтись не удаётся, и формула приобретает вид:

Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице
ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока
и описываются формулами:
X_C = 1/(2πƒС) ,   X_L = 2πƒL .

Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.

Количество вводимых элементов должно быть не менее одного, при наличии
индуктивного или емкостного элемента – необходимо указать значение частоты
f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.

Сопротивление R
Индуктивность L
Ёмкость С
Частота f
Реактивное сопротивление XC
Реактивное сопротивление XL
Полное сопротивление цепи Z

Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем
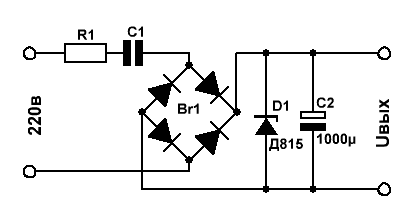
простенький бестрансформаторный источник питания.

Токозадающими цепями в данной схеме являются элементы R1 и С1.

Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом – 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в – 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока
нагрузки.
Зададимся номиналами R1 – 30 Ом, С1 – 1 Мкф, частотой сети f – 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет – надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости – 3,18 Мкф, при котором Z = 1,04кОм.

Всё – закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!

Мощность электрического тока является величиной, которая характеризует его свойства. Она определяется силой тока и напряжением. Единицей измерения является Ватт, в честь первооткрывателя этой величины. Обозначается она буквами Вт, в английском языке буквой W. В формулах эта характеристика имеет другое условное обозначение – латинская буква Р. Измеряется мощность тока ваттметром. Найти мощности нужно умножив силу тока на напряжение, то есть амперы на вольты получаем Ватты.

В статье будет рассказано подробно, о том, что такое мощность, как ее можно определить, от чего зависит и на что влияет.

Что такое мощность в электричестве

Механическая мощность как физическая величина равна отношению выполненной работы к некоторому промежутку времени. Поскольку понятие работы определяется количеством затраченной энергии, то и мощность допустимо представить как скорость преобразования энергий. Разобрав составляющие механической мощности, рассмотрим из чего складывается электрическая. Напряжение — выполняемая работа по перемещению одного кулона электрического заряда, а ток — количество проходящих кулонов за одну секунду. Произведение напряжения на ток показывает полный объем работы, выполненной за одну секунду.

Мощность электрического тока – количественная мера тока, характеризующая его энергетические свойства. Определяется основными параметрами – силой тока и напряжением. Измеряется мощность электрического тока прибором, который называется Ваттметр. Единица измерения — Ватт (Вт).

Проанализировав полученную формулу, можно заключить, что силовой показатель зависит одинаково от тока и напряжения. То есть, одно и тоже значение возможно получить при низком напряжении и большом тока, или при высоком напряжении и низком токе. Пользуясь зависимостью мощности от напряжения и силы тока, инженеры научились передавать электричество на большие расстояния путем преобразования энергии на понижающих и повышающих трансформаторных подстанциях.

Наука подразделяет электрическую мощность на:

• активную. Подразумевает преобразование мощности в тепловую, механическую и другие виды энергии. Показатель выражают в Ваттах и вычисляют по формуле U*I;
• реактивную. Эта величина характеризует электрические нагрузки, создаваемые в устройствах колебаниями энергии электромагнитного поля. Показатель выражается как вольт-ампер реактивный и представляет собой произведение напряжения на силу тука и угол сдвига.

Для простоты понимания смысла активной и реактивной мощности, обратимся к нагревательному оборудованию, где электрическая энергия преобразуется в тепловую.

Как измерить мощность

Знать силовые характеристики бытового оборудования необходимо всегда. Это требуется для расчета сечения проводки, учета расхода электроэнергии или электрификации дома. До начала монтажных работ такую информацию можно получить только путем сложения показателей мощности каждого отдельного устройства, добавив 10% запаса.

Определить потребляемую нагрузку дома поможет счетчик. Прибор показывает сколько киловатт было потрачено за один час работы оборудования. И для того чтобы убедиться в правильности показаний, владелец квартиры может проверить точность устройства с помощью электронных средств измерения. Сюда относится амперметр, вольтметр или мультиметр.

Также существуют ваттметры и варметры, которые показывают результаты измерений в ваттах. Во время снятия показания включенной оставить только активную нагрузку как лампочки и нагреватели. Далее померить токовое напряжение. В конце сверить показания счетчика с полученным результатом вычислений.

Мощность электрического тока расчет и формулы

Для вычисления мощности тока в ваттах, силу тока в амперах умножаем на напряжение в вольтах. Обозначить мощность электрического тока латинским символом P, то приведенное выше правило можно записать в виде математической формулы P = I × U (1).

Воспользуемся этой формулой на практике. Необходимо вычислить, какая мощность электрического тока требуется для накала нити лампы, если напряжение накала равно 4 в, а ток накала 75 мА. Р= 0,075 А × 4 В = 0,3 Вт Мощность электрического тока можно определить и другим способом. Например, нам известны сила тока и сопротивление цепи, а напряжение величина неизвестная, тогда мы воспользуемся соотношением из закона Ома: U=I × R Подставим правую часть формулы (1) IR вместо напряжения U. P = I× U = I×IR или Р = I2×R.

Рассмотрим пример расчета: какая мощность теряется в реостате сопротивлением в 5 Ом, если через него идет ток, силой 0,5 А. Пользуясь формулой (2), вычислим:. P= I2 × R = 0,52×5 =0,25×5 = 1,25 Вт. Кроме того, мощность электрического тока можно рассчитать если известны напряжение и сопротивление, а сила тока величина неизвестна.

Для этого вместо силы тока I в формулу подставляется отношение U/R и тогда формула приобретает следующий вид: Р = I × U=U2/R (3) Разберем очередной практический пример с использованием этой формулы, при 2,5 вольта падения напряжения на реостате сопротивлением в 5 Ом поглощаемая реостатом мощность будет определяться: Р = U2/R=(2,5)2/5=1,25 Вт; Выводы: Для нахождения мощности необходимо знать любые две из величин, из закона Ома. Мощность электрического тока равна работе тока, производимой в течение времени. P = A/t

Проходя по цепи, ток совершает работу. Как например, водный поток направить течь, на лопасти генератора, то пон будет совершать работу, вращая лопасти. Так же и ток совершает работу, двигаясь по проводнику. И эта работа тем выше, чем больше величина сила тока и напряжения. Работа электрического тока, совершаемая на участке цепи, прямо пропорциональна силе тока, напряжению и времени действия тока. Работа электрического тока обозначается латинским символом A. Так как, произведение I×U есть мощность, то формулу работы электрического тока можно записать: A = P×t

Единицей измерения работы электрического тока, является ватт в секундах или в джоулях. Поэтому, если мы хотим вычислить, какую работу осуществил ток, идя по цепи в течение временного интервала, мы должны умножить мощность на время Рассмотрим практический пример, через реостат с сопротивлением 5 Ом идет ток силой 0,5 А. Нужно вычислить, какую работу совершит ток в течение четырех часов. Работа в течение одной секунды будет: P=I2R = 0,52×5= 0,25×5 =1,25 Вт,

Тогда за 4 часа t=14400 секунд. Следовательно: А = Р×t= 1,25×14 400= 18 000 вт-сек. Ватт-секунда или один джоуль считаетсяя слишком малой велечиной для измерения работы. Поэтому на практике применяют единицу, называемую ватт-час (втч). Один ватт-час это эквивалентно 3 600 Дж. В электротехнике используются и еще большие единицы, гектоваттчас (гвтч) и киловаттчас (квтч): 1 квтч =10 гвтч =1000 втч = 3600000 Дж, 1 гвтч =100 втч = 360 000 Дж, 1 втч = 3 600 Дж.

Как рассчитать сопротивление и мощность

Допустим, требуется подобрать токоограничивающий резистор для блока питания схемы освещения. Нам известно напряжение питания бортовой сети «U», равное 24 вольта и ток потребления «I» в 0,5 ампера, который нельзя превышать. По выражению (9) закона Ома вычислим сопротивление «R». R=24/0,5=48 Ом. На первый взгляд номинал резистора определен. Однако, этого недостаточно. Для надежной работы семы требуется выполнить расчет мощности по току потребления.

Согласно действию закона Джоуля — Ленца активная мощность «Р» прямо пропорционально зависит от тока «I», проходящего через проводник, и приложенного напряжения «U». Эта взаимосвязь описана формулой Р=24х0,5=12 Вт.

Проведенный расчет мощности резистора по току его потребления показывает, что в выбираемой схеме надо использовать сопротивление величиной 48 Ом и 12 Вт. Резистор меньшей мощности не выдержит приложенных нагрузок, будет греться и со временем сгорит. Этим примером показана зависимость того, как на мощность потребителя влияют ток нагрузки и напряжение в сети.

Мощность тока

Разобравшись с понятием механической мощности, перейдём к рассмотрению электрической мощности (мощность электрического тока). Как Вы должны знать  U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока.

Активная электрическая мощность (это мощность, которая безвозвратно преобразуется в другие виды энергии — тепловую, световую, механическую и т.д.) имеет свою единицу измерения — Вт (Ватт). Она равна произведению 1 вольта на 1 ампер. В быту и на производстве мощность удобней измерять в кВт (киловаттах, 1 кВт = 1000 Вт). На электростанциях уже используются более крупные единицы — мВт (мегаватты, 1 мВт = 1000 кВт = 1 000 000 Вт).

Реактивная электрическая мощность — это величина, которая характеризует такой вид электрической нагрузки, что создаются в устройствах (электрооборудовании) колебаниями энергии (индуктивного и емкостного характера) электромагнитного поля. Для обычного переменного тока она равна произведению рабочего тока I и падению напряжения U на синус угла сдвига фаз между ними: Q = U*I*sin(угла). Реактивная мощность имеет свою единицу измерения под названием ВАр (вольт-ампер реактивный). Обозначается буквой «Q».

Простым языком активную и реактивную электрическую мощность на примере можно выразить так: у нас имеется электротехническое устройство, которое имеет нагревательные тэны и электродвигатель. Тэны, как правило, сделаны из материала с высоким сопротивлением. При прохождении электрического тока по спирали тэна, электрическая энергия полностью преобразуется в тепло. Такой пример характерен активной электрической мощности.

Электродвигатель этого устройства внутри имеет медную обмотку. Она представляет собой индуктивность. А как мы знаем, индуктивность обладает эффектом самоиндукции, а это способствует частичному возврату электроэнергии обратно в сеть. Эта энергия имеет некоторое смещение в значениях тока и напряжения, что вызывает негативное влияние на электросеть (дополнительно перегружая её).

Похожими способностями обладает и ёмкость (конденсаторы). Она способна накапливать заряд и отдавать его обратно. Разница ёмкости от индуктивности заключается в противоположном смещении значений тока и напряжения относительно друг друга. Такая энергия ёмкости и индуктивности (смещённая по фазе относительно значения питающей электросети) и будет, по сути, являться реактивной электрической мощностью.

Более подробно о свойствах реактивной мощности мы поговорим в соответствующей статье, а в завершении этой темы хотелось сказать о взаимном влиянии индуктивности и ёмкости. Поскольку и индуктивность, и ёмкость обладают способностью к сдвигу фазы, но при этом каждая из них делает это с противоположным эффектом, то такое свойство используют для компенсации реактивной мощности (повышение эффективности электроснабжения). На этом и завершу тему, электрическая мощность, мощность электрического тока.

Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что  делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.

В 1827 году  Георг Ом  опубликовал свои исследования, которые составляют основу формулы, используемую и по сей день. Ом выполнил большую серию экспериментов, которые показали связь между приложенным напряжением и током, протекающим через проводник.

Этот закон является эмпирическим, то есть основанный на опыте. Обозначение «Ом» принято в качестве официальной единицы СИ для электрического сопротивления.

Закон Ома для участка цепи гласит, что электрический ток в проводнике прямо пропорционален разности потенциалов в нем и обратно пропорционален его сопротивлению. Принимая во внимание, что сопротивление проводника (не путать с удельным сопротивлением) величина постоянная, можно оформить это следующей формулой:

где

• I — тока в амперах (А)
• V — напряжение в вольтах (В)
• R — сопротивления в омах (Ом)

Для наглядности: резистор имеющий сопротивление 1 Ом, через который протекает ток силой в 1 А на своих выводах имеет разность потенциалов (напряжение) в  1 В.

Немецкий физик Кирхгоф (известен своими правилами Кирхгофа) сделал обобщение, которое больше используется в физике:

где

• σ – проводимость материала
• J — плотность тока
• Е — электрическое поле.

Закон Ома и резистор

Резисторы являются пассивными элементами, которые оказывают сопротивление потоку электрического тока в цепи. Резистор, который функционирует в соответствии с законом Ома, называется омическим сопротивлением. Когда ток проходит через такой резистор, то падение напряжения на его выводах пропорционально величине сопротивления.

Формула Ома остается справедливой и для цепей с переменным напряжением и током. Для конденсаторов и катушек индуктивности закон Ома не подходит, так как их ВАХ (вольт-амперная характеристика) по сути, не является линейной.

Формула Ома действует так же для схем с несколькими резисторами, которые могут быть соединены последовательно, параллельно или иметь смешанное соединение. Группы резисторов, соединенные последовательно или параллельно могут быть упрощены в виде эквивалентного сопротивления.

В статьях о параллельном и последовательно соединении более подробно описано как это сделать.

Немецкий физик Георг Симон Ом опубликовал в 1827 свою полную теорию электричества под названием «теория гальванической цепи». Он нашел, что падение напряжения на участке цепи является результатом работы тока, протекающего через сопротивление этого участка цепи. Это легло в основу закона, который мы используем сегодня. Закон является одним из основных уравнений для резисторов. 

Закон Ома — формула

Формула закона Ома может быть использована, когда известно две из трех переменных. Соотношение между сопротивлением, током и напряжением может быть записано по-разному. Для усвоения и запоминания может быть полезен «треугольник Ома».

или

или

  Ниже приведены два примера использования такого треугольного калькулятора.

Закон Ома — мощность

Когда через резистор протекает электрический ток, он рассеивает определенную часть мощности в виде тепла.

Мощность является функцией протекающего тока I (А) и приложенного напряжения V (В):

где

• Р — мощность в ваттах (В)

В сочетании с законом Ома для участка цепи, формулу можно преобразовать в следующий вид:

или

Идеальный резистор рассеивает всю энергию и не сохраняет электрическую или магнитную энергию. Каждый резистор имеет предел мощности, которая может быть рассеяна, не оказывая повреждение резистору. Это мощность называется номинальной. 

Окружающие условия могут снизить или повысить это значение. Например, если окружающий воздух горячий, то способность рассеять излишнее тепло у резистора снижается, и на оборот, при низкой температуре окружающего воздух рассеиваемая способность резистора возрастает.

На практике, резисторы редко имеют обозначение номинальной мощности. Тем не менее, большинство из резисторов рассчитаны на 1/4 или 1/8 Вт.

Ниже приведена круговая диаграмма, которая поможет вам быстро определить связь между мощностью, силой тока, напряжением и сопротивлением. Для каждого из четырех параметров показано, как вычислить свое значение.

Закон Ома — калькулятор

Данный онлайн калькулятор закона Ома позволяет определить взаимосвязь между силой тока, электрическим напряжением, сопротивлением проводника и мощностью. Для расчета введите любые два параметра и нажмите кнопку расчет:

Для закрепления понимания работы закона Ома, приведем несколько задач для самостоятельного решения.

Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.

В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.

Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению

Так записывается основная формула:

Путем преобразования основной формулы можно найти и другие две величины:

      

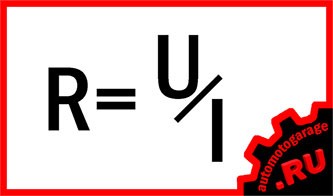
Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

Формула мгновенной электрической мощности:

Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.

Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.

Первая – мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.

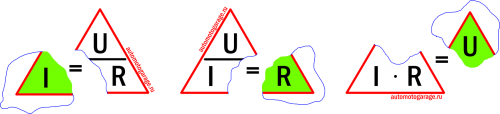
Вторая – метод треугольника. Его ещё называют магический треугольник закона Ома.

Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.

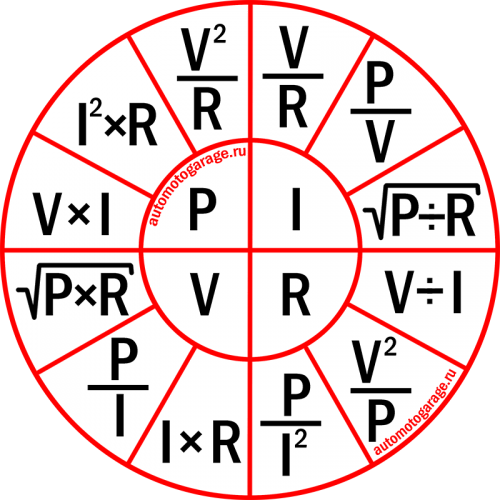
Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.

Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.

Этот круг также, как и треугольник можно назвать магическим.

Александр (Гость)

15 ноября 2020 / 07:52

Привет. У меня есть нерабочий строительный фен. Я нашёл, скажем так, новый нагреватель на замену нерабочего, но у него 3 вывода, т.е. на 2 рабочих положения. Но ещё одного вывода для запитки двигателя нет. Сопротивление обоих спиралей большое. Нагреватель я уже установил в корпус и вытаскивать его назад чревато поломкой. Вот я и подумал: возможно запитать двигатель автономным, не зависящим от спиралей, питанием. Двигатель, я думаю, на 12-18 вольт.

Павл (Гость)

21 марта 2023 / 00:24

Удивляюсь. Люди не выставляют размерность, а потом предъяляют претензии автору.

Расчет кто-то в комментариях делал на 3кВ и 1МОм. Дело в том что калькулятор считает сначала верхнюю строку (I). Если силу тока выставить до расчёта в мкА или в мА, то и расчёт будет верный – 3000 мкА или 3 мА.

С 5В и 1000 Ом ещё проще. 5 вольт – это напряжение, например, выходное блока питания ЗУ (у телефона и т.д.). Его никто не меряет чисто в амперах, даже производитель ЗУ ставит маркировку в мА. Итого, вычисляем: 5В на 1кОм – это 5мА и 0.03Вт

Размерность, господа, размерность важна!

Матвей (Гость)

6 апреля 2023 / 15:28

Калькулятор странный, например мне надо узнать какой будет ток, через резистор 2 вт 15 ом и 28 в
Выставляю эти значения, остается пустым сила тока, нажимаю рассчитать, а он сам меняет мощность на 52 вт, и уже от этого рисует мне 1.87А

Вася (Гость)

29 апреля 2023 / 10:37

Матвей. 1,87ампер потечет через резистор, а значит мощность нужна будет 52вт , для того, чтобы резистор выдержал на себе такое напряжение.