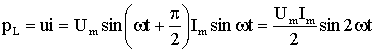Исследуем и рассчитываем мощность в цепи переменного тока
Содержание
- 1 Виды тока
- 2 Зачем нужно знать мощность электрооборудования
- 3 Виды мощности
- 4 Как измерить косинус «фи»
- 5 Как узнать мощность
- 6 Видео по теме
В процессе эксплуатации электрооборудования важную роль играет соответствие требуемой мощности и возможностей сети электропитания. Чтобы выполнить предварительные расчёты, необходимо понимать, какова природа электрической мощности и чем определяется её величина.
Виды тока
Техника может работать с использованием постоянного или переменного электрического тока. В первом случае сила тока на протяжении эксплуатации не меняется. Во втором она периодически меняется по абсолютной величине и знаку.
Наиболее часто переменный ток изменяется по синусоидальному закону, однако в некоторых случаях импульсы могут иметь другую, например, прямоугольную форму. В бытовых и производственных условиях часто для питания электроприборов требуется наличие однофазного или трехфазного переменного тока.
На представленном выше графике сила тока для активной мощности обозначена красным цветом. Для реактивной использованы обозначения с индексами L и C. На этом графике показан сдвиг фаз. Здесь видно, что ёмкостный ток отстаёт, а индуктивный опережает активный. При проведении расчетов для выбора автотрансформатора или других электроприборов важно правильно учитывать имеющиеся смещения.
Зачем нужно знать мощность электрооборудования
Каждый подключенный электроприбор для обеспечения своей работы будет потреблять часть мощности электросети. Если их работает одновременно несколько, то мощности складываются. Важно при расчете потребляемой электроэнергии учитывать:
- Мощность в цепи переменного тока или постоянного, которая обеспечивается поставщиком.
- Параметры защитных приборов, с помощью которых осуществляется регулирование рабочих характеристик оборудования.
- Конструкцию системы проводов и удлинителей.
- Наличие автотрансформатора или аналогичных устройств.
Если подаваемая мощность недостаточна, это способствует появлению перебоев в поставке электроэнергии. Защитные приборы должны быть настроены таким образом, чтобы при возникновении аварийной ситуации прерывать поступление электричества. Для этого в них должны быть заложены данные о том, какая величина мощности в цепях переменного или постоянного тока считается нормальной, а какая свидетельствует о возникновении проблемной ситуации.
Провода, удлинители и другие элементы электропроводки рассчитаны на определённые предельные значения. При их превышении они будут плавиться или перегорать. Перед подключением автотрансформатора или других электроприборов нужно предварительно узнать, соответствует ли требуемая им мощность имеющимся возможностям электросети.
Виды мощности
Полная мощность на участке цепи определяется как работа, выполняемая в течение единицы времени. Её также можно рассматривать как отношение используемой энергии к продолжительности интервала времени, на протяжении которого это происходит.
При работе электрического прибора часть мощность частично тратится на получение полезного эффекта. Такую мощность называют активной. Электрическая энергия при этом превращается в другой вид. Например, речь может идти о том, что она выделится в виде света или тепла.
Переменный ток при наличии в схеме ёмкости и индуктивности создаёт реактивную мощность. Она не расходуется, а преобразуется из одной формы в другую. Реактивная мощность, выделяемая в конкретной цепи переменного тока, считается паразитной. Если ее величина незначительная, то вся используемая энергия является активной.
Реактивная и активная мощности — это составляющие полной электрической мощности. Сложение осуществляется по векторным правилам. Чтобы рассчитать полную мощность, следует применить теорему Пифагора.
На приведённом рисунке длина гипотенузы выражает полную мощность, горизонтально расположенный катет — активную составляющую, а вертикально — реактивную. Как известно, квадрат гипотенузы — это сумма квадратов катетов.
В приведённой формуле используются следующие обозначения:
- С левой стороны знака равенства указана полная мощность.
- В качестве P рассматривается активная мощность.
- С помощью Q обозначена реактивная мощность.
Соотношение активной и реактивной мощности выражается через косинус угла «фи». Этот угол представляет собой фазовый сдвиг между электротоком и электронапряжением. Чтобы оценить реальную мощность работы оборудования, косинус «фи» часто указывают в технической документации электроприбора, как коэффициент мощности. Он полезен для определения особенностей использования автотрансформатора или других приборов.
Единицей измерения активной мощности является ватт. Для реактивной применяется вольт-ампер реактивный (вар). Полная мощность измеряется вольт-амперами.
Используется еще и такое понятие, как мгновенная мощность, которая постоянно меняется. Например, она может иметь нулевое значение в тех точках, где сила электротока также равняется нулю. На практике мгновенная мощность используется редко, но применяется её среднее значение за период.
Как измерить косинус «фи»
Обычно эта информация содержится в технической документации прибора. Если она не указана, то ее измеряют с помощью специального прибора — фазометра.
Чем больше рассматриваемая величина, тем выше будет эффективность электрооборудования. Если косинус небольшой, то выгодно улучшить ситуацию, используя компенсацию реактивной мощности переменного тока. Чтобы понять принцип работы, следует вспомнить, что реактивная мощность возникает из-за наличия ёмкости и индуктивности в электроцепи.
Для компенсации используют регулируемый узел, действующий противоположно реактивной составляющей электромощности. Например, регулировка может осуществляться при помощи дросселя с высокой индуктивностью. Его подключают последовательно с нагрузкой.
Как узнать мощность
Один из наиболее простых способов — измерение мощности с помощью ваттметра. Существуют различные виды таких устройств. Поскольку в быту не требуется особенно высокой точности, можно использовать довольно простые приборы.
Также можно провести вычисления, измерив напряжение, силу тока и сопротивление. Расчёт мощности осуществляется с помощью двух из этих трёх величин.
При использовании постоянного тока определение активной мощности выполняется с помощью следующего выражения:
Если нужно определить мощность однофазного переменного тока, используется формула:
Если ток трёхфазный, тогда мощность можно рассчитать по формуле:
Указанная выше формула мощности применяется при симметричном трёхфазном распределении. Если оно является асимметричным, тогда для каждой фазы мощность переменного тока вычисляется отдельно, а затем найденные значения складываются. Средняя мощность для переменного тока определяется интегральным исчислением.
Для определения реактивной мощности используют формулу:
Знание электрической мощности не только полезно само по себе, но оно помогает вычислить различные характеристики используемого электрооборудования. Обычно значение мощности и косинуса «фи» можно получить из технической документации. Например, зная напряжение, можно вычислить силу электрического тока, чтобы учесть её при подключении и обеспечении безопасности использования оборудования.
На представленной выше схеме во внутреннем круге указаны величины, которые требуется определить. Вдоль окружности приведены формулы, которыми следует воспользоваться для вычисления.
Сказанное можно пояснить на следующем примере. Допустим, нужно определиться с мощностью. В этом случае следует обратить внимание на левый нижний сектор чертежа. Зная две из трёх величин, через которые выражается мощность (напряжение, силу тока и сопротивление), можно подобрать подходящую формулу для вычисления.
Если требуется найти, чему равна сила тока, то это выполняется аналогичным образом. Разница состоит в том, что теперь следует работать с правым верхним сектором. Здесь потребуется знать две из следующих трёх величин: мощность, сопротивление и напряжение. Нужно подобрать подходящую формулу и выполнить соответствующие вычисления.
Видео по теме
Мощностные характеристики установки или сети являются основными для большинства известных электрических приборов. Активная мощность (проходящая, потребляема) характеризует часть полной мощности, которая передается за определенный период частоты переменного тока.
Определение
Активная и реактивная мощность может быть только у переменного тока, т. к. характеристики сети (силы тока и напряжения) у постоянного всегда равны. Единица измерений активной мощности Ватт, в то время, как реактивной – реактивный вольтампер и килоВАР (кВАР). Стоит отметить, что как полная, так и активная характеристики могут измеряться в кВт и кВА, это зависит от параметров конкретного устройства и сети. В промышленных цепях чаще всего измеряется в килоВаттах.
Электротехника используется активную составляющую в качестве измерения передачи энергии отдельными электрическими приборами. Рассмотрим, сколько мощности потребляют некоторые из них:
| Прибор | Мощность бытовых приборов, Вт/час |
| Зарядное устройство | 2 |
| Люминесцентная лампа ДРЛ | От 50 |
| Акустическая система | 30 |
| Электрический чайник | 1500 |
| Стиральной машины | 2500 |
| Полуавтоматический инвертор | 3500 |
| Мойка высокого давления | 3500 |
Исходя из всего, сказанного выше, активная мощность – это положительная характеристика конкретной электрической цепи, которая является одним из основных параметров для выбора электрических приборов и контроля расхода электричества.
Обозначение реактивной составляющей:
Это номинальная величина, которая характеризует нагрузки в электрических устройствах при помощи колебаний ЭМП и потери при работе прибора. Иными словами, передаваемая энергия переходит на определенный реактивный преобразователь (это конденсатор, диодный мост и т. д.) и проявляется только в том случае, если система включает в себя эту составляющую.
Расчет
Для выяснения показателя активной мощности, необходимо знать полную мощность, для её вычисления используется следующая формула:
S = U I, где U – это напряжение сети, а I – это сила тока сети.
Этот же расчет выполняется при вычислении уровня передачи энергии катушки при симметричном подключении. Схема имеет следующий вид:
Расчет активной мощности учитывает угол сдвига фаз или коэффициент (cos φ), тогда:
S = U * I * cos φ.
Очень важным фактором является то, что эта электрическая величина может быть как положительной, так и отрицательной. Это зависит от того, какие характеристики имеет cos φ. Если у синусоидального тока угол сдвига фаз находится в пределах от 0 до 90 градусов, то активная мощность положительная, если от 0 до -90 – то отрицательная. Правило действительно только для синхронного (синусоидального) тока (применяемого для работы асинхронного двигателя, станочного оборудования).
Также одной из характерных особенностей этой характеристики является то, что в трехфазной цепи (к примеру, трансформатора или генератора), на выходе активный показатель полностью вырабатывается.
Максимальная и активная обозначается P, реактивная мощность – Q.
Из-за того, что реактивная обуславливается движением и энергией магнитного поля, её формула (с учетом угла сдвига фаз) имеет следующий вид:
QL = ULI = I2xL
Для несинусоидального тока очень сложно подобрать стандартные параметры сети. Для определения нужных характеристик с целью вычисления активной и реактивной мощности используются различные измерительные устройства. Это вольтметр, амперметр и прочие. Исходя от уровня нагрузки, подбирается нужная формула.
Из-за того, что реактивная и активная характеристики связаны с полной мощностью, их соотношение (баланс) имеет следующий вид:
S = √P2 + Q2, и все это равняется U*I .
Но если ток проходит непосредственно по реактивному сопротивлению. То потерь в сети не возникает. Это обуславливает индуктивная индуктивная составляющая – С и сопротивление – L. Эти показатели рассчитываются по формулам:
Сопротивление индуктивности: xL = ωL = 2πfL,
Сопротивление емкости: хc = 1/(ωC) = 1/(2πfC).
Для определения соотношения активной и реактивной мощности используется специальный коэффициент. Это очень важный параметр, по которому можно определить, какая часть энергии используется не по назначению или «теряется» при работе устройства.
При наличии в сети активной реактивной составляющей обязательно должен рассчитываться коэффициент мощности. Эта величина не имеет единиц измерения, она характеризует конкретного потребителя тока, если электрическая система содержит реактивные элементы. С помощью этого показателя становится понятным, в каком направлении и как сдвигается энергия относительно напряжения сети. Для этого понадобится диаграмма треугольников напряжений:
К примеру, при наличии конденсатора формула коэффициента имеет следующий вид:
cos φ = r/z = P/S
Для получения максимально точных результатов рекомендуется не округлять полученные данные.
Компенсация
Учитывая, что при резонансе токов реактивная мощность равняется 0:
Q = QL — QC = ULI – UCI
Для того чтобы улучшить качество работы определенного устройства применяются специальные приборы, минимизирующие воздействие потерь на сеть. В частности, это ИБП. В данном приборе не нуждаются электрические потребители со встроенным аккумулятором (к примеру, ноутбуки или портативные устройства), но для большинства остальных источник бесперебойного питания является необходимым.
При установке такого источника можно не только установить негативные последствия потерь, но и уменьшить траты на оплату электричества. Специалисты доказали, что в среднем, ИБП поможет экономить от 20 % до 50 %. Почему это происходит:
- Значительно уменьшается нагрузка силовых трансформаторов;
- Провода меньше нагреваются, это не только положительно влияет на их работу, но и повышает безопасность;
- У сигнальных и радиоустройств уменьшаются помехи;
- На порядок уменьшаются гармоники в электрической сети.
В некоторых случаях специалисты используют не полноценные ИБП, а специальные компенсирующие конденсаторы. Они подходят для бытового использования, доступны и продаются в каждом электротехническом магазине. Для расчета планируемой и полученной экономии можно использовать все вышеперечисленные формулы.
RIR=UR; 1ωCIC=UC; ωLIL=UL.
Указанные выше формулы внешне могут напоминать закон Ома на участке цепи постоянного тока, но стоит заметить, что в этом случае вместо величин постоянных токов и напряжений на участке цепи, в них входят амплитудные значения напряжений и переменных токов.
Формулы, указанные выше, выражают собой закон Ома для переменного тока, который содержит один из элементов R, L и C.
R – активное сопротивление резистора.
1ωС – емкостное сопротивление конденсатора.
ωL – индуктивное сопротивление катушки в цепи переменного тока.
Движение переменного тока по участку цепи провоцирует электромагнитное поле выполнять работу, благодаря чему выделяется джоулево тепло.
Мгновенной мощностью в цепи называется произведение мгновенных значений тока и напряжения: p=J·u.
Прикладной интерес у нас вызывает среднее значение мощности за некоторый период переменного тока:
P=Pcα=I0U0cos ωt cos ωt+φ.
В приведенной выше формуле I0 и U0 являются амплитудными значениями тока и напряжения на выбранном участке цепи, а φ – фазовым сдвигом между током и напряжением. Черта же представляет собой символ усреднения. В случае, когда цепь содержит только резистор с сопротивлением R, то фазовый сдвиг φ будет равен нулю:
PR=IRURcos2ωt=IRUR2=IR2R2.
Действующие значения силы тока и напряжения
По причине необходимости совпадения с уравнением для мощности постоянного тока, нам приходится ввести определения действующих значений силы тока и напряжения:
IД=l02; UД=U02.
Мощность переменного тока на участке цепи
Средняя величина мощности переменного тока на участке цепи, включающем в себя резистор, равняется:
PR=IДUД.
Если в цепи содержится лишь конденсатор емкости C, то φ=π2. Отсюда, справедливо следующее выражение:
PC=ICUCcos ωt cosωt+π2=ICUCcos ωt-sin ωt=0.
Таким же способом можно проиллюстрировать, что PL=0.
Исходя из описанного выше получим следующие определение.
Мощность в цепи переменного тока выделяется только на активном сопротивлении, а среднее значение мощности переменного тока на конденсаторе и катушке индуктивности равняется нулю.
Теперь стоит рассмотреть электрическую цепь, включающую последовательно соединенные резистор, конденсатор и катушки, и подключенную к источнику переменного тока некой частоты ω. Следует выделить, что на всех участках цепи, соединенных последовательно, проходит один и тот же ток. Между напряжением внешнего источника e(t) и током J(t) проявляется фазовый сдвиг на определенный угол φ.
Исходя из приведенных выше фактов, мы можем записать:
J(t)=I0cos ωt; e(t)=δ0cos ωt+φ.
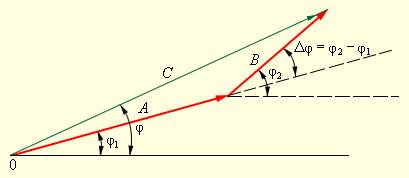
Данные формулы мгновенных значений тока и напряжения подходят к построениям, выполненным на векторной диаграмме (рис. 2.3.2).
Рисунок 2.3.2. Гармонические колебания A cos (ωt+φ1), B cos (ωt+φ2) и их суммы C cos (ωt+φ) на векторной диаграмме.
Средняя величина мощности, развиваемой источником переменного тока, может быть найдена из следующего выражения:
P=I0δ0cos ωt cos ωt+φ=I0δ02cos φ=IДδД cos φ.
Исходя из данных векторной диаграммы можно заявить, что UR=δ0·cos φ, следовательно,
P=I0UR2, а вся мощность, которую развивает источник питания, теряется в виде джоулева тепла на резисторе.
В прошлых темах нами было получено выражение, являющееся соотношением амплитуд тока I0 и напряжений δ0 в условиях последовательной RLC-цепи:
I0=δ0R2+ωL-1ωC2
Z=R2+ωL-1ωC2– это величина, имеющая название полное сопротивление цепи переменного тока.
Связь между амплитудными значениями тока и напряжения в цепи имеет вид:
ZI0=δ0.
Данное выражение представляет собой закон Ома для цепи переменного тока.
Закон Ома в условиях параллельной RLC-цепи
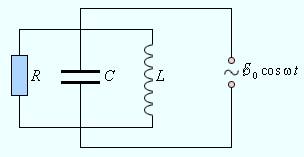
В различных расчетах, связанных с работой над цепями переменного тока, очень важное место занимает понятие полного сопротивления. Для его определения в цепи в большей части случаев практично использовать метод векторных диаграмм. В качестве примера, приведем параллельный подключенный к внешнему источнику переменного тока (рис. 2.4.1) RLC-контур:
Рисунок 2.4.1. Параллельный RLC-контур.
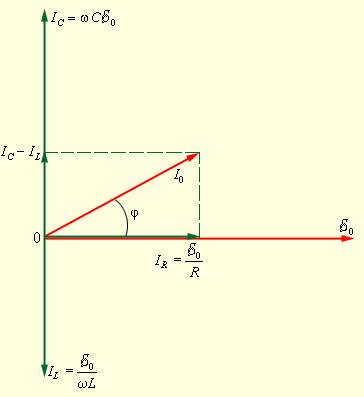
При построении диаграммы важно учесть, что в условиях параллельного соединения напряжение на всех элементах R, C и L идентично и равняется напряжению внешнего источника питания. Ток, текущий в разных ветвях цепи, различается не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Следовательно, полное сопротивление цепи невозможно вычислить опираясь на законы параллельного соединения цепей постоянного тока. Векторную диаграмму для параллельного RLC-контура можно увидеть на рис. 2.4.2.
Рисунок 2.4.2. Векторная диаграмма для параллельного RLC-контур.
Исходя из вида диаграммы, следует:
I0=δ01R2+ωL-1ωC2.
Соответственно, полное сопротивление параллельного RLC-контура выражается в виде следующего соотношения:
Z=11R2+ωL-1ωC2.
При параллельном резонансе (ω2=1LC) полное сопротивление цепи принимает свое максимальное значение, которое эквивалентно активному сопротивлению резистора:
Z=Zmax=R.
А значение фазового сдвига φ между током и напряжением при параллельном резонансе равняется нулю.
Все мы ежедневно сталкиваемся с электроприборами, кажется, без них наша жизнь останавливается. И у каждого из них в технической инструкции указана мощность. Сегодня мы разберемся что же это такое, узнаем виды и способы расчета.
Содержание
- 1 Мощность в цепи переменного электрического тока
- 1.1 Понятие активной мощности
- 1.2 Понятие реактивной мощности
- 1.2.1 Емкостные и индуктивные нагрузки
- 1.2.2 Коэффициент мощности cosφ
- 1.3 Понятие полной мощности. Треугольник мощностей
- 2
- 3 Как измеряют cosφ на практике
Мощность в цепи переменного электрического тока
Электроприборы, подключаемые к электросети работают в цепи переменного тока, поэтому мы будем рассматривать мощность именно в этих условиях. Однако, сначала, дадим общее определение понятию.
Мощность — физическая величина, отражающая скорость преобразования или передачи электрической энергии.
В более узком смысле, говорят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Если перефразировать данное определение менее научно, то получается, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый простой пример – это обычная лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше изначально этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше отдаст света.
Поскольку в данном случае происходит не только процесс преобразования электроэнергии в некоторую другую (световую, тепловую и т.д.), но и процесс колебания электрического и магнитного поля, появляется сдвиг фазы между силой тока и напряжением, и это следует учитывать при дальнейших расчетах.
При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.
Понятие активной мощности
Активная «полезная» мощность — это та часть мощности, которая характеризует непосредственно процесс преобразования электрической энергии в некую другую энергию. Обозначается латинской буквой P и измеряется в ваттах (Вт).
Рассчитывается по формуле: P = U⋅I⋅cosφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, cos φ – косинус угла сдвига фазы между напряжением и током.
ВАЖНО! Описанная ранее формула подходит для расчета цепей с напряжением 220В, однако, мощные агрегаты обычно используют сеть с напряжением 380В. В таком случае выражение следует умножить на корень из трех или 1.73
Понятие реактивной мощности
Реактивная «вредная» мощность — это мощность, которая образуется в процессе работы электроприборов с индуктивной или емкостной нагрузкой, и отражает происходящие электромагнитные колебания. Проще говоря, это энергия, которая переходит от источника питания к потребителю, а потом возвращается обратно в сеть.
Использовать в дело данную составляющую естественно нельзя, мало того, она во многом вредит сети питания, потому обычно его пытаются компенсировать.
Обозначается эта величина латинской буквой Q.
ЗАПОМНИТЕ! Реактивная мощность измеряется не в привычных ваттах (Вт), а в вольт-амперах реактивных (Вар).
Рассчитывается по формуле:
Q = U⋅I⋅sinφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, sinφ – синус угла сдвига фазы между напряжением и током.
ВАЖНО! При расчете данная величина может быть как положительной, так и отрицательной – в зависимости от движения фазы.
Емкостные и индуктивные нагрузки
Главным отличием реактивной (емкостной и индуктивной) нагрузки – наличие, собственно, емкости и индуктивности, которые имеют свойство запасать энергию и позже отдавать ее в сеть.
Индуктивная нагрузка преобразует энергию электрического тока сначала в магнитное поле (в течение половины полупериода), а далее преобразует энергию магнитного поля в электрический ток и передает в сеть. Примером могут служить асинхронные двигатели, выпрямители, трансформаторы, электромагниты.
ВАЖНО! При работе индуктивной нагрузки кривая тока всегда отстает от кривой напряжения на половину полупериода.
Емкостная нагрузка преобразует энергию электрического тока в электрическое поле, а затем преобразует энергию полученного поля обратно в электрический ток. Оба процесса опять же протекают в течение половины полупериода каждый. Примерами являются конденсаторы, батареи, синхронные двигатели.
ВАЖНО! Во время работы емкостной нагрузки кривая тока опережает кривую напряжения на половину полупериода.
Коэффициент мощности cosφ
Коэффициент мощности cosφ (читается косинус фи)– это скалярная физическая величина, отражающая эффективность потребления электрической энергии. Проще говоря, коэффициент cosφ показывает наличие реактивной части и величину получаемой активной части относительно всей мощности.
Коэффициент cosφ находится через отношение активной электрической мощности к полной электрической мощности.
ОБРАТИТЕ ВНИМАНИЕ! При более точном расчете следует учитывать нелинейные искажения синусоиды, однако, в обычных расчетах ими пренебрегают.
Значение данного коэффициента может изменяться от 0 до 1 (если расчет ведется в процентах, то от 0% до 100%). Из расчетной формулы не сложно понять, что, чем больше его значение, тем больше активная составляющая, а значит лучше показатели прибора.
Понятие полной мощности. Треугольник мощностей
Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буквой S.
Также рассчитать полную мощность можно путем перемножения напряжения и силы тока соответственно.
S = U⋅I
ВАЖНО! Полная мощность измеряется в вольт-амперах (ВА).
Треугольник мощностей – это удобное представление всех ранее описанных вычислений и соотношений между активной, реактивной и полной мощностей.
Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, то есть он является коэффициентом мощности.
Как найти активную, реактивную и полную мощности. Пример расчета
Все расчеты строятся на указанных ранее формулах и треугольнике мощностей. Давайте рассмотрим задачу, наиболее часто встречающуюся на практике.
Обычно на электроприборах указана активная мощность и значение коэффициента cosφ. Имея эти данные несложно рассчитать реактивную и полную составляющие.
Для этого разделим активную мощность на коэффициент cosφ и получим произведение тока и напряжения. Это и будет полной мощностью.
Далее, исходя из треугольника мощностей, найдем реактивную мощность равную квадрату из разности квадратов полной и активной мощностей.
Как измеряют cosφ на практике
Значение коэффициента cosφ обычно указано на бирках электроприборов, однако, если необходимо измерить его на практике пользуются специализированным прибором – фазометром. Также с этой задачей легко справится цифровой ваттметр.
Если полученный коэффициент cosφ достаточно низок, то его можно компенсировать практически. Осуществляется это в основном путем включения в цепь дополнительных приборов.
- Если необходимо скорректировать реактивную составляющую, то следует включить в цепь реактивный элемент, действующий противоположно уже функционирующему прибору. Для компенсации работы асинхронного двигателя, для примера индуктивной нагрузки, в параллель включается конденсатор. Для компенсации синхронного двигателя подключается электромагнит.
- Если необходимо скорректировать проблемы нелинейности в схему вводят пассивный корректор коэффициента cosφ, к примеру, это может быть дроссель с высокой индуктивностью, подключаемый последовательно с нагрузкой.
Мощность – это один из важнейших показателей электроприборов, поэтому знать какой она бывает и как рассчитывается, полезно не только школьникам и людям, специализирующимся в области техники, но и каждому из нас.
Мощности в цепях переменного тока
По аналогии с
мощностью в цепях постоянного тока
P = U I, в цепях переменного тока
рассматривают мгновенную мощность
p = u i. Для упрощения рассмотрим
мгновенную мощность в каждом из элементов
R, L и С отдельно.
Элемент r (резистор)
Зададим напряжение
и ток в виде соотношений
u(t)
= Um sin(ωt
+ ψu),
i(t)
= Im sin(ωt
+ ψi).
Известно,
что для резистора ψu =
ψi,
тогда для р получим
(2.32)
p(t)
= u(t) i(t) = Um Im sin2(ωt
+ ψi).
Из уравнения (2.32)
видно, что мгновенная мощность всегда
больше нуля и изменяется во времени. В
таких случаях принять рассматривать
среднюю за период Т мощность
(2.33)
.
Если
записать Um и
Im через
действующие значения U и I:
,
,
то получим
(2.34)
P = U I.
По форме уравнение
(2.34) совпадает с мощностью на постоянном
токе. Величину Р равную произведению
действующих значений тока и напряжения
называют активной мощностью. Единицей
ее измерения является Ватт (Вт).
Элемент l (индуктивность)
Известно,
что в индуктивности соотношение фаз
ψu = ψi + 90°.
Для мгновенной мощности имеет
(2.35)
.
Усредняя уравнение
(2.35) по времени за период Т получим
.
Для
количественной оценки мощности в
индуктивности используют величину
QL равную
максимальному значению рL
(2.36)
QL =
(Um Im)
/ 2
и
называют ее реактивной (индуктивной)
мощностью. Единицей ее измерения выбрали
ВАр (вольт-ампер реактивный). Уравнение
(2.36) можно записать через действующие
значения U и I и используя формулу
UL = I XL получим
(2.37)
QL = I2 XL.
Элемент с (ёмкость)
Известно,
что в емкости соотношение фаз ψu = ψi – 90°.
Для мгновенной мощности получаем
pC(t)
= u(t) I(t) = (Um Im)
/ 2 · sin(2ωt).
Среднее
значение за период здесь также равно
нулю. По аналогии с уравнением (2.36) вводят
величину QC = I2 XC,
которую называют реактивной (емкостной)
мощностью. Единицей ее измерения также
является ВАр.
Если в цепи
присутствуют элементы R, L и С, то активная
и реактивная мощности определяются
уравнениями
(2.37)
P
= U I cos φ,
(2.38)
Q = QL – QC,
(2.39)
Q
= U I sin φ,
где
φ
– угол
сдвига
фаз.
Вводят понятие
полной мощности цепи
(2.40)
.
С учетом уравнений
(2.37) и (2.39), (2.40) можно записать в виде
(2.41)
S = U I.
Единицей измерения
полной мощности является ВА – вольт-ампер.
Цепь переменного тока с индуктивностью
Как мы видели выше, при включении,
выключении и при всяком изменении
тока в электрической цепи вследствие
пересечения проводника своим же
собственным магнитным полем в нем
возникает индуктированная э. д. с. Эту
э. д. с. мы называли э. д. с. самоиндукции.
Э. д. с. самоиндукции, как указывалось,
имеет реактивный характер. Так, например,
при увеличении тока в цепи э. д. с.
самоиндукции будет направлена против
э. д. с. источника напряжения и поэтому
ток в электрической цепи не может
установиться сразу. И наоборот, при
уменьшении тока в цепи индуктируется
э. д. с. самоиндукции такого направления,
что, препятствуя убыванию тока, она
поддерживает этот убывающий ток.
Как нам уже известно, э. д. с. самоиндукции
зависит от скорости изменения тока в
цепи и от индуктивности этой цепи (числа
витков, наличия стальных сердечников):
В цепи переменного тока э. д. с. самоиндукции
возникает и действует непрерывно, так
как ток в цепи непрерывно изменяется.
На рис. 137 представлена схема
цепи переменного тока, содержащей
катушку с индуктивностью L
без стального сердечника.
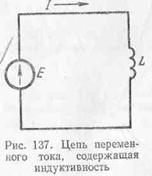
Для простоты будем считать сначала, что
активное сопротивление катушки г очень
мало и им можно пренебречь.
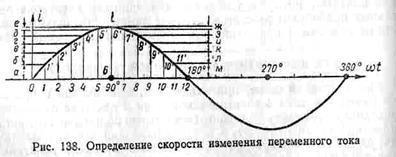
Рассмотрим внимательнее изменение
переменного тока за время одного
периода. На рис. 138 показана кривая
изменения переменного тока. Первая
половина периода разбита на мелкие
одинаковые части.
За промежуток времени 0—1
величина тока
изменилась от нуля до 1-1’. Прирост
величины тока за это время равен а.
За время, обозначенное
отрезком 1—2, мгновенная величина тока
выросла до 2—2′, причем прирост величины
тока равен б.
В течение времени, обозначенного
отрезком 2—3, ток увеличивается до
3—3′, прирост тока показывает отрезок в и
т. д.
Так, с течением времени переменный ток
возрастает до максимума (при 90°). Но,
как видно из чертежа, прирост тока
делается все меньше и меньше, пока,
наконец, при максимальном значении тока
этот прирост не станет равным нулю.
При дальнейшем изменении
тока от максимума до нуля убыль величины
тока становится все больше и
больше, пока, наконец около
нулевого значения ток, изменяясь с
наибольшей скоростью не исчезнет, но
тут же появляется вновь, протекая в
обратном направлении.
Рассматривая изменение
тока в течение периода, мы
видим, что с наибольшей скоростью
изменяется ток около своих нулевых
значений. Около максимальных значений
скорость изменения тока падает, а при
максимальном значении тока прирост его
равен нулю. Таким образом, переменный
ток меняется не только по величине и
направлению, но также и по скорости
своего изменения.
Переменный ток, проходя по виткам
катушки, создает переменное магнитное
поле. Магнитные линии этого поля,
пересекая витки своей же катушки,
индуктируют в них э. д. с. самоиндукции.
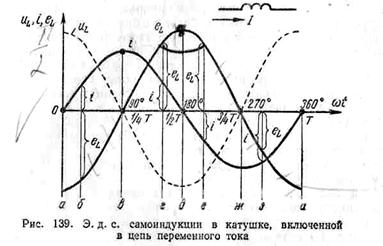
На рис. 139 кривая i показывает
изменение переменного тока в катушке.
Как было уже указано, величина э.
д. с. самоиндукции зависит от скорости
изменения тока и от индуктивности
катушки. Но так как индуктивность катушки
в нашем случае остается без изменения,
э. д. с. самоиндукции будет зависеть
только от скорости изменения тока. Выше
было показано, что наибольшая скорость
изменения тока имеет место около нулевых
значений тока. Следовательно,
наибольшее значение э. д. с. самоиндукции
имеет в те же моменты.
В момент а ток резко и быстро
увеличивается от нуля, а поэтому, как
следует из вышеприведенной формулы, э.
д. с. самоиндукции (кривая eL)
имеет отрицательное максимальное
значение. Так как ток увеличивается, то
э. д. с. самоиндукции, по правилу Ленца,
должна препятствовать изменению (здесь
увеличению) тока. Поэтому э. д. с.
самоиндукции при возрастании тока будет
иметь направление, обратное току
(положение б), что следует также из
указанной формулы. Скорость изменения
тока по мере приближения его к максимуму
уменьшается. Поэтому э. д. с. самоиндукции
также уменьшается, пока, наконец, при
максимуме тока, когда изменения его
будут равны нулю, она не станет равной
нулю (положение в).
Переменный ток, достигнув
максимума, начинает убывать. По правилу
Ленца, э. д. с. самоиндукции препятствует
току убывать и, направленная уже в
сторону протекания тока» будет его
поддерживать (положение г).
При дальнейшем изменении переменный
ток быстро убывает до нуля. Резкое
уменьшение тока в катушке повлечет за
собой
также быстрое уменьшение
магнитного поля и в результате
пересечения магнитными
линиями витков катушки в них будет
индуктироваться наибольшая э. д. с.
самоиндукции (положение д).
Во вторую половину периода изменения
тока картина повторяется и снова при
возрастании тока э.
д. с. самоиндукции
будет препятствовать ему, имея
направление, обратное току (положение е).
При убывании тока э. д. с.
самоиндукции, имея направление,
совпадающее с током, будет поддерживать
его, не давая ему исчезнуть сразу
(положение з).
На рисунке видно, что э. д. с. самоиндукции
отстает по фазе от тока на 90°, или на 1/4
периода. Так как магнитный поток совпадает
по фазе с током, то можно сказать, что
э. д. с, наводимая магнитным потоком,
отстает от него по фазе на 90°, или на 1/4
периода.
Нам уже известно, что две синусоиды,
сдвинутые одна относительно другой на
90′, можно изобразить векторами,
расположенными под углом 90° (рис.
140).

Так как э. д. с. самоиндукции в цепях
переменного тока непрерывно
противодействует изменениям тока,
то, чтобы ток мог протекать по виткам
катушки, напряжение сети должно
уравновешивать э. д. с. самоиндукции.
Иными словами, напряжение сети в каждый
момент времени должно быть равно и
противоположно э. д. с. самоиндукции.
Вектор напряжения сети,
равный и противоположный э. д. с.
самоиндукции EL,
мы обозначим через U (рис. 141). Только при
условии, что к зажимам катушки приложено
напряжение сети, равное и противоположное
э. д. с. самоиндукции, и, стало быть, это
напряжение сети U уравновешивает э.
д. с. самоиндукции ЕL по
катушке может проходить переменный
ток I.
Но в этом случае напряжение сети U будет
опережать по фазе ток I на
90°.
Следовательно, в цепи с
индуктивностью ток I отстает
от приложенного напряжения U по фазе
на 1/4 периода.

На векторной диаграмме
этому сдвигу фаз между напряжением U и
током I соответствует
угол а = 90° или
Таким образом, в цепях
переменного тока э. д. с. самоиндукции,
возникая и действуя непрерывно, вызывает
сдвиг фаз между током и напряжением.
Возвращаясь к рис. 139, мы видим, что
ток iпо
катушке будет проходить и тогда, когда
напряжение сети (кривая uL.)
равно нулю (положение в), и даже тогда,
когда напряжение сети направлено в
сторону, обратную току (положение г и
з).
Итак отметим, что в цепи переменного
тока, когда э. д. с. самоиндукции
отсутствует, напряжение сети и ток
совпадают по фазе. Индуктивная же
нагрузка в цепях переменного тока
(обмотки электродвигателей и
генераторов, обмотки трансформаторов,
индуктивные катушки) всегда вызывает
сдвиг фаз между током и напряжением.
Можно показать, что скорость
изменения, синусоидального тока
пропорциональна угловой частоте ω.
Следовательно, действующее значение
э. д. с. самоиндукции EL может
быть найдено по формуле
Как было отмечено выше, напряжение,
приложенное к зажимам цепи, содержащей
индуктивность, должно быть по величине
равно э. д. с. самоиндукции:
Поэтому
Обозначая
Формула закона Ома для цепи переменного
тока, содержащей индуктивность, имеет
вид
Величина xL называется
индуктивным сопротивлением цепи,
или реактивным сопротивлением
индуктивности, и измеряется в омах.
Таким образом, индуктивное сопротивление
представляет собой своеобразное
препятствие, которое цепь с индуктивностью
оказывает изменениям тока в ней. Оно
равно произведению индуктивности на
угловую частоту:
Так как индуктивное
сопротивление проводника зависит от
частоты переменного тока, то сопротивление
катушки, включаемой в цепь токов различной
частоты, будет
различным. Например,
если имеется катушка с
индуктивностью 0,05 гн,
то в цепи тока частотой 50 гц ее
индуктивное сопротивление будет
а в цепи тока частотой 400 гц
Та часть напряжения сети,
которая преодолевает (уравновешивает)
э. д. с. самоиндукции, называется
индуктивным падением напряжения (или
реактивной слагающей н
а п р я ж е н и я):
Рассмотрим теперь, какая мощность
потребляется от источника переменного
напряжения, если к зажимам его подключена
индуктивность.
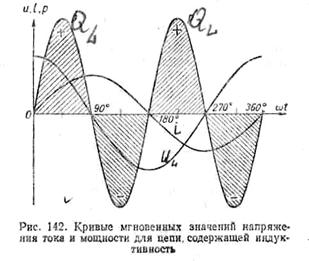
На рис. 342 даны кривые
мгновенных значений напряжения, тока
и мощности для этого случая. Мгновенное
значение мощности равно произведению
мгновенных значений напряжения и
тока:
Из чертежа видно, что
если u и i имеют
одинаковые знаки, то кривая р располагается
выше оси wt.
Если же u и
i имеют разные знаки, то кривая р
располагается ниже оси wt.
В первую четверть периода ток, а вместе
с ним и магнитный поток катушки
увеличиваются. Катушка потребляет из
сети мощность. Площадь, заключенная
между кривой р и осью wt, есть работа
(энергия) электрического тока. В первую
четверть периода энергия, потребляемая
из сети, идет на создание магнитного
поля вокруг витков катушки (мощность
положительная). Количество энергии,
запасаемое в магнитном поле за время
увеличения тока, можно определить по
формуле
Во вторую четверть периода
ток убывает. Э. д. с. самоиндукции, которая
в первую четверть периода стремилась
препятствовать возрастанию тока, теперь,
когда ток начинает уменьшаться, будет
препятствовать ему уменьшаться. Сама
катушка становится как бы генератором
электрической энергии. Она возвращает
в сеть энергию, запасенную в ее магнитном
поле. Мощность отрицательна, и на рис.
142 кривая р располагается ниже оси wt.
Во вторую половину периода явление
повторяется. Таким образом, между
источником переменного напряжения и
катушкой, содержащей индуктивность,
происходит обмен мощностью. В течение
первой и третьей четвертей периода
мощность поглощается катушкой, в течение
второй и четвертой четвертей мощность
возвращается источнику.
В этом случае в среднем
расхода энергии не будет, несмотря на
то что на зажимах цепи есть напряжение
U и в цепи протекает ток I.
Следовательно, средняя, или активная,
мощность цени, носящей чисто индуктивный
характер, равна нулю.
Из графика, изображенного
на рис. 142, видно, что мгновенная мощность
цепи с индуктивностью два раза в течение
каждого периода (когда wt
= 45°, 135° и т. д.) достигает максимального
значения,
равного
, Этой
величиной принято характеризовать
количественно процесс обмена энергией
между источником и магнитным полем.
Ее называют реактивной мощностью и
обозначают буквой Q.
Учитывая, что в рассматриваемой
цепи U = IxL,
получаем следующее выражение для
реактивной мощности: