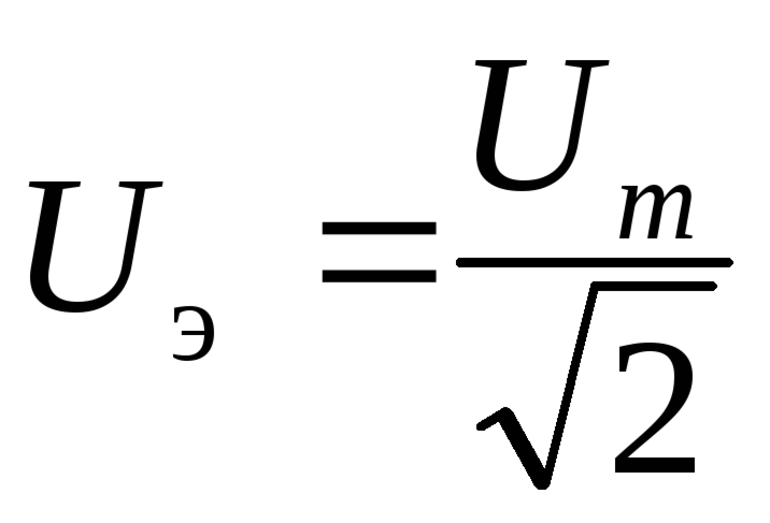Как найти мощность для переменного тока - Сайт, где вы сможете решить свои вопросы

Исследуем и рассчитываем мощность в цепи переменного тока

Содержание

1 Виды тока
2 Зачем нужно знать мощность электрооборудования
3 Виды мощности
4 Как измерить косинус «фи»
5 Как узнать мощность
6 Видео по теме

В процессе эксплуатации электрооборудования важную роль играет соответствие требуемой мощности и возможностей сети электропитания. Чтобы выполнить предварительные расчёты, необходимо понимать, какова природа электрической мощности и чем определяется её величина.

Виды тока

Техника может работать с использованием постоянного или переменного электрического тока. В первом случае сила тока на протяжении эксплуатации не меняется. Во втором она периодически меняется по абсолютной величине и знаку.

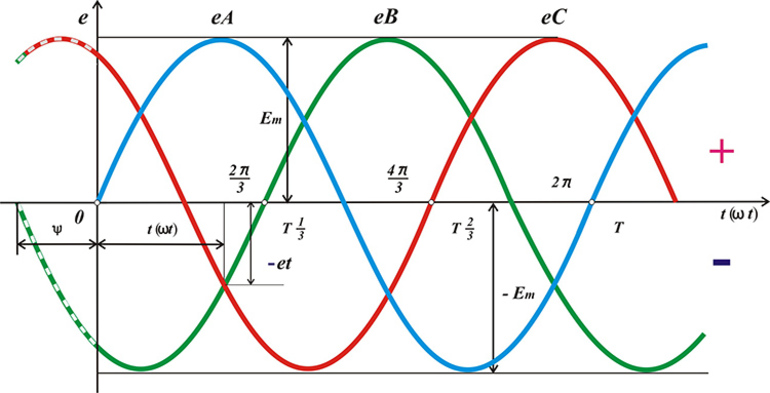
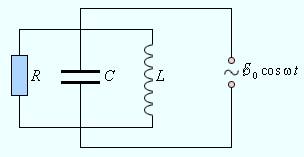
Наиболее часто переменный ток изменяется по синусоидальному закону, однако в некоторых случаях импульсы могут иметь другую, например, прямоугольную форму. В бытовых и производственных условиях часто для питания электроприборов требуется наличие однофазного или трехфазного переменного тока.

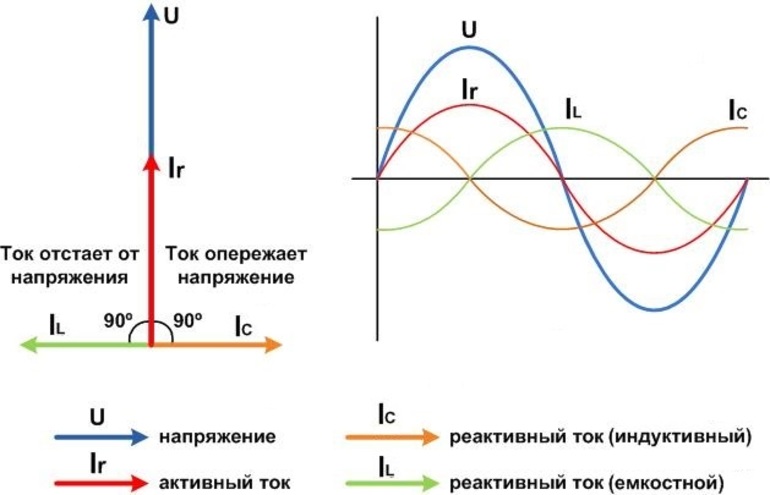
На представленном выше графике сила тока для активной мощности обозначена красным цветом. Для реактивной использованы обозначения с индексами L и C. На этом графике показан сдвиг фаз. Здесь видно, что ёмкостный ток отстаёт, а индуктивный опережает активный. При проведении расчетов для выбора автотрансформатора или других электроприборов важно правильно учитывать имеющиеся смещения.

Зачем нужно знать мощность электрооборудования

Каждый подключенный электроприбор для обеспечения своей работы будет потреблять часть мощности электросети. Если их работает одновременно несколько, то мощности складываются. Важно при расчете потребляемой электроэнергии учитывать:

Мощность в цепи переменного тока или постоянного, которая обеспечивается поставщиком.
Параметры защитных приборов, с помощью которых осуществляется регулирование рабочих характеристик оборудования.
Конструкцию системы проводов и удлинителей.
Наличие автотрансформатора или аналогичных устройств.

Если подаваемая мощность недостаточна, это способствует появлению перебоев в поставке электроэнергии. Защитные приборы должны быть настроены таким образом, чтобы при возникновении аварийной ситуации прерывать поступление электричества. Для этого в них должны быть заложены данные о том, какая величина мощности в цепях переменного или постоянного тока считается нормальной, а какая свидетельствует о возникновении проблемной ситуации.

Провода, удлинители и другие элементы электропроводки рассчитаны на определённые предельные значения. При их превышении они будут плавиться или перегорать. Перед подключением автотрансформатора или других электроприборов нужно предварительно узнать, соответствует ли требуемая им мощность имеющимся возможностям электросети.

Виды мощности

Полная мощность на участке цепи определяется как работа, выполняемая в течение единицы времени. Её также можно рассматривать как отношение используемой энергии к продолжительности интервала времени, на протяжении которого это происходит.

При работе электрического прибора часть мощность частично тратится на получение полезного эффекта. Такую мощность называют активной. Электрическая энергия при этом превращается в другой вид. Например, речь может идти о том, что она выделится в виде света или тепла.

Переменный ток при наличии в схеме ёмкости и индуктивности создаёт реактивную мощность. Она не расходуется, а преобразуется из одной формы в другую. Реактивная мощность, выделяемая в конкретной цепи переменного тока, считается паразитной. Если ее величина незначительная, то вся используемая энергия является активной.

Реактивная и активная мощности — это составляющие полной электрической мощности. Сложение осуществляется по векторным правилам. Чтобы рассчитать полную мощность, следует применить теорему Пифагора.

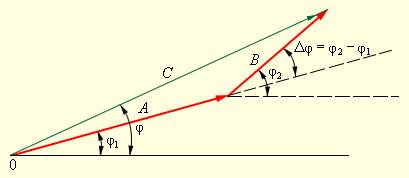
На приведённом рисунке длина гипотенузы выражает полную мощность, горизонтально расположенный катет — активную составляющую, а вертикально — реактивную. Как известно, квадрат гипотенузы — это сумма квадратов катетов.

В приведённой формуле используются следующие обозначения:

С левой стороны знака равенства указана полная мощность.
В качестве P рассматривается активная мощность.
С помощью Q обозначена реактивная мощность.

Соотношение активной и реактивной мощности выражается через косинус угла «фи». Этот угол представляет собой фазовый сдвиг между электротоком и электронапряжением. Чтобы оценить реальную мощность работы оборудования, косинус «фи» часто указывают в технической документации электроприбора, как коэффициент мощности. Он полезен для определения особенностей использования автотрансформатора или других приборов.

Единицей измерения активной мощности является ватт. Для реактивной применяется вольт-ампер реактивный (вар). Полная мощность измеряется вольт-амперами.

Используется еще и такое понятие, как мгновенная мощность, которая постоянно меняется. Например, она может иметь нулевое значение в тех точках, где сила электротока также равняется нулю. На практике мгновенная мощность используется редко, но применяется её среднее значение за период.

Как измерить косинус «фи»

Обычно эта информация содержится в технической документации прибора. Если она не указана, то ее измеряют с помощью специального прибора — фазометра.

Чем больше рассматриваемая величина, тем выше будет эффективность электрооборудования. Если косинус небольшой, то выгодно улучшить ситуацию, используя компенсацию реактивной мощности переменного тока. Чтобы понять принцип работы, следует вспомнить, что реактивная мощность возникает из-за наличия ёмкости и индуктивности в электроцепи.

Для компенсации используют регулируемый узел, действующий противоположно реактивной составляющей электромощности. Например, регулировка может осуществляться при помощи дросселя с высокой индуктивностью. Его подключают последовательно с нагрузкой.

Как узнать мощность

Один из наиболее простых способов — измерение мощности с помощью ваттметра. Существуют различные виды таких устройств. Поскольку в быту не требуется особенно высокой точности, можно использовать довольно простые приборы.

Также можно провести вычисления, измерив напряжение, силу тока и сопротивление. Расчёт мощности осуществляется с помощью двух из этих трёх величин.

При использовании постоянного тока определение активной мощности выполняется с помощью следующего выражения:

Если нужно определить мощность однофазного переменного тока, используется формула:

Если ток трёхфазный, тогда мощность можно рассчитать по формуле:

Указанная выше формула мощности применяется при симметричном трёхфазном распределении. Если оно является асимметричным, тогда для каждой фазы мощность переменного тока вычисляется отдельно, а затем найденные значения складываются. Средняя мощность для переменного тока определяется интегральным исчислением.

Для определения реактивной мощности используют формулу:

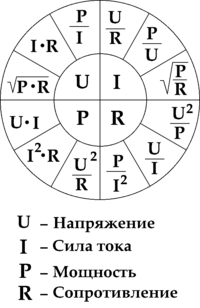
Знание электрической мощности не только полезно само по себе, но оно помогает вычислить различные характеристики используемого электрооборудования. Обычно значение мощности и косинуса «фи» можно получить из технической документации. Например, зная напряжение, можно вычислить силу электрического тока, чтобы учесть её при подключении и обеспечении безопасности использования оборудования.

На представленной выше схеме во внутреннем круге указаны величины, которые требуется определить. Вдоль окружности приведены формулы, которыми следует воспользоваться для вычисления.

Сказанное можно пояснить на следующем примере. Допустим, нужно определиться с мощностью. В этом случае следует обратить внимание на левый нижний сектор чертежа. Зная две из трёх величин, через которые выражается мощность (напряжение, силу тока и сопротивление), можно подобрать подходящую формулу для вычисления.

Если требуется найти, чему равна сила тока, то это выполняется аналогичным образом. Разница состоит в том, что теперь следует работать с правым верхним сектором. Здесь потребуется знать две из следующих трёх величин: мощность, сопротивление и напряжение. Нужно подобрать подходящую формулу и выполнить соответствующие вычисления.

Видео по теме

Источник

Классическая электродинамика

Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

Единицей измерения в Международной системе единиц (СИ) является ватт (русское обозначение: Вт, международное: W).

Мгновенная электрическая мощность[править | править код]

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки в точку , к величине пробного заряда. То есть можно сказать, что электрическое напряжение численно равно работе по переносу единичного заряда из точки в точку . Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу или над ним будет совершена работа, численно равная электрическому напряжению, действующему на участке цепи. Умножив напряжение на количество единичных зарядов, мы, таким образом, получаем работу, которую совершает электрическое поле по перемещению этих зарядов от начала участка цепи до его конца.
Мощность, по определению — это работа в единицу времени.

Введём обозначения:

— напряжение на участке A-B

(принимаем его постоянным на интервале Delta t

);

— количество зарядов, прошедших от

за время

;

— работа, совершённая зарядом

при движении по участку A-B

;

— мощность.

Записывая вышеприведённые рассуждения, получаем:

${displaystyle P_{A-B}={frac {A}{Delta t}}~.}$

Для единичного заряда на участке A-B :

${displaystyle P_{e(A-B)}={frac {U}{Delta t}}~.}$

Для всех зарядов:

${displaystyle P_{A-B}={frac {U}{Delta t}}cdot {Q}={U}cdot {frac {Q}{Delta t}}~.}$

Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть ${displaystyle textstyle I={frac {Q}{Delta t}}}$ по определению, в результате получаем:

${displaystyle P_{A-B}=Ucdot I~.}$

Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:

Если участок цепи содержит резистор c электрическим сопротивлением , то:

${displaystyle p(t)=i(t)^{2}cdot R={frac {u(t)^{2}}{R}}~.}$

Дифференциальные выражения для электрической мощности[править | править код]

Мощность, выделяемая в единице объёма, равна:

${displaystyle w={frac {dP}{dV}}=mathbf {E} cdot mathbf {j} ~,}$

где:

— напряжённость электрического поля;

— плотность тока.

Отрицательное значение скалярного произведения (векторы и противонаправлены или образуют тупой угол) означает, что в данной точке электрическая мощность не рассеивается, а генерируется за счёт работы сторонних сил.

В случае изотропной среды в линейном приближении:

${displaystyle w=sigma E^{2}={frac {E^{2}}{rho }}=rho j^{2}={frac {j^{2}}{sigma }}~,}$

где ${displaystyle textstyle sigma ,{overset {underset {mathrm {def} }{}}{=}},{frac {1}{rho }}}$ — удельная проводимость, величина, обратная удельному сопротивлению.

В случае наличия анизотропии (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла) в линейном приближении:

${displaystyle w=sigma _{alpha beta }E_{alpha }E_{beta }~,}$

где $sigma _{{alpha beta }}$ — тензор проводимости.

Мощность постоянного тока[править | править код]

Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:

Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:

${displaystyle P=I^{2}cdot R={frac {U^{2}}{R}}~,}$

где — электрическое сопротивление.

Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:

где — ЭДС.

Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность $p=I^{2}cdot r$ прибавляется к поглощаемой или вычитается из отдаваемой.

Мощность переменного тока[править | править код]

В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для большинства простых практических расчётов не слишком полезна непосредственно. Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.

Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол varphi (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.

Активная мощность[править | править код]

Единица измерения в СИ — ватт^[1].

Среднее за период значение мгновенной мощности называется активной электрической мощностью или электрической мощностью:

${displaystyle P={frac {1}{T}}int limits _{0}^{T}p(t)dt~.}$

В цепях однофазного синусоидального тока , где и — среднеквадратичные значения напряжения и тока, varphi — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи или её проводимость по формуле $P=I^{2}cdot r=U^{2}cdot g$ . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью активная связана соотношением .

В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отражённой мощностью.

Реактивная мощность[править | править код]

Единица измерения, по предложению Международной электротехнической комиссии, – вар (вольт-ампер реактивный); (русское обозначение: вар; международное: var). В терминах единиц СИ, как отмечено в 9-ом издании Брошюры СИ, вар когерентен произведению вольт-ампер. В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения в области «электротехника»^[1]^[2]:

{displaystyle Q=Ucdot Icdot sin varphi ~.}

Вар определяется как реактивная мощность цепи с синусоидальным переменным током при действующих значениях напряжения 1 В и тока 1 А, если сдвиг фазы между током и напряжением ${displaystyle textstyle {frac {pi }{2}}}$ ^[3].

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения и тока , умноженному на синус угла сдвига фаз varphi между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью и активной мощностью соотношением:

${displaystyle |Q|={sqrt {S^{2}-P^{2}}}~.}$

Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.

Необходимо отметить, что величина для значений varphi от 0 до плюс 90° является положительной величиной. Величина для значений varphi от 0 до −90° является отрицательной величиной. В соответствии с формулой , реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии, возвращаемой от индуктивной и ёмкостной нагрузки в источник переменного напряжения.

Полная мощность[править | править код]

Единица измерения — В·А, вольт-ампер (русское обозначение: В·А; международное: V·A). В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения «электротехника»^[1]^[2].

Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи и напряжения на её зажимах связана с активной и реактивной мощностями соотношением:

${displaystyle S={sqrt {P^{2}+Q^{2}}}~,}$

где:

— активная мощность;

— реактивная мощность (при индуктивной нагрузке

, а при ёмкостной

Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:

{displaystyle {vec {S}}={vec {P}}+{vec {Q}}~.}

Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.

Комплексная мощность[править | править код]

Мощность, аналогично импедансу, можно записать в комплексном виде:

${displaystyle {dot {S}}={dot {U}}{dot {I}}^{*}=I^{2}mathbb {Z} ={frac {U^{2}}{mathbb {Z} ^{*}}}~,}$

где:

— комплексное напряжение;

— комплексный ток;

— импеданс;

— оператор комплексного сопряжения.

Модуль комплексной мощности равен полной мощности Действительная часть равна активной мощности а мнимая — реактивной мощности с корректным знаком в зависимости от характера нагрузки.

Измерения[править | править код]

Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра, амперметра и фазометра.
Для измерения коэффициента реактивной мощности применяют фазометры
Государственный эталон мощности — ГЭТ 153—2012 Государственный первичный эталон единицы электрической мощности в диапазоне частот от 1 до 2500 Гц. Институт-хранитель: ВНИИМ

Потребление мощности некоторыми электроприборами[править | править код]

Значения потребляемой электрической мощности некоторых потребителей

Электрический прибор	Мощность,Вт
Лампочка фонарика	1
Сетевой роутер, хаб	10…20
Системный блок ПК	100…1700
Системный блок сервера	200…1500
Монитор для ПК ЭЛТ	15…200
Монитор для ПК ЖК	2…40
Лампа люминесцентная бытовая	5…30
Лампа накаливания бытовая	25…150
Холодильник бытовой	15…700
Электропылесос	100… 3000
Электрический утюг	300…2 000
Стиральная машина	350…2 000
Электрическая плитка	1000…2000
Сварочный аппарат бытовой	1000…5500
Двигатель лифта невысокого дома	3 000…15 000
Двигатель трамвая	45 000…75 000
Двигатель электровоза	650 000
Электродвигатель шахтной подъёмной машины	1 000 000…5 000 000
Электродвигатель прокатного стана	6 000 000…32 000 000

Выходная мощность[править | править код]

Измеряется как долговременная (RMS^[en]), так и кратковременная (PMO, PMPO) мощности, способные отдавать усилителями мощности.

также см.: КПД

См. также[править | править код]

Ваттметр
Электрический ток
Коэффициент мощности
Список параметров напряжения и силы электрического тока
Закон Ома
КПД

Примечания[править | править код]

↑ ¹ ² ³ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 26—27. — 240 с. — ISBN 5-7050-0118-5.
↑ ¹ ² Положение о единицах величин, допускаемых к применению в Российской Федерации Архивная копия от 2 ноября 2013 на Wayback Machine Утверждено Постановлением Правительства РФ от 31 октября 2009 г. N 879.
↑ Сена Л. А. Единицы физических величин и их размерности. — М.: Наука, 1977. — С. 213.

Литература[править | править код]

ГОСТ 8.417-2002 Единицы величин.
ПР 50.2.102-2009 Положение о единицах величин, допускаемых к применению в Российской Федерации.
Л. А. Бессонов . Теоретические основы электротехники. Электрические цепи: учебник

для бакалавров. — 12-е изд., испр. и доп. — М.: Юрайт, 2016. — 702 с. — (Бакалавр. Углубленный курс). — 1000 экз. — ISBN 978-5-9916-3210-2.

Гольдштейн Е. И., Сулайманов А. О., Гурин Т. С. Мощностные характеристики электрических цепей при несинусоидальных токах и напряжениях. ТПУ, — Томск, 2009, Деп. в ВИНИТИ, 06.04.09, № 193 — 2009. — 146 с.

Ссылки[править | править код]

Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. ToeHelp.Ru. Дата обращения: 7 марта 2022.
Для чего нужна компенсация реактивной мощности. Школа для электрика (2010). Дата обращения: 7 марта 2022.
. ред. Д. Макаров : Как рассчитать мощность электрического тока? Заметки электрика. ASUTPP. Дата обращения: 7 марта 2022.

Источник

Общее понятие

Электрическое напряжение определяется как отношение работы поля по переброске пробного заряда из одной заданной точки в другую к размеру потенциала. При дислокации единичного резерва выполняется работа, которая равняется напряжению на искомом участке. Общая мощность получают умножением работы электрического поля для единичного заряда на число потенциалов за определенную единицу времени.

В переменной электрической цепи выделяется 3 вида мощности:

активный P;
реактивный Q;
полного типа S.

В цепи переменного электричества формула для расчета постоянного тока применяется только для вычисления мгновенной мощности. Этот показатель претерпевает изменения во времени и почти не имеет практического смысла для всех остальных расчетов. Среднезначимый показатель мощности требует временной интеграции. Мгновенная мощность объединяется в течение определенного промежутка для расчета величины в магистрали с периодическим изменением силы переменного потока и синусоидального напряжения.

Применяется концепция комплексных чисел для связывания всех трех видов мощности. Это понятие обозначает, что в переменной цепи нагрузка выражается подобным числом так, что активная разновидность представляется действительной составляющей. Реактивный показатель выступает мнимым показателем, а полная мощность показывается в форме модуля. В этих расчетах принимает участие угол сдвига фаз φ, который является аргументом баланса мощностей в цепи переменного тока.

Активная мощность

Активная скорость преобразования выражается также через взаимное отношение силы потока, напряжения к значению активной составляющей сопротивления. В магистрали синусоидального и несинусоидального движения электронов активная нагрузка приравнивается к сумме аналогичных значений на отдельных участках.

Для определения среднего периодического размера используется активная мощность переменного тока, формула расчета P = U ^. I ^. cos φ (косинус), где:

U — мощность.
I — сила потока.
φ – угол смещения фаз.

Средний показатель мгновенной скорости преобразования в однофазной цепи берется в виде среднеквадратичного значения тока и напряжения с определенным углом сдвига. В цепях несинусоидального электричества мощность приравнивается к сумме соответствующих показателей отдельных перемещений. С помощью активной мощности характеризуется интенсивность необратимого видоизменения электроэнергии в другие разновидности, например, электромагнитную или тепловую.

Проходящая мощность используется в качестве активной в концепции длинных магистралей для анализа электромагнитных течений, протяженность которых сопоставляется с размерностью волны. Искомое значение рассчитывается как разница между понижающейся и отражающейся мощностями. От свойств коэффициента углового смещения зависят полученные показатели отрицательной или положительной нагрузки активного типа.

Реактивная характеристика

Для обозначения применяется дополнительно единица вольт-ампер реактивный (вар). В русских аналогах используется вар, а международные специалисты применяют var. В РФ единица допускается для электротехнических расчетов в форме внесистемного значения.

Нахождение производится по формуле P = U ^. I ^. sin φ (синус), где:

U — среднеквадратичная мощность.
I — среднеквадратичная сила потока.
φ – угол фазного смещения, значения синуса, определяются по таблицам.

При диапазоне показателя от 0 до 90º (ток отстает от напряжения, а нагрузка носит активно-индуктивный вид) синус φ будет иметь положительное значение. При угловом сдвиге от 0 до -90º (поток электронов опережает нагрузку, мощность отличается активно-емкостным свойством) константа всегда показывает отрицательный знак. Реактивная мощность характеризует напряженность, которая возникает в электромеханических приборах и цепях при изменении энергетических волн поля в магистрали переменного синусоидального потока.

В физическом смысле реактивная нагрузка показывает энергию, которая перекачивается от источника тока на конденсаторы, индукторы, двигательные обмотки, а впоследствии возвращается к источнику за один колебательный период. Реактивная мощность не принимает участия в работе электротока. В случае положительной характеристики устройство потребляет, а нагрузка с отрицательным знаком говорит о производстве энергии.

Это обстоятельство рассматривается в условном контексте, т. к. почти все энергопотребляющие приборы, например, двигатели асинхронной работы, а также полезная нагрузка, подаваемая через трансформатор, относятся к активно-индуктивным видам. Синхронные двигатели электростанций одновременно производят и потребляют энергию в зависимости от максимальной величины электротока возбуждения в роторных обмотках. Эта особенность применяется для координации уровня нагрузки в магистрали в электротехнике.

С помощью современных преобразователей производится компенсация реактивной нагрузки во избежание перегрузок и для увеличения коэффициента мощности электроустановок. Приборы более точно оценивают размер энергии, которая поступает в обратном направлении от индуктора к источнику переменного тока.

Полная нагрузка

Показатель используется в физике для описания потребляемой мощности, которая прилагается к подводящим агрегатам электросети с использованием резисторов. Суммируются параметры ЭДС распределительных щитков, кабелей, проводов, ЛЭП, трансформаторов.

Полную нагрузку можно рассчитать по формуле S = U ^. I, где:

S — параметр полной нагрузки (В/а).
U — расчетная нагрузка в генераторе.
I — комплексный показатель силы тока в сочетании с обмоточным значением.

Параметр темпа преобразований зависит от характеристик применяемого тока, а не от свойств фактически использованной нагрузки. По этой причине полная мощность распределительных электрощитов и трансформаторных агрегатов измеряется в вольт-амперах, а значение ватт к ней не применяется.

Работа в различных условиях

Модуль комплексного показателя интенсивности передвижения равняется показателю полной нагрузки. Действительная составляющая часть приравнивается к активной силе, а мнимая считается реактивным видом. Имеет место положительный или отрицательный знак, что зависит от интенсивности загруженности цепи. Комплексная мощность должна соответствовать сопряженному электрическому сопротивлению. Положительная нагрузка характеризуется соотношением Р > 0, а знак минус проявляется в случае Р < 0.

Измерение мощностных характеристик переменного потока электронов проводится при пропускании равного по значению тока по фазным проводникам. Показатели силы течения заряженных частиц с применением нулевого проводника имеют ничтожную размерность. Равномерная или симметричная фазовая нагрузка в трехфазной магистрали зависит от величины протекающих токов. Неравномерная или несимметричная нагрузка зависит от прохождения потока по нейтральным или нулевым кабелям. Общий мощностной уровень находится суммированием.

Если присутствует фазовый сдвиг между напряжением и силой тока, то он совпадает с углом смещения между векторными радиусами показателей электротока. В условиях переменного напряжения совпадение векторных радиусов тока и вольтажа отмечается только при отсутствии в цепи конденсаторов и катушек индукции. Установка индукторов не мешает совпадению фазных значений. При этом происходит векторное вращение равной интенсивности. График смещения внутреннего угла остается постоянным.

Если в магистрали происходит сдвиг напряжения и переменного тока, то мощностные показатели представляются значением с отрицательным знаком, так как калькулятор перемножает положительные и отрицательные величины. Продолжительность периодов зависит от уровня смещения фаз. При этом длительность отрицательных нагрузок определяет характеристики сдвига. При расчетах используются показатели сопротивления, которые знакомы из физического закона Ома.

Коэффициент скорости преобразования

Мощностной коэффициент является показателем потребления тока при присутствии реактивного компонента и искажающей нагрузки. Значение коэффициента отличается от понятия косинуса сдвигаемого угла. Второе понятие характеризуется смещением протекающего переменного тока, напряжения и используется только при синусоидальном токе и силе равного значения.

Коэффициент равняется отношению расходуемой нагрузки к ее полному значению. При этом работа совершается за счет активного вида преобразования. При синусоидальном токе и вольтаже полная нагрузка находится в виде суммы реактивной и активной форм. Активная нагрузка приравнивается к усредненному произведению силы тока и напряжения и не может быть выше произведения аналогичных среднеквадратических размерностей. Мощностной коэффициент показывается в диапазоне от 0 до 1 или ставится в процентах от 0 до 100.

При математическом расчете числовой множитель интерпретируется в качестве косинуса угла между токовыми векторами и направлением приложения вольтажа. Поэтому при синусоидальных характеристиках размерность коэффициента может совпадать с косинусом угла. Если применяется только синусоидальный вольтаж, а ток используется несинусоидальный с нагрузкой без реактивного компонента, то числовой переходник равняется части нагрузки при первых искажениях потребительского тока.

Если реактивный элемент присутствует в нагрузке, то, помимо мощностного коэффициента, указывается характер работы (емкостно-активный или индуктивно-активный). Коэффициент в этих случаях отличается и является отстающим или опережающим значением.

Практическое применение и коррекция

Если к розетке с синусоидальным напряжением 50 Гц и 230 В подсоединить нагрузку с опережением или отставанием тока от напряжения на какую-то угловую величину, то на активной внутренней катушке будет создаваться увеличенная мощность. Это значит, что при работе в таких условиях выделяется много тепла, и электростанция отводит его в увеличенном количестве, по сравнению с применением активной нагрузки.

Коэффициенты полезного действия и мощности отличаются друг от друга. Мощностной показатель не влияет на потребление приемника, подключенного к сети, но изменяет энергетические потери в подводных проводах и местах выработки энергии или ее преобразования. В доме электросчетчик не реагирует на проявление мощности, так как оплачивается только та энергия, за счет которой работают приборы.

КПД влияет на потребляемую активную нагрузку. Например, энергосберегающая лампа потребляет в полтора раза больше электричества, чем аналогичный прибор накаливания. Это говорит о высоком коэффициенте полезного действия у первой лампы. Но показатель нагрузки может быть низким и высоким в обоих вариантах.

Коррекция заключается в приведении потребления прибора с низким мощностным коэффициентом к стандартным показателям при питании от силовой цепи переменного тока. Технически это осуществляется применением действенной схемы на входном устройстве, которая помогает равномерно использовать фазную мощность и исключает перегрузку нулевого провода. При этом снижаются всплески потребительского тока на верхушке синусоиды питающего вольтажа.

Реактивная нагрузка корректируется при включении в магистраль элемента с обратным действием. Например, в двигателе переменного тока для компенсации действия ставится конденсатор параллельно питающей линии. Применяется система активного или пассивного корректора при изменении используемого тока во время колебательного периода подпитывающего напряжения для преобразования коэффициента. Простым примером является последовательное подключение дросселя. При этом конечные приборы потребляют ток непропорционально гармоничным искажениям. Катушка сглаживает волновые импульсы.

Источник

RIR=UR; 1ωCIC=UC; ωLIL=UL.

Указанные выше формулы внешне могут напоминать закон Ома на участке цепи постоянного тока, но стоит заметить, что в этом случае вместо величин постоянных токов и напряжений на участке цепи, в них входят амплитудные значения напряжений и переменных токов.

Формулы, указанные выше, выражают собой закон Ома для переменного тока, который содержит один из элементов R, L и C.

Определение 1

R – активное сопротивление резистора.

1ωС – емкостное сопротивление конденсатора.

ωL – индуктивное сопротивление катушки в цепи переменного тока.

Движение переменного тока по участку цепи провоцирует электромагнитное поле выполнять работу, благодаря чему выделяется джоулево тепло.

Определение 2

Мгновенной мощностью в цепи называется произведение мгновенных значений тока и напряжения: p=J·u.

Прикладной интерес у нас вызывает среднее значение мощности за некоторый период переменного тока:

P=Pcα=I0U0cos ωt cos ωt+φ.

В приведенной выше формуле I0 и U0 являются амплитудными значениями тока и напряжения на выбранном участке цепи, а φ – фазовым сдвигом между током и напряжением. Черта же представляет собой символ усреднения. В случае, когда цепь содержит только резистор с сопротивлением R, то фазовый сдвиг φ будет равен нулю:

PR=IRURcos2ωt=IRUR2=IR2R2.

Действующие значения силы тока и напряжения

Определение 3

По причине необходимости совпадения с уравнением для мощности постоянного тока, нам приходится ввести определения действующих значений силы тока и напряжения:

IД=l02; UД=U02.

Мощность переменного тока на участке цепи

Определение 4

Средняя величина мощности переменного тока на участке цепи, включающем в себя резистор, равняется:

PR=IДUД.

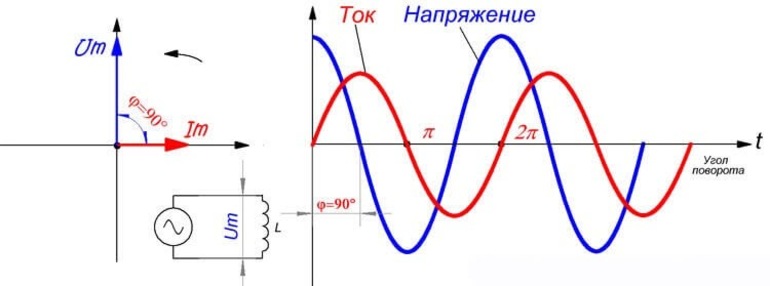
Если в цепи содержится лишь конденсатор емкости C, то φ=π2. Отсюда, справедливо следующее выражение:

PC=ICUCcos ωt cosωt+π2=ICUCcos ωt-sin ωt=0.

Таким же способом можно проиллюстрировать, что PL=0.

Исходя из описанного выше получим следующие определение.

Определение 5

Мощность в цепи переменного тока выделяется только на активном сопротивлении, а среднее значение мощности переменного тока на конденсаторе и катушке индуктивности равняется нулю.

Теперь стоит рассмотреть электрическую цепь, включающую последовательно соединенные резистор, конденсатор и катушки, и подключенную к источнику переменного тока некой частоты ω. Следует выделить, что на всех участках цепи, соединенных последовательно, проходит один и тот же ток. Между напряжением внешнего источника e(t) и током J(t) проявляется фазовый сдвиг на определенный угол φ.

Исходя из приведенных выше фактов, мы можем записать:

J(t)=I0cos ωt; e(t)=δ0cos ωt+φ.

Данные формулы мгновенных значений тока и напряжения подходят к построениям, выполненным на векторной диаграмме (рис. 2.3.2).

Рисунок 2.3.2. Гармонические колебания A cos (ωt+φ1), B cos (ωt+φ2) и их суммы C cos (ωt+φ) на векторной диаграмме.

Средняя величина мощности, развиваемой источником переменного тока, может быть найдена из следующего выражения:

P=I0δ0cos ωt cos ωt+φ=I0δ02cos φ=IДδД cos φ.

Исходя из данных векторной диаграммы можно заявить, что UR=δ0·cos φ, следовательно,
P=I0UR2, а вся мощность, которую развивает источник питания, теряется в виде джоулева тепла на резисторе.

В прошлых темах нами было получено выражение, являющееся соотношением амплитуд тока I0 и напряжений δ0 в условиях последовательной RLC-цепи:

I0=δ0R2+ωL-1ωC2

Определение 6

Z=R2+ωL-1ωC2– это величина, имеющая название полное сопротивление цепи переменного тока.

Определение 7

Связь между амплитудными значениями тока и напряжения в цепи имеет вид:

ZI0=δ0.

Данное выражение представляет собой закон Ома для цепи переменного тока.

Закон Ома в условиях параллельной RLC-цепи

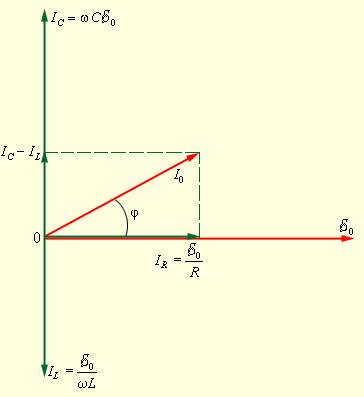
В различных расчетах, связанных с работой над цепями переменного тока, очень важное место занимает понятие полного сопротивления. Для его определения в цепи в большей части случаев практично использовать метод векторных диаграмм. В качестве примера, приведем параллельный подключенный к внешнему источнику переменного тока (рис. 2.4.1) RLC-контур:

Рисунок 2.4.1. Параллельный RLC-контур.

При построении диаграммы важно учесть, что в условиях параллельного соединения напряжение на всех элементах R, C и L идентично и равняется напряжению внешнего источника питания. Ток, текущий в разных ветвях цепи, различается не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Следовательно, полное сопротивление цепи невозможно вычислить опираясь на законы параллельного соединения цепей постоянного тока. Векторную диаграмму для параллельного RLC-контура можно увидеть на рис. 2.4.2.

Рисунок 2.4.2. Векторная диаграмма для параллельного RLC-контур.

Исходя из вида диаграммы, следует:

I0=δ01R2+ωL-1ωC2.

Определение 8

Соответственно, полное сопротивление параллельного RLC-контура выражается в виде следующего соотношения:

Z=11R2+ωL-1ωC2.

Определение 9

При параллельном резонансе (ω2=1LC) полное сопротивление цепи принимает свое максимальное значение, которое эквивалентно активному сопротивлению резистора:

Z=Zmax=R.

А значение фазового сдвига φ между током и напряжением при параллельном резонансе равняется нулю.

Источник

Большинство бытовых приборов, подключаемых к сети, характеризуются таким параметром, как электрическая мощность устройства. С физической точки зрения мощность представляет собой количественное выражение совершаемой работы. Поэтому для оценки эффективности того или иного устройства вам необходимо знать нагрузку, которую он будет создавать в цепи. Далее мы рассмотрим особенности самого понятия и как найти мощность тока, обладая различными характеристиками самого устройства и электрической сети.

Понятие электрической мощности и способы ее расчета

С электротехнической точки зрения она представляет собой количественное выражение взаимодействия энергии с материалом проводников и элементами при протекании тока в электрической цепи. Из-за наличия электрического сопротивления во всех деталях, задействованных в проведения электротока, направленное движение заряженных частиц встречает препятствие на пути следования. Это и обуславливает столкновение носителей заряда, электроэнергия переходит в другие виды и выделяется в виде излучения, тепла или механической энергии в окружающее пространство. Преобразование одного вида в другой и есть потребляемая мощность прибора или участка электрической цепи.

В зависимости от параметров источника тока и напряжения мощность также имеет отличительные характеристики. В электротехнике обозначается S, P и Q, единица измерения согласно международной системы СИ – ватты. Вычислить мощность можно через различные параметры приборов и электрических приборов. Рассмотрим каждый из них более детально.

Через напряжение и ток

Наиболее актуальный способ, чтобы рассчитать мощность в цепях постоянного тока – это использование данных о силе тока и приложенного напряжения. Для этого вам необходимо использовать формулу расчета: P = U*I

Где:

P – активная мощность;
U – напряжение приложенное к участку цепи;
I — сила тока, протекающего через соответствующий участок.

Этот вариант подходит только для активной нагрузки, где постоянный ток не обеспечивает взаимодействия с реактивной составляющей цепи. Чтобы найти мощность вам нужно выполнить произведение силы тока на напряжение. Обе величины должны находиться в одних единицах измерения – Вольты и Амперы, тогда результат также получится в Ваттах. Можно использовать и другие способы кВ, кА, мВ, мА, мкВ, мкА и т.д., но и параметр мощности пропорционально изменит свой десятичный показатель.

Через напряжение и сопротивление

Для большинства электрических устройств известен такой параметр, как внутреннее сопротивление, которое принимается за константу на весь период их эксплуатации. Так как бытовые или промышленные единицы подключаются к источнику с известным номиналом напряжения, определять мощность достаточно просто. Активная мощность находится из предыдущего соотношения и закона Ома для участка цепи, согласно которого ток на участке прямо пропорционален величине приложенного напряжения и имеет обратную пропорциональность к сопротивлению:

I = U/R

Если выражение для вычисления токовой нагрузки подставить в предыдущую формулу, то получится такое выражение для определения мощности:

P = U*(U/R)=U²/R

Где,

P – величина нагрузки;
U – приложенная разность потенциалов;
R – сопротивление нагрузки.

Через ток и сопротивление

Бывает ситуация, когда разность потенциалов, приложенная к электрическому прибору, неизвестна или требует трудоемких вычислений, что не всегда удобно. Особенно актуален данный вопрос, если несколько устройств подключены последовательно и вам неизвестно, каким образом потребляемая электроэнергия распределяется между ними. Подход в определении здесь ничем не отличается от предыдущего способа, за основу берется базовое утверждение, что электрическая нагрузка рассчитывается как P = U×I, с той разницей, что напряжение нам не известно.

Поэтому ее мы также выведем из закона Ома, согласно которого нам известно, что падение напряжения на каком-либо отрезке линии или электроустановки прямо пропорционально току, протекающему по этому участку и сопротивлению отрезка цепи:

U=I*R

после того как выражение подставить в формулу мощности, получим:

P = (I*R)*I =I²*R

Как видите, мощность будет равна квадрату силы тока умноженной на сопротивление.

Полная мощность в цепи переменного тока

Сети переменного тока кардинально отличаются от постоянного тем, что изменение электрических величин, приводит к появлению не только активной, но и реактивной составляющей. В итоге суммарная мощность будет также состоять активной и реактивной энергии:

Где,

S – полная мощность
P – активная составляющая – возникает при взаимодействии электротока с активным сопротивлением;
Q – реактивная составляющая – возникает при взаимодействии электротока с реактивным сопротивлением.

Также составляющие вычисляются через тригонометрические функции, так:

P = U*I*cosφ

Q = U*I*sinφ

что активно используется в расчете электрических машин.

Рис. 1. Треугольник мощностей

Пример расчета полной мощности для электродвигателя

Отдельный интерес представляет собой нагрузка, подключенная к трехфазной сети, так как электрические величины, протекающие в ней, напрямую зависят от номинальной нагрузки каждой из фаз. Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.

Особенность питания и асинхронной и синхронной электрической машины заключается в том, что на обмотки может подаваться и фазное и линейное напряжение. Тот или иной вариант, как правило, обуславливается способом соединения обмоток электродвигателя. Тогда мощность будет вычисляться по формуле:

S = 3*U_ф*I_ф

В случае выполнения расчетов с линейным напряжением, чтобы найти мощность формула примет вид:

Активная и реактивная мощности будут вычисляться по аналогии с сетями переменного тока, как было рассмотрено ранее.

Теперь рассмотрим вычисления на примере конкретной электрической машины асинхронного типа. Следует отметить, что официальная производительность, указываемая в паспортных данных электродвигателя – это полезная мощность, которую двигатель может выдать при совершении оборотов вала. Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.

Рис. 2. Шильд электродвигателя

Как видите, для вычислений с шильда мы возьмем следующую информацию об электродвигателе:

полезная производительность – 3 кВт, а в переводе на систему измерения – 3000 Вт;
коэффициент полезного действия – 80%, а в пересчете для вычислений будем пользоваться показателем 0,8;
тригонометрическая функция соотношения активных и реактивных составляющих – 0,74%;
напряжение, при соединении обмоток треугольником составит 220 В;
сила тока при том же способе соединения – 13,3 А.

С таким перечнем характеристик можно воспользоваться несколькими способами:

S = 1,732*220*13,3 = 5067 Вт

Чтобы найти искомую величину, сначала определяем активную составляющую:

P = P_{полезная} / КПД = 3000/0.8 = 3750 Вт

Далее полную по способу деления активной на коэффициент cos φ:

S = P/cos φ = 3750/0.74 = 5067 Вт

Как видите, и в первом, и во втором случае искомая величина получилась одинакового значения.

Примеры задач

Для примера рассмотрим вычисление на участках электрической цепи с последовательным и параллельным соединением элементов. Первый вариант предусматривает ситуацию, когда все детали соединяются друг за другом от одного полюса источника питания до другого.

Рис. 3. Последовательная расчетная цепь

Как видите на рисунке, в качестве источника мы используем батарейку с номинальным напряжением 9 В и три резистора по 10, 20 и 30 Ом соответственно. Так как номинальный ток нам не известен, расчет произведем через напряжение и сопротивление:

P = U²/R = 81 / (10+20+30) = 1.35 Вт

Для параллельной схемы подключения возьмем в качестве примера участок цепи с двумя резисторами и одним источником тока:

Рис. 4. Параллельная схема подключения

Как видите, для удобства расчетов нам нужно привести параллельно подключенные резисторы к схеме замещения, из чего получится:

R_общ = (R₁*R₂) / (R₁+R₂) = (10*15) / (10+15) = 6 Ом

Тогда искомый номинал нагрузки мы можем узнать через значение тока и сопротивления:

P = I²*R = 25*6 = 150 Вт

Видео по теме

Источник

Исследуем и рассчитываем мощность в цепи переменного тока

Виды тока

Зачем нужно знать мощность электрооборудования

Виды мощности

Как измерить косинус «фи»

Как узнать мощность

Видео по теме

Мгновенная электрическая мощность[править | править код]

Дифференциальные выражения для электрической мощности[править | править код]

Мощность постоянного тока[править | править код]

Мощность переменного тока[править | править код]

Активная мощность[править | править код]

Реактивная мощность[править | править код]

Полная мощность[править | править код]

Комплексная мощность[править | править код]

Измерения[править | править код]

Потребление мощности некоторыми электроприборами[править | править код]

Выходная мощность[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Общее понятие

Активная мощность

Реактивная характеристика

Полная нагрузка

Работа в различных условиях

Коэффициент скорости преобразования

Практическое применение и коррекция

Действующие значения силы тока и напряжения

Мощность переменного тока на участке цепи

Закон Ома в условиях параллельной RLC-цепи

Понятие электрической мощности и способы ее расчета

Через напряжение и ток

Через напряжение и сопротивление

Через ток и сопротивление

Полная мощность в цепи переменного тока

Пример расчета полной мощности для электродвигателя

Примеры задач

Видео по теме

Вам также может понравиться

Как найти сколько литров в аквариуме

Ошибка 413 атернос как исправить

Как найти номер абонента петроэлектросбыт по адресу

Добавить комментарий Отменить ответ