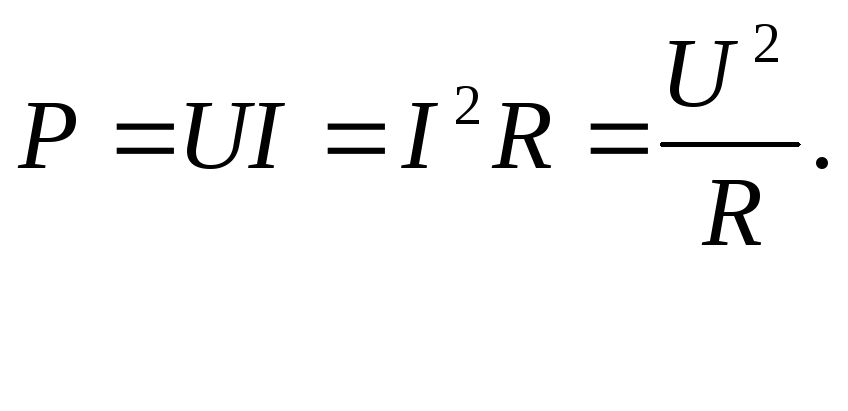Большинство бытовых приборов, подключаемых к сети, характеризуются таким параметром, как электрическая мощность устройства. С физической точки зрения мощность представляет собой количественное выражение совершаемой работы. Поэтому для оценки эффективности того или иного устройства вам необходимо знать нагрузку, которую он будет создавать в цепи. Далее мы рассмотрим особенности самого понятия и как найти мощность тока, обладая различными характеристиками самого устройства и электрической сети.
Понятие электрической мощности и способы ее расчета
С электротехнической точки зрения она представляет собой количественное выражение взаимодействия энергии с материалом проводников и элементами при протекании тока в электрической цепи. Из-за наличия электрического сопротивления во всех деталях, задействованных в проведения электротока, направленное движение заряженных частиц встречает препятствие на пути следования. Это и обуславливает столкновение носителей заряда, электроэнергия переходит в другие виды и выделяется в виде излучения, тепла или механической энергии в окружающее пространство. Преобразование одного вида в другой и есть потребляемая мощность прибора или участка электрической цепи.
В зависимости от параметров источника тока и напряжения мощность также имеет отличительные характеристики. В электротехнике обозначается S, P и Q, единица измерения согласно международной системы СИ – ватты. Вычислить мощность можно через различные параметры приборов и электрических приборов. Рассмотрим каждый из них более детально.
Через напряжение и ток
Наиболее актуальный способ, чтобы рассчитать мощность в цепях постоянного тока – это использование данных о силе тока и приложенного напряжения. Для этого вам необходимо использовать формулу расчета: P = U*I
Где:
- P – активная мощность;
- U – напряжение приложенное к участку цепи;
- I — сила тока, протекающего через соответствующий участок.
Этот вариант подходит только для активной нагрузки, где постоянный ток не обеспечивает взаимодействия с реактивной составляющей цепи. Чтобы найти мощность вам нужно выполнить произведение силы тока на напряжение. Обе величины должны находиться в одних единицах измерения – Вольты и Амперы, тогда результат также получится в Ваттах. Можно использовать и другие способы кВ, кА, мВ, мА, мкВ, мкА и т.д., но и параметр мощности пропорционально изменит свой десятичный показатель.
Через напряжение и сопротивление
Для большинства электрических устройств известен такой параметр, как внутреннее сопротивление, которое принимается за константу на весь период их эксплуатации. Так как бытовые или промышленные единицы подключаются к источнику с известным номиналом напряжения, определять мощность достаточно просто. Активная мощность находится из предыдущего соотношения и закона Ома для участка цепи, согласно которого ток на участке прямо пропорционален величине приложенного напряжения и имеет обратную пропорциональность к сопротивлению:
I = U/R
Если выражение для вычисления токовой нагрузки подставить в предыдущую формулу, то получится такое выражение для определения мощности:
P = U*(U/R)=U2/R
Где,
- P – величина нагрузки;
- U – приложенная разность потенциалов;
- R – сопротивление нагрузки.
Через ток и сопротивление
Бывает ситуация, когда разность потенциалов, приложенная к электрическому прибору, неизвестна или требует трудоемких вычислений, что не всегда удобно. Особенно актуален данный вопрос, если несколько устройств подключены последовательно и вам неизвестно, каким образом потребляемая электроэнергия распределяется между ними. Подход в определении здесь ничем не отличается от предыдущего способа, за основу берется базовое утверждение, что электрическая нагрузка рассчитывается как P = U×I, с той разницей, что напряжение нам не известно.
Поэтому ее мы также выведем из закона Ома, согласно которого нам известно, что падение напряжения на каком-либо отрезке линии или электроустановки прямо пропорционально току, протекающему по этому участку и сопротивлению отрезка цепи:
U=I*R
после того как выражение подставить в формулу мощности, получим:
P = (I*R)*I =I2*R
Как видите, мощность будет равна квадрату силы тока умноженной на сопротивление.
Полная мощность в цепи переменного тока
Сети переменного тока кардинально отличаются от постоянного тем, что изменение электрических величин, приводит к появлению не только активной, но и реактивной составляющей. В итоге суммарная мощность будет также состоять активной и реактивной энергии:

Где,
- S – полная мощность
- P – активная составляющая – возникает при взаимодействии электротока с активным сопротивлением;
- Q – реактивная составляющая – возникает при взаимодействии электротока с реактивным сопротивлением.
Также составляющие вычисляются через тригонометрические функции, так:
P = U*I*cosφ
Q = U*I*sinφ
что активно используется в расчете электрических машин.
Пример расчета полной мощности для электродвигателя
Отдельный интерес представляет собой нагрузка, подключенная к трехфазной сети, так как электрические величины, протекающие в ней, напрямую зависят от номинальной нагрузки каждой из фаз. Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.
Особенность питания и асинхронной и синхронной электрической машины заключается в том, что на обмотки может подаваться и фазное и линейное напряжение. Тот или иной вариант, как правило, обуславливается способом соединения обмоток электродвигателя. Тогда мощность будет вычисляться по формуле:
S = 3*Uф*Iф
В случае выполнения расчетов с линейным напряжением, чтобы найти мощность формула примет вид:
Активная и реактивная мощности будут вычисляться по аналогии с сетями переменного тока, как было рассмотрено ранее.
Теперь рассмотрим вычисления на примере конкретной электрической машины асинхронного типа. Следует отметить, что официальная производительность, указываемая в паспортных данных электродвигателя – это полезная мощность, которую двигатель может выдать при совершении оборотов вала. Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.
Как видите, для вычислений с шильда мы возьмем следующую информацию об электродвигателе:
- полезная производительность – 3 кВт, а в переводе на систему измерения – 3000 Вт;
- коэффициент полезного действия – 80%, а в пересчете для вычислений будем пользоваться показателем 0,8;
- тригонометрическая функция соотношения активных и реактивных составляющих – 0,74%;
- напряжение, при соединении обмоток треугольником составит 220 В;
- сила тока при том же способе соединения – 13,3 А.
С таким перечнем характеристик можно воспользоваться несколькими способами:
S = 1,732*220*13,3 = 5067 Вт
Чтобы найти искомую величину, сначала определяем активную составляющую:
P = Pполезная / КПД = 3000/0.8 = 3750 Вт
Далее полную по способу деления активной на коэффициент cos φ:
S = P/cos φ = 3750/0.74 = 5067 Вт
Как видите, и в первом, и во втором случае искомая величина получилась одинакового значения.
Примеры задач
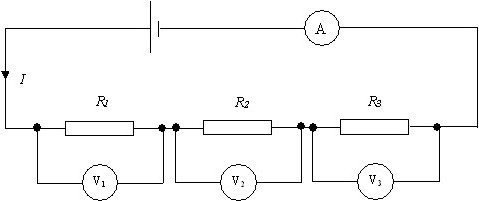
Для примера рассмотрим вычисление на участках электрической цепи с последовательным и параллельным соединением элементов. Первый вариант предусматривает ситуацию, когда все детали соединяются друг за другом от одного полюса источника питания до другого.
Как видите на рисунке, в качестве источника мы используем батарейку с номинальным напряжением 9 В и три резистора по 10, 20 и 30 Ом соответственно. Так как номинальный ток нам не известен, расчет произведем через напряжение и сопротивление:
P = U2/R = 81 / (10+20+30) = 1.35 Вт
Для параллельной схемы подключения возьмем в качестве примера участок цепи с двумя резисторами и одним источником тока:
Как видите, для удобства расчетов нам нужно привести параллельно подключенные резисторы к схеме замещения, из чего получится:
Rобщ = (R1*R2) / (R1+R2) = (10*15) / (10+15) = 6 Ом
Тогда искомый номинал нагрузки мы можем узнать через значение тока и сопротивления:
P = I2*R = 25*6 = 150 Вт
Видео по теме
Для школьников.
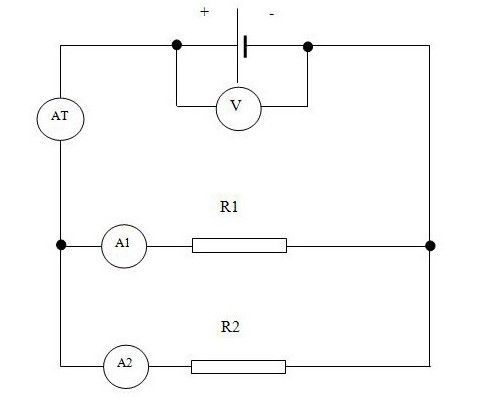
На рисунке изображена замкнутая электрическая цепь, состоящая из источника постоянного тока и переменной нагрузки во внешней части цепи.
Источником постоянного тока может быть электрическая машина, о которой говорится в статье “Искровой разряд“; батарея гальванических элементов, аккумулятор и др.
Роль источника тока заключается в создании (генерировании) электрической энергии: в разделении положительных и отрицательных зарядов; в создании и поддерживании разности потенциалов между конечными точками цепи, в которую включена нагрузка (электрическая лампочка, электроплитка. электродвигатель и т. д.).
При прохождении тока через нагрузку электрическая энергия превращается в другие виды энергии :тепловую (в электроплитке); в тепло и свет (в электрической лампе); в механическую энергию (в электродвигателе).
Превращение энергии из одного вида в другой всегда связано с работой.
При прохождении тока по проводнику совершается работа, её совершают электрические силы (или электрическое поле). Кратко эту работу называют работой тока.
Рассматривая участок цепи, по которому проходит ток, получим следующее выражение для работы тока:
Работа тока равна произведению напряжения между концами участка на протекающий ток и время его протекания.
В случае, если участок цепи однородный (не содержит источника тока), то
тогда получим ещё две формулы для работы тока:
Если ток проходит через неподвижный проводник, то единственным результатом работы тока является его нагревание. Тогда количество выделившейся теплоты
Это запись закона Джоуля – Ленца.
Если кроме нагревания ток совершает ещё механическую работу, например, приводя в действие электродвигатель (мотор), то работа
лишь частично переходит в тепло.
В этом случае работа тока больше количества выделившейся теплоты, но закон Джоуля – Ленца выполняется.
Работа, совершаемая током в единицу времени, называется мощностью тока:
Единицей мощности тока является 1 Вт:
1 Вт – мощность выделяемая током 1 А в проводнике, между концами которого поддерживается напряжение 1 В.
Основная формула мощности для участка цепи:
Мощность постоянного тока на любом участке цепи выражается произведением силы тока на напряжение между концами участка цепи.
Так как для однородного участка цепи
то мощность можно найти ещё по формулам:
Обычно говорят не о работе, а о потребляемой из сети некоторым прибором (электроплитка, лампочки и др.) или двигателем (мотором) мощности электрического тока. Говоря о мощности (например, электродвигателя), отмечают, что работа двигателя совершается за счёт тока.
На приборах часто отмечается потребляемая ими мощность – мощность, необходимая для нормальной работы этого прибора.
Согласно закону сохранения энергии, для замкнутой электрической цепи можно записать:
Здесь
есть полная или затраченная работа, совершаемая сторонними силами, существующими внутри источника, по переносу заряда по цепи.
В гальваническом элементе такими силами являются силы химической реакции.
– это полезная работа, совершаемая электрическим полем при прохождении тока через нагрузку;
это работа, совершаемая внутри источника, по преодолению его внутреннего сопротивления.
Так как работа, совершённая за единицу времени, есть мощность, то из уравнения (1) получим выражение для мощности:
Здесь
есть полная или затраченная мощность, это мощность развиваемая источником тока.
это мощность выделяемая внутри источника тока
это полезная мощность, создаваемая во внешней части цепи (на нагрузке).
Здесь U – напряжение на зажимах источника при замкнутой цепи (при разомкнутой цепи оно равно ЭДС источника).
Так как для однородного участка цепи напряжение равно произведению тока на сопротивление, то полезную мощность можно найти ещё по следующей формуле:
Ток в замкнутой цепи
тогда формулу для полезной мощности можно записать так:
Проанализируем зависимость полезной мощности от сопротивления нагрузки.
При коротком замыкании вся развиваемая источником мощность выделяется на его внутреннем сопротивлении в виде теплоты.
Таким образом, полезная мощность, развиваемая во внешней цепи, достигает максимального значения тогда, когда сопротивление нагрузки равно внутреннему сопротивлению источника.
На следующем рисунке показан график зависимости полезной мощности от сопротивления нагрузки.
Получена формула для нахождения максимальной полезной мощности
При этом ток в цепи в два раза меньше тока короткого замыкания:
Но чему при этом будет равно КПД источника?
Коэффициент полезного действия (КПД) источника показывает, какая часть затраченной (полной) работы источника пошла на пользу или КПД есть отношение полезной работы к затраченной:
Получается, что если добиваться максимальной мощности во внешней цепи, то получим КПД работы всего 50%, то есть половина затраченной мощности источника расходуется бесполезно – переходит в тепло, нагревая источник тока.
Выгоднее брать сопротивление нагрузки больше внутреннего сопротивления источника. Тогда ток в цепи уменьшится, а КПД источника увеличится.
Подумайте над решением следующих задач.
1. ЭДС аккумулятора 2 В, его внутреннее сопротивление 0,4 Ом, сопротивление внешней цепи 1 Ом. Найти разность потенциалов на зажимах аккумулятора и КПД его работы. Ответ: 1,43 В; 71 %.
2. Какую максимальную полезную мощность может выделить аккумулятор с ЭДС 10 В и внутренним сопротивлением 1 Ом? Каково при этом сопротивление внешней цепи? Ответ: 25 Вт; 1 Ом.
3. КПД источника тока, замкнутого на внешнее сопротивление R, равно 60%. Каков будет КПД источника, если внешнее сопротивление увеличить в 6 раз? Ответ: 90%.
Ответ: 7,7 Вт; 12 Вт; 40%; 25%.
Ответ: 2,7 10 4 кг.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Работа и мощность электрического тока. Лампы накаливания.
Следующая запись: Ещё раз о зарядке и разрядке конденсатора.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Все электронные устройства содержат резисторы, являющиеся их основным элементом. С его помощью изменяют величину тока в электрической цепи. В статье приведены свойства резисторов и методы расчёта их мощности.
Назначение резистора
Для регулировки тока в электрических цепях применяются резисторы. Это свойство определено законом Ома:
I=U/R (1)
Из формулы (1) хорошо видно, что чем меньше сопротивление, тем сильнее возрастает ток, и наоборот, чем меньше величина R, тем больше ток. Именно это свойство электрического сопротивления используется в электротехнике. На основании этой формулы создаются схемы делителей тока, широко применяющиеся в электротехнических устройствах.
В этой схеме ток от источника делится на два, обратно пропорциональных сопротивлениям резисторов.
Кроме регулировки тока, резисторы используются в делителях напряжения. В этом случае опять используется закон Ома, но немного в другой форме:
U=I∙R (2)
Из формулы (2) следует, что при увеличении сопротивления увеличивается напряжение. Это свойство используется для построения схем делителей напряжения.
Из схемы и формулы (2) ясно, что напряжения на резисторах распределяются пропорционально сопротивлениям.
Изображение резисторов на схемах
По стандарту резисторы изображаются прямоугольником с размерами 10 х 4 мм и обозначаются буквой R. Часто указывается мощность резисторов на схеме. Изображение этого показателя выполняется косыми или прямыми чёрточками. Если мощность более 2 Ватт, то обозначение производится римскими цифрами. Обычно это делается для проволочных резисторов. В некоторых государствах, например в США, применяются другие условные обозначения. Для облегчения ремонта и анализа схемы часто приводится мощность резисторов, обозначение которых выполняется по ГОСТ 2.728-74.
Технические характеристики устройств
Основная характеристика резистора – номинальное сопротивление Rн, которое указывается на схеме возле резистора и на его корпусе. Единица измерения сопротивления – ом, килоом и мегаом. Изготавливаются резисторы с сопротивлением от долей ома и до сотен мегаомов. Существует немало технологий производства резисторов, все они имеют и преимущества, и недостатки. В принципе, не существует технологии, которая позволила бы абсолютно точно изготавливать резистор с заданным значением сопротивления.
Второй важной характеристикой является отклонение сопротивления. Оно измеряется в % от номинального R. Существует стандартный ряд отклонения сопротивления: ±20, ±10, ±5, ±2, ±1% и далее вплоть до значения ±0,001%.
Следующей важной характеристикой является мощность резисторов. При работе они нагреваются от проходящего по ним тока. Если рассеиваемая мощность будет превышать допустимое значение, то устройство выйдет из строя.
Резисторы при нагревании изменяют своё сопротивление, поэтому для устройств, работающих в широком диапазоне температур, вводится ещё одна характеристика – температурный коэффициент сопротивления. Он измеряется в ppm/°C, то есть 10-6 Rн/°C (миллионная часть от Rн на 1°C).
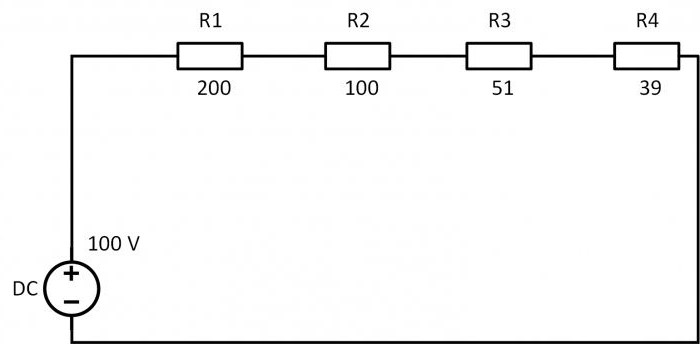
Последовательное соединение резисторов
Резисторы могут соединяться тремя разными способами: последовательным, параллельным и смешанным. При последовательном соединении ток поочерёдно проходит через все сопротивления.
При таком соединении ток в любой точке цепи один и тот же, его можно определить по закону Ома. Полное сопротивление цепи в этом случае равно сумме сопротивлений:
R=200+100+51+39=390 Ом;
I=U/R=100/390=0,256 А.
Теперь можно определить мощность при последовательном соединении резисторов, она рассчитывается по формуле:
P=I2∙R= 0,2562∙390=25,55 Вт.
Аналогично определяется мощность остальных резисторов:
P1= I2∙R1=0,2562∙200=13,11 Вт;
P2= I2∙R2=0,2562∙100=6,55 Вт;
P3= I2∙R3=0,2562∙51=3,34 Вт;
P4= I2∙R4=0,2562∙39=2,55 Вт.
Если сложить мощность резисторов, то получится полная P:
P=13,11+6,55+3,34+2,55=25,55 Вт.
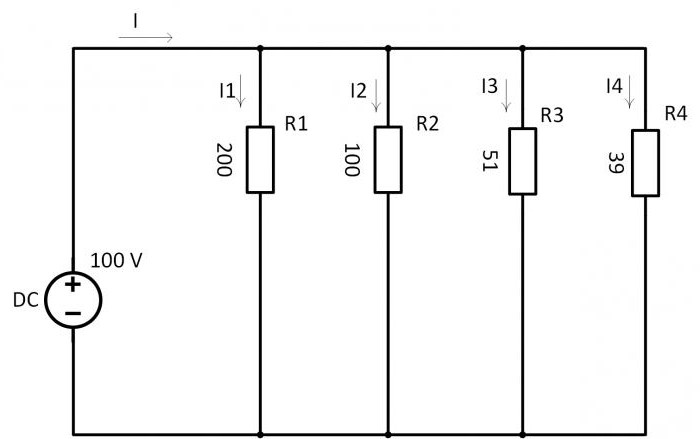
Параллельное соединение резисторов
При параллельном соединении все начала резисторов подключаются к одному узлу схемы, а концы – к другому. При таком соединении ток разветвляется и течёт по каждому устройству. Величина тока, согласно закону Ома, обратно пропорциональна сопротивлениям, а напряжение на всех резисторах одинаково.
Прежде чем найти ток, нужно рассчитать полную проводимость всех резисторов по общеизвестной формуле:
1/R=1/R1+1/R2+1/R3+1/R4=1/200+1/100+1/51+1/39=0,005+0,01+0,0196+0,0256= 0,06024 1/Ом.
Сопротивление – величина, обратная проводимости:
R=1/0,06024= 16,6 Ом.
Воспользовавшись законом Ома, находят ток через источник:
I= U/R=100∙0,06024=6,024 A.
Зная ток через источник, находят мощность параллельно соединённых резисторов по формуле:
P=I2∙R=6,0242∙16,6=602,3 Вт.
По закону Ома рассчитывается ток через резисторы:
I1=U/R1=100/200=0,5 А;
I2=U/R2=100/100=1 А;
I3=U/R1=100/51=1,96 А;
I1=U/R1=100/39=2,56 А.
Немного по другой формуле можно рассчитать мощность резисторов при параллельном соединении:
P1= U2/R1=1002/200=50 Вт;
P2= U2/R2=1002/100=100 Вт;
P3= U2/R3=1002/51=195,9 Вт;
P4= U2/R4=1002/39=256,4 Вт.
Если всё это сложить, то получится мощность всех резисторов:
P= P1+ P2+ P3+ P4=50+100+195,9+256,4=602,3 Вт.
Смешанное соединение
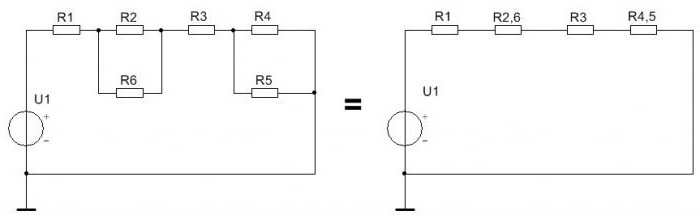
Схемы со смешанным соединением резисторов содержат последовательное и одновременно параллельное соединение. Эту схему несложно преобразовать, заменив параллельное соединение резисторов последовательным. Для этого заменяют сначала сопротивления R2 и R6 на их общее R2,6, используя формулу, приведённую ниже:
R2,6=R2∙R6/R2+R6.
Точно так же заменяются два параллельных резистора R4, R5 одним R4,5:
R4,5=R4∙R5/R4+R5.
В результате получается новая, более простая схема. Обе схемы приведены ниже.
Мощность резисторов на схеме со смешанным соединением определяется по формуле:
P=U∙I.
Для расчёта по этой формуле сначала находят напряжение на каждом сопротивлении и величину тока через него. Можно использовать другой метод, чтобы определить мощность резисторов. Для этого используется формула:
P=U∙I=(I∙R)∙I=I2∙R.
Если известно только напряжение на резисторах, то применяют другую формулу:
P=U∙I=U∙(U/R)=U2/R.
Все три формулы часто используются на практике.
Расчёт параметров схемы
Расчёт параметров схемы заключается в нахождении неизвестных токов и напряжений всех ветвей на участках электрической цепи. Имея эти данные, можно рассчитать мощность каждого резистора, входящего в схему. Простые методы расчёта были показаны выше, на практике же дело обстоит сложнее.
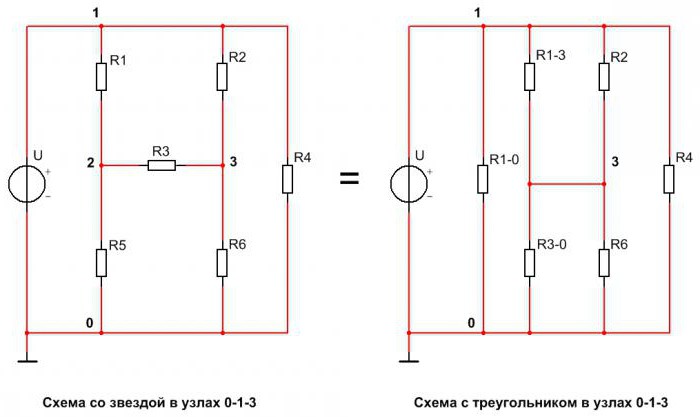
В реальных схемах часто встречается соединение резисторов звездой и треугольником, что создаёт значительные трудности при расчётах. Для упрощения таких схем были разработаны методы преобразования звезды в треугольник, и наоборот. Этот метод проиллюстрирован на схеме, представленной ниже:
Первая схема имеет в своём составе звезду, подключенную к узлам 0-1-3. К узлу 1 подсоединён резистор R1, к узлу 3 – R3, а к узлу 0 – R5. На второй схеме к узлам 1-3-0 подключены резисторы треугольника. К узлу 1 подключены резисторы R1-0 и R1-3, к узлу 3 – R1-3 и R3-0, а к узлу 0 – R3-0 и R1-0. Эти две схемы полностью эквивалентны.
Для перехода от первой схемы ко второй рассчитываются сопротивления резисторов треугольника:
R1-0=R1+R5+R1∙R5/R3;
R1-3=R1+R3+R1∙R3/R5;
R3-0=R3+R5+R3∙R5/R1.
Дальнейшие преобразования сводятся к вычислению параллельно и последовательно соединённых сопротивлений. Когда будет найдено полное сопротивление цепи, находят по закону Ома ток через источник. Используя этот закон, несложно найти токи во всех ветвях.
Как определить мощность резисторов после нахождения всех токов? Для этого используют общеизвестную формулу: P=I2∙R, применяя её для каждого сопротивления, найдём их мощности.
Экспериментальное определение характеристик элементов схемы
Для экспериментального определения нужных характеристик элементов требуется собрать заданную схему из реальных компонентов. После этого с помощью электроизмерительных приборов выполняют все необходимые измерения. Этот метод трудоёмкий и дорогостоящий. Разработчики электрических и электронных устройств для этой цели используют моделирующие программы. С помощью них производятся все необходимые вычисления, и моделируется поведение элементов схемы в различных ситуациях. Только после этого собирается опытный образец технического устройства. Одной из таких распространённых программ является мощная система моделирования Multisim 14.0 фирмы National Instruments.
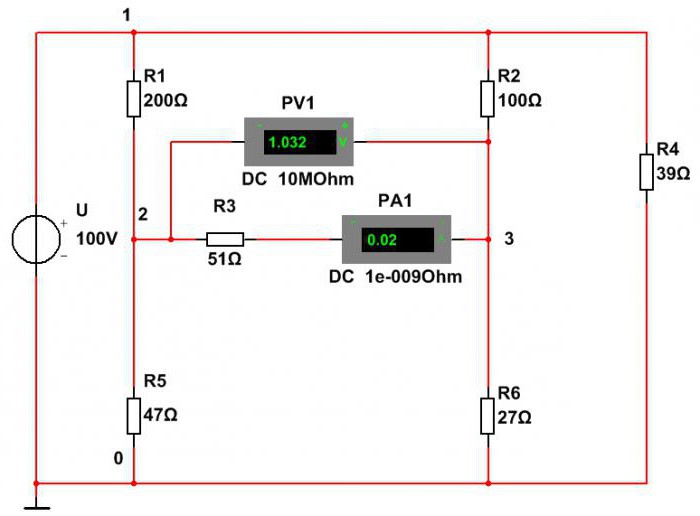
Как определить мощность резисторов с помощью этой программы? Это можно сделать двумя методами. Первый метод – это измерить ток и напряжение с помощью амперметра и вольтметра. Перемножив результаты измерений, получают искомую мощность.
Из этой схемы определяем мощность сопротивления R3:
P3=U∙I=1,032∙0,02=0,02064 Вт=20,6 мВт.
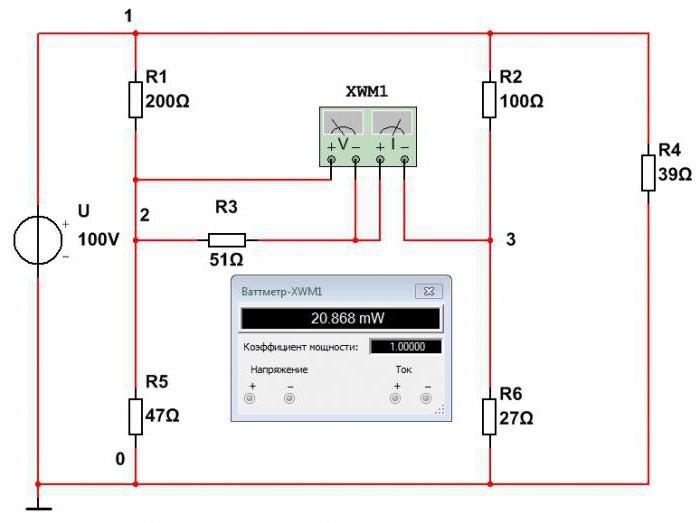
Второй метод – это непосредственное измерение мощности при помощи ваттметра.
Из этой схемы видно, что мощность сопротивления R3 равна P3=20,8 мВт. Расхождение из-за погрешности в первом методе больше. Точно так же определяются мощности остальных элементов.
Что такое мощность электрического тока
При описании электрической мощности в широком смысле чаще всего речь идет об энергии или силе, которой наделен некоторый объект либо действие. Например, ее можно определить для взрыва или же механизма, например двигателя. Этот параметр связан с силой и зависит от нее, потому эти явления нередко путают.
Отличие в том, что сила влияет на физические действия, то есть выполняется работа. Если она проделана за указанное время, то через эти два параметра можно вычислить значение мощности.
В случае с электричеством она бывает двух видов:
- Активная – превращается в энергию тепла, света, механических действий и т. д. Она измеряется в ваттах и вычисляется по формуле 1 Вт = 1 В х 1А. Но на практике этот показатель чаще всего выражен в киловаттах и мегаваттах.
- Реактивная – нагрузка, возникающая из-за колебаний внутри электромагнитного поля. Единица измерения – вольт-амперы (ВА), они вычисляются как Q=U x I x sin угла. Последнее означает изменение фазы между током и снижением напряжения.
На практике отличия обоих видов лучше всего рассмотреть на примере элементов для нагревания и электродвигателей. ТЭНы собраны из материала с высоким сопротивлением, поэтому всю полученную электроэнергию они превращают в тепловую. Электродвигатель же имеет детали, обладающие индуктивностью, то есть часть тока возвращается в сеть и может отрицательно влиять на нее, создавая перегрузки.
Как обозначается мощность
Р — мощность электрического тока обозначается (Вт).
В завершение следует отметить, что полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому данная величина трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Понятие полной мощности. Треугольник мощностей
Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буквой S.
Также рассчитать полную мощность можно путем перемножения напряжения и силы тока соответственно.
S = U⋅I
ВАЖНО! Полная мощность измеряется в вольт-амперах (ВА).
Треугольник мощностей – это удобное представление всех ранее описанных вычислений и соотношений между активной, реактивной и полной мощностей.
Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, то есть он является коэффициентом мощности.
Простое объяснение с формулами
Активная мощность (P)
Другими словами активную мощность можно назвать: фактическая, настоящая, полезная, реальная мощность. В цепи постоянного тока мощность, питающая нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, то есть
P = U I
потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.
Но при синусоидальных сигналах, то есть в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активная мощность), которая в действительности питает нагрузку, определяется как:
P = U I Cosθ
В цепи переменного тока, если она чисто активная (резистивная), формула для мощности та же самая, что и для постоянного тока: P = U I.
Формулы для активной мощности
P = U I – в цепях постоянного тока
P = U I cosθ – в однофазных цепях переменного тока
P = √3 UL IL cosθ – в трёхфазных цепях переменного тока
P = 3 UPh IPh cosθ
P = √ (S2 – Q2) или
P =√ (ВА2 – вар2) или
Активная мощность = √ (Полная мощность2 – Реактивная мощность2) или
кВт = √ (кВА2 – квар2)
Реактивная мощность (Q)
Также её мощно было бы назвать бесполезной или безваттной мощностью.
Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, известна как реактивная (Q).
Реактивной называется мощность, которая потребляется и затем возвращается нагрузкой из-за её реактивных свойств. Единицей измерения активной мощности является ватт, 1 Вт = 1 В х 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного поля или электрического поля в случае, соответственно, индуктивности или конденсатора.
Реактивная мощность определяется, как
Q = U I sinθ
и может быть положительной (+Ue) для индуктивной нагрузки и отрицательной (-Ue) для емкостной нагрузки.
Единицей измерения реактивной мощности является вольт-ампер реактивный (вар): 1 вар = 1 В х 1 А. Проще говоря, единица реактивной мощности определяет величину магнитного или электрического поля, произведённого 1 В х 1 А.
Все формулы мощности
Зная определения, несложно понять формулы мощности, используемые в разных разделах физики — в механике и электротехнике.
В механике
Механическая мощность (N) равна отношению работы ко времени, за которое она была выполнена.
Основная формула:
N = A / t, где A — работа, t — время ее выполнения.
Если вспомнить, что работой называется произведение модуля силы, модуля перемещения и косинуса угла между ними, мы получим формулу измерения работы.
Если направления модуля приложения силы и модуля перемещения объекта совпадают, угол будет равен 0 градусов, а его косинус равен 1. В таком случае формулу можно упростить:
A = F × S
Используем эту формулу для вычисления мощности:
N = A / t = F × S / t = F × V
В последнем выражении мы исходим из того, что скорость (V) равна отношению перемещения объекта на время, за которое это перемещение произошло.
В электротехнике
В общем случае электрическая мощность (P) говорит о скорости передачи энергии. Она равна произведению напряжения на участке цепи на величину тока, проходящего по этому участку.
P = I × U, где I — напряжение, U — сила тока.
В электротехнике существует несколько видов мощности: активная, реактивная, полная, пиковая и т. д. Но это тема отдельного материала, сейчас же мы потренируемся решать задачи на основе общего понимания этой величины. Посмотрим, как найти мощность, используя вышеуказанные формулы по физике.
Особенности расчёта в цепях переменного электричества
Чтобы выполнить расчёты P, потребляемой нагрузкой в цепях изменяющегося электричества, нужно чётко разделять схемы включения. Они могут быть однофазными и трёхфазными.
В однофазных цепях P находят, перемножив значение силы тока на значение напряжения (220 В). При этом учитывают наличие фазного сдвига между ними.
В трёхфазных сетях с напряжением 380 В рассматривают два случая:
- симметричная нагрузка по фазам;
- ассиметричная нагрузка фаз.
В первом случае P находят по формуле:
P = √3*U*I* cosφ.
Во втором случае необходимо рассчитывать P для каждой фазы (А, В, С). Общее значение P– это результат суммирования:
P общ = PфА + PфВ + PфС.
Внимание! Когда необходимо найти полную мощность трёхфазной цепи, находят по такому же принципу значения реактивной Q.
Рассчитать ток по мощности, зная, какое напряжение: фазное (220 В) или линейное (380 В), можно и в этом случае, выразив его из общей формулы P.
Формула мощности для постоянного электрического тока
Поэтому формулы мощности в электронике имеют вот такой вид:
Отсюда A=IUt
где,
А — это полезная работа, Джоули
t — время, секунды
U — напряжение, Вольты
I — сила тока, Амперы
P — собственно сама мощность, Ватты
R — сопротивление, Омы
Как вы можете заметить, формула P=I2 R говорит нам о том, что не всегда на маленьком сопротивлении вырабатывается большая мощность и то, что мощность очень сильно зависит от силы тока. А как поднять силу тока? Добавить напряжения ;-). Закон Ома работает всегда и везде.
А из формулы P=U2/R, можно увидеть, что чем меньше сопротивление и больше напряжение в цепи, тем больше мощность будет выделяться на нагрузке. А что такое выделение мощности на нагрузке? Это может быть тепло, свет, какая-либо механическая работа и тд. Короче говоря, выработка какой-либо полезной энергии для наших нужд.
Средняя P в активной нагрузке
В электрических сетях P измеряют при помощи специального прибора – ваттметра. Схемы подключения находятся в зависимости от способа подключения нагрузки.
При симметричной нагрузке P измеряется в одной фазе, а полученный результат умножают на три. В случае несимметричной нагрузки для измерения потребуется три прибора.
Параметры P электросети или установки являются важными данными электрического прибора. Данные по потреблению P активного типа передаются за определенный период времени, то есть передается средняя потребляемая P за расчетный период времени.
Формулы расчета мощности для однофазной и трехфазной схемы питания
Выше уже была представлена формула для одной фазы: P=U*I*cos(фи).
Отсюда следует, что в трехфазной сети показатель равен тройной мощности однофазной, соединенной в треугольник: P=3*U*I*cos(фи). На практике же инженеры пользуются формулой P=1,73*U*I*cos(фи).
Формулы для реактивной мощности
Q = U I sinθ
Реактивная мощность = √ (Полная мощность2 – Активная мощность2)
вар =√ (ВА2 – P2)
квар = √ (кВА2 – кВт2)
Полная мощность (S)
Полная мощность – это произведение напряжения и тока при игнорировании фазового угла между ними. Вся мощность в сети переменного тока (рассеиваемая и поглощаемая/возвращаемая) является полной.
Комбинация реактивной и активной мощностей называется полной мощностью. Произведение действующего значения напряжения на действующее значение тока в цепи переменного тока называется полной мощностью.
Она является произведением значений напряжения и тока без учёта фазового угла. Единицей измерения полной мощности (S) является ВА, 1 ВА = 1 В х 1 А. Если цепь чисто активная, полная мощность равна активной мощности, а в индуктивной или ёмкостной схеме (при наличии реактивного сопротивления) полная мощность больше активной мощности.
Формула для полной мощности
S = U I
Полная мощность = √ (Активная мощность2 + Реактивная мощность2)
kUA = √(kW2 + kUAR2)
Следует заметить, что:
- резистор потребляет активную мощность и отдаёт её в форме тепла и света.
- индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
- конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.
Все эти величины тригонометрически соотносятся друг с другом, как показано на рисунке:
Активная нагрузка (АН)
Подобной нагрузкой являются элементы приборов, имеющие активное сопротивление. Рабочая часть подобных аппаратов при прохождении через них электричества нагревается.
Ток, проходя через нагрузку, совершает работу, которая затрачивается на нагревание и выделение тепловой энергии. В чем измеряется такая нагрузка? Её измеряют в омах (Ом).
К примерам АН относятся: утюг, электроплита, спирали фена, нить накала лампы, резистивное сопротивление.
К сведению. АН ведёт себя одинаково, как при постоянном, так и при изменяющемся во времени токе.
Емкостная нагрузка
Устройства, способные запасаться энергией в электрическом поле и создавать рециркуляцию (полный или частичный возврат) мощности, именуют ёмкостной нагрузкой. Емкостная нагрузка (ЕН) при переменном напряжении, пропуская ток, сдвигает его фазу на 900 вперёд.
Основными элементами, относящимися к ЕН, считаются:
- конденсаторы;
- кабельные линии (ёмкость между жилами);
- ЛЭП (линии электропередач) сверхвысокого напряжения;
- генераторы, работающие в режиме перевозбуждения.
ЕН отдаёт реактивную мощность (Q).
Индуктивная нагрузка (ИН)
Нагрузка, в которой ток сдвинут по фазе назад от напряжения на 900, называется индуктивной. Она также потребляет Q.
Цепь с катушкой
При включении в сеть переменного напряжения катушки индуктивности (дросселя), у которой низкое активное сопротивление, в ней образуется ЭДС. Электродвижущая сила противостоит приложенному напряжению.
Важно! В случае чистой индуктивности L сопротивление синусоидальному току увеличивается с ростом частоты. Выделяемая на такой нагрузке средняя мощность P равна нулю.
Примерами ИН служат:
- асинхронные двигатели;
- электромагниты;
- дроссели;
- реакторы;
- трансформаторы;
- выпрямители.
Сюда же можно отнести тиристорные преобразователи.
Как узнать ток, зная мощность и напряжение
Для вычисления тока электросети по мощности и напряжению используют формулы:
- I=P/U – постоянный ток;
- I=P/(U*cos(фи)) — однофазная сеть;
- I=P/(1,73*U*cos(фи)) — трехфазная сеть.
Для простоты расчетов значение фи принимают равной 0,95.
Как узнать напряжение, зная силу тока
Для расчета напряжения используют формулы:
U=P/I – постоянный ток;
U=P/(I*cos(фи)) — однофазная сеть;
U=P/(1,73*I*cos(фи)) — трехфазная сеть.
Из выражения видно, что напряжение прямо пропорционально напряжению и обратно пропорционально силе тока.
Как рассчитать мощность, зная силу тока и напряжение
Силовую характеристику электроустановок рассчитывают по формуле:
P=U*I — постоянный ток;
P=U*I*cos(фи) – переменный ток однофазной сети.
P=1,73*U*I*cos(фи) — трехфазная сеть.
В статье приведены упрощенные формулы расчета активной мощности электросети, которые дают приблизительные результаты.
Для получения точных результатов, необходимо учитывать также реактивное и обычное сопротивление, а также потери.
Как правильно рассчитать
Активная мощность, как сделать правильный расчет?
Мощность электрического тока влияет на то, как быстро прибор сможет выполнить работу. К примеру, дорогой обогреватель, имеющий в 2 раза большую мощность, обогреет помещение быстрее, чем два дешевых, с меньшей в 2 раза мощностью. Получается, что выгоднее купить агрегат, имеющий большую мощность, чтобы быстрее обогреть холодное помещение. Но, в то же время, такой агрегат будет тратить существенно больше энергии, чем его более дешевый аналог.
Потребляемая мощность всех приборов в доме учитывается и при подборе проводки для прокладки в доме. Если не учитывать этого и в последующем включить в сеть слишком много приборов, то это вызовет перегрузку сети. Проводка не сможет выдержать мощность электрического тока всех приборов, что приведет к плавлению изоляции, замыканию и самовоспламенению проводки. В результате может начаться пожар, который может привести к непоправимым последствиям.
Однофазный синусоидальный ток в электрических цепях вычисляется по формуле Р = U x I x cos φ, где υ и Ι. Их обозначение шифруется следующим образом: среднеквадратичное значение напряжение и тока, а φ — фазный угол фаз между ними.
Для цепей несинусоидального тока электрическая ёмкость равна корню квадратному из суммы квадратов активной и реактивной производительности. Активная производительность характеризуется скоростью, которая имеет необратимый процесс преобразования электрической энергии в другие виды энергии. Данная ёмкость может вычисляться через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле P = I(2) x r = U(2) x g.

Следует заметить, что:
- резистор потребляет активную мощность и отдаёт её в форме тепла и света.
- индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
- конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.
В любой электрической цепи как синусоидального, так и несинусоидального тока активная способность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая емкость определяется как сумма пропускной способности отдельных фаз. С полной производительностью S, активная связана соотношением P = S x cos φ.
В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной производительностью.
Как найти реактивную полную мощность через активную? Данная производительность, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: Q = U x I x sin φ (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным).

Пример расчета мощности электрического тока
В конце концов, вы сможете проверить свои познания на 2-ух обычных примерах.
Представьте, что в первой задачке у вас есть резистор R = 50 Ом, через который течет электрический ток I = 0,3А. Какая электрическая мощность преобразуется в этом резисторе?
Вы можете отыскать решение, найдя соответствующую формулу и подставив в нее заданные значения. То есть у нас получается: P = I2R = 0,32 * 50 = 4,5 Вт
Во второй задаче дан резистор R, электрическое сопротивление которого 700 Ом. В техническом описании указано, что максимальная мощность этого резистора составляет 10 Вт. Насколько высоким может быть напряжение, подаваемое на этот резистор?
Для решения этой задачки подбираем подходящую формулу: P = U2/R, откуда мы находим Umax = Pmax * R = 700 * 10 = 83,67 В.
Это означает, что максимальное напряжение может составлять 83,67 В. Чтобы подстраховаться, следует выбирать электрическое напряжение значительно ниже этого предела.
Видео описание
Работа и мощность электрического тока.
Источники
- https://knigaelektrika.ru/teoriya/formula-moshhnosti-elektricheskogo-toka-raschet-po-moshhnosti-i-napryazheniyu.html
- https://rusenergetics.ru/polezno-znat/polnaya-moschnost
- https://odinelectric.ru/knowledgebase/aktivnaja-i-reaktivnaja-moshhnost-peremennogo-toka
- https://ElectroInfo.net/raznoe/aktivnaja-moshhnost-chto-takoe-aktivnaja-moshhnost.html
- https://skysmart.ru/articles/physics/moshnost
- https://amperof.ru/teoriya/raschet-moshhnosti.html
- https://www.RusElectronic.com/power/
- https://vdome.club/materialy/raschety/formula-moschnosti.html
- https://remont220.ru/osnovy-elektrotehniki/1090-formula-moshchnosti/
- https://khomovelectro.ru/articles/aktivnaya-reaktivnaya-i-polnaya-kazhushchayasya-moshchnosti.html
- https://www.asutpp.ru/moschnost-elektricheskogo-toka.html
- https://m-strana.ru/articles/elektricheskaya-moshchnost/
Как вам статья?

Павел
Бакалавр “210400 Радиотехника” – ТУСУР. Томский государственный университет систем управления и радиоэлектроники
Написать
Пишите свои рекомендации и задавайте вопросы
Энергия и мощность электрического тока
В любой замкнутой электрической цепи
источник затрачивает электрическую
энергию Wистна
перемещение единицы положительного
заряда по всей цепи: и на внутреннем и
на внешнем участках.
и
;
Энергия источника определяется
выражением: Wист=Eq=EIt=
(U0+U)It;
Энергия источника (полезная), которая
расходуется на потребителе: W=UIt;
Энергия источника (потери), которая
расходуется на внутреннем сопротивлении
источника: W=U0It;
Преобразование электрической энергии
в другие виды энергий происходит с
определенной скоростью. Эта скорость
определяет электрическую мощность
элементов электрической цепи:
;
Мощность источника определяется
соотношением:
Мощность потребителя определяется
соотношением:
Коэффициент полезного действияэлектрической цепиηопределяется
отношением мощности потребителя к
мощности источника:
Закон Джоуля – Ленца
Ток, протекая по проводнику, нагревает
его (в этом случае электрическая энергия
преобразуется в тепловую). Количество
выделенного тепла будет определяться
количеством электрической энергии,
затраченной в этом проводнике.
Дж.
(кал).
Коэффициент 0,24 (электротермический
эквивалент) устанавливает зависимость
между электрической и тепловой энергией.
Часть3: Режимы работы электрических цепей
В электрических цепях все основные
элементы делятся на активные и пассивные.
Активными считаются элементы, в которых
преобразование энергии сопровождается
возникновением ЭДС (аккумуляторы,
генераторы). Элементы, в которых ЭДС не
возникает, называются пассивными.
Параметры электрических цепей:
Ток в замкнутой цепи
;
Напряжение на клеммах источника
;
Падение напряжения на сопротивлении
источника
;
Полезная мощность (мощность потребителя)
.
Электрические цепи могут работать в
трех режимах:
-
режим холостого хода (цепь разомкнута)
R=∞:Iхх=0,U=E,
U0=0, P=0. -
режим короткого замыкания R=0:
-
режим нагрузки R≠0:
;
;
;
.
Условие максимальной отдачи мощности:
полезная мощность максимальна, когда
сопротивление потребителя R
станет равным внутреннему сопротивлению
источника R0.
КПД при максимальной отдаче мощности
равно 50%, к 100% КПД приближается в режиме,
близком к холостому ходу.
Нормальным (рабочим) режимом называют
такой режим работы цепи, при котором
ток, напряжение и мощность не превышают
номинальных значений, заданных
заводом-изготовителем.
Источники тока могут работать в режиме
генератора и в режиме нагрузки. Источники,
ЭДС которых совпадают с направлением
тока в цепи, работают в режиме генератора,
а источники , ЭДС которых не совпадают
с направлением тока, работают в режиме
потребителя.
Напряжение источника, работающего в
режиме генератора:
.
Напряжение источника, работающего в
режиме потребителя:
.
Тема 1.3
Расчет электрических цепей постоянного
тока
Основной целью расчета электрической
цепи является нахождение ее параметров:
ток, напряжение, сопротивление, мощность,
КПД. Значения параметров дают возможность
оценить условия и эффективность работы
электротехнического оборудования и
приборов во всех участках электрической
цепи.
Для расчета электрических цепей основой
служат законы Ома и Кирхгофа, Джоуля-Ленца.
Законы Кирхгофа
К характерным элементам электрической
цепи относятся ветвь, узел, контур.
Ветвью электрической цепи называется
ее участок, на всем протяжении которого
величина тока имеет одинаковое значение.
Ветви, которые содержат источники
питания называются активными, а которые
не содержат их – пассивными.
Узлом электрической цепи называется
точка соединения электрических ветвей.
Контуром электрической цепи называют
замкнутое соединение, в которое могут
входить несколько ветвей.
Первый закон Кирхгофа
Сумма токов входящих в узел равна сумме
токов, выходящих из узла. ИЛИ Сумма
токов, сходящихся в узле равна нулю.
∑I=0; – математическое
выражение первого закона Кирхгофа.
Второй закон Кирхгофа
Алгебраическая сумма ЭДС в замкнутом
контуре электрической цепи равна
алгебраической сумме падений напряжений
на всех участках этой цепи.
;
– математическое выражение второго
закона Кирхгофа.
Последовательное соединение
потребителей
Последовательным соединением участков
эй цепи называют соединение, при котором
через все участки цепи проходит один и
тот же ток.
Общее напряжение последовательно
соединенных элементов равно сумме
напряжений на каждом элементе согласно
второму закону Кирхгофа:
;
В соответствии с законом Ома:
;
Из этого соотношения следует:; Таким образом, общее сопротивление
цепи с последовательно соединенными
элементами равно сумме этих сопротивлений.
Параллельное сопротивление
потребителей
Параллельным соединением участков
электрической цепи называется соединение,
при котором все участки цепи присоединяются
к одной паре узлов, то есть находятся
под действием одного и того же напряжения.
Общий ток такого соединения согласно
первому закона Кирхгофа будет равен
сумме токов в отдельных ветвях:
;
В соответствии с законом Ома:;
Если поделить левую и правую части наU, получим:;
Обратная величина общего эквивалентного
сопротивления параллельно включенных
потребителей равна сумме обратных
величин этих потребителей.
Величина, обратная сопротивлению
определяет проводимость потребителя
g. Тогда для параллельно
соединенных потребителей справедливо:;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #