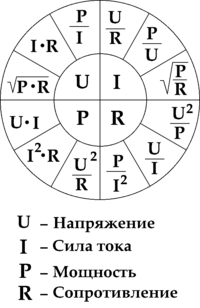
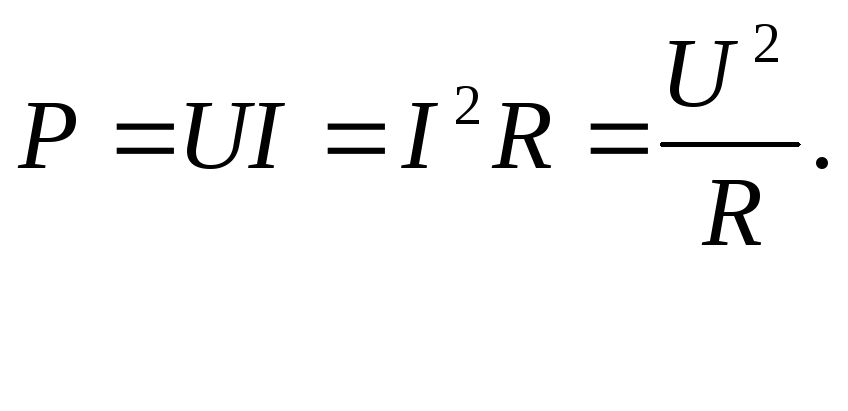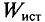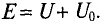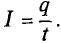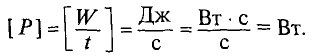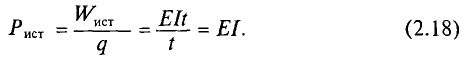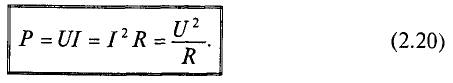Как найти мощность источника энергии - Сайт, где вы сможете решить свои вопросы

Как определить мощность источника тока

Содержание

1 Виды мощности
2 Активная и реактивная мощность
3 Как определяется мощность
4 Мощность источника питания
5 Видео по теме

Источники питания используются повсеместно. Их основная задача — преобразование параметров электроэнергии, поступающей из сети, в такие, которые необходимы для конкретного электротехнического устройства. Способность ИП выполнять данную задачу зависит от его мощности. Она является главной характеристикой любого блока питания. Чтобы оценить эффективность устройства, необходимо понимать, как найти мощность, если известны различные характеристики электрической цепи.

Виды мощности

При вычислении мощности возможны следующие ситуации:

Мгновенная мощность вычисляется для очень малого промежутка времени. Это значение важно знать в тех случаях, когда в разные моменты времени эта величина меняется. Проведение замеров позволит мастеру получить целостное представление об используемой мощности. Для постоянного тока данная характеристика постоянна.
Активное значение мощности применяется для определения постоянной величины, которая фактически является средним значением при наличии переменного тока. При этом мгновенные значения будут изменяться, а активная мощность будет в среднем характеризовать происходящие процессы. Активная мощность — это показатель выполнения полезной работы электрическим оборудованием.
Реактивная мощность относится к работе индуктивных и емкостных элементов электрических приборов. Она циклически переходит из одной формы в другую. При этом происходит перемещение зарядов, то есть, осуществляется электрическая работа, которая обычно не является полезной.

Активная и реактивная мощность

При работе электрического оборудования следует рассматривать полную мощность. Она показывает работу, которая проводится в единицу времени (в СИ в этом качестве рассматривается 1 секунда). При этом нужно помнить, что полная мощность складывается из активной и реактивной мощности.

Это разделение связано с используемым сопротивлением. Если электрические заряды преодолевают активное сопротивление, мощность также является активной. Она, как правило, относится к выполнению полезной работы.

При наличии переменного тока в электрической цепи присутствует реактивное сопротивление. Оно связано с работой электромагнитного поля и фактически сводится к периодическим изменениям, при которых энергия регулярно перетекает из одной формы в другую, практически не расходуясь.

В бытовых приборах и промышленном оборудовании в большинстве случаев присутствуют оба вида мощности. Активная играет основную роль при использовании постоянного тока или в тех случаях, когда её доля в общей мощности относительно высока.

Обычно в технической документации указывается параметр cosφ. Он может принимать значения от 0 до 1 включительно. Его величина показывает долю активной мощности в полной. Она будет высокой, например, в электронагревательных приборах, где значительная часть энергии тратится на выполнение полезной работы по обогреву помещения.

Надо учитывать, что наличие реактивной мощности оказывает разрушительное действие на прибор. Это может быть, например, связано с разрушением изоляции проводов и кабелей, с повышением риска возникновения короткого замыкания или с порчей оболочек электроприводов или трансформаторов.

Для получения полной мощности применяется векторное сложение активной и реактивной мощности. Её величину вычисляют по теореме Пифагора как длину гипотенузы прямоугольного треугольника, в котором катетами являются активная и реактивная мощности.

Как определяется мощность

Эта величина определяется на основе работы, выполненной при перемещении заряда. Мощность равна частному от деления её величины на потраченное для этого время. Из курса физики известно, что работу можно выразить как произведение разности потенциалов на перемещаемый заряд. Для вычисления заряда можно применить следующую формулу:

На основе сказанного можно привести такое равенство:

Из формулы видно, что мощность можно выразить как произведение напряжения и силы тока. Её можно преобразовать с использованием закона Ома:

Подставив это выражение в формулу мощности, выводят эквивалентные формы, которые могут быть более удобными в некоторых ситуациях.

Например, при рассмотрении последовательного соединения удобной будет формула с использованием силы тока и напряжения. Это связано с тем, что сила электротока на рассматриваемом участке является одинаковой.

При параллельном соединении одинаковым на различных участках будет электронапряжение. В данном случае производить вычисления проще с использованием формулы, которая выражает мощность через разницу потенциалов и сопротивление.

В международной системе измерений для мощности используется ватт. Иногда применяют эквивалентную единицу вольт*ампер. Широко используются значения, которые выражаются в единицах, кратных ваттам. В качестве примера можно привести киловатт и мегаватт, которые соответствуют тысяче и миллиону ватт соответственно.

У большинства электроприборов, используемых в быту, мощность находится в определённых пределах, которые примерно соответствуют значениям, указанным в следующей таблице:

В прошлом в качестве единицы измерения мощности активно использовалась лошадиная сила. Для ее выражения через ватты нужно применять следующую формулу:

Хотя классической единицей измерения энергии или выполненной работы является джоуль, для электрических приборов чаще используется ватт*час.

При описании электрических устройств или деталей часто указывают предельную мощность. В технической документации также может быть указана номинальная мощность оборудования. Режим работы устройства в этом случае считается оптимальным. Если реальная мощность будет выше, то это означает, что прибор эксплуатируется очень интенсивно.

Сказанное можно пояснить на следующем примере. Допустим, речь идёт о резисторе на 500 Ом. Пусть в технической документации сказано, что предельно допустимая мощность при его использовании составляет 10 Вт. В этом случае предельно допустимое напряжение определяется по формуле:

Из этого выражения можно найти напряжение. Для него будет правильным следующее равенство:

Подставляя конкретные значения, получаем, что квадратный корень нужно извлечь из произведения 500 * 10 = 5000. Он будет примерно равен 70.7. Таким образом, предельно допустимым напряжением для этого резистора будет 70.7 В.

Иногда возникает необходимость практически измерить мощность. Это можно сделать с помощью ваттметра.

Для определения мощности также используют амперметр и вольтметр. Первый присоединяют последовательно, второй — параллельно. Получив значения силы тока и напряжения, на их основе производят вычисления для определения мощности.

Мощность источника питания

В предыдущем разделе было рассмотрено понятие мощности и относящиеся к ней характеристики в применении к различным электрическим узлам или приборам. При рассмотрении источника элетротока потребуется учитывать имеющиеся в этом случае особенности.

Используемый ИП должен соответствовать параметрам электрической цепи, которую он питает. При этом необходимо обратить внимание на следующее:

Значение полной мощности электрической цепи.
ЭДС источника.
Внутренне сопротивление ИП.
Потери энергии внутри источника питания.
Значение полезной мощности.

Мощность источника тока должна превосходить мощность электроприбора не меньше, чем на 5-10%. Это позволит обеспечить электропитание даже в условиях интенсивного использования прибора. Энергия источника питания будет расходоваться на совершение полезной работы, а также на потери.

Для понимания особенностей работы источника питания важно знать разницу между электронапряжением на клеммах и электродвижущей силой. Практически в работающей цепи электроны перемещаются по замкнутому пути. Они переходят от отрицательной клеммы через электрическую цепь к положительной. Попадая внутрь батареи под воздействием электродвижущей силы, электроны будут вновь перемещаться на отрицательную клемму.

Нужно учитывать, что величина ЭДС не является независимой от нагрузки. Её точное значение можно узнать при измерении на холостом ходу. Чтобы вычислить мощность источника питания, можно воспользоваться формулой, которая выражает её через ЭДС и сопротивление. Для этого потребуется выполнить следующие действия:

Нужно определить величину электродвижущей силы (E) источника питания. Для этого замеряют разность потенциалов на клеммах на холостом ходу.
Далее требуется подключить нагрузку, которая имеет известное сопротивление (R).
Затем в электрической цепи измеряют силу тока (I), а также напряжение (U).
Теперь есть возможность узнать падение напряжения (U₀) внутри источника тока. Оно представляет собой разность между электродвижущей силой и напряжением в цепи.
Внутреннее сопротивление (R₀) вычисляется по формуле R₀ = U₀ / I.

Подставив полученные значения в формулу, выраженную через напряжение и сопротивление, можно определить мощность источника тока.

Полную мощность ИП можно представить как Р_полн = Р_полезн + Р_потерь.

Для определения полезной мощности используется одна из трех формул:

Мощность потерь, возникающая во внутренней цепи, то есть, в источнике тока, расходуется лишь на процессы, происходящие в самом ИТ и не может использоваться для каких-либо других целей. Ее вычисляют по формуле:

Для определения полной мощности можно воспользоваться одной из трех формул:

Используя приведённый здесь алгоритм, можно определить полезную мощность, которая создаётся рассматриваемым источником тока. Чтобы составить представление о зависимости полезной мощности и той, которая расходуется на нагрев ИТ, можно воспользоваться графиком. Из него видно, что полезная мощность сначала возрастает, а затем начинает убывать. Максимума она достигает в точке, в которой сопротивление нагрузки равно внутреннему сопротивлению источника электротока, то есть, R = r.

КПД при таком условии будет равен 50%. В общем случае коэффициент полезного действия находят по формуле:

Максимальная полезная мощность равняется половине полной. Следовательно

Из сказанного видно, что при подборе наиболее подходящего источника питания для электрического устройства нужно стремиться к тому, чтобы внутреннее сопротивление источника питания было равно сопротивлению нагрузки. Если оно значительно меньше, то существенная часть мощности в процессе эксплуатации будет рассеиваться в виде тепла. Приведённое требование соответствия величин называют условием согласования.

Важно отметить, что в качестве устройства питания не обязательно может использоваться батарея или аккумулятор. Отмеченная здесь закономерность будет действовать и в том случае, если речь идёт об использовании усилителя.

В качестве примера использования указанного правила можно привести подключение акустической системы к усилителю. В этом случае выходной импеданс последнего должен подбираться таким образом, чтобы быть примерно равным входному импедансу подключённых динамиков. На практике в технической документации усилителя указывают границы, в которых должна находиться соответствующая характеристика подключённых устройств.

Видео по теме

Источник

Классическая электродинамика

Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

Единицей измерения в Международной системе единиц (СИ) является ватт (русское обозначение: Вт, международное: W).

Мгновенная электрическая мощность[править | править код]

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки в точку , к величине пробного заряда. То есть можно сказать, что электрическое напряжение численно равно работе по переносу единичного заряда из точки в точку . Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу или над ним будет совершена работа, численно равная электрическому напряжению, действующему на участке цепи. Умножив напряжение на количество единичных зарядов, мы, таким образом, получаем работу, которую совершает электрическое поле по перемещению этих зарядов от начала участка цепи до его конца.
Мощность, по определению — это работа в единицу времени.

Введём обозначения:

— напряжение на участке A-B

(принимаем его постоянным на интервале Delta t

);

— количество зарядов, прошедших от

за время

;

— работа, совершённая зарядом

при движении по участку A-B

;

— мощность.

Записывая вышеприведённые рассуждения, получаем:

${displaystyle P_{A-B}={frac {A}{Delta t}}~.}$

Для единичного заряда на участке A-B :

${displaystyle P_{e(A-B)}={frac {U}{Delta t}}~.}$

Для всех зарядов:

${displaystyle P_{A-B}={frac {U}{Delta t}}cdot {Q}={U}cdot {frac {Q}{Delta t}}~.}$

Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть ${displaystyle textstyle I={frac {Q}{Delta t}}}$ по определению, в результате получаем:

${displaystyle P_{A-B}=Ucdot I~.}$

Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:

Если участок цепи содержит резистор c электрическим сопротивлением , то:

${displaystyle p(t)=i(t)^{2}cdot R={frac {u(t)^{2}}{R}}~.}$

Дифференциальные выражения для электрической мощности[править | править код]

Мощность, выделяемая в единице объёма, равна:

${displaystyle w={frac {dP}{dV}}=mathbf {E} cdot mathbf {j} ~,}$

где:

— напряжённость электрического поля;

— плотность тока.

Отрицательное значение скалярного произведения (векторы и противонаправлены или образуют тупой угол) означает, что в данной точке электрическая мощность не рассеивается, а генерируется за счёт работы сторонних сил.

В случае изотропной среды в линейном приближении:

${displaystyle w=sigma E^{2}={frac {E^{2}}{rho }}=rho j^{2}={frac {j^{2}}{sigma }}~,}$

где ${displaystyle textstyle sigma ,{overset {underset {mathrm {def} }{}}{=}},{frac {1}{rho }}}$ — удельная проводимость, величина, обратная удельному сопротивлению.

В случае наличия анизотропии (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла) в линейном приближении:

${displaystyle w=sigma _{alpha beta }E_{alpha }E_{beta }~,}$

где $sigma _{{alpha beta }}$ — тензор проводимости.

Мощность постоянного тока[править | править код]

Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:

Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:

${displaystyle P=I^{2}cdot R={frac {U^{2}}{R}}~,}$

где — электрическое сопротивление.

Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:

где — ЭДС.

Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность $p=I^{2}cdot r$ прибавляется к поглощаемой или вычитается из отдаваемой.

Мощность переменного тока[править | править код]

В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для большинства простых практических расчётов не слишком полезна непосредственно. Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.

Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол varphi (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.

Активная мощность[править | править код]

Единица измерения в СИ — ватт^[1].

Среднее за период значение мгновенной мощности называется активной электрической мощностью или электрической мощностью:

${displaystyle P={frac {1}{T}}int limits _{0}^{T}p(t)dt~.}$

В цепях однофазного синусоидального тока , где и — среднеквадратичные значения напряжения и тока, varphi — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи или её проводимость по формуле $P=I^{2}cdot r=U^{2}cdot g$ . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью активная связана соотношением .

В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отражённой мощностью.

Реактивная мощность[править | править код]

Единица измерения, по предложению Международной электротехнической комиссии, – вар (вольт-ампер реактивный); (русское обозначение: вар; международное: var). В терминах единиц СИ, как отмечено в 9-ом издании Брошюры СИ, вар когерентен произведению вольт-ампер. В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения в области «электротехника»^[1]^[2]:

{displaystyle Q=Ucdot Icdot sin varphi ~.}

Вар определяется как реактивная мощность цепи с синусоидальным переменным током при действующих значениях напряжения 1 В и тока 1 А, если сдвиг фазы между током и напряжением ${displaystyle textstyle {frac {pi }{2}}}$ ^[3].

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения и тока , умноженному на синус угла сдвига фаз varphi между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью и активной мощностью соотношением:

${displaystyle |Q|={sqrt {S^{2}-P^{2}}}~.}$

Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.

Необходимо отметить, что величина для значений varphi от 0 до плюс 90° является положительной величиной. Величина для значений varphi от 0 до −90° является отрицательной величиной. В соответствии с формулой , реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии, возвращаемой от индуктивной и ёмкостной нагрузки в источник переменного напряжения.

Полная мощность[править | править код]

Единица измерения — В·А, вольт-ампер (русское обозначение: В·А; международное: V·A). В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения «электротехника»^[1]^[2].

Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи и напряжения на её зажимах связана с активной и реактивной мощностями соотношением:

${displaystyle S={sqrt {P^{2}+Q^{2}}}~,}$

где:

— активная мощность;

— реактивная мощность (при индуктивной нагрузке

, а при ёмкостной

Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:

{displaystyle {vec {S}}={vec {P}}+{vec {Q}}~.}

Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.

Комплексная мощность[править | править код]

Мощность, аналогично импедансу, можно записать в комплексном виде:

${displaystyle {dot {S}}={dot {U}}{dot {I}}^{*}=I^{2}mathbb {Z} ={frac {U^{2}}{mathbb {Z} ^{*}}}~,}$

где:

— комплексное напряжение;

— комплексный ток;

— импеданс;

— оператор комплексного сопряжения.

Модуль комплексной мощности равен полной мощности Действительная часть равна активной мощности а мнимая — реактивной мощности с корректным знаком в зависимости от характера нагрузки.

Измерения[править | править код]

Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра, амперметра и фазометра.
Для измерения коэффициента реактивной мощности применяют фазометры
Государственный эталон мощности — ГЭТ 153—2012 Государственный первичный эталон единицы электрической мощности в диапазоне частот от 1 до 2500 Гц. Институт-хранитель: ВНИИМ

Потребление мощности некоторыми электроприборами[править | править код]

Значения потребляемой электрической мощности некоторых потребителей

Электрический прибор	Мощность,Вт
Лампочка фонарика	1
Сетевой роутер, хаб	10…20
Системный блок ПК	100…1700
Системный блок сервера	200…1500
Монитор для ПК ЭЛТ	15…200
Монитор для ПК ЖК	2…40
Лампа люминесцентная бытовая	5…30
Лампа накаливания бытовая	25…150
Холодильник бытовой	15…700
Электропылесос	100… 3000
Электрический утюг	300…2 000
Стиральная машина	350…2 000
Электрическая плитка	1000…2000
Сварочный аппарат бытовой	1000…5500
Двигатель лифта невысокого дома	3 000…15 000
Двигатель трамвая	45 000…75 000
Двигатель электровоза	650 000
Электродвигатель шахтной подъёмной машины	1 000 000…5 000 000
Электродвигатель прокатного стана	6 000 000…32 000 000

Выходная мощность[править | править код]

Измеряется как долговременная (RMS^[en]), так и кратковременная (PMO, PMPO) мощности, способные отдавать усилителями мощности.

также см.: КПД

См. также[править | править код]

Ваттметр
Электрический ток
Коэффициент мощности
Список параметров напряжения и силы электрического тока
Закон Ома
КПД

Примечания[править | править код]

↑ ¹ ² ³ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 26—27. — 240 с. — ISBN 5-7050-0118-5.
↑ ¹ ² Положение о единицах величин, допускаемых к применению в Российской Федерации Архивная копия от 2 ноября 2013 на Wayback Machine Утверждено Постановлением Правительства РФ от 31 октября 2009 г. N 879.
↑ Сена Л. А. Единицы физических величин и их размерности. — М.: Наука, 1977. — С. 213.

Литература[править | править код]

ГОСТ 8.417-2002 Единицы величин.
ПР 50.2.102-2009 Положение о единицах величин, допускаемых к применению в Российской Федерации.
Л. А. Бессонов . Теоретические основы электротехники. Электрические цепи: учебник

для бакалавров. — 12-е изд., испр. и доп. — М.: Юрайт, 2016. — 702 с. — (Бакалавр. Углубленный курс). — 1000 экз. — ISBN 978-5-9916-3210-2.

Гольдштейн Е. И., Сулайманов А. О., Гурин Т. С. Мощностные характеристики электрических цепей при несинусоидальных токах и напряжениях. ТПУ, — Томск, 2009, Деп. в ВИНИТИ, 06.04.09, № 193 — 2009. — 146 с.

Ссылки[править | править код]

Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. ToeHelp.Ru. Дата обращения: 7 марта 2022.
Для чего нужна компенсация реактивной мощности. Школа для электрика (2010). Дата обращения: 7 марта 2022.
. ред. Д. Макаров : Как рассчитать мощность электрического тока? Заметки электрика. ASUTPP. Дата обращения: 7 марта 2022.

Источник

Энергия и мощность электрического тока

В любой замкнутой электрической цепи
источник затрачивает электрическую
энергию W_истна
перемещение единицы положительного
заряда по всей цепи: и на внутреннем и
на внешнем участках.

и;

Энергия источника определяется
выражением: W_ист=Eq=EIt=
(U₀+U)It;

Энергия источника (полезная), которая
расходуется на потребителе: W=UIt;

Энергия источника (потери), которая
расходуется на внутреннем сопротивлении
источника: W=U₀It;

Преобразование электрической энергии
в другие виды энергий происходит с
определенной скоростью. Эта скорость
определяет электрическую мощность
элементов электрической цепи:

;

Мощность источника определяется
соотношением:

Мощность потребителя определяется
соотношением:

Коэффициент полезного действияэлектрической цепиηопределяется
отношением мощности потребителя к
мощности источника:

Закон Джоуля – Ленца

Ток, протекая по проводнику, нагревает
его (в этом случае электрическая энергия
преобразуется в тепловую). Количество
выделенного тепла будет определяться
количеством электрической энергии,
затраченной в этом проводнике.

Дж.

(кал).

Коэффициент 0,24 (электротермический
эквивалент) устанавливает зависимость
между электрической и тепловой энергией.

Часть3: Режимы работы электрических цепей

В электрических цепях все основные
элементы делятся на активные и пассивные.
Активными считаются элементы, в которых
преобразование энергии сопровождается
возникновением ЭДС (аккумуляторы,
генераторы). Элементы, в которых ЭДС не
возникает, называются пассивными.

Параметры электрических цепей:

Ток в замкнутой цепи
;

Напряжение на клеммах источника
;

Падение напряжения на сопротивлении
источника
;

Полезная мощность (мощность потребителя)
.

Электрические цепи могут работать в
трех режимах:

режим холостого хода (цепь разомкнута)
R=∞:I_хх=0,U=E,
U₀=0, P=0.
режим короткого замыкания R=0:
режим нагрузки R≠0:;;;.

Условие максимальной отдачи мощности:
полезная мощность максимальна, когда
сопротивление потребителя R
станет равным внутреннему сопротивлению
источника R₀.

КПД при максимальной отдаче мощности
равно 50%, к 100% КПД приближается в режиме,
близком к холостому ходу.

Нормальным (рабочим) режимом называют
такой режим работы цепи, при котором
ток, напряжение и мощность не превышают
номинальных значений, заданных
заводом-изготовителем.

Источники тока могут работать в режиме
генератора и в режиме нагрузки. Источники,
ЭДС которых совпадают с направлением
тока в цепи, работают в режиме генератора,
а источники , ЭДС которых не совпадают
с направлением тока, работают в режиме
потребителя.

Напряжение источника, работающего в
режиме генератора:
.

Напряжение источника, работающего в
режиме потребителя:
.

Тема 1.3

Расчет электрических цепей постоянного
тока

Основной целью расчета электрической
цепи является нахождение ее параметров:
ток, напряжение, сопротивление, мощность,
КПД. Значения параметров дают возможность
оценить условия и эффективность работы
электротехнического оборудования и
приборов во всех участках электрической
цепи.

Для расчета электрических цепей основой
служат законы Ома и Кирхгофа, Джоуля-Ленца.

Законы Кирхгофа

К характерным элементам электрической
цепи относятся ветвь, узел, контур.

Ветвью электрической цепи называется
ее участок, на всем протяжении которого
величина тока имеет одинаковое значение.
Ветви, которые содержат источники
питания называются активными, а которые
не содержат их – пассивными.

Узлом электрической цепи называется
точка соединения электрических ветвей.

Контуром электрической цепи называют
замкнутое соединение, в которое могут
входить несколько ветвей.

Первый закон Кирхгофа

Сумма токов входящих в узел равна сумме
токов, выходящих из узла. ИЛИ Сумма
токов, сходящихся в узле равна нулю.

∑I=0; – математическое
выражение первого закона Кирхгофа.

Второй закон Кирхгофа

Алгебраическая сумма ЭДС в замкнутом
контуре электрической цепи равна
алгебраической сумме падений напряжений
на всех участках этой цепи.

;
– математическое выражение второго
закона Кирхгофа.

Последовательное соединение
потребителей

Последовательным соединением участков
эй цепи называют соединение, при котором
через все участки цепи проходит один и
тот же ток.

Общее напряжение последовательно
соединенных элементов равно сумме
напряжений на каждом элементе согласно
второму закону Кирхгофа:
;

В соответствии с законом Ома:
;
Из этого соотношения следует:; Таким образом, общее сопротивление
цепи с последовательно соединенными
элементами равно сумме этих сопротивлений.

Параллельное сопротивление
потребителей

Параллельным соединением участков
электрической цепи называется соединение,
при котором все участки цепи присоединяются
к одной паре узлов, то есть находятся
под действием одного и того же напряжения.

Общий ток такого соединения согласно
первому закона Кирхгофа будет равен
сумме токов в отдельных ветвях:
;
В соответствии с законом Ома:;
Если поделить левую и правую части наU, получим:;

Обратная величина общего эквивалентного
сопротивления параллельно включенных
потребителей равна сумме обратных
величин этих потребителей.

Величина, обратная сопротивлению
определяет проводимость потребителя
g. Тогда для параллельно
соединенных потребителей справедливо:;

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В этой статье мы расскажем вам, что представляет собой мощность электрического тока и как её можно рассчитать.

Определение.

Мощность электрического тока (обозначается буквой P) — это физическая величина, определяемая как количество работы, которая совершается источником электрического напряжения для переноса электрического заряда (q) по проводнику за единицу времени t.

Если сказать в целом, то мощность электрического тока показывает, сколько электрической энергии преобразуется за определенное время. Она, в том числе, описывает энергопотребление потребителя.

Формулы

На многих бытовых электроприёмниках есть этикетки с указанием мощности. Мощность (P) говорит о работе (A), выполняемой электроприбором в единицу времени (t). Поэтому, дабы отыскать среднюю мощность электрического тока, необходимо поделить его работу на время, то есть P = A / t.

Давайте рассмотрим, что такое мощность электрического тока. Для этого рассмотрим электрическую цепь (см. рисунок 1), состоящую из источника тока, проводов и какого-либо электроприёмника, которым может быть резистор, аккумулятор, электродвигатель и т.д.

Рис. 1. Электрическая цепь, в которой напряжение и ток постоянны

Рекомендуемое электрическое напряжение также указывается на электрооборудовании. Как эти две величины связаны друг с другом? Из школьного курса физики мы знаем, что напряжение (U) между концами данного электроприёмника определяется следующим образом: U = A / q, где: A — работа, совершаемая источником электрического напряжения для переноса электрического заряда (q) по проводнику.

Величина электрического заряда рассчитывается по формуле: q = I * t

Имеем A = P * t; A = U*q, а q = I * t. После преобразования формул получаем: A = P*t = U*q = U*I*t

Отсюда следует (разделив обе стороны уравнения на t), что P = U*I. То есть мы можем сказать, что количество энергии, переданное от источника тока к резистору определяется по формуле: P = U * I

Из этой формулы можно найти, что U = P / I , I = P / U.

Согласно закону Ома для участка цепи I = U/R, где R — электрическое сопротивление участка цепи. Потому из формулы P = U*I следуют две другие формулы для мощности электрического тока, то есть P = U²/R, P = I²R.

Формулу P = I²R комфортно применять для электрических цепей с последовательным соединением проводников, потому что сила электрического тока при таком соединении в проводниках одинакова.

Для параллельно соединенных проводников работу и мощность удобнее выражать через одинаковое для их электрическое напряжение, исключая силу электрического тока, т.е. лучше применять формулу P = U²/R.

Если электроприборы соединены последовательно либо параллельно, их электрическая мощность суммируется. В данном случае для расчета полной мощности употребляется такая формула:

P_общ = P₁ + P₂ + … + P_n, где P₁, P₂, … — мощность отдельно взятых электроприёмников.

Единицы измерения и обозначение

Единицей измерения мощности в Международной системе единиц (СИ), является ватт. При этом русское обозначение: Вт, международное: W). 1 Вт = 1 Дж/c. Из формулы P = U*I следует, что: 1 ватт = 1 вольт * 1 ампер, или 1 Вт = 1 В*А.

Есть также единицы измерения мощности, кратные ваттам: гектаватт (гВт), киловатт (кВт), мегаватт (МВт). Другими словами 1 гВт = 100 Вт, 1 кВт = 1000 Вт, 1 МВт = 1 000 000 Вт.

Единицы мощности, применяемые в электротехнике, кратны ватту: микроватт (мкВт), милливатт (мВт), гектоватт (гВт), киловатт (кВт) и мегаватт (МВт). Другими словами, 1 мкВт = 1*10^-6 Вт, 1 мВт = 1*10^-3 Вт, 1 гВт = 1*10²Вт, 1 кВт = 1*10³ Вт, 1 МВт = 1*10⁶Вт.

Каждый электроприбор имеет определенную мощность (указана на приборе). Вот типовые значения мощности для некоторых электроприборов.

Прибор	Мощность, Вт
Телевизор в режиме ожидания	0,5
Лампа карманного фонарика	Около 1
Лампы накаливания	25-150
Холодильник	160
Электронагреватель	500-2000
Пылесос	До 1300-1800
Электрочайник	Около 2000
Утюг	1200-2200
Стиральная машина	До 2300

Раньше для обозначения мощности использовалась единица измерения — лошадиная сила (л.с.), которая известна и сейчас. Переведите из лошадиных сил в ватты, используя выражение: 1 л.с. = 735.5 Вт.

Пример расчета мощности электрического тока

В конце концов, вы сможете проверить свои познания на 2-ух обычных примерах.

Представьте, что в первой задачке у вас есть резистор R = 50 Ом, через который течет электрический ток I = 0,3А. Какая электрическая мощность преобразуется в этом резисторе?

Вы можете отыскать решение, найдя соответствующую формулу и подставив в нее заданные значения. То есть у нас получается: P = I²R = 0,3²* 50 = 4,5 Вт

Во второй задаче дан резистор R, электрическое сопротивление которого 700 Ом. В техническом описании указано, что максимальная мощность этого резистора составляет 10 Вт. Насколько высоким может быть напряжение, подаваемое на этот резистор?

Для решения этой задачки подбираем подходящую формулу: P = U²/R, откуда мы находим Umax = Pmax * R = 700 * 10 = 83,67 В.

Это означает, что максимальное напряжение может составлять 83,67 В. Чтобы подстраховаться, следует выбирать электрическое напряжение значительно ниже этого предела.

Более подробно о том как можно находить мощность электрического тока я писал в статье: https://www.asutpp.ru/kak-nayti-moschnost.html

Измерение мощности электрического тока

Вы сможете измерить силу электрического тока при помощи вольтметра и амперметра. Чтобы высчитать нужную мощность, помножьте электрическое напряжение на силу тока. Электрический ток и напряжение можно найти по показаниям приборов.

Рис. 2. Измерение мощности электрического тока

Помните, что вы всегда должны определять электрическое напряжение параллельно нагрузке и электрический ток последовательно.

Есть особые приборы – ваттметры, определяющие мощность электрического тока в цепи, которые, по сути, подменяют два устройства – амперметр и вольтметр.

Единицы измерения электрического тока, применяемые на практике

В паспортах потребителей электроэнергии – лампочки, плиты, электродвигатели – обычно указывают силу электрического тока в них. Исходя из мощности, найти работу электрического тока за данный промежуток времени довольно просто, нужно лишь использовать формулу A = P*t.

Выразив мощность в ваттах, а время в секундах, мы получим работу в джоулях: 1 Вт = 1 Дж/с, где 1 Дж = 1 Вт*с.

Но эту единицу работы неудобно применять на практике, так как электроприёмники потребляют ее в течение долгих периодов времени, как, к примеру, в бытовых устройствах – в течение нескольких часов, в электропоездах – в течение нескольких часов либо даже суток, а расчет потребленной энергии по электросчетчику в большинстве случаев делается раз в месяц.

Потому при расчете работы тока либо затраченной и выработанной электроэнергии во всех этих случаях нужно переводить эти промежутки времени в секунды, что усложняет расчеты.

Перышкин А.В. Физика 8. – М.: Дрофа, 2010. [2]

Потому на практике, при расчете работы электрического тока, более удобно выражать время в часах, а работу электрического тока не в джоулях, а в других единицах: например, ватт-час (Вт*ч), гектоватт*час (гВт*ч), киловатт-час (кВт*ч).

Перышкин А.В. Физика 8. – М.: Дрофа, 2010. [2]

Будут верны следующие соотношения:

1 Вт*ч = 3600 Дж;
1 гВт*ч = 100 Вт*ч = 360 000 Дж;
1 кВт*ч = 1000 Вт*ч = 3 600 000 Дж.

Задача. Существует электрическая лампа, рассчитанная на ток в мощностью 100 ватт. Лампа работает в течение 6 часов каждый день. Нам нужно отыскать работу электрического тока за один месяц (30 дней) и стоимость потребленной электроэнергии, предполагая, что тариф составляет 500 копеек за один кВт/ч.

Запишем условие задачки и решим ее.

Входные данные: P = 100 Вт, t = 6 ч * 30 = 180 ч, тариф = 500 к / кВт*ч .

Решение задачи. Мы знаем, что A = P*t, потому получаем: A = 100 Вт*180 ч = 18 000 Вт*ч = 18 кВт*ч.

Мы рассчитываем стоимость так: Стоимость = 500 к / кВт*ч * 18 кВт*ч = 9000 копеек = 90 рублей.

Ответ: A = 18 кВт*ч, стоимость израсходованной электроэнергии = 90 рублей.

Связь мощности тока с действием тока в электрической цепи

Сравнение мощности тока с номинальной мощностью электрического прибора позволяет определить, насколько сильно нагружен в электрической цепи прибор. Если мощность тока меньше номинального, то действие тока не достаточно интенсивно или совсем не проявляется. Подключение мощного прибора к слабому источнику тока не вызывает в нем никаких действий. Приборы, рассчитанные на малую мощность работы тока, при подключении к источникам, создающим сильное поле, сгорают.

Список использованной литературы

Физика, 8 класс, Исаченкова Л.А., Лещинский Ю.Д., Дорофейчик В.В., 2018
Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Энергия и мощность электрического тока

Энергия и мощность электрического тока:

В замкнутой электрической цепи источник затрачивает электhическую энергию

ЭДС источника определяется выражением 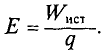Из этого выражения следует, что энергия, затраченная источником, равна

так как 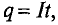что вытекает из определения величины тока

Энергия источника расходуется на потребителе (полезная энергия)

и на внутреннем сопротивлении источника (потери)

Потерей энергии в проводах, при незначительной их длине, можно пренебречь.

Из закона сохранения энергии следует

Во всех элементах электрической цепи происходит преобразование энергии (в источниках различные виды энергии преобразуются в электрическую, в потребителях — электрическая в другие виды энергии).

Скорость такого преобразования энергии определяет электрическую мощность элементов электрической цепи

Обозначается электрическая мощность буквой Р, а единицей электрической мощности является ватт, другими словами, 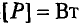(ватт)

Таким образом, мощность источника электрической энергии ‘ определяется выражением

Мощность потребителя, т.е. полезная, потребляемая мощность, будет равна

Если воспользоваться законом Ома для участка электрической цепи, то полезную мощность можно определить следующим выражением:

Потери мощности на внутреннем сопротивлении источника

Для любой замкнутой цепи должен сохраняться баланс мощностей

Так как электрическая мощность измеряется в ваттах, то единицей измерения электрической энергии является

Коэффициент полезного действия электрической цепи л определяется отношением полезной мощности (мощности потребителя) ко всей затраченной мощности (мощности источника)

Закон Джоуля — Ленца для тока
Режимы работы электрических цепей
Однофазные электрические цепи переменного тока
Однофазные цепи синусоидального тока
ЭДС и напряжение в электрической цепи
Закон Ома для участка цепи
Электрическое сопротивление
Закон Ома для замкнутой цепи

Источник

Как определить мощность источника тока

Виды мощности

Активная и реактивная мощность

Как определяется мощность

Мощность источника питания

Видео по теме

Мгновенная электрическая мощность[править | править код]

Дифференциальные выражения для электрической мощности[править | править код]

Мощность постоянного тока[править | править код]

Мощность переменного тока[править | править код]

Активная мощность[править | править код]

Реактивная мощность[править | править код]

Полная мощность[править | править код]

Комплексная мощность[править | править код]

Измерения[править | править код]

Потребление мощности некоторыми электроприборами[править | править код]

Выходная мощность[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Энергия и мощность электрического тока

Закон Джоуля – Ленца

Часть3: Режимы работы электрических цепей

Тема 1.3

Формулы

Единицы измерения и обозначение

Пример расчета мощности электрического тока

Измерение мощности электрического тока

Единицы измерения электрического тока, применяемые на практике

Связь мощности тока с действием тока в электрической цепи

Список использованной литературы

Энергия и мощность электрического тока

Вам также может понравиться

Как найти на пульте автонастройку

Как можно исправить отношения с мужчиной

Как найти айпи адрес асика через компьютер

Добавить комментарий Отменить ответ