Как определить мощность источника тока
Содержание
- 1 Виды мощности
- 2 Активная и реактивная мощность
- 3 Как определяется мощность
- 4 Мощность источника питания
- 5 Видео по теме
Источники питания используются повсеместно. Их основная задача — преобразование параметров электроэнергии, поступающей из сети, в такие, которые необходимы для конкретного электротехнического устройства. Способность ИП выполнять данную задачу зависит от его мощности. Она является главной характеристикой любого блока питания. Чтобы оценить эффективность устройства, необходимо понимать, как найти мощность, если известны различные характеристики электрической цепи.
Виды мощности
При вычислении мощности возможны следующие ситуации:
- Мгновенная мощность вычисляется для очень малого промежутка времени. Это значение важно знать в тех случаях, когда в разные моменты времени эта величина меняется. Проведение замеров позволит мастеру получить целостное представление об используемой мощности. Для постоянного тока данная характеристика постоянна.
- Активное значение мощности применяется для определения постоянной величины, которая фактически является средним значением при наличии переменного тока. При этом мгновенные значения будут изменяться, а активная мощность будет в среднем характеризовать происходящие процессы. Активная мощность — это показатель выполнения полезной работы электрическим оборудованием.
- Реактивная мощность относится к работе индуктивных и емкостных элементов электрических приборов. Она циклически переходит из одной формы в другую. При этом происходит перемещение зарядов, то есть, осуществляется электрическая работа, которая обычно не является полезной.
Активная и реактивная мощность
При работе электрического оборудования следует рассматривать полную мощность. Она показывает работу, которая проводится в единицу времени (в СИ в этом качестве рассматривается 1 секунда). При этом нужно помнить, что полная мощность складывается из активной и реактивной мощности.
Это разделение связано с используемым сопротивлением. Если электрические заряды преодолевают активное сопротивление, мощность также является активной. Она, как правило, относится к выполнению полезной работы.
При наличии переменного тока в электрической цепи присутствует реактивное сопротивление. Оно связано с работой электромагнитного поля и фактически сводится к периодическим изменениям, при которых энергия регулярно перетекает из одной формы в другую, практически не расходуясь.
В бытовых приборах и промышленном оборудовании в большинстве случаев присутствуют оба вида мощности. Активная играет основную роль при использовании постоянного тока или в тех случаях, когда её доля в общей мощности относительно высока.
Обычно в технической документации указывается параметр cosφ. Он может принимать значения от 0 до 1 включительно. Его величина показывает долю активной мощности в полной. Она будет высокой, например, в электронагревательных приборах, где значительная часть энергии тратится на выполнение полезной работы по обогреву помещения.
Надо учитывать, что наличие реактивной мощности оказывает разрушительное действие на прибор. Это может быть, например, связано с разрушением изоляции проводов и кабелей, с повышением риска возникновения короткого замыкания или с порчей оболочек электроприводов или трансформаторов.
Для получения полной мощности применяется векторное сложение активной и реактивной мощности. Её величину вычисляют по теореме Пифагора как длину гипотенузы прямоугольного треугольника, в котором катетами являются активная и реактивная мощности.
Как определяется мощность
Эта величина определяется на основе работы, выполненной при перемещении заряда. Мощность равна частному от деления её величины на потраченное для этого время. Из курса физики известно, что работу можно выразить как произведение разности потенциалов на перемещаемый заряд. Для вычисления заряда можно применить следующую формулу:
На основе сказанного можно привести такое равенство:
Из формулы видно, что мощность можно выразить как произведение напряжения и силы тока. Её можно преобразовать с использованием закона Ома:
Подставив это выражение в формулу мощности, выводят эквивалентные формы, которые могут быть более удобными в некоторых ситуациях.
Например, при рассмотрении последовательного соединения удобной будет формула с использованием силы тока и напряжения. Это связано с тем, что сила электротока на рассматриваемом участке является одинаковой.
При параллельном соединении одинаковым на различных участках будет электронапряжение. В данном случае производить вычисления проще с использованием формулы, которая выражает мощность через разницу потенциалов и сопротивление.
В международной системе измерений для мощности используется ватт. Иногда применяют эквивалентную единицу вольт*ампер. Широко используются значения, которые выражаются в единицах, кратных ваттам. В качестве примера можно привести киловатт и мегаватт, которые соответствуют тысяче и миллиону ватт соответственно.
У большинства электроприборов, используемых в быту, мощность находится в определённых пределах, которые примерно соответствуют значениям, указанным в следующей таблице:
В прошлом в качестве единицы измерения мощности активно использовалась лошадиная сила. Для ее выражения через ватты нужно применять следующую формулу:
Хотя классической единицей измерения энергии или выполненной работы является джоуль, для электрических приборов чаще используется ватт*час.
При описании электрических устройств или деталей часто указывают предельную мощность. В технической документации также может быть указана номинальная мощность оборудования. Режим работы устройства в этом случае считается оптимальным. Если реальная мощность будет выше, то это означает, что прибор эксплуатируется очень интенсивно.
Сказанное можно пояснить на следующем примере. Допустим, речь идёт о резисторе на 500 Ом. Пусть в технической документации сказано, что предельно допустимая мощность при его использовании составляет 10 Вт. В этом случае предельно допустимое напряжение определяется по формуле:
Из этого выражения можно найти напряжение. Для него будет правильным следующее равенство:
Подставляя конкретные значения, получаем, что квадратный корень нужно извлечь из произведения 500 * 10 = 5000. Он будет примерно равен 70.7. Таким образом, предельно допустимым напряжением для этого резистора будет 70.7 В.
Иногда возникает необходимость практически измерить мощность. Это можно сделать с помощью ваттметра.
Для определения мощности также используют амперметр и вольтметр. Первый присоединяют последовательно, второй — параллельно. Получив значения силы тока и напряжения, на их основе производят вычисления для определения мощности.
Мощность источника питания
В предыдущем разделе было рассмотрено понятие мощности и относящиеся к ней характеристики в применении к различным электрическим узлам или приборам. При рассмотрении источника элетротока потребуется учитывать имеющиеся в этом случае особенности.
Используемый ИП должен соответствовать параметрам электрической цепи, которую он питает. При этом необходимо обратить внимание на следующее:
- Значение полной мощности электрической цепи.
- ЭДС источника.
- Внутренне сопротивление ИП.
- Потери энергии внутри источника питания.
- Значение полезной мощности.
Мощность источника тока должна превосходить мощность электроприбора не меньше, чем на 5-10%. Это позволит обеспечить электропитание даже в условиях интенсивного использования прибора. Энергия источника питания будет расходоваться на совершение полезной работы, а также на потери.
Для понимания особенностей работы источника питания важно знать разницу между электронапряжением на клеммах и электродвижущей силой. Практически в работающей цепи электроны перемещаются по замкнутому пути. Они переходят от отрицательной клеммы через электрическую цепь к положительной. Попадая внутрь батареи под воздействием электродвижущей силы, электроны будут вновь перемещаться на отрицательную клемму.
Нужно учитывать, что величина ЭДС не является независимой от нагрузки. Её точное значение можно узнать при измерении на холостом ходу. Чтобы вычислить мощность источника питания, можно воспользоваться формулой, которая выражает её через ЭДС и сопротивление. Для этого потребуется выполнить следующие действия:
- Нужно определить величину электродвижущей силы (E) источника питания. Для этого замеряют разность потенциалов на клеммах на холостом ходу.
- Далее требуется подключить нагрузку, которая имеет известное сопротивление (R).
- Затем в электрической цепи измеряют силу тока (I), а также напряжение (U).
- Теперь есть возможность узнать падение напряжения (U0) внутри источника тока. Оно представляет собой разность между электродвижущей силой и напряжением в цепи.
- Внутреннее сопротивление (R0) вычисляется по формуле R0 = U0 / I.
Подставив полученные значения в формулу, выраженную через напряжение и сопротивление, можно определить мощность источника тока.
Полную мощность ИП можно представить как Рполн = Рполезн + Рпотерь.
Для определения полезной мощности используется одна из трех формул:
Мощность потерь, возникающая во внутренней цепи, то есть, в источнике тока, расходуется лишь на процессы, происходящие в самом ИТ и не может использоваться для каких-либо других целей. Ее вычисляют по формуле:
Для определения полной мощности можно воспользоваться одной из трех формул:
Используя приведённый здесь алгоритм, можно определить полезную мощность, которая создаётся рассматриваемым источником тока. Чтобы составить представление о зависимости полезной мощности и той, которая расходуется на нагрев ИТ, можно воспользоваться графиком. Из него видно, что полезная мощность сначала возрастает, а затем начинает убывать. Максимума она достигает в точке, в которой сопротивление нагрузки равно внутреннему сопротивлению источника электротока, то есть, R = r.
КПД при таком условии будет равен 50%. В общем случае коэффициент полезного действия находят по формуле:
Максимальная полезная мощность равняется половине полной. Следовательно
Из сказанного видно, что при подборе наиболее подходящего источника питания для электрического устройства нужно стремиться к тому, чтобы внутреннее сопротивление источника питания было равно сопротивлению нагрузки. Если оно значительно меньше, то существенная часть мощности в процессе эксплуатации будет рассеиваться в виде тепла. Приведённое требование соответствия величин называют условием согласования.
Важно отметить, что в качестве устройства питания не обязательно может использоваться батарея или аккумулятор. Отмеченная здесь закономерность будет действовать и в том случае, если речь идёт об использовании усилителя.
В качестве примера использования указанного правила можно привести подключение акустической системы к усилителю. В этом случае выходной импеданс последнего должен подбираться таким образом, чтобы быть примерно равным входному импедансу подключённых динамиков. На практике в технической документации усилителя указывают границы, в которых должна находиться соответствующая характеристика подключённых устройств.
Видео по теме
Большинство бытовых приборов, подключаемых к сети, характеризуются таким параметром, как электрическая мощность устройства. С физической точки зрения мощность представляет собой количественное выражение совершаемой работы. Поэтому для оценки эффективности того или иного устройства вам необходимо знать нагрузку, которую он будет создавать в цепи. Далее мы рассмотрим особенности самого понятия и как найти мощность тока, обладая различными характеристиками самого устройства и электрической сети.
Понятие электрической мощности и способы ее расчета
С электротехнической точки зрения она представляет собой количественное выражение взаимодействия энергии с материалом проводников и элементами при протекании тока в электрической цепи. Из-за наличия электрического сопротивления во всех деталях, задействованных в проведения электротока, направленное движение заряженных частиц встречает препятствие на пути следования. Это и обуславливает столкновение носителей заряда, электроэнергия переходит в другие виды и выделяется в виде излучения, тепла или механической энергии в окружающее пространство. Преобразование одного вида в другой и есть потребляемая мощность прибора или участка электрической цепи.
В зависимости от параметров источника тока и напряжения мощность также имеет отличительные характеристики. В электротехнике обозначается S, P и Q, единица измерения согласно международной системы СИ – ватты. Вычислить мощность можно через различные параметры приборов и электрических приборов. Рассмотрим каждый из них более детально.
Через напряжение и ток
Наиболее актуальный способ, чтобы рассчитать мощность в цепях постоянного тока – это использование данных о силе тока и приложенного напряжения. Для этого вам необходимо использовать формулу расчета: P = U*I
Где:
- P – активная мощность;
- U – напряжение приложенное к участку цепи;
- I — сила тока, протекающего через соответствующий участок.
Этот вариант подходит только для активной нагрузки, где постоянный ток не обеспечивает взаимодействия с реактивной составляющей цепи. Чтобы найти мощность вам нужно выполнить произведение силы тока на напряжение. Обе величины должны находиться в одних единицах измерения – Вольты и Амперы, тогда результат также получится в Ваттах. Можно использовать и другие способы кВ, кА, мВ, мА, мкВ, мкА и т.д., но и параметр мощности пропорционально изменит свой десятичный показатель.
Через напряжение и сопротивление
Для большинства электрических устройств известен такой параметр, как внутреннее сопротивление, которое принимается за константу на весь период их эксплуатации. Так как бытовые или промышленные единицы подключаются к источнику с известным номиналом напряжения, определять мощность достаточно просто. Активная мощность находится из предыдущего соотношения и закона Ома для участка цепи, согласно которого ток на участке прямо пропорционален величине приложенного напряжения и имеет обратную пропорциональность к сопротивлению:
I = U/R
Если выражение для вычисления токовой нагрузки подставить в предыдущую формулу, то получится такое выражение для определения мощности:
P = U*(U/R)=U2/R
Где,
- P – величина нагрузки;
- U – приложенная разность потенциалов;
- R – сопротивление нагрузки.
Через ток и сопротивление
Бывает ситуация, когда разность потенциалов, приложенная к электрическому прибору, неизвестна или требует трудоемких вычислений, что не всегда удобно. Особенно актуален данный вопрос, если несколько устройств подключены последовательно и вам неизвестно, каким образом потребляемая электроэнергия распределяется между ними. Подход в определении здесь ничем не отличается от предыдущего способа, за основу берется базовое утверждение, что электрическая нагрузка рассчитывается как P = U×I, с той разницей, что напряжение нам не известно.
Поэтому ее мы также выведем из закона Ома, согласно которого нам известно, что падение напряжения на каком-либо отрезке линии или электроустановки прямо пропорционально току, протекающему по этому участку и сопротивлению отрезка цепи:
U=I*R
после того как выражение подставить в формулу мощности, получим:
P = (I*R)*I =I2*R
Как видите, мощность будет равна квадрату силы тока умноженной на сопротивление.
Полная мощность в цепи переменного тока
Сети переменного тока кардинально отличаются от постоянного тем, что изменение электрических величин, приводит к появлению не только активной, но и реактивной составляющей. В итоге суммарная мощность будет также состоять активной и реактивной энергии:
Где,
- S – полная мощность
- P – активная составляющая – возникает при взаимодействии электротока с активным сопротивлением;
- Q – реактивная составляющая – возникает при взаимодействии электротока с реактивным сопротивлением.
Также составляющие вычисляются через тригонометрические функции, так:
P = U*I*cosφ
Q = U*I*sinφ
что активно используется в расчете электрических машин.
Пример расчета полной мощности для электродвигателя
Отдельный интерес представляет собой нагрузка, подключенная к трехфазной сети, так как электрические величины, протекающие в ней, напрямую зависят от номинальной нагрузки каждой из фаз. Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.
Особенность питания и асинхронной и синхронной электрической машины заключается в том, что на обмотки может подаваться и фазное и линейное напряжение. Тот или иной вариант, как правило, обуславливается способом соединения обмоток электродвигателя. Тогда мощность будет вычисляться по формуле:
S = 3*Uф*Iф
В случае выполнения расчетов с линейным напряжением, чтобы найти мощность формула примет вид:
Активная и реактивная мощности будут вычисляться по аналогии с сетями переменного тока, как было рассмотрено ранее.
Теперь рассмотрим вычисления на примере конкретной электрической машины асинхронного типа. Следует отметить, что официальная производительность, указываемая в паспортных данных электродвигателя – это полезная мощность, которую двигатель может выдать при совершении оборотов вала. Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.
Как видите, для вычислений с шильда мы возьмем следующую информацию об электродвигателе:
- полезная производительность – 3 кВт, а в переводе на систему измерения – 3000 Вт;
- коэффициент полезного действия – 80%, а в пересчете для вычислений будем пользоваться показателем 0,8;
- тригонометрическая функция соотношения активных и реактивных составляющих – 0,74%;
- напряжение, при соединении обмоток треугольником составит 220 В;
- сила тока при том же способе соединения – 13,3 А.
С таким перечнем характеристик можно воспользоваться несколькими способами:
S = 1,732*220*13,3 = 5067 Вт
Чтобы найти искомую величину, сначала определяем активную составляющую:
P = Pполезная / КПД = 3000/0.8 = 3750 Вт
Далее полную по способу деления активной на коэффициент cos φ:
S = P/cos φ = 3750/0.74 = 5067 Вт
Как видите, и в первом, и во втором случае искомая величина получилась одинакового значения.
Примеры задач
Для примера рассмотрим вычисление на участках электрической цепи с последовательным и параллельным соединением элементов. Первый вариант предусматривает ситуацию, когда все детали соединяются друг за другом от одного полюса источника питания до другого.
Как видите на рисунке, в качестве источника мы используем батарейку с номинальным напряжением 9 В и три резистора по 10, 20 и 30 Ом соответственно. Так как номинальный ток нам не известен, расчет произведем через напряжение и сопротивление:
P = U2/R = 81 / (10+20+30) = 1.35 Вт
Для параллельной схемы подключения возьмем в качестве примера участок цепи с двумя резисторами и одним источником тока:
Как видите, для удобства расчетов нам нужно привести параллельно подключенные резисторы к схеме замещения, из чего получится:
Rобщ = (R1*R2) / (R1+R2) = (10*15) / (10+15) = 6 Ом
Тогда искомый номинал нагрузки мы можем узнать через значение тока и сопротивления:
P = I2*R = 25*6 = 150 Вт
Видео по теме
Цепь постоянного тока
В цепи постоянного тока действуют постоянные напряжения, протекают постоянные токи и присутствуют только резистивные элементы (сопротивления).
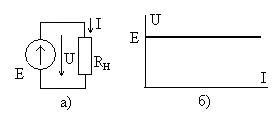
Идеальным источником напряжения называют источник, напряжение 
на зажимах которого, создаваемое внутренней электродвижущей силой (ЭДС 
), на зависит от формируемого им в нагрузке 
тока 
(рис. 6.1а). При этом имеет место равенство 
. Вольтамперная характеристика идеального источника напряжения показана на рис. 6.1б.
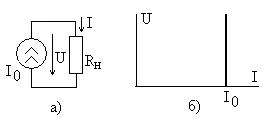
Идеальным источником тока 
называют источник, который отдает в нагрузку ток, не зависящий от напряжения на зажимах источника, 
Рис. 6.2а. Его вольтамперная характеристика показана на рис. 6.2б.
В сопротивлении 
связь между напряжением и током определяется законом Ома в виде
. (6.1)
Пример электрической цепи показан на рис. 6.3. В ней выделяются ветви, состоящие из последовательного соединения нескольких элементов (источника E и сопротивления 
) или одного элемента ( 
и 
) и узлы – точки соединения трех и более ветвей, отмеченные жирными точками. В рассмотренном примере имеется 
ветви и 
узла.
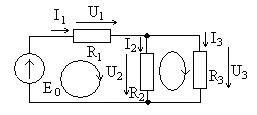
Кроме того, в цепи выделяются независимые замкнутые контуры, не содержащие идеальные источники тока. Их число равно 
. В примере на рис. 6.3 их число 
, например, контуры с ветвями E и , показанные на рис. 6.3 овалами со стрелками, указывающими положительное направление обхода контура.
Связь токов и напряжений в цепи определяется законами Кирхгофа.
Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю,
. (6.2)
Втекающие в узел токи имеют знак плюс, а вытекающие минус.
Второй закон Кирхгофа: алгебраическая сумма напряжений на элементах замкнутого независимого контура равна алгебраической сумме ЭДС идеальных источников напряжения, включенных в этом контуре,
. (6.3)
Напряжения и ЭДС берутся со знаком плюс, если их положительные направления совпадают с направлением обхода контура, в противном случае используется знак минус.
Для приведенного на рис. 6.3 примера по закону Ома получим подсистему компонентных уравнений
(6.4)
По законам Кирхгофа подсистема топологических уравнений цепи имеет вид
(6.5)
Расчет на основе закона Ома
Этот метод удобен для расчета сравнительно простых цепей с одним источником сигнала . Он предполагает вычисление сопротивлений участков цепи, для которых известна вели-
чина тока (или напряжения), с последующим определением неизвестного напряжения (или тока). Рассмотрим пример расчета цепи, схема которой приведена на рис. 6.4, при токе идеального источника 
А и сопротивлениях 
Ом, 
Ом, 
Ом. Необходимо определить токи ветвей 
и 
, а также напряжения на сопротивлениях 
, 
и 
.
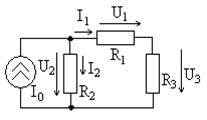Известен ток источника 
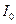, тогда можно вычислить сопротивление цепи 
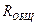относительно зажимов источника тока (параллельного соединения сопротивления 
и последовательно соединен-
Рис. 6.4 ных сопротивлений 
и 
),
.
Напряжение на источнике тока (на сопротивлении ) равно
В.
Затем можно найти токи ветвей
А,
А.
Полученные результаты можно проверить с помощью первого закона Кирхгофа в виде 
. Подставляя вычисленные значения, получим 
А, что совпадает с величиной тока источника.
Зная токи ветвей, нетрудно найти напряжения на сопротивлениях (величина уже найдена)
В,
В.
По второму закону Кирхгофа 
. Складывая полученные результаты, убеждаемся в его выполнении.
Расчет цепи по уравнениям Кирхгофа
Проведем расчет токов и напряжений в цепи, показанной на рис. 6.3 при 
и 
. Цепь описывается системой уравнений (6.4) и (6.5), из которой для токов ветвей получим
(6.6)
Из первого уравнения выразим 
, а из третьего
.
Тогда из второго уравнения получим
,
,
.
Из уравнений закона Ома запишем
.
.
Нетрудно убедиться, что выполняется второй закон Кирхгофа
.
Подставляя численные значения, получим
, 
,
, 
.
Эти же результаты можно получить, используя только закон Ома.
Мощность в цепи постоянного тока
Действующие в цепи идеальные источники тока и (или) напряжения отдают мощность в подключенную к ним цепь (нагрузку). Для цепи на рис. 6.1а отдаваемая идеальным источником напряжения мощность 
равна
, (6.7)
а в цепи на рис. 6.2а идеальный источник тока отдает в нагрузку мощность
. (6.8)
Подключенная к источнику внешняя резистивная цепь потребляет от него мощность, преобразуя ее в другте виды энергии, чаще всего в тепло.
Если через сопротивление протекает ток , а приложенное к нему напряжение равно , то для потребляемой сопротивлением мощности 
получим
. (6.9)
С учетом уравнений закона Ома (6.1) можно записать
. (6.10)
Если в цепи несколько сопротивлений, то сумма потребляемых ими мощностей равна суммарной мощности, отдаваемой в цепь всеми действующими в ней источниками. Это условие баланса мощностей.
Например, для цепи на рис. 6.3 в общем виде получим
. (6.11)
Подставляя в левую часть равенства (6.11) полученные ранее выражения для токов, получим
что соответствует правой части выражения (6.11).
Аналогичные расчеты можно проделать и для цепи на рис. 6.4.
Условие баланса мощностей позволяет дополнительно контролировать правильность расчетов.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9005 — 
| 7249 — 
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Цепь постоянного тока
В цепи постоянного тока действуют постоянные напряжения, протекают постоянные токи и присутствуют только резистивные элементы (сопротивления).
Идеальным источником напряжения называют источник, напряжение на зажимах которого, создаваемое внутренней электродвижущей силой (ЭДС ), на зависит от формируемого им в нагрузке тока (рис. 6.1а). При этом имеет место равенство . Вольтамперная характеристика идеального источника напряжения показана на рис. 6.1б.
Идеальным источником тока называют источник, который отдает в нагрузку ток, не зависящий от напряжения на зажимах источника, Рис. 6.2а. Его вольтамперная характеристика показана на рис. 6.2б.
В сопротивлении связь между напряжением и током определяется законом Ома в виде
. (6.1)
Пример электрической цепи показан на рис. 6.3. В ней выделяются ветви, состоящие из последовательного соединения нескольких элементов (источника E и сопротивления ) или одного элемента ( и ) и узлы – точки соединения трех и более ветвей, отмеченные жирными точками. В рассмотренном примере имеется ветви и узла.
Кроме того, в цепи выделяются независимые замкнутые контуры, не содержащие идеальные источники тока. Их число равно . В примере на рис. 6.3 их число , например, контуры с ветвями E и , показанные на рис. 6.3 овалами со стрелками, указывающими положительное направление обхода контура.
Связь токов и напряжений в цепи определяется законами Кирхгофа.
Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю,
. (6.2)
Втекающие в узел токи имеют знак плюс, а вытекающие минус.
Второй закон Кирхгофа: алгебраическая сумма напряжений на элементах замкнутого независимого контура равна алгебраической сумме ЭДС идеальных источников напряжения, включенных в этом контуре,
. (6.3)
Напряжения и ЭДС берутся со знаком плюс, если их положительные направления совпадают с направлением обхода контура, в противном случае используется знак минус.
Для приведенного на рис. 6.3 примера по закону Ома получим подсистему компонентных уравнений
(6.4)
По законам Кирхгофа подсистема топологических уравнений цепи имеет вид
(6.5)
Расчет на основе закона Ома
Этот метод удобен для расчета сравнительно простых цепей с одним источником сигнала . Он предполагает вычисление сопротивлений участков цепи, для которых известна вели-
чина тока (или напряжения), с последующим определением неизвестного напряжения (или тока). Рассмотрим пример расчета цепи, схема которой приведена на рис. 6.4, при токе идеального источника А и сопротивлениях Ом, Ом, Ом. Необходимо определить токи ветвей и , а также напряжения на сопротивлениях , и .
Известен ток источника 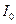, тогда можно вычислить сопротивление цепи 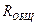относительно зажимов источника тока (параллельного соединения сопротивления и последовательно соединен-
Рис. 6.4 ных сопротивлений и ),
.
Напряжение на источнике тока (на сопротивлении ) равно
В.
Затем можно найти токи ветвей
А,
А.
Полученные результаты можно проверить с помощью первого закона Кирхгофа в виде . Подставляя вычисленные значения, получим А, что совпадает с величиной тока источника.
Зная токи ветвей, нетрудно найти напряжения на сопротивлениях (величина уже найдена)
В,
В.
По второму закону Кирхгофа . Складывая полученные результаты, убеждаемся в его выполнении.
Расчет цепи по уравнениям Кирхгофа
Проведем расчет токов и напряжений в цепи, показанной на рис. 6.3 при и . Цепь описывается системой уравнений (6.4) и (6.5), из которой для токов ветвей получим
(6.6)
Из первого уравнения выразим , а из третьего
.
Тогда из второго уравнения получим
,
,
.
Из уравнений закона Ома запишем
.
.
Нетрудно убедиться, что выполняется второй закон Кирхгофа
.
Подставляя численные значения, получим
, ,
, .
Эти же результаты можно получить, используя только закон Ома.
Мощность в цепи постоянного тока
Действующие в цепи идеальные источники тока и (или) напряжения отдают мощность в подключенную к ним цепь (нагрузку). Для цепи на рис. 6.1а отдаваемая идеальным источником напряжения мощность равна
, (6.7)
а в цепи на рис. 6.2а идеальный источник тока отдает в нагрузку мощность
. (6.8)
Подключенная к источнику внешняя резистивная цепь потребляет от него мощность, преобразуя ее в другте виды энергии, чаще всего в тепло.
Если через сопротивление протекает ток , а приложенное к нему напряжение равно , то для потребляемой сопротивлением мощности получим
. (6.9)
С учетом уравнений закона Ома (6.1) можно записать
. (6.10)
Если в цепи несколько сопротивлений, то сумма потребляемых ими мощностей равна суммарной мощности, отдаваемой в цепь всеми действующими в ней источниками. Это условие баланса мощностей.
Например, для цепи на рис. 6.3 в общем виде получим
. (6.11)
Подставляя в левую часть равенства (6.11) полученные ранее выражения для токов, получим
что соответствует правой части выражения (6.11).
Аналогичные расчеты можно проделать и для цепи на рис. 6.4.
Условие баланса мощностей позволяет дополнительно контролировать правильность расчетов.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8447 — | 7339 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Полная мощность источника тока:
P полн = P полезн + P потерь ,
где P полезн — полезная мощность, P полезн = I 2 R ; P потерь — мощность потерь, P потерь = I 2 r ; I — сила тока в цепи; R — сопротивление нагрузки (внешней цепи); r — внутреннее сопротивление источника тока.
Полная мощность может быть рассчитана по одной из трех формул:
P полн = I 2 ( R + r ), P полн = ℰ 2 R + r , P полн = I ℰ,
где ℰ — электродвижущая сила (ЭДС) источника тока.
Полезная мощность — это мощность, которая выделяется во внешней цепи, т.е. на нагрузке (резисторе), и может быть использована для каких-то целей.
Полезная мощность может быть рассчитана по одной из трех формул:
P полезн = I 2 R , P полезн = U 2 R , P полезн = IU ,
где I — сила тока в цепи; U — напряжение на клеммах (зажимах) источника тока; R — сопротивление нагрузки (внешней цепи).
Мощность потерь — это мощность, которая выделяется в источнике тока, т.е. во внутренней цепи, и расходуется на процессы, имеющие место в самом источнике; для каких-то других целей мощность потерь не может быть использована.
Мощность потерь, как правило, рассчитывается по формуле
P потерь = I 2 r ,
где I — сила тока в цепи; r — внутреннее сопротивление источника тока.
При коротком замыкании полезная мощность обращается в нуль
так как сопротивление нагрузки в случае короткого замыкания отсутствует: R = 0.
Полная мощность при коротком замыкании источника совпадает с мощностью потерь и вычисляется по формуле
где ℰ — электродвижущая сила (ЭДС) источника тока; r — внутреннее сопротивление источника тока.
Полезная мощность имеет максимальное значение в случае, когда сопротивление нагрузки R равно внутреннему сопротивлению r источника тока:
Максимальное значение полезной мощности:
P полезн max = 0,5 P полн ,
где P полн — полная мощность источника тока; P полн = ℰ 2 / 2 r .
В явном виде формула для расчета максимальной полезной мощности выглядит следующим образом:
P полезн max = ℰ 2 4 r .
Для упрощения расчетов полезно помнить два момента:
- если при двух сопротивлениях нагрузки R 1 и R 2 в цепи выделяется одинаковая полезная мощность, то внутреннее сопротивление источника тока r связано с указанными сопротивлениями формулой
- если в цепи выделяется максимальная полезная мощность, то сила тока I * в цепи в два раза меньше силы тока короткого замыкания i :
Пример 15. При замыкании на сопротивление 5,0 Ом батарея элементов дает ток силой 2,0 А. Ток короткого замыкания батареи равен 12 А. Рассчитать наибольшую полезную мощность батареи.
Решение . Проанализируем условие задачи.
1. При подключении батареи к сопротивлению R 1 = 5,0 Ом в цепи течет ток силой I 1 = 2,0 А, как показано на рис. а , определяемый законом Ома для полной цепи:
где ℰ — ЭДС источника тока; r — внутреннее сопротивление источника тока.
2. При замыкании батареи накоротко в цепи течет ток короткого замыкания, как показано на рис. б . Сила тока короткого замыкания определяется формулой
где i — сила тока короткого замыкания, i = 12 А.
3. При подключении батареи к сопротивлению R 2 = r в цепи течет ток силой I 2 , как показано на рис. в , определяемый законом Ома для полной цепи:
I 2 = ℰ R 2 + r = ℰ 2 r ;
в этом случае в цепи выделяется максимальная полезная мощность:
P полезн max = I 2 2 R 2 = I 2 2 r .
Таким образом, для расчета максимальной полезной мощности необходимо определить внутреннее сопротивление источника тока r и силу тока I 2 .
Для того чтобы найти силу тока I 2 , запишем систему уравнений:
i = ℰ r , I 2 = ℰ 2 r >
и выполним деление уравнений:
I 2 = i 2 = 12 2 = 6,0 А.
Для того чтобы найти внутреннее сопротивление источника r , запишем систему уравнений:
I 1 = ℰ R 1 + r , i = ℰ r >
и выполним деление уравнений:
I 1 i = r R 1 + r .
r = I 1 R 1 i − I 1 = 2,0 ⋅ 5,0 12 − 2,0 = 1,0 Ом.
Рассчитаем максимальную полезную мощность:
P полезн max = I 2 2 r = 6,0 2 ⋅ 1,0 = 36 Вт.
Таким образом, максимальная полезная мощность батареи составляет 36 Вт.
На этой странице вы узнаете
- Где самое большое сопротивление в теле человека?
- Какой ученый променял бильярд на физику?
- К чему может привести авария среди электронов?
Весь современный мир держится на электричестве. Наряду с глобальной интернет-сетью, наш мир «опутан» сетью электрических проводов. Что такого происходит в этих тоненьких проводах, что от них зависит жизнь целого города? Давайте поближе познакомимся с электрическим током и узнаем, откуда он появляется.
Мы с вами уже познакомились с электрическими схемами в теме «Законы постоянного тока», где выяснили, какие приборы существуют и как используются в схемах. В этой статье мы поговорим о том, как в элементарных электрических цепях появляется ток. Начало положено, сопротивление бесполезно.
Источник тока
Как мы уже выяснили, электрические схемы не могут работать просто так. Представим, что вы хотите поехать на машине, в которой нет бензина. Конечно, машина не заведется, так как ее нужно заправить. Электрические схемы работают по такому же принципу. Если их не подпитывать током, то они не будут работать.
Электрический ток — это направленное, упорядоченное движение электрических зарядов. Поэтому, чтобы поддерживать в цепи ток длительное время, в нем должен быть участок, на котором будет происходить перенос зарядов против сил электростатического поля (поля, создаваемого неподвижными зарядами). То есть, то место, где электроны будут принудительно приходить в движение.
Источник тока — элемент электрической цепи, в котором на заряды действует сторонняя сила, задающая направление движения зарядов (тока).
Перемещение зарядов на этом участке возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними силами. Эти силы приводят заряды в движение. Благодаря этому поддерживается ток в цепи. Действие сторонних сил характеризуется величиной, называемой электродвижущей силой источника тока (ЭДС), о которой поговорим чуть позднее.
Примером источника тока может служить обычная батарейка. Вы наверняка замечали, что на пальчиковых батарейках с одной стороны пишется «плюс», а с другой — «минус». Это означает, что электрический ток пойдет от положительной части батарейки к отрицательной. А почему ток выходит из одной части, но заходит в другую?
Для объяснения этого явления рассмотрим картинку ниже. Главным критерием рабочей электрической цепи является ее замкнутость, то есть вся цепь неразрывно связана. Подключим нашу батарейку (источник тока) к электрической цепи, которую также называют внешней электрической цепью.
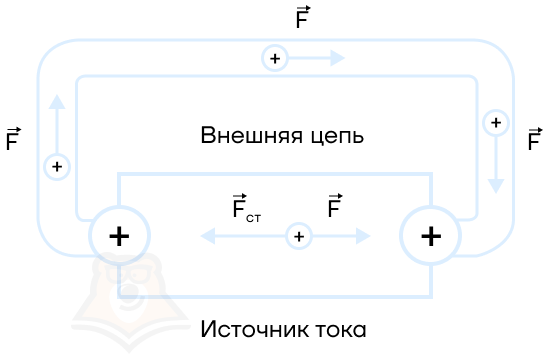
Как мы видим на этом рисунке, на заряды внутри источника тока действует сторонняя сила ((F_{ст})), от плюса к плюсу) и сила электростатического поля ((F)), которая направлена от плюса к минусу. Без действия сторонних сил внутри источника положительный заряд будет двигаться от «+» к «-» (по направлению силы (F)).
Мы действуем сторонними силами так, чтобы он стал двигаться к «+» (по направлению (F_{ст})), то есть против сил электростатического поля. Тогда заряды вылетают из источника тока и далее по внешней цепи, уже под действием обычного электростатического поля, движутся по стандартным законам от «+» к «-». Это и есть наш долгожданный электрический ток – движущиеся заряды. Если бы мы не действовали сторонними силами, все заряды бы просто сидели на месте («+» окружили бы «-», и наоборот). То есть, сама сторонняя сила задает направление движения заряда.
После того как заряд выходит из источника тока, на него действует только одна сила F. Поэтому он обходит всю цепь и возвращается в этот же источник тока. Там на него вновь действует сторонняя сила, ну а дальше вы уже знаете.
Если бы в источнике тока не было сторонних сил, то все положительные заряды застряли бы у минуса.
Основные параметры источника тока
Как и любой другой элемент электрической цепи, источник тока обладает своими характеристиками, которые могут меняться в зависимости от условий использования. Главными характеристиками являются ЭДС источника тока (электродвижущая сила) и его внутреннее сопротивление.
ЭДС источника тока (ε) — это физический параметр, который характеризует работу сторонних сил ((А_{ст})), затраченную на перемещение зарядов (q) внутри источника.
(ε) – ЭДС источника тока (В);
(А_{ст})– работа сторонних сил (Дж);
(q) – заряд, помещенный внутри источника (Кл).
Внутреннее сопротивление определяет количество потерь энергии при прохождении тока через источник тока.
Стоит понимать, что внутреннее сопротивление появляется из-за неидеальности реальных предметов. Только у идеальных источников тока отсутствует внутреннее сопротивление.
Однако при расчете характеристик электрических схем никакой сложности не возникает, так как мы просто представляем, что в цепи появляется дополнительный резистор (на схемах обозначается прямоугольником и буквой R), сопротивление которого будет равняться внутреннему сопротивлению источника тока.
Раз уж мы затронули расчеты электрических схем, то пора вплотную к ним приблизиться.
Закон Ома для участка цепи
Георг Ом рос в небогатой семье. Также он был довольно азартным человеком, любил играть в бильярд в компании друзей. В университетские годы Ом был лучшим игроком в бильярд среди студенческой молодежи, показывал прекрасные результаты в конькобежном спорте.
Но его очень манили точные науки: физика и математика. Однажды он смог собрать всю свою волю «в кулак» и начать проводить опыты в лаборатории обычной школы, где работал учителем. И так он окончательно вжился в статус ученого-физика. После этого он играл в бильярд только для получения удовольствия, а не использовал его как способ заработка.
Дальше мы с вами поговорим о напряжении на элементах электрической цепи, и, в частности, на источнике тока. Поэтому вспомним, что такое напряжение из темы «Законы постоянного тока». Напряжение – физическая величина, которая показывает, какую работу сторонние силы должны приложить, чтобы перенести заряд от одной точки до другой.
Так как у источника тока имеется внутреннее сопротивление, значит, внутри него также будет и напряжение. Чтобы найти его, воспользуемся законом Ома — умножим внутреннее сопротивление источника тока r на сам ток I и получим:
Ur = Ir.
Также мы можем найти напряжение, которое будет выделяться на внешней цепи. Для этого снова умножим ток I на общее сопротивление цепи R:
UR = IR.
Оказывается, что не вся энергия источника тока уходит в цепь. Как раз таки та часть энергии, которая уходит на преодоление внутреннего сопротивления, и будет характеризовать потери. Тогда мы можем записать еще одну формулу для нахождения ЭДС источника тока:
ε – ЭДС источника тока (В);
UR – напряжение на самой электрической цепи (В);
Ur – напряжение внутри источника тока (В).
Теперь давайте подставим вместо напряжений полученные формулы через токи и сопротивления и выразим силу тока. Так мы получим закон Ома для полной цепи:
I – ток в цепи (А);
ε – ЭДС источника тока (В);
R – сопротивление в цепи (Ом);
r – внутреннее сопротивление источника (Ом).
Сила тока в цепи с заданным источником тока (при неизменной ЭДС и с постоянным внутренним сопротивлением) зависит только от сопротивления внешней цепи R.
Самое большое электрическое сопротивление на теле человека — поверхность верхнего рогового слоя кожи человека. Оно может достигать 40000–100000 Ом. Но это не значит, что можно хвататься за оголенные провода голыми руками! Этого сопротивления далеко не достаточно, чтобы защитить человека от опасного электрического тока.
Резко уменьшают сопротивление человека потливость кожного покрова, переутомление, нервное возбуждение. Значение снижается до 800–1000 Ом. Поэтому даже самое небольшое напряжение может вызвать ожог кожи.
Задачи на данную тему встречаются в №12 ЕГЭ. Давайте рассмотрим один пример.
Задача. Найдите внутреннее сопротивление источника ЭДС, если сопротивление в цепи R = 4 Ом, а ЭДС ε=10 В. Сила тока в цепи 2 А.
Решение.Воспользуемся законом Ома для полной цепи и выразим из него внутреннее сопротивление источника ЭДС:
(I=frac{ε}{R + r}),
(r=frac{ε}{I}-R=frac{10}{2}-4=1) (Ом).
Ответ: 1 Ом
Короткозамкнутая цепь
Рассмотрим частный случай электрической цепи, в котором источник тока будет подключен сам на себя. Иначе говоря, он будет короткозамкнутым.
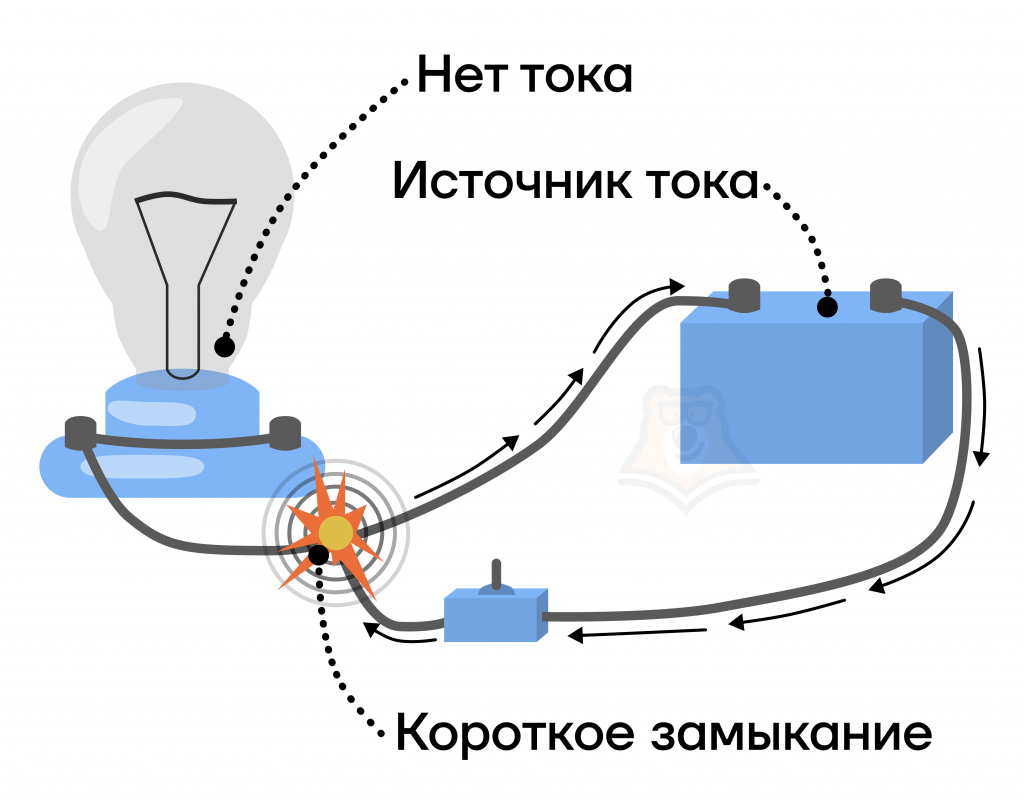
В этом случае отсутствует сопротивление внешней цепи и закон Ома для цепи будет выглядеть так:
(I_{кз}) – ток короткого замыкания (А);
(ε) – ЭДС источника тока (В);
(r) – сопротивление источника ЭДС (Ом).
Короткое замыкание — это такой случай соединения проводов, при котором практически весь ток проходит по пустому проводу и возвращается в источник тока.
Короткое замыкание приводит к сильному нагреву, расплавлению металлов, а иногда и к пожарам.
Если сравнить поток электронов с потоком машин, то ток короткого замыкания – это авария на автодороге. Один поток машин решил влезть в другой. В результате на дороге образовалась авария. Но машины продолжают налетать одна на другую (как в метель в Норильске).
При коротком замыкании сила тока будет увеличиваться до тех пор, пока отключающие механизмы не прекратят поступление силы тока.
Теперь, когда мы уже рассмотрели основные характеристики источника тока, можем перейти к мощности и КПД источника тока.
Мощность и КПД источника тока
Мы уже не раз говорили о том, что при протекании тока выделяется энергия. Источники тока не исключение. При подключении их к цепи на них выделяется энергия. При этом энергия выделяется и в самой цепи.
Чтобы найти мощность передачи энергии (P), выделяемой источником тока, необходимо умножить силу тока на ЭДС этого источника тока. Тогда получим:
(P_{ист}) – мощность источника тока (Вт);
(ε) – ЭДС источника тока (В);
(I) – сила тока (А).
При этом часть этой мощности уходит на элементы внешней цепи, а другая часть – на преодоление внутреннего сопротивления источника тока:
(εI = I^2R + I^2r).
Тогда мощность, выделяемая на внешней цепи:
(P_R=I^2R).
А мощность, которая теряется на внутреннее сопротивление источника тока:
(P_r=I^2r).
Теперь давайте рассмотрим коэффициент полезного действия (КПД, ) источника тока. Как мы уже говорили ранее, часть ЭДС источника тока уходит на внутреннее сопротивление, а часть – на внешнюю цепь. При этом вспомним, что КПД – это отношение полезной мощности к затраченной.
Запишем формулы для мощности:
(P_{ист}=εI=I^2(R+r)),
(P_R=IU =I^2R).
Тогда КПД:
(eta) – КПД источника тока;
(ε) – ЭДС источника тока (В);
(U) – напряжение на внешней цепи (В);
(I) – сила тока (А):
(R) – сопротивление на внешней цепи (Ом);
(r) – сопротивление источника тока (Ом).
Также задачи на тему ЭДС встречаются и в №16 ЕГЭ. Сложность данных задач заключается в установлении правильной зависимости величин друг от друга.
Задача.Определите, как изменятся сила тока (А) в цепи и сопротивление резистора (Б), если ЭДС источника тока заменить на такую же ЭДС, но с большим внутренним сопротивлением.
1) увеличится
2) уменьшится
3) не изменится
Решение.
Б) Внешнее сопротивление никак не зависит от источника тока. Поэтому оно не изменится — выбираем ответ 3.
А) Запишем закон Ома для полной цепи:
(I=frac{ε}{R + r})
При увеличении внутреннего сопротивления знаменатель увеличится. Следовательно, сила тока уменьшится, так что вариант 2 тоже нам подходит.
Ответ: 23
Мы с вами выяснили, что источники тока – элементы электрической цепи, без которых самой цепи не существовало бы. Хотя, конечно, она бы существовала, но была бы бесполезной. Однако и они «не без греха», так как существует опасное внутреннее сопротивление, которое является головной болью для многих инженеров. А все потому, что оно снижает КПД источников тока. Дальше вы можете ознакомиться с полноценными электрическими схемами и посмотреть, как ток ведет себя за пределами источника тока.
Термины
Напряжение – произведение сопротивления элемента и протекающего через него тока.
Резистор (или резистивный элемент) – элемент электрической цепи, который может только потреблять энергию и не может ее создавать.
Сторонние силы — это все внешние силы, воздействующие на заряд.
Электростатическое поле — невидимое поле, создаваемое постоянными электрическими зарядами.
Фактчек
- ЭДС источника тока (ε) — это физический параметр, который характеризует работу, затраченную на перемещение зарядов внутри источника сторонними силами: (ε =frac{А_{cт}}{q}).
- Внутреннее сопротивление (r) — определяет количество потерь энергии при прохождении тока через источник тока.
- Закон Ома для полной цепи: Сила тока в замкнутой цепи равна отношению ЭДС цепи к ее полному сопротивлению: (I =frac{ε}{R + r}).
- Предельное значение силы тока для данного источника тока называется током короткого замыкания: (I_{кз} =frac{ε}{r}).
- Полная мощность цепи — это есть мощность источника тока: (P_ист=εI).
Проверь себя
Задание 1.
Как рассчитывается ЭДС источника тока?
- (ε =frac{А_{ст}}{q})
- (ε =frac{U}{q})
- (ε =frac{А_{ст}}{I})
- (ε =frac{А_{ст}}{qt})
Задание 2.
Короткое замыкание — это:
- Соединение концов участка цепи проводником, сопротивление которого очень мало по сравнению с сопротивлением участка цепи.
- Соединение концов участка цепи проводником, сопротивление которого очень велико по сравнению с сопротивлением участка цепи.
- Соединение концов участка цепи проводником, сопротивление которого не зависит от сопротивления участка цепи.
- Отсутствие электрического тока в цепи.
Задание 3.
Чему равно ЭДС источника тока?
- (ε = U_R- U_r)
- (ε = U_R+ U_r)
- (ε = U_R U_r)
- (ε = U_R)
Задание 4.
От чего зависит сила тока в цепи с заданным источником тока?
- от внутреннего сопротивления цепи
- от внутреннего сопротивления источника тока
- от внешнего сопротивления цепи
- не зависит ни от каких величин
Задание 5.
Где самое большое сопротивление в человеке?
- в сердце
- в пищеварительной системе
- на коже
- в голове
Ответы: 1. — 1; 2. — 1; 3. — 2; 4. — 3; 5. — 3.
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
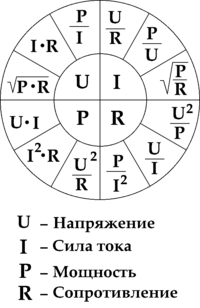
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Единицей измерения в Международной системе единиц (СИ) является ватт (русское обозначение: Вт, международное: W).
Мгновенная электрическая мощность[править | править код]
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки 
в точку 
, к величине пробного заряда. То есть можно сказать, что электрическое напряжение численно равно работе по переносу единичного заряда из точки в точку . Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу или над ним будет совершена работа, численно равная электрическому напряжению, действующему на участке цепи. Умножив напряжение на количество единичных зарядов, мы, таким образом, получаем работу, которую совершает электрическое поле по перемещению этих зарядов от начала участка цепи до его конца.
Мощность, по определению — это работа в единицу времени.
Введём обозначения:
— напряжение на участке (принимаем его постоянным на интервале );- — количество зарядов, прошедших от к за время ;
- — работа, совершённая зарядом при движении по участку ;
- — мощность.
Записывая вышеприведённые рассуждения, получаем:
Для единичного заряда на участке 
:
Для всех зарядов:
Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть 
по определению, в результате получаем:
Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:
Если участок цепи содержит резистор c электрическим сопротивлением 
, то:
Дифференциальные выражения для электрической мощности[править | править код]
Мощность, выделяемая в единице объёма, равна:
где:
- — напряжённость электрического поля;
- — плотность тока.
Отрицательное значение скалярного произведения (векторы 
и 
противонаправлены или образуют тупой угол) означает, что в данной точке электрическая мощность не рассеивается, а генерируется за счёт работы сторонних сил.
В случае изотропной среды в линейном приближении:
где 
— удельная проводимость, величина, обратная удельному сопротивлению.
В случае наличия анизотропии (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла) в линейном приближении:
где 
— тензор проводимости.
Мощность постоянного тока[править | править код]
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:
Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:
где — электрическое сопротивление.
Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:
где 
— ЭДС.
Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность 
прибавляется к поглощаемой или вычитается из отдаваемой.
Мощность переменного тока[править | править код]
В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для большинства простых практических расчётов не слишком полезна непосредственно. Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол 
(сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.
Активная мощность[править | править код]
Единица измерения в СИ — ватт[1].
Среднее за период 
значение мгновенной мощности называется активной электрической мощностью или электрической мощностью:
В цепях однофазного синусоидального тока 
, где 
и 
— среднеквадратичные значения напряжения и тока, — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи 
или её проводимость 
по формуле 
. В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью 
активная связана соотношением 
.
В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отражённой мощностью.
Реактивная мощность[править | править код]
Единица измерения, по предложению Международной электротехнической комиссии, – вар (вольт-ампер реактивный); (русское обозначение: вар; международное: var). В терминах единиц СИ, как отмечено в 9-ом издании Брошюры СИ, вар когерентен произведению вольт-ампер. В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения в области «электротехника»[1][2]:
Вар определяется как реактивная мощность цепи с синусоидальным переменным током при действующих значениях напряжения 1 В и тока 1 А, если сдвиг фазы между током и напряжением 
[3].
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения и тока , умноженному на синус угла сдвига фаз между ними: 
(если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью и активной мощностью 
соотношением:
Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.
Необходимо отметить, что величина 
для значений от 0 до плюс 90° является положительной величиной. Величина для значений от 0 до −90° является отрицательной величиной. В соответствии с формулой 
, реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.
Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии, возвращаемой от индуктивной и ёмкостной нагрузки в источник переменного напряжения.
Полная мощность[править | править код]
Единица измерения — В·А, вольт-ампер (русское обозначение: В·А; международное: V·A). В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения «электротехника»[1][2].
Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи и напряжения на её зажимах 
связана с активной и реактивной мощностями соотношением:
где:
- — активная мощность;
- — реактивная мощность (при индуктивной нагрузке , а при ёмкостной ).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Комплексная мощность[править | править код]
Мощность, аналогично импедансу, можно записать в комплексном виде:
где:
- — комплексное напряжение;
- — комплексный ток;
- — импеданс;
- — оператор комплексного сопряжения.
Модуль комплексной мощности 
равен полной мощности 
Действительная часть 
равна активной мощности 
а мнимая 
— реактивной мощности 
с корректным знаком в зависимости от характера нагрузки.
Измерения[править | править код]
- Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра, амперметра и фазометра.
- Для измерения коэффициента реактивной мощности применяют фазометры
- Государственный эталон мощности — ГЭТ 153—2012 Государственный первичный эталон единицы электрической мощности в диапазоне частот от 1 до 2500 Гц. Институт-хранитель: ВНИИМ
Потребление мощности некоторыми электроприборами[править | править код]
| Электрический прибор | Мощность,Вт |
|---|---|
| Лампочка фонарика | 1 |
| Сетевой роутер, хаб | 10…20 |
| Системный блок ПК | 100…1700 |
| Системный блок сервера | 200…1500 |
| Монитор для ПК ЭЛТ | 15…200 |
| Монитор для ПК ЖК | 2…40 |
| Лампа люминесцентная бытовая | 5…30 |
| Лампа накаливания бытовая | 25…150 |
| Холодильник бытовой | 15…700 |
| Электропылесос | 100… 3000 |
| Электрический утюг | 300…2 000 |
| Стиральная машина | 350…2 000 |
| Электрическая плитка | 1000…2000 |
| Сварочный аппарат бытовой | 1000…5500 |
| Двигатель лифта невысокого дома | 3 000…15 000 |
| Двигатель трамвая | 45 000…75 000 |
| Двигатель электровоза | 650 000 |
| Электродвигатель шахтной подъёмной машины | 1 000 000…5 000 000 |
| Электродвигатель прокатного стана | 6 000 000…32 000 000 |
Выходная мощность[править | править код]
Измеряется как долговременная (RMS[en]), так и кратковременная (PMO, PMPO) мощности, способные отдавать усилителями мощности.
- также см.: КПД
См. также[править | править код]
- Ваттметр
- Электрический ток
- Коэффициент мощности
- Список параметров напряжения и силы электрического тока
- Закон Ома
- КПД
Примечания[править | править код]
- ↑ 1 2 3 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 26—27. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Положение о единицах величин, допускаемых к применению в Российской Федерации Архивная копия от 2 ноября 2013 на Wayback Machine Утверждено Постановлением Правительства РФ от 31 октября 2009 г. N 879.
- ↑ Сена Л. А. Единицы физических величин и их размерности. — М.: Наука, 1977. — С. 213.
Литература[править | править код]
- ГОСТ 8.417-2002 Единицы величин.
- ПР 50.2.102-2009 Положение о единицах величин, допускаемых к применению в Российской Федерации.
- Л. А. Бессонов . Теоретические основы электротехники. Электрические цепи: учебник
для бакалавров. — 12-е изд., испр. и доп. — М.: Юрайт, 2016. — 702 с. — (Бакалавр. Углубленный курс). — 1000 экз. — ISBN 978-5-9916-3210-2.
- Гольдштейн Е. И., Сулайманов А. О., Гурин Т. С. Мощностные характеристики электрических цепей при несинусоидальных токах и напряжениях. ТПУ, — Томск, 2009, Деп. в ВИНИТИ, 06.04.09, № 193 — 2009. — 146 с.
Ссылки[править | править код]
- Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. ToeHelp.Ru. Дата обращения: 7 марта 2022.
- Для чего нужна компенсация реактивной мощности. Школа для электрика (2010). Дата обращения: 7 марта 2022.
- . ред. Д. Макаров : Как рассчитать мощность электрического тока? Заметки электрика. ASUTPP. Дата обращения: 7 марта 2022.
