Как найти мощность критерия мат статистика - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 августа 2018 года; проверки требуют 3 правки.

Статистическая мощность в математической статистике — вероятность отклонения основной (или нулевой) гипотезы при проверке статистических гипотез в случае, когда конкурирующая (или альтернативная) гипотеза верна. Чем выше мощность статистического теста, тем меньше вероятность совершить ошибку второго рода. Величина мощности также используется для вычисления размера выборки, необходимой для подтверждения гипотезы с необходимой силой эффекта.

Применение[править | править код]

Величина мощности при проверке статистической гипотезы зависит от следующих факторов:

величины уровня значимости, обозначаемого греческой буквой , на основании которого принимается решение об отвержении или принятии альтернативной гипотезы;
величины эффекта (то есть разности между сравниваемыми средними);
размера выборки, необходимой для подтверждения статистической гипотезы.

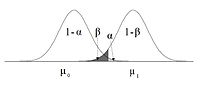
Основные параметры для определения мощности показаны на схеме.

Уровень значимости ( alpha ) выбирается исследователем и определяет вероятность совершения ошибки первого рода. Вероятность того, что альтернативная гипотеза верна, но решение принимается в пользу нулевой гипотезы (ошибка второго рода), обозначается греческой буквой beta . Тогда вероятность принятия правильного решения при истинной альтернативной гипотезе (мощность) равна 1-beta .

При известном стандартном отклонении генеральной совокупности и заданном уровне значимости мощность 1-beta можно вычислить с использованием Z-критерия по формуле

${displaystyle {1-beta }=Pleft(Z>{frac {mu {_{0}}+1{,}64(SE)-mu _{1}}{SE}}right)}$ ,

где $mu {_{0}}$ есть среднее при нулевой гипотезе, $mu {_{1}}$ — среднее при альтернативной гипотезе, — величина критического значения Z-статистики при одностороннем Z-тесте, и — стандартная ошибка.

Величина эффекта определяет вероятность совершения ошибки второго рода. Коэффициент величины эффекта называется мерой эффекта . Был введён в употребление Дж. Коэном и вычисляется как отношения разности между сравниваемыми средними к стандартному отклонению
$d={frac {mu {_{0}}-mu {_{1}}}{sigma }}$ .

Размер выборки, необходимой для подтверждения статистической гипотезы, влияет на статистическую мощность, так как с увеличением выборки уменьшается стандартная ошибка, а следовательно, увеличивается мощность.

См. также[править | править код]

Проверка статистических гипотез
Ошибки первого и второго рода
Статистический критерий
Уровень значимости

Литература[править | править код]

Кендалл М., Стьюарт А. Статистические выводы и связи. — М.: Наука, 1973.
Hays, W. Statistics (5th ed.). Cengage Learning, 1994.

Источник

Принимаемая

Гипотеза

Верная гипотеза

Н₀

Н₁

Н₀

Н₁

Мощностью
критерия
1-

называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.

Задача:
построить критическую область таким
образом, чтобы мощность критерия была
максимальной.

Наилучшей
критической областью
(НКО) называют критическую область,
которая обеспечивает минимальную ошибку
второго рода

Пусть
проверяется H₀:

,
а

–
критическая область критерия с заданным
уровнем значимости

.
Функцией
мощности
критерия
называется
вероятность отклонения Н_о
как функция параметра

,
т.е.

–
ошибка 1-ого
рода

–
мощность критерия

Лемма
Неймана-Пирсона.

При
проверке простой гипотезы Н₀
против простой альтернативной гипотезы
Н₁
наилучшая критическая область (НКО)
критерия заданного уровня значимости
α состоит из точек выборочного пространства
(выборок объема n),
для которых справедливо неравенство:

–
константа, зависящая от α;

–
элементы выборки;

L–функция
правдоподобия при условии, что
соответствующая гипотеза верна.

Соседние файлы в папке Экзамен

#
#
#
08.12.202010.47 Кб26Диаграмма 1.xlsx
#
#
#
08.12.202027.14 Кб27РГР задание 5.xls
#
#
#

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Методика проверки статистических гипотез
2 Альтернативная методика на основе достигаемого уровня значимости
3 Типы критической области
4 Ошибки первого и второго рода
5 Свойства статистических критериев
6 Типы статистических гипотез
7 Типы статистических критериев
- 7.1 Критерии согласия
- 7.2 Критерии сдвига
- 7.3 Критерии нормальности
- 7.4 Критерии однородности
- 7.5 Критерии симметричности
- 7.6 Критерии тренда, стационарности и случайности
- 7.7 Критерии выбросов
- 7.8 Критерии дисперсионного анализа
- 7.9 Критерии корреляционного анализа
- 7.10 Критерии регрессионного анализа
8 Литература
9 Ссылки

Статистическая гипотеза (statistical hypothesys) — это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.

Проверка статистической гипотезы (testing statistical hypotheses) — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.

Статистический тест или статистический критерий — строгое математическое правило, по которому принимается или отвергается статистическая гипотеза.

Методика проверки статистических гипотез

Пусть задана случайная выборка — последовательность объектов из множества .
Предполагается, что на множестве существует некоторая неизвестная вероятностная мера .

Методика состоит в следующем.

Формулируется нулевая гипотеза о распределении вероятностей на множестве . Гипотеза формулируется исходя из требований прикладной задачи. Чаще всего рассматриваются две гипотезы — основная или нулевая и альтернативная . Иногда альтернатива не формулируется в явном виде; тогда предполагается, что означает «не ». Иногда рассматривается сразу несколько альтернатив. В математической статистике хорошо изучено несколько десятков «наиболее часто встречающихся» типов гипотез, и известны ещё сотни специальных вариантов и разновидностей. Примеры приводятся ниже.
Задаётся некоторая статистика (функция выборки) $T:: X^m to mathbb{R}$ , для которой в условиях справедливости гипотезы выводится функция распределения и/или плотность распределения . Вопрос о том, какую статистику надо взять для проверки той или иной гипотезы, часто не имеет однозначного ответа. Есть целый ряд требований, которым должна удовлетворять «хорошая» статистика . Вывод функции распределения при заданных и является строгой математической задачей, которая решается методами теории вероятностей; в справочниках приводятся готовые формулы для ; в статистических пакетах имеются готовые вычислительные процедуры.
Фиксируется уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Это должно быть достаточно малое число . На практике часто полагают .
На множестве допустимых значений статистики выделяется критическое множество наименее вероятных значений статистики , такое, что $mathbb{P}{TinOmega_alphaleft|H_0right.} = alpha$ . Вычисление границ критического множества как функции от уровня значимости является строгой математической задачей, которая в большинстве практических случаев имеет готовое простое решение.
Собственно статистический тест (статистический критерий) заключается в проверке условия:

Итак, статистический критерий определяется статистикой
и критическим множеством , которое зависит от уровня значимости alpha .

Замечание.
Если данные не противоречат нулевой гипотезе, это ещё не значит, что гипотеза верна.
Тому есть две причины.

Альтернативная методика на основе достигаемого уровня значимости

Широкое распространение методики фиксированного уровня значимости было вызвано сложностью вычисления многих статистических критериев в докомпьютерную эпоху. Чаще всего использовались таблицы, в которых для некоторых априорных уровней значимости были выписаны критические значения. В настоящее время результаты проверки гипотез чаще представляют с помощью достигаемого уровня значимости.

Достигаемый уровень значимости (пи-величина, англ. p-value) — это наименьшая величина уровня значимости,
при которой нулевая гипотеза отвергается для данного значения статистики критерия

$p(T) = min { alpha:: TinOmega_alpha },$

где
— критическая область критерия.

Другая интерпретация:
достигаемый уровень значимости p(T) — это вероятность при справедливости нулевой гипотезы получить значение статистики, такое же или ещё более экстремальное, чем

Если достигаемый уровень значимости достаточно мал (близок к нулю), то нулевая гипотеза отвергается.
В частности, его можно сравнивать с фиксированным уровнем значимости;
тогда альтернативная методика будет эквивалентна классической.

Типы критической области

Обозначим через t_alpha значение, которое находится из уравнения , где — функция распределения статистики .
Если функция распределения непрерывная строго монотонная,
то t_alpha есть обратная к ней функция:

$t_alpha = F^{-1}(alpha)$

Значение t_alpha называется также alpha –квантилем распределения F(t) .

На практике, как правило, используются статистики с унимодальной (имеющей форму пика) плотностью распределения.
Критические области (наименее вероятные значения статистики) соответствуют «хвостам» этого распределения.
Поэтому чаще всего возникают критические области одного из трёх типов:

Левосторонняя критическая область:

определяется интервалом

пи-величина:

Правосторонняя критическая область:

определяется интервалом $Omega_alpha = (t_{1-alpha},,+infty)$

пи-величина:

Двусторонняя критическая область:

определяется двумя интервалами $Omega_alpha = (-infty,, t_{alpha/2}) cup (t_{1-alpha/2},,+infty);$

пи-величина:

p(T) = min left{ 2F(T),; 2(1-F(T)) right}.

Ошибки первого и второго рода

Ошибка первого рода или «ложная тревога» (англ. type I error, error, false positive) — когда нулевая гипотеза отвергается, хотя на самом деле она верна. Вероятность ошибки первого рода:

$alpha = mathbb{P}left{ TinOmega_alpha | H_0 right}.$

Ошибка второго рода или «пропуск цели» (англ. type II error, error, false negative) — когда нулевая гипотеза принимается, хотя на самом деле она не верна. Вероятность ошибки второго рода:

$beta(H_1) = mathbb{P}left{ TnotinOmega_alpha | H_1 right}.$

	Верная гипотеза

Результат применения критерия		верно принята	неверно принята (Ошибка второго рода)
	неверно отвергнута (Ошибка первого рода)	верно отвергнута

Свойства статистических критериев

Мощность критерия:
$1 - beta(H) = mathbb{P}left{ TinOmega_alpha | H right}$ — вероятность отклонить гипотезу H_0 , если на самом деле верна альтернативная гипотеза .
Мощность критерия является числовой функцией от альтернативной гипотезы .

Несмещённый критерий:

для всех альтернатив
или, что то же самое,
$mathbb{P}left{ TinOmega_alpha | H right} geq mathbb{P}left{ TinOmega_alpha | H_0 right}$
для всех альтернатив .

Состоятельный критерий:
при для всех альтернатив .

Равномерно более мощный критерий.
Говорят, что критерий с мощностью является равномерно более мощным, чем критерий с мощностью , если выполняются два условия:

;
для всех рассматриваемых альтернатив , причём хотя бы для одной альтернативы неравенство строгое.

Типы статистических гипотез

Простая гипотеза однозначно определяет функцию распределения на множестве . Простые гипотезы имеют узкую область применения, ограниченную критериями согласия (см. ниже). Для простых гипотез известен общий вид равномерно более мощного критерия (Теорема Неймана-Пирсона).

Сложная гипотеза утверждает принадлежность распределения к некоторому множеству распределений на . Для сложных гипотез вывести равномерно более мощный критерий удаётся лишь в некоторых специальных случаях.

Типы статистических критериев

В зависимости от проверяемой нулевой гипотезы статистические критерии делятся на группы, перечисленные ниже по разделам.

Наряду с нулевой гипотезой, которая принимается или отвергается по результату анализа выборки, статистические критерии могут опираться на дополнительные предположения, которые априори предпологаются выполненными.

Параметрические критерии предполагают, что выборка порождена распределением из заданного параметрического семейства. В частности, существует много критериев, предназначенных для анализа выборок из нормального распределения. Преимущество этих критериев в том, что они более мощные. Если выборка действительно удовлетворяет дополнительным предположениям, то параметрические критерии дают более точные результаты. Однако если выборка им не удовлетворяет, то вероятность ошибок (как I, так и II рода) может резко возрасти. Прежде чем применять такие критерии, необходимо убедиться, что выборка удовлетворяет дополнительным предположениям. Гипотезы о виде распределения проверяются с помощью критериев согласия.

Непараметрические критерии не опираются на дополнительные предположения о распределении. В частности, к этому типу критериев относится большинство ранговых критериев.

Критерии согласия

Критерии согласия проверяют, согласуется ли заданная выборка с заданным фиксированным распределением, с заданным параметрическим семейством распределений, или с другой выборкой.

Критерий Колмогорова-Смирнова
Критерий хи-квадрат (Пирсона)
Критерий омега-квадрат (фон Мизеса)

Критерии сдвига

Специальный случай двухвыборочных критериев согласия.
Проверяется гипотеза сдвига, согласно которой распределения двух выборок имеют одинаковую форму и отличаются только сдвигом на константу.

Критерий Стьюдента
Критерий Уилкоксона-Манна-Уитни

Критерии нормальности

Критерии нормальности — это выделенный частный случай критериев согласия.
Нормально распределённые величины часто встречаются в прикладных задачах, что обусловлено действием закона больших чисел.
Если про выборки заранее известно, что они подчиняются нормальному распределению, то к ним становится возможно применять более мощные параметрические критерии.
Проверка нормальность часто выполняется на первом шаге анализа выборки, чтобы решить, использовать далее параметрические методы или непараметрические.
В справочнике А. И. Кобзаря приведена сравнительная таблица мощности для 21 критерия нормальности.

Критерий Шапиро-Уилка
Критерий асимметрии и эксцесса

Критерии однородности

Критерии однородности предназначены для проверки нулевой гипотезы о том, что
две выборки (или несколько) взяты из одного распределения,
либо их распределения имеют одинаковые значения математического ожидания, дисперсии, или других параметров.

Критерии симметричности

Критерии симметричности позволяют проверить симметричность распределения.

Одновыборочный критерий Уилкоксона и его модификации: критерий Антилла-Кёрстинга-Цуккини, критерий Бхаттачария-Гаствирса-Райта
Критерий знаков
Коэффициент асимметрии

Критерии тренда, стационарности и случайности

Критерии тренда и случайности предназначены для проверки нулевой гипотезы об
отсутствии зависимости между выборочными данными и номером наблюдения в выборке.
Они часто применяются в анализе временных рядов, в частности, при анализе регрессионных остатков.

Критерии выбросов

Критерии дисперсионного анализа

Критерии корреляционного анализа

Критерии регрессионного анализа

Литература

Вероятность и математическая статистика: Энциклопедия / Под ред. Ю.В.Прохорова. — М.: Большая российская энциклопедия, 2003. — 912 с.
Кобзарь А. И. Прикладная математическая статистика. Справочник для инженеров и научных работников. — М.: Физматлит, 2006. — 816 с.

Ссылки

Statistical hypothesis testing — статья в англоязычной Википедии.

Источник

Мощность исследования¶

Статистическая мощность – вероятность, с которой искомый эффект будет обнаружен, при условии, что он имеет место.
Величина мощности также используется для вычисления размера выборки, необходимой для подтверждения гипотезы с необходимой мерой эффекта.

Рис. 10 Параметры для определения мощности критерия¶

Уровень значимости ((alpha)) выбирается исследователем и определяет вероятность совершения ошибки первого рода – «обнаружения» эффекта, которого на самом деле нет, когда случайность принимаем за истинный результат. Вероятность того, что альтернативная гипотеза верна, но решение принимается в пользу нулевой гипотезы (ошибка второго рода), обозначается греческой буквой (beta). Тогда вероятность принятия правильного решения при истинной альтернативной гипотезе (мощность) равна (1-beta).

При планировании исследования желаемая мощность обычно принимается равной 0.8 или 0.9.

Эффект действия фактора – это разница между нулевой и альтернативной гипотезами, выраженная в сигмах.

G*Power – популярная программа для вычисления статистической мощности для многих различных тестов. G*Power также может использоваться для вычисления размеров эффекта.

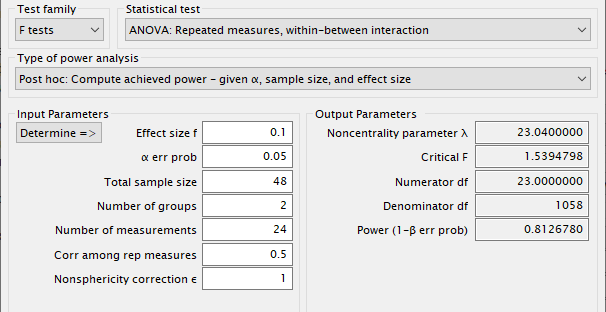
Расчет мощности с параметрами для экспресс варианта теста Баланс внимания приведен на рисунке Рис. 11.

Рис. 11 Окно результатов программы G*Power при выполнении расчета мощности¶

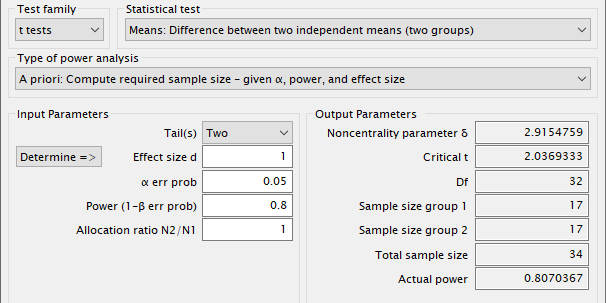
Другой «априорный» тип анализа мощности применяют, когда надо найти размер выборки для заданных уровня значимости и мощности, 0.05 и 0.8 соответственно. При сбалансированных выборках одинакового размера отношение N1 к N2 равно 1.

Рис. 12 Окно результатов программы G*Power при расчете размера выборки¶

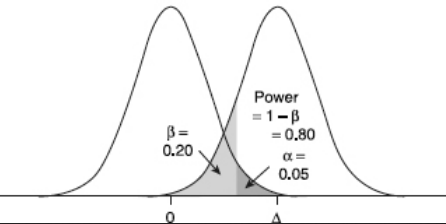
Таким образом, мы отвечаем на вопрос, сколько наблюдений требуется для выборки каждого типа, чтобы, по крайней мере, обнаружить эффект в 1 сигму с 80%-ной вероятностью обнаружения эффекта, если он истинен (20% ошибки типа II), и 5%-ной вероятностью обнаружения эффекта, если такого эффекта нет (ошибка типа I).

Анализ мощности обычно выполняется до проведения исследования. Перспективный или априорный анализ мощности может быть использован для оценки любого из четырех параметров мощности, но чаще всего используется для оценки требуемых размеров выборки.

Для несложных видов анализа вроде теста Стьюдента вычисление мощности сводится к расчету доли одного распределения, разрезанного в точке, рассчитанной как доля в другом распределении, сдвинутом на размер эффекта Рис. 10.

import scipy.stats as stats

n = 48
ncond = 2
effect = 1.
power = 0.8
alpha = 0.05
beta = 1 - power
n_group = n // ncond
df = n_group - 1

# позиция относительно H0
crit = stats.t.ppf(1-alpha/2, df)
# доля в H1 до позиции, сдвинутой на эффект
stats.t.cdf(crit + effect, df)

Для точного расчёта используют нецентральное распределение Стьюдента, у которого ошибка растет с ростом «нецентральности».
Уровень значимости делим на 2, поскольку для двухстороннего теста вероятность распределяется на два хвоста в случае положительного и отрицательного эффекта.

crit = stats.t.ppf(1-alpha/2, df)
1 - stats.nct.cdf(crit, df, effect*np.sqrt(n_group))

Поскольку приходится отнимать от единицы, то можно заменить на прямую и инвертированную «функции выживания» (англ. survival function).

crit = stats.t.isf(alpha/2, df)
stats.nct.sf(crit, df, effect*np.sqrt(n_group))

from statsmodels.stats.power import ttest_power
ttest_power(effect, n_group, alpha)

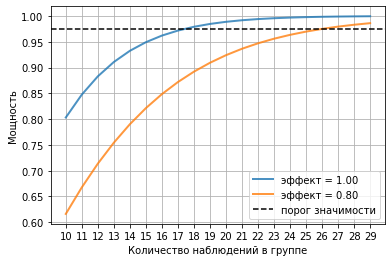
Построим график роста мощности с увеличением размера выборки для заданных эффектов.

nn = arange(10,30)    
popo = ttest_power(effect, nn, alpha)
plot(nn, popo, lw=2, alpha=0.8, label='эффект = %4.2F' % effect)
effect2 = 0.8
popo = ttest_power(effect2, nn, alpha)
plot(nn, popo, lw=2, alpha=0.8, label='эффект = %4.2F' % effect2)
axhline(1 - alpha/2, color='k', ls='--', label='порог значимости')
xticks(nn)
grid(True)
xlabel('Количество наблюдений в группе')
ylabel('Мощность');
legend();

В пакете statsmodels есть специальные средства для решения этой задачи. При этом используют scipy.optimize для нахождения значения, удовлетворяющего уравнению расчета мощности.
Параметр, который нужно найти, передается в метод ...solve_power() с пустым значением None.

from statsmodels.stats.power import tt_ind_solve_power

result = tt_ind_solve_power(effect, power=power, nobs1=None, ratio=1.0, alpha=alpha)
print(f'Размер выборки: {result:.3f}')

Для достоверного обнаружения разницы в 1 сигму (для времени реакции это около 100 мс) нужно по крайней мере 17 значений на группу.

Если выборку сделать больше, то можно будет обнаруживать разницу менее 1 сигмы. Помните, что рост дискриминационной способности статистического метода (размер ошибки) обратно пропорционален корню квадратному от размера выборки, т.е. значительное увеличение выборки ведет лишь к незначительному росту мощности.
Так в надежном варианте теста «Баланс внимания» 32 предъявления для каждого из шести видов стимуляции (2 модальности и 3 частоты предъявления). С учётом того, что 1-2 стимула могут быть пропущены, рабочий размер выборки можно считать 30 штук.

result = tt_ind_solve_power(effect_size=None, power=power, nobs1=30, ratio=1.0, alpha=alpha)
print(f'Обнаруживаемая разница: {result:.3f} σ')

Обнаруживаемая разница: 0.736 σ

Источник

Применение[править | править код]

См. также[править | править код]

Литература[править | править код]

Материал из MachineLearning.

Содержание

Методика проверки статистических гипотез

Альтернативная методика на основе достигаемого уровня значимости

Типы критической области

Ошибки первого и второго рода

Свойства статистических критериев

Типы статистических гипотез

Типы статистических критериев

Критерии согласия

Критерии сдвига

Критерии нормальности

Критерии однородности

Критерии симметричности

Критерии тренда, стационарности и случайности

Критерии выбросов

Критерии дисперсионного анализа

Критерии корреляционного анализа

Критерии регрессионного анализа

Литература

Ссылки

Мощность исследования¶

Вам также может понравиться

Как найти сохраненные пароли на моем компьютере

Как исправить ошибки реестра недвижимости

Как найти молярну масу

Добавить комментарий Отменить ответ