Как найти мощность маховика

Unit Converter

4.1 Подбор электродвигателя.

Для подбора
электродвигателя применяем метод,
основанный на использовании кривой
избыточных моментов.

Для построения
кривой избыточных моментов необходимо
построить на кривой моментов сил
сопротивления (M_Q)
усреднённый и принимаемый постоянным
момент сил движущихся (M_P).
Основанием служит условие установившегося
движения M_P=M_Q.

Кривая избыточных
моментов приведена на листе 4.

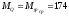
Нм (определяется
из равенства площадей).

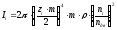
Расчётный момент
электродвигателя:

Нм,

где

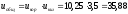
Требуемая мощность
электродвигателя:

кВт, где η – К.П.Д.
электродвигателя (принимаем
).

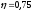По ГОСТ 19523-74
выбираем электродвигатель 4А80В4У3,
мощностью 1,5
кВт, частотой вращения

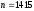
мин^-1.

4.2 Расчёт маховика.

Момент инерции
маховика:

,
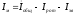
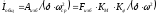где А_изб –
наибольшая избыточная работа, δ=1/40
– коэффициент неравномерности хода
машины, ω_ср
– угловая скорость вала, на котором
устанавливается маховик, F_изб
– определяем,
как площадь М_изб
над средним моментом.

с^-1

К_М=0,5
– масштабный коэффициент момента,
К_φ=π/180
рад/мм – масштабный коэффициент угла
поворота кривошипа.

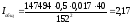
кгм²

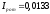
кгм²

кгм²,
(для
зубчатых колес);

Центральный момент
инерции колеса Z₁:

кгм².

Центральный момент
инерции колеса Z₂:

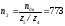
мин^-1;

кгм².

Центральный момент
инерции колеса Z₃:

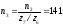
мин^-1;

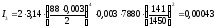
кгм².

Центральный момент
инерции колеса Z₄:

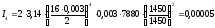
кгм².

Центральный момент
инерции колеса Z₅:

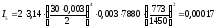
кгм².

Центральный момент
инерции колеса Z₆:

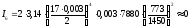
кгм².

Центральный момент
инерции колеса Z₇:

кгм².

Центральный момент
инерции колеса Z₈:

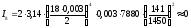
кгм².

Центральный момент
инерции колеса Z₉:

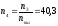
мин^-1;

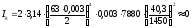
кгм².

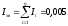
кгм².

Момент инерции
маховика:

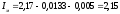
кгм²

Диаметр маховика:

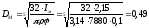
м

Ширина маховика:
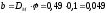м

Скорость маховика:
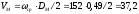м/с

м/с, следовательно,
материал маховика – сталь.

Произведем расчет
другим, более точным методом.

Для этого кривую
моментов сопротивления перестроим в
аппроксимированный график. Заменим
холмообразный участок кривой рабочего
хода равновеликим прямоугольником,
высота которого принимается М_Q
max
,а основание определяется из равенства
площадей. Участок кривой обратного хода
ползуна так же представляем прямоугольником,
высота которого равна 5% от М_Q
max.

Аппроксимированный
график приведен на листе 4.

Определяем время
цикла, время рабочего хода и время
обратного хода:

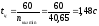
масштаб:

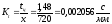
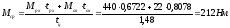
_{Расчетный
приведенный
момент двигателя:}

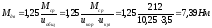
_{Расчетная
мощность двигателя:}

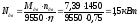
По ГОСТ 19523-74
выбираем электродвигатель 4А80В4У3,
мощностью 1,5
кВт, частотой вращения

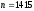
мин^-1.

Для определения
момента инерции маховика вычисляем:

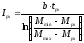
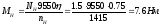
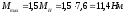
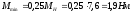
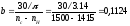
Так как I_рх
>I_ох,
то необходимо выбрать более мощный
двигатель и повторить расчет.

По ГОСТ 19523-74
выбираем электродвигатель 4А112L4У3,
мощностью 4 кВт, частотой вращения

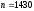
мин^-1.

Для определения
момента инерции маховика вычисляем:

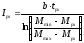
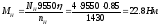
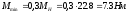
Так как I_рх
<I_ох,
то данный двигатель удовлетворяет нашим
условиям.

Момент инерции
маховика:

кгм²

Диаметр маховика:

м

Ширина маховика:
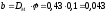м

Скорость маховика:
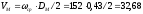м/с

м/с, следовательно,
материал маховика – сталь.

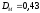
Принимаем:

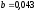м,
м,
электродвигатель 4А112L4У3,
мощностью

4 кВт, частотой
вращения

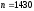
мин^-1.

Заключение

В
результате проведения расчетов по
данному курсовому проекту удалось
выбрать электродвигатель, необходимый
для корректной работы данного кулисного
механизма с учетом технологической
нагрузки, рассчитать размеры самого
механизма и маховика, установить силы,
действующие в звеньях механизма. Все
эти полученные данные необходимы при
создании строгального станка с
однокулисным механизмом.

Список литературы

1. Кореняко А. С.
Курсовое проектирование по теории
механизмов и машин. Киев: Вища школа,
1970.

2. Раскин Я. М. Атлас
схем и примеры выполнения задач анализа
и синтеза современных механизмов.
Днепропетровск: ДМетИ, 1975.

3. Кожевников С.
Н., Раскин Я. М. Конспект лекций по ТММ,
ч. 1 и 2. Днепропетровск: ДМетИ, 1971.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Измерение мощности на динамометрическом стенде, вроде все просто, но почему так много вопросов возникает? Мощность — с колес, с маховика. Единицы измерения мощности в лошадиных силах индикаторная (механическая), а может метрическая или киловаттах. Думаю, многим будет интересно с этим раз и навсегда разобраться.

Что бы лучше в этом разобраться начнем с Джемса Уатта и его парового двигателя, и постепенно дойдем до самых современных методов измерения мощности, используемых в автомобильной промышленности и гоночной индустрии.

Джеймс Уатт (1736-1819) был ученым из Шотландии, инженером, изобретателем, а также инноватором, человеком, который смог извлечь выгоду из своего изобретения. Более того, можно сказать, что он был одним из первых тюнеров двигателей. Все началось с того, что к нему обратился его друг профессор физики Джон Андерсон с просьбой отремонтировать действующий макет паровой машины Ньюкомена. Паровая машина Ньюкомена существовала уже пятьдесят лет до него, и применялась большей частью для откачки воды и поднятия угля из шахт, однако, за всё это время она ни разу не была усовершенствована, и мало кто разбирался в принципе её работы.

Первым значительным усовершенствованием Уатта на паровой машине стало внедрение в 1769 году изолированной камеры для конденсации. А в 1782 году он изобретает машину двойного действия. В итоге, после “тюнинга” от Уатта эффективность паровой машины увеличилась более чем в четыре раза и стала легко управляемой.

К сожалению, машина оставалась бесполезной для изобретателя, как и любое другое изобретение без создания коммерческого спроса. Необходимо было начать продвижение изобретения.

И тогда Уатт предложил использовать паровую машину с доработанным механизмом для поднятия угля из шахты, и тем самым заменить традиционный источник энергии — лошадь. Лошади в то время были использованы для подъема угля до уровня земли. Но как объяснить прижимистым шахтовладельцам, что им предлагают купить более эффективную альтернативу, и оценить преимущества нового приспособления?
Уатт сделал измерения на нескольких лошадях и рассчитал производительность средней рабочей лошади в течение всего рабочего дня. После расчетов именно Уатт дает название этой единице измерения – “Лошадиная сила”, которое в дальнейшем звучит как BHP (brake horsepower) и imp HP (imperial horsepower). Теперь он мог шахтовладельцам показать выгоду, т.е. сколько лошадей они могли бы заменить при использовании одного парового двигателя, а для себя начинать рассчитывать прибыль в предвкушении радужных перспектив.

Однако, все попытки Уатта поставить свои изобретения на коммерческую основу не имели успеха до тех пор, пока не состоялась судьбоносная встреча с предпринимателем Мэттью Болтоном. Совместная компания «Boulton and Watt» (англ. Boulton and Watt) успешно работала на протяжении двадцати пяти лет, в результате чего Уатт становится весьма и весьма состоятельным человеком.

А вот дальше начинается небольшая путаница. Изначально Уатт использовал индикаторные единицы измерения (Imperial units) т.е. фунт и фут (pounds and feet) и следующий расчет – средняя лошадь способна поднять груз 550 фунтов на высоту 10 футов за 10 секунд.

Остальная Европа хотела определение на основе метрических единиц. Это почти, но не совсем, то же самое. Английская или индикаторная (imperial) лошадиная сила при преобразовании в метрическую, показывает на 1.5% более высокие числа. Метрическая л.с., используемая в большинстве европейских стран, определяется как 75 кгс·м/с, то есть как мощность, затрачиваемая при равномерном вертикальном поднимании груза массой в 75 кг со скоростью 1 метр в секунду при стандартном ускорении свободного падения (9,80665 м/с²).

На Втором Конгрессе Британской Научной ассоциации в 1882 году принимается уже новая единица измерения мощности — ватт (обозначение: Вт, W), названая в честь Джеймса Уатта (Ватта), создателя универсальной паровой машины. До этого же при большинстве расчётов использовались введённые Джеймсом Уаттом лошадиные силы.

Ватт – единица измерения мощности в Международной системе единиц (СИ).
1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль. Таким образом, ватт является производной единицей измерения и связан с другими единицами СИ следующими соотношениями:

Вт = Дж / с = кг·м²/с³
Вт = H·м/с

Или, если через лошадей, то поднятие груза 1000 Ньютонов (98.1 кг) на высоту 1 метр за 1 секунду. Единица измерения кВ (киловатт)

Мощность в киловаттах всегда и во всем мире будет одинакова, а вот лошадиные силы разные. Для перевода можно использовать следующие коэффициенты:

1 кВт = 1.34 л.с – английское обозначение HP. Используется в основном в Англии и США.
1 кВт = 1.36 л.с — Лошадиная сила (русское обозначение: л. с.; английское: hp; немецкое: PS; французское:CV) — внесистемная единица мощности. Используется в большинстве европейских стран и России.

1 HP Англо-американская л.с. равняется = 1.015 Русско-европейской л.с.

Также для пересчета англо-американского крутящего момента в международную систему СИ:

1 lb-ft = 1.36 Нм

КРУТЯЩИЙ МОМЕНТ

Крутящий момент (Torque) является хорошим индикатором способности двигателя выполнять работу. Момент силы имеет размерность “сила на расстояние” и имеет единицу измерения N-m или lbf-ft.
Совпадение размерностей этих величин — не случайность; момент силы 1 Н·м, приложенный через целый оборот, совершает механическую работу и сообщает энергию 2π джоулей

Т = 2πW

Где:
T = крутящий момент
Wb = эффективная работа за один оборот

Крутящий момент на самом деле то, что вы чувствуете во время вождения автомобиля. Давайте представим, что мы хотим растолкать автомобиль. Когда мы начинаем толкать авто, которое трудно сдвинуть с места, мы прилагаем усилие или крутящий момент, передающийся на колеса, даже если машина остается бездвижна. Только, когда мы сдвинем авто с места, будет произведена работа. Время, в течение которого мы толкаем, и определяет мощность, которую мы имеем.

Для демонстрации концепции, давайте представим, что у машины нет аэродинамического сопротивления, трения и т.д., и попросим 120 килограммового штангиста растолкать машину, начиная с 0 км/час, пока он не достигнет своей максимальной скорости (где-то 20 км/час). В этой точке он больше не будет прилагать усилие (момент), а просто будет бежать с машиной (не забывайте, что в нашем эксперименте нет сопротивления, потерь и т.д.). Скорее всего, он разовьет 20 км/час (свой максимум) через 50 метров. Если же мы попросим растолкать машину 90 килограммового Чемпиона мира в беге на 100 метров, то он скорее всего через 50 метров достигнет только 15 км/час, но будет продолжать разгонять (ускорять) машину. Когда он достигнет скорости 20 км/в час, то он будет продолжать ускорятся, прилагать момент для ускорения машины, скажем до 30 км в час. Для того, чтобы протолкать машину на 100 метров штангист и бегун затратят одинаковое количество времени, и точку 100 метров они достигнут в один момент времени. Это значит, что у штангиста и бегуна одинаковая мощность. Если же машину будет толкать здоровенный мужик с моментом и силой, как у штангиста, и скоростью, как у бегуна, то он будет продолжать ускоряться, толкая машину, и в точке 50 метров при достижении скорости 20 км/ч. И в итоге затратит меньше времени на 100 метров, так как его мощность больше, чем у штангиста и бегуна. Если все это перевести на язык машин, то штангист это Американский 5 литровый Шеви, бегун – Хонда интегра 1.8, а здоровенный мужик – Порше турбо.

Теперь мы понимаем, что мощность и крутящий момент величины, связанные между собой. В тематических автомобильных журналах и на интернет форумах чаще всего используют формулу, описывающую соотношение между крутящим моментом и мощностью. Кривая мощности и крутящего момента всегда будут пересекаться при частоте вращения коленчатого вала 5252 об/мин в английской (imperial) системе измерения и при 9549 об/мин при использовании kW” and “Nm” (международная система СИ).

ИЗМЕРЕНИЕ МОЩНОСТИ “Dynamometer”. Какая разница между мощностью с колес и на маховике?

Ключ к пониманию чего-нибудь заключается в определении основных слов объекта (предмета) “Dynamometer” – состоит из двух слов (dynamo) — это греческое слово обозначающее “power in motion” – мощность, сила в движении. Второе слово “meter” также имеет греческое происхождение – измерение. Или просто Дино – можно описать, как стенд (машина) для измерения мощности в движении.
Существует два типа Дино (стендов) – моторный стенд (engine dynamometers) и роликовый, барабанный, колесный стенд (chassis dynamometers). Для того, чтобы измерить мощность двигателя на моторном стенде, необходимо его снять с машины и установить на моторный стенд, подключив напрямую к маховику. Для этого используются специальные адаптеры, также необходимо подключить систему охлаждения и т.д. Данная процедура занимает много времени. Поэтому этот вид стендов в основном используют разработчики моторов.

Для тюнинга автомобилей такой вид стендов используется редко из-за сложности подключения, больших трудозатрат и т.д. Для целей доводки двигателей более эффективен колесный стенд по экономическим соображениям. Гораздо дешевле использовать колесный стенд, и вот о них мы сегодня и поговорим.
Колесный стенд – специально спроектирован для измерения мощности. Двигатель, генерирует мощность на маховике, которая в свою очередь передается в КПП через сцепление. КПП далее передает мощность через дифференциалы, привода, карданный вал на колеса. Все эти механизмы поглощают часть мощности и как результат, мощность, поставляемая к колесам – меньше, чем на маховике двигателя.
Мощность на колесах это то, что определяет характеристику, эффективность автомобиля.

Количество потерь варьируется от автомобиля к автомобилю, очень много зависит от типа трансмиссии, размера и давления в шинах, температуры КПП, подшипников и т.д и даже от того, как автомобиль пристегнут к стенду.

Колесные стенды делятся на несколько типов: инерционные, нагрузочные со своей классификацией. Большинство колесных стендов спроектированы на измерение мощности только с колес, но есть те, которые способны сделать замер мощности не только с колес, но и с маховика. Для этого, данный тип стендов производит замер не только мощности с колес, но и определяет потери, вот для этого и измеряют свободный выбег.

Выбег: Свободное движение системы вращающихся масс стенда и колеса (колес) с испытуемой шиной, затухающее под действием сил сопротивления их вращению.

Давайте взглянем на результаты замера на популярном автомобиле Skoda Octavia II с двигателем 1.8 TSI

Как я уже писал выше, на замер мощности с колес оказывает влияние множество факторов (размер колес, сход-развал, давление и тип шин, температура и вязкость масла в КПП, редукторах и т.д.), но эти погрешности в основном относятся к возникающим потерям, которые измеряются отдельно, после замера мощности с колес методом выбега.

На данном примере я покажу, как влияет замер мощности в зависимости от выбранной передачи. Первое условие – необходимо выбрать передачу, на которой происходит замер, как можно ближе к передаточному соотношению 1:1. В основном это предпоследняя передача в КПП. Скажем, на 5-ти ступенчатой КПП это будет 4-я передача. На испытуемой Шкоде установлена 7-ми ступенчатая КПП DSG. Для наглядности мы сделаем замер на 5-й и 6-й (жирные линии) передаче и наложим полученные графики замеров друг на друга.

Как мы видим максимальная мощность и крутящий момент, на маховике, в обоих случаях практически идентичен (207 л.с, 270 Нм). А вот потери (зеленные линии) сильно отличаются – 54.5 л.с на 6-ой передачи против 40.6 л.с. на 5-ой. Разница составила 14 л.с и соответственно мощность с колес отличается на такую же величину (147,5 л.с против 162 л.с с колес). Вывод – если вы решили сравнить данные замеров мощностных характеристик двух автомобилей, то, как минимум, (если не учитывать также значительные потери от размера колес и т.д.), необходимо знать на какой передаче был сделан замер (может там вообще на 3-й передаче).

Далее, точка максимальной мощности с колес и с маховика очень редко приходятся на одни и те же обороты двигателя. Если посмотреть на выше указанный график, то максимальная мощность с колес при замере на предпоследней передаче приходится на 4800 об/мин, а с маховика в обоих замерах на 5400 об/мин.

Объяснение этому очень простое. Как мы уже рассмотрели, мощность является соотношением крутящего момента умноженного на частоту вращения и поделенное на константу (в зависимости от системы измерения). Следовательно, после того, как кривая момента начинает падать, начинается и уменьшение прироста мощности, НО! возникающие потери продолжают только увеличиваться, соответственно мощность с колес не только будет иметь меньший прирост с увеличением оборотов двигателя, а также может начать падать (как в примере жирная синяя линия). Ситуация еще больше усугубляется на автомобилях 4х4, так как там значительно выше потери в сравнении с передним приводом рассматриваемым в данном примере.

Возникающие потери в основном зависят от скорости автомобиля (скорости вращения колес) – чем выше скорость, тем больше потери. Поэтому при замере на разных передачах, на одних и тех же частотах вращения двигателя будут различные потери и естественно различные значения мощности с колес.

Возможно, для одного поста много информации, которой хотелось поделиться. В дальнейшем, я расскажу о различных факторов, влияющих на точность замера, при работе на дино стендах, исходя из своего многолетнего опыта. И, конечно, раскрою многие секреты “читерства”на дино-стендах, не только сленгом все больше прорастая в российскую реальность после 15 летнего заграничного путешествия . Уже 3 месяца в России, продолжение следует…

С уважением
Barik

Маховик вращается по закону, выражаемому уравнением ?=A+Bt+Ct2, где A=2 рад, B=32 рад/с, С=—4 рад/с2. Найти среднюю мощность , развиваемую силами, действующими на маховик

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,415
• гуманитарные 33,633
• юридические 17,906
• школьный раздел 608,079
• разное 16,856

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Школе NET

Register

Do you already have an account? Login

Login

Don’t you have an account yet? Register

Newsletter

Submit to our newsletter to receive exclusive stories delivered to you inbox!

• Главная 
• Вопросы & Ответы 
• Вопрос 6592357

Главный Попко

Маховик вращается по закону, выражаемому уравнением ?=A+Bt+Ct2, где A=2 рад, B=32 рад/с, С=—4 рад/с2. Найти среднюю мощность , развиваемую силами, действующими на маховик Маховик вращается по закону, выражаемому уравнением ?=A+Bt+Ct2, где A=2 рад, B=32 рад/с, С=—4 рад/с2. Найти среднюю мощность , развиваемую силами, действующими на маховик при его вращении, до остановки, если его момент инерции J=100 кг*м2.

Маховик вращается по закону выражаемого уравнением чему равна мощность

Маховик вращается по закону, выражаемому уравнением ϕ = 5 + 6t–2t2?

Физика | 10 — 11 классы

Маховик вращается по закону, выражаемому уравнением ϕ = 5 + 6t–2t2.

Момент инерции маховика равен 50 кг⋅м2.

Найти закон, по которому меняется вращающий момент M = M(t).

угловое ускорение ε = φ'(t) = 6 — 4t

M(t) = J * ε = 50(6 — 4t) = 300 — 200t.

Определить тормозящий момент, которым можно остановить за 20 с маховое колесо массой 50 кг и радиусом 0, 30 м, вращающееся с частотой 20 об / с?

Определить тормозящий момент, которым можно остановить за 20 с маховое колесо массой 50 кг и радиусом 0, 30 м, вращающееся с частотой 20 об / с.

Массу маховика считать распределенной по ободу.

Чему равна работа, совершаемая тормозящим моментом?

Двигатель равномерно вращает маховик?

Двигатель равномерно вращает маховик.

После отключения двигателя маховик делает в течении 30 сек .

120 об и останавливается.

Момент инерции маховика 0.

3 кг / м2 Считая что угловое ускорение маховика после отключения двигателя постоянно, определить мощность двигателя при равномерном вращении маховика (Ответ : P = 25 вт).

Маховик равномерно вращается с угловой скоростью 628 рад / с?

Маховик равномерно вращается с угловой скоростью 628 рад / с.

Найти период вращения маховика?

Маховое колесо, имеющее момент инерции 245кг * м ^ 3, вращается, делая 20 об / с?

Маховое колесо, имеющее момент инерции 245кг * м ^ 3, вращается, делая 20 об / с.

Через минуту после того как на колесо перестал действовать вращающий момент, оно остановилось.

Найти : 1) момент сил трения, 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.

Маховик вращается с постоянным угловым ускорением 2 рад / с ^ 2?

Маховик вращается с постоянным угловым ускорением 2 рад / с ^ 2.

После начала движения полное ускорение маховика стало равно 0, 15м / с ^ 2.

Найти радиус кольца.

Маховик вращается по закону, выражаемому уравнением φ = A + Вt + Сt2, где A = 2 рад, В = 16 рад / с, С = — 2 рад / с2?

Маховик вращается по закону, выражаемому уравнением φ = A + Вt + Сt2, где A = 2 рад, В = 16 рад / с, С = — 2 рад / с2.

Момент инерции J маховика равен 50 кг * м2.

Найти законы, по которым меняются вращающий момент M и мощность N.

Чему равна мощность в момент времени t = 3 с?

Помните решить задачу?

Помните решить задачу.

Маховик, массу которого, равную 5 кг, можно считать распределенной по ободу радиусом 20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр, с угловой скоростью 720 об / мин.

При торможении маховик полностью останавливается через 20 с.

Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки.

Маховик, вращающийся угловой скоростью 8π с ^ — 1, делает 1000 оборотов за время?

Маховик, вращающийся угловой скоростью 8π с ^ — 1, делает 1000 оборотов за время.

Маховик А приводиться во вращение так, как показано на рис?

Маховик А приводиться во вращение так, как показано на рис.

Момент инерции маховика I, радиус r, масса груза равна m, коэффициент то между грузом и наклонной плоскостью u.

Найдите угловое ускорение!

Как найти момент инерции тела если оно вращается вокруг оси не проходящей через центр масс?

Как найти момент инерции тела если оно вращается вокруг оси не проходящей через центр масс.

На этой странице вы найдете ответ на вопрос Маховик вращается по закону, выражаемому уравнением ϕ = 5 + 6t–2t2?. Вопрос соответствует категории Физика и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

V = 300 м / с n = 3 * 10 ^ 20 м ^ — 3M = 32 * 10 ^ — 3 кг / моль p = ? P = n * k * T = (1 / 3) * n * mo * v² mo — масса молекулы кислородаmo = M / Na Na — число Авогадро Na = 6 * 10 ^ 23p = (1 / 3) * n * M * v² / Na = 3 * 10 ^ 20 * 32 * 10 ^ — 3 * 9..

Пройденный путь, это площадь трапеции на графике S = (10 + 20) * 4 / 2 = 60 м.

S = (vo + v) * t / 2 = (10 + 20) * 4 / 2 = 60 м = = = = = = = = = = = = = = = =.

1) Дано : U = 120B, f = 50 Гц, C = 74, 8 мкФ. Определяем : ω = 2πf = 2 * 50 * π = 100π 1 / c. Xc = 1 / (ωC) = 1 / (100π * 7, 48 * 10⁻⁵) = 1 / 0, 023499 4 = 42, 5548Ом. I = U / Xc = 120 / 42. 5548 = 2, 819894 А. Qc = I² * Xc = 2, 819894² * 42, 55..

10г = 0, 01кг Импульс пули до удара о стену р1 = mV1 Импульс пули после удара о стену р2 = mV2 Уменьшение импульса р1 — р2 = m(V1 — V2) = 0, 01 кг * (600м / с — 200м / с) = 0, 01 * 400 = 4 кг * м / с Это численно.

С — Цельсия? Тогда, кпд = (Tнагр. — Тхол. / Тнагр. ) * 100% = (700 — 280 / 700) * 100% = 60%.

Конечно же, это масса. Ответ 2.

Физическая величина — 2) масса.

К по­ло­жи­тель­но за­ря­жен­но­му элек­тро­мет­ру под­нес­ли от­ри­ца­тель­но за­ря­жен­ный пред­мет. По­ка­за­ние элек­тро­мет­раумень­шит­ся.

Маховик вращается по закону выражаемого уравнением чему равна мощность

Вопрос по физике:

Маховик вращается по закону, выражаемому уравнением φ=A+Вt+Сt2, где A=2 рад, В=16 рад/с, С=-2 рад/с2. Момент инерции J маховика равен 50 кг*м2. Найти законы, по которым меняются вращающий момент M и мощность N. Чему равна мощность в момент времени t=3 с? пСодробным объяснением пожалуйста.

Ответы и объяснения 1

Запишем уравнение вращательного движения, подставив исходные данные в виде:
φ = -2*t² + 16*t +2

Угловая скорость — первая производная от угла:
ω = φ’ = -4*t + 16

Угловое ускорение — первая производная от угловой скорости:
ε = ω’ = — 4

Запишем основное уравнение динамики вращательного движения:
M = J*ε
Тогда:
M = 50*(-4) = — 200 Н*м (момент отрицательный — «тормозящий»)

Мощность:
N = M*ω
В момент времени t=4 с:
ω(t) = -4*t+16
ω(4) = -4*4+16 =0

N= — 200*0 = 0 (Тело перестало вращаться)

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Физика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.

[spoiler title=”источники:”]

http://shkolenet.ru/QA/6592357/

http://usbravo.ru/makhovik-vrashchayetsya-po-zakonu-vyrazhayemogo-uravneniyem-chemu-ravna-moshchnost/

[/spoiler]

Маховик вращается по закону Ф= 2+4t+t^2. Момент инерции маховика J=100 кг*м^2 . Чему равны мощность, развиваемая моховиком, и его кинетическая энергия через t=5 секунд после начала вращения?

Уравнение вращательного движения в общем виде записывается так:

$phi(t)=phi_0+w_0t+frac{varepsilon t^2}{2}$         (1)

где  $phi(t),;phi_0,;w_0,;t,;varepsilon$     – соответственно угол поворота от оси отсчета в момент времени t, начальный угол поворота от этой оси, начальная угловая скорость, время, угловое ускорение.  

 Сравнив (1) с заданным в условии выражением, нетрудно сопоставить значения величин   начального угла поворота,  начальной угловой скорости и углового ускорения.

Кинетическая энергия тела, вращающегося относительно неподвижной оси можно определить по формуле: 

$E_k=frac{Jw^2}{2}$       (2) 

В формуле (2) нам надо подставить значение угловой скорости w в момент времени t=5 c.

Угловая скорость может быть выражена при равноускоренном круговом движении формулой:

$w=w_0+varepsilon t$           (3)   

Тогда (2) принимает вид:

$E_k=frac{J(w_0+varepsilon t)^2}{2}=frac{100*(4+1*5)^2}{2}=4050$ Дж

Мгновенная мощность при вращательном движении может быть выражена формулой:

$N=Jw(t)varepsilon(t)$


$N=J*(w_0+varepsilon t)*varepsilon(t)$


$N=100*(4+1*5)*1=900$  Вт