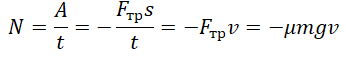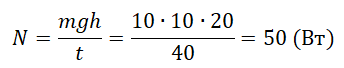Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 декабря 2020 года; проверки требуют 48 правок.
| Мощность | |
|---|---|
| P, N | |
| Размерность | L2MT−3 |
| Единицы измерения | |
| СИ | Вт |
| СГС | эрг·с−1 |
Мо́щность — скалярная физическая величина, характеризующая мгновенную скорость передачи энергии от одной физической системы к другой в процессе её (энергии) использования и в общем случае определяемая через соотношение переданной энергии к времени передачи. В системе СИ единицей измерения мощности является ватт, равный энергии в 1 джоуль, переданной за время в 1 секунду (1 Вт ≡ 1 Дж/с), а любое числовое значение мощности, указываемое в каких-либо информационных источниках, по умолчанию подразумевает именно такой секундный временной промежуток.[1][2]
Смысл понятия на примерах[править | править код]
Электрическая лампочка мощностью 100 Вт для своей работы по освещению ежесекундно расходует 100 Дж энергии, за 1 час – 0.1 кВт*ч (360000 Дж).
Электродвигатель заявленной мощностью 1 кВт для совершения работы способен ежесекундно передавать посредством вращения 1 кДж энергии, чего должно хватать для подъёма груза массой 100 кг на высоту 1 метр за 1 секунду. При этом электрическая мощность этого двигателя будет выше 1 кВт, так как КПД электродвигателя всегда ниже 100% и не вся электрическая мощность может быть преобразована в работу на валу.
Автомобильный двигатель внутреннего сгорания нетто-мощностью 100 кВт (136 л.с.) способен ежесекундно передавать автомобилю энергию в 100 кДж., что обычно позволяет современному легковому автомобилю разгоняться до скорости порядка 200 км/ч. При этом не имеют значения ни тип двигателя (бензиновый или дизельный), ни его рабочий объём, ни особенности его внешней скоростной характеристики.
Значение мощности в 6000 МВт у Красноярской ГЭС означает, что данная ГЭС способна ежесекундно вырабатывать энергию в 6000 МДж, что эквивалентно энергии, получаемой от работы 60 тысяч автомобильных двигателей, работающих на режиме максимальной мощности из примера выше и что без учёта потерь на передачу и трансформацию электроэнергии позволяет обеспечить электроэнергией 60 миллионов 100-ваттных электрических ламп.
Используемые обозначения[править | править код]
Актуальные международные стандарты серии ISO/IEC 80000 предписывают обозначать мощность символом P прописной буквой как для формул механики, так и для формул электродинамики.[3][4] Этимология обозначения — либо от лат. potestas, либо от англ. power.
В русскоязычной литературе по физике мощность в формулах механики и гидродинамики может обозначаться символом N, но этимология данного обозначения точно не ясна.
Основные формулы[править | править код]
Основное определение мощности:
(где P – мощность, E – энергия, t – время).
Определение среднего значения мощности за промежуток времени 
:
Интеграл по времени от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:
Единицы измерения[править | править код]
В Международной системе единиц (СИ) единицей измерения мощности является ватт (Вт), равный одному джоулю в секунду (Дж/с).[5]
В теоретической физике, астрофизике, в качестве единицы для мощности часто используют эрг в секунду (эрг/с), являющуюся внесистемной.
Распространённой единицей измерения мощности автомобильных, локомотивных и судовых ДВС является лошадиная сила. Однако в своих рекомендациях Международная организация законодательной метрологии (МОЗМ) относит лошадиную силу к числу единиц измерения, «которые должны быть изъяты из обращения как можно скорее там, где они используются в настоящее время, и которые не должны вводиться, если они не используются»[6].
| Единицы | Вт | кВт | МВт | кгс·м/с | эрг/с | л. с.(мет.) | л. с.(анг.) |
|---|---|---|---|---|---|---|---|
| 1 ватт | 1 | 10−3 | 10−6 | 0,102 | 107 | 1,36⋅10−3 | 1,34⋅10−3 |
| 1 киловатт | 103 | 1 | 10−3 | 102 | 1010 | 1,36 | 1,34 |
| 1 мегаватт | 106 | 103 | 1 | 102⋅103 | 1013 | 1,36⋅103 | 1,34⋅103 |
| 1 килограмм-сила-метр в секунду | 9,81 | 9,81⋅10−3 | 9,81⋅10−6 | 1 | 9,81⋅107 | 1,33⋅10−2 | 1,31⋅10−2 |
| 1 эрг в секунду | 10−7 | 10−10 | 10−13 | 1,02⋅10−8 | 1 | 1,36⋅10−10 | 1,34⋅10−10 |
| 1 лошадиная сила (метрическая) | 735,5 | 735,5⋅10−3 | 735,5⋅10−6 | 75 | 7,355⋅109 | 1 | 0,9863 |
| 1 лошадиная сила (английская) | 745,7 | 745,7⋅10−3 | 745,7⋅10−6 | 76,04 | 7,457⋅109 | 1,014 | 1 |
Мощность в механике[править | править код]
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
|
- где — вектор силы;
- — вектор скорости;
- — угол между вектором скорости и силы;
- — модуль вектора силы;
- — модуль вектора скорости.
Частный случай мощности при вращательном движении:
|
- где — момент силы (Н*м);
- — угловая скорость (рад/с);
- — частота вращения (число оборотов в минуту, об/мин).
Электрическая мощность[править | править код]
Электри́ческая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Мгновенная электрическая мощность 
участка электрической цепи:
- где — мгновенный ток через участок цепи;
- — мгновенное напряжение на этом участке.
При изучении сетей переменного тока, помимо мгновенной мощности, соответствующей общефизическому определению, вводятся также понятия:
- активной мощности, равной среднему за период значению мгновенной мощности,
- мгновенная активная мощность:
- реактивной мощности, которая соответствует энергии, циркулирующей без диссипации от источника к потребителю и обратно,
- мгновенная реактивная мощность:
-
- при
- при
- при
- полной мощности, вычисляемой как произведение действующих значений тока и напряжения без учёта сдвига фаз.
- мгновенная полная мощность:
- где — амплитуда тока;
- — амплитуда напряжения;
- — угол между начальным углом напряжения и начальным углом силы тока —
- — угловая скорость;
- — время.
Приборы для измерения электрической мощности и мощности излучения[править | править код]
Аналоговый стрелочный ваттметр
- Ваттметры (в том числе варметры) — измерительные приборы, предназначенные для определения мощности электрического тока или электромагнитного излучения.
По назначению и диапазону частот ваттметры можно разделить на три категории — низкочастотные (и постоянного тока), радиочастотные и оптические.
Ваттметры радиодиапазона по назначению делятся на два вида: проходящей мощности, включаемые в разрыв линии передачи, и поглощаемой мощности, подключаемые к концу линии в качестве согласованной нагрузки. В зависимости от способа функционального преобразования измерительной информации и её вывода оператору ваттметры бывают аналоговые (показывающие и самопишущие) и цифровые.
Гидравлическая мощность[править | править код]
Мощность гидромашины или гидроцилиндра равна произведению перепада давления на машине (разности давлений на входе и выходе) на расход жидкости:
- где — расход жидкости, м3/с;
- — перепад давления, Па.
К примеру, насос НП-89Д, стоящий на Су-24, Ту-134 и Ту-154, имеет производительность 55 л/мин (~0,000917 м3/с) при давлении 210 кгс/см2 (21 МПа)[7] — следовательно, его гидравлическая мощность составляет примерно 19,25 кВт.
См. также[править | править код]
- Удельная мощность
- Активная мощность
- Реактивная мощность
- Светимость
- Энергия
- Мощность взрывного устройства
- Мощность звука
- Усилитель мощности
Примечания[править | править код]
- ↑ Мощность — статья из Физической энциклопедии
- ↑ Физика . — С. 100. Глава 6 «Работа и энергия», § 3 «Мощность».
- ↑ ISO 80000-4:2019 «Quantities and units — Part 4: Mechanics» Item 4.27. Дата обращения: 2 апреля 2021. Архивировано 1 апреля 2021 года.
- ↑ Физика . — С. 100. Глава 6 «Работа и энергия», параграф 3 «Мощность».
- ↑ ГОСТ 8.417-2002 . — С. 5. П.5.2 «Производные единицы СИ», таблица 3 « Производные единицы СИ, имеющие специальные наименования и обозначения».
- ↑ Международный документ МОЗМ D2. Узаконенные (официально допущенные к применению) единицы измерений. Приложение В. Дата обращения: 5 апреля 2013. Архивировано из оригинала 14 октября 2013 года.
- ↑ НП-89Д. Описание. Технические характеристики. Агрегаты производства ОАО ММЗ Знамя. Дата обращения: 15 апреля 2018. Архивировано 15 апреля 2018 года.
Литература[править | править код]
- ГОСТ 8.417-2002. «Государственная система обеспечения единства измерений. Единицы величин». — Москва: Стандартинформ, 2002. — 39 с.
- Орир Дж. Физика, полный курс = Physics by Jay Orear, Cornell University / пер. с англ. и научная редактура Ю. Г. Рудого и А. В. Беркова. — 2-е. — Москва: «Издательство «КДУ», 2010. — С. 100-101. — 752 с. — ISBN 978-5-98227-366-6.
Ссылки[править | править код]
- Электрическая работа и мощность
- Влияние формы электрического тока на его действие. Журнал «Радио», номер 6, 1999 г. Архивная копия от 11 июня 2008 на Wayback Machine
- Гидравлическая мощность и КПД центробежных насосов
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).
Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.
Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.
Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.
Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения |
Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости |
Модуль силы упругости: Fупр = kx Работа силы упругости:
|
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:
Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.
Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.
A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:
Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела |
Работа при равномерном прямолинейном движении определяется формулой: A = Fтs Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:
|
Мощность при равномерном подъеме груза |
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:
|
Мгновенная мощность при неравномерном движении |
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:
|
Мощность силы трения при равномерном движении по горизонтали |
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:
|
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:
Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:
Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство |
Работа полезная и полная |
КПД |
| Неподвижный блок, рычаг |
Aполезн = mgh Асоверш. |
 |
| Наклонная плоскость |
Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
 |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
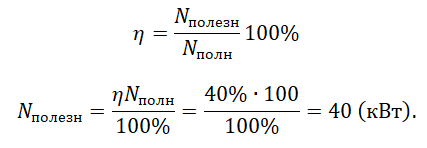
Задание EF17557
Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?
Ответ:
а) 916 Вт
б) 3300 Вт
в) 82500 Вт
г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17574
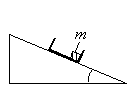С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
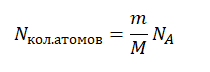
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
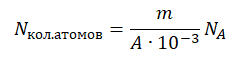
Энергия, выделенная всеми атомами, равна:
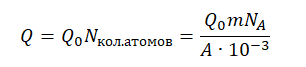
Теперь можем вычислить КПД:
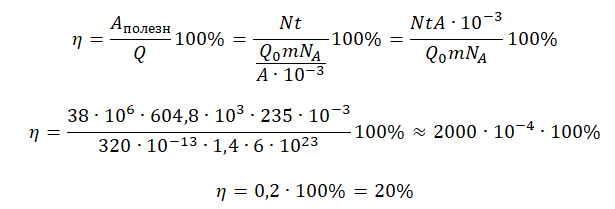
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 11.8k
Мощность
Для характеристики работоспособности и быстроты совершения работы введено понятие мощности.
Мощность — работа, выполненная в единицу времени:
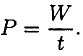
Единицы измерения мощности: ватты, киловатты,
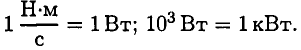
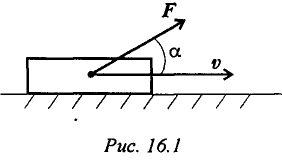
Мощность при поступательном движении (рис. 16.1)
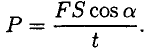
Учитывая, что
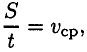
получим
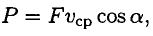
где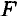 
— модуль силы, действующей на тело; 
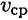— средняя скорость движения тела.
Средняя мощность при поступательном движении равна произведению модуля силы на среднюю скорость перемещения и на косинус угла между направлениями силы и скорости.
Мощность при вращении (рис. 16.2)
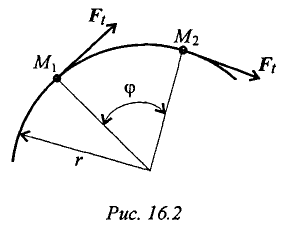
Тело движется по дуге радиус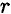 
из точки 
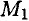в точку 
.
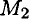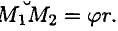
Работа силы:
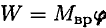
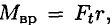
где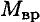 
— вращающий момент.
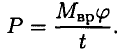
Учитывая, что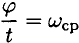 
, получим 
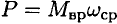, где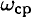 
— средняя угловая скорость.
Мощность силы при вращении равна произведению вращающего момента на среднюю угловую скорость.
Если при выполнении работы усилие машины и скорость движения меняются, можно определить мощность в любой момент времени, зная значения усилия и скорости в данный момент.
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Другими словами, работа – мера воздействия силы.
Определение механической работы
Работа А, совершаемая постоянной силой F→, – это физическая скалярная величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы F→ и перемещением s→.
Данное определение рассматривается на рисунке 1.
Формула работы записывается как,
A=Fs cos α.
Работа – это скалярная величина. Единица измерения работы по системе СИ – Джоуль (Дж).
Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.
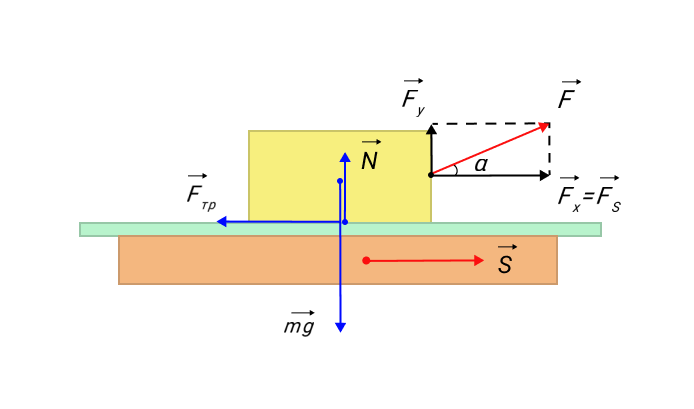
Рисунок 1. Работа силы F→: A=Fs cos α=Fss
При проекции Fs→ силы F→ на направление перемещения s→ сила не остается постоянной, а вычисление работы для малых перемещений Δsi суммируется и производится по формуле:
A=∑∆Ai=∑Fsi∆si.
Данная сумма работы вычисляется из предела (Δsi→0), после чего переходит в интеграл.
Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком Fs(x)рисунка 2.
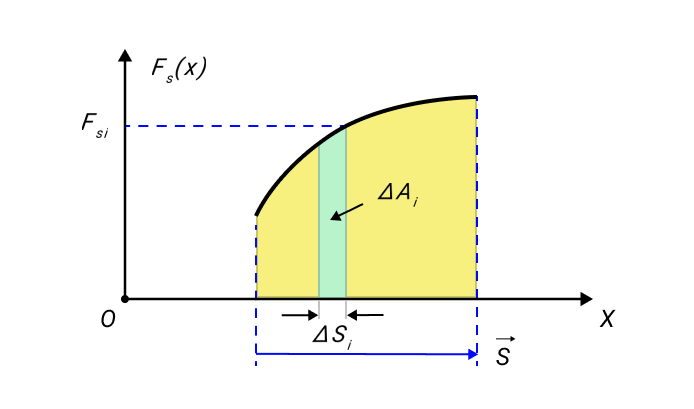
Рисунок 2. Графическое определение работы ΔAi=FsiΔsi.
Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F→, модуль которой пропорционален удлинению пружины. Это видно на рисунке 3.
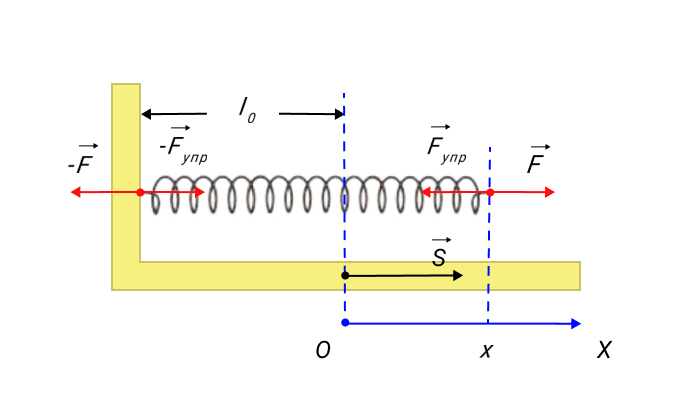
Рисунок 3. Растянутая пружина. Направление внешней силы F→ совпадает с направлением перемещения s→. Fs=kx, где k обозначает жесткость пружины.
F→упр=-F→
Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.
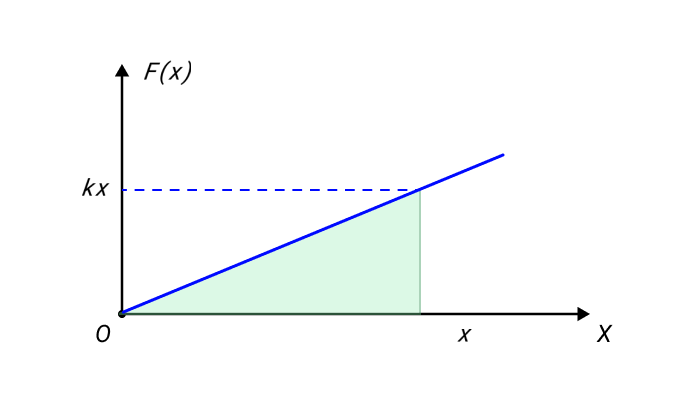
Рисунок 4. Зависимость модуля внешней силы от координаты при растяжении пружины.
Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид
A=kx22.
Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F→упр равняется работе внешней силы F→, но с противоположным знаком.
Если на тело действует несколько сил, то их общая работа равняется сумме всех работ, совершаемых над телом. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.
Мощность
Мощностью называют работу силы, совершаемую в единицу времени.
Запись физической величины мощности, обозначаемой N, принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:
N=At.
Система СИ использует в качестве единицы мощности ватт (Вт). 1 Ватт – это мощность, которую совершает работу в 1 Дж за время 1 с.
Помимо Ватта, существуют и внесистемные единицы измерения мощности. Например, 1 лошадиная сила примерна равна 745 Ваттам.
