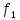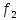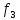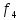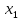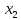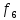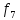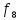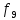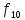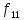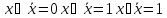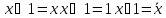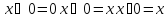Функции, определенные
на множестве E2={0,1}
и принимающее значение на множестве
называются булевыми функциями или
функция алгебры логики.
Функцию F
алгебры логики удобно задавать при
помощи таблицы, в которой аргументы
расположены в порядке возрастания, т.е.
будем считать что аргументы упорядочены
в алфавитном порядке, т.е. будем обозначать,
что аргумент(0,0,0,1) предшествует({)
аргументу (0,0,1,0), а аргумент
(0,0,1,0){(1,0,0,1).
Наборы
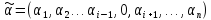 ,
,
 будем называть соседними поi-й
будем называть соседними поi-й
координате, а наборы
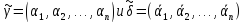 называются противоположными.
называются противоположными.
Символом
 будем обозначать количество наборов
будем обозначать количество наборов
переменных, при которых функция принимает
значение 1.
Свойства
булевой функции:
-
x◦y=y◦x
(коммутативность операций, где ◦
обозначает операции
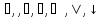
-
x◦(x◦y)=(x◦y)◦z
ассоциативность -
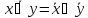
-
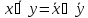 правило де
правило де
моргана -
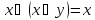 правило поглощения
правило поглощения -
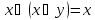 правило поглощения
правило поглощения -
Дистрибутивность
конъюнкции отн. Дизъюнкции. -
Дистрибутивность
конъюнкции отн. Суммы по модулю.
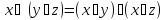
-
Дистрибутивность
дизъюнкции отн. Конъюнкции.
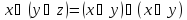
-
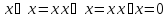
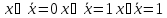
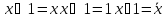
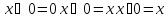
Совокупность всех
булевых функций относительно операций
логического умножения, сложения,
отрицания является алгеброй булевой
функций. Соотношение между булевой
алгеброй и алгеброй Кантора и есть
изоморфизм, т.к. любая алгебра обладающая
свойствами 1-10 называется булевой
алгеброй.
Функцию f,
определенную на множестве всех n-мерных
векторов
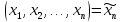 ,
,
где числа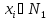 ,
,
будем называть булевой функцией отn
переменных и будем записывать в виде
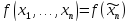 .
.
Мощность множества
всех булевых функций от n
переменных для фиксированного n-
это количество булевых функций от n
переменных. Мощность высчитывается по
формуле
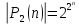
8. Элементарные булевы функции.
Будем
рассматривать следующие элементарные
функции:
-
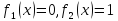 наз. Тождественный
наз. Тождественный
нуль и тождественная единица. -
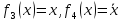 наз. Тождественная
наз. Тождественная
функция истинности и отрицание
 .
. -
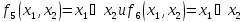 конъюнкция
конъюнкция
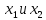 и дизъюнкция
и дизъюнкция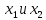 .
. -
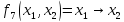 импликация
импликация
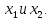
-
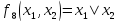 функция Шеффера
функция Шеффера
(отр. конъюнкция
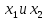 )).
)). -
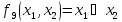 эквивалентности
эквивалентности
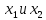 .
. -
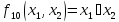 сумма по модулю
сумма по модулю
2 (отр. Эквивалентности
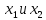 )
) -
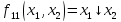 стрелка Пирса,
стрелка Пирса,
(отр. дизъюнкция
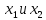 ).
).
Таблица
истинности для функции
с
одной переменной.
|
x |
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
Таблица истинности
для функций с 2 переменными
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
9. Формулы. Основные эквивалентности формул.
В каждой формуле
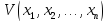
над полем Р сопоставляется функция
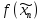 из Р2
из Р2
множество
всех возможных булевых функций.
Формулы V
и G
считаются эквивалентными, если
соответствующие им функции fu
= hg
равны.
Правила: 1.
Внешние скобки в формулах как правило
опускаются.
2.
Формула U G
G
записывается в виде U●G
или UG.
При
этом считают, что знак отрицания связывает
сильнее, чем логическое
 знак умножить связывает сильнее, чем
знак умножить связывает сильнее, чем
знак любой из операций или
А
знак = связывает слабее, чем вышеперечисление
операции в формуле.
Функции
f1
– f11
– Элементарные
функции подчиняются следующим
эквивалентности:
-
x◦y=y◦x
(коммутативность операций, где ◦
обозначает операции
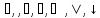
-
x◦(x◦y)=(x◦y)◦z
ассоциативность -
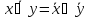
-
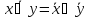 правило де
правило де
моргана -
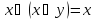 правило поглощения
правило поглощения -
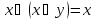 правило поглощения
правило поглощения -
Дистрибутивность
конъюнкции отн. Дизъюнкции. -
Дистрибутивность
конъюнкции отн. Суммы по модулю.
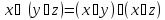
-
Дистрибутивность
дизъюнкции отн. Конъюнкции.
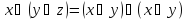
-
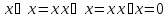
-
-
(дополнительные
не из наших лекций)Выражение эквивалентности
через другие операции:
x~y
=
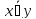 =x⊕y⊕1
=x⊕y⊕1
x~y
=
(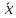 ∨y)&(x∨
∨y)&(x∨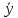 )
)
= x&y
∨
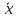 &
&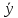
-
Выражение
⊕
через другие операции:
x
⊕
y =
(x&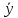 )∨
)∨
(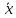 &y)
&y)
= (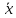 ∨
∨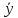 )
)
& (x
∨
y)
-
Выражение
импликации через другие операции:
x→y
=
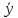 →
→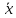 x→y=
x→y=
xy⊕x⊕1
x→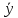 =
=
y→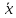
x→y
=
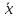 ∨y
∨y
x→y=
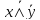
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Остался вопрос про аксиому выбора…
Если я правильно понял, проблема касается не только бесконечных, но и конечных множеств. А именно – множество рассматривается как некий мешок с элементами, а как они там лежат – мы не знаем.
Договоримся о том, что элементы одного множества все-таки чем-либо отличаются между собой. Например, если рассматриваем множество светловолосых людей, то разные люди из этого множества будут отличаться отпечатками пальцев. В противном случае мы получим множество тождественных элементов – типа {2 2 2 2}, и нам будет все равно, какой из элементов будет выбран в качестве представителя.
Пусть есть некий Оракул, который умеет производить стандартные операции с множествами. Например, если мы ему дадим два множества и скажем “Объедини” – он выдаст нам один мешок с объединенным множеством. В том числе Оракул может по команде “Подмножество” собрать и отдать нам подмножество элементов, удовлетворяющих некоторому точно заданному критерию, – например выделить из множества светловолосых людей с голубыми глазами.
Пусть мы имеем множество  , элементами которого являются множества мощности
, элементами которого являются множества мощности  . Тогда мы можем взять числовую прямую
. Тогда мы можем взять числовую прямую  и для каждого элемента
и для каждого элемента  дать Оракулу следующие команды:
дать Оракулу следующие команды:
1) “Декартово произведение”: 
2) “Множество всех подмножеств”: 
3) “Подмножество”: 
4) “Подмножество”: 
5) “Прообраз”: 
Объединение всех  и даст искомое множество представителей, поскольку
и даст искомое множество представителей, поскольку  , так?
, так?
Какая тогда из команд Оракула неверна в отсутствие аксиомы выбора?
Добавлено спустя 32 минуты 21 секунду:
А, Оракул, пожалуй, не сможет найти  …
… ![]()
This answer is based on, but differs slightly from, user Asaf Karaglia’s above.
First, observe that by definition, ${text{all real functions of real variable}}:= {f: ; f: mathbb{R}tomathbb{R}} := mathbb{R}^mathbb{R}$.
The question is about $|{text{all real functions of real variable}}|$, so examine an arbitrary real function of real variable: $f,colon,mathbb{R}tomathbb{R}.$
By inspection, $f,colon,mathbb{R}tomathbb{R} := {(r, f(r)) : r in mathbb{R}} quad subseteq quad P(mathbb{R} times mathbb{R})$.
Thus, $color{green}{|mathbb{R}^{mathbb{R}}| le |P(mathbb{R}timesmathbb{R})|}$.
Before continuing, let’s try to simplify $|P(mathbb{R}timesmathbb{R})|$. Observe that $|mathbb{R}| = |mathbb{R}^k| , forall , k in mathbb{N}$. Its proof by mathematical induction requires the induction hypothesis of $|mathbb{R}| = |mathbb{R}^2|$, one proof of which is : $|mathbb{N}| = |mathbb{N}timesmathbb{N}| implies |mathbb{R}| = |2^{mathbb{N}}| = |2^{mathbb{N}timesmathbb{N}}| = |2^mathbb{N}times 2^mathbb{N}| = |mathbb{R}timesmathbb{R}|$.
Verily, $mathbb{R} neq mathbb{R}^2$. Howbeit, for infinite sets $A,B$: $|A| = |B| Longrightarrow require{cancel} cancel{Longleftarrow} |P(A)| = |P(B)|$.
(The converse is discussed here.)
Thus, $|P(mathbb{R})| = |P(mathbb{R}timesmathbb{R})| implies color{green}{|mathbb{R}^mathbb{R}| le |P(mathbb{R}timesmathbb{R})|} = |P(mathbb{R})|$. Now scrutinise $|P(mathbb{R})|$:
● $color{#A9057D}{|P(mathbb{R})| = |2^{mathbb{R}}|}$, where $2^{mathbb{R}} := {f : ; f: mathbb{R} to {0,1}}$,
● Every $f: mathbb{R} to {0,1}$ is a particular case of a function from $mathbb{R}$ to $mathbb{R}$, thus $color{#EC5021}{2^{mathbb{R}} subsetneq mathbb{R}^mathbb{R}}$.
Altogether, $color{#A9057D}{|P(mathbb{R})| =} color{#EC5021}{|2^mathbb{R}| le} color{green}{|mathbb{R}^mathbb{R}| le |P(mathbb{R}timesmathbb{R})|} = |P(mathbb{R})|$
$implies |P(mathbb{R})| qquad qquad quad leq |mathbb{R}^mathbb{R}| leq |P(mathbb{R})| implies color{#A9057D}{underbrace{|P(mathbb{R})|}_{= |2^mathbb{R}|}} = |mathbb{R}^mathbb{R}| $.
Мо́щность, или кардина́льное число́, мно́жества (лат. cardinalis ← cardo «главное обстоятельство; основа; сердце») — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.
В основе этого понятия лежат естественные представления о сравнении множеств:
- любые два множества, между элементами которых может быть установлено взаимно-однозначное соответствие (биекция), содержат одинаковое количество элементов (имеют одинаковую мощность, равномощны);
- обратно: равномощные множества должны допускать такое взаимно-однозначное соответствие;
- часть множества не превосходит полного множества по мощности (то есть по количеству элементов).
До того, когда была построена теория мощности множеств, множества различались по признакам: пустое/непустое и конечное/бесконечное, также конечные множества различались по количеству элементов. Бесконечные же множества нельзя было сравнить.
Мощность множеств позволяет сравнивать бесконечные множества.
Например, счётные множества являются самыми «маленькими» бесконечными множествами.
Мощность множества 

Иногда встречаются обозначения 


Определение[править | править код]
Если принять аксиому выбора, мощность множества формально будет определяться как наименьшее порядковое число 


Если не принимать аксиому выбора, то требуется иной подход. Самое первое определение мощности множества 
![[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fadb3aef0836cb1d004479f470703a45972bf8fe)



![[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fadb3aef0836cb1d004479f470703a45972bf8fe)


![[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fadb3aef0836cb1d004479f470703a45972bf8fe)
![[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fadb3aef0836cb1d004479f470703a45972bf8fe)
Формальный порядок среди кардинальных чисел вводится следующим образом: 









Множество 












Связанные определения[править | править код]
- Для мощностей, как и в случае конечных множеств, имеются понятия: «равенство», «больше», «меньше». То есть для любых множеств
и
возможно только одно из трёх:
, или
и
равномощны;
, или
мощнее
, то есть
содержит подмножество, равномощное
, но
и
не равномощны;
, или
мощнее
— в этом случае
содержит подмножество, равномощное
, но
и
не равномощны.
- Множества
и
называются эквивалентными, если существует взаимно однозначное отображение множества
на множество
.[1]
Примеры[править | править код]
- Множество называется счётным, если оно равномощно множеству всех натуральных чисел
. Счётными множествами являются:
- Бесконечные множества, неравномощные множеству
, называются несчётными. По теореме Кантора несчётным является множество всех возможных бесконечных последовательностей, составленных из цифр 0 и 1. Мощность этого множества называется континуум.
- Мощность множества вещественных чисел
равна континууму.
Свойства[править | править код]
Арифметика кардинальных чисел[править | править код]
Обычные арифметические операции над числами натурального ряда можно обобщить на случай кардинальных чисел. Можно также показать, что в случае конечных кардинальных чисел эти операции совпадают с соответствующим арифметическими действиями над числами. Помимо этого, операции над кардинальными числами сохраняют многие свойства обычных арифметических операций.
Следующее по порядку кардинальное число[править | править код]
Если принять аксиому выбора, то для каждого кардинального числа 



Если 

В случае бесконечных 
Через 


Сложение кардинальных чисел[править | править код]
Если множества 





Нейтральность нуля относительно сложения:
Ассоциативность:
Коммутативность:
Монотонность (неубывание) сложения по обоим аргументам:
Если аксиому выбора принять верной, то сумму двух бесконечных кардинальных чисел можно легко вычислить.
Если одно из чисел 

Вычитание[править | править код]
При соблюдении аксиомы выбора для любого бесконечного кардинального числа 







Умножение кардинальных чисел[править | править код]
Произведение двух кардинальных чисел выражается через декартово произведение множеств:

Свойства нуля:
Нейтральность единицы относительно умножения:
Ассоциативность:
Коммутативность:
Монотонность (неубывание) умножения по обоим аргументам:
Дистрибутивность умножения относительно сложения:
По аналогии со сложением, произведение двух бесконечных кардинальных чисел можно легко вычислить при соблюдении аксиомы выбора. Если числа 

Деление[править | править код]
При соблюдении аксиомы выбора для любой пары кардинальных чисел 









Возведение кардинальных чисел в степень[править | править код]
Возведение в степень определяется следующим образом:
,
где 


(в частности,
), см. «Пустая функция»
Монотонность:
Заметим, что 





Все последующие утверждения, приведённые в этом разделе, опираются на аксиому выбора.
Если 


Если кардинальное число 


Если 

.
Используя теорему Кёнига, можно доказать, что для любого бесконечного кардинального числа 
,
где 

Извлечение корней[править | править код]
Если соблюдать аксиому выбора, то для любого бесконечного кардинала 




Логарифмы[править | править код]
При соблюдении аксиомы выбора кардинальное число 







Логарифмом бесконечного кардинального числа 


Континуум-гипотеза[править | править код]
Согласно континуум-гипотезе, между 







См. также[править | править код]
- Порядковое число
Примечания[править | править код]
- ↑ Мельников О. В., Ремеслеников В. Н., Романьков В. А. Общая алгебра. Том 1. — М., Наука, 1990. — с. 31
- ↑ Мельников О. В., Ремеслеников В. Н., Романьков В. А. Общая алгебра. Том 1. — М., Наука, 1990. — с. 32
Литература[править | править код]
- А. А. Болибрух, Проблемы Гильберта (100 лет спустя), Глава 2 Первая проблема Гильберта: континуум-гипотеза Архивная копия от 3 июня 2004 на Wayback Machine, Библиотека «Математическое просвещение», Выпуск 2
- Р. Курант, Г. Роббинс, Что такое математика? Глава II, § 4.
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 109-110. — 383 с. — ISBN 5-09-001287-3.
- Брудно А. Л. Теория функций действительного переменного. — М.: Наука, 1971. — 119 с.
Множество всех функций из $%mathbb R$% в $%mathbb R$% имеет мощность больше континуума, поэтому для отдельных классов функций представляет интерес доказательство того, что их континуум. Скажем, для непрерывных функций это так, потому что они однозначно определяются значениями в рациональных точках. А множество отображений счётного множества в $%mathbb R$% континуально: $%mathbb R^{mathbb N}sim(2^{mathbb N})^{mathbb N}sim2^{mathbb Ntimesmathbb N}sim2^{mathbb N}simmathbb R$%.
Ясно, что функций не меньше континуума, и тогда с учётом теоремы Кантора – Бернштейна достаточно доказывать, что их не больше континуума.
С монотонными функциями дело обстоит чуть сложнее, потому что они значениями в рациональных точках в общем случае не определяются. Рассмотрим функцию $%f(x)=0$% при $%x < sqrt2$%, $%f(x)=1$% при $%x > sqrt2$%, и тогда для $%f(sqrt2)$% годится любое значение из отрезка $%[0;1]$%.
Тем не менее, значения в рациональных точках однозначно определяют значения в точках непрерывности. Если $%x_0$% — точка разрыва, то рассмотрим два числа: $%a=suplimits_{x < x_0}f(x)$% и $%b=inflimits_{x > x_0}f(x)$%. При этом $%a < b$%, и возникает интервал $%(a,b)$%, из которого функция не принимает значений. Для каждой точки разрыва, такой интервал свой в силу монотонности, и разные интервалы не пересекаются. Их множество не более чем счётно ввиду наличия в каждом интервале своей рациональной точки. Тем самым, множество точек разрыва не более чем счётно.
Заметим, что множество (не более чем) счётных подмножеств континуума имеет мощность континуума. Это доказывается стандартно: берём интервал $%(0;1)$%, и элементы счётного подмножества записываем в виде строк как двоичные дроби. Получается матрица, элементы которой нумеруем некоторым способом. Это даёт новое число, которое хранит информацию о всех элементах подмножества: зная это число, можно восстановить матрицу.
Теперь заметим, что монотонная функция однозначно определяется такими данными: 1) значения в рациональных точках; 2) множество точек разрыва; 3) значения в точках разрыва. Получается, что функций не больше, чем элементов $%mathbb R^3$%, то есть не больше континуума. Это завершает доказательство.