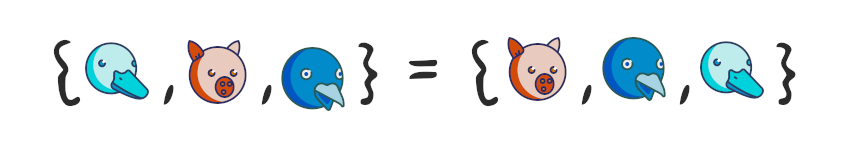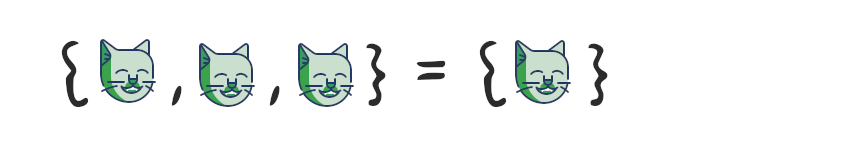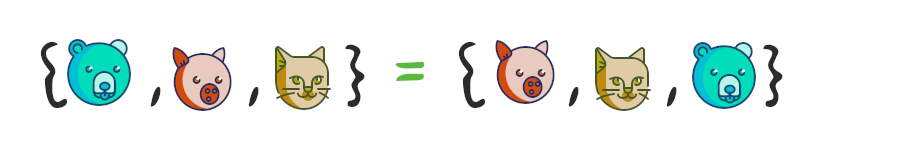Информатика, 10 класс. Урок № 10.
Тема — Некоторые сведения из теории множеств
Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором, создателем теории множеств.

Георг Кантор
(1845—1918)
Немецкий математик, создатель теории множеств
Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое. Под множеством мы можем понимать: учеников класса, фрукты, деревянные предметы, числа и т. д.
Например:
|
|
Множество учеников класса |
|
|
Множество деревянных предметов |
|
|
Множество чисел |
|
|
Множество фруктов |
Множества принято обозначать прописными буквами латинского алфавита (A,B,C,D и т. д.).
Множество можно задать перечислением всех его элементов, заключенных в фигурные скобки:
|
|
|
|
A={Маша, Ваня, Петя….} |
B={Банан, яблоко, виноград….} |
|
|
|
|
C={миска, подставка под карандаши, разделочная доска….} |
D={1,2,3,4,5….} |
Из некоторых элементов одного множества можно составить новое. Тогда такое множество Е принято называть подмножеством D:
D={1,2,3,4,5,6,7,8…}
E={2,4,6,8…}
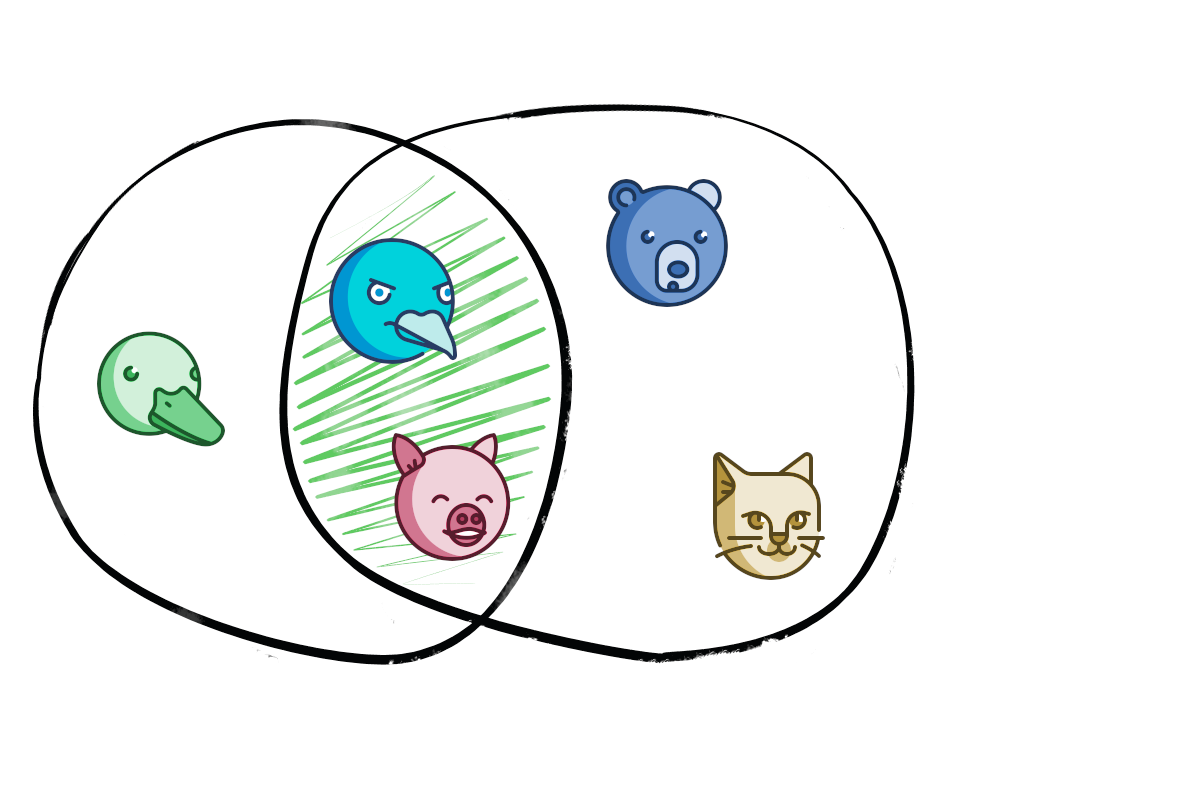
Для наглядности множества можно изображать в виде окружности, так называемых кругов Эйлера, где элементы, входящие в множество, изображают внутри круга, а остальные вне:
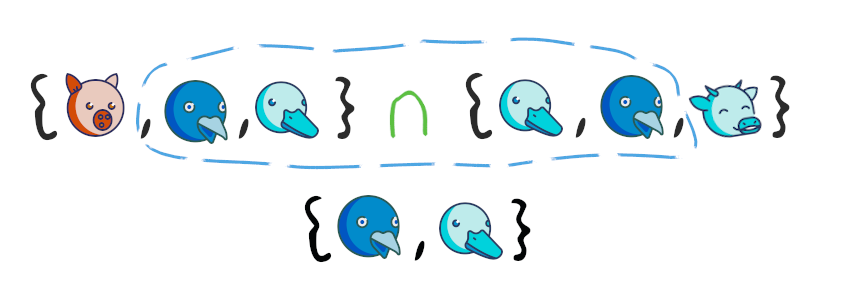
Пересечением множеств называется множество их общих элементов.
Например:
Пусть множество A будет состоять из элементов 1,3,6,9,12,15, а множество B из элементов 2,4,6,8,10,12. Тогда в пересечение этих множеств будет входить 2,6,12:
A={1,3,6,9,12,15}
B={2,4,6,8,10,12}
A⋂B={2,6,12}
Множество может не содержать элементы, тогда оно будет называться пустым.
Если множества не имеют общих элементов, то их пересечение — пустое множество:
С⋂D=ø
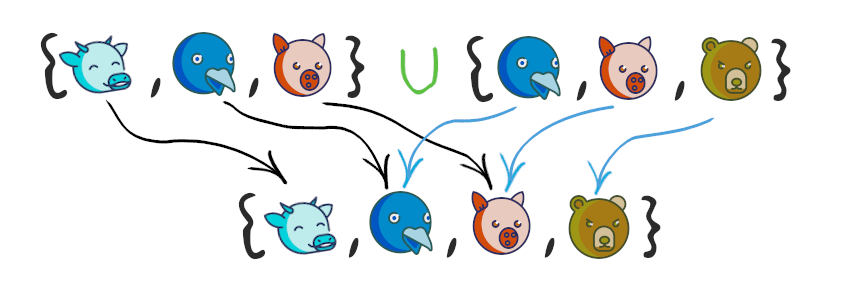
Объединением двух множеств называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов:
A={1,3,6,9}
B={2,4,6,8}
A⋃B={1,2,3,4,6,8,9}
Разностью множеств А и В называется множество элементов, принадлежащих множеству А, которые не принадлежат множеству В:
A={1,3,6,9}
B={2,4,6,8}
AB={1,3,9}
Если множество А является подмножеством B, то дополнением называется разность множества А и В:
A={2,4,6}
B={1,2,3,4,5,6}
Мощностью множества называется число его элементов: A={1,2,3,4,5,6}
|A|=5
Таким образом, мощность непересекающихся множеств будет являться суммой мощностей каждого множества:
A={1,3,5,7}
B={2,4,6,8}
|A⋃B|=8
Для вычисления мощности пересекающихся множеств можно использовать принцип включений и исключений:
|A⋃B|= |A|+|B|–| A⋂B|
A={1,2,3,4,5,6}
B={2,4,6,8}
|A⋃B|=6+4–3=7
Для вычисления мощности пересечения трех множеств принцип включений и исключений выглядит так:
|A⋃B⋃С|= |A|+|B|+|C|–|A⋂B|–|A⋂C|-|B⋂C|+|A⋂B⋂C|
Задание №1.
В классе 17 пловцов, 8 борцов и 13 футболистов. Известно, что в классе 25 детей, а ребят занимающихся футболом и плаваньем — 10, борьбой и плаваньем — 3, борьбой и футболом — 2 и только один ребенок занимается всеми тремя видами спорта. Сколько детей в классе не занимаются спортом?
Дано:
|A|=17, |B|=8, |C|=13
|A⋂B|=3, |A⋂C|=10, |B⋂C|=2
|A⋂B⋂C|=1
по формуле включения:
|A⋃B⋃С|= |A|+|B|+|C|–|A⋂B|–|A⋂C|–|B⋂C|+|A⋂B⋂C|=17+8+13–3–10–2+1=24
Таким образом, в классе 24 ребенка занимаются хотя бы одним видом спорта, ответ 1
Задание №2.
- Множество общих элементов двух множеств
- Совокупность объектов произвольной природы, которая рассматривается как единое целое
- Число элементов множества
- Множество элементов, не входящих в подмножество
- Множество, состоящее из всех элементов двух (или более) множеств и не содержащее никаких других элементов
Проверьте свои ответы:
- Пересечение
- Множество
- Мощность
- Дополнение
- Объединение
Задание №3
Закрасьте область цветом:
- Зеленым — R(PQ)
- Красным — (P⋂R)Q
- Желтым — (P∪Q)R
Ваше решение должно быть таким:
Всем привет! Я Елена, и на канале TeachYOU мы разбираем задачи из экзаменов по информатике. Обычно я пишу статьи с разбором задач из ЕГЭ, но этот материал пригодится и 9му классу, и 11му. Если вы готовитесь к ЕГЭ и считаете, что эта тема вам не нужна, то советую заглянуть в задания 279 (прототип 24), 5627 (прототип 9) и 2557 (прототип 8) с kompege. Они намного проще решаются, когда обладаешь навыком решения задач на круги Эйлера.
Множества
Чтобы начать говорить о кругах Эйлера, нужно ввести понятие множества. Множество – это набор объектов, объединенных каким-то признаком. Например, множество квадратных объектов, множество предметов, изучаемых в 9 классе и пр.
Рассмотрим множество объектов оранжевого цвета. В него входят рыжий кот, спасательный жилет, апельсин, осенний кленовый лист, и много других объектов оранжевого цвета. На рисунке изобразим круг и будем предполагать, что все оранжевые предметы находятся внутри него:
Теперь возьмем множество животных кошачьего семейства. Здесь будут домашние кошки, тигры, львы, гепарды и остальные представители данного семейства.
Пересечение множеств
Заметим, что рыжий кот входит в оба множества. Поэтому, если мы изобразим эти множества рядом, должны будем расположить их следующим образом:
Область, в которой сидит рыжий кот, называется пересечением множеств. Множества принято обозначать заглавными латинскими буквами: A, B, C, … Пересечение обозначают символом & : A & B, читается как “пересечение множеств A и B“.
В общем случае произвольные два множества располагаются именно так: есть элементы, входящие в оба множества (то есть пересечение множеств непустое), а есть элементы, которые не входят только в одно из множеств.
Объединение
В гости к Пете едет его любимая бабушка. Она поинтересовалась у внука, что можно купить ему в подарок. Он сказал, что любит книжки и машины. В магазине бабушка увидела разные игрушки, и в блокноте изобразила круги Эйлера – один с множеством машин, второй – с множеством книжек. В пересечение этих кругов попала книга о машинах. Вне кругов расположились шарик, вертолет, матрешка и медвежонок – они не входят в множество предполагаемых подарков для Пети:
Область, похожая на перевернутую восьмерку, иллюстрирует множество машинок и книжек – подходящих подарков. Такое множество называется объединением. В него входят все элементы изначальных множеств, причем те, которые находятся на пересечении, входят только один раз:
Мощность множеств
Мощность множества – это количество элементов в нем. Обозначается так: |A|. Мощность множества может быть равна нулю (пустое множество), конечному числу (мощность множества десятичных цифр равна 10) или равна бесконечности (мощность множества натуральных чисел).
Частные случаи расположения элементов двух множеств
Случай 1. Равенство
Рассмотрим картинку с изображениями людей.
Выберем из них два множества:
- А – люди с длинными волосами
- В – женщины
Получилось, что в оба множества входят одни и те же элементы. В этом случае говорят о равенстве множеств:
- A = B – множество А равно множеству В
- A & B = A (= B) – пересечение множеств совпадает с множеством А (или В)
- А | В = А (=В) – объединение множеств равно множеству А (или В)
Что в этом случае происходит с мощностями множеств?
- |A | B| = |A & B| = |A| = |B|
Случай 2. Включение
Все элементы одного множества могут входить в другое множество – тогда говорят о включении одного множества в другое (A ⊂ B). Пусть А – множество домашних кошек. Оно включено в B – множество представителей семейства кошачьих (также можно сказать “множество домашних кошек является подмножеством множества представителей семейства кошачьих”).
Заметим, что пересечение множеств в этом случае совпадает с множеством домашних кошек, а объединение – с множеством представителей семейства кошачьих:
- A ⊂ B (А включено в В, А является подмножеством В)
- A & B = A (пересечение множеств совпадает с множеством А)
- A | B = B (объединение множеств равно множеству В)
Для мощностей множеств можно сформулировать следующие утверждения:
- |A| < |B|
- |A & B| = |A|
- |A | B| = |B|
Случай 3. Непересечение
Бывает, что у множеств нет общих элементов. Про такие множества говорят, что они не пересекаются или что их пересечение равно пустому множеству (A & B = ∅). Давайте изобразим множества представителей кошачьих и собачьих (сложно придумать животного, которое будет одновременно кошкой и собакой):
- A & B = ∅ – множества не пересекаются (пересечение множеств равно пустому множеству)
О мощностях:
- |A & B| = 0
- |A | B| = |A| + |B|
Формула включения/исключения для двух областей
Вернемся к примеру с бабушкой и Петей. Пусть бабушка хочет посчитать, сколько вариантов выбрать один подарок у нее есть. Она знает мощность множества А – подарков на “машинную” тематику, мощность множества книг В и мощность их пересечения A&B.
То, что хочет найти бабушка, называется мощностью объединения множеств A | B. Логично предположить, что для его поиска нужно сложить мощности множеств A и B: 4 “машинковых” подарка + 3 книги = 7 подарков. Но на картинке видно, что всего подарков 6! Дело в том, что при суммировании мощностей множеств A и B элемент, находящийся на их пересечении, мы посчитали два раза. Тогда его нужно один раз отнять. Итого формула нахождения мощности множества объединения двух множеств такова:
|A | B| = |A| + |B| – |A & B|
Ее называют формулой включения – исключения.
Задание 8 ОГЭ по информатике
Наконец мы добрались до заданий из ОГЭ. Оговорюсь, что знание теории, описанной выше, поможет решить не все задачи – в сборниках встречаются задания на три множества. Подобные мы разберем в другой раз.
Задание 1369 с сайта К.Ю. Полякова
Задание: Ниже приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
шахматы | теннис 7770
теннис 5500
шахматы & теннис 1000
Сколько страниц будет найдено по запросу
шахматы?
Решение: обозначим множество страниц, которое находится по запросу шахматы как Ш, а по запросу теннис как Т. Тогда формула включения-исключения примет вид:
|Ш | Т| = |Ш| + |Т| – |Ш & Т|
Подставим в нее известные величины:
7770 = |Ш| + 5500 – 1000
И выразим неизвестную:
|Ш| = 7770 – 5500 + 1000 = 3270
Ответ: 3270
Задание 1365 с сайта К.Ю. Полякова
Задание: Ниже приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
лебедь & (рак | щука) 320
лебедь & рак 200
лебедь & рак & щука 50
Сколько страниц будет найдено по запросу
лебедь & щука?
Решение: может показаться, что эта задача на три множества и силами теории, описанной в этой статье, ее не решить. Но давайте заметим, что во всех строках условия встречается “лебедь &”. Предлагаю на данном этапе не углубляться в теорию множеств, а довериться мне и сократить на лебедя:
лебедь & (рак | щука) 320лебедь & рак 200лебедь & рак & щука 50
Сколько страниц будет найдено по запросу
лебедь & щука?
Теперь это задача на два множества (я их фамильярно называю задачами на два кружочка). Выписываем формулу:
|Р | Щ| = |Р| + |Щ| – |Р & Щ|
Подставляем известные величины, выражаем неизвестную:
|Щ| = 320 + 50 – 200 = 170.
Ответ: 170
Домашнее задание
Сайт К.Ю. Полякова, номера 1368, 1357, 1351, 1364, 1362.
Что с тремя множествами?
Я буду писать статью о трех множествах, где расскажу и об общем случае их пересечения, и о частном под кодовым названием “микки-маус” (или “гусеничка”). Если вам важно, чтобы этот материал вышел поскорее, напишите об этом в комментариях или поставьте лайк – тогда я узнаю, что вы его ждете.
Успехов вам с подготовкой от меня и канала TeachYOU 🙂
Время на прочтение
11 мин
Количество просмотров 93K
Python и теория множеств
В Python есть очень полезный тип данных для работы с множествами – это set. Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.
Следует сразу сделать оговорку, что эта статья ни в коем случае не претендует на какую-либо математическую строгость и полноту, скорее это попытка доступно продемонстрировать примеры использования множеств в языке программирования Python.
- Множество
- Множества в Python
- Хешируемые объекты
- Свойства множеств
- Принадлежность множеству
- Мощность множества
- Перебор элементов множества
- Отношения между множествами
- Равные множества
- Непересекающиеся множества
- Подмножество и надмножество
- Операции над множествами
- Объединение множеств
- Добавление элементов в множество
- Пересечение множеств
- Разность множеств
- Удаление элементов из множества
- Симметрическая разность множеств
- Заключение
- Полезные ссылки
Множество
Множество – это математический объект, являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества. Или другими словами:
Множество – это не более чем неупорядоченная коллекция уникальных элементов.
Что значит неупорядоченная? Это значит, что два множества эквивалентны, если содержат одинаковые элементы.
Элементы множества должны быть уникальными, множество не может содержать одинаковых элементов. Добавление элементов, которые уже есть в множестве, не изменяет это множество.
Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества – бесконечными. Конечное множество, как следует из названия, можно задать перечислением его элементов. Так как темой этой статьи является практическое использование множеств в Python, то я предлагаю сосредоточиться на конечных множествах.
Множества в Python
Множество в Python можно создать несколькими способами. Самый простой – это задать множество перечислением его элементов в фигурных скобках:
fruits = {"banana", "apple", "orange"}Единственное ограничение, что таким образом нельзя создать пустое множество. Вместо этого будет создан пустой словарь:
wrong_empty_set = {}
print(type(wrong_empty_set))
# Вывод
<class "dict">Для создания пустого множества нужно непосредственно использовать set():
correct_empty_set = set()
print(type(correct_empty_set))
# Вывод
<class "set">Также в set() можно передать какой-либо объект, по которому можно проитерироваться (Iterable):
color_list = ["red", "green", "green", "blue", "purple", "purple"]
color_set = set(color_list)
print(color_set)
# Вывод (порядок может быть другим):
{"red", "purple", "blue", "green"}Ещё одна возможность создания множества – это использование set comprehension. Это специальная синтаксическая конструкция языка, которую иногда называют абстракцией множества по аналогии с list comprehension (Списковое включение).
numbers = [1, 2, 2, 2, 3, 3, 4, 4, 5, 6]
# Единственное отличие со списковыми включениями - это
# использование фигурных скобок вместо квадратных
even_numbers = {
number for number in numbers
if number % 2 == 0
}
print(even_numbers)
# Вывод (порядок может быть другим):
{2, 4, 6}Хешируемые объекты
Существует ограничение, что элементами множества (как и ключами словарей) в Python могут быть только так называемые хешируемые (Hashable) объекты. Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
# Множество кортежей (tuple)
records = {
("Москва", 17_200_000),
("Санкт-Петербург", 5_400_000),
("Новосибирск", 1_600_000),
("Москва", 17_200_000),
}
for city, population in records:
print(city)
# Вывод (порядок может быть другим):
Москва
Новосибирск
Санкт-ПетербургОбъекты пользовательских классов являются хешируемыми по умолчанию. Но практического смысла чаще всего в этом мало из-за того, что сравнение таких объектов выполняется по их адресу в памяти, т.е. невозможно создать два “равных” объекта.
class City:
def __init__(self, name: str):
self.name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}Скорее всего мы предполагаем, что объекты City("Moscow") должны быть равными, и следовательно в множестве cities должен находиться один объект.
Этого можно добиться, если определить семантику равенства для объектов класса City:
class City:
def __init__(self, name: str):
# Атрибут name не должен изменяться, пока объект существует
# Для простоты пометим этот атрибут как внутренний
self._name = name
def __hash__(self) -> int:
""" Хеш от объекта
"""
return hash((self._name, self.__class__))
def __eq__(self, other) -> bool:
""" Определяем семантику равентсва (оператор ==)
"""
if not isinstance(other, self.__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'Чтобы протокол хеширования работал без явных и неявных логических ошибок, должны выполняться следующие условия:
- Хеш объекта не должен изменяться, пока этот объект существует
- Равные объекты должны возвращать одинаковый хеш
moscow = City("Moscow")
moscow_again = City("Moscow")
print(moscow == moscow_again and hash(moscow) == hash(moscow_again))
# Вывод:
True
# Теперь множество городов работает более логично и интуитивно
cities = {City("Moscow"), City("Kazan"), City("Moscow")}
print(cities)
# Вывод (порядок может быть другим):
{City("Kazan"), City("Moscow")}Свойства множеств
Тип set в Python является подтипом Collection (про коллекции), из данного факта есть три важных следствия:
- Определена операция проверки принадлежности элемента множеству
- Можно получить количество элементов в множестве
- Множества являются iterable-объектами
Принадлежность множеству
Проверить принадлежит ли какой-либо объект множеству можно с помощью оператора in. Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за O(1) с теми же оговорками, которые существуют для хеш-таблиц.
tremendously_huge_set = {"red", "green", "blue"}
if "green" in tremendously_huge_set:
print("Green is there!")
else:
print("Unfortunately, there is no green...")
# Вывод:
Green is there!
if "purple" in tremendously_huge_set:
print("Purple is there!")
else:
print("Unfortunately, there is no purple...")
# Вывод:
Unfortunately, there is no purple...Мощность множества
Мощность множества – это характеристика множества, которая для конечных множеств просто означает количество элементов в данном множестве. Для бесконечных множеств всё несколько сложнее.
even_numbers = {i for i in range(100) if i % 2 == 0}
# Мощность множества
cardinality = len(even_numbers)
print(cardinality)
# Вывод:
50Перебор элементов множества
Как уже было отмечено выше, множества поддерживают протокол итераторов, таким образом любое множество можно использовать там, где ожидается iterable-объект.
colors = {"red", "green", "blue"}
# Элементы множества можно перебрать с помощью цикла for
for color in colors:
print(color)
# Вывод (порядок может быть другим):
red
green
blue
# Множества можно использовать там, где ожидается iterable-объект
color_counter = dict.fromkeys(colors, 1)
print(color_counter)
# Вывод (порядок может быть другим):
{"green": 1, "red": 1, "blue": 1}Отношения между множествами
Между множествами существуют несколько видов отношений, или другими словами взаимосвязей. Давайте рассмотрим возможные отношения между множествами в этом разделе.
Равные множества
Тут всё довольно просто – два множества называются равными, если они состоят из одних и тех же элементов. Как следует из определения множества, порядок этих элементов не важен.
my_fruits = {"banana", "apple", "orange", "orange"}
your_fruits = {"apple", "apple", "banana", "orange", "orange"}
print(my_fruits == your_fruits)
# Вывод:
TrueНепересекающиеся множества
Если два множества не имеют общих элементов, то говорят, что эти множества не пересекаются. Или другими словами, пересечение этих множеств является пустым множеством.
even_numbers = {i for i in range(10) if i % 2 == 0}
odd_numbers = {i for i in range(10) if i % 2 == 1}
# Очевидно, что множества чётных и нечётных чисел не пересекаются
if even_numbers.isdisjoint(odd_numbers):
print("Множества не пересекаются!")
# Вывод:
Множества не пересекаются!Подмножество и надмножество
Подмножество множества S – это такое множество, каждый элемент которого является также и элементом множества S. Множество S в свою очередь является надмножеством исходного множества.
# Множество чисел Фибоначчи меньших 100
fibonacci_numbers = {0, 1, 2, 3, 34, 5, 8, 13, 21, 55, 89}
# Множество натуральных чисел меньших 100
natural_numbers = set(range(100))
# Множество чисел Фибоначчи является подмножеством множества
# натуральных чисел
if fibonacci_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!
# В свою очередь множество натуральных чисел является
# надмножеством множества чисел Фибоначчи
if natural_numbers.issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!Пустое множество является подмножеством абсолютно любого множества.
empty = set()
# Методы issubset и issuperset могут принимать любой iterable-объект
print(
empty.issubset(range(100))
and empty.issubset(["red", "green", "blue"])
and empty.issubset(set())
)
# Вывод:
TrueСамо множество является подмножеством самого себя.
natural_numbers = set(range(100))
if natural_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!Операции над множествами
Рассмотрим основные операции, опредяляемые над множествами.
Объединение множеств
Объединение множеств – это множество, которое содержит все элементы исходных множеств. В Python есть несколько способов объединить множества, давайте рассмотрим их на примерах.
my_fruits = {"apple", "orange"}
your_fruits = {"orange", "banana", "pear"}
# Для объединения множеств можно использовать оператор `|`,
# оба операнда должны быть объектами типа set
our_fruits = my_fruits | your_fruits
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Также можно использовать ментод union.
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}Добавление элементов в множество
Добавление элементов в множество можно рассматривать как частный случай объединения множеств за тем исключением, что добавление элементов изменяет исходное множество, а не создает новый объект. Добавление одного элемента в множество работает за O(1).
colors = {"red", "green", "blue"}
# Метод add добаляет новый элемент в множество
colors.add("purple")
# Добавление элемента, который уже есть в множестве, не изменяет
# это множество
colors.add("red")
print(colors)
# Вывод (порядок может быть другим):
{"red", "green", "blue", "purple"}
# Метод update принимает iterable-объект (список, словарь, генератор и т.п.)
# и добавляет все элементы в множество
numbers = {1, 2, 3}
numbers.update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}Пересечение множеств
Пересечение множеств – это множество, в котором находятся только те элементы, которые принадлежат исходным множествам одновременно.
def is_prime(number: int) -> bool:
""" Возвращает True, если number - это простое число
"""
assert number > 1
return all(number % i for i in range(2, int(number**0.5) + 1))
def is_fibonacci(number: int) -> bool:
""" Возвращает True, если number - это число Фибоначчи
"""
assert number > 1
a, b = 0, 1
while a + b < number:
a, b = b, a + b
return a + b == number
# Множество простых чисел до 100
primes = set(filter(is_prime, range(2, 101)))
# Множество чисел Фибоначчи до 100
fibonacci = set(filter(is_fibonacci, range(2, 101)))
# Множество простых чисел до 100, которые одновременно являются
# числами Фибоначчи
prime_fibonacci = primes.intersection(fibonacci)
# Или используя оператор `&`, который определён для множеств
prime_fibonacci = fibonacci & primes
print(prime_fibonacci)
# Вывод (порядок может быть другим):
{2, 3, 5, 13, 89}При использовании оператора & необходимо, чтобы оба операнда были объектами типа set. Метод intersection, в свою очередь, принимает любой iterable-объект. Если необходимо изменить исходное множество, а не возращать новое, то можно использовать метод intersection_update, который работает подобно методу intersection, но изменяет исходный объект-множество.
Разность множеств
Разность двух множеств – это множество, в которое входят все элементы первого множества, не входящие во второе множество.
i_know: set = {"Python", "Go", "Java"}
you_know: dict = {
"Go": 0.4,
"C++": 0.6,
"Rust": 0.2,
"Java": 0.9
}
# Обратите внимание, что оператор `-` работает только
# для объектов типа set
you_know_but_i_dont = set(you_know) - i_know
print(you_know_but_i_dont)
# Вывод (порядок может быть другим):
{"Rust", "C++"}
# Метод difference может работать с любым iterable-объектом,
# каким является dict, например
i_know_but_you_dont = i_know.difference(you_know)
print(i_know_but_you_dont)
# Вывод:
{"Python"}Удаление элементов из множества
Удаление элемента из множества можно рассматривать как частный случай разности, где удаляемый элемент – это одноэлементное множество. Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность O(1).
fruits = {"apple", "orange", "banana"}
# Удаление элемента из множества. Если удаляемого элемента
# нет в множестве, то ничего не происходит
fruits.discard("orange")
fruits.discard("pineapple")
print(fruits)
# Вывод (порядок может быть другим):
{"apple", "banana"}
# Метод remove работает аналогично discard, но генерирует исключение,
# если удаляемого элемента нет в множестве
fruits.remove("pineapple") # KeyError: "pineapple"Также у множеств есть метод differenсe_update, который принимает iterable-объект и удаляет из исходного множества все элементы iterable-объекта. Этот метод работает аналогично методу difference, но изменяет исходное множество, а не возвращает новое.
numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
even_numbers_under_100 = (i for i in range(1, 101) if i % 2 == 0)
numbers.difference_update(even_numbers_under_100)
print(numbers)
# Вывод (порядок может быть другим):
{1, 3, 5, 7, 9}Симметрическая разность множеств
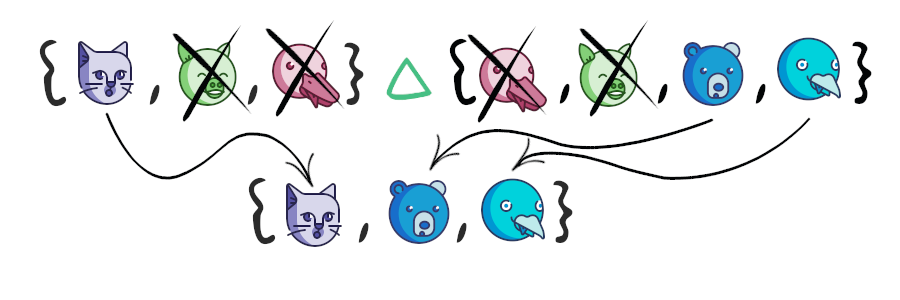
Симметрическая разность множеств – это множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам. Также симметрическую разность можно рассматривать как разность между объединением и пересечением исходных множеств.
non_positive = {-3, -2, -1, 0}
non_negative = {0, 1, 2, 3}
# Обратите внимание, что оператор `^` может применяться
# только для объектов типа set
non_zero = non_positive ^ non_negative
print(non_zero)
# Вывод (порядок может быть другим):
{-1, -2, -3, 1, 2, 3}Как видно из примера выше, число 0 принадлежит обоим исходным множествам, и поэтому оно не входит в результирующее множество. Для операции симметрической разности, помимо оператора ^, также существует два специальных метода – symmetric_difference и symmetric_difference_update. Оба этих метода принимают iterable-объект в качестве аргумента, отличие же состоит в том, что symmetric_difference возвращает новый объект-множество, в то время как symmetric_difference_update изменяет исходное множество.
non_positive = {-3, -2, -1, 0}
non_negative = range(4)
non_zero = non_positive.symmetric_difference(non_negative)
print(non_zero)
# Вывод (порядок может быть другим):
{-1, -2, -3, 1, 2, 3}
# Метод symmetric_difference_update изменяет исходное множество
colors = {"red", "green", "blue"}
colors.symmetric_difference_update(["green", "blue", "yellow"])
print(colors)
# Вывод (порядок может быть другим):
{"red", "yellow"}Заключение
Я надеюсь, мне удалось показать, что Python имеет очень удобные встроенные средства для работы с множествами. На практике это часто позволяет сократить количество кода, сделать его выразительнее и легче для восприятия, а следовательно и более поддерживаемым. Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Полезные ссылки
Множества (Статья на Википедии)
Документация по типу set
Iterable-объекты (Глоссарий Python)
Hashable-объекты (Глоссарий Python)
Sets in Python
Set Theory: the Method To Database Madness
Информатика. 10 класса. Босова Л.Л. Оглавление
§ 17. Некоторые сведения из теории множеств
17.1. Понятие множества
С понятием множества вы познакомились на уроках математики ещё в начальной школе, а затем работали с ним при изучении математики и информатики в основной школе.
Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое.
Примерами множеств могут служить: множество всех учеников вашего класса, множество всех жителей Санкт-Петербурга, множество всех натуральных чисел, множество всех решений некоторого уравнения и т. п.
Множества принято обозначать прописными буквами латинского алфавита (А, В, С, …). Объекты, входящие в состав множества, называются его элементами.
Множество можно задать следующими способами:
1) перечислением всех его элементов;
2) характеристическим свойством его элементов.
В первом случае внутри фигурных скобок перечисляются все объекты, составляющие множество. Каждый объект, входящий в множество, указывается в фигурных скобках лишь один раз.
Например, запись М = {1, 3, 5, 7, 9} означает, что множество М состоит из чисел 1, 3, 5, 7 и 9. Точно такой же смысл будет иметь запись М = {3, 1, 5, 9, 7}. Иначе говоря, порядок расположения элементов в фигурных скобках значения не имеет. Важно точно указать, какие именно объекты являются элементами множества.
Например:
• число 5 является элементом множества М: 5 ? М 1);
• число 4 не является элементом множества М: 4 ? М.
1) Символ ? называется знаком принадлежности.
Это же множество можно задать с помощью характеристического свойства образующих его элементов — такого свойства, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит. В нашем примере можно говорить о множестве натуральных однозначных нечётных чисел.
В рассматриваемом множестве М содержится 5 элементов. Это обозначают так: |М| = 5. Можно составить множество, содержащее любое число элементов. Например, множество всех корней уравнения х2 — 4х — 5 = 0 конечно (два элемента), а множество всех точек прямой бесконечно. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом ?.
Первый способ задания множеств применим только для конечных множеств, да и то при условии, что число элементов множества невелико. Вторым способом можно задавать как конечные, так и бесконечные множества.
Из некоторых элементов множества М можно составить новое множество, например Р: Р = {1, 3, 5}.
Если каждый элемент множества Р принадлежит множеству М, то говорят, что Р есть подмножество М, и записывают: Р ? М.
Само множество М является своим подмножеством, т. к. каждый элемент М принадлежит множеству М. Пустое множество также является подмножеством М.
Работая с объектами какой-то определённой природы, всегда можно выделить «самое большое» или универсальное множество, содержащее все возможные подмножества. Пусть А — множество чётных чисел, В — множество натуральных чисел, С — множество чисел, кратных пяти.
Тогда самым большим множеством, содержащим в себе множества А, В и С, а также другие подобные множества, будет множество целых чисел. Универсальное множество будем обозначать буквой U.
Для наглядного изображения множеств используются круги Эйлера (рис. 4.1). Точки внутри круга считаются элементами множества.

Рис. 4.1. Графическое изображение множеств: 1) х ? М, 2) х ? М
17.2. Операции над множествами
Над множествами, как и над числами, производят некоторые операции.
Пересечением двух множеств X и Y называется множество их общих элементов.
Пересечение множеств обозначают с помощью знака ?: Х ? У. На рисунке 4.2 закрашено множество X ? Y.

Рис. 4.2. Графическое изображение множества X ? Y
Пусть множества X и Y состоят из букв:
X = {ш к, о, л, а};
У = {у, р, о, к}.
Эти множества имеют общие элементы: к, о.
X ? У = { к, о}.
Множества М и X не имеют общих элементов, их пересечение — пустое множество:
М ? Х = ?.
Пересечение множеств М и Р есть множество Р, а пересечение множеств М и М есть множество М:
М ? Р = Р;
М ? М = М.
Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.
Объединение множеств обозначают с помощью знака ?: X ? У.
На рисунке 4.3 закрашено множество X ? У.

Рис. 4.3. Графическое изображение множества X ? У
Для наших примеров:
Х ? У = {ш, к, о, л, а, у, р};
М ? X = {1, 3, 5, 7, 9, ш, к, о, л, а};
М ? Р = М; М ? М = М.
Подумайте, возможно ли равенство: А ? В = А ? В.
Пересечение и объединение выполняются для любой пары множеств. Третья операция — дополнение — имеет смысл не для всех множеств, а только тогда, когда второе множество является подмножеством первого.
Пусть множество Р является подмножеством множества М. Дополнением Р до М называется множество, состоящее из тех элементов М, которые не вошли в Р.
Дополнение Р до М обозначают
= {7, 9}.
Дополнение М до М есть пустое множество, дополнение пустого множества до М есть
Особый интерес представляет дополнение некоторого множества В до универсального множества U. Например, если В — это множество точек, принадлежащих некоторому отрезку, то его дополнением
до универсального множества U, которым в данном случае является множество всех точек числовой прямой, является множество точек, не принадлежащих данному отрезку.
В общем случае можем записать:
(рис. 4.4)

Рис. 4.4. Дополнение множества В до универсального множества
На рисунке 4.5 видно, что множество А ? В будет совпадать с универсальным, если А будет совпадать с множеством
или содержать его в качестве подмножества. В первом случае, т. е. при А =
мы имеем дело с минимальным множеством А, таким что A ? В = U.

Рис. 4.5. Выбор такого множества А, что А ? В = U
Каким должно быть множество А для того, чтобы множество
? В совпадало с универсальным множеством?
Для ответа на этот вопрос воспользуйтесь рисунком 4.6.

Рис. 4.6. Выбор такого множества А, что ? В = U
17.3. Мощность множества
Мощностью конечного множества называется число его элементов.
Мощность множества X обозначается |Х|.
В рассмотренных выше примерах |Х| = 5, |М| = 5.
Число элементов объединения двух непересекающихся множеств равно сумме чисел элементов этих множеств. Так, в объединении множеств М и X содержится 10 элементов: |М ? Х| = 10.
Если же множества пересекаются, то число элементов объединения находится сложнее. Так, X состоит из 5 элементов, множество Y — из 4, а их объединение — из 7. Сложение чисел 5 и 4 даёт нам число 9. Но в эту сумму дважды вошло число элементов пересечения. Чтобы получить правильный результат, надо к числу элементов X прибавить число элементов Y и из суммы вычесть число элементов пересечения. Полученная формула подходит для любых двух множеств: |Х ? Y| = |Х| + |Y| — |Х ? Y|. Это частный случай так называемого принципа включений-исключений.
Принципом включений-исключений называется формула, позволяющая вычислить мощность объединения (пересечения) множеств, если известны их мощности и мощности всех их пересечений (объединений).
Для случая объединения трёх множеств формула имеет вид:
Аналогичные формулы справедливы и для пересечения множеств:

Пример. В зимний оздоровительный лагерь отправляется 100 старшеклассников. Почти все они увлекаются сноубордом, коньками или лыжами. При этом многие из них занимаются не одним, а двумя и даже тремя видами спорта. Организаторы выяснили, что всего кататься на сноуборде умеют 30 ребят, на лыжах — 28, на коньках — 42. Всего умением кататься на лыжах и сноуборде из них могут похвастаться 8 ребят, на лыжах и коньках — 10, на сноуборде и коньках — 5, но только трое из них владеют всеми тремя видами спорта.
Сколько ребят не умеет кататься ни на сноуборде, ни на лыжах, ни на коньках?
Обозначим через S, L и К множества сноуборд истов, лыжников и любителей коньков соответственно. Тогда |S| = 30, |L| = 28 и |К| = 42. При этом |S ? L| = 8, |К ? L| = 10, |S ? К| = 5, |S ? L ? K| = 3.
Объединение множеств S, L и К — это множество ребят, увлекающихся хотя бы каким-то видом спорта.
По формуле включений-исключений находим:
|S ? L ? К| = 30 + 28 + 42 — 8 — 10 — 5 + 3 = 80.
Таким образом, из 100 старшеклассников 20 не умеют кататься ни на сноуборде, ни на лыжах, ни на коньках.
САМОЕ ГЛАВНОЕ
Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое.
Пересечением двух множеств X и Y называется множество их общих элементов.
Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.
Пусть множество Р является подмножеством множества М. Дополнением Р до М называется множество, состоящее из тех элементов М, которые не вошли в Р.
Мощностью конечного множества называется число его элементов.
Формула включений-исключений позволяет вычислить мощность объединения (пересечения) множеств, если известны их мощности и мощности всех их пересечений (объединений).
Вопросы и задания
1. Если множество X — это множество натуральных чисел, делящихся нацело на 2, а У — множество натуральных чисел, делящихся нацело на 3, то что будет
2. Пусть множество X — это множество натуральных чисел, делящихся нацело на 18, a Y — множество натуральных чисел, делящихся нацело на 14. Укажите наименьшее число, входящее
3. Пусть А, В и С — некоторые множества, обозначенные кругами, U — универсальное множество.
4. В первую смену в лагере «Дубки» отдыхали: 30 отличников, 28 победителей олимпиад и 42 спортсмена. При этом 10 человек были и отличниками, и победителями олимпиад, 5 — отличниками и спортсменами, 8 — спортсменами и победителями олимпиад, 3 — и отличниками, и спортсменами, и победителями олимпиад. Сколько ребят отдыхало в лагере?
5. Старшеклассники заполняли анкету с вопросами об экзаменах по выбору. Оказалось, что выбрали они информатику, физику и обществознание. В классе 38 учеников. Обществознание выбрал 21 ученик, причём трое из них выбрали ещё и информатику, а шестеро — ещё и физику. Один ученик выбрал все три предмета. Всего информатику выбрали 13 учеников, пятеро из которых указали в анкете два предмета. Надо определить, сколько же учеников выбрали физику.
*6. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Сколько человек знают все три языка?
§ 16. Кодирование звуковой информации
Глава 4. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И АЛГЕБРЫ ЛОГИКИ
§ 17. Некоторые сведения из теории множеств
§ 18. Алгебра логики

Помогите склепать программу в единое целое
первую часть я понял, а вот в-ю (выделяет из него подмножество Y1, представляющее собой цифры, входящие в Y.
Определить мощность множества Y.) и как определяется мощность???????????
Код:
| Pascal | ||
|
Мощность – это количество элементов во множестве. Определить например так
Код:
| Pascal | ||
|
Вторая часть, не проверял
Код:
| Pascal | ||
|