Как найти мощность множества всех натуральных чисел - Сайт, где вы сможете решить свои вопросы

Мо́щность, или кардина́льное число́, мно́жества (лат. cardinalis ← cardo «главное обстоятельство; основа; сердце») — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.

В основе этого понятия лежат естественные представления о сравнении множеств:

любые два множества, между элементами которых может быть установлено взаимно-однозначное соответствие (биекция), содержат одинаковое количество элементов (имеют одинаковую мощность, равномощны);
обратно: равномощные множества должны допускать такое взаимно-однозначное соответствие;
часть множества не превосходит полного множества по мощности (то есть по количеству элементов).

До того, когда была построена теория мощности множеств, множества различались по признакам: пустое/непустое и конечное/бесконечное, также конечные множества различались по количеству элементов. Бесконечные же множества нельзя было сравнить.

Мощность множеств позволяет сравнивать бесконечные множества.
Например, счётные множества являются самыми «маленькими» бесконечными множествами.

Мощность множества обозначается через |A| .
Иногда встречаются обозначения , и .

Определение[править | править код]

Если принять аксиому выбора, мощность множества формально будет определяться как наименьшее порядковое число alpha , при котором между и alpha можно установить биективное соответствие. Данное определение также называется распределением кардинальных чисел по фон Нейману.

Если не принимать аксиому выбора, то требуется иной подход. Самое первое определение мощности множества (оно неявно присутствует в работах Кантора и явным образом сформулировано у Фреге, а также в Principia Mathematica) представляет собой класс [X] всех множеств, равномощных . В аксиоматических системах, основанных на теории ZFC, такое определение неприменимо, поскольку при непустом такая совокупность слишком велика, чтобы подходить под определение множества. Точнее, если , то существует инъективное отображение универсального множества в [X] , при котором каждое множество переходит в , откуда, в силу аксиомы ограничения размера следует, что [X] — собственный класс. Данное определение можно использовать в теории типов и «новых основаниях»^[en], а также в связанных с ними аксиоматических системах. В случае ZFC определение можно использовать, если ограничить коллекцию [X] равномощными множествами с наименьшим рангом (этот приём, предложенный Даной Скоттом, работает благодаря тому, что совокупность объектов, обладающих заданным рангом, является множеством).

Формальный порядок среди кардинальных чисел вводится следующим образом: означает, что множество можно инъективно отобразить на . Согласно теореме Кантора — Бернштейна, из пары неравенств и следует, что |X|=|Y| . Аксиома выбора эквивалентна утверждению о том, что для любых множеств и выполняется по крайней мере одно из неравенств или .

Множество называется бесконечным по Дедекинду^[en], если в нём существует такое собственное подмножество , что |X|=|Y| . В противном случае множество называется конечным по Дедекинду. Конечные кардинальные числа совпадают с обычными натуральными числами или нулём, — иначе говоря, множество конечно тогда и только тогда, когда при некотором натуральном или при n=0 (если множество пустое). Все остальные множества бесконечны. При соблюдении аксиомы выбора можно доказать, что определения по Дедекинду совпадают со стандартными. Кроме того, можно доказать, что мощность множества натуральных чисел aleph_0 (алеф-нуль, или алеф-0, — название образовано от первой буквы еврейского алфавита aleph ) представляет собой наименьшее бесконечно большое кардинальное число, то есть в любом бесконечном множестве есть подмножество мощности aleph_0 . Следующее по порядку кардинальное число обозначается aleph_1 и так далее, число алефов бесконечно. Любому порядковому числу alpha соответствует кардинальное число $aleph _{alpha }$ , причём таким образом можно описать любое бесконечно большое кардинальное число.

Связанные определения[править | править код]

Для мощностей, как и в случае конечных множеств, имеются понятия: «равенство», «больше», «меньше». То есть для любых множеств и возможно только одно из трёх:
1. , или и равномощны;
2. , или мощнее , то есть содержит подмножество, равномощное , но и не равномощны;
3. , или мощнее — в этом случае содержит подмножество, равномощное , но и не равномощны.
Множества и называются эквивалентными, если существует взаимно однозначное отображение множества на множество .^[1]

Примеры[править | править код]

Множество называется счётным, если оно равномощно множеству всех натуральных чисел . Счётными множествами являются:

Бесконечные множества, неравномощные множеству , называются несчётными. По теореме Кантора несчётным является множество всех возможных бесконечных последовательностей, составленных из цифр 0 и 1. Мощность этого множества называется континуум.

Мощность множества вещественных чисел равна континууму.

Свойства[править | править код]

Арифметика кардинальных чисел[править | править код]

Обычные арифметические операции над числами натурального ряда можно обобщить на случай кардинальных чисел. Можно также показать, что в случае конечных кардинальных чисел эти операции совпадают с соответствующим арифметическими действиями над числами. Помимо этого, операции над кардинальными числами сохраняют многие свойства обычных арифметических операций.

Следующее по порядку кардинальное число[править | править код]

Если принять аксиому выбора, то для каждого кардинального числа kappa можно определить следующее за ним число $kappa ^{+}>kappa$ , причём между kappa и $kappa ^{+}$ нет других кардинальных чисел.
Если kappa конечно, то кардинальное число, следующее по порядку, совпадает с .
В случае бесконечных kappa следующее кардинальное число отличается от следующего порядкового числа.

Через ${displaystyle kappa ^{-}}$ обозначают предыдущее кардинальное число для числа kappa если таковое существует; в противном случае, ${displaystyle kappa ^{-}=kappa }$ .

Сложение кардинальных чисел[править | править код]

Если множества и не имеют общих элементов, то сумма мощностей определяется мощностью их объединения. При наличии общих элементов исходные множества можно заменить непересекающимися множествами той же мощности — например, заменить на , а на .

Нейтральность нуля относительно сложения:

Ассоциативность:

Коммутативность:

Монотонность (неубывание) сложения по обоим аргументам:

kappa leq mu rightarrow kappa +nu leq mu +nu .

kappa leq mu rightarrow nu +kappa leq nu +mu .

Если аксиому выбора принять верной, то сумму двух бесконечных кардинальных чисел можно легко вычислить.
Если одно из чисел kappa или бесконечно, то

Вычитание[править | править код]

При соблюдении аксиомы выбора для любого бесконечного кардинального числа sigma и произвольного кардинального числа существование kappa , при котором , эквивалентно неравенству . Такое kappa единственно (и совпадает с sigma ) тогда и только тогда, когда .

Умножение кардинальных чисел[править | править код]

Произведение двух кардинальных чисел выражается через декартово произведение множеств:

Свойства нуля:

{displaystyle kappa cdot mu =0rightarrow kappa =0lor mu =0}

Нейтральность единицы относительно умножения:

Ассоциативность:

(kappa cdot mu )cdot nu =kappa cdot (mu cdot nu )

Коммутативность:

Монотонность (неубывание) умножения по обоим аргументам:

kappa leq mu rightarrow kappa cdot nu leq mu cdot nu .

kappa leq mu rightarrow nu cdot kappa leq nu cdot mu .

Дистрибутивность умножения относительно сложения:

kappa cdot (mu +nu )=kappa cdot mu +kappa cdot nu

(mu +nu )cdot kappa =mu cdot kappa +nu cdot kappa

По аналогии со сложением, произведение двух бесконечных кардинальных чисел можно легко вычислить при соблюдении аксиомы выбора. Если числа kappa и отличны от нуля и хотя бы одно из них бесконечно, то

Деление[править | править код]

При соблюдении аксиомы выбора для любой пары кардинальных чисел и , где бесконечно, а не равно нулю, существование kappa , при котором , эквивалентно неравенству . Такое kappa единственно (и совпадает с ) тогда и только тогда, когда mu <pi .

Возведение кардинальных чисел в степень[править | править код]

Возведение в степень определяется следующим образом:

$|X|^{{|Y|}}=|X^{Y}|$

где $X^{Y}$ обозначает множество всех функций из в .

$kappa ^{0}=1$

(в частности, $0^{0}=1$

), см. «Пустая функция»

$1leq mu rightarrow 0^{mu }=0$

$1^{mu }=1$

$kappa ^{1}=kappa$

$kappa ^{{mu +nu }}=kappa ^{mu }cdot kappa ^{nu }$

$kappa ^{{mu cdot nu }}=(kappa ^{mu })^{nu }$

$(kappa cdot mu )^{nu }=kappa ^{nu }cdot mu ^{nu }$

Монотонность:

${displaystyle (1leq nu land kappa leq mu )rightarrow nu ^{kappa }leq nu ^{mu }}$

$kappa leq mu rightarrow kappa ^{nu }leq mu ^{nu }$

Заметим, что $2^{{|X|}}$ представляет собой мощность булеана и, следовательно, $2^{{|X|}}>|X|$ для любого множества (см. Диагональный метод Кантора). Отсюда следует, что среди кардинальных чисел нет наибольшего (поскольку для любого кардинального числа kappa можно указать большее число $2^{kappa }$ ). В действительности класс всех кардинальных чисел является собственным (хотя в некоторых системах аксиом теории множества этого доказать нельзя — к таковым, например, относится система «Новых оснований»^[en]).

Все последующие утверждения, приведённые в этом разделе, опираются на аксиому выбора.

Если kappa и — конечные числа, большие 1, а — бесконечное кардинальное число, то ${displaystyle kappa ^{nu }=mu ^{nu }.}$
Если кардинальное число kappa бесконечно, а конечно и отлично от нуля, то $kappa ^{mu }=kappa$ .

Если и , причём хотя бы одно из них бесконечно, то

${displaystyle max{kappa ,2^{mu }}leq kappa ^{mu }leq max{2^{kappa },2^{mu }}}$

Используя теорему Кёнига, можно доказать, что для любого бесконечного кардинального числа kappa выполняются неравенства:

${displaystyle kappa <kappa ^{operatorname {cf} (kappa )}}$

${displaystyle kappa <operatorname {cf} (2^{kappa })}$

где обозначает конфинальность kappa .

Извлечение корней[править | править код]

Если соблюдать аксиому выбора, то для любого бесконечного кардинала kappa и конечного кардинала mu >0 существует кардинальное число , при котором $nu ^{mu }=kappa$ , причём .

Логарифмы[править | править код]

При соблюдении аксиомы выбора кардинальное число lambda , удовлетворяющее условию $mu ^{lambda }=kappa$ , при заданном бесконечном kappa и конечном mu >1 , существует не всегда. Если же такое lambda существует, то оно бесконечно и меньше kappa , причём любое конечное кардинальное число nu >1 также будет удовлетворять равенству $nu ^{lambda }=kappa$ .

Логарифмом бесконечного кардинального числа kappa называется наименьшее кардинальное число , удовлетворяющее условию $kappa leq 2^{mu }$ . Несмотря на то, что логарифмы бесконечно больших кардинальных чисел лишены некоторых свойств, характерных для логарифмов положительных вещественных чисел, они оказываются полезными в некоторых областях математики — в частности, при изучении кардинальных инвариантов топологических пространств.

Континуум-гипотеза[править | править код]

Согласно континуум-гипотезе, между aleph_0 и $2^{aleph_0}$ не существует других кардинальных чисел. Кардинальное число $2^{aleph_0}$ также обозначается и представляет собой мощность континуума (то есть множества вещественных чисел). В данном случае $2^{{aleph _{0}}}=aleph _{1}$ . Обобщённая континуум-гипотеза отрицает существование кардинальных чисел, заключённых строго между |X| и $2^{{|X|}}$ , для любого бесконечного множества . Континуум-гипотеза является независимой от стандартной аксиоматизации теории множеств, то есть системы аксиом Цермело-Френкеля в сочетании с аксиомой выбора (см. Теория множеств Цермело-Френкеля).

См. также[править | править код]

Порядковое число

Примечания[править | править код]

↑ Мельников О. В., Ремеслеников В. Н., Романьков В. А. Общая алгебра. Том 1. — М., Наука, 1990. — с. 31
↑ Мельников О. В., Ремеслеников В. Н., Романьков В. А. Общая алгебра. Том 1. — М., Наука, 1990. — с. 32

Литература[править | править код]

А. А. Болибрух, Проблемы Гильберта (100 лет спустя), Глава 2 Первая проблема Гильберта: континуум-гипотеза Архивная копия от 3 июня 2004 на Wayback Machine, Библиотека «Математическое просвещение», Выпуск 2
Р. Курант, Г. Роббинс, Что такое математика? Глава II, § 4.
Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 109-110. — 383 с. — ISBN 5-09-001287-3.
Брудно А. Л. Теория функций действительного переменного. — М.: Наука, 1971. — 119 с.

Источник

Мощность множества

Множество равномощно множеству , если существует биекция fcolon Ato B .

Из того, что существует биекция fcolon Ato B , следует, что соответствие $f^{-1}$ есть биекция на . Поэтому если равномощно , то и равномощно , и мы можем говорить, что множества и равномощны.

Факт равномощности множеств и будем записывать так: Asim B .

Из определения равномощности и свойств биекции также следует, что для любого множества имеет место Asim A (тождественное отображение есть биекция множества на себя); а для любых множеств A,,B,,C из Asim B и Bsim C следует Asim C (композиция биекций есть биекция).

Таким образом, отношение равномощности множеств есть отношение эквивалентности, заданное на “множестве всех множеств” (на самом деле на множестве всех подмножеств некоторого универсального множества).

Примечание. Зачастую в литературе по теории множеств равномощные множества и называют “эквивалентными множествами”. Однако следует различать общее понятие отношения эквивалентности и его частный случаи — эквивалентность, или равномощность, множеств.

Если мы обозначим через |A| класс эквивалентности множества по отношению sim , то утверждение о равномощности множеств и можно записать так: |A|=|B| .

Этот класс эквивалентности |A| называют мощностью множества .

Конечные множества $A={a_1,ldots,a_n}$ и $B={b_1,ldots,b_n}$ равномощны тогда и только тогда, когда множества и состоят из одного и того же числа элементов, т.е. n=m . Отсюда, в частности, следует, что конечное множество не является равномощным никакому своему собственному подмножеству. Это свойство конечных множеств можно сформулировать так.

Теорема 1.8. Если — конечное множество и fcolon Ato A — инъекция, то она является сюръекцией и, следовательно, биекцией.

В силу приведенных выше соображений мощностью конечного множества $A={a_1,ldots, a_n}$ можно считать натуральное число , так как, задавая такое число, мы задаем и класс всех (попарно равномощных) множеств вида ${a_1,ldots,a_n}$ . Обратно, каждый такой класс однозначно определяет натуральное число как число элементов в каждом множестве данного класса. Естественно считается, что мощность пустого множества равна нулю.

Перейдем теперь к исследованию мощности бесконечных множеств. Таковы хорошо известные нам ещё со школы числовые множества mathbb{N},,mathbb{Z},,mathbb{Q},,mathbb{R} и mathbb{C} .

Любое множество, равномощное множеству всех натуральных чисел, называют счетным. Мощность счетного множества обозначают aleph_0 (читается “алеф нуль”).

Любую биекцию nucolonmathbb{N}to M называют нумерацией счетного множества ; если элемент есть nu(n) для некоторого ninmathbb{N} , то этот элемент обозначаем через a_n , называя натуральное число номером элемента a_n относительно данной нумерации .

Таким образом, элементы счетного множества можно перенумеровать, записав их в виде последовательности a_1,ldots,a_n,ldots или ${a_n}_{ninmathbb{N}}$ . Другими словами, счетное множество есть область значений некоторой функции натурального аргумента.

Пример 1.21. а. Множество всех нечетных натуральных чисел счетно. Нумерацию можно задать так: nu(n)=2n-1,~ ninmathbb{N}

б. Множество всех натуральных чисел, делящихся на заданное число kgeqslant2 , счётно. Нумерацию можно задать так: nu(n)=kn,~ ninmathbb{N} . В частности, при k=2 получаем, что множество всех четных чисел счётно. Этот и предыдущий примеры показывают, что бесконечное (счетное) множество может иметь собственное равномощное ему подмножество.

в. Множество mathbb{Z} всех целых чисел счётно. Нумерацию можно установить так:

$nu(n)= begin{cases}dfrac{n}{2}-1,& text{if}quad n=2k;\[7pt] -dfrac{n+1}{2},& text{if}quad n=2k-1.end{cases}(kin mathbb{Z})$

Свойства счётных множеств

Рассмотрим свойства счетных множеств.

Теорема 1.9. Любое бесконечное множество содержит счетное подмножество.

Доказательство. Пусть M_0 — бесконечное множество. Значит, оно не пусто и существует элемент a_1in M_0 . Положим $M_1=M_0 setminus{a_1}$ . Множество M_1 не пусто, так как в противном случае имело бы место равенство $M_0={a_1}$ , что противоречит предположению о бесконечности M_0 . Выберем элемент a_2in M_1 и положим

$M_2= M_1setminus {a_2}= M_0setminus {a_1,a_2}.$

Множество M_2 также не пусто, поскольку иначе мы бы имели $M_0={a_1,a_2}$ и множество M_0 было бы конечным.

Методом математической индукции можно показать, что для любого множество $M_n=M_0 setminus {a_1,ldots,a_n}$ , где $a_1in M_0,ldots,a_nin M_{n-1}$ , не пусто. Тогда существует элемент $a_{n+1}=M_n$ и $a_{n+1}notin M_{n+1}= M_n setminus {a_{n+1}}$ . Таким образом, все элементы $a_n,~nin mathbb{N}$ , попарно различны и множество ${a_ncolon, nin mathbb{N}}$ счетно, а его нумерация может быть задана так: nu(n)=a_n .

Теорема 1.10. В любом бесконечном множестве можно выделить два не пересекающихся между собой счетных подмножества.

Доказательство. Разобьем множество натуральных чисел на два подмножества:

$mathbb{N}_1={ncolon, n=2k-1,~ kin mathbb{N}}$ (множество нечетных чисел),
$mathbb{N}_2={ncolon, n=2k,~ kin mathbb{N}}$ (множество четных чисел).

Оба этих множества счетны (см. пример 1.21).

Согласно теореме 1.9, бесконечное множество содержит некоторое счетное подмножество . Пусть установлена некоторая его нумерация. Разобьем это подмножество на два подмножества: всех элементов с четными и всех элементов с нечетными номерами. По построению эти подмножества не пересекаются и являются счетными, поскольку счётны множества четных и нечетных чисел.

Теорема 1.11. Любое подмножество счетного множества конечно или счетно.

Доказательство.Пустое подмножество конечно по определению. Пусть — счетное множество, а — его некоторое непустое подмножество. Поскольку множество счетно, можно считать, что задана некоторая его нумерация. Следовательно, каждый элемент подмножества имеет свой номер. Запишем номера элементов множества в порядке возрастания: i_1,ldots, i_n, ldots . Если среди них есть наибольший номер i_p , то подмножество конечно. В противном случае получим счетное подмножество ${a_{i_1}, a_{i_2},ldots,a_{i_n},ldots}$ , нумерация которого установлена так: $nu(n)=a_{i_n}$ .

Если множество конечно или счетно, его называют не более чем счетным. Семейство $(A_i)_{iin I}$ множеств называют не более чем счетным, если множество (индексов) не более чем счетно.

Теорема 1.12. Объединение любого не более чем счетного семейства счетных множеств счетно.

Пусть $(A_i)_{iin I}$ — конечное или счетное семейство счетных множеств. Рассмотрим сначала случай, когда множества A_i попарно не пересекаются.

В этом случае нумерация объединения конечного семейства счетных множеств может быть проведена по схеме, изображенной на рис. 1.14, а нумерация объединения счетного семейства счетных множеств — по схеме, приведенной на рис. 1.15.

Схемы нумераций объединений конечного и счётного семейств счётных множеств

Пусть теперь $(A_i)_{iinmathbb{N}}$ — произвольное счетное семейство счетных множеств, т.е. множества A_i могут пересекаться. В этом случае, применяя указанные на рис. 1.14 и 1.15 схемы нумерации к конечному или счетному объединению счетных множеств, следует пропускать каждый раз элементы, которые уже получили номера.

Полезно отметить также и следующий факт.

Теорема 1.13. Объединение конечного и счетного множеств счетно.

Теорема 1.14. Пусть — бесконечное множество, а — его не более чем счетное подмножество. Если множество Msetminus N бесконечно, то оно равномощно множеству .

По теореме 1.10 в множестве Msetminus N , поскольку оно бесконечно, можно выбрать счетное подмножество . Ясно, что Ncap N'=varnothing . Множество Ncup N' является счетным как объединение двух счетных множеств или объединение счетного и конечного множеств. Поэтому существует биекция fcolon Ncup N'to N' . Поскольку

bigl(M setminus (Ncup N')bigr)cup (Ncup N')=M,qquad M setminus (Ncup N')cup N'= M setminus N.

то требуемую биекцию на Msetminus N строим так: на подмножестве Msetminus (Ncup N') , общем для и , эта биекция совпадает с тождественным отображением; на подмножестве Ncup N' эта биекция есть биекция .

Следствие 1.1. Если — бесконечное множество, а — не более чем счетное множество, то Msim Mcup N .

Существуют бесконечные множества, не являющиеся счетными. Это вытекает из следующих рассуждений.

Рассмотрим множество всех последовательностей нулей и единиц, т.е. последовательностей вида

${alpha_1,alpha_2,ldots,alpha_n,ldots}$ , где $alpha_iin {0;1}$ для каждого igeqslant1 .

Обозначим множество таких “двоичных” последовательностей через ${0;1}^{omega}$ .

Теорема Кантора

Теорема 1.15 (Кантора). Множество ${0;1}^{omega}$ не есть счетное множество.

Пусть множество ${0;1}^{omega}$ и счетное. Тогда существует биекция $varphicolonmathbb{N}{0;1}^{omega}$ . Выпишем все последовательности varphi(n):

$begin{aligned}&varphi(1)= {alpha_{11},alpha_{12},ldots,alpha_{1n},ldots},\ &varphi(2)= {alpha_{21},alpha_{22},ldots,alpha_{2n},ldots},\ &cdotscdotscdotscdotscdots\ &varphi(n)= {alpha_{n1},alpha_{n2},ldots,alpha_{nn},ldots},\ &cdotscdotscdotscdotscdots end{aligned}$

Построим последовательность $beta={beta_1,ldots,beta_n,ldots}$ : положим beta_i=1 , если $alpha_{ii}=0$ , и beta_i=0 , если $alpha_{ii}=1$ . Ясно, что эта последовательность не совпадает ни с одной из последовательностей varphi(n) , а это противоречит допущению, что любая последовательность из ${0;1}^{omega}$ есть varphi(k) для некоторого .

Итак, mathbb{N} не равномощно ${0;1}^{omega}$ .

В то же время ${0;1}^{omega}$ содержит подмножество последовательностей, в каждой из которых только один член отличен от нуля. Это подмножество равномощно множеству всех одноэлементных подмножеств mathbb{N} и, следовательно, самому . Следовательно, множество ${0;1}^{omega}$ бесконечно, но не равномощно счетному множеству и потому не является счетным.

Теорема 1.16. Множество $2^{mathbb{N}}$ всех подмножеств множества натуральных чисел и множество ${0;1}^{omega}$ равномощны.

Определим отображение varphi множества $2^{mathbb{N}}$ на множество ${0;1}^{omega}$ следующим образом: если Xsubseteq mathbb{N} , то varphi(X)_i=1 при iin X и varphi(X)_i=0 при inotin X .

Тем самым подмножеству ставится в соответствие последовательность varphi(X) , i-й член которой равен единице тогда и только тогда, когда число есть элемент множества . Докажем, что varphi — биекция $2^{mathbb{N}}$ на ${0;1}^{omega}$ .

Покажем, что отображение varphi — инъекция. Пусть и — различные подмножества mathbb{N} . Тогда найдется число iin Xsetminus Y или число jin Ysetminus X . В первом случае в последовательности varphi(X) i-й член будет равен единице, а в последовательности varphi(Y) — нулю. Таким образом, varphi(X)ne varphi(Y) . Во втором случае varphi(Y)_j=1, varphi(X)_j=0 и опять . Следовательно, отображение varphi — инъекция.

Покажем, что varphi — сюръекция. Возьмем произвольную последовательность $alphain{0;1}^{omega}$ . Образуем множество $X_{alpha}={icolon, alpha_i=1}$ . Ясно, что $varphi(X_{alpha})=alpha$ . Таким образом, для любой последовательности $alphain{0;1}^{omega}$ существует подмножество $X_{alpha}in2^{mathbb{N}}$ , такое, что $varphi(X_{alpha})=alpha$ . Следовательно, varphi — сюръекция.

Таким образом, мы показали, что varphi — биекция, а множества $2^{mathbb{N}}$ и ${0;1}^{omega}$ равномощны.

Множество мощности континуум (континуальное множество)

Мощность множества $2^{mathbb{N}}$ обозначают и называют мощностью континуума, а любое множество, эквивалентное множеству $2^{mathbb{N}}$ , называют множеством мощности континуума или континуальным множеством.

Теорема 1.17. Множество действительных чисел отрезка [0;1] равномощно множеству всех последовательностей нулей и единиц ${0;1}^{omega}$ .

Каждое действительное число из отрезка [0;1] представим в виде бесконечной дроби в двоичной системе счисления. Число 1 представим в виде периодической дроби, содержащей бесконечное число единиц — 0,!1(1) . Конечные рациональные дроби представим как бесконечные, дополнив справа бесконечным числом нулей. Таким образом, каждое число из [0;1] представлено в виде последовательности нулей и единиц. Кроме этого, выбросим счетное множество всех периодических дробей вида 0,alpha_0alpha_1ldotsalpha_k0(1) , поскольку каждая такая дробь представляет то же самое число, что и дробь 0,alpha_0 alpha_1 ldots alpha_k1(0) , где $alpha_iin{0;1}$ для всякого i=overline{1,k} . Легко видеть, что полученное таким образом множество двоичных дробей равномощно множеству ${0;1}^{omega}$ .

Следствие 1.2. $[0;1]sim2^{mathbb{N}}$ .

Выше была доказана равномощность множеств $(0;1)^{omega}$ и $2^{mathbb{N}}$ . Тогда имеем $[0;1]sim {0;1}^{omega}sim 2^{mathbb{N}}$ .

Теорема 1.18. Следующие множества равномощны:

1) множество действительных чисел отрезка [0;1] ;
2) множество действительных чисел интервала (0;1) ;
3) множество действительных чисел отрезка [a;b] ;
4) множество действительных чисел интервала (a;b) ;
5) множество действительных чисел (числовая ось) mathbb{R} ;
6) множество всех подмножеств множества натуральных чисел $2^{mathbb{N}}$ .

Покажем равномощность множеств [0;1] и (0;1) . Из множества действительных чисел отрезка [0;1] выделим двухэлементное подмножество {0;1} . Разностью этих множеств будет множество действительных чисел интервала (0;1) , и, согласно теореме 1.14, [0;1]sim(0;1) .

Отображение y=(b-a)x+a задает биекцию множества [0;1] на множество [a;b] . Следовательно, эти множества равномощны. Заметим, что аналогично доказывается равномощность (0;1) и (a;b) .

Покажем, что (0;1)simmathbb{R} . Биекцию можно установить, например, с помощью функции $y=frac{1}{pi}operatorname{arctg}x+frac{1}{2}$ .

Поскольку равномощность [0;1] и 2W ранее доказана, имеем

$[0;1]sim (0;1)sim [a;b]sim (a;b)sim mathbb{R}sim 2^{mathbb{N}}.$

Замечание 1.7. Заметим, что если в условиях теоремы 1.14 множество несчетно, а — его счетное подмножество, то множество Msetminus N бесконечно, ибо иначе получилось бы, что множество M=(Msetminus N)cup N счетно как объединение конечного и счетного множеств.

Таким образом, можно утверждать, что для любого несчетного множества и его не более чем счетного подмножества имеет место равенство |Msetminus N|=|M| .

Сравнение мощностей множеств

До сих пор речь шла о равенстве мощностей. Однако мощности разных множеств можно в определенном смысле сравнивать, говоря о большей или меньшей мощности.

Считают, что мощность множества не превышает мощность множества B~(|A|leqslant|B|) , если равномощно некоторому подмножеству множества . Можно показать, что из соотношений и |B|leqslant|A| следует, что |A|=|B| .

Мощность множества считается строго меньшей мощности множества B~(|A|<|B|) , если множества и неравномощны и существует собственное подмножество множества , равномощное множеству , то есть

(Ansim B) и (exists C subset B)(Asim C) .

Можно доказать, что из |A|leqslant|B| и |B|leqslant|C| следует |A|leqslant|C| .

Таким образом, на множестве всех мощностей (т.е. на множестве всех классов эквивалентности по отношению sim ) установлено отношение порядка.

Из определения сразу следует, что мощность любого конечного множества строго меньше мощности aleph_0 , а из доказательства теоремы 1.15 вытекает, что aleph_0<c . Кроме того, согласно теореме 1.9, мощность счетного множества aleph_0 является наименьшей на множестве всех бесконечных мощностей (т.е. мощностей бесконечных множеств). Можно сказать, что всякое бесконечное множество не менее чем счетно.

Без доказательства приведем две важные теоремы.

Теорема Кантора–Бернштейна

Теорема 1.19 (Кантора–Бернштейна). Для любых двух множеств и имеет место в точности одно из следующих трех условий: либо |A|<|B| , либо |B|<|A| , либо |B|=|A| .

Таким образом, любые два множества сравнимы по мощности. Другими словами, “шкала мощностей” линейно упорядочена.

Теорема 1.20. Для любого множества верно неравенство |2^A|>|A| .

В силу теоремы 1.20 нет наибольшей мощности, так как для любого множества существует множество большей мощности — его булеан. Заметим, что для счетного множества теорема 1.20 сводится к теореме Кантора 1.15.

Теорема 1.21 (теорема о квадрате). Для любого бесконечного множества его декартов квадрат Mtimes M равномощен самому множеству .

Доказательство проведем для частных случаев счетного и континуального множеств.

Сначала обратимся к счетному множеству. Для доказательства утверждения достаточно показать, что mathbb{N}times mathbb{N}sim mathbb{N} , т.е. задать на mathbb{N}timesmathbb{N} некоторую нумерацию. Рассмотрим множество $A_i= {(i,j)colon, jinmathbb{N}}$ упорядоченных пар. Это множество счетно по построению. Легко видеть, что справедливо равенство

$mathbb{N}times mathbb{N}= bigcuplimits_{iinmathbb{N}}A_i,,$

откуда, согласно теореме 1.12, вытекает счетность декартова квадрата mathbb{N}times mathbb{N} множества как счетного объединения счетных множеств.

Перейдем к континуальному множеству. Докажем, что множество всех упорядоченных пар двоичных последовательностей эквивалентно множеству всех таких последовательностей, т.е. $2^{mathbb{N}}times 2^{mathbb{N}}sim 2^{mathbb{N}}$ .

Паре последовательностей (alpha,beta)) поставим в соответствие последовательность

alpha_0,~ beta_0,~ alpha_1,~ beta_1,~ ldots,~ alpha_n,~ beta_m,~ ldots

Это соответствие будет взаимно однозначным, т.е. установлена биекция между $2^{mathbb{N}}times 2^{mathbb{N}}$ и $2^{mathbb{N}}$ .

Получается, что — как это ни удивительно — в квадрате “столько же” точек, сколько и в каждой его стороне. Можно обобщить это утверждение для произвольной конечной декартовой степени множества .

Следствие 1.3. Множество рациональных чисел mathbb{Q} счетно.

Каждому рациональному числу, представленному несократимой дробью a/b , однозначно соответствует упорядоченная пара (a;b) , и, напротив, любая упорядоченная пара (a;b) взаимно простых целых чисел и однозначно определяет несократимую дробь a/b и, значит, рациональное число. Следовательно, множество mathbb{Q} эквивалентно некоторому бесконечному подмножеству множества mathbb{Z}times mathbb{Z} . Поскольку множество счетно, из теоремы 1.11 вытекает, что любое его бесконечное подмножество счетно. Таким образом, множество mathbb{Q} счетно.

В заключение приведем сводку результатов по мощностям некоторых конечных множеств.

Теорема 1.22. Если и — конечные множества и |M|=m , a |N|=n , то:

1) мощность множества всех отображений в равна n^m ;
2) мощность множества всех биекций из на себя равна
3) мощность множества всех инъекций из в (mleqslant n) равна $A_n^m=frac{n!}{(n-m)!}$ ;
4) мощность множества всех подмножеств множества равна 2^n ;
5) мощность множества всех k-элементных подмножеств множества равна $C_n^k=frac{n!}{k!(n-k)!}$ ;
6) мощность прямого произведения Mtimes N равна mcdot n .

Напомним, что в комбинаторике число P_n называют числом перестановок элементов, число A_n^m — числом размещений без повторений из элементов по , число C_n^k (обозначаемое также tbinom{n}{k} ) — числом сочетаний из элементов по . Эти числа называются также биномиальными коэффициентами, поскольку

$(a+b)^n=sumlimits_{k=0}^{n} C_n^k a^{n-k}b^k$ (формула бинома Ньютона).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Пусть
даны конечные множества
и,
число элементов которых равноисоответственно. В зависимости от величини,
возможны следующие ситуации:

, ,.

Какое
из этих соотношений имеет место, можно
решить двумя способами. Можно пересчитать
число элементов каждого из множеств и
сравнить полученные числа. А можно
сравнить два множества путем установления
взаимно однозначного соответствия
между их элементами.

Определение
1: Назовем
два множества эквивалентными,
если существует взаимно однозначное
соответствие между их элементами.

Обозначают:
.
Определенное нами бинарное отношение
эквивалентности между множествами
обладает свойствами:

1)
рефлексивность:
,

2)
симметричность:
из того, что
следует, что,

3)
транзитивность:
если
и,
то,
т.е. действительно являетсяэквивалентностью.

Таким
образом, всевозможные множества
распадаются на классы эквивалентных
между собой множеств. В один класс
эквивалентности попадают множества,
состоящие из одного и того же числа
элементов.

Поставим
в соответствие каждому классу эквивалентных
между собой множеств некоторый символ,
который назовемкардинальным
числом или мощностью
любого из множеств данного класса.

Например,
линейная функция
устанавливает взаимно однозначное
соответствие между точками интервалаи точками интерваладля любого.
Функцияустанавливает взаимно однозначное
соответствие между всеми точками
интервалаи точками прямой линии.

Замечание:
Понятие
мощности для конечного множества
совпадает с понятием числа элементов
этого множества. Кардинальное число –
это количество элементов во множестве.

Определение
2: Множества,
обладающие одинаковой мощностью,
называются равномощными
(эквивалентными).

Два
конечных множества будут равномощными,
если в них содержится одинаковое число
элементов. Если имеем дело с бесконечными
множествами, то вопросы, связанные с
мощностями, решаются путём установления
соответствия между элементами этих
множеств.

Возвращаясь,
к примеру, можно отметить, что множество
точек любого интервала и прямой –
равномощны. Это означает, что на прямой
и в интервале одинаковое количество
точек. Кардинальное число для бесконечного
множества – это число, обозначаемое
специальным символом или буквой.

При
сравнении мощностей бесконечных множеств
удобно пользоваться следующими
вспомогательными теоремами.

Теорема
1 (о
мощности промежуточного множества):
Пусть
,
причем,
тогда.

Т.е.
теорема утверждает, что, если мощности
крайних множеств одинаковы, то и мощность
среднего (промежуточного множества),
будет такой же.

Доказательство:
По условию теоремы, крайние множества
равномощны, т. е.
.
Это значит, что можно установить взаимно
однозначное соответствие между элементами
этих множеств. Пусть при этом собственной
частимножествабудет соответствовать собственная
часть множества,
которую назовем.
Итак,,
где.
В свою очередь, множествубудет соответствовать множество,
т.е.,
где.
Продолжая этот процесс неограниченно,
получим последовательность множеств:

таких,
что
,,,…

Кроме того, имеют
место следующие эквивалентности:

Обозначим
через
общую часть множеств.
Представим теперь множестваив виде сумм попарно непересекающихся
частей:

Эти
части эквивалентны, так как слагаемые
первой и второй строки либо совпадают,
либо эквивалентны. Что и требовалось
доказать.

Теорема
2
(Кантора-Бернштейна):
Если каждое из двух данных множеств
эквивалентно некоторой части другого
множества, то данные множества
эквивалентны.

Доказательство:Пусть даны
два множества
и,
причёми.
Частиипредполагаем собственными, т.к. иначе
теорема очевидна. Поставим элементы
множестваво взаимно однозначное соответствие
элементам множестваи назовем,
ту собственную часть множества,
которая составлена из элементов,
соответствующих элементам множества.
Тогда,
причем,,
следовательно, используя свойство
транзитивности отношения эквивалентности,
имеем:.
Согласно предыдущей теореме,,
но,
значит данные множества эквивалентны:.
Теорема доказана.

Следствие:
Таким
образом, при сравнении двух бесконечных
множеств возможны следующие случаи:

1)
между элементами множеств можно
установить взаимно однозначное
соответствие, тогда данные множества
равномощны;

2)
между элементами множеств нельзя
установить взаимно однозначное
соответствие, но можно установить
взаимно однозначное соответствие между
элементами одного из них и собственной
частью другого, тогда мощность одного
множества больше мощности другого.

Далее
рассмотрим наиболее распространенные
виды множеств в зависимости от их
мощности.

Теорема
3: Мощность
множества всех подмножеств любого
непустого множества
больше, чем мощность данного множества.

Доказательство:
Пусть дано
непустое множество
.
Обозначим множество всех его подмножеств.
Мы покажем, чтоне эквивалентнои что, кроме того,эквивалентно некоторой части множества.
Будем считать, что во множество подмножестввместе с другими входят несобственные
подмножества множества.
Докажем неэквивалентность множестви.
Доказательство проведём от противного.
Предположим, что.
Тогда каждому элементусоответствует некоторое подмножествотого же множества,
являющегося элементом множества.
В данной ситуации возможны два случая.
Либо элементпринадлежит тому подмножеству, которому
тот соответствует, либо нет. Разобьём
в соответствии с этим все элементы
множествана две категории: «включенные» элементы
и «не включенные». Обе категории не
пусты. Так, элемент множества,
соответствующий всему множествукак подмножеству, является включенным,
а элемент множества,
соответствующий его пустому подмножеству
– не включённым. Рассмотрим подмножествомножества,
составленное из всех не включённых
элементов. Пусть этому элементу множествасоответствует некоторый элемент.
Тогда окажется, чтоне может быть ни включенным, ни не
включенным элементом. В самом деле, если
он включенный, то,
что невозможно т.к.составлено из не включенных элементов.
Если– не включённый элемент, то он должен
принадлежать,
где собраны не включенные элементы, но
тогда он оказывается включенным. Значит,
и этот случай невозможен. Пришли к
противоречию, которое возникло из-за
неверного допущения. Тем самым доказано,
что множестваине эквивалентны.

Доказательство
того, что
,
где– собственное подмножество множества,
очень просто. Достаточно взять в качествевсе одноэлементные подмножества
множестваи поставить каждому из них в соответствие
тот
же элемент,
из которого это одноэлементное множество
состоит. Теорема доказана.

Следствие:
Из доказанной
теоремы следует, что для каждого
кардинального числа существует большее
кардинальное число.

В
последующих рассуждениях важное место
занимает множество натуральных чисел.

Определение
3: Множество,
эквивалентное множеству чисел натурального
ряда, называется счетным.

Натуральный
ряд чисел – это счётное множество. Все
множества, равномощные множеству
,
имеют такую же мощность.

Теорема
4: Для того
чтобы множество
было счетным, необходимо и достаточно,
чтобы его элементы можно было
«перенумеровать», т.е. представить в
форме последовательности:

. (1)

Доказательство:
Если
множество
представлено в форме (1), то достаточно
каждому элементупоставить в соответствие его индекс,
чтобы получить взаимно однозначное
соответствие между множествоми,
так что– счётно.

Обратно,
если
– счётно, то существует взаимно однозначное
соответствиемежду множествамии.
Обозначимчерези получим представление в форме (1).

Теорема
5: Из всякого
бесконечного множества
всегда можно выделить счётное подмножество.

Доказательство:
Пусть
– бесконечное множество. Возьмем в этом
множестве произвольный элемент.
Т.к.бесконечно, то в нём есть и другие
элементы. Можно выбрать элемент.
По тем же соображениям множествоне пусто и в нём можно выбрать элемент.
Ввиду бесконечности множестваэтот процесс можно продолжать
неограниченно. В результате получили
последовательность элементов:.
Эта выбранная последовательность и
образует счётное подмножество,
т. к. все элементы в ней перенумерованы.
Что и требовалось доказать.

Следствие:
Таким
образом, мощность счётного множества
наименьшая из всех мощностей бесконечных
множеств. Всем множествам, эквивалентным
множеству
,
ставится в соответствие одно и то же
кардинальное число.

Теорема
6: Всякое
бесконечное подмножество счётного
множества счётно.

Доказательство:
Пусть
– счетное множество, а– его бесконечное подмножество. Так как
множество– счётно, то все его элементы можно
перенумеровать, т. е. представить в виде
последовательности:.
Будем перебирать один за другим элементы
множествав порядке возрастания их номеров. При
этом нам будут встречаться элементы
множества.
Соотнося каждому элементу множестваномер «встречи» с ним, мы перенумеруем
множество,
причём, в силу бесконечности,
на его нумерацию пойдут все натуральные
числа.

Следствие:
Если из счётного множества удалить
конечное подмножество, то оставшееся
множество будет счётным.

Перечислим ещё
некоторые свойства счётных множеств.

Так
как для любого натурального числа
множество вида– счетно, тогда сумма конечного и счётного
множества без их общих элементов является
счётным множеством.

Сумма
конечного или счетного числа попарно
не пересекающихся счетных множеств
есть счётное множество. Покажем
схематически, как можно занумеровать
полученную сумму для конечного числа
слагаемых:,
где множестваимеют следующий вид:

Расположим
элементы данных множеств так, как
показано на рисунке. Таким образом,
натуральные номера присваиваются
сначала первым элементам данных множеств,
затем – вторым и т. д.

Далее
рассмотрим сумму (объединение) счётного
числа попарно не пересекающихся счётных
множеств:
.

Н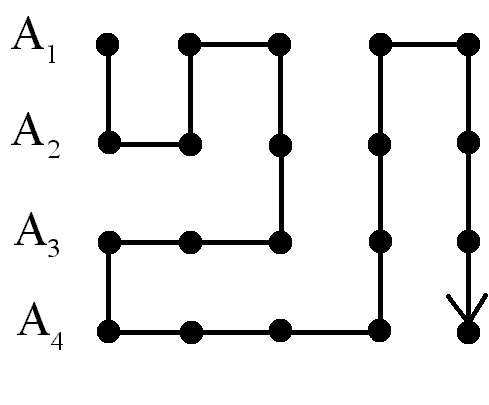а
рисунке показана примерная схема
нумерации элементов данных множеств.
Пользуясь рассмотренными свойствами
счётных множеств, можно всех целых чисел– счётно:

Это
множество – есть объединение конечного
числа счётных множеств, следовательно,
оно является счётным.

Также
схематически можно показать, что
множество всех точек плоскости с
целочисленными координатами счетно.
Отсюда нетрудно вывести, что множество
всех рациональных чисел также счетно.

Ниже рассмотрим
множества, мощность которых отлична от
мощности счётного множества.

Теорема
7: Множество
всех последовательностей из нулей и
единиц не счетно.

Доказательство:
Рассматриваемое
множество, очевидно, является бесконечным.
Поэтому достаточно доказать, что не
существует взаимно однозначного
отображения множества натуральных
чисел на множество двоичных
последовательностей. Докажем это
утверждение методом от противного.
Предположим, что множество всех двоичных
последовательностей можно перенумеровать,
т.е. любой последовательности из нулей
и единиц можно поставить в соответствие
некоторый натуральный номер. Схематически
это соответствие можно представить
следующим образом:

. . . . . . . . . . . . .
. . . . . . ,

Где
– это элементы двоичных последовательностей,
т. е. 0 или 1.

Покажем,
что существует двоичная последовательность,
которая при этом не получит номера.
Построим такую последовательность
следующим образом. Выберем первый её
элемент(если,
то;
если,
то).
Аналогично выбираем остальные элементы:,,…,и т.д. Тем самым, для всех индексовбудет выбран элемент(если,
то;
если,
то).
Тогда построенная последовательностьне совпадает с первой последовательностью,
так как.
Она не совпадает со второй последовательностью,
т.к.и т.д. Последовательностьне совпадает с последовательностью,
получившей номер,
т.к.и т.д. Таким образом, последовательностьне
может получить номера вопреки
предположению. Это означает, что множество
всех двоичных последовательностей не
эквивалентно множеству натуральных
чисел. Тем самым доказано, что множество
двоичных последовательностей нечетно.

Замечание:
Метод доказательства, примененный в
теореме 7, называют Канторовым
диагональным методом.
Его можно использовать при решении
задач и при доказательстве подобных
утверждений.

Применяя
Канторов диагональный метод, можно,
например, доказать, что множество всех
точек отрезка
несчетно.

Нетрудно
показать, что мощность множества всех
двоичных последовательностей равна
мощности множества всех действительных
чисел отрезка
,
или мощности всех последовательностей
натуральных чисел. Все эти множества
являются несчётными, а также равномощными,
значит, им соответствует одно и то же
кардинальное число.

Действительно,
каждую цифру в десятичной записи числа
или каждое натуральное число можно
зашифровать конечным набором из 0 и 1,
поэтому любое действительное число
отрезка
или любую последовательность натуральных
чисел можно зашифровать последовательностью
из нулей и единиц.

На
протяжении трех лет (с 1871 по 1874г.)
основатель теории множеств Георг Кантор
искал доказательство того, что взаимно
однозначное соответствие между точками
отрезка и точками квадрата невозможно.
Неожиданно ему удались построить
соответствие, которое он считал
невозможным! Математику Дедекинду он
писал: «И вижу это, но не верю». Но интуиция
подвела и здесь.

Дадим
эскиз доказательства Кантора. Каждую
точку квадрата можно задать её координатамии.
Эти числа можно записать, как бесконечные
десятичные дроби, т.к.и.
не больше 1.

Пусть
,(для простоты мы взяли внутренние точки
квадрата). Выпишем число,
десятичные знаки которого получаются
«перемешиванием» десятичных знаков
чиселиследующим образом:.

Точка
принадлежит отрезку,
причем соответствиеявляется взаимно однозначным. Таким
образом, установлено взаимно однозначное
соответствие между всеми точками
квадрата и частью точек отрезка.
Это показывает, что множество, точек
квадрата имеет не большую мощность, чем
множества точек отрезка. Но его мощность
и не меньшее, а потому эти мощности
совпадают. Не только квадрат, но и куб,
и вообще любая геометрическая фигура,
содержащая хотя бы одну лини, имеет
столько же точек и отрезок. Такие
множества назовёммножествами
мощности континуум
(от латинского слова continuum
– непрерывный).

Перечисленные
выше множества точек отрезка
,
множество всех двоичных последовательностей
и др. имеют мощность континуум. Можно
показать, что множество всех подмножеств
любого счетного множества имеет мощность
континуум.

Возникает
вопрос, существует ли множество, мощность
которого больше мощности счетного
множества и меньше, чем континуум. Эта
задача получила название проблемы
континуума.
Над этой проблемой думали многие
выдающиеся математики, начиная с Г.
Кантора, но до 60-х годов XX века эта
проблема оставалась нерешенной. В
течение многих лет думал над этой
проблемой один из крупнейших математиков
Н.Н. Лузин. Правда, в ходе размышлений
над проблемой континуума Н.Н Лузин решил
целый ряд труднейших задач теории
множеств и создал целый раздел математики
– дескриптивную теорию множеств.

Неудачи
попыток решить проблему континуума не
были случайными. Оказалось, что положение
дел здесь напоминает историю постулата
параллельных прямых. Этот постулат
пытались на протяжении двух тысячелетий
вывести из остальных аксиом евклидовой
геометрии. После работ Лобачевского,
Гильберта и ряда других ученых выяснилось,
что пятый постулат не противоречит
остальным аксиомам, но и не может быть
выведен из них. Точно так же после работ
К. Гёделя, П. С. Новикова, Дж. Коэна и
других выяснилось, что утверждение об
отсутствии множества промежуточной
мощности является аксиомой теории
множеств. Не существует мощности,
большей, чем мощность счётного множества,
и меньшей мощности континуум. Если
множество имеет мощность, большую
мощности счётного множества, то данное
множество имеет мощность континуум.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Подписывайтесь на канал в Яндекс. Дзен или на канал в телеграм “Математика не для всех”, чтобы не пропустить интересующие Вас материалы. Также есть группы в VK, Одноклассниках и Facebook : всё для математического просвещения!

Что нужно знать для разрешения парадокса бесконечного отеля? Теория множеств - 7

В прошлом материале я рассказывал про парадокс бесконечного отеля. Тогда я обещал дать теоретическую основу, которая поможет разрешить его. Итак, встречайте материал про мощность множеств. Это уже 7-ая часть моего курса по теории множеств (ознакомьтесь, если еще не читали его). Поехали!

Что такое мощность множества ?

Мощность множества – это действительно удивительное понятие из мира математики. Поняв его, вы узнаете, что сравнивать можно не только множества из конечного числа элементов, но и бесконечные. Более того и среди бесконечных множеств существуют более и менее “мощные”.

Источник: https://24smi.org/public/media/resize/660x-/celebrity/2017/12/20/ymdb0nsndrjt-kardinal-rishele.jpg

Мощность на английском языке читается как cardinality. Поэтому вместо мощности множества часто употребляют кардинальное число множества.

Разговор о нём обычно начинают с такого мысленного эксперимента:

Как понять, кого больше в комнате: стульев или находящихся в ней людей, не пересчитывая их?

Самым логичным решением будет сопоставление: нужно попросить каждого человека занять стул. В итоге мы получим либо свободные стулья, либо оставшихся стоять людей. С точки зрения теории множеств мы попытались произвести биекцию – однозначное сопоставление множества людей и множества стульев.

Данный пример имеет ключевое значение для понимания мощности бесконечных множеств: если возможна биекция бесконечного множества стульев и бесконечного множества людей, мы можем заключить, что эти бесконечные множества равны или по-другому “равномощны”.

Вот небольшой пример: множество натуральных чисел n равномощно множеству квадратов этих натуральных чисел:

Операция отображения

Действительно, каждому натуральному числу мы можем однозначно сопоставить его квадрат : 2 -4, 7 – 49, 90 – 8100 и так далее до бесконечности. Отсюда делается вывод, что указанные множества равномощны.

Возникает резонный вопрос: если между бесконечными множествами можно поставить знак равенства, то можно ли для других бесконечных множеств поставить знак больше или меньше? Но обо всём по порядку.

Свойство равномощности множеств (конечных и бесконечных)

Существует три основных свойства:

Отношение равномощности симметрично: если множество А равномощно множеству В, то верно и обратное утверждение.
Отношение равномощности рефлексивно: каждое множество равномощно самому себе.
Отношение равномощности транзитивно: если множество А равномощно множеству В, а множество В равномощно множеству С, то множество А равномощно множеству С.

Счетные множества

Определение. Счетными множествами называются бесконечные множества, равномощные множеству натуральных чисел. Иначе говоря, если мы можем “занумеровать” элементы исходного множества, используя 1,2,3 и т.д, то оно является счетным.

Счетные множества – самые “маленькие” из бесконечных множеств. Их принято обозначать следующим образом:

Чтобы показать, что множество счётное, надо выписать все его элементы по одному разу таким образом, чтобы не пропустить ни один элемент. Например, вот так можно показать, что множество целых чисел Z (если забыли, что это за множество, читайте этот материал) – счетное и равномощно множеству натуральных чисел:

Насчет “натуральности” 0 позиции математиков разнятся

Мы очевидным образом занумеровали все целые числа: дело в шляпе!

Первым свойством счетных множеств является тот факт, что их сложение или прямое произведение также является счётным множеством.

Иными словами, сложение алефа-ноль с алефом-ноль будет равно алефу-ноль.

Второе свойство еще более важное: в каждом бесконечном счетном множестве есть подмножество той же мощности. Звучит странно, но если взять множество натуральных чисел и его подмножество четных натуральных чисел, то они равномощны!

Невероятно, но факт!

Может показаться, что часть равна целому! Ох уж эти бесконечности!

Из текста материала становится ясно, что существуют и бОльшие бесконечные множества, такие как “алеф-один” и т.д. Такие множества называются “несчетными”. О них мы поговорим в следующем материале: пока что мы изучили достаточно информации, чтобы полностью разрешить парадокс бесконечного отеля.

*******************************************

Спасибо за прочтение, разрешение парадокса будет в следующем материале! Надеюсь, было очень интересно и познавательно! Буду рад, если Вы поддержите меня ПОДПИСКОЙ, ЛАЙКОМ или даже критическим комментарием.

Первый урок по теории множеств.

Путеводитель по каналу “Математика не для всех”

******************************************

Источник

: May 4 2009, 11:06

Category:

Наука
Cancel

16.2 Мощность множества

Мощность множества — это обобщение понятия количества (числа элементов множества), которое имеет смысл для всех множеств, включая бесконечные.

Существуют бо́льшие, есть ме́ньшие бесконечные множества, среди них счётное множество является самым маленьким.

Определение

Два множества называются равномощными, если между ними существует биекция. Существование биекции между множествами есть отношение эквивалентности, а мощность множества — это соответствующий ему класс эквивалентности.

Пример

Множество чётных целых чисел имеет такую же мощность, что и множество целых чисел . Определим так: . f — биекция, поэтому

Свойства

Два конечных множества равномощны тогда и только тогда, когда они состоят из одинакового числа элементов. То есть для конечного множества понятие мощности совпадает с привычным понятием количества.
Для бесконечных множеств мощность множества может совпадать с мощностью его собственного подмножества, например .
Теорема Кантора гарантирует существование более мощного множества для любого данного: Множество всех подмножеств множества A мощнее A, или | 2^A | > | A | .
С помощью канторова квадрата можно также доказать следующее полезное утверждение: Декартово произведение бесконечного множества A с самим собой равномощно A.

Связанные определения

Следуя Кантору, мощность множества называется кардинальным числом, и обозначается мощность такого множества A через | A | (сам Кантор использовал обозначение ). Иногда встречается обозначение .

Мощность множества натуральных чисел обозначается символом («алеф-нуль»). Множество называется бесконечным, если его мощность , таким образом, счётные множества — это «самые маленькие» из бесконечных множеств. Следующие кардинальные числа в порядке возрастания обозначаются .

Про множества, равномощные множеству всех вещественных чисел, говорят, что они имеют мощность континуума, и мощность таких множеств обозначается символом c. Континуум-гипотеза утверждает, что .

Для мощностей, как и в случае конечных множеств, имеются понятия: равенство, больше, меньше. То есть для любых множеств A и B возможно только одно из трёх:

| A | = | B | или A и B равномощны;
| A | > | B | или A мощнее B, т. е. A содержит подмножество, равномощное B, но A и B не равномощны;
| A | < | B | или B мощнее A, в этом случае B содержит подмножество, равномощное A, но A и B не равномощны.

Ситуация, в которой A и B не равномощны и ни в одном из них нет части, равномощной другому, невозможна. Это следует из теоремы Цермело. Иначе это означало бы существование несравнимых между собой мощностей (что в принципе возможно, если не принимать аксиому выбора).

Ситуация, в которой | A | > | B | и | A | < | B | , невозможна по теореме Кантора — Бернштейна.

Источник

Определение[править | править код]

Связанные определения[править | править код]

Примеры[править | править код]

Свойства[править | править код]

Арифметика кардинальных чисел[править | править код]

Следующее по порядку кардинальное число[править | править код]

Сложение кардинальных чисел[править | править код]

Вычитание[править | править код]

Умножение кардинальных чисел[править | править код]

Деление[править | править код]

Возведение кардинальных чисел в степень[править | править код]

Извлечение корней[править | править код]

Логарифмы[править | править код]

Континуум-гипотеза[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Мощность множества

Свойства счётных множеств

Теорема Кантора

Множество мощности континуум (континуальное множество)

Сравнение мощностей множеств

Теорема Кантора–Бернштейна

Что такое мощность множества ?

Свойство равномощности множеств (конечных и бесконечных)

Счетные множества

16.2

Мощность множества

Определение

Пример

Свойства

Связанные определения

Вам также может понравиться

Как можно найти транспортный налог

Как найти песни на башкирском языке

Как найти работника в цех

Добавить комментарий Отменить ответ