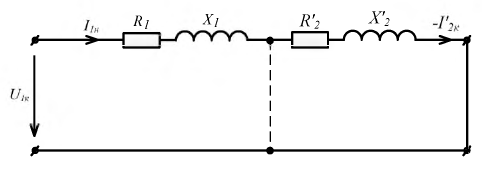
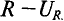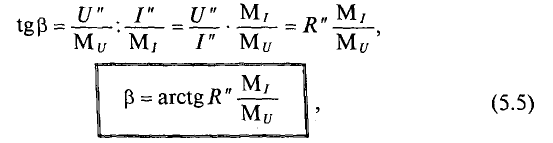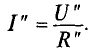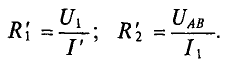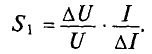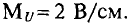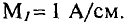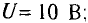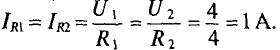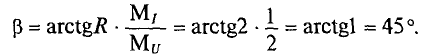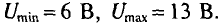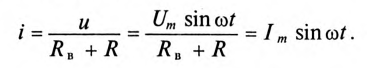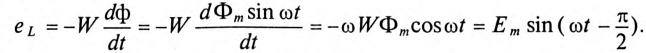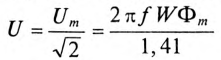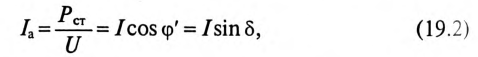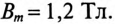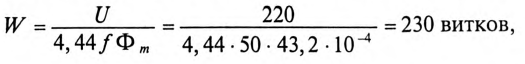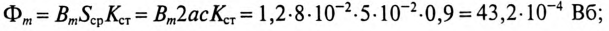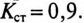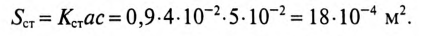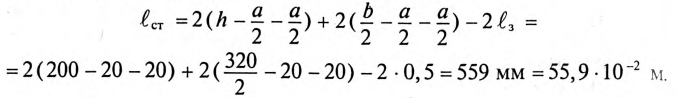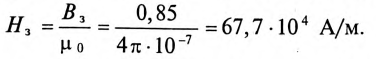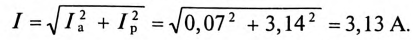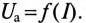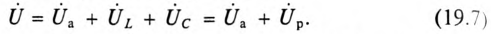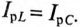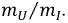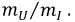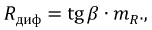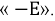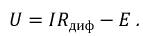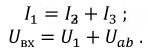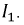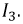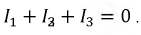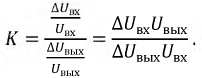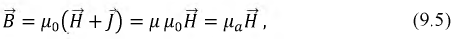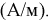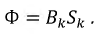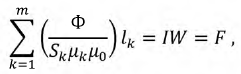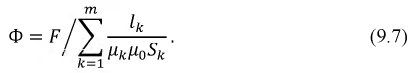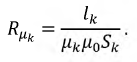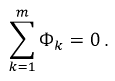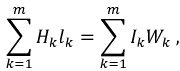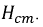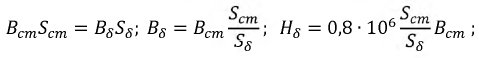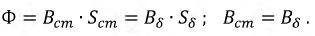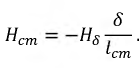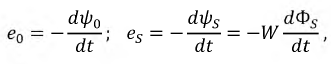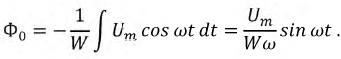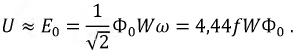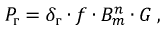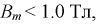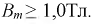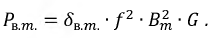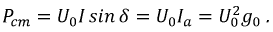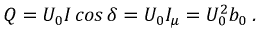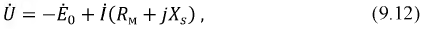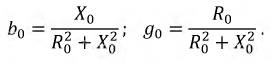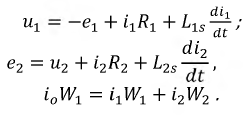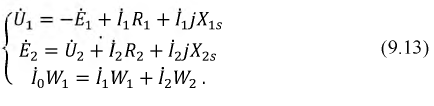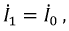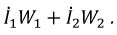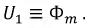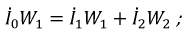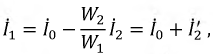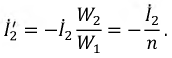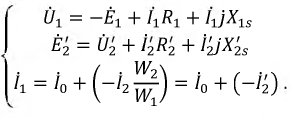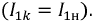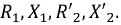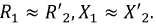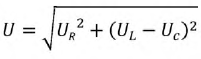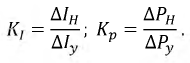Карточка № 2.11б (432). Расчет сложных электрических цепей
|
Являются ли контурные токи реальными |
Да |
188 |
|||||
|
токами ветвей? |
|||||||
|
Нет |
192 |
||||||
|
Это |
зависит |
от расположения ветви |
189 |
||||
|
(внешнее или внутреннее) |
|||||||
|
На сколько сокращается число уравнений при |
На число узлов в схеме |
194 |
|||||
|
использовании метода контурных токов? |
|||||||
|
На число независимых контуров в схеме |
186 |
||||||
|
На число узлов в схеме без одного |
197 |
||||||
|
На число независимых контуров в схеме |
176 |
||||||
|
без одного |
|||||||
|
Как выбирается направление контурных токов? |
По часовой стрелке |
180 |
|||||
|
Против часовой стрелки |
172 |
||||||
|
Произвольно |
179 |
||||||
|
Когда можно воспользоваться методом |
Когда |
сложная |
цепь содержит всего два |
182 |
|||
|
узлового напряжения? |
источника |
||||||
|
Когда сложная цепь содержит всего два |
177 |
||||||
|
узла |
|||||||
|
Для расчета любой сложной цепи |
181 |
||||||
|
Выберите |
правильную |
формулу |
У1я |
I2=(E2–Uab)G2 |
185 |
||
|
определения I2 в этой цепи |
|||||||
|
I2=(-E2–Uab)G2 |
190 |
||||||
|
I2=(-E2+Uab)G2 |
185 |
||||||
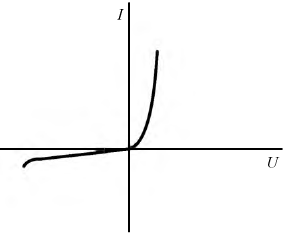
До сих пор рассматривались линейные цепи. В отличие от линейной цепи, у которой сопротивления нагрузки не зависят ни от тока, ни от напряжения, т. е. являются постоянными,
нелинейная цепь содержит один или несколько нелинейных элементов.
Нелинейным называется элемент, который не обладает постоянным сопротивлением. Примерами нелинейных элементов являются лампы накаливания, электронные, полупроводниковые и ионные приборы.
В нелинейной цепи между током и напряжением нет линейной пропорциональной зависимости, следовательно, закон Ома неприменим для расчета таких цепей.
Расчет нелинейных цепей, как правило, производят графическими методами. Для этой цепи задаются вольт–амперные характеристики нелинейных элементов, которые представляют собой зависимость тока в элементе от напряжения на его зажимах: I=f(U).
На рис. 2.16 представлены вольт–амперные характеристики нелинейных элементов — лампы накаливания с металлической нитью (кривая 1) и лампы накаливания с угольной нитью (кривая 3). Для сравнения показана вольт–амперная характеристика линейного элемента (прямая 2). Рассмотрим методы расчета нелинейных цепей.
Последовательное соединение.
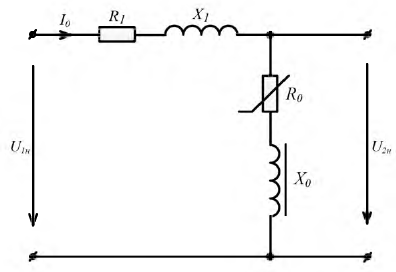
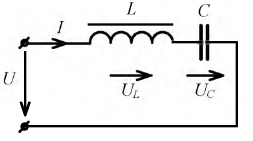
Задача состоит в том, чтобы по заданному напряжению U0 и вольт–амперным характеристикам нелинейных элементов НЭ1, НЭ2 найти ток I0 и напряжения U1, U2 на элементах неразветвленной цепи (рис. 2.17).

|
Рис. 2.16. Вольт–амперные характеристики линейного и |
Рис. 2.17. Последовательное соединение нелинейных |
|
нелинейных элементов |
элементов |
Так как элементы НЭ1 и НЭ2 соединены последовательно, то через них будет проходить одинаковый ток. Воспользуемся этим для построения общей характеристики цепи (рис. 2.18) (здесь I=f1(U) и I=f2(U)) —вольт–амперные характеристики первого и второго нелинейных элементов).
Зададимся произвольными токами I‘ и I ” и произведем для них сложение характеристик по напряжению, т. е. используем свойство последовательного соединения сопротивлений: общее напряжение равно сумме напряжений на участках. Так, например, точку А‘ общей характеристики получаем в результате сложения абсцисс А0′А1′ и А0′А2′ . Точно так же получаем точку А” и т. д.
Соединив точки А‘, А” и т. д. плавной кривой, получаем общую вольт–амперную характеристику I=f(U) цепи. Теперь отложим на оси абсцисс отрезок, соответствующий в масштабе значению U0. Перпендикуляр, восставленный из точки, соответствующей U0, до пересечения с общей характеристикой, определяет силу тока I0 цепи. Отрезки прямых А0А1 и А0А2, проведенных через точку А параллельно оси абсцисс, определяют напряжения U, U2 на нелинейных элементах НЭ и
НЭ2.
|
Рис. 2.18. Графический расчет неразветвленной цепи |
Рис. 2.19. Параллельное соединение нелинейных |
|
элементов |
Рис. 2.20. Графический расчет разветвленной цепи
Параллельное соединение.
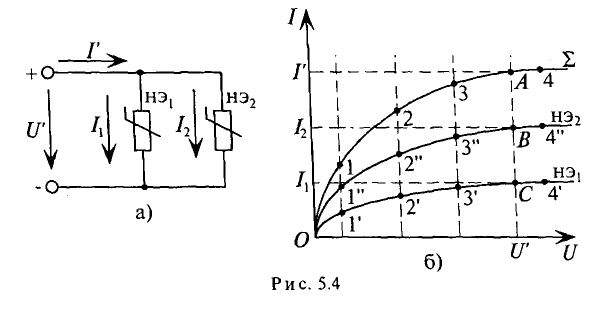
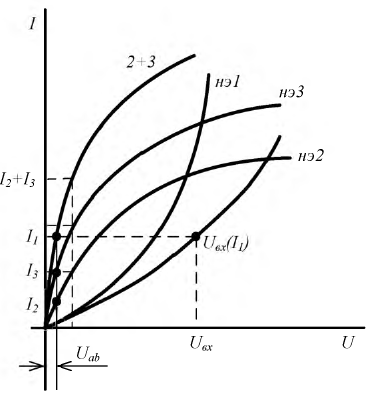
По заданному напряжению U0 и вольт–амперным характеристикам нелинейных элементов НЭ1, НЭ2 найдем общий ток I0 и токи I1 и I 2 в ветвях цепи (рис. 2.19).
Так как элементы НЭ и НЭ2 соединены параллельно, на них будет одинаковое напряжение. Воспользуемся этим для построения общей характеристики цепи (рис. 2.20). Зададимся произвольными напряжениями U’ и U” и, используя первый закон Кирхгофа, сложим характеристики по току. Операция сложения аналогична описанной, однако теперь складываются ординаты выбранных точек. Получив общую характеристику I=f’(U), находим токи I0, I1, I2. Для этого по оси абсцисс откладываем заданное напряжение U0.
Перпендикуляр О‘А, восставленный из точки О‘ до пересечения с общей характеристикой, определяет в масштабе силу тока I0 цепи, а его отрезки О‘А1 и О‘А2 — соответственно токи I1 и I2.
Рассмотренные методы расчета широко используются при анализе цепей, содержащих электронные и полупроводниковые приборы.
Карточка № 2.12 (397).
Нелинейные электрические цепи
|
Было установлено, что закон Ома неприменим к нелинейным |
Нет |
193 |
|
|
цепям. Применимы ли к нелинейным цепям законы |
|||
|
Кирхгофа? |
Да |
175 |
|
|
Какую из приведенных здесь формул можно использовать |
Р= I2R |
184 |
|
|
для определения мощности нелинейного элемента? |
|||
|
P=UI |
174 |
||
|
P=U2/R |
199 |
||
|
Все три |
191 |
||
|
Можно ли применить графический метод расчета к линейным |
Можно |
183 |
|
|
цепям? |
|||
|
Нельзя |
198 |
||
|
Можно ли так подобрать два нелинейных элемента, чтобы их |
Нельзя |
173 |
|
|
общая вольт–амперная характеристика стала линейной? |
|||
|
Можно |
187 |
||
|
При изменении тока, проходящего через проволочное |
Да |
200 |
|
|
сопротивление, меняется температура этого сопротивления. |
|||
|
Применим ли закон Ома к такому сопротивлению? |
Нет |
196 |
|
|
Это зависит от |
значения |
178 |
|
|
температурного коэффициента |
|||
|
сопротивления α |
|||
Соседние файлы в папке РГР 2
- #
- #
Содержание:
Расчет нелинейных электрических цепей:
Законы Кирхгофа в первой форме записи (
Приведение нелинейных цепей к линейным
Такое приведение можно сделать, если нелинейные элементы цепи работают в узком диапазоне напряжений и токов, где соответствующие участки вольтамперных характеристик близки к прямым.
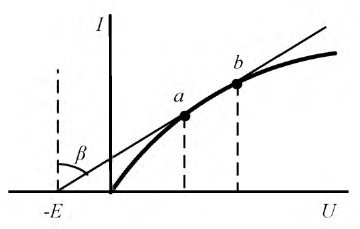
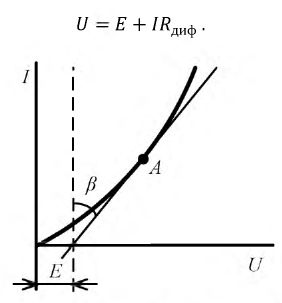
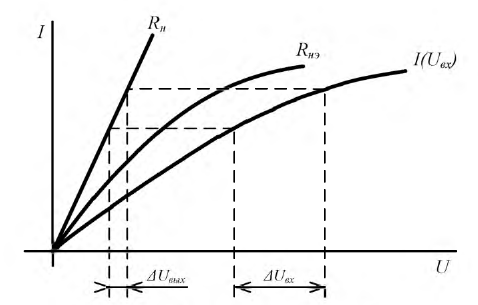
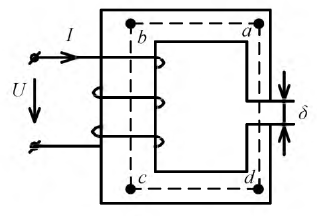
Пусть это, например, имеет место для участков ab и cd характеристик 1 и 2 (рис. 4.1) нелинейных резисторов R1 и R2 цепи рис. 4.2, а. Так как продолжения этих прямых составляют с осью токов углы 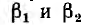
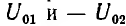
где R11 и R12 — дифференциальные сопротивления этих резисторов, имеющие постоянные значения на участках ab и cd; k — масштабный коэффициент.
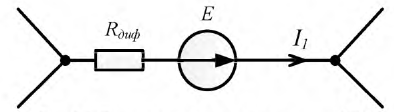
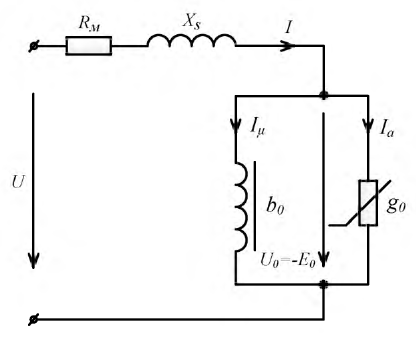
Следовательно, каждый такой нелинейный элемент может быть представлен в виде эквивалентной схемы, состоящей из последовательного соединения — резисторов R11 или R12 и источника напряжения U01 или — U02 включенного навстречу внешнему напряжению, так как последнее должно преодолеть напряжение этого источника.
В результате нелинейная цепь рис. 4.2, а заменяется линейной цепью рис. 4.2, б. Так как при принятом положительном направлении напряжение U02 второго источника отрицательно, его направление совпадает с напряжением U всей цепи. Полученная цепь рис. 4.2, б рассчитывается обычными методами. Решение будет правильным только в том случае, если токи I1 и I2 не выйдут за пределы участков ab и cd (см. рис. 4.1).
Графические методы расчета нелинейных цепей
Вольтамперная характеристика одиночного нелинейного резистора (см. рис. 1.9—1.11) сразу позволяет определить ток по заданному напряжению или напряжение по заданному току. При последовательном соединении любого числа нелинейных и линейных резисторов вольтамперная характеристика всей цепи строится путем суммирования ординат характеристик отдельных резисторов в соответствии с зависимостью
На рис. 4.3 показано такое построение для двух последовательно соединенных резисторов. По характеристике всей цепи для заданного значения напряжения U’ определяется соответствующий ему ток I’, а по Рис. 4.3 нему — напряжения 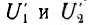
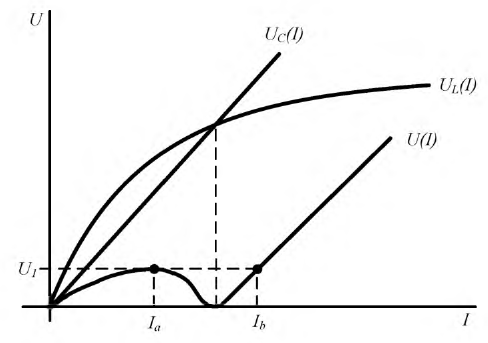
Если нужно определить ток и напряжения на участках цепи из двух приемников только при одном значении напряжения U всей цепи, нет надобности строить вольтамперную характеристику всей цепи, следует лишь отложить горизонталь для заданного значения U, а oт нее вниз — характеристику U2 (I) (рис. 4.4, а). Её пересечение с характеристикой U1(I) даст рабочую точку и определит тем самым ток I’ цепи и напряжения U’1 и U’2 на участках.
Рис. 4.4, а иллюстрирует также графическое решение задачи определения тока и напряжения цепи при питании нелинейного резистора с вольтамперной характеристикой Ul (I) от источника напряжения с нелинейной внешней характеристикой U2 (I).
При параллельном соединении нескольких линейных и нелинейных резисторов вольтамперная характеристика всей цепи строится путем суммирования абсцисс характеристик, т. е. токов отдельных резисторов:
На рис. 4.5 показано такое построение для двух параллельно соединенных резисторов. По характеристике для всей цепи для любого заданного тока I определяется напряжение U’, а по нему — токи I1‘ и I2‘ участков цепи.
Для определения токов ветвей только при одном значении тока I всей цепи можно применить упрощенное построение, аналогичное рис. 4.4, а и показанное на рис. 4.4, б для резисторов с теми же вольтамперными характеристиками. Характеристика U (I2) строится влево от вертикали для заданного значения I. Ее пересечение с характеристикой U (I1) определяет напряжение U’ цепи и токи I1‘ и I2‘ на ее участках.
При смешанном соединении, например при расчете цепи рис. 4.6, а, также строится вольтамперная характеристика всей цепи по характеристикам отдельных резисторов (рис. 4.6, б). С помощью суммирования абсцисс, т. е. токов I2 и I3, строится характеристика параллельного разветвления U23 (I1), затем, суммируя ординаты этой характеристики и характеристики Ul (I1), т. е. напряжения U23 и U1 строят характеристику U(I1) всей цепи. По этой характеристике для заданного напряжения U’ определяется ток I’1 цепи,
после чего по характеристикам Ul (I1) и U23 (I1), находят напряжения 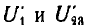
Совершенно аналогичны построения, если цепь со смешанным соединением, помимо линейных и нелинейных резисторов, содержит источники электрической энергии, например источники напряжения, вольтамперные характеристики которых без учета внутренних сопротивлений представляют собой прямые, параллельные оси абсцисс.
Их ординаты и следует алгебраически просуммировать с ординатами
вольтамперных характеристик участков (в том числе внутренних сопротивлений), соединенных последовательно с этими источниками, чтобы получить полные характеристики ветвей. При этом необходимо соблюдать правило знаков. Так как напряжение всей ветви должно преодолевать э. д. с. включенного в ветвь источника, то при э. д. с., направленной навстречу току (рис. 4.7, а), нужно при суммировании брать ее с положительным знаком (рис. 4.7, б), и наоборот.
После построения аналогичных характеристик для всех ветвей подобно предыдущему постепенно строится характеристика всей цепи и по заданному ее напряжению обратным построением определяются напряжения и токи всех ветвей цепи. Аналогичным образом решаются задачи при заданных источниках тока.
Если любая сложная цепь содержит одну нелинейную ветвь, для расчета может быть применен метод эквивалентного источника энергии: вся цепь, кроме нелинейной ветви, заменяется эквивалентным источником напряжения или тока, после чего задача сводится к только что рассмотренной задаче последовательного или параллельного соединения двух элементов — нелинейной ветви и внутреннего сопротивления (проводимости) эквивалентного источника. Это позволит определить ток или напряжение нелинейной ветви, после чего может быть рассчитана линейная часть цепи.
Метод последовательных приближений
Этот метод, называемый также итерационным, является приближенным аналитическим способом решения нелинейных алгебраических уравнений.
В качестве примера рассматривается расчет простой цепи рис. 4.8, состоящей из резистора с нелинейным сопротивлением R(I) с заданной вольтамперной характеристикой, питаемого от источника напряжения с заданной постоянной э. д. с. 
Расчет этой цепи может быть произведен по уравнению
где n — порядковый номер приближения.
Задавшись произвольно нулевым приближением тока I0, по вольтамперным характеристикам находят соответствующие ему напряжения: U0 на внешнем сопротивлении R0 и U0B на внутреннем сопротивлении R0B. Затем определяют эти сопротивления и суммарное сопротивление цепи:
а из исходного уравнения — первое приближение тока
Исходя из этого значения тока, весь ход расчета повторяется для определения второго приближения I2 и так до тех пор, пока из-за сходимости итерационного процесса результат не начнет практически повторяться.
Как известно из математики, итерация в зависимости от вида характеристик может дать расходящийся процесс. Тогда сходимость можно получить на основе исходного уравнения для другой величины, например для напряжения на приемнике:
В случае сложной цепи, например моста с двумя нелинейными резисторами (рис. 4.9), исходные уравнения могут быть составлены по методу контурных токов. При этом контуры должны быть выбраны так, чтобы контурный ток нелинейных ветвей одновременно был их действительным током. В противном случае действительный ток нельзя находить путем алгебраического суммирования проходящих по нелинейной ветви двух контурных токов, так как принцип наложения для нелинейных сопротивлений неприменим.
Правильный выбор контурных токов показан на рис. 4.9. Здесь токи нелинейных участков цепи
Тогда система уравнений получает вид:
Если нелинейное сопротивление R2(I2) с увеличением тока убывает, a R3(I3) — возрастает, можно показать, что для обеспечения сходимости итерационного процесса из этой системы уравнений надо найти ток I3 = IA и напряжение U2 = R2IB = R2I2 выразив их через все постоянные заданные величины и нелинейные сопротивления R2 и R3. Результаты расчетов целесообразно вносить в табл. 4.1,
из которой видны последовательность и способ получения отдельных величин.
Таблица 4.1
Закончив вычисления после практической сходимости итерационного процесса и определив тем самым напряжения и токи нелинейных
участков цепи, на основе законов Кирхгофа определяют напряжения
и токи всех линейных участков, например ток I1 из уравнения
Нелинейные электрические цепи постоянного тока
В автоматике, электронике и радиотехнике широко применяются элементы электрических цепей, имеющие нелинейную зависимость между током и напряжением U = f(I).
Электрическая цепь, в которую входят нелинейные элементы, называется нелинейной.
Нелинейную вольт-амперную характеристику имеют электровакуумные приборы (см. рис. 2.6), фотоэлементы (см. рис. 2.7), газоразрядные приборы (см. рис. 2.8—2.10), полупроводниковые приборы (см. рис. 2.15).
Большую группу нелинейных элементов представляют нелинейные сопротивления: терморезисторы, варисторы, бареттеры и др.
В данной главе рассмотрены принципы решения некоторых задач расчета электрических цепей с нелинейными элементами на основе их вольт-амперных характеристик.
Эквивалентные схемы простейших нелинейных цепей
Для нелинейных электрических цепей остаются справедливыми законы Ома и Кирхгофа. Однако рассмотренные ранее методы расчета для нелинейных цепей непосредственно применить нельзя.
Аналитический расчет нелинейной цепи можно выполнить при условии, что вольт-амперные характеристики нелинейных элементов выражаются относительно простыми уравнениями I = f(U). Например, для электронной лампы известна зависимость I = kU3/2. Кроме того, характеристики некоторых нелинейных элементов в определенном интервале изменения напряжения и тока прямолинейны или близки к прямой. В таких случаях можно составить для нелинейного элемента эквивалентную схему замещения с линейными элементами и ввести ее в аналитический расчет.
В других случаях схемы замещения остаются нелинейными, но с их помощью достигаются упрощения схем нелинейных цепей.
Статическое и динамическое сопротивления нелинейного элемента
У нелинейных элементов различают статическое и динамическое сопротивления (рис. 6.1, а).
Статическим сопротивлением в данной точке a вольт-амперной характеристики называют отношение напряжения к току, соответствующих этой точке:
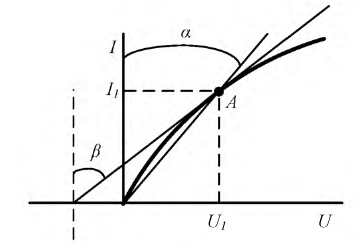
где mu и m — масштабы напряжения и тока; mR = mu /mi — масштаб сопротивления.
Динамическое сопротивление в точке a определяется отношением бесконечно малых приращений напряжения dU и тока dI:
Динамическое сопротивление пропорционально тангенсу угла наклона касательной к вольт-амперной характеристике в точке a.
Рис. 6.1. Вольт-амперная характеристика и схема замещения нелинейного элемента
Приведение нелинейных цепей к линейным
Если продолжить линейный участок h-b-a характеристики до пересечения с осью напряжения, то он пересечет ее в точке f.
Отрезок 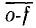
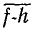
На основании уравнения (6.3) нелинейный элемент можно представить схемой последовательного соединения э. д. с. Е0 = U0 и динамического сопротивления Rдин (рис. 6.1, б). При этом
Аналогичную схему замещения можно получить для нелинейного элемента с вольт-амперной характеристикой, обращенной выпуклостью к оси токов (рис. 6.2, а). Э. д. с. Е0 в этом случае будет направлена по направлению тока. На примере данной характеристики покажем, что нелинейный элемент можно представить схемой параллельного соединения источника тока и динамической проводимости Gдин.
В линейной части характеристики ток можно представить в виде суммы
Этому равенству соответствует схема замещения рис. 6.2, б.
Рис. 6.2. Вольт-амперная характеристика и схема замещения нелинейного элемента
Рис. 6.3. Вольт-амперные характеристики и схемы замещения нелинейного двухполюсника
После замены нелинейных элементов эквивалентными схемами замещения с линейными элементами нелинейную цепь можно рассчитать одним из методов, применяемых для расчета линейных цепей.
Нелинейный активный двухполюсник
Нелинейный элемент, вольт-амперная характеристика которого не проходит через начало координат (рис. 6.3, а), можно представить схемой последовательного соединения постоянной э. д. с. и нелинейного сопротивления.
Если характеристику нелинейного элемента перенести так, чтобы она проходила через начало координат, то получится зависимость I(U) нелинейного сопротивления эквивалентной схемы, в которую кроме этого нелинейного сопротивления последовательно включен источник э. д. с. Е0.
Эквивалентная схема рис. 6.3, б представляет собой активный нелинейный двухполюсник, для которого справедливо уравнение по второму закону Кирхгофа. В данном случае
Эту схему вводить в аналитический расчет нельзя, так как она остается нелинейной в отличие от схемы рис. 6.1, б или 6.2, б, но ее можно использовать для упрощения более сложной схемы, в которую она входит как часть.
В некоторых случаях полезно или необходимо обратное построение: по известной вольт-амперной характеристике нелинейного сопротивления и величине э. д. с. Е последовательно с ним включенного источника строят вольт-амперную характеристику активного нелинейного двухполюсника (рис. 6.3, в).
Графический расчет нелинейных электрических цепей
Многие нелинейные элементы, применяемые в практике, имеют вольт-амперные характеристики, у которых нет линейных участков, и уравнения для их аналитического выражения.
Расчет цепей, содержащих такие элементы, осуществляется графическими методами, которые применимы при любом виде вольт-амперных характеристик и дают результаты достаточной точности.
Исходные данные для расчета (вольт-амперные характеристики элементов цепи) задаются в виде графиков или таблиц.
Задачу определения тока одного элемента по напряжению этого элемента или обратную задачу решают просто: заданную величину отмечают на оси координат, находят соответствующую ей точку кривой, а затем на другой оси определяют искомую величину.
Рассмотрим, как решаются такие задачи, когда несколько элементов соединены между собой в нелинейной цепи.
Последовательное соединение двух нелинейных элементов
Для расчета такой цепи (рис. 6.4, а) заданные вольт-амперные характеристики элементов и I(U1) и I(U2) строят в общей системе координат (рис. 6.4, б).
Далее строят вольт-амперную характеристику I(U) всей цепи, выражающую зависимость тока в цепи от общего напряжения.
Ток I обоих участков цепи одинаков, а общее напряжение U = U1 + U2.
Для построения общей вольт-амперной характеристики достаточно сложить абсциссы исходных кривых I(U1) и I(U2).
Проведем прямую, параллельную оси абсцисс и соответствующую току I1. Отрезки 1-2 и 1-3 в выбранном масштабе выражают напряжения U1, U2 на участках. Сложив эти отрезки, на той же прямой получим точку 4 общей вольт-амперной характеристики.
Для других значений тока аналогично найден еще ряд точек, через которые проведена общая вольт-амперная характеристика.
Построение вольт-амперных характеристик (рис. 6.4, б) является подготовительным этапом для решения различных задач, относящихся к подобным цепям. Требуется, например, определить ток в цепи и напряжения U1 и U2 на участках, если общее напряжение U известно.
На оси абсцисс находим точку 5, определяющую напряжение U (отрезок 0-5 в масштабе напряжений выражает напряжение в цепи). Через нее проводим перпендикуляр к оси абсцисс до пересечения с общей вольт-амперной характеристикой I(U) в точке 4. Из точки 4 проводим линию, параллельную оси абсцисс. Отрезок 5-4 выражает ток в цепи, а отрезки 1-2 и 1-3 — напряжения на участках (соответственно U1 и U2).
Параллельное соединение двух нелинейных элементов
При параллельном соединении двух нелинейных элементов (рис. 6.5, а) к ним приложено одно и то же напряжение U, а ток в неразветвленной части цепи равен сумме токов в ветвях: I = I1 + I2.
Для построения общей вольт-амперной характеристики I(U) нужно для ряда значений U сложить ординаты вольт-амперных характеристик элементов, как показано на рис. 6.5, б. При напряжении U1 (отрезок 0-1) сумма отрезков 1-2 (ток I1) и 1-3 (ток I2) равна отрезку 1-4 (ток I).
Предположим, что по заданному значению U = U1 нужно определить токи в ветвях и общий ток I. На оси абсцисс откладываем отрезок 0-1, выражающий напряжение U1, и через точку 1 проводим линию, параллельную оси ординат. Определяем точки 2, 3, 4 пересечения прямой с вольт-амперными характеристиками. Отрезки 1-2, 1-3, 1-4 в масштабе токов выражают токи в цепи I1, I2, I.
Аналогично решают задачи при параллельном соединении нелинейного элемента с линейным, а также при большем числе линейных и нелинейных элементов.
Смешанное соединение нелинейных элементов
При смешанном соединении нелинейных элементов графический расчет цепи производится методом «свертывания» схемы: в соответствии со схемой соединения элементов складываются их вольт-амперные характеристики.
Рассмотрим решение этой задачи применительно к схеме рис. 6.6, а.
Рис. 6.4. К расчету нелинейной электрической цепи при последовательном соединении элементов
Рис. 6.5. К расчету нелинейной электрической цепи при параллельном соединении элементов
Рис. 6.6. К расчету нелинейной электрической цепи при смешанном соединении элементов
По заданным характеристикам I2(U2), I3(U3) параллельно соединенных элементов строится вольт-амперная характеристика участка цепи между точками b, c.
Для примера на рис. 6.6, б при напряжении U2 (отрезок 0-1) определены токи I2 (отрезок 1-2) и I3 (отрезок 1-3), а затем ток I1 = I2 + I3 (отрезок 1-4).
Далее строим вольт-амперную характеристику I1(U) всей цепи, учитывая, что участок цепи между точками b, c включен последовательно с нелинейным элементом на участке a-b. Для примера при токе I1 (отрезок 0-7) определены напряжения U1 (отрезок 7-5) и U2 (отрезок 7-4), а также общее напряжение U = U1 + U2 (отрезок 7-6).
После построения вольт-амперных характеристик порядок решения задачи зависит от ее условия. Пусть задано напряжение в цепи. Требуется определить токи в схеме и напряжения на участках.
Отложив на оси абсцисс отрезок 0-11, выражающий напряжение U, проведем линию 11-6 параллельно оси ординат до пересечения с кривой I1(U). Отрезком 11-6 определяется ток I1 в неразветвленной части цепи. Прямая, параллельная оси абсцисс, проведенная через точку 6, пересекает кривые I1(U1) и I2(U2) в точках 5 и 4. Отрезками 7-4 и 7-5 определяются напряжения U2 и U1 на участках. Напряжение U2 — общее для параллельно соединенных участков с токами I2 и I3. Для определения этих токов через точку 4 проводится прямая, параллельная оси ординат. Пересечение этой прямой с кривыми I2(U2) и I3(U2) в точках 2 и 3 дает отрезки 1-2 и 1-3, определяющие токи I2 и I3.
Рис. 6.7. К задаче 6.6
Задача 6.6.
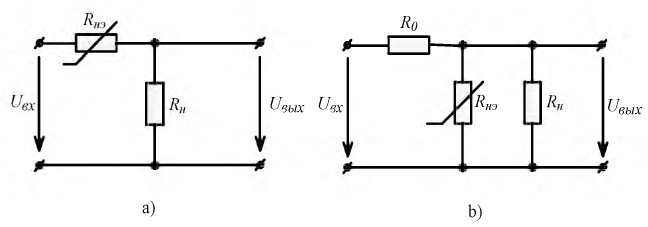
Для поддержания постоянным тока нагрузки при колебаниях входного напряжения U последовательно с нагрузочным резистором Rн = 1 Ом (рис. 6.7, а) включен бареттер Б, вольт-амперная характеристика которого дана в табл. 6.2.
Таблица 6.2
| U, В | 0 | 0,5 | 1 | 2 | 4 | 6 | 8 | 10 | 12 | 14 |
| I, А | 0 | 1 | 1,6 | 2 | 2,1 | 2,15 | 2,2 | 2,25 | 2,5 | 3,2 |
Построить график изменения тока в цепи при изменении входного напряжения
Решение. Определим ток в цепи и напряжение на участках графически. Для этого на одном чертеже построим вольт-амперные характеристики бареттера и нагрузочного резистора (рис. 6.7, б), выбрав предварительно масштабы по обеим осям.
Для построения на миллиметровой бумаге рекомендуются масштабы:
напряжений mu = 2 В/см; токов mi = 1 А/см.
Вольт-амперная характеристика нагрузочного резистора — прямая, проходящая через начало координат под углом α к оси токов (см. пунктир Oa на рис. 6.7,6). Определим угол
Ток в цепи и падение напряжения U1 связаны между собой двумя зависимостями: вольт-амперной характеристикой нелинейного элемента I(U1) и уравнением 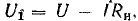
Построим указанную прямую при заданной величине Rн = 1 Ом и входном напряжении V = 8 В. Для этого определим положение точек, в которых прямая пересекается с осями координат:
при I = 0
при U1 = 0
Прямая, построенная по двум точкам, пересекается с вольт-амперной характеристикой нелинейного элемента в точке b.
Спроектируем эту точку на оси координат и найдем величины тока и напряжения на участках: I = 2.2 А; U1 = 5,8 В; U2 = 2,2 В. Аналогично находим те же величины для других напряжений U, для чего прямую перемещаем параллельно самой себе (на рис. 6.7, б показаны такие характеристики для U = 6 и 10 В).
График I(U) для заданной цепи построен на рис. 6.7, в. Из графика видно, что при изменении входного напряжения в пределах от 5до 13 В ток в цепи остается практически постоянным.
Примеры упрощения схем нелинейных цепей
Расчеты разветвленных нелинейных электрических цепей при наличии в схеме произвольного количества элементов представляют значительные трудности. В зависимости от вида схемы принимается тот или другой путь расчета, но во всех случаях основой является систематическое упрощение схемы. Рассмотрим некоторые конкретные примеры.
Цепь с двумя узлами
Между двумя узлами 1 и 2 (рис. 6.8) включены три ветви, две из которых представляют собой последовательное соединение нелинейного сопротивления и постоянной э. д. с.
Рис. 6.8. Схема нелинейной электрической цепи с двумя узлами
Рис. 6.9. К расчету нелинейной электрической цепи с двумя узлами
Нелинейные сопротивления заданы вольт-амперными характеристиками I1(U1); I2(U2); I3(U3) (рис. 6.9).
Ток каждой ветви можно выразить в зависимости от напряжения между узлами: U1.2 = Е1 — U1(I1); U1.2 = E2 — U2(I2); U1.2 = U3(I3).
Построение кривых I1(U1.2) и I2(U1.2) проводится так: для ряда значений тока определяют разность э. д. с. и соответствующих значений напряжения; через полученные точки проводят кривые. Кривая I3(U1.2) совпадает с заданной кривой I3(U3), так как U1.2 = U3.
Далее строится кривая (I1 + I2)(U1.2); для ряда значений U1.2 определяют сумму токов I1 + I2, которая согласно первому закону Кирхгофа равна I3 : I1 + I2 = I3.
Поэтому точка 3, в которой пересекаются кривые (I1 + I2) и I3(U3), определяет величину тока I3 (отрезок 3-4). Опустив перпендикуляр к оси U через точку 3, находят другие величины: ток I1 — отрезок 1-4; ток I2 — отрезок 2-4; напряжение U1.2 — отрезок 0-4.
Заметим, что кривая (I1 + I2)(U1.2) является вольт-амперной характеристикой нелинейного активного двухполюсника, эквивалентного двум ветвям исходной схемы. Построение этой кривой означает замену двух ветвей (1 и 2) одной ветвью, что является упрощением заданной схемы. Нетрудно представить, что такой путь можно применить при наличии в схеме большего числа ветвей и постепенно привести ее к схеме простейшего активного нелинейного двухполюсника.
Цепь с одним нелинейным сопротивлением
Предположим, что в разветвленную цепь входит несколько линейных элементов, в том числе источники э. д. с., и одно нелинейное сопротивление (рис. 6.10, а). Ветвь с нелинейным сопротивлением можно выделить, а оставшуюся линейную часть представить в виде активного двухполюсника.
Включим в нелинейную ветвь э.д.с. E’ такой величины, чтобы ток в ней уменьшился до нуля. Для активного линейного двухполюсника такое состояние является режимом холостого хода, поэтому Е’ = Ux, где Ux — напряжение холостого хода.
Для того чтобы получить ток, т. е. возвратиться к первоначальному режиму, можно в нелинейную ветвь включить еще одну э. д. с. Е”, равную по величине Е’, но направленную ей встречно (рис. 6.10., б). Можно сказать, что ток в нелинейной ветви вызывает только э. д. с. Е”, а остальные э. д. с. (Е’ и активного двухполюсника) тока не вызывают и их можно из схемы исключить, накоротко замкнув точки, к которым эти источники присоединены.
В результате получается схема последовательного соединения пассивного линейного двухполюсника с активным нелинейным двухполюсником (рис. 6.10, в).
Отсюда следует порядок расчета первоначально заданной нелинейной цепи: 1) определяют напряжение холостого хода и входное сопротивление линейного двухполюсника (рис. 6.10, г); 2) находят, например графически, ток и напряжение в нелинейной ветви; 3) определяют токи в линейной части цепи, считая сопротивление нелинейной ветви R = U/I постоянным.
Рис. 6.10. К расчету разветвленной электрической цепи с одним нелинейным элементом
Цепь с двумя нелинейными сопротивлениями
В сложную цепь могут входить два нелинейных сопротивления, которые простым преобразованием не приводятся к одному сопротивлению (рис. 6.11, а).
Упрощение и расчет такой цепи можно осуществить в следующем порядке. Выделим нелинейные сопротивления, а оставшуюся часть цепи представим активным линейным четырехполюсником, у которого к первичным и вторичным зажимам присоединено по одному нелинейному сопротивлению.
В каждой нелинейной ветви можно провести преобразования, такие же как на рис. 6.10, и провести аналогичные рассуждения (рис. 6.11, б). В данном случае линейный четырехполюсник можно представить Т-образной схемой замещения и получить схему с двумя узлами, изображенную на рис. 6.11, в.
Рис. 6.11. К расчету разветвленной электрической цепи с двумя нелинейными элементами
Затем надо определить сопротивления Т-схемы четырехполюсника и решить задачу так, как указано в начале этого параграфа. При необходимости от Т-схемы четырехполюсника известными способами можно перейти к исходной схеме, считая при этом сопротивления нелинейных ветвей постоянными, так как токи в них найдены.
Подобный путь применяют для расчета цепей с тремя (и более) нелинейными сопротивлениями.
Метод последовательных приближений
Суть этого метода заключается в предварительном выборе ожидаемого результата и последовательной его проверке и уточнении.
Рассмотрим метод на примере относительно простой цепи последовательного соединения двух нелинейных сопротивлений рис. 6.4, а. Даны напряжение на зажимах цепи и вольт-амперные характеристики нелинейных элементов.
Ток в цепи по закону Ома
где n — порядковый номер приближения.
Первое значение тока I1 в цепи выбирают ориентировочно, если имеются для этого какие-то основания, а если их нет, то произвольно. По вольт-амперным характеристикам определяют напряжения на нелинейных элементах U1 и U2 и затем по закону Ома — сопротивления R1 и R2:
По формуле (6.6) находят второе приближение тока:
По найденной величине тока I2 и вольт-амперным характеристикам снова определяют напряжения на нелинейных элементах и их сопротивления, а затем опять находят ток и так до тех пор, пока результат на начнет практически повторяться. Обычно достаточно точный ответ достигается после 4-5 повторений расчета, если процесс приближений обладает сходимостью. В случае расходящегося процесса задачу следует решать на основе уравнения для другой величины [вместо (6.6)], например для напряжения на одном из нелинейных элементов
Задача 6.7.
Лампа накаливания включена параллельно с линейным резистором R2 = 30 Ом (рис. 6.12, а). Построить зависимость эквивалентного сопротивления Rэк цепи от напряжения U на его зажимах.
Методом последовательных приближений определить напряжение U при токе в неразветвленной части цепи I = 5 А. Вольт-амперная характеристика лампы задана в табл. 6.3.
Таблица 6.3
| U, В | 0 | 20 | 40 | 60 | 80 | 100 | 120 |
| I, А | 0 | 0,6 | 1,1 | 1,5 | 1,85 | 2,15 | 2,4 |
Решение. Построим вольт-амперные характеристики элементов цепи. На рис. 6.12, б: I1(U) — характеристика лампы и I2(U) — характеристика резистора R2. Сложив ординаты этих характеристик при различных значениях напряжения, получим вольт-амперную характеристику всей цепи, т. е. зависимость тока в неразветвленной части цепи от приложенного напряжения I(U). Эквивалентное сопротивление схемы найдем как отношение Rэк = U/I для различных значений приложенного напряжения.
Результаты вычислений приведены на графике рис. 6.12, б.
Нелинейные электрические цепи постоянного тока
Нелинейными называются цепи, в которые включены нелинейные элементы (нэ).
Элемент электрической цепи, сопротивление которого зависит от чины и направления тока в нем или от напряжения, называется нелинейным. Нелинейными такие элементы называются потому, что их вольт-амперная характеристика (т. е. зависимость тока от напряжения, приложенного к элементу) 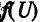
Примерами нелинейных элементов могут служить электронные газонаполненные лампы, полупроводниковые приборы, ламп накаливания и пр. нелинейную цепь наряду с нелинейными элементами могут быть включены линейные. Сопротивление линейных элементов практически не зависит от тока или напряжения (резистор). Вольт-амперная характеристика линейного элемента — прямая линия, ходящая через начало координат, точку О (рис. 5.1).
Вторую точку (точку А) для построения вольт-амперной характеристики линейного элемента определяют вычислением тока Г в линейном менте при произвольно выбранном напряжении U’, приложенном к этому элементу, т.е. 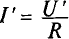
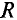
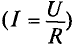
Для расчета нелинейных цепей рационально использовать графо-аналитический метод, который предусматривает построение суммарной вольт-амперной характеристики цепи. По суммарной характеристике и характеристикам элементов определяются искомые величины (обычно токи и напряжения).
Построение суммарной вольт-амперной характеристики нелинейной цепи зависит от схемы соединения элементов нелинейной цепи и производится по заданным вольт-амперным характеристикам нелинейных элементов и построенным характеристикам линейных элементов, если они включены в цепь.
Кроме того, если в нелинейной цепи имеется линейный элемент, то расчет нелинейной цепи можно производить построением так называемой нагрузочной характеристики (рис. 5.36).
Неразветвленная нелинейная цепь
В неразветвленной нелинейной электрической цепи все элементы соединены последовательно и по всем элементам проходит одинаковый ток (рис. 5.2а).
Для расчета цепи с последовательно соединенными нелинейными элементами 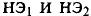
При последовательном соединении элементов для построения суммарной вольт-амперной характеристики суммируются абсциссы (напряжения) вольт-амперных характеристик элементов при различных токах (например, в точках 1, 2, 3, 4 рис. 5.26).
Зная напряжение, приложенное к цепи (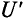
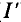
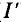
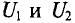
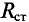
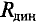
Статическое сопротивление 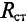
Вычислить статические сопротивления нелинейных элементов в режиме работы рассматриваемой цепи, т. е. сопротивления для С и В вольт-амперных характеристик (при токе 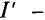
Динамическое сопротивление нелинейных элементов (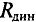
где 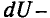
Вели в неразветвленную нелинейную цепь включен линейный элемент с заданным сопротивлением R, то для расчета такой нелинейной цепи можно произвести суммирование абсцисс (напряжений) всех элементов цепи, включая линейный, построив предварительно его вольт-амперную характеристику в той же системе ординат (рис. 5.1).
По суммарной вольт-амперной характеристике нелинейной пи определяется режим работы цепи и ее элементов. Для расчета нелинейной цепи с последовательно включенным линейным элементом с сопротивлением R (рис. 5.3а) можно воспользоваться построением нагрузочной характеристики рис. 5.36).
Нагрузочная характеристика представляет собой прямую линию, проведенную через две точки А и В (рис. 5.36). Точка А расположена на оси ординат (ток). Точка В- на оси абсцисс (напряжение).
Построение нагрузочной характеристики осуществляется с использованием двух уравнений (5.3 и 5.4) для рассматриваемой цепи в системе координат
Откуда
Точка В соответствует величинам 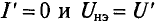
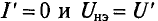
- отрезок DC – ток цепи
,
- отрезок OD – напряжение на нелинейном элементе
,
- отрезок DB — напряжение на линейном элементе
Такой метод расчета неразветвленных нелинейных цепей называется методом пересечений.
На рис. 5.36 можно проследить изменения режима работы цепи (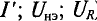
Если точка А, соответствующая измененному значению напряжения сети U’ или сопротивления линейного элемента R (см. (5.4)), выходит за пределы графика (рис. 5.36), то определяют 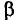
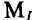
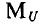
Тогда нагрузочную характеристику из точки В доводят только до сечения с вольт-амперной характеристикой нелинейного мента (точка С’ рис. 5.36) и определяют режим работы цепи, соответствующий измененному значению сопротивления линейного элемента R или напряжения сети V.
Разветвленная нелинейная цепь
В разветвленной нелинейной электрической цепи нелинейные менты могут быть соединены параллельно. При параллельном соединении нелинейных элементов напряжение на всех элементах будет одинаковым.
Для расчета цепи с параллельным соединением нелинейных ментов 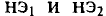
При заданном значении тока в неразветвленной части нелинейной цепи Г по суммарной вольт-амперной характеристике (точка А) можно определить напряжение цепи U’. Это напряжение создает ток в первом элементе 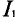
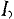
Если задано напряжение U’, приложенное к элементам, то по суммарной вольт-амперной характеристике определяется ток в неразветвленной части цепи (точка А), а по вольт-амперным характеристикам элементов определяются токи 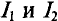
Включение в нелинейную цепь линейного элемента не меняет характера и порядка расчета.
Нелинейная цепь со смешанным соединением элементов
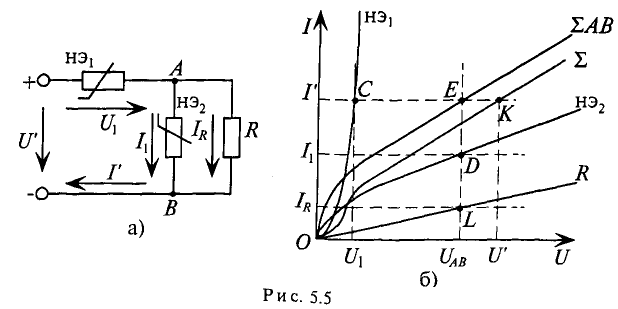
Расчет нелинейной цепи при смешанном соединении элементов (в общем виде) рассмотрен на примере 5.1 (рис. 5.5).
Пример 5.1
По заданному напряжению цепи U’ требуется определить токи 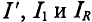
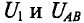
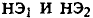
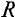
Решение
По заданному сопротивлению Я линейного элемента строится вольт-амперная характеристика этого элемента (см. рис. 5.1). Линейный элемент с сопротивлением 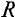
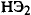
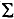
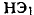
Участок АВ соединен последовательно с нелинейным элементом 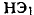
Напряжение цепи U’, по суммарной характеристике цепи К) определяется ток в неразветвленной части цепи рис. 5.56). Этот ток создает падение напряжения 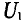
Напряжение на участке АВ (UAB) в разветвленной цепи создает А (точка D) и (точка L).
Определив напряжения и токи нелинейных элементов, можно определить статические сопротивления этих элементов в заданном режиме работы цепи
Таким образом, по вольт-амперным характеристикам соединен-смешанно элементов и их суммарным характеристикам можно определить все параметры нелинейной цепи (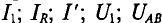
Стабилизаторы тока и напряжения
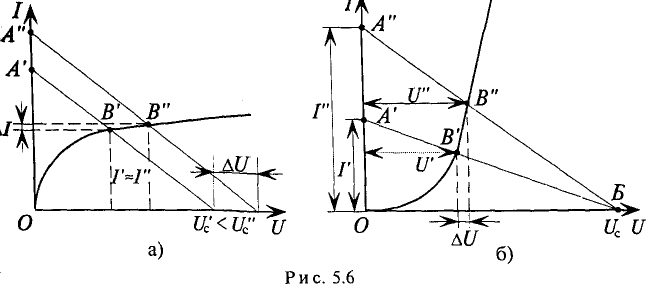
Есть такие нелинейные элементы, вольт-амперная характеристика которых имеет участки, параллельные оси абсцисс или оси ординат (рис. 5.6). Такие нелинейные элементы применяют в качестве стабилизаторов тока (рис. 5.6а) и стабилизаторов напряжения ис. 5.66).
В качестве стабилизатора тока можно использовать, например бареттер (стальная нить в атмосфере водорода). На участке В’В’ (рис. 5.6а) характеристика бареттера почти параллельна оси абсцисс. Если бареттер включить последовательно с участком (io цепи (рис. 5.8), то ток 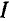
Эффективность стабилизации характеризует коэффициент стабилизации, показывающий, во сколько раз относительное изменение тока 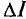
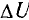
Для стабилизации напряжения применяют газоразрядные или полупроводниковые (кремниевые) стабилизаторы. Рабочий участок В’В” вольт-амперной характеристики стабилизатора напряжения почти параллелен оси ординат (рис. 5.66). Стабилизатор напряжения включается параллельно сопротивлению 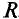
Последовательно с разветвленным участком (ab) включается балластное сопротивление 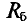
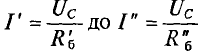
Пример 5.2
Для стабилизации напряжения и тока накала электронной лампы (4 В; I А) включен бареттер Б (рис. 5.8а), вольт-амперная характеристика которого приведена на рис. 5.86.
Определить все токи и напряжения на бареттере U1 и нити накала U2, если напряжение сети 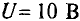
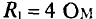
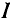
Решение
Масштаб напряжения на графике
Масштаб тока на графике принят
Нагрузочная характеристика строится в координатах:
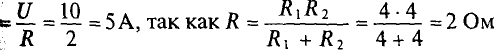
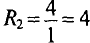
Следовательно, точка пересечения вольт-амперной характеристики бареттера и нагрузочной характеристики В (рис. 5.86) сет координаты 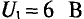
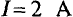
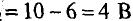
Нагрузочная характеристика проведена под углом 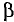
Нагрузочные характеристики, соответствующие пределам изменил напряжений сети, при которых ток цепи 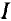
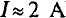
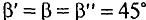
Таким образом, как следует из графиков рис. 5.86, эти напряжения соответственно равны
Определение нелинейных электрических цепей переменного тока
Нелинейные элементы
Нелинейными электрическими цепями переменного тока называются цепи, в состав которых входят один или несколько нелинейных сопротивлений (нелинейных элементов) переменного тока.
Характерной чертой нелинейных элементов переменного тока являются нелинейная вольт-амперная, кулон-вольтовая, вебер-амперная и другие характеристики.
Переменному току оказывают сопротивление активные сопротивления, индуктивности и емкости. В соответствии с этим нелинейные сопротивления переменного тока могут быть разделены на три группы: 1) группа нелинейных активных сопротивлений; 2) группа нелинейных индуктивных сопротивлений; 3) группа нелинейных емкостных сопротивлений.
Каждая из этих групп сопротивлений подразделяется на управляемые и неуправляемые.
- В качестве управляемых нелинейных активных сопротивлений широкое распространение получили электронные и полупроводниковые приборы, магнитные усилители и другие устройства. Неуправляемыми нелинейными активными сопротивлениями являются электрическая дуга, полупроводниковые выпрямители, лампы накаливания и др. Нелинейные элементы этой группы способствуют созданию несинусоидальных токов в электрических цепях.
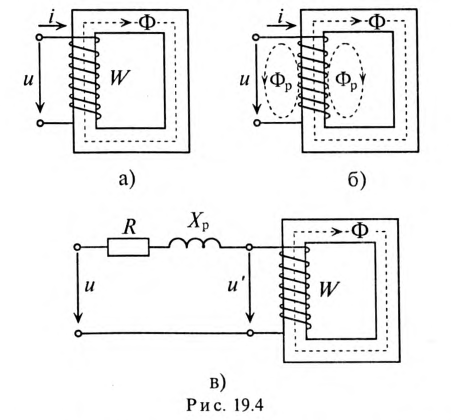
- Под нелинейными индуктивными сопротивлениями, или иначе нелинейными индуктивностями, понимают катушки с ферромагнитными сердечниками, для которых зависимость магнитного потока в сердечнике от тока в катушке нелинейна. Катушка с ферромагнитным сердечником в цепи переменного тока искажает форму кривой тока, т. е. является генератором несинусоидального тока. Катушку со стальным сердечником называют дросселем (рис. 19.4).
- Для нелинейных конденсаторов зависимость заряда Q на обкладках от напряжения, приложенного к конденсатору, нелинейна. Нелинейные конденсаторы называют варикоидами или вари капами. Пространство между обкладками нелинейного конденсатора заполнено сегнетодиэлектриком, диэлектрическая проницаемость которого зависит от напряженности электрического поля между обкладками конденсатора. Сегнетодиэлектрики обладают гистерезисом, т.е. отставанием изменения электрического смещения в диэлектрике от изменения электрического поля в нем.
Такие явления, как выпрямление переменного тока в постоянный, стабилизация напряжения, умножение и деление частоты, получение сигналов различной формы и т. д., можно получить только в нелинейных цепях переменного тока.
В настоящей главе рассматривается работа двух нелинейных элементов: вентили (1-я группа нелинейных активных сопротивлений) и катушки с ферромагнитным сердечником (2-я группа нелинейных индуктивных сопротивлений).
Выпрямители – источники несинусоидального тока
Выпрямителями называют аппараты, преобразующие переменный ток в постоянный.
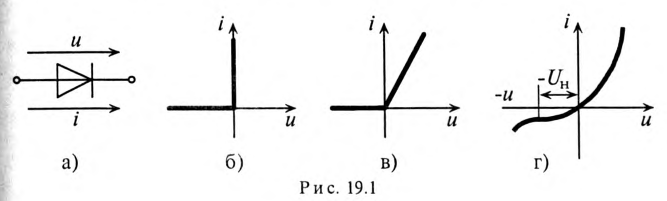
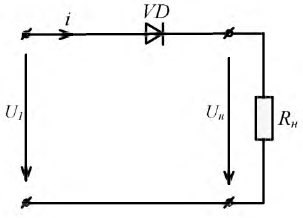
Основным элементом любого выпрямителя является электрический вентиль. Электрический вентиль обладает малым сопротивлением в прямом направлении и большим в обратном направлении. Вентиль имеет нелинейную вольт-амперную характеристику (рис. 19.1), поскольку обладает практически односторонней проводимостью. Графическое изображение электрического вентиля в электрических схемах и положительное направление прямого напряжения и тока показано на рис. 19.1а.
Вентиль, сопротивление которого в прямом направлении равно нулю, а в обратном – бесконечно большое, считается идеальным вентилем. Характеристика идеального вентиля дана на рис. 19.1б. Вентиль, сопротивлением которого в прямом направлении пренебречь нельзя, а обратным током можно пренебречь, имеет вольт-амперную характеристику, изображенную на рис. 19.1в. Вольт-амперная характеристика реального полупроводникового вентиля изображена на рис. 19.1г.
Как видно, если к реальному вентилю приложено увеличивающееся по величине обратное напряжение 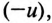
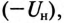
Основными параметрами вентилей наряду с вольт-амперной характеристикой являются допустимая температура, плотность тока и допустимое обратное напряжение.
В выпрямителях вентиль включается по различным схемам.
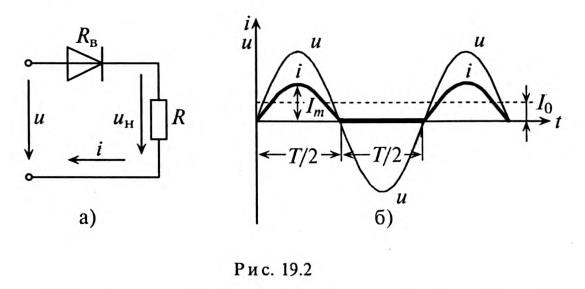
В схеме однополупериодного выпрямителя вентиль включается последовательно с потребителем R, ток которого необходимо выпрямить (рис. 19.2а).
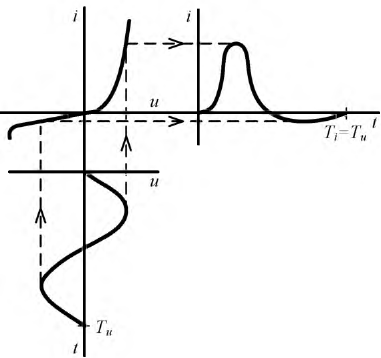
Если к цепи, изображенной на рис. 19.2а, приложено синусоидальное напряжение 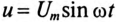
В течение же отрицательного полупериода напряжения 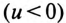
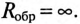
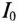
Таким образом, на сопротивлении R в результате выпрямления синусоидального напряжения и создается несинусоидальный ток и несинусоидальное напряжение
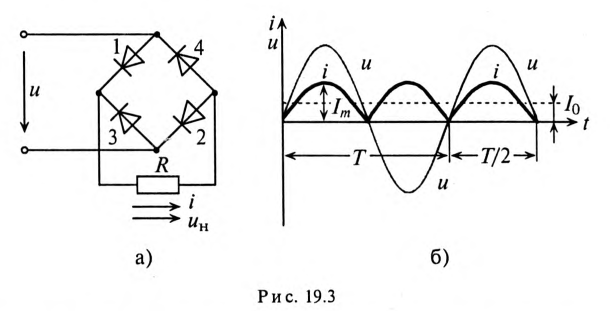
Если вентили включены по мостовой схеме (рис. 19.3а) и к мосту подведено синусоидальное напряжение 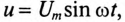
В положительный полупериод синусоидального напряжения и ток проходит через вентили 1, 2 и через потребитель слева направо (рис. 19.3а). В отрицательный полупериод напряжения и ток проходит через вентили 3, 4 и через потребитель также слева направо. Таким образом, ток через потребитель изменяется по величине, но не меняется по направлению (рис. 19.3б), т.е. через потребитель проходит пульсирующий ток, который складывается из постоянной составляющей и четных гармоник. Таким же будет и напряжение 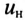
При выпрямлении трехфазного тока (см. кривую 7 таблицы 18.1) несинусоидальный ток раскладывается на постоянную составляющую и гармоники, кратные трем, т. е. 3, 6, 9 и т.д. При этом постоянная составляющая тока (напряжения) на потребителе увеличивается, а пульсации уменьшаются (по сравнению с однофазным током). Для уменьшения пульсаций на потребителе в любой схеме соединения вентилей используются электрические фильтры (см. § 18.7).
Катушка с ферромагнитным сердечником
Наиболее распространенным нелинейным элементом переменного тока в электрических машинах, трансформаторах и других аппаратах является катушка со стальным сердечником (рис. 19.4).
Если магнитный поток в сердечнике изменяется по синусоидальному закону 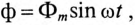
Если пренебречь активным сопротивлением катушки, то напряжение, приложенное к ней, равно по величине и противоположно по знаку ЭДС самоиндукции, определяемой по (11.9):
где 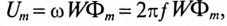
или
Если к катушке со стальным сердечником приложено синусоидальное напряжение, то в сердечнике возникает синусоидальный магнитный поток.
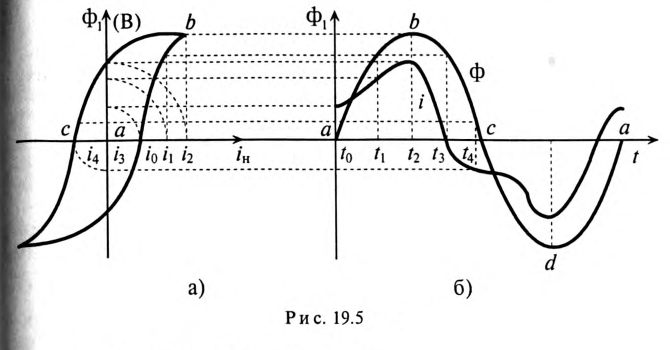
Ток в катушке при этом оказывается несинусоидальным. Это связано с нелинейной зависимостью между магнитим потоком и током 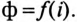
Для каждого момента времени 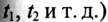
Как видно (рис. 19.56), кривая тока при синусоидальном магнитном потоке несинусоидальна.
Кривая намагничивания ферромагнитного материала (рис. 8.3) выражает зависимость индукции В в ферромагнитном материале от напряженности Я магнитного поля в катушке. Напряженность Н в катушке пропорциональна току I в катушке. Магнитный поток в ферромагнитном материале 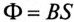
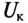
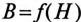
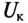
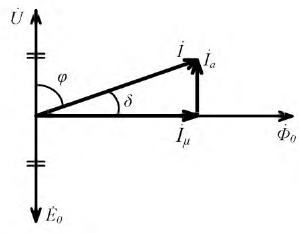
Мощность потерь. Векторная диаграмма катушки со стальным сердечником
При расчете цепи катушки со стальным сердечником несинусоидальный намагничивающий ток 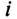
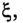
Значение коэффициента 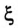
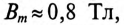
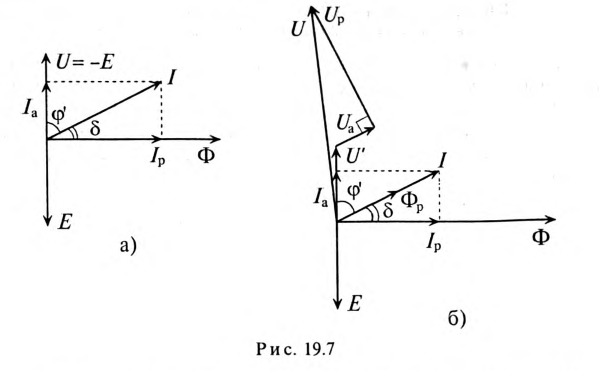
При синусоидальном токе векторная диаграмма для катушки (без активного сопротивления) со стальным сердечником (без рассеяния) может быть построена как для идеальной индуктивности (рис. 11.4б), т. е. ток отстает от напряжения на угол 90°.
Если учесть потери на циклическое перемагничивание в сердечнике 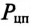
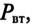
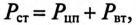
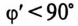
совпадающая по фазе с напряжением, и реактивная составляющая тока
Реактивная составляющая тока, совпадающая по фазе с магнитным потоком и намагничивающая сердечник, называется намагничивающим током катушки.
Угол 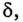
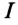
Потери в стали (магнитные потери) можно определить выражением
где G — масса ферромагнитного сердечника, кг; 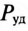
Удельную мощность потерь вычисляют по формуле
где 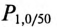
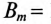
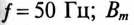
Значения 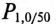
Если не пренебрегать активным сопротивлением катушки R, то падение напряжения на этом сопротивлении 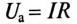
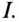
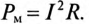
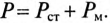
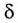
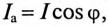
Большая часть магнитного потока, т. е. основной поток Ф, замыкается в сердечнике, а незначительная часть потока 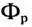
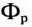
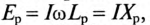
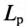
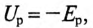
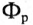
Следовательно, напряжение на зажимах катушки со стальным сердечником складывается из напряжения 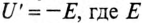
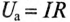
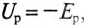
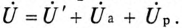
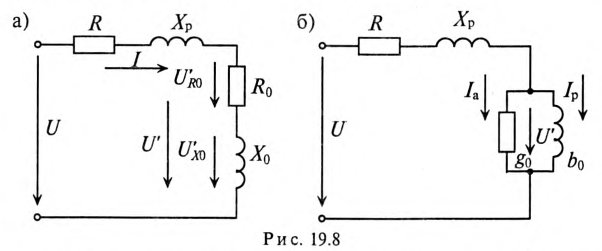
Схема замещения
Эквивалентная схема катушки со стальным сердечником изображена на рис. 19.4в. На эквивалентной схеме выделены активное сопротивление R и индуктивное сопротивление рассеяния 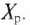
Напряжение 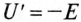
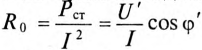
Эти соображения легли в основу построения схемы замещения катушки со стальным сердечником (рис. 19.8а).
Реальная катушка (рис. 19.4а) и схема ее замещения (рис. 19.8б) при одинаковых напряжениях на зажимах U имеют одинаковые токи и мощности.
Активная составляющая тока определяет активную проводимость идеальной катушки 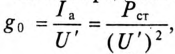
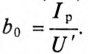
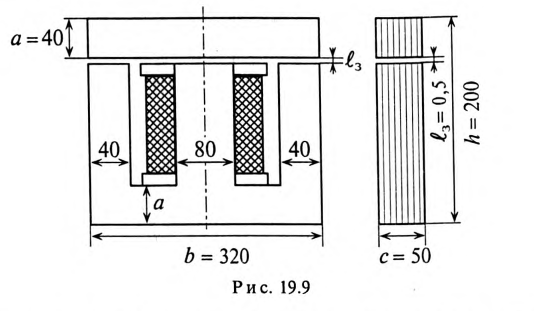
Пример 19.1
На среднем стержне Ш-образного магнитопровода (рис. 19.9), выполненного из листовой 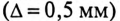
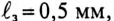
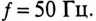
Определить число витков обмотки W, ток в обмотке 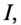
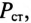
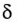
Решение
По выражению (19.1) определяется число витков обмотки
где
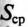
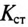
Расчет намагничивающего тока 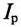
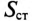
Длина средней линии половины сердечника
Напряженность магнитного поля в магнитопроводе (Приложение 5) для стали Э42 (1512) 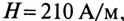
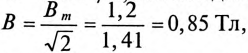
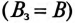
Поправочный коэффициент 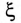
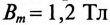
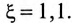
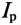
Масса стали сердечника
где 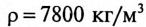
Потери в стали
где 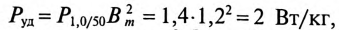
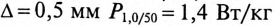
Активная составляющая тока обмотки обусловлена этими потерями, т. е.
Ток в обмотке (рис. 19.7) будет равен
Коэффициент мощности цепи 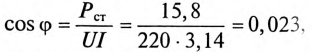
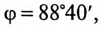
Феррорезонанс
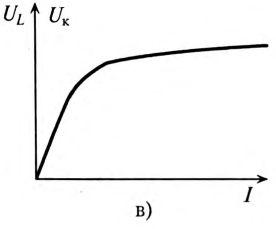
В цепи с нелинейной индуктивностью (катушка со стальным сердечником) существует нелинейная зависимость напряжения на индуктивности 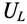
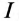
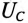
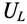
Цепи, содержащие нелинейную индуктивность и линейную емкость, называют феррорезонансными, а явление равенства напряжений 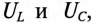
Для объяснения явления феррорезонанса можно воспользоваться вольт-амперной характеристикой нелинейной индуктивности 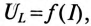
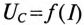
При построении суммарной вольт-амперной характеристики
рассматриваемой цепи исходят из того, что напряжение источника U уравновешивается суммой напряжений:
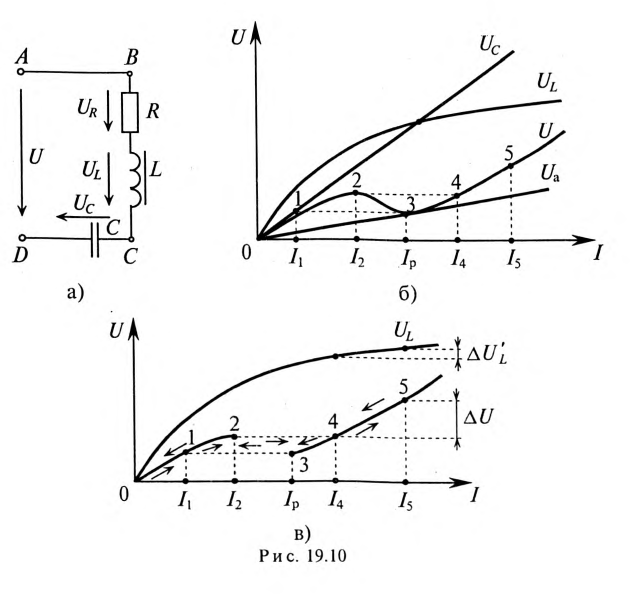
Из векторной диаграммы для рассматриваемой цепи (рис. 12.46) следует, что индуктивное напряжение UL опережает по фазе ток на угол 90°, а емкостное напряжение Uc — отстает на 90 (Для упрощения несинусоидальные величины заменены эквивалентными синусоидальными, т. е. вольт-амперная характеристика нелинейной катушки UL=f(I) аналогична характеристике, показанной на рис. 19.5в.) Следовательно,, реактивные напряжения UL и Uc находятся в противофазе, т. е. Up = UL – Uc.
Величину емкости можно подобрать так, чтобы прямая Uc=f(I) пересекла кривую UL=f(I). Точка их пересечения и является том кой феррорезонанса напряжений (UL = Uc), при котором Up = UL – Uс =0. Следовательно, 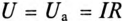
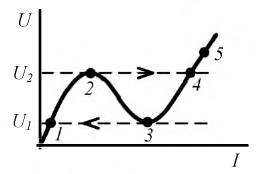
Из графика (рис. 19.106) следует, что с увеличением тока I напряжение U сначала растет (участок 0—2), затем уменьшается (участок 2—3), достигая минимального значения при феррорезонансе (точка 3), затем снова растет (участок 3—5).
Из того же графика видно, что при непрерывном увеличении напряжения источника U ток плавно увеличивается до значения 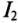
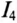
При плавном уменьшении напряжения U ток 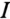
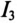
Характерно, что при каждом скачке тока 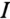
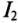
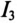
Явление «опрокидывания фазы» проиллюстрировано на рис. 19.10в, на котором показаны кривые напряжений U=f(I) и UL =f(I). Из кривой UL =f(I) видно, что напряжение на выводах катушки (точки В и С схемы — рис. 19.10а) остается почти неизменным (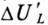
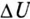
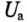
Это явление используется в феррорезонансных стабилизаторах напряжения, в которых значительное изменение входного напряжения (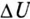
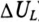
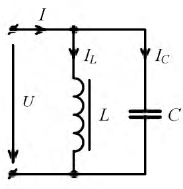
При параллельном соединении катушки с ферромагнитным сердечником и конденсатора может возникнуть феррорезонанс токов, если
Элементы нелинейных цепей, их характеристики и параметры
Все ранее выполненные исследования касались анализа режима работы линейных электрических цепей. В их составе присутствовали исключительно линейные элементы, ток и напряжение в которых были связаны линейным уравнением. В подавляющем большинстве реальных цепей зависимость тока от напряжения в большей или меньшей степени отлична от линейной и в этом случае говорят о нелинейных цепях.
Цепь считается нелинейной, если емкость, сопротивление или индуктивность любого участка является функцией напряжения и тока, а также их направления. Особо подчеркнем, что принцип наложения в таких цепях неприменим. В отличие от линейных элементов, характеристики которых задаются аналитическими функциями, нелинейные задаются экспериментальными зависимостями, с помощью таблиц или приближенными эмпирическими формулами. Все это усложняет расчет цепей и требует специальных методов расчета.
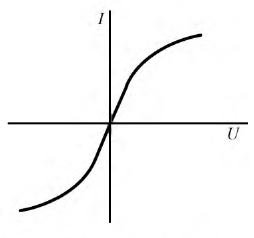
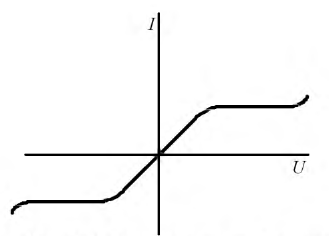
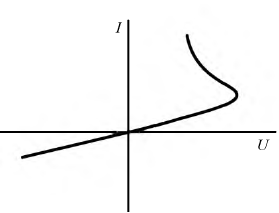
Нелинейное сопротивление характеризуется нелинейной вольтамперной характеристикой, нелинейная катушка задаётся вебер-амперной характеристикой, ёмкость характеризуется кулон-вольтной характеристикой. Все перечисленные зависимости весьма разнообразны, но их можно систематизировать по двум основным группам: симметричные и несимметричные. Нелинейный элемент будет иметь симметричную характеристику, если форма кривой не зависит от направления тока или направления приложенного напряжения, в противном случае характеристика становится несимметричной. На рис. 9.1-9.2 изображены симметричные вольтамперные характеристики (В.А.Х.) и, соответственно, на рис. 9.3-9.4 – несимметричные.
Рис. 9.1. В.А.Х. лампы накаливания
Рис. 9.2. В.А.Х. характеристика бареттера
Рис. 9.3. В.А.Х. электрической дуги
Рис. 9.4. В.А.Х. диода
Нелинейные элементы могут быть подразделены на управляемые и неуправляемые. Отличительной особенностью управляемых элементов является наличие семейства характеристик: транзисторы, тиристоры, магнитные усилители и т.д.
Статистические и дифференциальные характеристики нелинейных элементов
Режим работы нелинейного элемента (НЭ) во многом зависит от положения рабочей точки на характеристике (рис. 9.5). Пусть точка 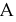
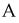
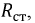
Сопротивление 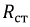
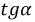
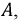
Дифференциальное сопротивление 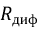
Рис. 9.5. В.А.Х. НЭ
Численно дифференциальное сопротивление равно тангенсу угла наклона касательной 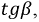
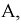
Замена нелинейного элемента линейным и источником ЭДС – один из вариантов линеаризации цепи.
Если заранее известен участок 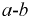
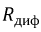
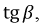
где 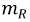
Рис. 9.6. Линеаризация НЭ
Следовательно, уравнение электрического равновесия на основании рис. 9.6 примет вид:
Таким образом, исходный нелинейный элемент (рис. 9.7) заменяется на линейный, схема замещения которого изображена рис. 9.8.
Рис. 9.7. Исходный НЭ
Рис. 9.8. Эквивалентная схема замещения НЭ
При ином наклоне характеристики НЭ (рис. 9.9) получим:
Рис. 9.9. Вольт-амперная характеристика НЭ
Расчет электрической цепи при смешанном соединении нелинейных элементов
Рассмотрим общий принцип расчета нелинейных цепей с использованием графоаналитического метода.
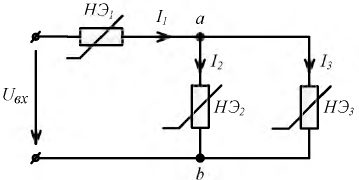
Пусть дана цепь, содержащая три нелинейных элемента, каждый из которых задан своей вольтамперной характеристикой (рис. 9.10-9.11).
Рис. 9.10. Исследуемая цепь с НЭ
Применительно к цепи по рис. 9.10 запишем уравнения по законам Кирхгофа:
Рис. 9.11. В.А.Х. элементов исходной цепи
Расчет будем вести в следующей последовательности.
Произвольно задаваясь значениями напряжения 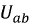
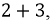
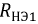
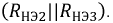
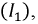
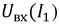
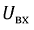
Из точки ординаты, соответствующей току 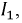
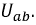
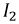
Метод двух узлов
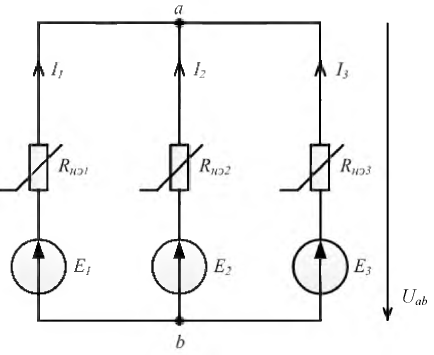
Для нелинейной цепи, имеющей два узла, расчет можно вести методом двух узлов. Покажем его применимость на примере цепи следующего вида (рис. 9.12).
Рис. 9.12. Нелинейная электрическая цепь
Каждый из элементов 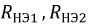
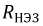
Напряжение на каждом из элементов может быть определено следующим образом:
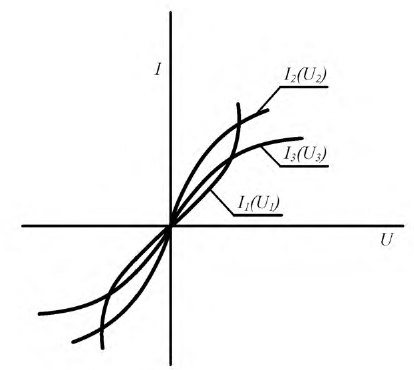
Рис. 9.13. В.А.Х. нелинейных элементов
Поскольку напряжение 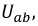
Трансформируем данные функции относительно общего напряжения 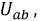
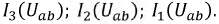
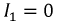
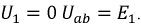
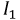
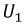
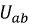
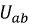
Задаваясь рядом значений 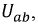
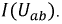
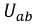
Первый и третий токи положительны, а второй ток отрицателен, т.е. его направление на схеме нужно изменить на противоположное.
Стабилизация напряжения и тока с помощью нелинейных элементов
В линейных цепях это явление не может быть реализовано.
В основе стабилизации лежит наличие у В.А.Х. элемента участков практически параллельных осям напряжений или токов.
Основная задача стабилизации состоит в том, что при существенных изменениях входных напряжений выходные напряжения или токи меняются незначительно. Вводится коэффициент стабилизации, например, по напряжению:
Качество стабилизации зависит не только от наличия элемента с требуемой характеристикой, но и поддержания требуемого режима работы этого элемента, т.е. стабильности рабочей точки. Изобразим простейшие схемы стабилизации (рис. 9.14,a,b).
Рис. 9.14. Схемы стабилизации напряжения: а) последовательная, b) параллельная
Рассмотрим процесс стабилизации на примере последовательной цепи (рис. 9.14,а).
При значительном изменении напряжения на входе 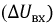
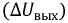
Рис. 9.15. Стабилизация напряжения
Метод эквивалентного генератора
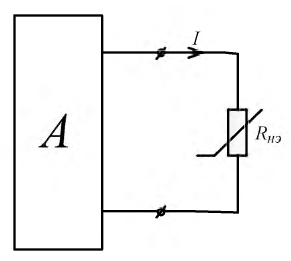
Если в схеме есть один нелинейный элемент, а остальные – линейные и необходимо рассчитать ток через нелинейный элемент, то выделяют ветвь с нелинейным элементом, а оставшуюся линейную схему представляют в виде активного двухполюсника (рис. 9.16).
Рис. 9.16. Активный двухполюсник, нагруженный нелинейным сопротивлением
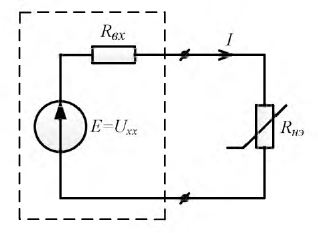
Активный линейный двухполюсник замещается источником ЭДС и некоторым внутренним линейным сопротивлением 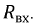
После проведенных преобразований, рассмотренных выше, определение тока в ветви с нелинейным элементом не представляет трудностей.
Нелинейные магнитные цепи при постоянных токах
Самостоятельную группу нелинейных цепей образуют магнитные цепи. Магнитной цепью называется совокупность устройств, содержащих ферромагнитные тела, процессы в которых описываются понятиями магнитодвижущей или намагничивающей силы (МДС), магнитного потока и падения магнитного напряжения или разности магнитных потенциалов. Из курса физики известен закон полного тока, который формулируется так: циркуляция вектора напряженности вдоль замкнутого контура равна алгебраической сумме токов, охваченных этим контуром, т. е.:
Этот закон связывает магнитное поле с напряженностью 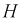
Магнитная индукция 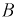
где 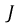
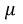
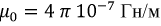
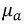
В системе СИ единица индукции В – тесла 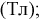
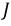
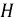
Магнитный поток 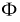
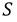
Для ферромагнитных материалов связь между 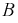
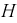
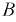
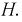
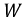
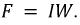
Рис. 9.18. Неразветвленный магнитопровод переменного сечения с зазором
Поскольку магнитопровод неразветвлен и его сечение на разных участках неодинаково, то и магнитная индукция также не одинакова, а магнитный поток 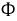
Используя данное соотношение, подставим его в (9.6) и получим следующее выражение:
откуда:
Выражение (9.7) есть закон Ома для магнитных цепей.
Магнитное сопротивление участка цепи длиной 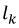
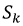
Разветвленные магнитные цепи, как и электрические цепи, можно описать законами Кирхгофа.
Первый закон Кирхгофа: алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю:
Второй закон Кирхгофа: алгебраическая сумма падений магнитных напряжений в контуре равна алгебраической сумме МДС, действующих в этом контуре:
где 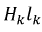
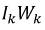
Постоянный магнит
Постоянный магнит нашел широкое практическое применение (генераторы тока, магнето, преобразующие элементы приборов магнитоэлектрической системы, динамики, громкоговорители и т.д.). Рассмотрим принцип расчета постоянного магнита. Если на замкнутый магнитопровод, выполненный из магнитотвердого материала (широкая петля гистерезиса) намотать обмотку и пропустить через неё ток, то магнитопровод можно довести до насыщения. Затем ток уменьшить до нуля, при этом напряженность также снижается до нуля, а индукция не обращается в нуль (кривая размагничивания стали, рис. 9.19). После этого катушку снимают и остается рассчитать магнитную индукцию 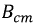
Рис. 9.19. Кривая размагничивания стали
Для получения реального магнита в магнитопроводе делают тонкий пропил, при этом будем считать, что площадь сечения магнитопровода с пропилом и площадь без пропила стали одинаковы. Будем полагать известными кривую размагничивания магнитопровода, длину воздушного зазора 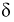
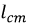
Нуль в правой части уравнения объясняется отсутствием катушки на магнитопроводе.
Если зазор достаточно мал, то потоком рассеяния в зазоре можно пренебречь:
где 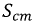
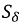
Так как магнитопровод не разветвленный, то магнитный поток в пропиле и стали, будет одинаков:
После этого магнитопровод перестает быть однородным и из уравнения (9.8) получим:
Тогда:
Таким образом, между 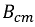
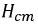
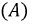
Особенности работы нелинейных элементов в цепях переменного тока
Работа нелинейных элементов в цепях переменного тока приводит к возникновению явлений, принципиально невозможных в линейных цепях, причем на этих особенностях базируются принципы действия новых приборов. С помощью нелинейных элементов осуществляется выпрямление переменного тока, умножение и деление частоты, стабилизация напряжения, усиление сигнала и т.д. Работа нелинейных элементов и электрических цепей, в которые входят эти элементы, описывается нелинейными дифференциальными уравнениями, точных методов решения которых в математике не существует. Поэтому для проведения инженерных расчетов применяют различные приближенные методы расчёта этих дифференциальных уравнений и в соответствии с этим существуют разные методы расчета нелинейных цепей на переменном токе. Назовем некоторые из них.
- Метод малого параметра и условной линеаризации. Основан на пренебрежении относительно малыми величинами. При этом полученная условно линейная цепь рассчитывается известными методами расчета линейных цепей, но с учетом нелинейной зависимости между действующими значениями токов и напряжений.
- Метод аналитической аппроксимации нелинейной характеристики. Основан на замене нелинейной зависимости неким аналитическим выражением так, чтобы оно достаточно точно описывало нелинейную зависимость и полученное дифференциальное уравнение решалось относительно просто.
- Метод кусочно-линейной аппроксимации и припасовывания линейного решения. Основан на замене нелинейной характеристики ломаной кривой и применении на каждом участке ломаной кривой методов линейной электротехники, а переход от одного участка ломаной кривой к другому участку осуществляется соответствующим выбором постоянных интегрирования.
- Итерационный метод. Основан на подстановке некоторого приближенного решения в исходное уравнение и последующем уточнении этого решения.
Нелинейные магнитные цепи при периодических процессах
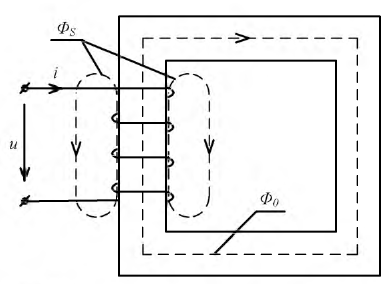
Нелинейные магнитные цепи при периодических процессах также нашли широкое практическое применение, это различного рода электромагнитные аппараты и устройства, основным элементом которых является катушка с ферромагнитным сердечником (рис. 9.20). Исследование ее режимов работы позволит сделать количественную и качественную оценку происходящих в ней явлений.
Рис. 9.20. Катушка с ферромагнитным сердечником
В катушке с ферромагнитным сердечником необходимо выделить два магнитных потока: основной 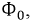
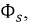
где 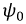
С учетом того, что сама обмотка, выполненная из медного провода, имеет сопротивление 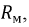
Уравнение (9.10) нелинейно, т.к. 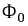
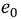
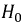
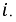
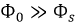
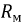
Идеальная катушка индуктивности
Таким образом, уравнение равновесия идеальной катушки имеет вид:
Будем считать, что напряжение сети изменяется по косинусоидальному закону 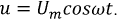
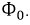
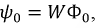
Действующее значение напряжения, выраженное через магнитный поток:
Магнитный поток, так же, как и приложенное напряжение, изменяется по синусоидальному закону. ЭДС самоиндукции отстает от магнитного потока на угол 90°, в свою очередь напряжение и ЭДС находятся в противофазе, поэтому напряжение опережает магнитный поток на 90°.
Определим форму тока в катушке, считая, что магнитопровод изготовлен из магнитомягкого материала. Для решения этой задачи воспользуемся графоаналитическим методом (рис. 9.21).
Рис. 9.21. Графическое определение закона изменения тока в катушке
Форма тока получилась несинусоидальная, что указывает на искажение тока в нелинейных цепях и, соответственно, усложняет расчет. Если учесть петлю гистерезиса реального магнитопровода, то форма кривой тока еще более усложнится (рис. 9.22).
Рис. 9.22. Графическое определение закона изменения тока при учете петли гистерезиса
Появление угла 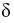
Уравнение электрического равновесия идеальной катушки запишется в виде:
Анализ поведения тока идеальной катушки позволяет построить векторную диаграмму (рис. 9.23).
Рис. 9.23. Векторная диаграмма идеальной катушки
Из векторной диаграммы следует, что угол сдвига между током и напряжением катушки 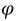
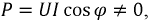
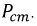
Потери на гистерезис
Мощность этой составляющей потерь зависит от целого ряда факторов. Одной из эмпирических зависимостей, полученных для расчета потерь на перемагничивание, является формула Штейнмеца:
где 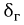
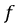
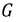
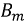
Степень 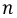
1) 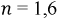
2) 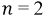
Потери на вихревые токи
Вихревые токи возникают ввиду того, что магнитопровод, изготовленный из стали, является проводящим, и под действием наведенной ЭДС линии тока расположены в контуре, перпендикулярно силовым линиям. Величина наведенной ЭДС зависит от частоты и магнитной индукции и мощность, расходуемая на тепловые потери, вызванные вихревыми токами, рассчитывается по формуле:
где 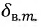
Для уменьшения этих потерь поступают следующим образом: магнитопровод набирают из листов стали, изолированных друг от друга с помощью лака или добавляют в ферромагнитный материал примеси, увеличивающие удельное сопротивление стали. Так как 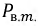
1) при
2) при
На очень высоких частотах магнитопровод изготавливают из магнитодиэлектриков – ферритов, которые представляют собой смесь из мелких ферромагнитных частиц и диэлектрика.
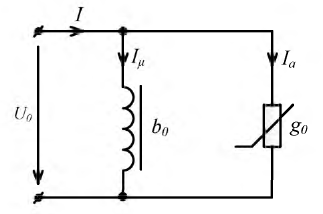
Схема замещения идеальной катушки
На векторной диаграмме идеальной катушки (рис. 9.23) показано разложение вектора тока на активную 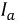
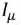
Рис. 9.24. Схема замещения идеальной катушки
Активная составляющая тока протекает по нелинейной активной проводимости 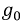
Реактивная составляющая тока протекает по нелинейной индуктивности и, соответственно, реактивная мощность:
Векторная диаграмма и схема замещения реальной катушки
Возвращаясь к уравнению (9.10) и учитывая, что несинусоидальный ток заменен эквивалентным синусоидальным, перепишем это уравнение в комплексной форме:
где 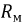
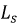
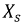
На основании уравнения (9.12) схема замещения реальной катушки примет вид (рис. 9.25):
Рис. 9.25. Последовательно-параллельная схема замещения реальной катушки
Параметры схемы замещения могут быть получены на основании экспериментальных измерений напряжения, тока и мощности, потребляемой катушкой из цепи. По результатам этих измерений вначале строят более простую – последовательную схему замещения (рис. 9.26).
Параметры последовательной и последовательно-параллельной схем замещения связаны между собой следующими соотношениями:
На основании схемы замещения можно построить и векторную диаграмму (рис. 9.27).
Рис. 9.26. Последовательная схема замещения реальной катушки
Рис. 9.27. Векторная диаграмма реальной катушки
Трансформатор с ферромагнитным сердечником
Основным элементом трансформатора является рассмотренная выше катушка с ферромагнитным сердечником и дополнительно намотанной на него второй катушкой. По сравнению с линейным трансформатором у трансформатора с ферромагнитным сердечником резко увеличивается магнитный поток, что в свою очередь приводит к увеличению мощности, передаваемой из одной обмотки в другую, но трансформатор с ферромагнитным сердечником становится нелинейным и в его магнитопроводе появляются потери. Как и при анализе работы катушки, используют понятия эквивалентных синусоид. Потому напряжения, токи и магнитный поток считают синусоидальными. Подавляющее большинство трансформаторов конструируется с максимальной близостью к линейным. Область использования трансформаторов весьма широка – это силовые, измерительные, согласующие, сварочные и т.д. Так как принцип работы воздушного трансформатора ранее был подробно рассмотрен, то ограничимся лишь составлением и анализом схемы замещения трансформатора с сердечником (рис. 9.28).
Рис. 9.28. Схема замещения трансформатора с ферромагнитным сердечником
Запишем уравнения трансформатора для мгновенных величин токов и напряжений. Первые два – это уравнения электрического равновесия для первичной и вторичной цепи, третье – уравнение намагничивающих сил:
В комплексной форме эта система уравнений примет вид:
Некоторого пояснения требует уравнение магнитного равновесия.
В режиме холостого хода 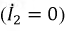
где 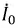
При этом МДС первичной обмотки равна 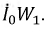
Поскольку подводимое к первичной обмотке напряжение не изменилось, то не изменился и магнитный поток трансформатора:
Следовательно, МДС в режиме холостого хода и в нагрузочном режиме равны:
Тогда:
где:
У приведенной схемы замещения трансформатора (рис. 9.28) все вторичные параметры изменились и поэтому уравнения (9.13), описывающие его работу, видоизменятся:
Для составления схемы замещения трансформатора необходимо определить ее параметры, т. е. сопротивления 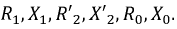
Опыт холостого хода.
Проводится при номинальном первичном напряжении 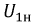
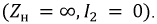
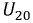
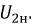
Рис. 9.29. Схема замещения трансформатора при опыте XX
Ток холостого хода 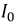
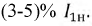
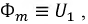
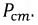
Примечание: сопротивлением 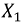
Поскольку у трансформаторов малы активные сопротивления обмоток, а также потоки рассеяния, то можно принять 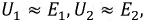
Опыт короткого замыкания.
Проводится при замкнутой накоротко вторичной обмотке трансформатора 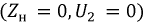
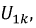
Так как 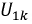
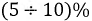
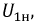
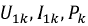
Примечание. При приведении вторичной обмотки к первичной сопротивления
Для режима короткого замыкания схема замещения представлена на рис. 9.30. Пунктиром показано положение ветви намагничивания.
Рис. 9.30. Схема замещения трансформатора в режиме КЗ
В режиме КЗ намагничивающей составляющей 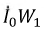
Тогда коэффициент трансформации можно определить следующим образом:
Векторная диаграмма трансформатора под нагрузкой
Используя систему уравнений (9.13), а также соотношения, полученные выше, построим векторную диаграмму, приняв для определенности, что трансформатор работает под нагрузкой при
Рис. 9.31. Векторная диаграмма трансформатора, работающего под нагрузкой
Построение диаграммы начнем с вектора 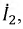
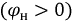
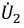
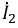
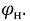
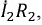
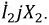
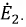
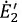
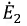
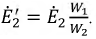
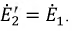
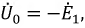
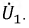
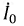
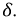
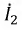
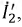
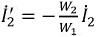
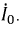
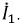
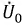
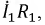
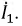
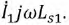
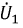
Феррорезонансные явления
В нелинейных цепях, составленных из нелинейных индуктивностей и линейных емкостей или наоборот, линейных индуктивностей и нелинейных емкостей возможны резонансные явления, как и в линейных цепях, но они характеризуются рядом особенностей. Феррорезонанс – это резонанс в цепи, содержащей катушку с ферромагнитным сердечником, который последовательно или параллельно подсоединен к линейному конденсатору. В линейных цепях резонанс возникал при изменении каких-либо параметров цепи: индуктивности 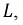
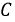
Феррорезонанс напряжений
Феррорезонанс напряжений возникает в последовательном колебательном контуре (рис. 9.32).
Рис. 9.32. Схема для исследования феррорезонанса напряжения
На рис. 9.33 построены В.А.Х. линейной емкости 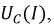
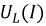
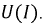
Рис. 9.33. Вольтамперные характеристики цепи при феррорезонансе напряжений
График зависимости 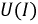
При работе схемы от источника напряжения и плавном росте напряжения до 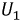
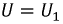
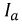
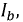
Модуль напряжения сети подсчитывается по приведенной ниже формуле:
Скачкообразное изменение тока при увеличении напряжения выше 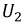
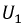
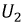
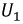
Рис. 9.34. Реальная вольт-амперная характеристика цепи при феррорезонансе напряжений
Феррорезонанс токов
Феррорезонанс токов наблюдается при параллельном соединении нелинейной индуктивности и линейного конденсатора (рис. 9.35).
Рис. 9.35. Схема для исследования феррорезонанса токов
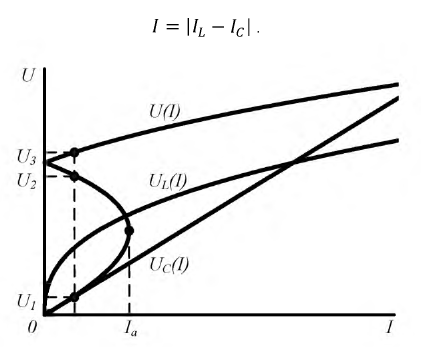
Будем полагать, что известны В.А.Х. идеальной нелинейной индуктивности и идеальной емкости, построенные для действующих значений. На рис. 9.36 построены В.А.Х. рассматриваемых элементов и суммарная В.А.Х., полученная на основании уравнения:
Рис. 9.36. Вольтамперные характеристики цепи при феррорезонансе токов
Из построений следует, что одному и тому же значению тока в диапазоне 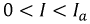
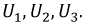
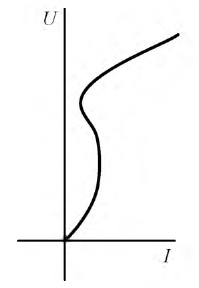
В реальной цепи при учете потерь и высших гармоник общая В.А.Х. цепи имеет вид, показанный на рис. 9.37.
При плавном изменении напряжения источника можно получить всю кривую 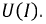
Рис. 9.37. Реальная вольт-амперная характеристика цепи при феррорезонансе токов
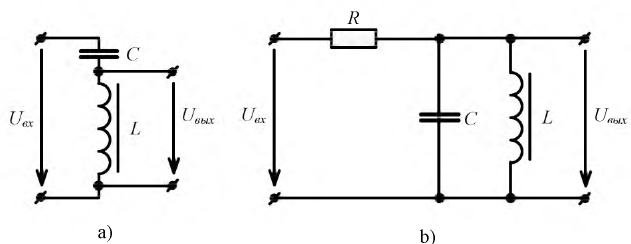
На практике он используется при создании так называемых ферромагнитных стабилизаторов напряжения. Ниже (рис. 9.38,a,b) приведены примеры простейших схем стабилизации.
Рис. 9.38 а,b. Схемы ферромагнитных стабилизаторов напряжения
Ферромагнитный усилитель
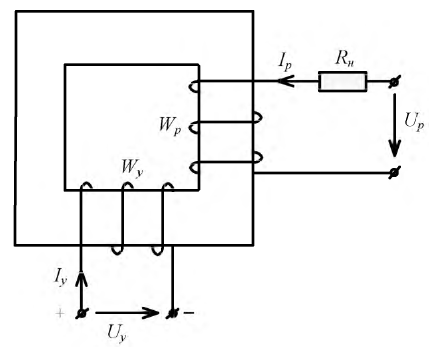
Нелинейность свойств магнитопроводов лежит в основе работы многих устройств, среди которых особое место отводится управляемым нелинейным элементам. Примером таких устройств являются магнитные усилители, способные усиливать ток и мощность при сохранении формы выходного напряжения. Результирующий магнитный поток магнитного усилителя является суммой магнитных потоков, создаваемых МДС на различных частотах, источниками которых в магнитном усилителе служат рабочая обмотка и обмотка управления. Общий принцип работы простейшего магнитного усилителя рассмотрим на примере схемы рис. 9.39.
Рис. 9.39. Схема простейшего магнитного усилителя
На ферромагнитный сердечник наматывают две обмотки: 
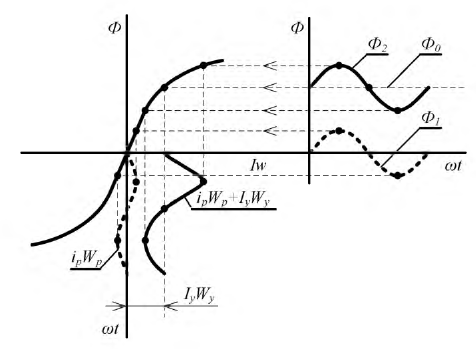
Рассмотрим принцип работы магнитного усилителя. Для этого сделаем ряд графических построений (рис. 9.40) и при этом будем считать, что вебер-амперная характеристика магнитопровода известна. Используем магнитопровод из магнитомягкого материала (узкая петля гистерезиса).
При отсутствии тока в обмотке управления 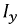
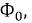
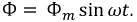
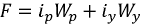
Рис. 9.40. Схема усиления сигнала
Напишем уравнение электрического равновесия для рабочей обмотки магнитного усилителя:
Из данного уравнения следует, что уменьшение ЭДС самоиндукции в рабочей обмотке приведет к увеличению тока, протекающего через сопротивление нагрузки 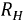
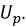
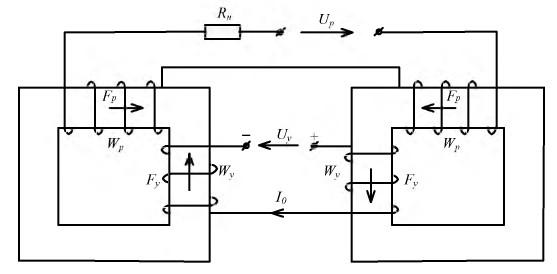
Рис. 9.41. Схема магнитного усилителя мощности
Эффективность работы магнитного усилителя определяется коэффициентами усиления по току и мощности:
Оптимальный режим работы магнитного усилителя можно рассчитать, если известно семейство его вольтамперных характеристик (рис. 9.42).
На основании второго закона Кирхгофа и учитывая, что 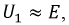
Рис. 9.42. Семейство В.А.Х. магнитного усилителя
Данное уравнение представляет собой уравнение окружности радиусом 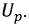
Вентиль в цепи синусоидального тока
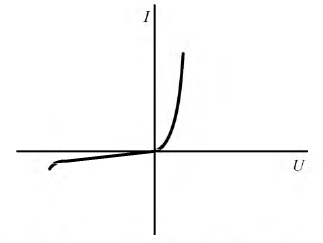
Полупроводниковые электронные приборы с практически односторонней проводимостью носят название вентиля (диода). Они относятся к классу активных нелинейных сопротивлений, которые так же задаются нелинейной В.А.Х. Кроме того, они относятся к классу безынерционных нелинейных элементов. На рис. 9.43 приведена В.А.Х. диода.
Рис. 9.43. Вольтамперная характеристика вентиля
Главное назначение вентиля – выпрямление переменного тока. Рассмотрим простейшую схему однополупериодного выпрямителя (рис. 9.44).
Рис. 9.44. Схема однополупериодного выпрямителя
Реализация принципа выпрямления тока в нагрузке иллюстрируется рис. 9.45.
Рис. 9.45. Графическое определение временной зависимости тока 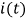
Из построения видно, что при отрицательной полуволне напряжения источника амплитуда тока резко уменьшается, а большей амплитуде входного напряжения соответствует больший выпрямительный эффект. Ток и, соответственно, падение напряжения на нагрузке имеют явно выраженную несинусоидальную форму и поэтому могут быть разложены в ряд, который содержит постоянную составляющую, первую и все четные гармоники. Если на нагрузке необходимо иметь постоянное напряжение, то перед нагрузкой включают фильтры, не пропускающие первую и все гармоники более высокого порядка. Аналогично работают выпрямители, построенные по более сложным схемам.
- Магнитные цепи и их расчёт
- Цепи переменного тока
- Символический метод расчета цепей
- Четырехполюсники
- Линейные и нелинейные резисторы
- Индуктивность и ее расчет
- Энергия в электрических цепях
- Линейные электрические цепи
A1
2.00
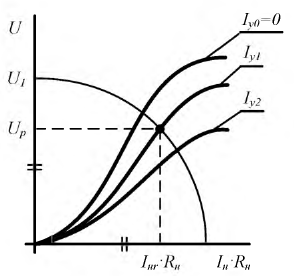
Найдите максимальную мощность $P_1$, выделяющуюся на нелинейном элементе.
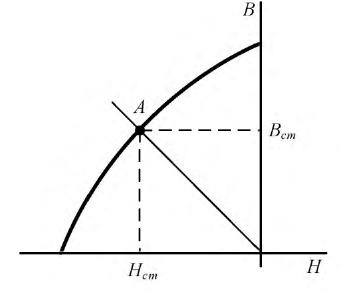
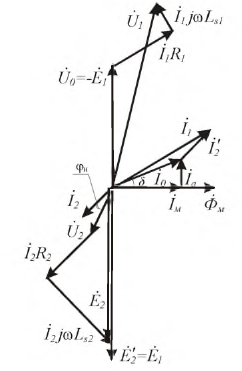
Обозначим за $A$ точку на графике вольт-амперной характеристики нелинейного элемента, а за $O$ — центр окружности. Пусть $OA$ составляет угол $varphi$ с осью напряжений $frac{U}{U_0}=x$. Тогда
$$P_{НЭ}=IU={U_0}{I_0}sinvarphi cosvarphi=frac{{U_0}{I_0}sin 2varphi}{2}
$$
В начальный момент угол $varphi$ принимает значение $pi/3$, поэтому в процессе дальнейшей зарядки конденсатора величина $2varphi$ принимает значения $frac{2pi}{3}leqvarphileq2pi$.
Таким образом, максимальная мощность, выделяющаяся на нелинейном элементе достигается в момент замыкания ключа и равна
Ответ:
$$P_1=frac{{U_0}{I_0}sqrt{3}}{4}$$
A2
8.00
Найдите максимальную скорость изменения энергии конденсатора $P_2$ и время после замыкания ключа $Delta t$, через которое она достигается.
Скорость изменения энергии конденсатора
$$frac{dW}{dt}={I_C}{U_C}={U_0}{I_0}sinvarphi(1-cosvarphi)$$
Величина $sinvarphi(1-cosvarphi)$ является площадью равнобедренного треугольника с основанием $2sinvarphi$ и высотой $(1-cosvarphi)$, вписанного в окружность единичного радиуса. Максимум площади достигается в случае равностороннего треугольника. Таким образом, в этот момент времени $varphi$ принимает значение $2pi/3$, а максимальная площадь равняется $S_{max}=3sqrt{3}/4$
Окончательно
$$P_2=frac{3sqrt{3} {U_0}{I_0}}{4}$$
Найдём время, через которое $varphi$ принимает значение $2pi/3$. Рассмотрим изменение напряжения на конденсаторе с течением времени. Поскольку суммарное напряжение на нелинейном элементе и конденсаторе сохраняется
$$frac{dU_C}{dt}=-{U_0}frac{dx}{dt}$$
Величину $frac{dx}{dt}$ найдём из условия движения точки $A$ по окружности с некоторой угловой скоростью $omega$
$$frac{dx}{dt}=-{omega}sinvarphi Rightarrow frac{dU_C}{dt}={omega},{U_0}sinvarphi$$
С другой стороны
$$q_C=CU_C$$
Откуда
$$I_C=Cfrac{dU_C}{dt}={I_0}sinvarphi$$
Комбинируя два выражения для $frac{dU_C}{dt}$
$$omega=frac{I_0}{CU_0}=mathrm{const}$$
Таким образом, $OA$ вращается с постоянной угловой скоростью и к моменту достижения максимальной скорости изменения конденсатора поворачивается на угол $pi/3$, откуда сразу получим выражение для времени
$${Delta}t=frac{{pi}CU_0}{3I_0}$$
Ответ:
$$P_2=frac{3sqrt{3} {U_0}{I_0}}{4}$$
$${Delta}t=frac{{pi}CU_0}{3I_0}$$
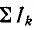
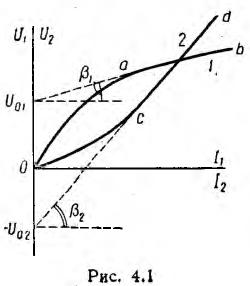
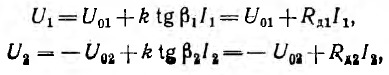
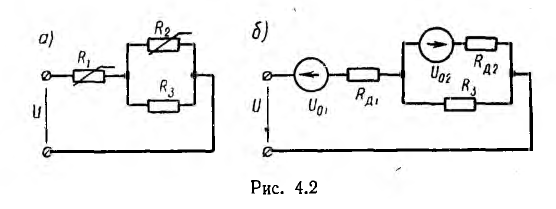
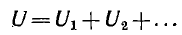
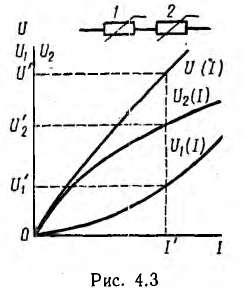
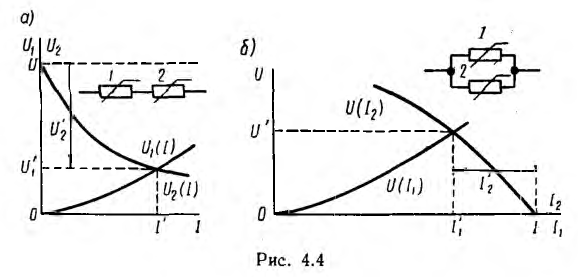
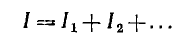
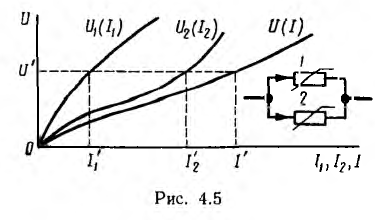
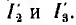
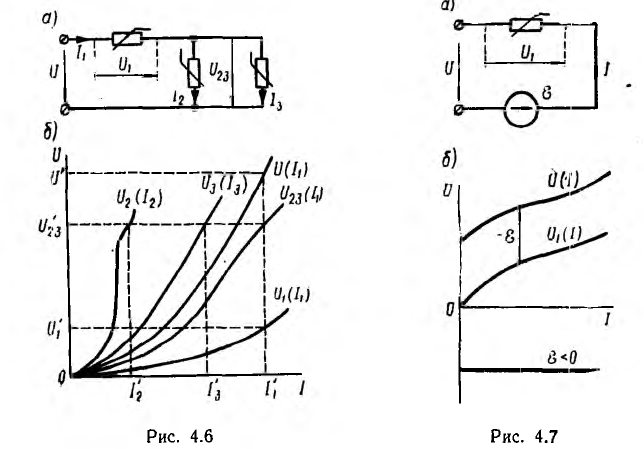
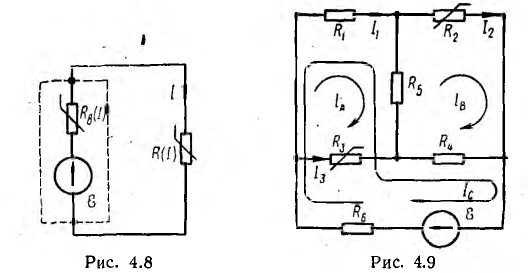
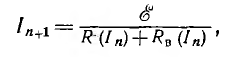
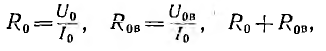
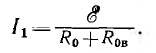
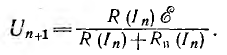
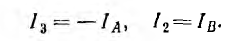
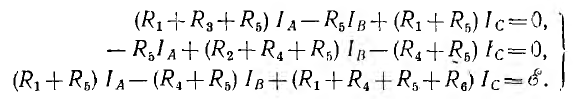
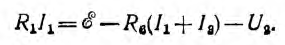
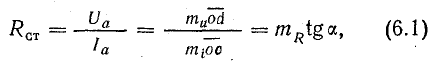
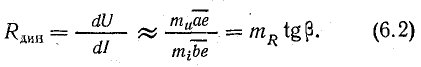
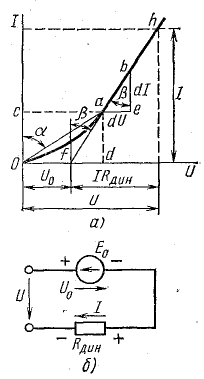

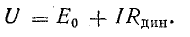

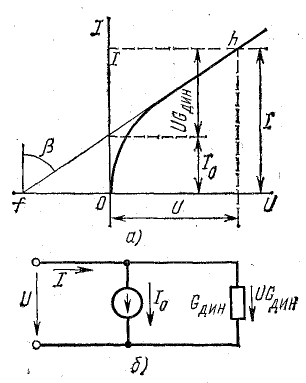
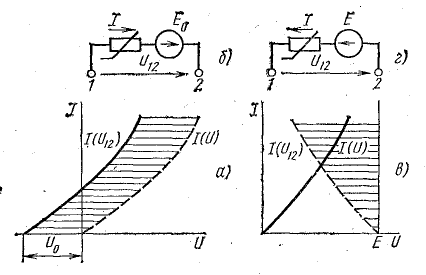
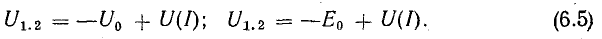
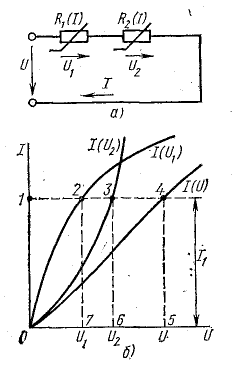
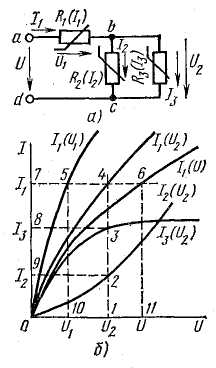
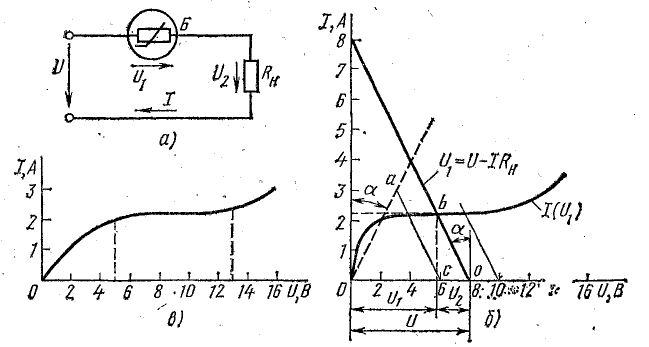
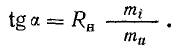
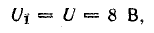
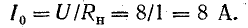
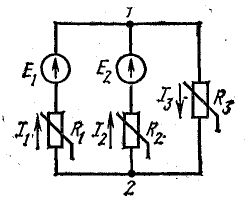
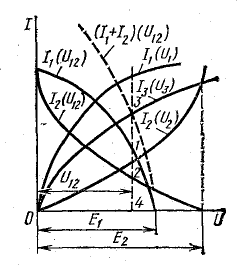
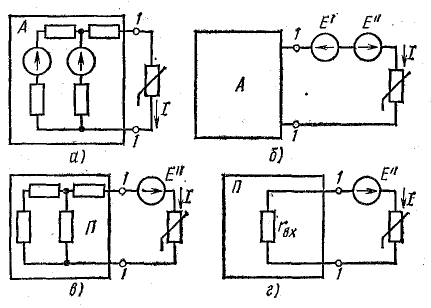
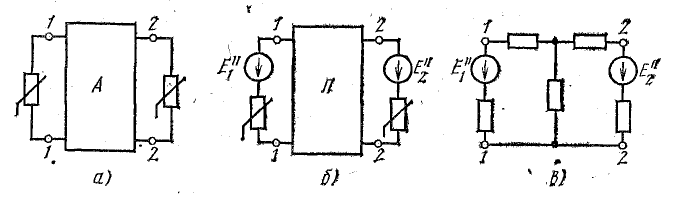
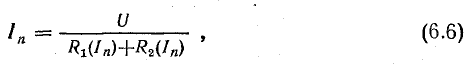
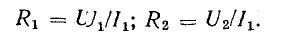
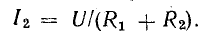
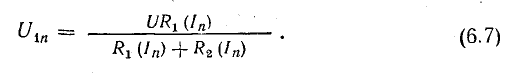
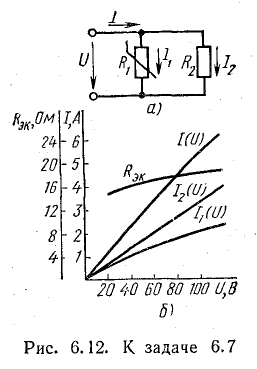
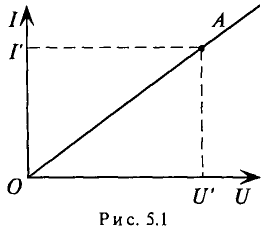
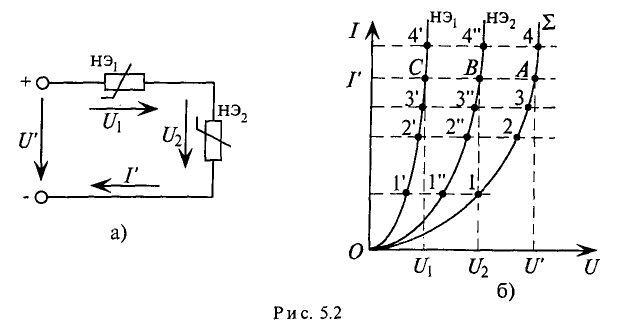

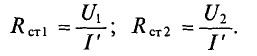

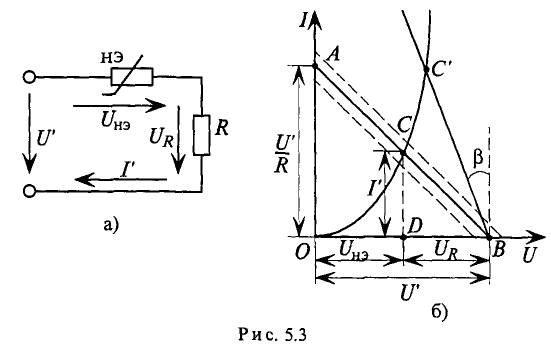
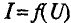
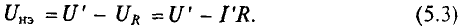
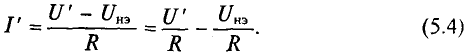
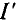 ,
,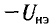 ,
,