У этого термина существуют и другие значения, см. Исключение.
Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре[1].
Например, в случае двух множеств 

В сумме 


Таким же образом и в случае 

Формулировка[править | править код]
Формулу включений-исключений можно сформулировать в разных формах.
В терминах множеств[править | править код]
Пусть 

При 
В терминах свойств[править | править код]
Принцип включений-исключений часто приводят в следующей альтернативной формулировке
[2].
Пусть дано конечное множество 








Формулировка принципа включений-исключений в терминах множеств эквивалентна формулировке в терминах свойств.
Действительно, если множества 




Если теперь вместо «элемент 



Обозначим через 



Доказательство[править | править код]
Существует несколько доказательств формулы включений-исключений.
Доказательство по индукции
Формулу включений-исключений можно доказать по индукции
[1]
[3].
При 

Пусть формула верна для 

Пусть каждый элемент множества 

Применим формулу включений-исключений для свойств 

Теперь применим формулу для свойств 



Наконец, применим формулу для одного свойства 



Комбинируя выписанные три формулы, получим формулу включений-исключений для 

■
Комбинаторное доказательство
Рассмотрим произвольный элемент 
Если элемент 


Пусть элемент 








При 

Таким образом, правая часть формулы включений-исключений учитывает каждый элемент, не имеющий указанных свойств точно по одному разу, а каждый элемент, обладающий хотя бы одним из свойств — нуль раз. Следовательно, она равна количеству элементов, не обладающих ни одним из свойств 

■
Доказательство через индикаторные функции
Пусть 




Индикаторная функция их дополнений 

а индикаторная функция пересечения дополнений:

Раскрывая скобки в правой части и ещё раз используя тот факт, что индикаторная функция пересечения множеств равна произведению их индикаторных функций, получаем:

Это соотношение — одна из форм принципа включений-исключений. Оно выражает собой логическое тождество[1] и верно для произвольных множеств 




получим формулировку принципа включений-исключений в терминах мощностей множеств (или в терминах свойств).
■
Топологическое доказательство
Применение[править | править код]
Задача о беспорядках[править | править код]
Классический пример использования формулы включений-исключений — задача о беспорядках[2].
Требуется найти число перестановок 



Пусть 










Это соотношение можно преобразовать к виду

Нетрудно видеть, что выражение в скобках является частичной суммой ряда 



Вычисление функции Эйлера[править | править код]
Другой пример применения формулы включений-исключений — нахождение явного выражения для функции Эйлера 


Пусть каноническое разложение числа 

Число 








Количество 



По формуле включений-исключений находим

Эта формула преобразуется к виду:

Вариации и обобщения[править | править код]
Принцип включения-исключения для вероятностей[править | править код]
Пусть 

Эта формула выражает принцип включений-исключений для вероятностей. Её можно получить из принципа включений-исключений в форме индикаторных функций:

Пусть 





Принцип включений-исключений в пространствах с мерой[править | править код]
Пусть 



Очевидно, принцип включений-исключений для вероятностей и для мощностей конечных множеств являются частными случаями этой формулы. В первом случае мерой является, естественно, вероятностная мера в соответствующем вероятностном пространстве: 

Вывести принцип включений-исключений для пространств с мерой можно также, как для указанных частных случаев, из тождества для индикаторных функций:

Пусть 




Тождество максимумов и минимумов[править | править код]
Формула включений-исключений может рассматриваться как частный случай тождества максимумов и минимумов:
Это соотношение справедливо для произвольных чисел 





Обращение Мёбиуса[править | править код]
Пусть 




Тогда имеет место следующая формула обращения[6]
[7]:
Это утверждение является частным случаем общей формулы обращения Мёбиуса для алгебры инцидентности[en] совокупности 


Покажем, как из этой формулы следует принцип включения-исключения для конечных множеств.
Пусть дано семейство подмножеств 







Тогда функция 
даёт количество элементов, каждый из которых входит во все множества 

Заметим далее, что 
С учётом сделанных замечаний запишем формулу обращения Мёбиуса:
Это есть в точности формула включений-исключений для конечных множеств, только в ней не сгруппированы слагаемые, относящиеся к одинаковым значениям 
История[править | править код]
Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильва[en] в 1854 году[1].
Но ещё в 1713 году Николай Бернулли[en] использовал этот метод для решения задачи Монмора[en], известной как задача о встречах (фр. Le problème des rencontres)[8], частным случаем которой является задача о беспорядках. Также формулу включений-исключений связывают с именем английского математика Джозефа Сильвестра[9].
См. также[править | править код]
- Формула Грассмана
- Неравенство Буля[en]
Примечания[править | править код]
- ↑ 1 2 3 4 5 Риордан Дж. Введение в комбинаторный анализ = An Introduction to Combinatorial Analysis. — М.: Изд-во иностранной литературы, 1963. — С. 63—66. — 289 с.
- ↑ 1 2 3 Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 18-20. — 424 с.
- ↑ 1 2
Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 69—73. — 309 с. - ↑
Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 266. — 309 с. - ↑ Боровков, А. А. Теория вероятностей. — 2-е изд. — М.: «Наука», 1986. — С. 24. — 431 с.
- ↑ Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 30-31. — 424 с.
- ↑ Стенли Р. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 103—107. — 440 с.
- ↑ Weisstein, Eric W. Derangement (англ.) на сайте Wolfram MathWorld.
- ↑
Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 264. — 309 с.
Литература[править | править код]
- Риордан Дж. Введение в комбинаторный анализ = An Introduction to Combinatorial Analysis. — М.: Изд-во иностранной литературы, 1963. — 289 с.
- Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — 309 с.
- Стенли Р. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: Мир, 1990. — 440 с.
- Холл М. Комбинаторика = Combinatorial Theory. — М.: Мир, 1970. — 424 с.
- И. Яглом. Заплаты на кафтане // Квант. — 1974. — № 2. — С. 13—21.
Ссылки[править | править код]
- Weisstein, Eric W. Inclusion-Exclusion Principle (англ.) на сайте Wolfram MathWorld.
Множество –
совокупность определенных различаемых
объектов, для которых можно установить
принадлежит данный объект множеству
или нет.
Число элементов
конечного множества М называется его
мощностью |М|.
-
Мощность объединения
двух множеств: -
Мощность объединения
трех множеств: -
Мощность объединения
N
множеств:
Пример:
-
Векторы. Прямое произведение множеств. Мощности прямого произведения множеств.
Вектор (или кортеж)
– это упорядоченный набор элементов.
Элементы вектора называются координатами
или компонентами. Число координат –
длина вектора (размерность).
Координаты вектора
могут совпадать. Два вектора равны, если
они имеют одинаковую длину и равны
соответствующие координаты.
Прямым (декартовым)
произведением множеств А и В (А x
В) называется множество всех векторов
(a,
b),
таких, что a
∈
A,
b
∈
B:
Если А=В, то А х
А=А2.
Прямым произведением
множества
называется множество всех векторов
длины m,
таких, что
.
Пусть
– конечные множества. Соответственно
мощности этих множеств равны:
.
Тогда мощность
прямого произведения N
множеств равна произведению мощностей
соответствующих множеств, т.е.
.
-
Отношения. Основные понятия отношений (отношения; унарные, бинарные, n-местные отношения)
Отношения – один
из способов задания связи между элементами
множества.
Унарные или
одноместные отношения – отражают
наличие определенного признака Р у
элемента множества М.
Тогда все такие
элементы a
из множества М, которые отличаются
данным признаком R,
образующие подмножества в М, называются
унарными отношением R.
Бинарные отношения
– используются для определения
взаимосвязи, которыми характеризуются
парные элементы во множестве М.
Тогда все пары вида
(a,
b)
из множества М, между которыми имеют
отношения, образ подмножества пар из
всех пар элементов М х М=М2,
называется бинарным отношением М.
Могут рассматриваться
N-местные
отношения. Под N-местными
отношениями понимают подмножество R
прямого произведения N
множеств, n:
R
М1
х М2
х…х Мn,
элементы a1,
a2,…,an,
где (а1
принадл М1
и т.д.) находятся в отношении R,
если (а1, а2,…,аn)
принадл. R.
-
Отношения. Бинарные отношения. Основные понятия (определение, обозначения, область определения, область значений, способы задания бинарных отношений). Привести примеры.
Отношения – один
из способов задания связи между элементами
множества.
Бинарным отношением
R из множества A в множество B называется
подмножество прямого произведения A и
B и обозначается:
D(R)
– область определения. ={a:
(a,
b)
∈R}
Q(R)
– область значения. ={b:
(a, b) ∈R}
Первый способ
задания множества состоит в 1
непосредственном перечислении таких
пар. Ясно, что он приемлем лишь в случае
конечного множества R.
Второй удобный
способ задания отношения R
на конечном множестве — матричный. Все
элементы нумеруются, и матрица отношения
R
определяется своими элементами для
всех i
и j.
Известным примером такого задания
отношений являются турнирные таблицы
(если ничьи обозначить нулями, как и
проигрыш, то матрица изобразит отношение
«xi
— победитель yj»).
-
Отношения.
Свойства бинарных отношений
(рефлексивность, антирефлексивность,
симметричность, антисимметричность,
транзитивность). Привести примеры.
Графические особенности диаграммы
(бинарное отношение задано в виде
диаграммы состоящей из узлов и стрелок)
в зависимости от характера свойств
бинарного отношения.
Отношения – один
из способов задания связи между элементами
множества.
-
В математике
бинарное отношение R на множестве X
называется рефлексивным, если всякий
элемент этого множества находится в
отношении R с самим собой.
-
В математике
бинарное отношение R на множестве X
называется антирефлексивным, если
всякий элемент этого множества не
находится в отношении R с самим собой.
-
В математике
бинарное отношение R на множестве X
называется симметричным, если для
каждой пары элементов множества (a,b)
выполнение отношения
влечёт выполнение отношения
.
-
В математике
бинарное отношение R на множестве X
называется антисимметричным, если для
каждой пары элементов множества a,b
выполнение отношений aRb и bRa влечёт a =
b, или, что то же самое, выполнение
отношений aRb и bRa возможно только для
равных a и b.
-
В математике
бинарное отношение R на множестве X
называется транзитивным, если для любых
трёх элементов множества a,b,c выполнение
отношений aRb и bRc влечёт выполнение
отношения aRc.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Достаточно часто в математической науке возникает ряд трудностей и вопросов, причем многие ответы не всегда проясняются. Не исключением стала такая тема, как мощность множеств. По сути, это не что иное как численное выражение количества объектов. В общем смысле множество является аксиомой, у него нет определения. В основе лежат любые объекты, а точнее их набор, который может носить пустой, конечный или бесконечный характер. Кроме этого, он содержит числа целые или натуральные, матрицы, последовательности, отрезки и прямые.
О существующих переменных
Нулевой или пустой набор, не имеющий собственного значения, считается элементом мощности, так как это подмножество. Сбор всех подмножеств непустого множества S является множеством множеств. Таким образом, набор мощности заданного множества считается многим, мыслимым, но единым. Это множество называется множеством степеней S и обозначается P (S). Если S содержит N элементов, то P (S) содержит 2 ^ n подмножеств, так как подмножество P (S) является либо ∅, либо подмножеством, содержащим r элементов из S, r = 1, 2, 3, … Составленное из всего бесконечного множества M называется степенным количеством и символически обозначается P (M).
Элементы теории множеств
Эта область знаний была разработана Джорджем Кантором (1845-1918 годы жизни). Сегодня она используется почти во всех отраслях математики и служит ее фундаментальной частью. В теории множеств элементы представлены в форме списка и заданы типами (пустой набор, одноэлементный, конечные и бесконечные множества, равные и эквивалентные, универсальные), объединение, пересечение, разность и дополнение чисел. В повседневной жизни часто говорится о коллекции таких объектов, как куча ключей, стая птиц, пачка карточек и т. д. В математике 5 класса и не только, встречаются натуральные, целые, простые и составные числа.
Можно рассмотреть следующие множества:
- натуральные числа;
- буквы алфавита;
- первичные коэффициенты;
- треугольники с разными значениями сторон.
Видно, что эти указанные примеры представляют собой четко определенные множества объектов. Рассмотрим еще несколько примеров:
- пять самых известных ученых мира;
- семь красивых девушек в обществе;
- три лучших хирурга.
Эти примеры мощности множества не являются четко определенными коллекциями объектов, потому, что критерий “наиболее известных”, “самых красивых”, “лучших” варьируется от человека к человеку.
Наборы
Это значение представляет собой четко определенное количество различных объектов. Предположив, что:
- набор слов является синонимом, агрегатом, классом и содержит элементы;
- объекты, члены являются равными по значению терминами;
- наборы обычно обозначаются прописными буквами A, B, C;
- элементы набора представлены маленькими буквами a, b, c.
Если «a» – элемент множества A, то говорится, что «a» принадлежит A. Обозначим фразу «принадлежит» греческим символом «∈» (epsilon). Таким образом, выходит, что a ∈ A. Если ‘b’ – элемент, который не принадлежит A, это представляется как b ∉ A. Некоторые важные наборы, используемые в математике 5 класса, представляют, используя три следующих метода:
- заявки;
- реестров или табличные;
- правило создания построения.
При детальном рассмотрении форма заявления основана на следующем. В этом случае задано четкое описание элементов множества. Все они заключены в фигурные скобки. Например:
- множество нечетных чисел, меньших 7 – записывается как {меньше 7};
- набор чисел больше 30 и меньше 55;
- количество учеников класса, вес которых больше, чем учителя.
В форме реестра (табличной) элементы набора перечислены в паре скобок {} и разделены запятыми. Например:
- Пусть N обозначает множество первых пяти натуральных чисел. Следовательно, N = → форма реестра
- Набор всех гласных английского алфавита. Следовательно, V = {a, e, i, o, u, y} → форма реестра
- Множество всех нечетных чисел меньше 9. Следовательно, X = {1, 3, 5, 7} → форма реестра
- Набор всех букв в слове «Математика». Следовательно, Z = {M, A, T, H, E, I, C, S} → Форма реестра
- W – это набор последних четырех месяцев года. Следовательно, W = {сентябрь, октябрь, ноябрь, декабрь} → реестр.
Стоит отметить, что порядок, в котором перечислены элементы, не имеет значения, но они не должны повторяться. Установленная форма построения, в заданном случае правило, формула или оператор записываются в пару скобок, чтобы набор был корректно определен. В форме set builder все элементы должны обладать одним свойством, чтобы стать членом рассматриваемого значения.
В этой форме представления набора элемент множества описывается с помощью символа «x» или любой другой переменной, за которой следует двоеточие («:» или «|» используется для обозначения). Например, пусть P – множество счетных чисел, большее 12. P в форме set-builder написано, как – {счетное число и больше 12}. Это будет читаться определенным образом. То есть, «P – множество элементов x, такое, что x является счетным числом и больше 12».
Решенный пример с использованием трех методов представления набора: количество целых чисел, лежащих между -2 и 3. Ниже приведены примеры различных типов наборов:
- Пустой или нулевой набор, который не содержит какого-либо элемента и обозначается символом ∅ и считывается как phi. В форме списка ∅ имеет написание {}. Пустым является конечное множество, так как число элементов 0. Например, набор целых значений меньше 0.
- Очевидно, что их не должно быть <0. Следовательно, это пустое множество.
- Набор, содержащий только одну переменную, называется одноэлементным множеством. Не является ни простым, ни составным.
Конечное множество
Множество, содержащее определенное число элементов, называется конечным либо бесконечным множеством. Пустое относится к первому. Например, набор всех цветов в радуге.
Бесконечное количество – это набор. Элементы в нем не могут быть перечислены. То есть, содержащий подобные переменные, называется бесконечным множеством. Примеры:
- мощность множества всех точек в плоскости;
- набор всех простых чисел.
Но стоит понимать, что все мощности объединения множества не могут быть выражены в форме списка. К примеру, вещественные числа, так как их элементы не соответствуют какой-либо конкретной схеме.
Кардинальный номер набора – это число различных элементов в заданном количестве A. Оно обозначается n (A).
Например:
- A {x: x ∈ N, x <5}. A = {1, 2, 3, 4}. Следовательно, n (A) = 4.
- B = набор букв в слове ALGEBRA.
Эквивалентные наборы для сравнения множеств
Две мощности множества A и B являются таковыми, если их кардинальное число одинаково. Символом для обозначения эквивалентного набора является «↔». Например: A ↔ B.
Равные наборы: две мощности множества A и B, если они содержат одни и те же элементы. Каждый коэффициент из A является переменной из B, и каждый из B является указанным значением A. Следовательно, A = B. Различные типы объединения множеств в мощности и их определения объясняются с помощью указанных примеров.
Сущность конечности и бесконечности
Каковы различия между мощностью конечного множества и бесконечного?
Для первого значения характерно следующее название, если оно либо пустое, либо имеет конечное число элементов. В конечном множестве переменная может быть указана, если она имеет ограниченный счет. Например, с помощью натурального числа 1, 2, 3. И процесс листинга заканчивается на некотором N. Число различных элементов, отсчитываемых в конечном множестве S, обозначается через n (S). А также называется порядком или кардинальным. Символически обозначается по стандартному принципу. Таким образом, если множество S является русским алфавитом, то оно содержит в себе 33 элемента. Также важно запомнить, что элемент не встречается более одного раза в наборе.
Бесконечное количество в множестве
Множество называется бесконечным, если элементы не могут быть перечислены. Если оно имеет неограниченное (то есть несчетное) натуральное число 1, 2, 3, 4 для любого n. Множество, которое не является конечным, называется бесконечным. Теперь можно обсудить примеры рассматриваемых числовых значений. Варианты конечного значения:
- Пусть Q = {натуральные числа меньше 25}. Тогда Q – конечное множество и n (P) = 24.
- Пусть R = {целые числа между 5 и 45}. Тогда R – конечное множество и n (R) = 38.
- Пусть S = {числа, модуль которых равен 9}. Тогда S = {-9, 9} является конечным множеством и n (S) = 2.
- Набор всех людей.
- Количество всех птиц.
Примеры бесконечного множества:
- количество существующих точек на плоскости;
- число всех пунктов в сегменте линии;
- множество положительных целых чисел, кратных 3, является бесконечным;
- все целые и натуральные числа.
Таким образом, из приведенных выше рассуждений понятно, как различать конечные и бесконечные множества.
Мощность множества континуум
Если провести сравнение множества и других существующих значений, то к множеству присоединено дополнение. Если ξ – универсальное, а A – подмножество ξ, то дополнение к A является количеством всех элементов ξ, которые не являются элементами A. Символически обозначается дополнение A относительно ξ как A’. К примеру, 2, 4, 5, 6 являются единственными элементами ξ, которые не принадлежат A. Следовательно, A’= {2, 4, 5, 6}
Множество с мощностью континуум имеет следующие особенности:
- дополнением универсального количества является пустое рассматриваемое значение;
- эта переменная нулевого множества является универсальным;
- количество и его дополнение являются непересекающимися.
Например:
- Пусть количество натуральных чисел является универсальным множеством и А – четное. То, тогда A ‘{x: x – множество нечетное с такими же цифрами}.
- Пусть ξ = множество букв в алфавите. A = набор согласных. Тогда A ‘= количество гласных.
- Дополнением к универсальному множеству является пустое количество. Можно обозначить через ξ. Тогда ξ ‘= Множество тех элементов, которые не входят в ξ. Пишется и обозначается пустое множество φ. Поэтому ξ = φ. Таким образом, дополнение к универсальному множеству является пустым.
В математике «континуум» иногда используется для обозначения реальной линии. И в более общем плане, для описания подобных объектов:
- континуум (в теории множеств) – вещественная линия или соответствующее кардинальное число;
- линейный – любое упорядоченное множество, которое разделяет определенные свойства реальной прямой;
- континуум (в топологии) – непустое компактное связное метрическое пространство (иногда хаусдорфово);
- гипотеза о том, что никакие бесконечные множества больше целых чисел, но меньшие, чем действительные числа;
- мощность континуума – кардинальное число, представляющее размер множества действительных чисел.
По существу дела, континуум (измерение), теории или модели, которые объясняют постепенные переходы из одного состояния в другое без каких-либо резких изменений.
Проблемы объединения и пересечения
Известно, что пересечение двух или более множеств – это количество, содержащее все элементы, которые являются общими в этих значениях. Задачи Word на множествах решаются, чтобы получить основные идеи о том, как использовать свойства объединения и пересечения множеств. Решенные основные проблемы слов на множествах выглядят так:
- Пусть A и B – два конечных множества. Они представляют собой такие, что n (A) = 20, n (B) = 28 и n (A ∪ B) = 36, находится n (A ∩ B).
Связь в наборах с использованием диаграммы Венна:
- Объединение двух множеств может быть представлено заштрихованной областью, представляющей A ∪ B. A ∪ B, когда A и B – непересекающиеся множества.
- Пересечение двух множеств может быть представлено диаграммой Венна. С затененной областью, представляющей A ∩ B.
- Разность двух наборов может быть представлена диаграммами Венна. С заштрихованной областью, представляющей A – B.
- Связь между тремя наборами, использующими диаграмму Венна. Если ξ представляет универсальное количество, то A, B, C – три подмножества. Здесь все три набора являются перекрывающимися.
Обобщение информации о множестве
Мощность множества определяется как общее количество отдельных элементов в наборе. А последнее указанное значение описывается как количество всех подмножеств. При изучении подобных вопросов требуются методы, способы и варианты решения. Итак, у мощности множества примерами могут служить следующие:
Пусть A = {0,1,2,3}| | = 4, где | A | представляет мощность множества A.
Теперь можно найти свой набор мощности. Это тоже довольно просто. Как уже сказано, набор мощности установлен из всех подмножеств заданного количества. Поэтому нужно в основном определить все переменные, элементы и другие значения A, которые {}, {0}, {1}, {2}, {3}, {0,1}, {0,2}, {0,3}, {1,2}, {1,3}, { 2,3}, {0,1,2}, {0,1,3}, {1,2,3}, {0,2,3}, {0,1,2,3}.
Теперь мощность выясняет P = {{}, {0}, {1}, {2}, {3}, {0,1}, {0,2}, {0,3}, {1,2}, {1,3}, {2,3}, {0,1,2}, {0,1,3}, {1,2,3}, {0,2,3}, {0,1,2,3}}, который имеет 16 элементов. Таким образом, мощность множества A = 16. Очевидно, что это утомительный и громоздкий метод решения этой проблемы. Однако есть простая формула, по которой, непосредственно, можно знать количество элементов в множестве мощности заданного количества. | P | = 2 ^ N, где N – число элементов в некотором A. Эта формула может быть получена применением простой комбинаторики. Таким образом, вопрос равен 2 ^ 11, поскольку число элементов в множестве A равно 11.
Итак, множеством является любое численно выраженное количество, которое может быть всевозможным объектом. К примеру, машины, люди, числа. В математическом значении это понятие шире и более обобщенное. Если на начальных этапах разбираются числа и варианты их решения, то в средних и высших стадиях условия и задачи усложнены. По сути, мощность объединения множества определена принадлежностью объекта к какой-либо группе. То есть один элемент принадлежит к классу, но имеет одну или несколько переменных.
Скачать материал

Скачать материал


- Сейчас обучается 87 человек из 36 регионов




- Сейчас обучается 27 человек из 18 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Теория множеств
Элементы математической логики -
2 слайд
Множество
Многое, мыслимое нами как единое целоеГеорг Кантор
Совокупность элементов, удовлетворяющих какому-либо характеристическому свойству
-
3 слайд
Георг Кантор
Немецкий математикСоздатель теории множеств
1904 г медаль Сильвестра Лондонского королевского общества
1845 1918
«Никто не изгонит нас из рая, который основал Кантор»
Давид Гильберт -
4 слайд
Пример
Множество студентов группы
Множество людей в аудитории
Множество бутылок в ближайшем магазине
Множество атомов Вселенной
Множество натуральных чисел -
5 слайд
Натуральные числа
1, 2, 3, 4, 5, …
Числа, используемые для счёта в природе
от лат. naturalis — естественный= {1, 2, 3, 4, 5, …}
-
-
7 слайд
Целые числа
-3, -2, -1, 0, 1, 2, 3, 4, 5, …
от нем. zahl — число= {…-2,-1,0,1, 2,…}
-
-
9 слайд
Рациональные числа
1/2, -3, -5/6, 0, 5, …
от лат. quotient — отношениецелые числа
конечные десятичные дроби
бесконечные периодические десятичные дроби -
-
11 слайд
С
D
бесконечная непериодическая десятичная дробь -
12 слайд
1
1
?
катет
катет
гипотенуза -
13 слайд
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
a
b
c -
14 слайд
1
1
бесконечная непериодическая десятичная дробь -
15 слайд
Иррациональные числа
Бесконечные непериодические десятичные дроби -
16 слайд
Действительные числа
Рациональные числа + иррациональные
от лат. realis — действительныйДействительные = вещественные
-
-
18 слайд
Квадратное уравнение
x2+x+1=0
ax2+bx+c=0
a,b,c коэффициенты
Дискриминант
D = b2 – 4ac ≥ 0 -
19 слайд
Квадратное уравнение
x2+x+1=0
a = 1, b = 1, c = 1
D = 12 – 4∙1 ∙ 1 = -3 < 0Арифметический квадратный корень не извлекается из отрицательных чисел
-
20 слайд
Джироламо Кардано
Итальянский математик, инженер, философ, медик и астрологВ его честь формулы решения кубического уравнения, карданов подвес и карданный вал
1501 1576
1545 г. Великое искусство, или об алгебраических правилах -
-
22 слайд
Комплексные числа
от лат. complex — тесно связанный
z = a + bi
Действительная часть
Re(z) = a
Мнимая часть
Im(z) = b -
-
24 слайд
Множество
Совокупность элементов, объединённых каким-либо характеристическим свойством (признаком) -
25 слайд
Подмножество
Множество К называется подмножеством множества А, если любой элемент множества К принадлежит множеству АK A
А
К
x -
26 слайд
Подмножество
Множество К называется подмножеством множества А, если любой элемент множества К принадлежит множеству Ах К х А
-
27 слайд
Кванторы
Специальные математические символы, облегчающие запись математических выраженийГеорг Кантор
Кантор придумал кванторы
-
28 слайд
Кванторы
– квантор всеобщности«для любого»
All (англ)
-
29 слайд
Кванторы
– квантор существования«существует»
Exist (англ)
-
30 слайд
Счётное множество
Множество , в котором столько же элементов, сколько во множестве натуральных чисел -
31 слайд
Равные множества
Если A = B , тоA B и B A
-
32 слайд
Универсальное множество
Множество , которому принадлежат все элементы, обладающие данным характеристическим свойством -
33 слайд
Континуальное множество
Множество , в котором столько же элементов, сколько во множестве действительных чисел -
34 слайд
Равные множества
Множества, состоящие из одинаковых элементовА = {1, 2, 4, 8, 16}
B = {20, 21, 22, 23, 24}
C = {x : x= 2n, n = 0, 1, 2, 3, 4}A = B = C
-
35 слайд
Задача
На множестве U всех букв русского алфавита заданы множества
А = {ё, к, л, м,н} В ={к, о, з, ё, л}
С = {б, ы, ч, о, к}Найдите следующие множества и изобразите их кругами Эйлера
1) AUB 2) A∩B 3) (A∩B)UC
4) (AUC)∩B 5) U(AUB UС) -
36 слайд
Диаграммы Венна
А = 6 В =6 С = 7
А
С
В -
37 слайд
Задача
Даны числовые промежутки
А= [-4; 5], В =(2; 6), С = (5, 10]Найдите следующие множества и изобразите их на числовой прямой и кругами Эйлера
1) AUB 2) A∩B 3) (СUB)(A∩B)
4) (A∩B)UC 5) (AUB ) (A∩B) -
38 слайд
Формула мощности объединения множеств
-
39 слайд
Задача 1
В Ивдельском филиале Уральского промышленно-экономического техникума 2 группы программистов.
В группе ИзПу-108 учится 11 человек.
В группе ИзПу-304 – 9 человек.Сколько всего студентов-программистов в Ивдельском филиале?
-
40 слайд
Обозначения
А – множество студентов группы ИзПу-108
А=11В – множество студентов группы ИзПу-304
В=9 -
41 слайд
Диаграммы Венна
А
В
АUВ =А +В =11+9=20 -
42 слайд
Задача 11
Все студенты группы ИзПу-108 очень любят заниматься рукоделием. При этом они предпочитают только 2 вида рукоделия: плетение из бисера и вышивку крестиком.1. 7 человек плетут фенечки из бисера.
2. 6 студентов занимаются вышивкой крестиком.
3. 2 человека занимаются обоими видами рукоделия.Сколько студентов в группе ИзПу-108?
-
43 слайд
Обозначения
А – множество студентов группы ИзПу-108, увлекающихся бисероплетением
А=7В – множество студентов группы ИзПу-108, вышивающих крестиком
В=6 -
44 слайд
Обозначения
А∩В – множество студентов группы ИзПу-108, увлекающихся бисероплетением и вышивкой одновременноА∩В=2
-
45 слайд
Диаграммы Венна
А
В
АUВ =А +В =13 -
46 слайд
Диаграммы Венна
А
В
АUВ =А +В – А∩В =13-2=11 -
47 слайд
Формула мощности объединения двух множеств
АUВ =А +В – А∩В -
48 слайд
Формула мощности объединения трёх множеств
-
49 слайд
Задача 111
Все студенты группы ИзПу-108 очень любят заниматься спортом.При этом они предпочитают только 3 вида спорта: синхронное плавание, кёрлинг и спортивное перетягивание каната.
Сколько студентов в этой талантливой группе, если:
-
50 слайд
Задача 111
1. 6 человек плавают синхронно.
2. 6 студентов занимаются кёрлингом.
3. 7 человек перетягивают канат.
4. Двое кёрлингистов также занимаются синхронным плаванием.
5. Перетягивать канат любят четыре человека из команды кёрлингистов.
6. Синхронным плаванием и перетягиванием каната одновременно увлекаются 3 человека.
7. Всеми тремя видами спорта занимается только 1 студент -
51 слайд
Обозначения
А – множество студентов ИзПу-108, занимающихся в секции синхронного плавания
А=6В – множество студентов-кёрлингистов группы ИзПу-108
В=6С – множество студентов группы ИзПу-108, любящих перетягивать канат
С=7 -
52 слайд
Обозначения
А∩B – множество студентов ИзПу-108, занимающихся синхронным плаванием и кёрлингом одновременно
А∩B=2В∩C – множество студентов-кёрлингистов группы ИзПу-108, любящих перетягивать канат
В∩С=4 -
53 слайд
Обозначения
А∩С – множество студентов группы
ИзПу-108, занимающихся перетягиванием каната и синхронным плаванием
А∩С=3А∩В∩С – множество студентов группы ИзПу-108, занимающихся всеми тремя видами спорта
А∩В∩С=1 -
54 слайд
Диаграммы Венна
А = 6 В =6 С = 7
А
С
В -
55 слайд
Диаграммы Венна
А∩В = 2
А
С
В -
56 слайд
Диаграммы Венна
В∩С = 4
А
С
В -
57 слайд
Диаграммы Венна
А∩С = 3
А
С
В -
58 слайд
Формула мощности объединения трёх множеств
АUВUС =
=А +В+С –
-А∩В -А∩С -С∩В -
59 слайд
Формула мощности объединения трёх множеств
АUВUС =
=6+6+7-2-4-3=10 -
60 слайд
Диаграммы Венна
А
С
В -
61 слайд
Диаграммы Венна
А∩В∩ С = 1
А
С
В -
62 слайд
Формула мощности объединения трёх множеств
АUВUС =
=А +В+С –
-А∩В -А∩С -С∩В +
+ А∩В ∩С -
63 слайд
Формула мощности объединения трёх множеств
АUВUС =
=6+6+7-2-4-3+1=11 -
64 слайд
Задача 1V
Из 35 студентов, побывавших на каникулах в Москве, все, кроме двоих, делились впечатлениями.
О посещении Большого театра с восторгом вспоминали 12 чел., Кремля – 14, а 16 – о концерте. По три студента запомнили посещение театра и Кремля, а также театра и концерта, четверо – концерта и пребывания в Кремле.
Сколько студентов сохранили воспоминания одновременно о театре, концерте и Кремле? -
-
66 слайд
Обозначения
U – множество студентов, посетивших Москву – универсальное множество
U=35А – множество запомнивших Большой театр
А=12В – множество студентов, рассказывавших о Кремле
В=14 -
67 слайд
Обозначения
С – множество студентов, вспоминавших о концерте
С=16А∩В – множество тех, кто рассказывал о Большом театре и Кремле
А∩В =3А∩С – множество тех, кто делился впечатлениями о Большом театре и концерте
А∩С =3 -
68 слайд
Обозначения
B∩С – множество тех, кто делился впечатлениями о Кремле и концерте
B∩С =4D = U /(АUВUС) – множество тех, кто не стал делиться воспоминаниями
D=2А∩В∩С – множество тех, кто сохранил воспоминания о Большом театре, Кремле и концерте.
А∩В∩С =? -
69 слайд
А∩В∩С =
АUВUС -А -В-С +
+А∩В +А∩С +С∩В -
70 слайд
А∩В∩С =
АUВUС -А -В-С +
+А∩В +А∩С +С∩В -
71 слайд
АUВUС =U -D
АUВUС =35 -2=33
А∩В∩С = 33 -12 -14–16 +3+3+ 4 = 1
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 255 998 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 19.07.2020
- 970
- 13

- 19.07.2020
- 896
- 13
- 19.07.2020
- 1452
- 20
- 18.07.2020
- 418
- 7
- 18.07.2020
- 194
- 5
Рейтинг:
5 из 5
- 18.07.2020
- 381
- 3
- 18.07.2020
- 555
- 9
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
-
Курс повышения квалификации «Развитие информационно-коммуникационных компетенций учителя в процессе внедрения ФГОС: работа в Московской электронной школе»
-
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
-
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
Нахождение мощности объединения множеств
-
Мощность объединения двух множеств:
(
рис.
2.4).Рис.
2.4.
-
Мощность объединения трех множеств:
(
рис.
2.5).Рис.
2.5.
Доказательство:
-
Мощность объединения
множеств:
Теорема.
– некоторые множества, тогда мощность объединения
множеств определяется по формуле
Правая часть этой формулы является суммой
слагаемых,
-е по порядку слагаемое имеет вид
, где
есть сумма чисел мощностей
по всем возможным пересечениям k разных множеств из множеств
Пример. На потоке из 100 студентов 28 человек изучают английский язык, 30 человек – немецкий язык, 42 человека – французский язык. Причем 8 человек изучают два языка – английский и немецкий, 10 человек изучает английский и французский языки, 5 человек – немецкий и французский языки. 3 человека изучают все 3 языка. Сколько студентов не изучает ни один из перечисленных языков?
Пусть
– множество студентов,
(студентов).
– множество студентов, изучающих английский язык,
;
– множество студентов, изучающих немецкий язык
,
– множество студентов, изучающих французский язык,
.
Соответственно множества студентов, изучающих по 2 или
3 иностранных языка заданы следующим образом:.
– множество студентов, изучающих иностранные языки.
– множество студентов, не изучающих иностранный язык.
Векторы и прямые произведения
Векторы. Проекция вектора
Вектор (или кортеж) – это упорядоченный набор элементов. Например, 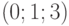
Координаты вектора могут совпадать 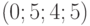
Два вектора равны, если они имеют одинаковую длину и равны соответствующие координаты: 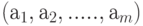
Проекцией вектора 


Проекцией вектора 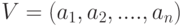

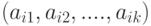
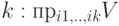
Пример: 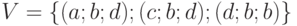
Прямое произведение
Прямым (декартовым) произведением множеств 


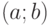
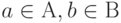
Если 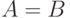
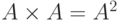


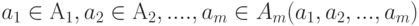
Примеры.
-
Множество
– множество точек плоскости, точнее пар вида
, где
и являются координатами.
-
.
Тогда
– множество всех 64 клеток шахматной доски.
-
– множество букв, символов, знаков препинания и т. д. Тогда элементы множества
– слова длины
. Множество всех слов
составляет язык.
-
.
Следовательно,
.
Теорема о мощности прямого произведения
Пусть 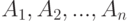

Тогда мощность прямого произведения 
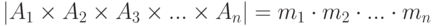
Доказательство методом математической индукции.
Для 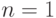
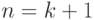
По предположению 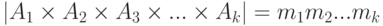
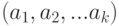
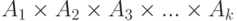




Таким образом, из всех 
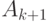
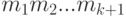


Следствие:



















































![ЗадачаДаны числовые промежутки
А= [-4; 5], В =(2; 6), С = (5, 10]
Найдите... ЗадачаДаны числовые промежутки
А= [-4; 5], В =(2; 6), С = (5, 10]
Найдите...](https://documents.infourok.ru/e9d67147-884c-4c4c-9159-9082866e400c/0/slide_37.jpg)


































 (
(
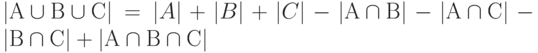 (
(
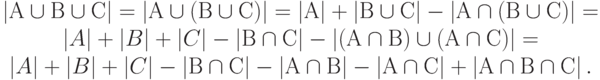
 – некоторые
– некоторые ![begin{array}
left| А_1 cup А_2 cup .... cup A_n | = left| A_1 right| + left| A_2 right| +...+\
+ left| A_n right| - left[ left| А_1 cap А_2 right| + left| А_1 cap А_3 right| + ...+ left| A_{n-1} cap A_n right| right] + \
left[ left| А_1 cap А_2 cap А_3 right| + left| А_1 cap А_2 cap А_4 right| + ... + left| A_{n-2} cap А_{n-1} cap А_n right| right] -...\
+ (-1)^{n-1} left| А_1 cap А_2 cap....A_n right| .\
end{array}](https://intuit.ru/sites/default/files/tex_cache/bac8852a09e893409db8a79ded1a28ca.png)
 -е по порядку слагаемое имеет вид
-е по порядку слагаемое имеет вид  , где
, где 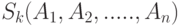 есть сумма чисел
есть сумма чисел 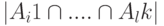 по всем возможным
по всем возможным 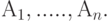
 –
–  (студентов).
(студентов).  –
–  ;
;  –
– 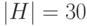 ,
,  –
–  .
.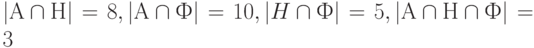 .
. –
– 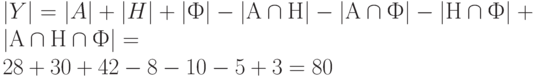
 – множество студентов, не изучающих иностранный язык.
– множество студентов, не изучающих иностранный язык.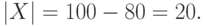
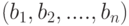

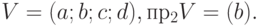


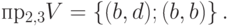


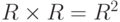 –
– 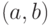 , где
, где  и являются координатами.
и являются координатами. .
.
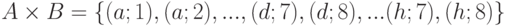 –
– 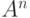 – слова длины
– слова длины 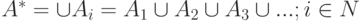 составляет язык.
составляет язык.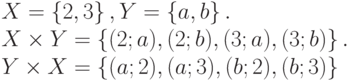 .
.
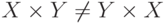 .
.
