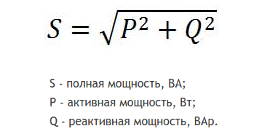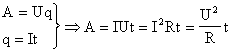Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при параллельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
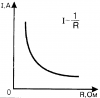
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное.
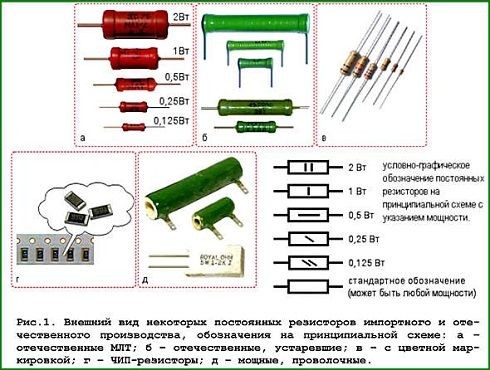
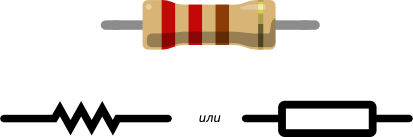
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
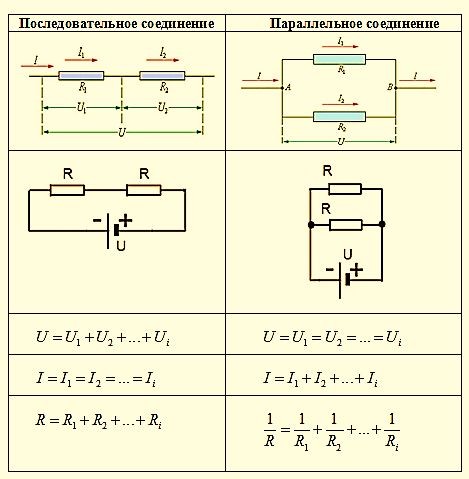
Для соединения резисторов в схемах используются три разных способа подключения — параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
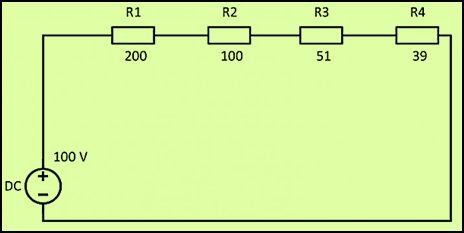
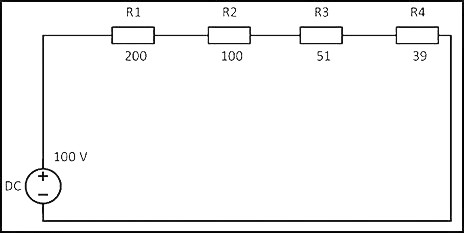
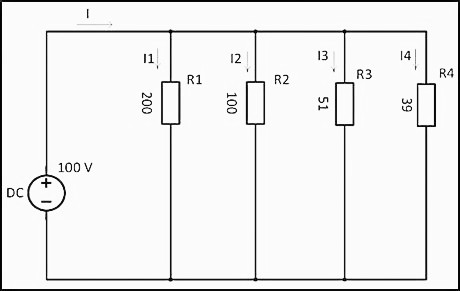
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I2 x R = 0,2562 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I2 x R1 = 0,2562 x 200 = 13,11 Вт;
- P2 = I2 x R2 = 0,2562 x 100 = 6,55 Вт;
- P3 = I2 x R3 = 0,2562 x 51 = 3,34 Вт;
- P4 = I2 x R4 = 0,2562 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при параллельном соединение
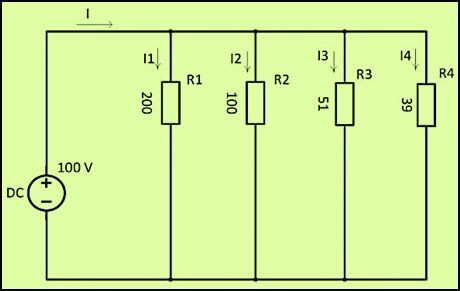
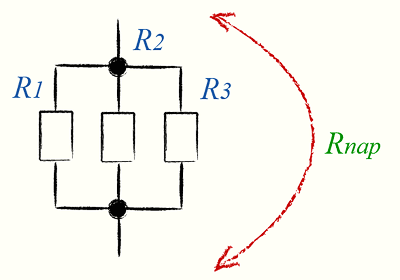
При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом: P = I2 x R = 6,0242 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов: P1 = U2/R1 = 1002/200 = 50 Вт; P2 = U2/R2 = 1002/100 = 100 Вт; P3 = U2/R3 = 1002/51 = 195,9 Вт; P4 = U2/R4 = 1002/39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и параллельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
Резистор и сопротивление
Теория
Резистор — искусственное «препятствие» для тока. Сопротивление в чистом виде. Резистор ограничивает силу тока, переводя часть электроэнергии в тепло. Сегодня невозможно изготовить ни одно, сколько-нибудь функциональное, электронное устройство без резисторов. Они используются везде: от компьютеров до систем охраны.
Сопротивление резистора — его основная характеристика. Основной единицей электрического сопротивления является Ом. На практике используются также производные единицы — килоом (кОм), мегаом (МОм), гигаом (ГОм), которые связаны с основной единицей следующими соотношениями:
1 кОм = 1000 Ом,
1 МОм = 1000 кОм,
1 ГОм = 1000 МОм
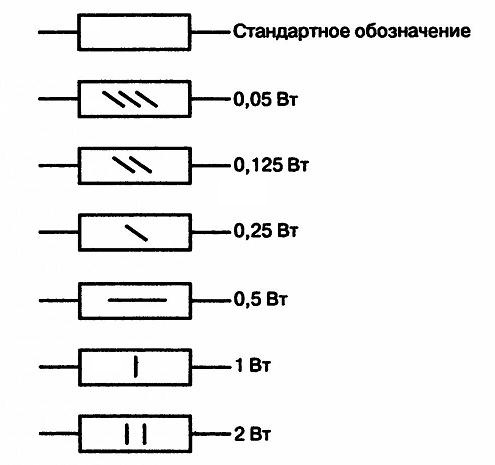
Ниже на рисунке видна маркировка резисторов на схемах:
Наклонные линии обозначают мощность резистора до 1 Вт. Вертикальные линии и знаки V и X (римские цифры), указывают на мощность резистора в несколько Ватт, в соответствии со значением римской цифры.
Для соединения резисторов в схемах используются три разных способа подключения: параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
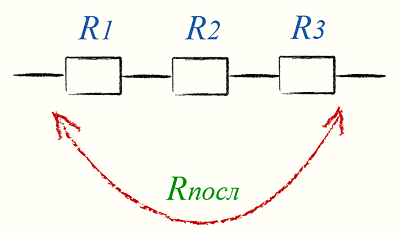
Последовательное соединение резисторов
Последовательное соединение резисторов применяется для увеличения сопротивления. Т.е. когда резисторы соединены последовательно, общее сопротивление равняется сумме сопротивлений каждого резистора. Например, если резисторы R1 и R2 соединены последовательно, их общее сопротивление высчитывается по формуле:
Rобщ = R1 + R2
Это справедливо и для большего количества соединённых последовательно резисторов:
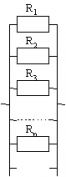
Rобщ = R1 + R2 + R3 + … + Rn
Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.
При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.
Мощность при последовательном соединении
При соединении резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат:
R = 200 + 100 + 51 + 39 = 390 Ом
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять
I = U/R = 100 В/390 Ом = 0,256 A
На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле:
P = I2 x R = 0,2562 x 390 = 25,55 Вт
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
P1 = I2 x R1 = 0,2562 x 200 = 13,11 Вт;
P2 = I2 x R2 = 0,2562 x 100 = 6,55 Вт;
P3 = I2 x R3 = 0,2562 x 51 = 3,34 Вт;
P4 = I2 x R4 = 0,2562 x 39 = 2,55 Вт.
Если сложить полученные мощности, то общая Р составит:
Робщ = 13,11 + 6,55 + 3,34 + 2,55 = 25,55 Вт
Параллельное соединение резисторов
Параллельное соединение резисторов необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним.
Расчет параллельного сопротивления двух параллельно соединённых резисторов R1 и R2 производится по следующей формуле:
Rобщ = (R1 × R2) / (R1 + R2)
Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:
1 / Rобщ = 1 / R1 + 1 / R2 + … + 1 / Rn
Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.
Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.
Мощность при параллельном соединении
При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
1/R = 1/200 + 1/100 + 1/51 + 1/39 ≈ 0,06024 Ом
R = 1 / 0,06024 ≈ 16,6 Ом
Используя значение напряжения 100 В, по закону Ома рассчитывается сила тока
I = U/R = 100 В x 0,06024 Ом = 6,024 A
Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом
P = I2 x R = 6,0242 x 16,6 = 602,3 Вт
Расчет силы тока для каждого резистора выполняется по формулам:
I1 = U/R1 = 100/200 = 0,5 A;
I2 = U/R2 = 100/100 = 1 A;
I3 = U/R3 = 100/51 = 1,96 A;
I4 = U/R4 = 100/39 = 2,56 A
На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов:
P1 = U2/R1 = 1002/200 = 50 Вт;
P2 = U2/R2 = 1002/100 = 100 Вт;
P3 = U22/R3 = 1002/51 = 195,9 Вт;
P4 = U22/R4 = 1002/39 = 256,4 Вт
Если сложить полученные мощности, то общая Р составит:
Робщ = 50 + 100 + 195,9 + 256,4 = 602,3 Вт
Калькулятор
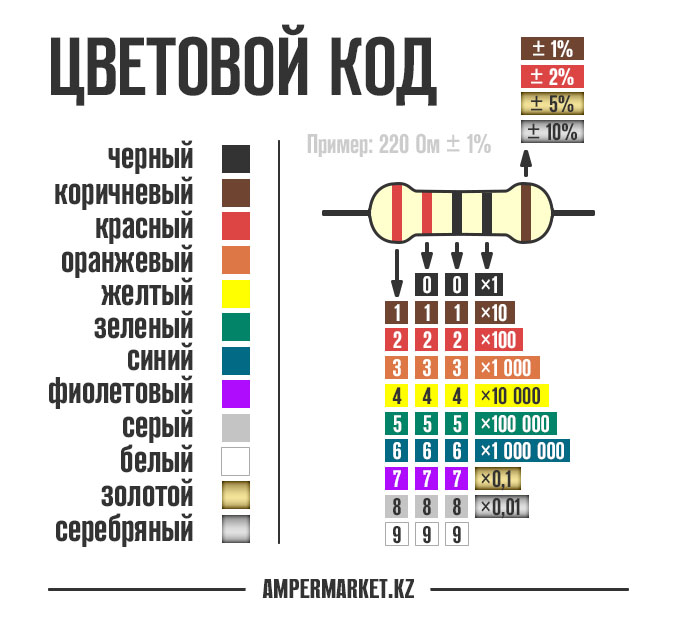
Цветовая маркировка резисторов
Наносить номинал резистора на корпус числами — дорого и непрактично: они получаются очень мелкими. Поэтому номинал и допуск кодируют цветными полосками. Разные серии резисторов содержат разное количество полос, но принцип расшифровки одинаков. Цвет корпуса резистора может быть бежевым, голубым, белым. Это не играет роли. Если не уверены в том, что правильно прочитали полосы, можете проверить себя с помощью мультиметра или калькулятора цветовой маркировки.
Калькулятор цветовой маркировки резисторов
Основные характеристики
| Сопротивление (номинал) | R | Ом |
| Точность (допуск) | ± | % |
| Мощность | P | Ватт |
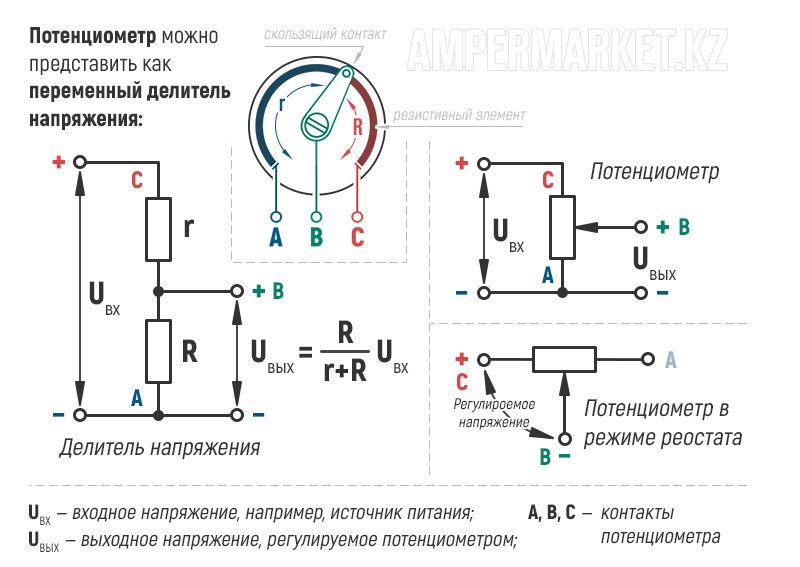
Переменный резистор
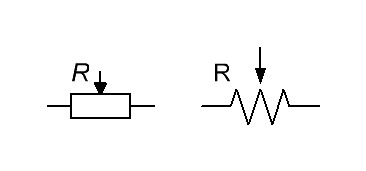
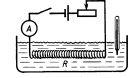
Переменный резистор — это резистор, у которого электрическое сопротивление между подвижным контактом и выводами резистивного элемента можно изменять механическим способом. Переменные резисторы (их также называют реостатами или потенциометрами) предназначены для постепенного регулирования силы тока и напряжения. Разница в том, что реостат регулирует силу тока в электрической цепи, а потенциометр — напряжение. Выглядят переменные резисторы так:
На радиосхемах переменные резисторы обозначаются прямоугольником с пририсованной к их корпусу стрелочкой.
Регулировать величину сопротивления переменных резисторов можно с помощью вращения специальной ручки. Те из резисторов, у которых регулировка сопротивления резистора может осуществляться только с помощью отвертки или специального ключа-шестигранника, называются подстроечными переменными резисторами.
Термисторы, варисторы и фоторезисторы
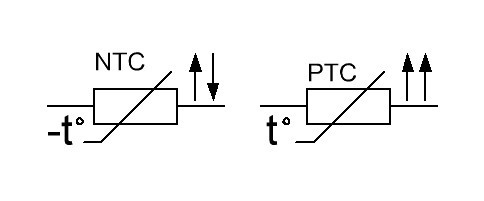
Кроме реостатов и потенциометров есть и другие виды резисторов: термисторы, варисторы и фоторезисторы. Термисторы, в свою очередь, делятся на термисторы и позисторы. Позистор – это термистор, у которого сопротивление возрастает вместе с ростом температуры окружающей среды. У термисторов, наоборот, чем выше температура вокруг, тем меньше сопротивление. Это свойство обозначают как ТКС – тепловой коэффициент сопротивления.
В зависимости от ТКС (отрицательный он или положительный) обозначают на схеме термисторы следующим образом:
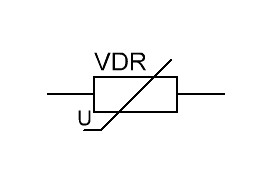
Следующий особый класс резисторов – это варисторы. Они изменяют силу сопротивления в зависимости от подаваемого на них напряжения. Зная свойства варистора, можно догадаться, что такой резистор защищает электрическую цепь от перенапряжения.
На схемах варисторы обозначаются так:
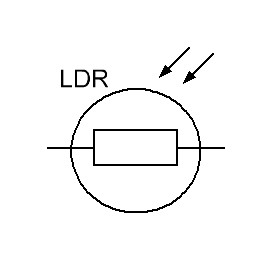
В зависимости от интенсивности освещения изменяет свое сопротивление еще один вид резисторов – фоторезисторы. Причем не важно, каков источник освещения: искусственный или естественный. Их особенность еще и в том, что ток в них протекает как в одном, так и в другом направлении, то есть еще говорят, что фоторезисторы не имеют p-n перехода.
А на схемах изображаются так:
В физике достаточно много внимания уделено энергии и мощности устройств, веществ или тел. В электротехнике эти понятия играют не менее важную роль чем в других разделах физики, ведь от них зависит насколько быстро установка выполнит свою работу и какую нагрузку понесут линии электропередач. Исходя из этих сведений подбираются трансформаторы для подстанций, генераторы для электростанций и сечение проводников передающих линий. В этой статье мы расскажем, как найти мощность электрического прибора или установки, зная силу тока, напряжение и сопротивление.
- Определение
- Формулы для расчётов цепи постоянного тока
- Для переменного тока
- Пример расчёта полной мощности для электродвигателя
- Расчет для параллельного и последовательного подключения
- Заключение
Определение
Мощность – это скалярная величина. В общем случае она равна отношению выполненной работы ко времени:
P=dA/dt
Простыми словами эта величина определяет, как быстро выполняется работа. Она может обозначаться не только буквой P, но и W или N, измеряется в Ваттах или киловаттах, что сокращенно пишется как Вт и кВт соответственно.
Электрическая мощность равна произведению тока на напряжение или:
P=UI
Как это связано с работой? U – это отношение работы по переносу единичного заряда, а I определяет, какой заряд прошёл через провод за единицу времени. В результате преобразований и получилась такая формула, с помощью которой можно найти мощность, зная силу тока и напряжение.
Формулы для расчётов цепи постоянного тока
Проще всего посчитать мощность для цепи постоянного тока. Если есть сила тока и напряжение, тогда нужно просто по формуле, приведенной выше, выполнить расчет:
P=UI
Но не всегда есть возможность найти мощность по току и напряжению. Если вам они не известны – вы можете определить P, зная сопротивление и напряжение:
P=U2/R
Также можно выполнить расчет, зная ток и сопротивление:
P=I2*R
Последними двумя формулами удобен расчёт мощности участка цепи, если вы знаете R элемента I или U, которое на нём падает.
Для переменного тока
Однако для электрической цепи переменного тока нужно учитывать полную, активную и реактивную, а также коэффициент мощности (соsФ). Подробнее все эти понятия мы рассматривали в этой статье: https://samelectrik.ru/chto-takoe-aktivnaya-reaktivnaya-i-polnaya-moshhnost.html.
Отметим лишь, что чтобы найти полную мощность в однофазной сети по току и напряжению нужно их перемножить:
S=UI
Результат получится в вольт-амперах, чтобы определить активную мощность (ватты), нужно S умножить на коэффициент cosФ. Его можно найти в технической документации на устройство.
P=UIcosФ
Для определения реактивной мощности (вольт-амперы реактивные) вместо cosФ используют sinФ.
Q=UIsinФ
Или выразить из этого выражения:
И отсюда вычислить искомую величину.
Найти мощность в трёхфазной сети также несложно, для определения S (полной) воспользуйтесь формулой расчета по току и фазному напряжению:
S=3UфIф
А зная Uлинейное:
S=1,73*UлIл
1,73 или корень из 3 – эта величина используется для расчётов трёхфазных цепей.
Тогда по аналогии чтобы найти P активную:
P=3UфIф*cosФ=1,73*UлIл*cosФ
Определить реактивную мощность можно:
Q=3UфIф*sinФ=1,73*UлIл*sinФ
На этом теоретические сведения заканчиваются и мы перейдём к практике.
Пример расчёта полной мощности для электродвигателя
Мощность у электродвигателей бывает полезная или механическая на валу и электрическая. Они отличаются на величину коэффициента полезного действия (КПД), эта информация обычно указана на шильдике электродвигателя.
Отсюда берём данные для расчета подключения в треугольник на Uлинейное 380 Вольт:
- Pна валу=160 кВт = 160000 Вт
- n=0,94
- cosФ=0,9
- U=380
Тогда найти активную электрическую мощность можно по формуле:
P=Pна валу/n=160000/0,94=170213 Вт
Теперь можно найти S:
S=P/cosφ=170213/0,9=189126 Вт
Именно её нужно найти и учитывать, подбирая кабель или трансформатор для электродвигателя. На этом расчёты окончены.
Расчет для параллельного и последовательного подключения
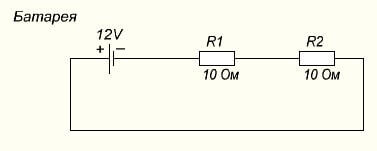
При расчете схемы электронного устройства часто нужно найти мощность, которая выделяется на отдельном элементе. Тогда нужно определить, какое напряжение падает на нём, если речь идёт о последовательном подключении, или какая сила тока протекает при параллельном включении, рассмотрим конкретные случаи.
Здесь Iобщий равен:
I=U/(R1+R2)=12/(10+10)=12/20=0,6
Общая мощность:
P=UI=12*0,6=7,2 Ватт
На каждом резисторе R1 и R2, так как их сопротивление одинаково, напряжение падает по:
U=IR=0,6*10=6 Вольт
И выделяется по:
Pна резисторе=UI=6*0,6=3,6 Ватта
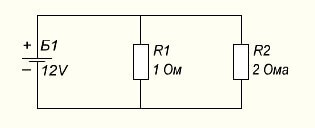
Тогда при параллельном подключении в такой схеме:
Сначала ищем I в каждой ветви:
I1=U/R1=12/1=12 Ампер
I2=U/R2=12/2=6 Ампер
И выделяется на каждом по:
PR1=12*6=72 Ватта
PR2=12*12=144 Ватта
Выделяется всего:
P=UI=12*(6+12)=216 Ватт
Или через общее сопротивление, тогда:
Rобщее=(R1*R2)/( R1+R2)=(1*2)/(1+2)=2/3=0,66 Ом
I=12/0,66=18 Ампер
P=12*18=216 Ватт
Все расчёты совпали, значит найденные значения верны.
Заключение
Как вы могли убедиться найти мощность цепи или её участка совсем несложно, неважно речь идёт о постоянке или переменке. Важнее правильно определить общее сопротивление, ток и напряжение. Кстати этих знаний уже достаточно для правильного определения параметров схемы и подбора элементов – на сколько ватт подбирать резисторы, сечения кабелей и трансформаторов. Также будьте внимательны при расчёте S полной при вычислении подкоренного выражения. Стоит добавить лишь то, что при оплате счетов за коммунальные услуги мы оплачиваем за киловатт-часы или кВт/ч, они равняются количеству мощности, потребленной за промежуток времени. Например, если вы подключили 2 киловаттный обогреватель на пол часа, то счётчик намотает 1 кВт/ч, а за час – 2 кВт/ч и так далее по аналогии.
Напоследок рекомендуем просмотреть полезное видео по теме статьи:
Также читают:
- Как определить потребляемую мощность приборов
- Как рассчитать сечения кабеля
- Маркировка резисторов по мощности и сопротивлению
На чтение 7 мин. Просмотров 7.2k. Опубликовано 18.05.2020
Ни одна электрическая схема не обходится без резисторов. Что это такое, для чего он нужен и какими способами их подключают в электрическую цепь рассмотрим подробно.
Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.
- С левого края – левый.
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.
При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.
Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Последовательное подключение
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.
При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.
Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Какая мощность тока при последовательном и параллельном соединении
Определение мощности отдельного резистивного элемента производится по формуле
P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.
Мощность при параллельном соединении
Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где
- R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
- I – сила тока в цепи.
При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.
Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.
Мощность при последовательном соединении
Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где
- R – рассчитанное нами сопротивление для определенной схемы;
- U – падение напряжения на данном резистивном элементе.
Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.
Как правильно рассчитать сопротивление
Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где
- U – падение напряжение на конкретном резистивном элементе;
- I – ток, протекающий через него.
При последовательном соединении
Для двух элементов считаем Rобщ = R1+R2.
Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.
При параллельном соединении
Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).
Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле
Rобщ = 1/(1/R1+1/R2+1/R3+…+1/Rn).
Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.
Как рассчитать сложные схемы соединения резисторов
Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.

- R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
- R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
- R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.
Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.
Преобразование «звезда-треугольник»
Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:
- «звезда» – соединение трех ветвей с одним общим узлом;
- «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.
Справка: Узел – точка, в которой соединяются три и более проводника электрической цепи.
Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».
Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».
RA = RAB RAC/(RAB+RAC+RDC).
Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.
RAB=(RARB+RARC+RBRС)/RC
О разнице подключения звезда и треугольник читайте здесь.
Чему равна сила тока в цепи при параллельном соединении резисторов
Согласно правилу Кирхгофа ток, поступающий в узел, равен току, выходящему из узла, – величина тока до группы параллельных резисторов и после нее должна быть неизменной.
Ток в группе параллельных резисторов распределяется по цепи в зависимости от их номинала, после прохождения через сопротивления суммируется в узле и выходит из него неизменным I = I1+I2+I3+…+In.
Как определить величину эквивалентного сопротивления при последовательном соединении резисторов
Справка: Эквивалентом сопротивления называется замена части схемы, состоящей из нескольких резистивных элементов, одним элементом.
Для последовательного соединения эквивалентное сопротивление равно сумме сопротивлений резисторов, включенных в группу, для расчета применяется формула Rэкв = R1+R2+…+Rn.
Например: Нужно посчитать эквивалентное сопротивление данной схемы.

Выделяем первую группу из последовательно соединенных элементов – R2, R3, R4.
Считаем сопротивление Rобщ1 = R2+R3+R4.
Выделяем вторую группу из последовательных элементов R1, R5, R6.
Считаем сопротивление Rобщ2 = R1+R5+R6.
Получаем величину двух эквивалентных сопротивлений Rобщ1 и Rобщ2, соединенных параллельно.
Делаем расчет всей схемы Rэкв= Rобщ1× Rобш2/ (Rобщ1+ Rобщ2).
Зная способы соединения и формулы расчета можно рассчитать любую сложную схему соединения резистивных элементов, однако существует множество онлайн калькуляторов, которые сделают это быстрей человека, достаточно только ввести нужные параметры компонентов схемы.
| Закон Ома для участка цепи. | ||
|
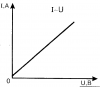
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению этого участка. Выполняется для металлов и электролитов. |
|
|
|
Закон Джоуля – Ленца. Дж. Джоуль (1841—1843) Э. X. Ленц (1842—1843) независимо друг от друга экспериментально установили |
|
|
|
В электрической цепи происходит преобразование энергии упорядоченного движения заряженных частиц в тепловую. Согласно з-ну сохранения энергии работа тока равна количеству выделившегося тепла. |
|
|
|
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток: |
|
|
|
Работа и мощность электрического тока. |
||
|
Работа электрического тока: |
|
|
|
Мощность электрического тока (работа в единицу времени): |
|
|
|
В электричестве иногда применяется внесистемная единица работы – кВт.ч (киловатт-час). |
1 кВт.ч = 3,6.106 Дж. |
|
|
Виды соединения проводников. |
||
|
Последовательное соединение. 1. Сила тока во всех последовательно соединенных участках цепи одинакова: I1=I2=I3=…=In=… 2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке: U=U1+U2+…+Un+… 3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка: R=R1+R2+…+Rn+… Если все сопротивления в цепи одинаковы, то: R=R1. N При последовательном соединении общее сопротивление увеличивается (больше большего). |
Параллельное соединение. 1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках. I=I1+I2+…+In+… |
|
|
2. Напряжение на всех параллельно соединенных участках цепи одинаково: U1=U2=U3=…=Un=… 3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению): Если все сопротивления в цепи одинаковы, то: При параллельном соединении общее сопротивление уменьшается (меньше меньшего). |
||
|
4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. A=I2Rt=I2(R1+R2+…+Rn+…)t. 5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. силы тока во всех участках одинаковы, то: U1:U2:…:Un:… = R1:R2:…:Rn:… Для двух резисторов: |
4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. 5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. напряжения на всех участках одинаковы, то: I1R1= I2R2=…= I3R3=… Для двух резисторов: |