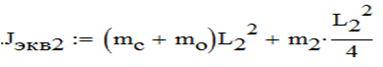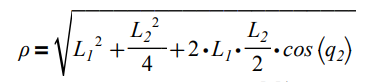Как найти мощность привода

1. Расчёт привода

1.1 Определение требуемой мощности электродвигателя

Требуемая мощность
электродвигателя определяется по
формуле

кBт,

где

– общий КПД привода,

где ₁=0,965
– КПД закрытой цилиндрической зубчатой
передачи в масляной ванне с учетом
потерь в подшипниках,

₂=0,91
– КПД цепной втулочно-роликовой передачи
с учетом потерь в подшипниках. [1, т.3]

Находим требуемую
мощность электродвигателя

=
6,834 кBт.

1.2 Выбор
электродвигателя по ГОСТ

Выбираем
электродвигатель по ГОСТ [1,т. 4] при
условии:

Р_дв

Р_тр

Выбираем
электродвигатель с числом оборотов
970.

Тип электродвигателя
АО 2-52-6

Р_дв
= 7,5 кBт,

n_дв
= 970 об/мин
– число оборотов вала двигателя

1.3 Выбор диаметр
вала электродвигателя

Выбираем диаметр
вала электродвигателя по типоразмеру
[1, т. 6]

d­_дв
= 38 мм.

1.4 Определение
мощностей

Определяем мощность
на каждом валу привода:

кBт – мощность на ведущем
валу привода,

кBт – мощность на
промежуточном валу привода,

кBт – мощность на ведомом
валу привода.

1.5 Определение
передаточных отношений редуктора

Передаточное
число показывает во сколько раз снижается
угловая скорость и частота вращения
выходной величины по сравнению с
входной.

Определяем общее
передаточное отношение

где

об/мин – число оборотов вала
электродвигателя,

=
об/мин – число оборотов ведущего вала
привода,

Тогда общее
передаточное отношение примет вид

Разбиваем общее
передаточное отношение по ступеням
привода

где u₁
–
передаточное число закрытой зубчатой
передачи,

u₂
– передаточное
число цепной втулочно-роликовой
передачи.

Принимаем для
редуктора u₁
= 3,15 [1, т. 7
], тогда u₂
=

1.6 Определение
числа оборотов и угловых скоростей
привода

Определяем угловые
скорости и число оборотов привода, на
каждом валу привода:

n₁
= 970 об/мин,

рад/с – угловая скорость и число оборотов
ведущего вала привода,

об/мин – число
оборотов выходного вала цилиндрического
редуктора,

1/с – угловая
скорость выходного вала цилиндрического
редуктора,

об/мин
– число оборотов ведомого вала привода,

1/с – угловая
скорость вращения ведомой звездочки
цепной передачи.

1.7 Определение крутящих моментов на каждом валу привода

– крутящий момент
на ведущем валу привода,

– крутящий момент
на выходном валу цилиндрического
редуктора,

– крутящий момент
на ведомом валу привода.

2. Расчет втулочной
муфты и соединение с валом.

2.1 Выбор муфты по диаметру вала двигателя по гост

d_дв = 38 мм – диаметр
вала двигателя

Определяем
расчетный крутящий момент

,

где К_р=1,5
– коэффициент режима работы для привода
электродвигателя,

Т₁
= 74 Нм
– номинальный крутящий момент.

Муфту выбираем при условии:

Т_р ≤ [Т_р]

[T_p]
=200 Н·м – максимально допустимый
крутящий момент.

Выбираем муфту по справочнику в зависимости от крутящего момента [2, т.17.2].

Размеры втулочной
муфты:

D = 55 мм – наружный
диаметр муфты,

L
= 105 мм – длина муфты,

l
= 25 мм – расстояние до отверстия под
штифт.

2.2 Расчет втулки
на кручение:

– касательное
напряжение кручения.

где


– допускаемое
напряжение кручения;

W_ρ
– полярный момент сопротивления:

где

– коэффициент отношения диаметров.

.
Условие прочности выполняется.

Соседние файлы в папке Расчёт привода,муфты

• #
• #

В электромеханике существует много приводов, которые работают с постоянными нагрузками без изменения скорости вращения. Их используют в промышленном и бытовом оборудовании как, например, вентиляторы, компрессоры и другие. Если номинальные характеристики неизвестны, то для расчетов используют формулу мощности электродвигателя. Вычисления параметров особенно актуальны для новых и малоизвестных приводов. Калькуляция выполняется с использованием специальных коэффициентов, а также на основе накопленного опыта работы с подобными механизмами. Данные необходимы для правильной эксплуатации электрических установок.

Что такое электродвигатель?

Электрический двигатель представляет собой устройство, которое преобразует электрическую энергию в механическую. Работа большинства агрегатов зависит от взаимодействия магнитного поля с обмоткой ротора, которая выражается в его вращении. Функционируют они от источников питания постоянного или переменного тока. В качестве питающего элемента может выступать аккумулятор, инвертор или розетка электросети. В некоторых случаях двигатель работает в обратном порядке, то есть преобразует механическую энергию в электрическую. Такие установки находят широкое применение на электростанциях, работающие от потока воздуха или воды.

Электродвигатели классифицируют по типу источника питания, внутренней конструкции, применению и мощности. Также приводы переменного тока могут иметь специальные щетки. Они функционируют от однофазного, двухфазного или трехфазного напряжения, имеют воздушное или жидкостное охлаждение. Формула мощности электродвигателя переменного тока

P = U х I,

где P – мощность, U – напряжение, I – сила тока.

Приводы общего назначения со своими размерами и характеристиками находят применение в промышленности. Самые большие двигатели мощностью более 100 Мегаватт используют на силовых установках кораблей, компрессорных и насосных станций. Меньшего размера используют в бытовых приборах, как пылесос или вентилятор.

Конструкция электрического двигателя

Привод включает в себя:

• Ротор.
• Статор.
• Подшипники.
• Воздушный зазор.
• Обмотку.
• Коммутатор.

Ротор – единственная подвижная деталь привода, которая вращается вокруг своей оси. Ток, проходя через проводники, образует индукционное возмущение в обмотке. Формируемое магнитное поле взаимодействует с постоянными магнитами статора, что приводит в движение вал. Их рассчитывают по формуле мощности электродвигателя по току, для которой берется КПД и коэффициент мощности, в том числе все динамические характеристики вала.

Подшипники расположены на валу ротора и способствуют его вращению вокруг своей оси. Внешней частью они крепятся к корпусу двигателя. Вал проходит через них и выходит наружу. Поскольку нагрузка выходит за пределы рабочей зоны подшипников, ее называют нависающей.

Статор является неподвижным элементом электромагнитной цепи двигателя. Может включать в себя обмотку или постоянные магниты. Сердечник статора выполнен из тонких металлических пластин, которые называют пакетом якоря. Он призван снижать потери энергии, что часто происходит с твердыми стержнями.

Воздушный зазор – расстояние между ротором и статором. Эффективным является небольшой промежуток, так как он влияет на низкий коэффициент работы электродвигателя. Ток намагничивания растет с увеличением размера зазора. Поэтому его всегда стараются делать минимальным, но до разумных пределов. Слишком маленькое расстояние приводит к трению и ослаблению фиксирующих элементов.

Обмотка состоит из медной проволоки, собранной в одну катушку. Обычно укладывается вокруг мягкого намагниченного сердечника, состоящего из нескольких слоев металла. Возмущение индукционного поля происходит в момент прохождения тока через провода обмотки. В этот момент установка переходит в режим конфигурации с явными и неявными полюсами. В первом случае магнитное поле установки создает обмотка вокруг полюсного наконечника. Во втором случае, в распределенном поле рассредотачивается слотов полюсного наконечника ротора. Двигатель с экранированными полюсами имеет обмотку, которое сдерживает магнитное возмущение.

Коммутатор используют для переключения входного напряжения. Состоит из контактных колец, расположенных на валу и изолированных друг от друга. Ток якоря подается на щетки контактов ротационного коммутатора, который приводит к изменению полярности и заставляет вращаться ротор от полюса к полюсу. При отсутствии напряжения мотор прекращает крутиться. Современные установки оборудованы дополнительными электронным средствами, которые контролируют процесс вращения.

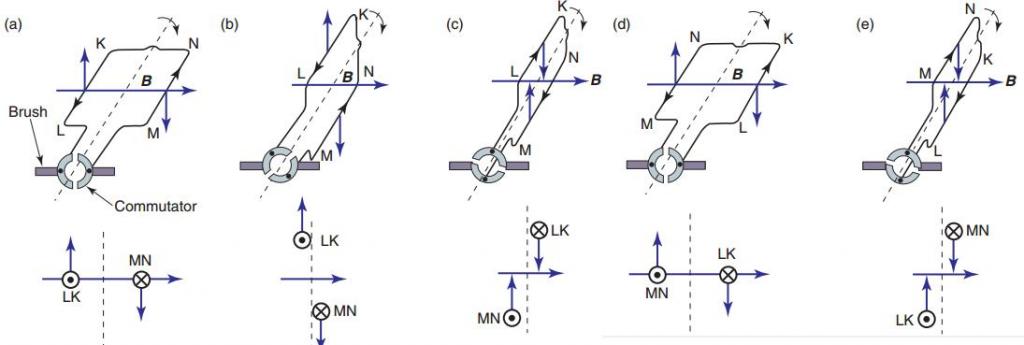
Принцип действия

По закону Архимеда ток в проводнике создает магнитное поле, в котором действует сила F1. Если из этого проводника изготовить металлическую рамку и поместить ее в поле под углом 90°, то края будут испытывать силы, направленные в противоположную сторону относительно друг друга. Они создают крутящий момент относительно оси, который начинает ее вращать. Витки якоря обеспечивают постоянное кручение. Поле создается электрическими или постоянными магнитами. Первый вариант выполнен в виде обмотки катушки на стальном сердечнике. Таким образом, ток рамки генерирует индукционное поле в обмотке электромагнита, которое порождает электродвижущую силу.

Рассмотрим более подробно работу асинхронных двигателей на примере установок с фазным ротором. Такие машины работают от переменного тока с частотой вращения якоря, не равной пульсации магнитного поля. Поэтому их еще называют индукционными. Ротор приводится в движение за счет взаимодействия электрического тока в катушках с магнитным полем.

Когда во вспомогательной обмотке отсутствует напряжение, устройство находится в состоянии покоя. Как только на контактах статора появляется электрический ток, образуется постоянное в пространстве магнитное поле с пульсацией +Ф и -Ф. Его можно представить в виде следующей формулы:

n_пр = n_обр = f₁ × 60 ÷ p = n₁

где:

n_пр – количество оборотов, которое совершает магнитное поле в прямом направлении, об/мин;

n_обр – число оборотов поля в обратном направлении, об/мин;

f₁ – частота пульсации электрического тока, Гц;

p – количество полюсов;

n₁ – общее число оборотов в минуту.

Испытывая пульсации магнитного поля, ротор получает начальное движение. По причине неоднородности воздействия потока, он будет развиваться крутящий момент. По закону индукции, в короткозамкнутой обмотке образуется электродвижущая сила, которая генерирует ток. Его частота пропорциональна скольжению ротора. Благодаря взаимодействию электрического тока с магнитным полем создается крутящий момент вала.

Для расчетов производительности существуют три формулы мощности асинхронного электродвигателя. По сдвигу фаз используют

S = P ÷ cos (alpha), где:

S – полная мощность, измеряемая в Вольт-Амперах.

P – активная мощность, указываемая в Ваттах.

alpha – сдвиг фаз.

Под полной мощностью понимаются реальный показатель, а под активной – расчетный.

Виды электродвигателей

По источнику питания приводы разделяют на работающие от:

• Постоянного тока.
• Переменного тока.

По принципу работы их, в свою очередь, делят на:

• Коллекторные.
• Вентильные.
• Асинхронные.
• Синхронные.

Вентильные двигатели не относят к отдельному классу, так как их устройство является вариацией коллекторного привода. В их конструкцию входит электронный преобразователь и датчик положения ротора. Обычно их интегрируют вместе с платой управления. За их счет происходит согласованная коммутация якоря.

Синхронные и асинхронные двигатели работают исключительно от переменного тока. Управление оборотами происходит с помощью сложной электроники. Асинхронные делятся на:

• Трехфазные.
• Двухфазные.
• Однофазные.

Теоретическая формула мощности трехфазного электродвигателя при соединении в звезду или треугольником

P = 3 * U_ф * I_ф * cos(alpha).

Однако для линейных значений напряжения и тока она выглядит как

P = 1,73 × U_ф × I_ф × cos(alpha).

Это будет реальный показатель, сколько мощности двигатель забирает из сети.

Синхронные подразделяются на:

• Шаговые.
• Гибридные.
• Индукторные.
• Гистерезисные.
• Реактивные.

В своей конструкции шаговые двигатели имеют постоянные магниты, поэтому их не относят к отдельной категории. Управление работой механизмов производится с помощью частотных преобразователей. Существуют также универсальные двигатели, которые функционируют от постоянного и переменного тока.

Общие характеристики двигателей

Все моторы имеют общие параметры, которые используются в формуле определения мощности электродвигателя. На их основе можно рассчитать свойства машины. В разной литературе они могут называться по-разному, но означают они одно и то же. В список таких параметров входит:

• Крутящий момент.
• Мощность двигателя.
• Коэффициент полезного действия.
• Номинальное количество оборотов.
• Момент инерции ротора.
• Расчетное напряжение.
• Электрическая константа времени.

Вышеуказанные параметры необходимы, прежде всего, для определения эффективности электрических установок, работающих за счет механической силы двигателей. Расчетные величины дают лишь приблизительное представление о реальных характеристиках изделия. Однако эти показатели часто используют в формуле мощность электродвигателя. Именно она определяет результативность машин.

Вращательный момент

Этот термин имеет несколько синонимов: момент силы, момент двигателя, Вращательный момент, вертящий момент. Все они используются для обозначения одного показателя, хотя с точки зрения физики эти понятия не всегда тождественны.

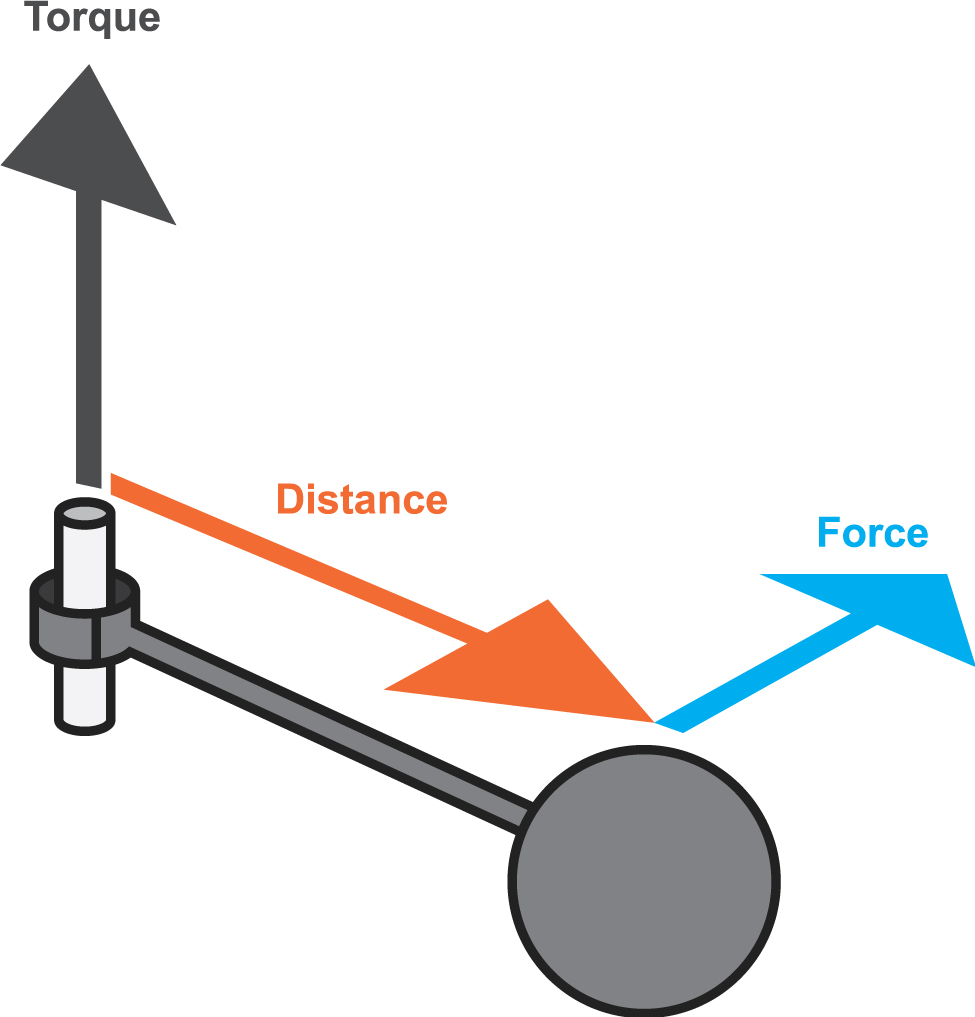
В целях унификации терминологии были разработаны стандарты, которые приводят все к единой системе. Поэтому в технической документации всегда используются словосочетание “крутящий момент”. Он представляет собой векторную физическую величину, которая равна произведению векторных значений силы и радиуса. Вектор радиуса проводится от оси вращения к точке приложенной силы. С точки зрения физики разница между крутящим и вращательным моментом заключается в точке прикладывания силы. В первом случае это внутреннее усилие, во втором – внешнее. Измеряется величина в ньютон-метрах. Однако в формуле мощности электродвигателя крутящий момент используется как основное значение.

Рассчитывается он как

M = F × r, где:

M – крутящий момент, Нм;

F – прикладываемая сила, H;

r – радиус, м.

Для расчета номинального вращающего момента привода используют формулу

Мном = 30Р_ном ÷ pi × н_ном, где:

Р_ном – номинальная мощность электрического двигателя, Вт;

н_ном – номинальное число оборотов, мин^-1.

Соответственно, формула номинальной мощности электродвигателя бедует выглядеть следующим образом:

Рном = М_ном * pi*н_ном / 30.

Обычно все характеристики указаны в спецификации. Но бывает, что приходится работать с совершенно новыми установками, информацию о которых найти очень сложно. Для расчета технических параметров таких устройств берут данные их аналогов. Также всегда известны только номинальные характеристики, которые даются в спецификации. Реальные данные необходимо рассчитывать самостоятельно.

Мощность двигателя

В общем смысле данный параметр представляет собой скалярную физическую величину, которая выражена в скорости потребления или преобразования энергии системы. Он показывает, какую работу механизм выполнит за определенную единицу времени. В электротехнике характеристика отображает полезную механическую мощность на центральном вале. Для обозначения показателя используют литеру P или W. Основной единицей измерения является Ватт. Общая формула расчета мощности электродвигателя может быть представлена как:

P = dA ÷ dt, где:

A – механическая (полезная) работа (энергия), Дж;

t – затраченное время, сек.

Механическая работа также является скалярной физической величиной, выражаемой действием силы на объект, и зависящей от направления и перемещения этого объекта. Она представляет собой произведение вектора силы на путь:

dA = F × ds, где:

s – пройденное расстояние, м.

Она выражает дистанцию, которую преодолеет точка приложенной силы. Для вращательных движений она выражается как:

ds = r × d(teta), где:

teta – угол оборота, рад.

Таким образом можно вычислить угловую частоту вращения ротора:

omega = d(teta) ÷ dt.

Из нее следует формула мощности электродвигателя на валу: P = M × omega.

Коэффициент полезного действия электромотора

КПД – это характеристика, которая отражает эффективность работы системы при преобразовании энергии в механическую. Выражается отношением полезной энергии к потраченной. По единой системе единиц измерений он обозначается как “eta” и является безразмерным значением, исчисляемым в процентах. Формула КПД электродвигателя через мощность:

eta = P₂ ÷ P₁, где:

P₁ – электрическая (подаваемая) мощность, Вт;

P₂ – полезная (механическая) мощность, Вт;

Также он может быть выражен как:

eta = A ÷ Q × 100 %, где:

A – полезная работа, Дж;

Q – затраченная энергия, Дж.

Чаще коэффициент вычисляют по формуле потребляемой мощности электродвигателя, так как эти показатели всегда легче измерить.

Снижение эффективности работы электродвигателя происходит по причине:

• Электрических потерь. Это происходит в результате нагрева проводников от прохождения по ним тока.
• Магнитных потерь. Вследствие излишнего намагничивания сердечника появляется гистерезис и вихревые токи, что важно учитывать в формуле мощности электродвигателя.
• Механических потерь. Они связаны с трением и вентиляцией.
• Дополнительных потерь. Они появляются из-за гармоник магнитного поля, так как статор и ротор имеют зубчатую форму. Также в обмотке присутствуют высшие гармоники магнитодвижущей силы.

Следует отметить, что КПД является одним из самых важных компонентов формулы расчета мощности электродвигателя, так как позволяет получить цифры, наиболее приближенные к действительности. В среднем этот показатель варьирует от 10% до 99%. Она зависит от конструктивного устройства механизма.

Номинальное количество оборотов

Еще одним ключевым показателем электромеханических характеристик двигателя является частота вращения вала. Он выражается в числе оборотов в минуту. Часто его используют в формуле мощности электродвигателя насоса, чтобы узнать его производительность. Но необходимо помнить, что показатель всегда разный для холостого хода и работы под нагрузкой. Показатель представляет физическую величину, равной количеству полных оборотов за некий промежуток времени.

Расчетная формула частоты оборотов:

n = 30 × omega ÷ pi, где:

n – частота вращения двигателя, об/мин.

Для того, чтобы найти мощность электродвигателя по формуле оборотистости вала, необходимо привести ее к расчету угловой скорости. Поэтому P = M × omega будет выглядеть следующим образом:

P = M × (2pi × n ÷ 60) = M × (n ÷ 9,55), где

t = 60 секунд.

Момент инерции

Этот показатель представляет собой скалярную физическую величину, которая отражает меру инертности вращательного движения вокруг собственной оси. При этом масса тела является величиной его инертности при поступательном движении. Основная характеристика параметра выражена распределением масс тела, которая равна сумме произведений квадрата расстояния от оси до базовой точки на массы объекта.В Международной системе единиц измерения он обозначается как кг·м² и имеет рассчитывается по формуле:

J = ∑ r² × dm, где

J – момент инерции, кг·м² ;

m – масса объекта, кг.

Моменты инерции и силы связаны между собой соотношением:

M – J × epsilon, где

epsilon – угловое ускорение, с^-2.

Показатель рассчитывается как:

epsilon = d(omega) × dt.

Таким образом, зная массу и радиус ротора, можно рассчитать параметры производительности механизмов. Формула мощности электродвигателя включает в себя все эти характеристики.

Расчетное напряжение

Его еще называют номинальным. Оно представляет собой базовое напряжение, представленное стандартным набором вольтажа, которые определяется степенью изоляции электрического оборудования и сети. В действительности оно может отличаться в разных точках оборудования, но не должно превышать предельно допустимых норм рабочих режим, рассчитанных на продолжительное функционирование механизмов.

Для обычных установок под номинальным напряжением понимают расчетные величины, для которых они предусмотрены разработчиком в нормальном режиме работы. Перечень стандартного вольтажа сети предусмотрен в ГОСТ. Эти параметры всегда описаны в технических характеристиках механизмов. Для расчета производительности используют формулу мощности электродвигателя по току:

P = U × I.

Электрическая константа времени

Представляет собой время, необходимое для достижения уровня тока до 63 % после подачи напряжения на обмотки привода. Параметр обусловлен переходными процессами электромеханических характеристик, так как они быстротечны ввиду большого активного сопротивления. Общая формула расчета постоянной времени:

t_e = L ÷ R.

Однако электромеханическая константа времени t_m всегда больше электромагнитной t_e. Первый параметр получается из уравнения динамических характеристики двигателя при сохранении условии, когда ротор разгоняется с нулевой скоростью до максимальных оборотов холостого хода. В этом случае уравнение принимает вид

M = M_ст + J × (d(omega) ÷ dt), где

M_ст = 0.

Отсюда получаем формулу:

M = J × (d(omega) ÷ dt).

По факту электромеханическую константу времени рассчитывают по пусковому момент – M_п. Механизм, работающий в идеальных условиях, с прямолинейными характеристиками будем иметь формулу:

M = M_п × (1 – omega ÷ omega₀), где

omega₀ – скорость на холостом ходу.

Такие расчеты используют в формуле мощности электродвигателя насоса, когда ход поршня напрямую зависит от оборотистости вала.

Основные формулы расчета мощности двигателей

Для вычисления реальных характеристик механизмов всегда нужно учитывать много параметров. в первую очередь нужно знать, какой ток подается на обмотки электродвигателя: постоянный или переменный. Принцип их работы отличается, следовательно, отличаются метод вычислений. Если упрощенный вид расчета мощности привода выглядит как:

P_эл = U × I, где

I – сила тока, А;

U – напряжение, В;

P_эл – подведенная электрическая мощность. Вт.

В формуле мощности электродвигателя переменного тока необходимо также учитывать сдвиг фаз (alpha). Соответственно, расчеты для асинхронного привода выглядят как:

P_эл = U × I × cos(alpha).

Кроме активной (подведенной) мощности существует также:

• S – реактивная, ВА. S = P ÷ cos(alpha).
• Q – полная, ВА. Q = I × U × sin(alpha).

В расчетах также необходимо учитывать тепловые и индукционные потери, а также трение. Поэтому упрощенная модель формулы для электродвигателя постоянного тока выглядит как:

P_эл = Pмех + Ртеп +Ринд + Ртр_, где

Рмех – полезная вырабатываемая мощность, Вт;

Ртеп – потери на образование тепла, ВТ;

Ринд – затраты на заряд в индукционной катушке, Вт;

Рт – потери в результате трения, Вт.

Заключение

Электродвигатели находят применение практически во всех областях жизни человека: в быту, в производстве. Для правильного использования привода необходимо знать не только его номинальные характеристики, но и реальные. Это позволит повысить его эффективность и снизить затраты.

Мощность электродвигателя – паспортная характеристика прибора, превращающего электрическую энергию в кинетическую. Это один из ключевых параметров при выборе устройства для обслуживания различного оборудования. Она всегда указывается в сопроводительной документации и дополнительно «штампуется» на шильднике электрического двигателя, закрепленном на его корпусе.

Но документы не всегда сохраняются, а надпись на шильднике может затереться. В таких случаях для дальнейшей эксплуатации, проверки, подключения может потребоваться расчет мощности электродвигателя. Он производится разными способами, о которых и расскажем.

Способы расчета мощности электродвигателя

Учитывая широкое распространение, неудивительно, что формул мощности электродвигателя существует довольно много. Самые простые в плане применения на производстве – следующие три подхода.

1. Расчет мощности электродвигателя по току. Для определения фактического показателя прибор надо подключить (напряжение – фиксированное) и изменять ток поочередно на каждой из обмоток при помощи амперметра. Алгоритм действий такой:
   • берется количество замеров;
   • определяется сила тока в Амперах для каждого замера;
   • все показатели суммируются и делятся на количество замеров;
   • среднее значение силы тока умножаем на напряжение и получаем мощность электродвигателя в кВт (или Ваттах).
2. Расчет мощности электродвигателя по размерам. Надо измерить диаметр и длину сердечника статора, узнать частоту оборотов вала.
3. Расчет мощности электродвигателя асинхронного по силе тяги:
   • тахометром определяем частоту вращения вала;
   • штангенциркулем меряем радиус вала (если нет циркуля, можно взять обычную линейку);
   • динамометр используем, чтобы замерять тяговое усилие устройства;
   • формула мощности электродвигателя выглядит как P = F (тяговая сила)*n (частота вращения)*r (радиус вала)*2*3,14.

Формула мощности электродвигателя

Формула мощности электродвигателя может учитывать массу нюансов технологического процесса. Благодаря развитию IT-технологий сегодня найти способы расчета такого показателя не составляет труда. А вот выбрать в огромном количестве предложенных вариантов тот, который подойдет именно вам, как показывает практика, не так-то просто.

Чтобы вы не растерялись в огромном количестве методичек и рекомендаций интернета, предлагаем универсальный вариант формулы, который подойдет практически для любого случая. Выглядит она следующим образом.

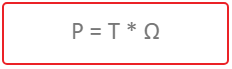
,где:

• P – потребляемая мощность электродвигателя (номинальная);
• T – необходимый момент вращения на валу;
• Ω – угловая скорость.

У экспликатов тоже есть свои формулы.

1. Вращающий момент (T) считается как произведение требуемого усилия тяги и радиуса рабочего органа подключаемого механизма.
   • Усилие тяги (обозначается как Ft) можно рассчитать по формуле Ft = t*M*2,5, где t –коэффициент трения (берется из таблицы данных, для подшипников качения, например, он известен и равняется 0,02), а М – масса груза, который перемещает оборудование. Произведение корректируется на коэффициент Ньютона, который тоже известен и составляет 2,5.
   • Радиус элемента вращения измеряют или берут из проектных/паспортных данных.
2. Угловую скорость определяют так: Ω = число Пи (π, принимается как 3,14)*n/30 (n – частота вращательного движения механизма, которое приводит в действие электродвигатель – берется из паспорта). Чтобы электродвигателя хватило с учетом возможных перегрузок привода, угловая скорость, рассчитанная приведенным способом, корректируется в большую сторону на коэффициент 1,5.

При расчете мощности электродвигателя надо делать поправку на тип соединения обмоток статора, от которого зависит значение рабочего тока. В соединениях типа «звезда» ток меньше в 1,73 раза, чем в соединениях «треугольник». Соответственно, для «звезды» показатель тоже надо уменьшать в 1,73 раза.

Расчет мощности электродвигателя для оборудования

Чтобы определить, какой мощности электродвигатель нужен для обслуживания конкретного механизма, надо знать его (механизма) потребляемую мощность. Она обычно указывается для каждой категории установок и приборов, прописывается в паспортной документации и известна производителю. Если фактической информации по показателю нет, ее можно получить:

• по результатам теоретических расчетов;
• эмпирически, использовав результаты многочисленных опытов;
• методом снятия нагрузочных диаграмм, если опытной базы эксплуатации еще не накоплено (оборудование малоизученно), здесь нужны самопишущие приборы;
• через применение нормативов потребления энергии (статистических данных), которые учитывают удельные расходы электрической энергии при создании конкретного продукта.

Когда потребление известно, останется подставить его в формулу следующего вида.

, где:

• Рм – определенная теоретически/эмпирически или паспортная мощность оборудования;
• – коэффициент полезного действия промежуточной передачи.

Расчетный показатель используется для выбора по каталогу продукции ПТЦ «Привод». При этом ориентироваться следует на номинальные мощностные показатели электродвигателя с небольшим запасом.

Проверять электрический двигатель по нагрузке или перегреву необходимости нет. Наш производственно-технический центр на этапе контроля качества готовых изделий проводит все испытания и расчеты с максимальным использованием материалов, которые заложены в моделях при номинальном расчете мощности электродвигателя. А вот контроль достаточности момента пуска для некоторых видов подключаемых механизмов может быть полезен. Это в особенности касается устройств с увеличенным сопротивлением трения на старте (транспортеры, рабочие узлы станков металлорезки).

Энергетическая эффективность электродвигателя

Как и у всех электроприборов, потребляющих электрическую энергию (платный ресурс), электродвигатель имеет свой класс энергоэффективности. От этого показателя зависят расходы производства на работу устройства. Он, в свою очередь, зависит от коэффициента полезного действия двигателя и указывается в технической документации. Как показывает практика, даже в средней категории электродвигателей (55 кВт) предпочтение версиям с более высоким классом энергоэффективности позволяет существенно снизить расходы энергии (экономия до 10 тыс. кВт в год).

Вы можете подобрать установку оптимального класса энергоэффективности по каталогу продукции ПТЦ «Привод» – в описании моделей есть вся необходимая информация. Здесь же можно заказать регулятор мощности электродвигателя, который тоже помогает сократить расход энергии и обеспечивает плавную работу устройства без рывков (увеличивает срок его службы).

Энергетический расчёт и выбор на этой основе исполнительных двигателей

Блог компании Специальный Технологический Центр

Разберём, как можно выбрать исполнительные двигатели для своего проекта, самоделки и иных целей. Будет использоваться подход к синтезу, который получил название синтеза цифровой системы по ее непрерывному аналогу. Начальным этапом процесса проектирования является выполнение энергетического расчёта и выбор на этой основе исполнительных двигателей, механических передач и силовых преобразователей (усилителей мощности), в совокупности обеспечивающих возможность реализации силового воздействия на объект управления.

1. Энергетический расчёт.

Целью энергетического расчета является рациональный выбор исполнительных элементов приводов системы, которые обладают энергетическими возможностями для обеспечения механического объекта управления по заданному закону во всех предусмотренных режимах работы. Задача энергетического расчета состоит в анализе сил (моментов сил) и скоростей, которые должны развивать приводы системы и выборе исполнительных элементов, энергетически обеспечивающих возможность получения требуемых сил и скоростей движения механических объектов управления и удовлетворяющих заданным критериям эффективности такого выбора.

Считаем, что динамическая жёсткость приводов бесконечно высока и поэтому взаимовлияние степеней подвижности манипулятора не проявляется. Тогда можно считать, что при движении одного из звеньев второе звено остаётся неподвижным.

Примем себе техническое задание:

Спроектировать привода для двухзвенного плоского манипулятора робота.  Возьмём для этого упрощенную модель двухзвенного механизма манипулятора (рис.1), имеющего “плечевое” и “локтевое” звенья, причем рабочий орган (РО) условно считается закрепленным непосредственно на конце “локтевого” звена.

На рисунке приняты обозначения:

q₁ и q₂ – обобщённые координаты манипуляционного механизма. Они представляют собой углы поворота “плечевого” и “локтевого” звеньев манипулятора, соответственно. Угол q₁ определяется как отклонение “плечевого” звена от вертикали, а угол q₂ определяется как отклонение “локтевого” звена от продольной оси “плечевого” звена. Положительные значения этих углов соответствуют вращению звеньев по часовой стрелке;

L₁ и L₂ – длины «плечевого» и «локтевого» звеньев, соответственно. L₂ – расстояние от оси поворота “локтевого” звена до центра масс рабочего органа с объектом манипулирования;

m₁ и m₂ – массы «плечевого» и «локтевого» звеньев, соответственно.

Считается, что каждая из этих масс сосредоточена в центре соответствующего звена;

m₀ – суммарная масса рабочего органа и объекта манипулирования;

m_ДВ1 и m_ДВ2 – массы исполнительных двигателей;

V и a – скорость и ускорение конечной точки манипулятора соответственно;

R – расстояние от оси вращения «плечевого» звена до конечной точки манипулятора;

M₁ и M₂ – моменты сил, развиваемые приводами и действующие на звенья манипулятора.

Таблица 1. Параметры манипуляционного механизма:

Таблица 2. Основные требования к исполнительной системе робота:

1.1 Выбор двигателя и редуктора привода второго звена.

Кинематический анализ:

Найдём максимальные значения угловой скорости и углового ускорения для второго звена манипулятора.

Максимальное угловое ускорение 2-го звена:

Максимальная угловая скорость рабочего движения 2-го звена:

Максимальное угловое ускорение рабочего движения 2-го звена:

Максимальный суммарный момент сил  M2max , который должен развивать привод второго звена, определяется по формуле.

η – КПД механической передачи.

Статический момент относительно оси вращения 2-го звена определяется по формуле:

где g =9.807 м/с2 –  ускорение свободного падения.

Mст2  имеет максимальное значение при выполнении условия sin(q1+q2)=1. Mст2 = 30.4 Н*м.

Для вычисления динамического момента, действующего на второе звено, находим эквивалентный момент инерции Jэкв2 этого звена по формуле:

Jэкв2 = 0.62 кг*м2

Максимальное значение динамического момента (для режима переброски) получим:

       

С целью обеспечения точной работы приводов манипулятора могут быть

выбраны волновые или планетарные редукторы. Предварительно выбираем волновой редуктор HDUR-32 компании Harmonic drive gearing. По данным производителя КПД такого редуктора η2̗ = 0.85 В этом случае максимальный суммарный момент сил M2max , который должен развивать привод второго звена:

Оценка мощности двигателя второго звена:

Максимальное значение мощности механического движения второго звена:

Требуемую мощность двигателя второго звена P2 выбираем из условия.

P2≈(2…3)*P2max.  P2= 420 Вт

Выбор исполнительного двигателя производим по требуемой мощности. Выбираем двигатель TETRA 85SR2.2, обладающий следующими параметрами:

Pн2 = 650 Вт – номинальная мощность.

Мн2 = 2.2  ̗- номинальный момент Н*м.

 J дв2 =1.8Έ10˕4 кг*Ем2  – момент инерции ротора.

mдв2 = 4.2 кг – масса двигателя.

 n2ном  =  3000 об/мин – номинальная частота вращения.

Rя  = 19.76  Ом – активное сопротивление якоря.

U2ном = 250 В – номинальное напряжение якоря.

Определение требуемого передаточного отношения и марки редуктора.

Оценка значения передаточного отношения редуктора привода второго звена:

Выбираем редуктор HDUR FDD-32-260, обладающий следующими параметрами:

i_р2 = 260 – передаточное отношение.

m_p2 ̗= 1.7 кг- масса редуктора.

Для дальнейших расчётов и выбора компонентов привода первого звена принимаем массу привода второго звена равной:

Теперь проверим выполнения необходимых условий правильности выбора

двигателя и редуктора. Проверяем выбранный двигатель по моменту:

Следовательно, подсистема «двигатель-редуктор» способна создавать момент, не меньше требуемого.

1.2 Выбор двигателя и редуктора привода первого звена.

Кинематический анализ манипуляционного механизма

Расчёты проводятся в соответствии с кинематической схемой и схемой действия сил, представленной на рис. 3

В таком положении момент М1 первого звена будет иметь значения, наиболее близкие к максимально возможным значениям. Скорость вращения первого звена Ω1 определяется по формуле:

где q2 – обобщённая координата, характеризующая положение второго звена

относительно продольной оси первого звена. Таким образом, видно, что скорость вращения первого звена Ω1 зависит от обобщенной координаты q2

Угловое ускорение, с которым движется первое звено, определяется по формуле:

Следовательно, угловое ускорение тоже зависит от q2.

Силовой анализ манипуляционного механизма.

Определяется момент сил, который должен развивать привод первого звена. При этом считаем, что силы приложены в центрах масс первого и второго звеньев, рабочего органа и объекта манипулирования

Статический момент Мст1 действующий относительно оси поворота первого звена, зависит от обобщённых координат:

Динамический момент Mдин1 , зависящий от углового ускорения ε1 и

эквивалентного момента инерции Jэкв1 вычисляется по формуле:

Эквивалентный момент инерции манипуляционного механизма, перемещаемого первым приводом, можно оценить по формуле:

где ρ – расстояние от оси вращения первого звена до центра масс второго звена, причём

Максимальное значение суммарного момента М1 можно определить, варьируя значения переменных q1 и q2. Для упрощения решения задачи будем рассматривать конфигурацию манипулятора, представленную на рис. 3, при которой рабочий орган находится на горизонтальной прямой линии, проходящей через ось вращения первого звена. Тогда между переменными q1 и q2 будет существовать связь следующего вида:

КПД редуктора привода первого звена примем η1̗0.85

Оценка мощности механического движения первого звена.

Для определения максимального значения мощности механического движения первого звена воспользуемся графиком зависимости требуемой мощности P1 от обобщенной координаты q2.

P1max = 303 Вт. Примем q2pmax = 58 град.

1.3 Выбор двигателя привода первого звена.

Выбираем двигатель по мощности из расчета P1≈(2…3)*P1max. P1 = 2.5 * P1max = 757.5 Вт.

Выбираем двигатель ESA 3L обладающий следующими параметрами:

Pн1 = 800 Вт – номинальная мощность.

Мн1 = 1.75 Н*м – номинальный момент.

Jдв1 = 0.64 * 10^-4 кг*м^2 – момент инерции ротора.

Mдв1 = 3.05 кг – масса двигателя.

n1ном = 3000 обмин – номинальная частота вращения.

Rя1 = 5.24 Ом – сопротивление якоря.

U1ном = 250 В – номинальное напряжение якоря.

Iяном = 2.5 А – номинальный ток якоря.

Tэ = 0.00275  – электромагнитная постоянная времени.

Вычислим номинальную угловую скорость двигателя:

Выбираем редуктор аналогичный редуктору второго звена HDUR-32-260

обладающий следующими параметрами:

i = 260 – передаточное отношение.

m 1.7 кг- масса редуктора.