Пример расчета реактивной мощности асинхронного двигателя
В данной статье будет рассматриваться пример расчета реактивной мощности асинхронного двигателя.
Пример
Определить реактивную мощность асинхронного двигателя типа АИР132М2 с нагрузкой 100 и 50%.
Исходные данные
Технические характеристики двигателя определяются по каталогу согласно таблице 1:
- Рн = 11 кВт – номинальная активная мощность;
- сosϕн = 0,89 – коэффициент мощности;
- Uн = 380В – номинальное напряжение при схеме соединения обмоток статора в треугольник;
- ηн = 0,884 – коэффициент полезного действия.
Таблица 1 — Технические характеристики электродвигателей типа АИР
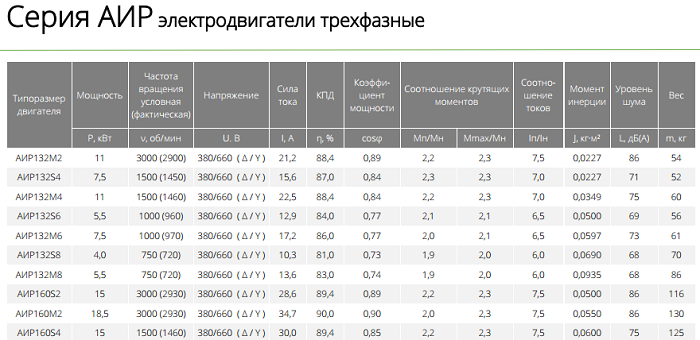
Решение
1. Определяем коэффициент реактивной мощности АД, зная значение cosϕ:
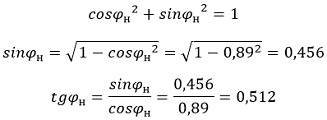
2. Определяем реактивную мощность двигателя при нагрузке 100% по выражению 22 [Л1, с.33]:
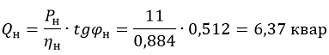
3. Определяем номинальный ток двигателя:
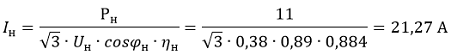
4. Измеряем ток холостого хода двигателя при расцепленной муфте: Iх.х.= 5,3 А.
Если же измерить ток холостого хода нет возможности, можно принять, что ток холостого хода лежит в пределах от 25 до 60%*Iн согласно [Л1, с.32]. Такие большие значения тока холостого хода связаны из-за относительно большого воздушного зазора между статором и ротором. На преодоление этого воздушного зазора магнитным потоком требуется большая намагничивающая сила обмотки двигателя, что приводит к большему намагничивающему току и к значительно большему току холостого хода асинхронного двигателя по сравнению с трансформатором (у трансформатора ток холостого хода составляет 2-6% номинального тока).
5. Определяем реактивную мощность двигателя при нагрузке 50% по выражению 24 [Л1, с.34], при этом Рн = 5,5 кВт:
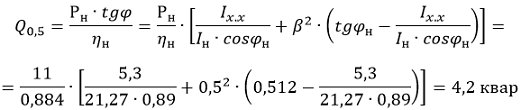
6. Определяем коэффициент реактивной мощности при нагрузке 50% по выражению 13 [Л1, с.19]:
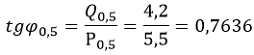
Литература:
- Реактивная мощность (2-е издание) Минин Г.П. 1978 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
коэффициент реактивной мощности, реактивная мощность двигателя, холостой ход двигателя
Благодарность:
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding» и «PayPal».
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.
2.1. Двигатель и силовая установка
Следует различать
понятия двигатель
и силовая
установка.
Двигателем
принято называть устройство, участвующее
в создании тяги (или мощности), необходимой
для движения летательного аппарата.
Двигатель является составной частью
силовой установки, той ее частью, которая
изготавливается и поставляется
двигательным заводом.
Авиационной
силовой установкой называют
конструктивно объединенную совокупность
двигателя с входным и выходным устройствами
(с теми их элементами, которые
изготавливаются на самолетостроительном
заводе), встроенную в конструкцию планера
(фюзеляжа или крыла) или скомпонованную
в отдельных двигательных гондолах.
Силовая
установка, помимо двигателя, входного
и выходного устройств, включает в себя
еще системы топливопитания, смазки,
запуска и автоматического управления,
обеспечивающие ее надежное функционирование,
а также узлы крепления, необходимые для
передачи усилий от двигателя к планеру.
В теории авиадвигателей эти системы и
узлы не рассматриваются.
2.2. Тяга реактивного двигателя
Под тягой
двигателя Р
понимают тягу
без учета внешних сопротивлений входных
и выходных устройств и других элементов
силовой установки.
Тяга реактивного двигателя определяется
по формуле:
.
(2.1)
Эта формула получила
наименование формулы
Стечкина.
Она
была впервые получена Борисом
Сергеевичем Стечкиным
в его знаменитой работе «Теория воздушного
реактивного двигателя», опубликованной
в 1929 г. Она выведена в предположении,
что двигатель расположен в мотогондоле,
векторы скорости истечения и скорости
полета параллельны оси двигателя, а
внешнее обтекание двигателя является
идеальным, т.е. происходит без трения,
отрыва потока и без скачков уплотнения.
В формуле Стечкина
в ряде случаев могут быть сделаны
упрощения. Так, если пренебречь тем, что
расходы воздуха на входе в двигатель
и газа на выходе из него
отличаются, получим.
.
(2.2)
отличается от
по той причине, что в ГТД подводится
топливо и могут быть отборы воздуха на
нужды летательного аппарата.
При полном расширении газа в сопле до
атмосферного давления (рс=рН)
формула тяги приобретает еще более
простой вид
.
(2.3)
2.3. Эффективная тяга силовой установки
Под эффективной тягой силовой
установки Рэфпонимают
ту часть силы тяги двигателя, которая
непосредственно используется для
движения самолета, т.е. идет на совершение
полезной работы по преодолению лобового
сопротивления и инерции летательного
аппарата. ВеличинаРэфравна
тяге двигателяРза вычетом всех
внешних сопротивлений, создаваемых
самой силовой установкой.
По физическому смыслу Рэфявляется равнодействующей всех сил
давления и трения, действующих на
элементы проточной части со стороны
газового потока, протекающего через
силовую установку изнутри, и внешнего
потока воздуха, обтекающего силовую
установку снаружи. Задача определения
эффективной тяги сводится к нахождению
векторной суммы всех указанных сил. Эти
силы принято разделять на внутренние
(вн) и наружные (нар).
Внутренние силы
представляют собой сумму сил давления
и трения, действующих на рабочие
поверхности силовой установки изнутри.
Величина равнодействующей внутренних
сил зависит от термодинамического
совершенства рабочего процесса двигателя
и практически не зависит от способа
установки двигателя на летательном
аппарате.
Наружные силы
представляют
собой совокупность сил давления и
трения, действующих на силовую установку
со стороны обтекающего ее внешнего
потока. Эти
силы существенно зависят от способа
размещения силовой установки на
летательном аппарате.
Рассмотрим наиболее
простой с точки зрения учета условий
внешнего обтекания случай – изолированная
силовая установка в отдельной мотогондоле.
Наружная поверхность
силовой установки здесь условно разделена
на три части: лобовую часть вх–М,
центральную часть М–и кормовую часть
–c.
Набегающий
поток воздуха разделяется поверхностью
тока Н–1–2–вх
на внутренний, проходящий через двигатель,
и внешний, обтекающий силовую установку
снаружи. Сечения в невозмущенном потоке
перед силовой установкой, на входе в
воздухозаборник и на выходе из сопла
двигателя обозначим Н–Н,
вх–вх
и с–с.
Соответственно, площади нормальных
сечений будут FН,
Fвх
и Fс.
Главной причиной
возникновения внешнего сопротивления
силовой установки при сверхзвуковых
скоростях полета является повышение
давления на головном участке гондолы
вх–М
и наличие разрежения на ее кормовом
участке
–c.
К этому прибавляется сопротивление от
сил трения по всей поверхности гондолы
от сечения вх–вх
до сечения с–с.
Эффективная тяга силовой установки,
согласно определению, равна
, (2.4)
где Rвн– равнодействующая
сил давления и трения, действующих на
внутренние поверхности силовой установки;
Rнар– равнодействующая сил
давления и трения, действующих на всю
наружную поверхность гондолывх–М––c.
Зная характер
распределения давлений по наружной
поверхности гондолы, величину силы Rнар
можно определить непосредственным
интегрированием сил давления и трения
по этой поверхности. Тогда
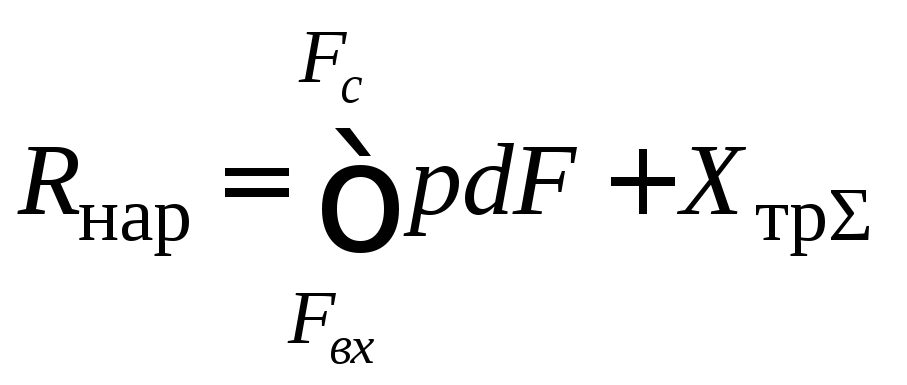
(2.5)
где
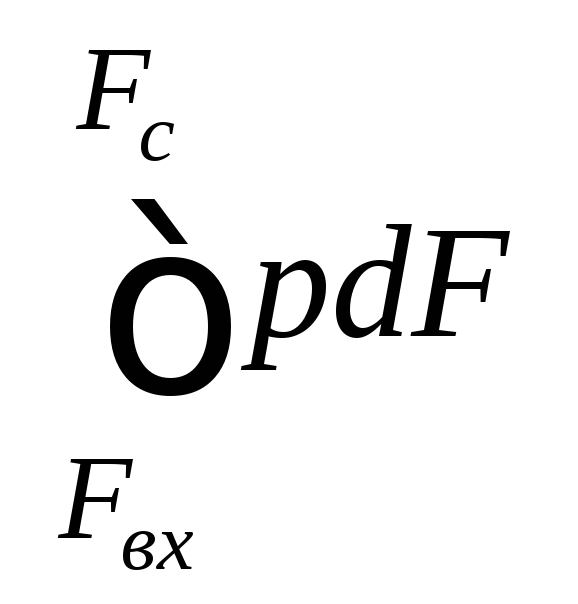
– равнодействующие сил давления и
трения, приложенные к наружной поверхности
гондолы;dF =dS cos
– проекция элемента поверхности
гондолы на плоскость, перпендикулярную
направлению полета (
– угол между нормалью к элементу
поверхности и этой плоскостью).
Величину Rвнопределим,
пользуясь уравнением сохранения
количества движения для некоторого
контрольного объема, включающего все
внутренние поверхности силовой установки.
В качестве такого контрольного объема
выберем объем внутренней струи,
заключенный между сечениямиН–Нис–с.
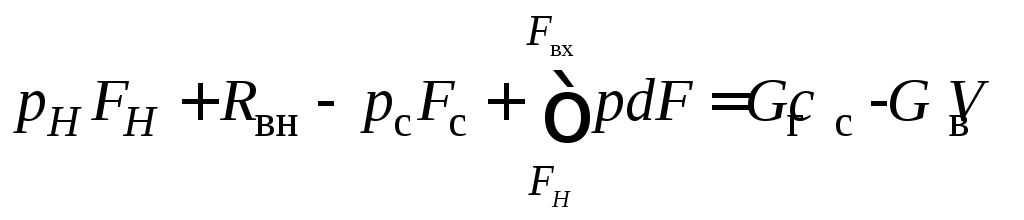
где pН FНиpсFс– силы давления,
приложенные к торцевым поверхностям
выделенного участка струи;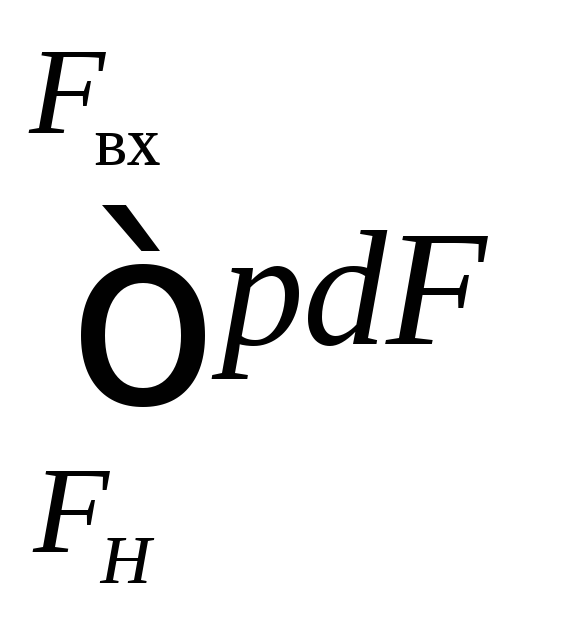
равнодействующая сил давления, приложенных
к боковой поверхности струи токаН–1–2–вх;Rвн –
равнодействующая сил давления и трения,
действующих на внутренние поверхности
силовой установки (равная по модулю
силе,
действующей со стороны СУ на выделенный
контрольный объем газа).
Отсюда находим

(2.7)
Подставляя выражения Rнариз
(2.6) иRвниз (2.8) в уравнение
(2.5), получим

(2.8)
Для перехода от абсолютных давлений к
избыточным воспользуемся следующим
очевидным тождеством:
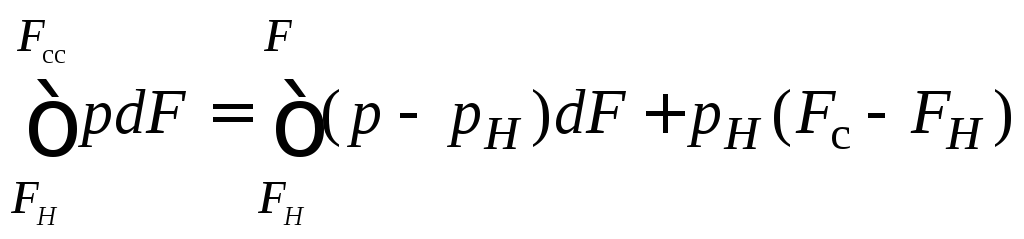
Оно позволяет выражение (2.9) привести к
виду
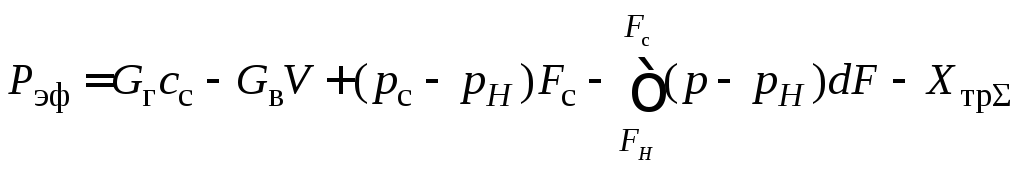
Эта формула
является общим выражением эффективной
тяги для силовой установки рассмотренной
схемы. При
этом необходимо иметь в виду, что тяга
реактивного двигателя является векторной
величиной. Если формулу (2.9) представить
в векторной форме, то вектор тяги
необязательно будет направлен вдоль
оси двигателя, как было принято при
выводе, а может отклоняться от нее,
например, при полетах со значительными
углами атаки или при повороте сопла.
Мощность ракетного двигателя
Мощность ракетного двигателя
Мощность, развиваемая двигателем, т. е. механическая работа, совершаемая им в единицу времени (секунду), является важнейшей характеристикой любого двигателя. Это и естественно, если иметь в виду, что именно совершение этой механической работы за счет израсходования определенного количества энергии другого вида — тепловой, электрической или еще какой-либо — и является назначением всякого двигателя. В соответствии с этим двигатели подразделяются на электрические, тепловые и т. д.
Обычно мощность, развиваемая каким-либо двигателем, может быть использована самыми разнообразными способами. Для этого вал двигателя связывают с тем или иным потребителем механической работы. Так, например, поршневой двигатель внутреннего сгорания может быть установлен на электростанции и вращать ротор динамомашины, тогда мощность двигателя будет преобразовываться в электрическую энергию; он может вращать трансмиссию в цехе и приводить таким образом в движение станки; может быть установлен на автомобиле для привода его ведущих колес; наконец, может вращать пропеллер самолета и т. д. Во всех этих случаях мощность двигателя будет неизменной, она будет только по-разному расходоваться. В частности, для нас очень важно, что мощность такого двигателя, установленного, допустим, на самолете, будет также одинаковой, вне зависимости от того, неподвижен ли самолет, стоящий на аэродроме, или летит со скоростью в сотни километров в час.
Именно этим свойством обычного поршневого авиационного двигателя объясняется то, что он перестал удовлетворять требованию непрерывного роста скорости полета, характерному для современной авиации.
Действительно, мощность, потребная для полета данного самолета, очень быстро растет при увеличении скорости полета, пропорционально кубу этой скорости. Значит, при увеличении скорости полета в два раза потребная мощность вырастет соответственно в восемь раз. Еще значительнее становится рост потребной мощности при приближении скорости полета к скорости звука, т. е. скорости, с которой звук распространяется в воздухе (немногим более 1200 км/час вблизи земли), что объясняется дополнительным сопротивлением, связанным с явлением сжимаемости воздуха при этих скоростях.
Установка на самолетах все более мощных двигателей приводит лишь к незначительному увеличению скорости полета. Более мощные двигатели оказываются и более тяжелыми (вес двигателя увеличивается почти пропорционально его мощности), а также большими по размерам, вследствие чего для их установки требуются и большие по размерам самолеты. Но это в свою очередь увеличивает мощность, потребную для полета с данной скоростью.
Выход из этого заколдованного круга был найден применением двигателей принципиально иного типа — двигателей прямой реакции в частности, ракетных. Поэтому не без основания говорят что применение реактивных двигателей в авиации представляет собой настоящую техническую революцию.
Ракетный двигатель в смысле развиваемой им мощности ведет себя совсем иначе, чем, например, поршневые двигатели внутреннего сгорания.
B этом легко убедиться.
Как известно, мощность — это работа, произведенная за секунду, работа же есть действие силы на некотором пути. Поэтому величина работы определяется произведением силы на пройденный в направлении ее действия путь, а мощность соответственно равна произведению силы на скорость. Если мощность измерять в лошадиных силах, то, как известно, величину секундной работы в килограммометрах нужно еще разделить на 75, так как 1 л. с. = 75 кгм/сек; таким образом:
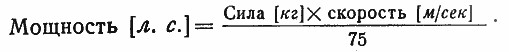
Чему же равна мощность ракетного двигателя? Так как реактивная сила, т. е. тяга, развиваемая двигателем, от скорости передвижения не зависит, то мощность ракетного двигателя оказывается прямо пропорциональной скорости полета.
Когда двигатель неподвижен — например, испытывается на станке, — его мощность равна нулю, несмотря на то, что тяга, развиваемая двигателем, может быть при этом очень велика. Мощность становится значительной лишь при больших скоростях передвижения.
Это свойство ракетного двигателя характеризует его как двигатель специфически транспортный; мало того, как двигатель для аппаратов, передвигающихся с очень большими скоростями, возможными лишь в воздухе и вне пределов атмосферы, т. е. двигатель для самолетов, снарядов, ракет.
На малых скоростях ракетный двигатель развивает весьма незначительную мощность, но зато при увеличении скорости мощность возрастает и может достигать значений, недосягаемых для других тепловых двигателей. Это обстоятельство позволяет получить с помощью ракетного двигателя скорость полета значительно большую, чем с помощью обычных (поршневых) авиационных двигателей.
Как велика может быть мощность ракетного двигателя, видно из следующего примера, относящегося к одной дальнобойной ракете.
На этой ракете установлен ракетный двигатель (он будет описан подробно в разделе о жидкостно-реактивных двигателях), развивающий тягу в 25 тонн. При запуске ракеты, когда скорость ее равна нулю, мощность двигателя также равна нулю. Но когда ракета, примерно через 1 мин. после старта, достигает высоты около 40 км, ее скорость становится очень большой, порядка 1500 м/сек (около 5500 км/час). Подсчитаем по нашей формуле мощность, которую развивает двигатель в этот момент:
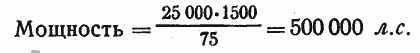
Конечно, такую колоссальную мощность (полмиллиона лошадиных сил!) не в состоянии развить ни один тепловой двигатель при тех размерах и весе, которые имеет двигатель этой ракеты.
Ракетный двигатель совершает полезную работу за счет израсходования скоростной энергии газов, вытекающих из двигателя в атмосферу.
Доля тепловой энергии топлива, переходящей в скоростную энергию газов и, следовательно, величина этой скоростной энергии, от скорости полета не зависит.
В то же время мощность двигателя при изменении скорости полета меняется.
Это означает, что в зависимости от скорости полета скоростная энергия вытекающих из двигателя газов по-разному используется для совершения полезной работы[3].
Преобразование скоростной энергии газов в полезную работу двигателя полностью определяется скоростью полета. Некоторые характерные в этом отношении (режимы полета ракеты или самолета с ракетным двигателем представлены на фиг. 8. Верхний рисунок на этой фигуре соответствует режиму взлета — двигатель работает, но ракета неподвижна, скорость полета равна нулю. При этом полезная работа, т. е. мощность двигателя, тоже равна нулю. Куда же расходуется скоростная энергия струи газов, с большой скоростью вытекающих из двигателя? Очевидно газы, которые в этом случае мчатся относительно земли со скоростью, равной скорости истечения, уносят с собой эту скоростную энергию, которая затем бесполезно рассеивается в атмосфере.
Но вот ракета взлетела и начинает полет со все увеличивающейся скоростью. При этом разность между скоростью истечения и скоростью полета становится все меньше. Поэтому молекулы газа движутся относительно земли в сторону, противоположную направлению полета, со все меньшей скоростью. Это значит, что скоростная энергия, уносимая с собой молекулами, становится все меньшей. Следовательно, все большая часть скоростной энергии струи преобразовывается в полезную работу, сообщается ракете.
Весьма характерным является момент, когда увеличивающаяся скорость полета становится равной скорости истечения газов из двигателя, что соответствует среднему рисунку на фиг. 8. Очевидно что при этом скорость газов относительно земли становится равной нулю, т. е. относительно неподвижного наблюдателя газы будут неподвижными. Но это означает, что скоростная энергия этих газов равна нулю и, следовательно, вся скоростная энергия струи переходит в полезную работу. Однако следует иметь в виду, что это отвечает очень большой скорости полета, так как скорость истечения газов из ракетного двигателя равна 1500–2500 м/сек, т. е. примерно 5000-10000 км/час. Следовательно, этот случай может иметь место только при полете в самых верхних слоях атмосферы и вне ее. При скоростях полета до 1000–1200 км/час в полезную работу переходит менее четверти скоростной энергии струи.
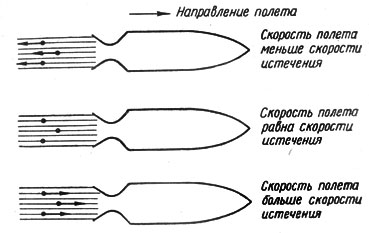
Фиг. 8. Характерные режимы полета ракеты (точками условно обозначены молекулы газа, стрелками — направление их скорости относительно неподвижного наблюдателя).
При дальнейшем увеличении скорости полета молекулы газа, как это показано на нижнем рисунке фиг. 8, движутся относительно неподвижного наблюдателя в том же направлении, что и ракета, со скоростью, равной разности скорости полета и скорости истечения. При этом энергия, отдаваемая струей ракете, т. е. совершаемая ракетой полезная работа, даже превышает скоростную энергию струи. Противоречие здесь, конечно, лишь кажущееся, что становится очевидным, если рассматривать не только тепловую, но и скоростную энергию сжигаемого топлива, приобретенную им в результате ускорения ракеты в течение предшествующего полета.
Для уменьшения потерь скоростной энергии отходящих газов на малых скоростях полета на выходе из ракетного двигателя могут быть установлены специальные насадки, расположенные с некоторым зазором вокруг выходного сечения реактивного сопла[4]. При полете в атмосфере через кольцевую щель между таким насадком и соплом подсасывается воздух, который примешивается к струе отходящих газов, уменьшая их скорость, но зато увеличивая массу. Это может привести к существенному повышению тяги и, следовательно, мощности; например, когда двигатель неподвижен, т. е. скорость полета равна нулю, то такой, как говорят, эжекционный подсос воздуха, увлекаемого струей выходящих газов, увеличивает тягу двигателя на 1/3. Но когда скорость полета увеличивается, этот выигрыш в тяге резко падает: так, при скорости полета, составляющей всего 5 % от скорости истечения, выигрыш в тяге уменьшается наполовину. При еще больших скоростях вместо выигрыша может получиться даже уменьшение тяги.
Читайте также
4. МОЩНОСТЬ ВЗРЫВА
4. МОЩНОСТЬ ВЗРЫВА
При постройке железной дороги Кангауз — Сучан на Дальнем Востоке необходимо было проложить выемку в Бархатном перевале в скальном грунте. Специалисты подсчитали, что по старому способу, без применения взрывчатых веществ, прокладка выемки потребует не
ТАКТИКО-ТЕХНИЧЕСКИЕ ДАННЫЕ РАЗЛИЧНЫХ ТИПОВ РАКЕТ И РАКЕТНОГО ВООРУЖЕНИЯ. ВЕЛИКОБРИТАНИЯ
ТАКТИКО-ТЕХНИЧЕСКИЕ ДАННЫЕ РАЗЛИЧНЫХ ТИПОВ РАКЕТ И РАКЕТНОГО ВООРУЖЕНИЯ. ВЕЛИКОБРИТАНИЯ
О разработках ракет и реактивных снарядов в Великобритании почти нет опубликованных данных. Однако нужно признать, что сделано не многое. Официально сообщается, что все разработки
4. Мощность взрыва
4. Мощность взрыва
При постройке железной дороги Кангауз — Сучан на Дальнем Востоке необходимо было проложить выемку в Бархатном перевале в скальном грунте. Специалисты подсчитали, что по старому способу, без применения взрывчатых веществ, прокладка выемки потребует не
КЛАССИФИКАЦИЯ РАКЕТНОГО ОРУЖИЯ
КЛАССИФИКАЦИЯ РАКЕТНОГО ОРУЖИЯ
БАЛЛИСТИЧЕСКИЕ РАКЕТЫ (СУХОПУТНЫЕ И МОРСКИЕ)Межконтинентальные баллистические ракеты (МБР) Баллистические ракеты подводных лодок (БРПЛ) Баллистические ракеты средней дальности (БРСД) Баллистические ракеты оперативно-тактические и
Выхлоп двигателя дымный. В картер двигателя поступает повышенный объем газов
Выхлоп двигателя дымный. В картер двигателя поступает повышенный объем газов
Диагностирование двигателя по цвету дыма из выхлопной трубы
Сине-белый дым – неустойчивая работа двигателя. Рабочая фаска клапана подгорела. Оценить состояние газораспределительного
2. СВОЙСТВА РАКЕТНОГО ДВИГАТЕЛЯ
2. СВОЙСТВА РАКЕТНОГО ДВИГАТЕЛЯ
Основные свойства ракетного двигателя мы уже знаем.Первое свойство заключается в отсутствии специального движителя, назначение которого выполняет сам двигатель. Это оказывается возможным потому, что тяга представляет собой реакцию
Тяга ракетного двигателя
Тяга ракетного двигателя
Создание реактивной тяги есть назначение всякого ракетного двигателя; поэтому величина тяги является важнейшей характеристикой двигателя.Тяга современных ракетных двигателей колеблется от нескольких килограммов до десятков тонн, в
Экономичность ракетного двигателя
Экономичность ракетного двигателя
Наряду с мощностью важнейшей характеристикой каждого двигателя является его экономичность. Если речь идет о тепловом двигателе, то экономичность его определяется расходом топлива на единицу мощности, т. е. на 1 л. с. Экономичный
3.4.1. Что такое мощность микроволн
3.4.1. Что такое мощность микроволн
В микроволновых печах в зависимости от приготавливаемого блюда можно изменять уровень мощность микроволн:80-150 Вт – режим поддержания готового блюда в горячем состоянии;• 160–300 Вт – размораживание и приготовление «деликатных»
Электрические измерения: напряжение, ток, сопротивление, мощность
Электрические измерения: напряжение, ток, сопротивление, мощность
Измерять в быту электрические параметры приходится не часто, а некоторым — и никогда.Напряжение в сети либо есть, либо его нет, и определяют это просто подключив нагрузку — проще всего настольную лампу.
Двигатель не развивает полную мощность. Его приемистость недостаточна
Двигатель не развивает полную мощность. Его приемистость
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока
Реактивная мощность связана с полной мощностью и активной :
Зная Активную мощность и Полную мощность определяем Реактивную мощность из прямоугольного треугольника
Если рассмотреть Физически «реактивная мощность» — это, энергия, затрачиваемая на перемагничивание короткозамкнутой обмотки асинхронного двигателя при его работе, то есть ЛЮБОЙ асинхронный двигатель потребляет реактивную мощность из сети независимо от момента на своем валу.
Реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Отрицательное значение активной мощности нагрузки характеризовало бы нагрузку как генератор энергии. Активное, индуктивное, ёмкостное сопротивление не могут быть источниками постоянной энергии.
Так же есть :
Полная мощность тока
Активная мощность тока
В формуле мы использовали :
— Реактивная мощность
— Напряжение в цепи
— Сила тока
— Угол сдвига фаз
— Полная мощность тока
— Активная мощность тока
Как посчитать теоретическую мощность реактивного двигателя?
Гуру
(3389),
закрыт
11 лет назад
Михаил Ермилов
Просветленный
(42561)
11 лет назад
Вы очень-очень подробно описали свои расчёты – и с ними всё в порядке. Тот результат, который вы получили, является безукоризненной аппроксимацией, пригодной для малых скоростей судна. Действительно, пока катер движется со скоростью V, много меньшей скоростью истечения воды V1, сила тяги почти постоянна, а значит, полезная мощность примерно прямо пропорциональна скорости катера V. Правильный вывод. . Ваша ошибка (если уж вам хочется так говорить) – не в расчётах, а в том, что вы распространили их на любые V. То, что полученный результат не верен для больших скоростей, понятно и без формул; представьте себе, что катер идёт со скоростью V1. При этом выброшенная вода будет неподвижна относительно Земли, и, следовательно, никакого импульса катеру не передаст – сила тяги равна нулю! Более аккуратные расчёты приводят к диффер. уравнению. Причём при малых t его точное решение совпадёт с вашим, а при больших временах выйдет на стационарное выражение с некоторой V=const, зависящей от силы трения.


