Измерение мощности шума
Измерение
любой статистической характеристики
шума включает операцию усреднения. При
теоретическом анализе случайных
процессов средние значения определяются
путем усреднения по статистическому
ансамблю реализаций: все допустимые
значения усредняемой величины суммируются
с весами, равными вероятности этих
значений. Экспериментатор же располагает
лишь одной реализацией
![]() ,
,
и определение средних значений
производится путем усреднения по этой
единственной реализации –усреднения
по времени.
Возможность такого усреднения основана
на том, что случайный процесс обладает
конечной памятью – временем корреляции.
Поэтому одну реализацию в принципе
можно разбить на отдельные независимые
участки, и получить тем самым подобие
статистического ансамбля. Процессы,
для которых усреднение по времени
(предполагается, что интервал усреднения
можно брать сколь угодно большим)
эквивалентно усреднению по ансамблю,
называются эргодическими.
Примером
временного усреднения, важным для
практики, служит определение мощности
шума:
![]() , (27)
, (27)
где
![]() – начало интервала усреднения,
– начало интервала усреднения,![]() –
–
длительность усреднения.
Если
проводить эту процедуру для различных
реализаций статистического ансамбля,
получаемые значения средней по времени
мощности будут отличаться друг от друга.
Среднее этих значений равно дисперсии
шума
![]() ,
,
вычисленной по ансамблю:![]() .
.
Отклонение получаемых значений от
величины дисперсии![]() являетсястатистической
являетсястатистической
ошибкой
измерения мощности
![]() .
.
Величина
ошибки зависит от соотношения длительности
усреднения
![]() и времени корреляции шума
и времени корреляции шума![]() .
.
Она будет небольшой по сравнению с
величиной дисперсии![]() ,
,
если длительность усреднения намного
превышает время корреляции. При выполнении
этого условия среднеквадратичная
относительная ошибка измерения мощности
шума, имеющего постоянную спектральную
плотность и полосу частот![]() ,
,
определяется выражением:
![]() , (28)
, (28)
Измерение
спектральной плотности по существу
является измерением мощности составляющих
шума в достаточно узкой полосе частот,
выделяемых с помощью фильтра, и последующем
делением значения мощности на ширину
полосы. Из выражения (28) видно, что
улучшение спектрального разрешения
(уменьшение ширины полосы частот) и
уменьшение ошибки измерения спектральной
плотности являются противоречивыми
требованиями, и их соотношение выбирается
из компромиссных соображений.
Операция
усреднения по времени
![]() в спектральном представлении является
в спектральном представлении является
фильтром низких частот, который пропускает
низкочастотные компоненты входного
сигнала, включая постоянную составляющую,
и подавляет высокочастотные, начиная
с частоты порядка![]() .
.
Для временного усреднения флуктуаций
в принципе могут использоваться любые
низкочастотные фильтры. В частности,
при аналоговой обработке сигналов часто
применяются интегрирующиеRC
-цепочки. В этом случае выражение для
относительной ошибки измерения мощности
имеет вид:
![]() ,
,
где
– постоянная времени цепочки. (29)
Функциональная
схема измерения мощности шума показана
на Рис.6. Она содержит: источник шумового
сигнала, представленный генератором
напряжения eR(t)
и внутренним сопротивлением источника
R,
усилитель с регулируемым коэффициентом
усиления K,
фильтр, задающий полосу частот измерения
шума f,
квадратичный или линейный детектор,
фильтр низких частот, выполняющий
функцию усреднения, и выходной индикатор.

Для
квадратичного детектора (выходной
сигнал детектора пропорционален квадрату
входного сигнала) и в предположении,
что спектральная плотность источника
шума SR(f)
постоянна в пределах полосы пропускания
фильтра, показание индикатора A
пропорционально спектральной плотности.
В соответствии с (5), (6) его можно выразить
в виде:
![]() , (30)
, (30)
где
– постоянная, учитывающая нерегулируемые
коэффициенты передачи фильтров, детектора
и индикатора,
= f.
Для линейного детектора (выходной сигнал
детектора пропорционален модулю входного
сигнала) и гауссовского шума показание
A
пропорционально квадратному корню из
спектральной плотности:
![]() , (31)
, (31)
где
также является некоторой постоянной.
Значение
постоянной
в выражении (30) или (31) можно
определить, если заведомо известна
спектральная плотность источника
шумового сигнала. Обычно для калибровки
используются специальные генераторы
шума или тепловой шум измеряемой системы.
Для
сравнения шумов, генерируемых различными
источниками или одним и тем же источником
при различных условиях, удобно использовать
относительное измерение. Если входной
шум со спектральной плотностью S0
вызывает показание индикатора A0
при величине коэффициента усиления K0,
а шум со спектральной плотностью S
вызывает показание индикатора A
при величине коэффициента усиления K,
то отношение этих спектральных плотностей
(для измерителя с линейным детектором)
определяется выражением:
![]() . (32)
. (32)
Если
одна из спектральных плотностей известна,
тем самым определяется величина другой.
Соседние файлы в папке Лабы
- #
06.06.201518.63 Кб53.1.xlsx
- #
- #
06.06.201563.46 Кб12Броуновское движение 1.xlsx
- #
06.06.201534.81 Кб5Броуновское движение 2.xlsx
- #
- #
06.06.201518.87 Кб7Ударная волна 1.xlsx
- #
06.06.201517.53 Кб5Ударная волна 2.xlsx
5.3.1. Дистанционное уравнение
5.3.1.1. Возвращаясь к дистанционному уравнению
5.3.2. Мощность принятого сигнала как функция частоты
5.3.3. Потери в тракте зависят от частоты
5.3.4. Мощность теплового шума
5.3.1. Дистанционное уравнение
Основная задача бюджета канала — доказать, что система связи будет работать согласно плану; т.е. качество сообщений (достоверность передачи) будет удовлетворять заданным требованиям. Бюджет канала отслеживает “потери” и “прибыли” (усиление и ослабление) передаваемого сигнала от начала его формирования в передатчике до полного получения в приемнике. Вычисления показывают, чему равно отношение ![]() в приемнике и какой запас прочности существует. Процесс вычисления бюджета канала начинается с дистанционного уравнения, связывающего принятую мощность с расстоянием между передатчиком и приемником. Вывод этого уравнения дан ниже.
в приемнике и какой запас прочности существует. Процесс вычисления бюджета канала начинается с дистанционного уравнения, связывающего принятую мощность с расстоянием между передатчиком и приемником. Вывод этого уравнения дан ниже.
В системах радиосвязи несущая распространяется от передатчика посредством передающей антенны. Передающая антенна — это устройство, преобразовывающее электрические сигналы в электромагнитные поля. В приемнике принимающая антенна выполняет обратное преобразование; она превращает электромагнитные поля в электрические сигналы. Вывод уравнения, связывающего приемник и передатчик, обычно начинается с рассмотрения ненаправленного источника радиоизлучения, равномерно передающего в 4π стерадиан. На рис. 5.3 показан идеальный источник, называемый изотропным излучателем (isotropic radiator). Поскольку площадь поверхности сферы радиуса d равна 4πd, плотность мощности p(d) данной сферы с центром в источнике излучения связана с переданной мощностью Рt.
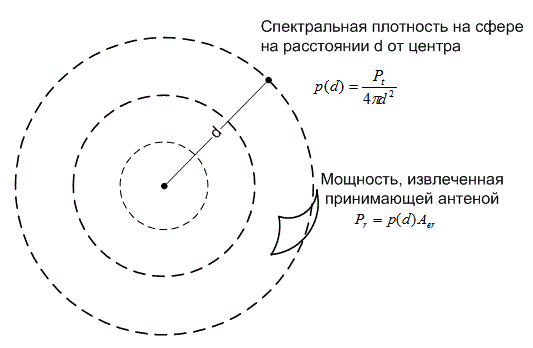
Рис. 5.3. Дистанционное уравнение. Выражение принятой мощности через расстояние
![]() (5.1)
(5.1)
Мощность, извлеченную принимающей антенной, можно записать следующим образом.
![]() (5.2)
(5.2)
Здесь параметр Аer — это сечение захвата (эффективная площадь) принимающей антенны, определяемое следующим образом.
![]() (5.3)
(5.3)
Если рассматриваемая антенна является передающей, ее эффективная площадь обозначается как Аet. Если не указано, выполняет ли антенна принимающую или передающую функцию, эффективная площадь обозначается через Ае.
Эффективная площадь антенны Аe, и ее физическая площадь поверхности Арсвязаны коэффициентом эффективности η.
![]() (5.4)
(5.4)
Это говорит о том, что не вся мощность падающего луча была извлечена; вследствие различных механизмов [3] происходят потери. Номинальное значение η для параболической антенны составляет 0,55, а для рупорной — 0,75.
Определим параметр антенны, который связывает выходную (или входную) мощность с мощностью изотропного излучателя и именуется коэффициентом направленного действия.
![]() (5.5)
(5.5)
При отсутствии любых диссипативных потерь или потерь вследствие несогласованности импедансов коэффициент направленного действия антенны (в направлении максимальной интенсивности излучения) определяется из формулы (5.5). В то же время, если существует некоторая диссипация или несогласованность, коэффициент направленного действия антенны уменьшается на множитель, соответствующий объему потерь [4]. В данной главе мы будем предполагать, что диссипативные потери равны нулю, а импедансы согласованы идеально. Таким образом, формула (5.5) описывает максимальный коэффициент направленного действия антенны; как показано на рис. 5.4, его можно рассматривать как результат концентрации изотропного излучения в некоторой ограниченной области, меньшей 4я стерадиан. Теперь мы можем определить эффективную излученную мощность относительно изотропного излучателя (эффективная изотропно-излучаемая мощность — effective isotropic radiated power, EIRP) как произведение переданной мощности Рt и коэффициента усиления передающей антенны Gt.
EJRP = PtGt, (5.6)
Пример 5.1. Эффективная изотропно-излучаемая мощность
Покажите, что при надлежащем выборе антенн можно получить одинаковое значение EIRP как при использовании передатчика с Рt = 100 Вт, так и при использовании передатчика с Рt = 0,1Вт.
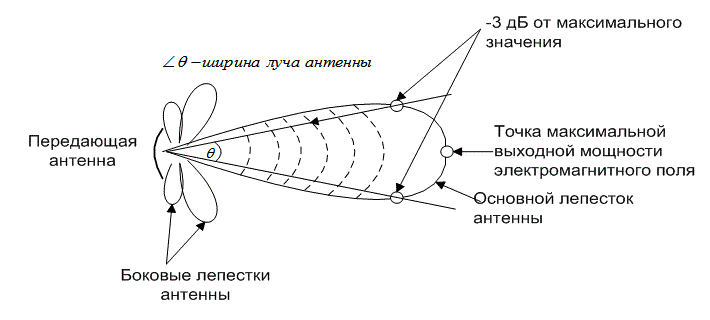
Рис. 5.4. Коэффициент направленного действия антенны — результат концентрации изотропного излучения
Решение
На рис. 5.5, а показан передатчик с Рt = 100 Вт, соединенный с изотропной антенной; значение EIRP = PtGt = 100 х 1 = 100 Вт. На рис. 5.5, б показан передатчик с Рt = 0,1 Вт, соединенный с антенной, имеющей Gt = 1000; EIRP=PtGt = 0,1 x 1000 = 100 Вт. Если измерители напряженности поля расположены так, как показано на рисунке, то измеряемая с их помощью эффективная мощность не будет отличаться.

а)

б)
Рис. 5.5. Два различных способа получения одинакового значения EIRP
5.3.1.1. Возвращаясь к дистанционному уравнению
Если антенна передатчика имеет некоторый коэффициент направленного действия, отличающийся от предоставляемого изотропной антенной, в уравнении (5.2) мы меняем Рt на EIRP, что дает следующее.
![]() (5.7)
(5.7)
Связь между коэффициентом усиления антенны G и эффективной площадью Аe дается выражением [4].
![]() (5.8)
(5.8)
Здесь λ — длина волны несущей. Длина волны λ и частота f связаны соотношением λ = c/f, где с — скорость света (![]() м/с). Теорема взаимности утверждает, что для данной антенны при данной длине волны коэффициенты направленного действия приема и передачи идентичны [4].
м/с). Теорема взаимности утверждает, что для данной антенны при данной длине волны коэффициенты направленного действия приема и передачи идентичны [4].
Зона обзора антенны является мерой телесного угла, в котором сконцентрирована большая часть мощности поля. Зона обзора — это мера анизотропных свойств антенны; она обратно пропорциональна усилению антенны, т.е. антеннам с большим коэффициентом усиления соответствует более узкая зона обзора. Часто зону обзора выражают не через телесный угол, а через плоский угол раствора антенны (beamwidth), измеряемый в радианах или градусах. На рис. 5.4 показана диаграмма направленности антенны и дана иллюстрация общего определения угла раствора антенны. Угол раствора — это угол, образованный точками, в которых максимальная мощность поля ослаблена на 3 дБ. Как угол раствора зависит от частоты сигнала и размера антенны? Из уравнения (5.8) можно видеть, что усиление антенны увеличивается с уменьшением длины волны (увеличением частоты); также усиление антенны увеличивается с увеличением эффективной площади. Увеличение усиления антенны равносильно фокусировке плотности потока энергии в меньшем угле раствора; следовательно, увеличение частоты сигнала или размера антенны приводит к сужению угла раствора.
Эффективную площадь изотропной антенны можно вычислить, положив в уравнении (5.8) G=1, что позволяет получить следующее выражение для Аe.
![]() (5.9)
(5.9)
Затем для нахождения принятой мощности Рr, при изотропной принимающей антенне, подставляем уравнение (5.9) в уравнение (5.7), что дает следующее.
![]() (5.10)
(5.10)
Здесь совокупность коэффициентов ![]() называется потерями в тракте (path loss) или потерями в свободном пространстве (free-space loss) и обозначается через Ls. Формула (5.10) показывает, что мощность, принятая изотропной антенной, равна эффективной переданной мощности, сниженной только за счет потерь в тракте связи. Если принимающая антенна не является изотропной, то после замены в уравнении (5.7) Аer выражением
называется потерями в тракте (path loss) или потерями в свободном пространстве (free-space loss) и обозначается через Ls. Формула (5.10) показывает, что мощность, принятая изотропной антенной, равна эффективной переданной мощности, сниженной только за счет потерь в тракте связи. Если принимающая антенна не является изотропной, то после замены в уравнении (5.7) Аer выражением ![]() из уравнения (5.8) получаем более общую формулу.
из уравнения (5.8) получаем более общую формулу.
![]() (5.11)
(5.11)
Здесь Gr — коэффициент усиления принимающей антенны. Полученное уравнение (5.11) называется дистанционным.
5.3.2. Мощность принятого сигнала как функция частоты
Поскольку и передающую, и принимающую антенны можно выразить через усиление или площадь, Рr можно выразить четырьмя различными способами.
![]() (5.12)
(5.12)
![]() (5.13)
(5.13)
![]() (5.14)
(5.14)
![]() (5.15)
(5.15)
В этих выражениях Аer и Аet — эффективные площади принимающей и передающей антенн.
В уравнениях (5.12)-(5.15) зависимая переменная — это мощность принятого сигнала Рr, а независимые переменные — это такие параметры, как переданная мощность, коэффициент усиления антенны, площадь антенны, длина волны и расстояние между антеннами. Допустим, возник вопрос: как меняется принятая мощность при увеличении длины волны (или уменьшении частоты), при фиксированных остальных параметрах? Если рассматривать уравнения (5.12) и (5.14), то кажется, что Рr и длина волны вообще не связаны. Из уравнения (5.13) величина Рr вроде бы обратно пропорциональна квадрату длины волны, а из уравнения (5.15) она прямо пропорциональна квадрату длины волны. Нет ли здесь противоречия? Разумеется, нет; кажущаяся противоречивость уравнений (5.12)-(5.15) исчезает, если вернуться к формуле (5.8) и вспомнить, что коэффициент усиления антенны и ее площадь связаны через длину волны. Когда следует употреблять каждое из уравнений (5.12Н5.15) для определения зависимости Рr от длины волны? Представим уже сконструированную систему, т.е. антенны уже построены (зафиксированы Аet и Аer). В этом случае подходящим выбором для вычисления Рr является уравнение (5.13), сформулированное для антенн фиксированного размера. Из этого уравнения видим, что принятая мощность увеличивается при уменьшении длины волны.
Рассмотрим уравнение (5.12), где независимыми переменными являются Gt и Aer. Итак, желательно, чтобы Gt и Аer были фиксированными при вычислении зависимости Рr от длины волны. Как изменится усиление при передаче на фиксированное расстояние, если уменьшить независимую переменную λ? Gt увеличится (см. уравнение (5.8)). Но мы не хотим увеличения Gt — оно нужно нам фиксированным. Другими словами, чтобы обеспечить неизменность Gt, нам необходимо уменьшать размер передающей антенны при уменьшении длины волны. Рассуждая подобным образом, приходим к выводу, что уравнение (5.12) удобно использовать при фиксированном усилении передающей антенны (или растворе антенны) и при переменном параметре Аet. Подобным образом уравнение (5.14) используется при фиксированных Аet и Gr a уравнение (5.15) — при фиксированных коэффициентах усиления передающей и принимающей антенн (или растворах антенн).
На рис. 5.6 показано спутниковое приложение, где для обзора земной поверхности требуется луч со спутниковой антенны (раствор антенны равен порядка 17°). Поскольку коэффициент усиления спутниковой антенны Gt должен быть фиксированным, результирующая мощность Рr (см. уравнение (5.12)) не зависит от длины волны. Если передача ведется на определенной частоте ![]() , то изменение ее на f2, где
, то изменение ее на f2, где ![]() , приведет к уменьшению обзора (поскольку при данной антенне увеличится Gt); таким образом, для поддержания требуемого обзора или раствора антенны размер этой антенны должен быть уменьшен. Итак, при увеличении несущей частоты антенны обзор земной поверхности уменьшается.
, приведет к уменьшению обзора (поскольку при данной антенне увеличится Gt); таким образом, для поддержания требуемого обзора или раствора антенны размер этой антенны должен быть уменьшен. Итак, при увеличении несущей частоты антенны обзор земной поверхности уменьшается.
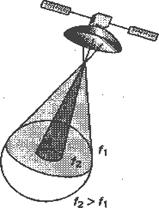
Рис. 5.6. Принятая мощность как функция частоты
5.3.3. Потери в тракте зависят от частоты
Из уравнения (5.10) можно видеть, что потери в тракте Ls зависят от длины волны (частоты). Довольно часто возникает вопрос: почему потери в тракте, подчиняющиеся простому геометрическому закону ослабления (ослабление обратно пропорционально квадрату расстояния), зависят от частоты? Ответ заключается в том, что потери в тракте, выраженные в уравнении (5.10), определены для изотропной принимающей антенны (Gr=1). Вообще, потери в тракте — это весьма удобный параметр; он представляет гипотетическую потерю мощности, которая произойдет, если принимающая антенна будет изотропной. Из рис. 5.3 и уравнения (5.1) видно (из чисто геометрических соображений), что плотность мощности p(d) — это функция расстояния, p(d) не является функцией частоты. В то же время, поскольку потери в тракте заданы для Gr= 1, когда мы находим некоторую мощность Рr с помощью изотропной антенны, результат описывается выражением (5.10). Снова акцентируем внимание на том, что Ls можно рассматривать как совокупность параметров, которой было присвоено неудачное имя потери в тракте. Название представляет чисто геометрический эффект и не акцентирует внимания на том, что Gr= 1. Пожалуй, лучшим названием было бы потери распространения при единичном усилении. В системах радиосвязи потери в тракте — это наибольший единичный источник ослабления мощности сигнала. В спутниковых системах потери в тракте для канала связи со спутником в полосе С (6 ГГц) обычно составляют порядка 200 дБ.
Пример 5.2. Проект антенны для измерения потерь в тракте
Предложите эксперимент для измерения потерь в тракте Ls при частотах f1 = 30 МГц и f2 = 60 МГц, если расстояние между передатчиком и приемником равно 100 км. В обоих случаях найдите эффективную площадь принимающей антенны и вычислите потери в тракте в децибелах.
Решение
Два канала измерения Ls для частот f1 и f 2 показаны на рис. 5.7. Для обоих приемников удельная мощность p(d) одинакова и равна следующему.
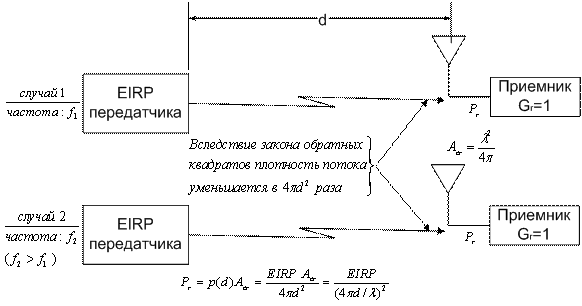
Рис. 5.7. Зависимость потерь в тракте от частоты. Предполагаемый эксперимент измерения потерь для двух различных частот
![]()
Это снижение удельной мощности происходит исключительно вследствие закона обратных квадратов. Действительная мощность, полученная каждым приемником, находится, как показано на рис. 5.7, посредством умножения плотности мощности p(d) в приемнике на эффективную площадь собирающей антенны Аer. Поскольку потери в тракте определены для Gr=1, эффективные площади Аer1 и Аer2 для частот f1 и f2 находятся с использованием уравнения (5.9).
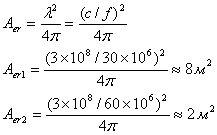
Далее для обоих случаев находим потери в тракте (в децибелах).
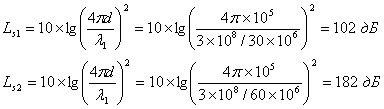
5.3.4. Мощность теплового шума
Тепловой шум вызывается тепловым движением электронов во всех проводящих элементах. Он создается в местах соединения антенны и приемника и в первых каскадах приемника. Спектральная плотность мощности шума постоянна для всех частот, вплоть до 1012 Гц, что определило название белый шум. Как показывалось в разделе 1.5.5, процесс теплового шума в приемниках системы связи моделируется как процесс аддитивного белого гауссового шума (additive white Gaussian noise — AWGN). Физическая модель [5, 61 теплового шума — это генератор шума со среднеквадратическим напряжением холостого хода, равным ![]() , где
, где
k (константа Больцмана) = ![]() Дж/К или Вт/КГц
Дж/К или Вт/КГц
= -228,6 дБВт/КГц,
Т — температура, Кельвин
W — ширина полосы, Герц
и
![]() — сопротивление, Ом
— сопротивление, Ом
Максимальная мощность теплового шума N, которую можно подать с выхода генератора шума на вход усилителя, равна следующему.
![]() (5.16)
(5.16)
Следовательно, максимальная номинальная односторонняя спектральная плотность мощности шума N0 (мощность шума на 1 Гц полосы) на выходе усилителя равна следующему.
![]() (5.17)
(5.17)
Может показаться, что мощность шума должна зависеть от значения сопротивления — но это не так. Рассмотрим такой аргумент. Соединим электрически большое и малое сопротивление так, чтобы они формировали замкнутую пару и их физические температуры были одинаковы. Если бы мощность шума зависела от сопротивления, то наблюдался бы поток полезной мощности от большего сопротивления к меньшему; большее сопротивление охлаждалось бы, а меньшее — нагревалось. Но это противоречит нашему жизненному опыту, не говоря уже о втором начале термодинамики. Следовательно, мощность, поступающая от большего сопротивления к меньшему, должна равняться мощности, получаемой этим большим сопротивлением.
Как видно из уравнения (5.16), мощность, подаваемая источником теплового шума, зависит от температуры окружающей среды источника (шумовой температуры). Это позволяет ввести для источников шума полезное понятие эффективной шумовой температуры (причем источники не обязательно должны быть тепловыми по природе — галактика, атмосфера, интерферирующие сигналы), влияющей на работу принимающей антенны. Эффективная шумовая температура подобного источника шума определяется как температура гипотетического источника теплового шума, дающего эквивалентную паразитную мощность. Подробнее шумовая температура рассматривается в разделе 5.5.
Пример 5.3. Максимальная номинальная мощность шума
Используя генератор со среднеквадратическим напряжением, равным ![]() , покажите, что максимальная мощность шума, которую можно подать из такого источника на усилитель, равна
, покажите, что максимальная мощность шума, которую можно подать из такого источника на усилитель, равна ![]() .
.
Решение
Теорема из области теории электрических цепей утверждает, что максимальная мощность подается на нагрузку, если полное сопротивление (импеданс) нагрузки равно комплексно сопряженному импедансу генератора [7]. В нашем случае импеданс генератора — это чистое сопротивление, ![]() ; следовательно, условие передачи максимальной мощности удовлетворяется, если сопротивление усилителя равно 9t. Пример подобной схемы приведен на рис. 5.8. Источник теплового шума представлен электрически эквивалентной моделью, состоящей из бесшумного сопротивления, последовательно соединенного с идеальным генератором напряжения со среднеквадратическим напряжением
; следовательно, условие передачи максимальной мощности удовлетворяется, если сопротивление усилителя равно 9t. Пример подобной схемы приведен на рис. 5.8. Источник теплового шума представлен электрически эквивалентной моделью, состоящей из бесшумного сопротивления, последовательно соединенного с идеальным генератором напряжения со среднеквадратическим напряжением ![]() . Теперь входное сопротивление усилителя равно
. Теперь входное сопротивление усилителя равно ![]() . Напряжение шума, поступающего на вход усилителя, равно всего половине напряжения генератора, что следует из основных законов электрических схем. Таким образом, мощность шума, поданную на вход усилителя, можно выразить следующим образом.
. Напряжение шума, поступающего на вход усилителя, равно всего половине напряжения генератора, что следует из основных законов электрических схем. Таким образом, мощность шума, поданную на вход усилителя, можно выразить следующим образом.
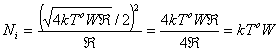

Рис. 5.8. Электрическая модель максимального теплового шума на входе усилителя
- Звуковое Оборудование
- Световое Оборудование
- Полезные статьи по организации светового и звукового пространства
- Инструменты
- Шоу-бизнес
- Программы для музыканта
- Видеоконференции и их использование
Главная › Библиотека › Звуковое Оборудование › Что такое шум
Что такое шум?
Шумы создаются звуковыми волнами, возникающими при расширении и сжатии в воздухе и других средах. В системах кондиционирования и вентиляции шумы могут возникать и распространяться в воздухе, корпусах воздуховодов, передвигающихся по трубам жидкостях и т.д.
Шумы могут иметь различную частоту и интенсивность.
Скорость распространения звука
Шум распространяется с гораздо меньшей скоростью, чем световые волны. Скорость звука в воздухе – примерно 330 м/с. В жидкостях и твердых телах скорость распространения шума выше, она зависит от плотности и структуры вещества.
Пример: скорость звука в воде равна 1.4 км/с, а в стали – 4.9 км/с.
Частота шума
Основной параметр шума – его частота (число колебаний в секунду). Единица измерения частоты – 1 герц (Гц), равный 1 колебанию звуковой волны в секунду.
Человеческий слух улавливает колебания частот от 20 Гц до 20000Гц. При работе систем кондиционирования учитывают обычно спектр частот от 60 до 4000Гц.
Для физических расчетов слышимая полоса частот делится на 8 групп волн. В каждой группе определена средняя частота: 62 Гц, 125 Гц, 250 Гц, 500 Гц, 1000 Гц, 2 кГц, 4 кГц и 8 кГц. Любой шум раскладывается по группам частот, и можно найти распределение звуковой энергии по различным частотам.
Мощность звука
Мощность звука какой-либо установки – это энергия, которая выделяется установкой в виде шума за единицу времени. Измерять силу шума в стандартных единицах мощности неудобно, т.к. спектр звуковых частот очень широк, и мощность звуков отличается на много порядков.
Пример: сила шума при поступлении в помещение воздуха под низким давлением равна одной стомиллиардной ватта, а при взлете реактивного самолета сила шума достигает 1000 Вт.
Поэтому уровень мощности звука измеряют в логарифмических единицах – децибелах (дБ). В децибелах сила шума выражается двух- или трехзначными числами, что удобно для расчетов.
Уровень мощности звука в дБ – функция отношения мощности звуковых волн возле источника шума к нулевому значению W0, равному 10-12Вт. Уровень мощности рассчитывается по формуле:
Lw = 10lg(W/W0)
Пример: если мощность звука вблизи источника равна 10 Вт, то уровень мощности составит 130 дБ, а если мощность звука равна 0.001 Вт, то уровень мощности – 90 дБ.
Мощность звука и уровень мощности независимы от расстояния до источника шума. Они связаны лишь с параметрами и режимом работы установки, поэтому важны для проектирования и сравнения различных систем кондиционирования и вентиляции.
Уровень мощности нельзя измерить непосредственно, он определяется косвенно специальным оборудованием.
Уровень давления звука
Уровень давления звука Lp – это ощущаемая интенсивность шума, измеряемая в дБ.
Lp = P/P0
Здесь P – давление звука в измеряемом месте, мкПа, а P0 = 2 мкПа – контрольная величина.
Уровень звукового давления зависит от внешних факторов: расстояния до установки, отражения звука и т.д. Наиболее простой вид имеет зависимость уровня давления от расстояния. Если известен уровень мощности шума Lw, то уровень звукового давления Lp в дБ на расстоянии r (в метрах) от источника вычисляется так:
Lp = Lw – lgr – 11
Пример: мощность звука холодильного блока равна 78 дБ. Уровень звукового давления на расстоянии 10 м от него равен: (78 – lg10 – 11) дБ = 66 дБ.
Если известен уровень звукового давления Lp1 на расстоянии r1 от источника шума, то уровень звукового давления Lp2 на расстоянии r2 будет вычисляться так:
Lp2 = Lp1 – 20*lg(r2/r1)
Пример: Уровень звукового давление на расстоянии 1 м от установки равно 65 дБ. Тогда уровень звукового давления на расстоянии 10 м от нее равен: (65 – 20*lg10) дБ = (65 – 20) дБ = 45 дБ..
Вообще, в открытом пространстве уровень звукового давления снижается на 6 дБ при увеличении расстояния до источника шума в 2 раза. В помещении зависимость будет сложнее из-за поглощения звука поверхностью пола, отражения звука и т.д.
Громкость шума
Чувствительность человека к звукам разной частоты неодинакова. Она максимальна к звукам частотой около 4 кГц, стабильна в диапазоне от 200 до 2000 Гц, и снижается при частоте менее 200 Гц (низкочастотные звуки).
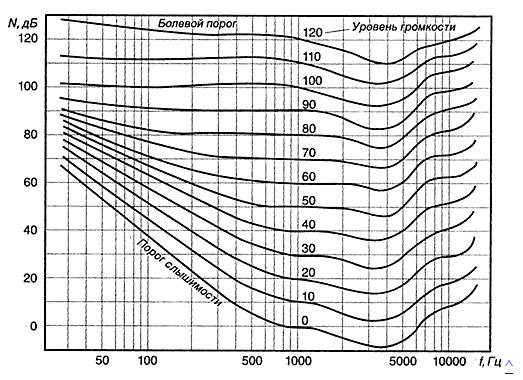
Громкость шума зависит от силы звука и его частоты. Громкость звука оценивают, сравнивая ее с громкостью простого звукового сигнала частотой 1000Гц. Уровень силы звука частотой 1000Гц, столь же громкого, как измераемый шум, называется уровнем громкости данного шума. На приведенной ниже диаграмме показана зависимость силы звука от частоты при постоянной громкости.
При малом уровне громкости человек менее чувствителен к звукам очень низких и высоких частот. При большом звуковом давлении ощущение звука перерастает в болевое ощущение. На чатоте 1 кГц болевой порог соответствует давлению 20 Па и силе звука 10 Вт/кв.м.
Диаграмма кривых равной громкости
Шумовые характеристики оборудования
Шумовые характеристики оборудования представляют в виде таблиц, где содержатся:
- уровень мощности шума в дБ с разбивкой по полосам частот
- общий уровень звукового давления
Звуковое давление в помещениях нормируется санитарными нормативами, допустимые значения различны для разных частот. Шум, создаваемый системами вентиляции и кондиционирования, принимают на 5 дБ ниже допустимого уровня шума в помещении (СНиП 11-12-77).
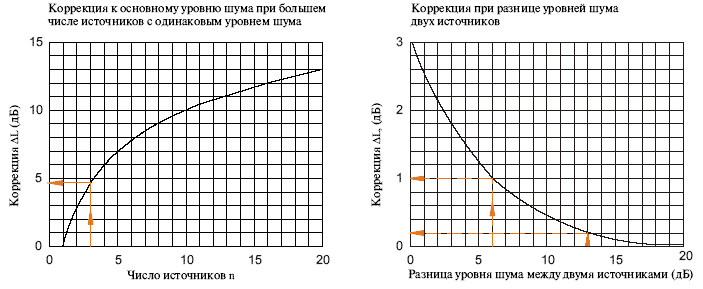
Суммирование источников шума
Шум от нескольких источников не соответствует сумме шумов от каждого источника в отдельности. Для двух находящихся рядом установок шум определяется следующим образом:
- Если показатели уровня шума одинаковы, то суммарный уровень шума на 3 дБ превышает уровень шума каждой установки.
- Если разница уровней шума превышает 10 дБ, суммарный уровень шума равен величине большего из двух шумов.
Например, общий шум от двух установок с уровнями 30 и 60 дБ, равен 60 дБ.
- Если разница уровней шума не более 10 дБ, нужно воспользоваться приведенной ниже таблицей. Вычисляем разность уровней шума установок.
Например, L1 = 52 дБ, а L2 = 48 дБ. Разность равна 4 дБ. В верхней строке таблицы найдем 4 дБ, тогда в нижней строке видим показатель 1.5 дБ. Прибавим этот показатель к большему уровню шума: 52 дБ + 1.5 дБ = 53.5 дБ. Это и будет общий уровень шума от двух установок.
| Разница уровней шума, дБ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Показатель-добавка, дБ | 2.6 | 2.1 | 1.8 | 1.5 | 1.2 | 1.0 | 0.8 | 0.6 | 0.5 | 0.4 |
Если источников шума более двух, метод расчета не меняется, и источники рассматриваются парами, начиная с самых слабых.
Например, есть четыре установки с уровнями шума 25 дБ, 38 дБ, 43 дБ и 50 дБ.
Сначала делаем подсчет для двух слабейших установок: 38 – 25 = 13 дБ. Разница больше 10 дБ, и эту установку вообще не учитываем.
Для установок 38 и 43 дБ: 43 – 38 = 5 дБ, поправка из таблицы равна 1.2 дБ. Суммарный шум трех установок: 43 + 1.2 = 44.2 дБ.
Теперь найдем полный шум всех установок. 50 – 44.2 = 5.8 дБ. Округляя разность уровней шума до 6 дБ, по таблице находим поправку 1.0 дБ.
Итак, общий уровень шума четырех установок равен 50 + 1 = 51 дБ.
Вы можете оставить свой комментарий.
Общие данные о звуке и шуме
Введение
Тон, звук, шум представляют собой механические вибрации
материальных частиц в эластичной среде. Когда тон и звук
являются помехой тогда говорим о шуме. Обычная звуковая волна колеблется
с небольшой амплитудой.
В случае взрыва амплитуды очень большие. В жидкостях и газах
звуковая волна – продольная, частицы колеблются в направлении распространения
волны. В твердых телах звуковые волны могут быть и поперечными.
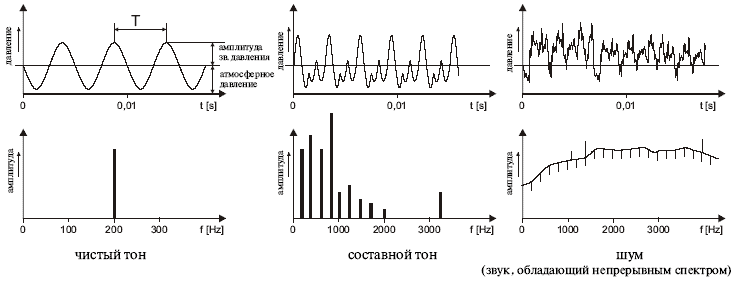
Обозначения акустических величин:
| c | м/сек | – скорость звука |
|
||||||||||||||
| l | м | – длина волны | |||||||||||||||
| f | Гц | – частота | |||||||||||||||
| T | сек | – продолжительность одного периода | |||||||||||||||
| дБ | – логарифмическая единица уровня звука | ||||||||||||||||
| LpA | дБ | – уровень звуковой мощности | |||||||||||||||
| LWA | дБ (A) | – уровень звуковой мощности по отношению к А фильтру | |||||||||||||||
| Lv | дБ | – общий уровень звуковой мощности вентилятора | |||||||||||||||
| z | – число лопаток вентилятора | ||||||||||||||||
| fon | фон | – единица уровня громкости | |||||||||||||||
| De | дБ | – демпфирование (ослабление) звукового давления | |||||||||||||||
| a | – коэффициент абсорбции звука |
Звуковое давление – переменное давление, которое при расширении
звукового вала суммируется с атмосферным давлением. Звуковое
давление очень мало по сравнению с атмосферным. Минимальное
давление, регистрируемое
человеческим ухом составляет всего 0,00002 Па (т.е. 2*10 -5 Н/м2),
а звуковое давление, вызывающее боль в ушах приблизительно
20 Па (т.е. 20 Н/м2). Для упрощения измерений в практике чаще
всего измеряют звуковое давление, т.к. его изменения ухо
воспринимает как звук. Звуковое
давление уменьшается обратно пропорционально с расстоянием
от источника звука. Так например удвоение расстояния уменьшает
уровень шума на 6 дБ,
в соответствии со следующей формулой:
De=Lv-LpA=10 log 4 p r22/r12
Пример ослабления шума вентилятора на определенном расстоянии в свободном
пространстве:
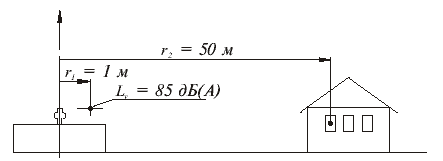
При условии, что на расстоянии г1 от вентилятора, звуковое поле уже
сформировалось, действительно выражение для приблизительного
вычисления.
De = 20 log r2 + 14 дБ(А) = 20 log 50 + 14 = 48 дБ(А)
Уровень звукового давления на расстоянии r2 составляет:
LpA = Lv – De = 85 – 48 = 37 дБ(А)
(В расчете не приняты во внимание абсорбция и отражение шума
от объектов)
Сила (интенсивность) звука I (Вт/м2)
– количество звуковой энергии, которая в единицу времена
проходит через единичную площадь, перпендикулярную к направлению
распространения звука.
Звуковая мощность Р (Вт) – произведение силы звука
и поверхности, через которую звук проходит. Диапазон звуковых
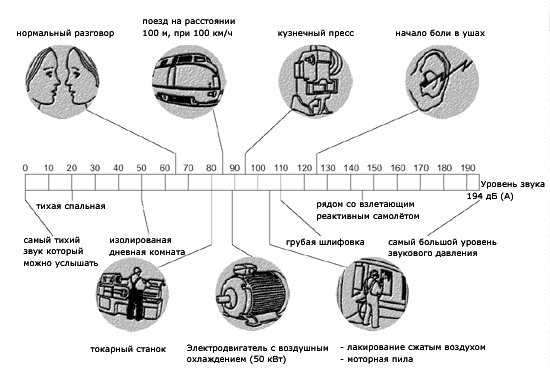
давлений, чувствуемых человеческим ухом огромен. Сравнивая
диапазон от порога слышимости до границы боли, отношение
минимального и максимального звуковых давлений 1:106,
а минимальной и максимальной звуковых мощностей даже 1:1012.
Поэтому для показа этих отношений используют логарифмическую
скалу, ввиду того, что ухо обладает логарифмической характеристикой.
Из-за этого данные отношения можно показать значительно
меньшими числами -децибелами, а умножение и деление сводится
на суммирование и вычитание.
Уровни акустических величин Цель введения данных
величин – получение различных параметров как например звуковое
давление, сила звука, мощность звука и т.п. в сравнении
с базовыми значениями. Логарифмические соотношения между
значениями данных параметров являются безразмерными относительными
величинами. Так например уровень звукового давления – безразмерная
величина, показывающая во сколько раз наблюдаемый звуковой
вал сильнее базового. Таким образом диапазон давлений от
1:1 000 000 сведен на уровень от О до 120 дБ (см. таблицу).
LpW= 10 log (p/p0) (дБ), где p0(10-12 Вт)
– сила звука на пороге слышимости
Выражение для уровня звукового давления на частоте 1000
Гц
LpA= 20 log (p/p0)
(дБ), где p0(10-5 Вт) – звуковое
давление на пороге слышимости
Пример:
– Измерено звуковое давление р = 10-1 Па.
– Каков уровень звукового давления LpA ?
Решение:
Отношение давлений: p/p0= 10-1/(2*10-5)=
5000 = 5 * 1000
Из таблицы считываем:
– отношению звуковых давлений 5 соответствует 14 дБ
– отношению звуковых давлений 1000 соответствует 60 дБ
Уровень звукового
давления LpA = 74 дБ
Соотношения силы звука и звуковых давлений в диапазоне
от порога чувствительности до границы боли
| Децибелы | <– Отношения силы звука Отношения звуковой мощности –> |
Децибелы | Уровень громкости |
| 0 | 1 | 0 | Порог чувствительности (измерен в лабораториях) |
| 3 | 2 | 6 | |
| 4,8 | 3 | 9,5 | |
| 6 | 4 | 12 | Шуршание листьев на очень слабом ветре |
| 7 | 5 | 14 | |
| 7,8 | 6 | 15,6 | |
| 8,5 | 7 | 16,9 | |
| 9 | 8 | 18,1 | |
| 9,5 | 9 | 19,1 | |
| 10 | 10 | 20 | Шепот, библиотека |
| 20 | 100 | 40 | Приглушенный разговор |
| 30 | 1 000 | 60 | Нормальный разговор |
| 40 | 10 000 | 80 | Грузовой автомобиль на расстоянии 5 м |
| 50 | 100 000 | 100 | Самый сильный человеческий голос |
| 60 | 1 000 000 | 120 | Выстрел из ружья под ухом |
| 70 | 10 000 000 | ||
| 80 | 100 000 000 | ||
| 90 | 1 000 000 000 |
||
| 100 | 10 000 000 000 |
||
| 110 | 100 000 000 000 |
||
| 120 | 1 000 000 000 000 (1012) |
Уровень громкости – фон – величина, численно равная уровню
звукового давления чистого тона с частотой 1000 Гц, вызывающего
такое же ощущение как и испытываемый звук.
При борьбе с шумом необходимо иметь в виду, что чувство неприятности не зависит
от абсолютной величины уровня шума, а от перемены, которую какой-либо источник
звука вызывает по отношению к уровню громкости окружающей среды. При этом
увеличение уровня громкости на 10 дБ вызывает чувство неприятности.
Графики одинаковой громкости, как их чувствует ухо, в соответствии
с ДИН 45630, лист 2.
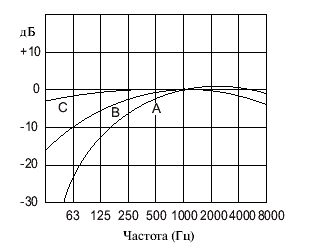
Графики оценивания А, В, С.
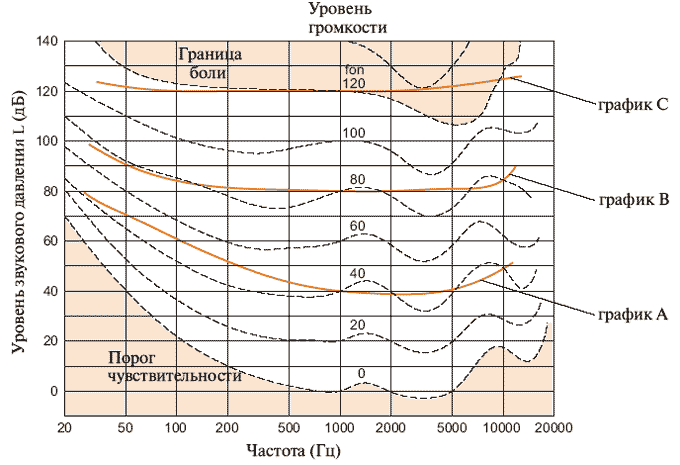
Уровень звукового давления (дБ) и уровень громкости (фон)
при частоте 1 000 Гц имеют одинаковые значения.
Критерии оценки шума
При оценке шума в настоящее время применяют два основных правила:
- Измерение уровня громкости или звукового давления
LpA при помощи акустического измерителя с корректирующей
характеристикой типа А/дБ(А)/, при этом разрешенный уровень
LpA задан. - Измерение уровня звукового давления по октавам и сравнение
с NR (или NC) характеристикой, нормализированным по ИСО.
В качестве критерия для оценки шума в области вентиляции и кондиционирования
в Европе приняты NR (noisie rating) характеристики. В акустические измерители
встроены фильтры с А, В и С характеристиками, и тогда на измерителе (анализаторе
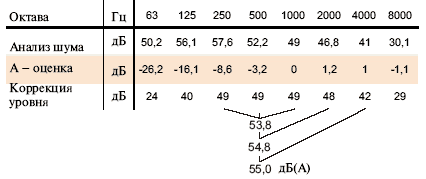
шума) считывают уровни на средних частотах спектра. Если шум какого-либо
источника обладает одинаковой интенсивностью во всех 8-ми октавах спектра,
тогда шум каждой октавы меньше шума источника на 9 дБ, т.к. общая разница
звукового давления
| LpA=10 log*n + L1 (дБ) |
| n – число источников шума |
| L1 – интенсивность шума в каждой из 8-ми октав (или в каждом из 8-ми источников) |
Когда отдельные уровни источника звукового давления, измеренные по октавам,
повторяют одну из NR характеристик, определенный уровень
звукового давления LpA такого источника расположен ВЫШЕ значения граничной
характеристики
на 7 до 10 дБ. При шуме, создаваемом вентилятором, разница
составляет около 5 дБ. т.к. спектр данного шума во всех октавах не достигает
NR
характеристику.
NR характеристики одинаковой громкости (в соответствии с А характеристикой)
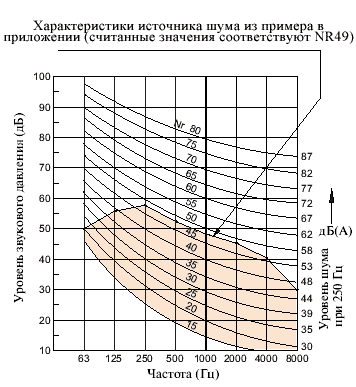 |
Коррекционные коэффициенты для характеристик оценки
Затененная область иллюстрирует рекомендуемые значения |
|
Пример: результаты измерения шума по А-характеристике Задано: LpA = 55 дБ Решение: (обозначено на диаграмме |
Вместо верхней таблицы при акустических расчетах можно использовать и диаграмму с обратнопропорциональными характеристиками в соответствии с нижним рисунком. |
|
|
Предписанные критерии уровня шума для различных помещений
в соответствии с ДИН 4109 и VDI2058 (от 1973 года)
| Типы помещений | Уровень шума (ДБ) |
Среднее время эха (с) |
NR – характеристики | ||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
| * зависит от назначения |
| Максимальные уровни шумов по VDI2058 | |||
| в чисто промышленном районе | 70 дБ(А) | ||
| в преобладающе промышленном районе | днем | 65 дБ(А) | |
| ночью | 50 дБ(А) | ||
| в смешанном районе | днем | 60 дБ(А) | |
| ночью | 45 дБ(А) | ||
| в преобладающе жилом районе | днем | 55 дБ(А) | |
| ночью | 40 дБ(А) | ||
| в исключительно жилом районе | днем | 55 дБ(А) | |
| ночью | 30 дБ(А) | ||
| в санаториях | днем | 45 дБ(А) | |
| ночью | 35 дБ(А) | ||
| в чисто жилом районе | днем | 35 дБ(А) | |
| ночью | 25 дБ(А) |
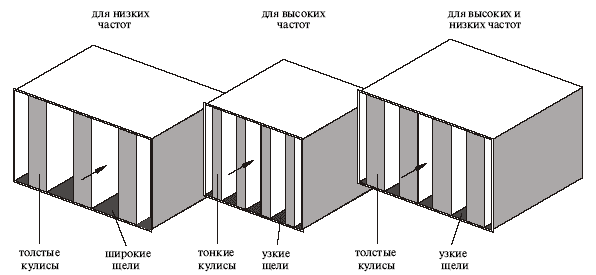
Абсорбционные глушители звука
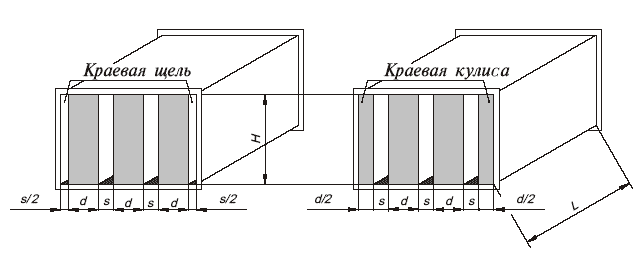
|
| Эскиз глушителей с одинаковыми акустическими характеристиками |
Приблизительные значения глушения можно рассчитать по выражению:
| De =3a*(L/s) (дБ), где | |
| a – коэффициент абсорбции половины кулисы | |
| L – длина глушителя | |
| s – расстояние между кулисами |
Верхняя формула действительна при ограничении
l > 2 s или f < c/(2*s),
т.к. вне данного диапазона появляются высшие, очень направленные частоты.
Максимальное глушение ввиду эффекта интерференции (сдвиг фаз при l/2)
звуковых волн особенно проявляется при d = l/
4, т.е. при f=c/ = c/4d.
Из этого видно, что для глушения нижних частот необходима большая толщина
кулис. Ввиду прохождения звука по листовым стенкам глушителя, максимальное
приглушение составляет 40 дБ. Если необходимо большее глушение, тогда общее
глушение делят на 2 глушителя, а между собой их соединяют эластичным переходником.
При скоростях воздуха, больших 20 м/сек, или при загрязненном воздухе, кулисы
обкладывают перфорированным листом, что очень незначительно влияет на глушение
шума. Если же из – за большой влажности или других гигиенических причин,
под перфорированным листом установить ПХВ пленку – это значительно ухудшает
эффект глушения.
Основные критерии при выборе глушителей