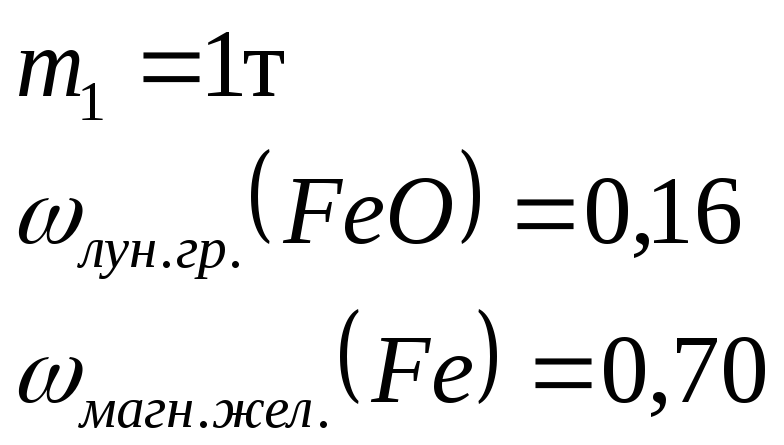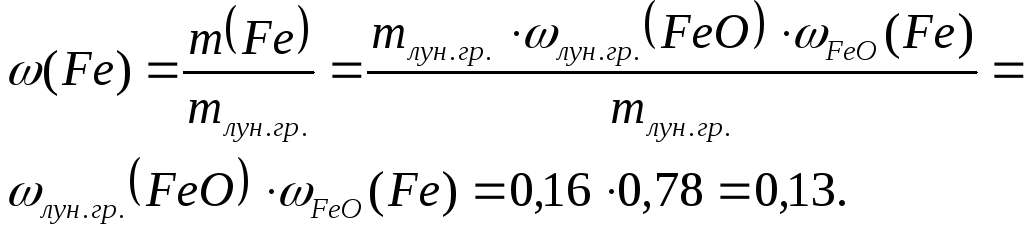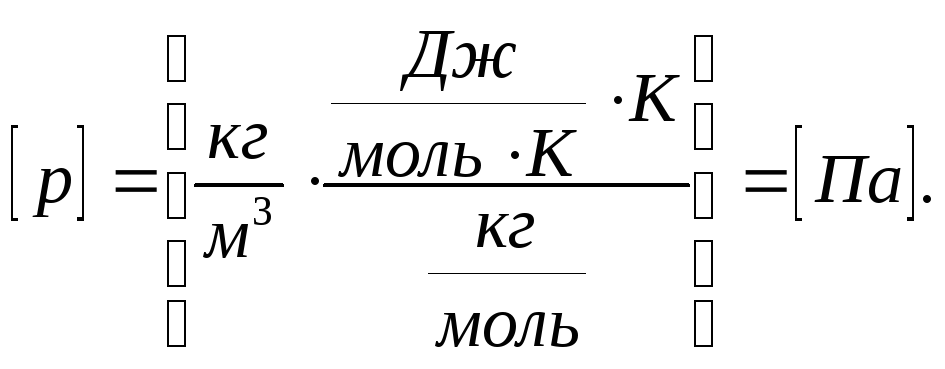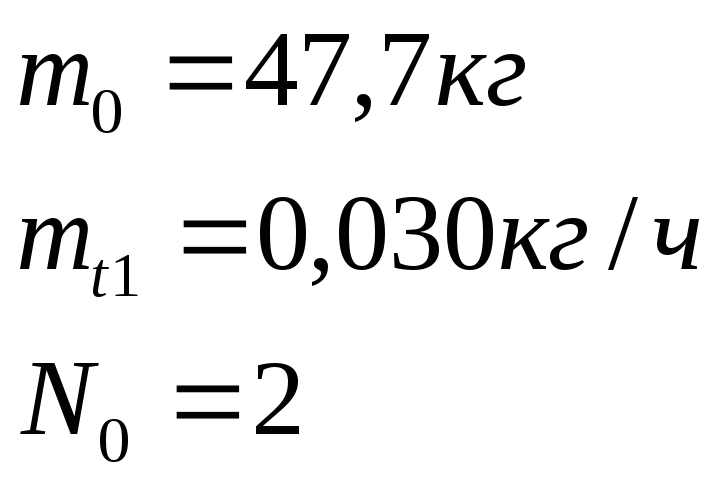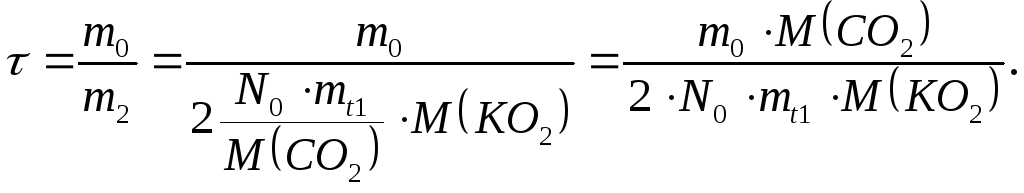Решение
Энергетическая
светимость Солнца (как абсолютно черного
тела) по закону Стефана-Больцмана равна:
.
С другой стороны по определению
,
гдеE–
излучаемая энергия, S–
площадь излучающей поверхности, t-время,
в течении которого происходит излучение,
N–
мощность излучения.
Т.о.,
(Считаем Солнце шаром с радиусом 7108
м). Получаем,
что мощность излучения Солнца составляет
3,91026
Вт
35. Найти солнечную
постоянную К, т.е. количество лучистой
энергии, посылаемой Солнцем в единицу
времени через единичную площадку,
перпендикулярную к солнечным лучам и
находящуюся на таком же расстоянии от
него, как и Земля. Температура поверхности
Солнца 5800 К. Излучение Солнца считать
близким к излучению абсолютно черного
тела.
Решение.
Энергетическая
светимость Солнца (как абсолютно черного
тела) по закону Стефана-Больцмана равна:
.
А мощность солнечного излучения
,
гдеr–
радиус Солнца. Т.к. солнечная энергия
не теряется, то на расстоянии орбиты
Земли
.
Получаем
.Откуда
,Е=1389 Вт/м2.
36. Известно,
что атмосфера Земли поглощает 10% лучистой
энергии, посылаемой Солнцем. Определите
максимальную и минимальную мощность
излучения L,
получаемую от Солнца горизонтальным
участком Земли, на котором расположен
город Калуга. Площадь города принять
равной 50 км2.
Излучение Солнца считать близким к
излучению абсолютно черного тела.
Решение
Максимальная
мощность излучения Lmax,
получаемая от Солнца горизонтальным
участком Земли, будет в тот день, когда
высота Солнца над горизонтом наибольшая
(это день летнего солнцестояния).
Определим в этот день высоту Солнца в
Калуге.
Широта Калуги
=54
31,
а склонение Солнца =23,5,
тогда hmax=90-
54,5+
23,5=59
(по формуле h
= 90-
+ ).
Мощность излучения,
получаемая от Солнца горизонтальным
участком, равна
,
гдеЕ –
солнечная постоянная для Земли, S
– площадь участка, перпендикулярного к
солнечным лучам, равная
(S
– площадь
данного участка (города Калуги)),
n–
коэффициент
поглощения земной атмосферы.
Т
.о.,
,Lmax=51010
Вт.
Минимальная
мощность излучения Lmin,
получаемая от Солнца горизонтальным
участком Земли, будет в тот день, когда
высота Солнца над горизонтом наименьшая
(это день зимнего солнцестояния).
Определим в этот день высоту Солнца в
Калуге. Склонение Солнца в этот день
=-23,5,
тогда hmin=90-
54,5-
23,5=12.
Минимальная же мощность излучения Lmin
будет равна
,
Lmin=
1,21010
Вт.
37. В 1947 г в
западных отрогах Сихотэ-Алиня (Приморский
край) упал огромный железо-никелевый
метеорит. Во время движения в атмосфере
он разбился на многочисленные осколки
и рассеялся металлическим дождем на
площади 35 км2.
Масса метеорита оценивается в 60 т, общий
вес собранных осколков достиг 27 т. В
Калужском государственном музее истории
космонавтики им. К.Э. Циолковского
хранится осколок сихоте-алиньского
метеорита массой 7,7 кг. Оцените массу
никеля в этом метеорите, если процентное
содержание железа в нем 93,3%, а никеля –
6%.
|
Дано:
|
Решение:
Рассчитаем массу
|
|
|
Ответ: 0,46 кг никеля.
38. Видеокамеры
лунного зонда «Клементина» запечатлели
поверхность Луны на 11 частотах видимого
и инфракрасного диапазона спектра.
Съемка на волнах 750 и 950 нм позволила
составить карту распределения железа
в поверхностных лунных грунтах. Наибольшая
концентрация этого металла (до 16% оксида
железа (II))
отмечена в морях видимой стороны,
наименьшая – в центральных областях
обратной стороны. В будущем, для нужд
лунного производства, предполагается
наладить получение железа на Луне. На
Земле одной из наиболее богатых железом
горных пород является магнитный железняк,
содержащий до 70% железа. Сравните массу
лунного грунта, богатого железом, и
магнитного железняка, которые необходимо
переработать для получения металлического
железа массой 1,0 т.
|
Дано:
|
Решение:
1. Рассчитаем
|
|
|
2.
Найдем массовую долю железа в лунном
грунте.
Рассчитаем
массовую долю железа в оксиде железа
(II),
как отношение относительной атомной
массы железа к относительной молекулярной
массе оксида железа (II):
Массу
железа в лунном грунте можно вычислить
по формуле:
Рассчитаем массовую
долю железа в лунном грунте:
3. Рассчитаем массу
лунного грунта, содержащую 1,0 т железа:
Ответ: 1,4 т магнитного
железняка; 7,7 т лунного грунта.
30. В Калужском
Государственном музеи истории космонавтики
среди образцов минералов, доставленных
с поверхности Луны автоматической
станцией «Луна-24», представлен оливин.
На Земле оливин распространенный
силикатный минерал состав которого
плавно меняется от Mg2SiO4
(фостерит) до Fe2SiO4
(фаялит). Рассчитайте массовые доли
кислорода в фостерите и фаялите.
|
Дано:
|
Решение:
Рассчитаем
|
|
|
,
Ответ: 45,7%, 31,4%.
40. Фотосфера –
единственный на Солнце слой (не считая
солнечной атмосферы), где водород
существует в форме нейтральных атомов.
Рассчитайте давление водорода в нижних
слоях фотосферы Солнца, если плотность
вещества в ней составляет 510-4
кг/м3,
а температура 6000 К.
|
Дано:
|
Решение: Запишем |
|
|
.
Подставим числовые
данные
Проверим единицы
измерения
Ответ: 2,5104
Па.
ТЕМА «ОСНОВЫ
КОСМОНАВТИКИ»
41. В фантастической
повести «Вне Земли», написанной
Циолковским в 1896 г, есть такие строки:
«… Сейчас на своей ракете мы летаем
вокруг Земли на расстоянии 1000 км, делая
полный оборот в 100 минут…». Подтвердите
расчетами, что корабль, находясь на
данной высоте, двигается с указанным
периодом.
Решение.
Спутник движется
с постоянной по модулю скоростью по
круговой орбите радиусом R+H
под действием силы всемирного тяготения,
следовательно, по
закону Ньютона
,
ускорение ракеты
,
где
–
период обращения,
–
масса ракеты,
–
масса Земли. Получим
,
откуда
.
Учитывая, что
,
получим более рациональную для расчета
формулу
.
После подстановки численных данных
найдем, что Т105
мин.
42.
Первый
искусственный спутник Земли представлял
собой шар диаметром 580 мм (Его копию
можно увидеть в Калужском государственном
музее истории космонавтики им. К.Э.
Циолковского). Посчитайте, на каком
расстоянии от земного наблюдателя
должен был бы двигаться этот спутник,
чтобы с его помощью можно было бы хоть
мгновение наблюдать полное солнечное
затмение? Оцените (очень приблизительно),
каков был бы период обращения этого
спутника вокруг Земли?
Справочные данные
(округлённые): Диаметр Земли 12700 км.
Диаметр Солнца 1400000 км. Диаметр Луны
3500 км. Расстояние Земля-Солнце 150000000 км.
Расстояние Земля-Луна 380000 км. Звёздный
период обращения Луны вокруг Земли 27,3
средних солнечных суток.
Решение
Видимый
угловой размер спутника должен быть
таким как и видимый угловой размер
Солнца, т.е. примерно 1/2 углового градуса,
поэтому расстояние от наблюдателя до
спутника должно быть во столько раз
меньше, чем от наблюдателя до Солнца,
во сколько раз диаметр спутника меньше
диаметра Солнца
.
Откуда
.
Следовательно, высота спутника не должна
превышать 62 м. На такой высоте слишком
велико сопротивление атмосферы, поэтому
спутник не сможет сделать ни одного
оборота.
43. Одной из
достопримечательностей города Калуги
является космический корабль «Восток»,
установленный на возвышении берега
Яченского водохранилища. На космических
кораблях этой серии для регенерации
кислорода, необходимого для дыхания
экипажа, использовали надпероксид калия
(КО2),
который, взаимодействуя с выдыхаемым
космонавтами углекислым газом образует
кислород и карбонат калия. На борту
космического корабля находится 47,7 кг
КО2.
Космонавт в течение часа выдыхает 30 г
углекислого газа. Определите, в течение
скольких суток будет обеспечиваться
на орбите жизнедеятельность экипажа,
состоящего из двух человек?
|
Дано:
|
Решение:
1. Запишем уравнение
2. |
|
|
3. Найдем, какая
масса надпероксида калия расходуется
за 1 час.
За 1 час два
космонавта выдыхают углекислый газ
массой
или количеством вещества
Значит, согласно уравнению реакции за
1 час расходуется надпероксид калия
количеством вещества
или массой
4. Время
жизнедеятельности экипажа на орбите
можно определить как отношение массы
надпероксида калия, находящейся на
корабле, к его массе, расходуемой экипажем
за час.
5. Подставим в
полученную формулу числовые значения
Получаем 
Проверим единицы измерения 
Ответ: 246 ч или 10
суток.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
10.02.201513.05 Mб18жизнь растений т 4.djvu
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Оценка энергии солнечного излучения
Интенсивность солнечного света, которая достигает земли меняется в зависимости от времени суток, года, местоположения и погодных условий. Общее количество энергии, подсчитанное за день или за год, называется иррадиацией (или еще по-другому «приход солнечной радиации») и показывает, насколько мощным было солнечное излучение. Иррадиация измеряется в Вт*ч/м² в день, или другой период.
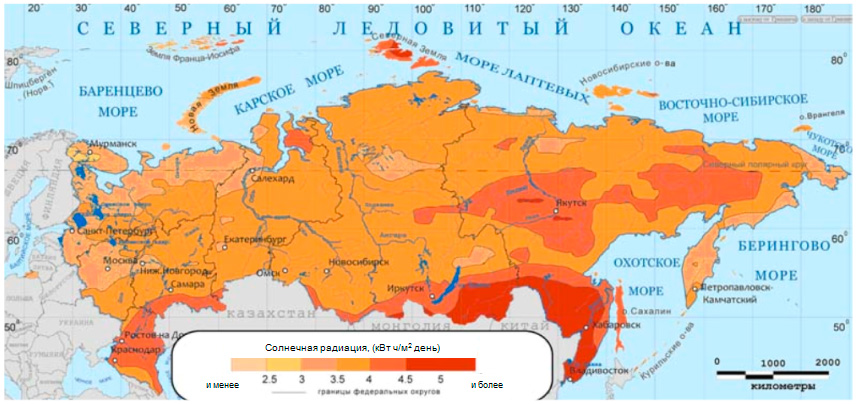
Интенсивность солнечного излучения в свободном пространстве на удалении, равном среднему расстоянию между Землей и Солнцем, называется солнечной постоянной. Ее величина — 1353 Вт/м². При прохождении через атмосферу солнечный свет ослабляется в основном из-за поглощения инфракрасного излучения парами воды, ультрафиолетового излучения — озоном и рассеяния излучения частицами атмосферной пыли и аэрозолями. Показатель атмосферного влияния на интенсивность солнечного излучения, доходящего до земной поверхности, называется «воздушной массой» (АМ). АМ определяется как секанс угла между Солнцем и зенитом.
На рис.1 показано спектральное распределение интенсивности солнечного излучения в различных условиях. Верхняя кривая (АМ0) соответствует солнечному спектру за пределами земной атмосферы (например, на борту космического корабля), т.е. при нулевой воздушной массе. Она аппроксимируется распределением интенсивности излучения абсолютно черного тела при температуре 5800 К. Кривые АМ1 и АМ2 иллюстрируют спектральное распределение солнечного излучения на поверхности Земли, когда Солнце в зените и при угле между Солнцем и зенитом 60°, соответственно. При этом полная мощность излучения — соответственно порядка 925 и 691 Вт/м². Средняя интенсивность излучения на Земле примерно совпадает с интенсивностью излучения при АМ=1,5 (Солнце — под углом 45° к горизонту) [1].
Около поверхности Земли можно принять среднюю величину интенсивности солнечной радиации 635 Вт/м². В очень ясный солнечный день эта величина колеблется от 950 Вт/м² до 1220 Вт/м². Среднее значение — примерно 1000 Вт/м² [860 ккал/(м²ч)]. Пример: Интенсивность полного излучения в Цюрихе (47°30′ с. ш., 400 м над уровнем моря) на поверхности, перпендикулярной излучению:1 мая 12 ч 00 мин 1080 Вт/м²;21 декабря 12 ч 00 мин 930 Вт/м².
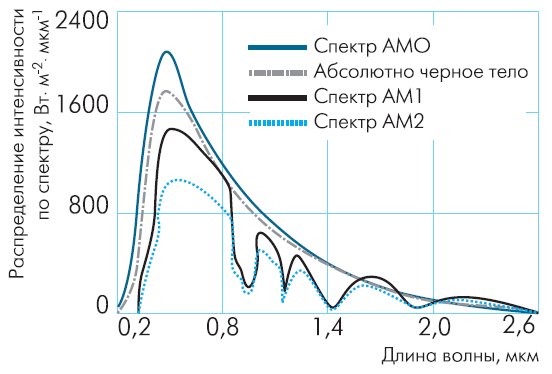
Для упрощения вычисления по приходу солнечной энергии, его обычно выражают в часах солнечного сияния с интенсивностью 1000 Вт/м². Т.е. 1 час соответствует приходу солнечной радиации в 1000 Вт*ч/м². Это примерно соответствует периоду, когда солнце светит летом в середине солнечного безоблачного дня на поверхность, перпендикулярную солнечным лучам.
Пример
Яркое солнце светит с интенсивностью 1000 Вт/м² на поверхность, перпендикулярную солнечным лучам. За 1 час на 1 м² падает 1 кВт*ч энергии (энергия равна произведению мощности на время). Аналогично, средний приход солнечной радиации в 5 кВт*ч/м² в течение дня соответствует 5 пиковым часам солнечного сияния в день. Не путайте пиковые часы с реальной длительностью светового дня. За световой день солнце светит с разной интенсивностью, но в сумме она дает такое же количество энергии, как если бы оно светило 5 часов с максимальной интенсивностью. Именно пиковые часы солнечного сияния используются в расчетах солнечных энергетических установок.
Приход солнечной радиации меняется в течение дня и от места к месту, особенно в горных районах. Иррадиация меняется в среднем от 1000 кВт*ч/м² в год для северо-европейских стран, до 2000-2500 кВт*ч/м² в год для пустынь. Погодные условия и склонение солнца (которое зависит от широты местности), также приводит к различиям в приходе солнечной радиации.
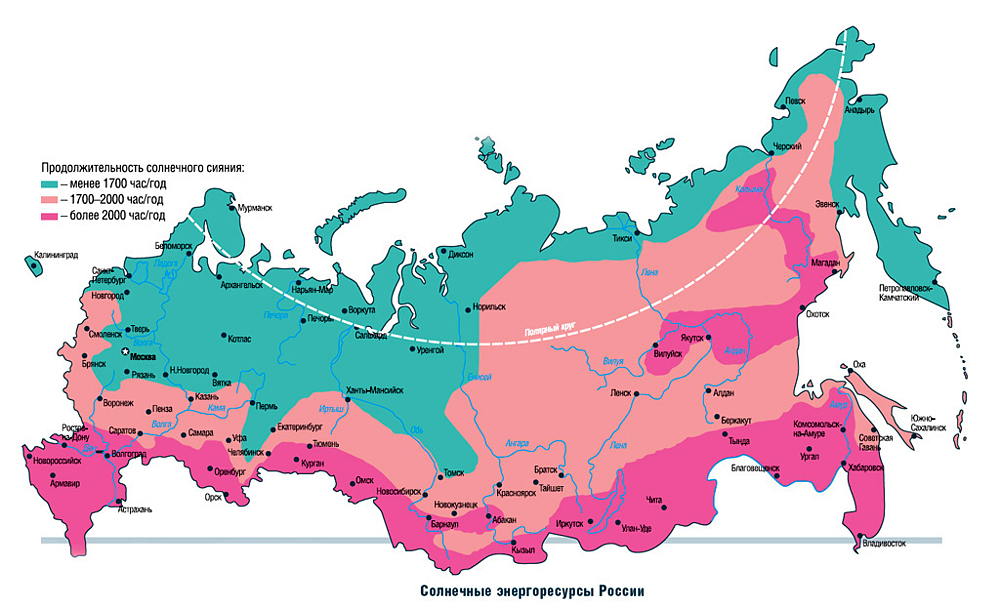
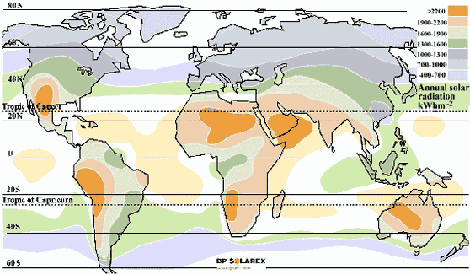
В России, вопреки распространённому мнению, очень много мест, где выгодно преобразовывать солнечную энергию в электроэнергию при помощи солнечных батарей. Ниже приведена карта ресурсов солнечной энергии в России. Как видим, на большей части России можно успешно использовать солнечные батареи в сезонном режиме, а в районах с числом часов солнечного сияния более 2000 часов/год — круглый год. Естественно, в зимний период выработка энергии солнечными панелями существенно снижается, но все равно стоимость электроэнергии от солнечной электростанции остается существенно ниже, чем от дизельного или бензинового генератора.
Особенно выгодно применение солнечных батарей там, где нет централизованных электрических сетей и энергообеспечение обеспечивается за счет дизель-генераторов. А таких районов в России очень много.
Более того, даже там, где сети есть, использование работающих параллельно с сетью солнечных батарей позволяет значительно снизить расходы на электроэнергию. При существующей тенденции на повышении тарифов естественных энергетических монополий России, установки солнечных батарей становится умным вложением денег.
Эта статья прочитана 62506 раз(а)!
Продолжить чтение
-
66
Классификация солнечных фотоэлектрических электростанций – Автономные, соединенные с сетью, резервные. Солнечные батареи в системах электроснабжения. -
60
Инверторы для фотоэлектрических систем Инверторы используются для преобразования постоянного тока от аккумуляторов или солнечных модулей в переменный ток, аналогичный тому, который присутствует в сетях централизованного электроснабжения. В системах электроснабжения с солнечными батареями применяются следующие типы инверторов: Сетевые фотоэлектрические инверторы В… -
54
Фотоэлектрические комплекты: Состав Для того, чтобы использовать солнечную энергию для питания ваших потребителей, одной солнечной батареи недостаточно. Кроме солнечной батареи нужно еще несколько составляющих. Типичный состав автономного фотоэлектрического комплекта следующий: фотоэлектрическая батарея контроллер заряда аккумуляторной батареи аккумуляторная батарея провода, коннекторы,… -
54
Как работают MPPT контроллеры? Что такое MPPT контроллеры, для чего они нужны и в чем их отличие от контроллеров с ШИМ описано по ссылке. На этой странице дана более подробная техническая информация Методы поиска точки максимальной мощности (ТММ) солнечной батареи… -
54
Эффективность работы солнечных батарей и коллекторов зимой Солнечные батареи могут быть великолепной частью вашего дома. Они определённо позволяют экономить вам деньги в течение длительного срока и постоянно могут снижать ваши счета за электроэнергию. Мы все знаем, что солнечные батареи преобразуют… -
54
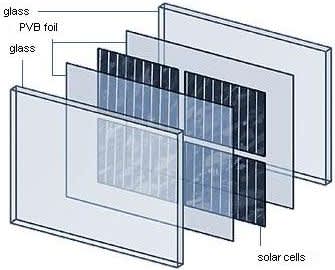
Солнечные фотоэлектрические модули с двойным стеклом Модули с двойным остеклением (double glass) Солнечные модули с двойным стеклом появились на рынке сравнительно недавно – 5-7 лет назад, но до недавнего времени они были дороже обычных модулей. В 2017 году они стали…
Каждый сходит с ума по-своему. У меня тоже имеется индивидуальная, запатентованная технология.
Недавно меня крайне заинтересовал вопрос: какую площадь имеет такая часть поверхности Солнца, которая излучает ровно столько энергии, сколько Земля получает от всего Солнца в целом? Как вам вопрос?
Поискав готовый ответ на просторах интернета, я ничего толкового не нашел. Зато приметил на нескольких форумах обсуждающийся похожий вопрос: какая доля всей излучаемой солнечной энергии достается Земле? И тут же во всех источниках дается приблизительно такое решение: доля солнечной радиации, которую получает Земля, равна отношению площади сечения Земли диаметральной плоскостью к площади сферы c радиусом, равным радиусу земной орбиты.
Ну что же, давайте проверять.
Для начала придется сделать несколько допущений. Во всех дальнейших расчетах мы будем предполагать, что: Земля и Солнце являются идеальными шарами; Земля обращается вокруг Солнца по круговой орбите; излучение исходит от Солнца и распределяется в пространстве равномерно. Решать задачу мы будем исключительно на геометрическом уровне и не будем брать в расчет, что некоторая часть излучения вовсе не доходит до Земли, поглощаясь и отражаясь по пути сначала космической пылью и газами, а затем и земной атмосферой.
Для расчетов возьмем справочные средние значения нужных нам величин.
Радиус Земли r1 = 6 371 км.
Расстояние от центра Земли до центра Солнца R = 149 597 870 км.
Искомая доля излучения = π(r1)2 / 4πR2 = 0,000000000453…
То есть Земля получает приблизительно одну двухмиллиардную часть от общего солнечного излучения.
Теперь вычисляем площадь такой части поверхности Солнца, которая выдает именно эту долю излучения. Очевидно, что она будет равна произведению площади поверхности всего Солнца на только что найденную долю.
Радиус Солнца r2 = 695 700 км.
Искомая площадь части поверхности:
S = 4π(r2)2 х 0,000000000453… = 2 757,771439343673… кв. километров.
Однако, выпив и рассудив трезво, я обнаружил, что такое решение нельзя назвать правильным. Если бы нам нужно было только оценить порядок этой величины, то можно было бы согласиться и с таким результатом. Но меня интересует точное решение, поэтому для его поиска придется немного пораскинуть мозгами. Хорошо бы заиметь какое-нибудь ненаглядное пособие.
Скажите мне, Киса, как художник – художнику: вы рисовать умеете? Нет? Я тоже. Но надо.
Рисовать мы будем на плоскости, а представлять нарисованное – в пространстве.
Рисуем Землю, рисуем Солнце. Рисуем, конечно, без соблюдения масштабов. Пунктирной линей разделяем Землю по диаметру. Для наглядности чертим круговую орбиту, по которой Земля обращается вокруг Солнца.
Проводим из центра Солнца касательные к окружности Земли (красные линии). Также проводим касательные между окружностями Земли и Солнца (синие линии).
Посмотрите, в каких точках красные касательные соприкасаются с Землей. Эти точки не совпадают с условными полюсами Земли, через которые проведена пунктирная линия.
А ведь в ранее рассмотренном алгоритме, который предлагают на различных сайтах и форумах, мы брали в расчет площадь сечения Земли, которое проходит через ее центр.
Теперь становится понятно, что приведенное выше решение является неверным.
Конечно же, невозможно провести из центра Солнца красные касательные к окружности Земли так, чтобы они коснулись Земли в точках условных полюсов. И чем ближе будут находиться друг к другу Земля и Солнце, или, чем больше будет отношение радиуса Земли к радиусу Солнца, тем дальше от полюсов будут отодвинуты точки, в которых красные касательные касаются Земли.
Теперь соединим отрезком точки пересечения красных касательных с поверхностью Солнца.
Этот отрезок отсекает часть Солнца. Перенеся построенную модель с плоскости в пространство, мы получим отсеченный от Солнца шаровой сегмент. Площадь его боковой (то есть выпуклой) поверхности, без учета площади основания, и будет равна той самой площади части Солнца, которую я ищу (вспомните мучивший меня вопрос).
Возможно, некоторый читатель воскликнет: не может быть! Ведь излучение исходит от Солнца не только перпендикулярно его поверхности! Солнце освещает Землю не только с части поверхности, ограниченной двумя красными касательными, но также и с других участков поверхности, что находятся между красными и синими касательными!
Конечно, это так. Но излучение, исходящее от Солнца с части поверхности, ограниченной двумя красными касательными, не всё идет на Землю, а частично уходит и в других направлениях. И если мы допускаем, что излучение исходит от Солнца и распределяется в пространстве равномерно, то становится очевидным, что количество излучения, исходящего от участков поверхности, находящихся между красными и синими касательными и направленного при этом на Землю, будет абсолютно равно количеству излучения, исходящему от части поверхности, ограниченной двумя красными касательными, но при этом не направленному в сторону Земли.
Следовательно, для вычисления нужной нам величины достаточно иметь только лишь рассмотренный выше отсеченный от Солнца шаровой сегмент. Если кто-то этого пока не понял, значит нужно поработать с более тщательным представлением модели сначала на плоскости, а потом и в пространстве.
Итак, мы будем искать площадь боковой (выпуклой) поверхности шарового сегмента, полученного отсечением части Солнца по точкам, где красные касательные пересекаются с его поверхностью.
Площадь боковой поверхности шарового сегмента:
S = 2πr2h, где r2 – радиус Солнца, h – высота шарового сегмента.
Теперь нам необходимо найти высоту шарового сегмента. Без тригонометрии здесь уже не обойтись. Проводим отрезки от центра Земли к точкам, в которых красные касательные касаются Земли. Соединяем отрезком центры Земли и Солнца.
Всем образующимся на нашей модели точкам даем имена.
Малюсенький отрезочек между точкой L и необозначенной точкой на поверхности Солнца – это и есть высота шарового сегмента, которую нам нужно найти. Точку на поверхности Солнца я не стал обозначать, чтобы она не сливалась с точкой L.
Но если увеличить картинку, то можно обозначить и вторую точку. Высота шарового сегмента равна длине отрезка NL.
Возвращаемся к предыдущей полной картинке, чтобы она была здесь, перед глазами.
Касательные, проведенные к окружности, всегда перпендикулярны радиусу, проведенному в точке касания.
Таким образом, мы имеем большой прямоугольный треугольник ACB и входящий в него маленький прямоугольный треугольник KLB. Углы ACB и KLB – прямые. Теперь нам нужно выяснить, чему равны острые углы треугольников.
Синус угла ABC будет равен отношению радиуса Земли к расстоянию между Землей и Солнцем.
sin (ABC) = AC / AB = 6 371 / 149 597 870 = 0,000042587504…
Зная синус угла ABC, определяем, что сам угол ABC = 0,002440084283… градуса.
Очевидно, что также и угол LBK = 0,002440084283… градуса.
Далее, угол LKB = 90 – 0,002440084283… = 89,997559915716… градусов.
Вычисляем длину отрезка LB, ведь нам теперь известны все углы и гипотенуза маленького треугольника, которая равна радиусу Солнца.
LB = KB х sin (LKB) = 695 699,999369105998… км.
Определяем высоту шарового сегмента:
NL = NB – LB = 0,000630894001… км, то есть всего около 63 сантиметров!
Площадь боковой поверхности шарового сегмента:
S = 2πr2h = 2 757,771440594113… кв. километров.
Это и есть та самая часть поверхности Солнца, которая излучает ровно столько энергии, сколько Земля получает от всего Солнца в целом. Сей участок сравним по площади с Москвой в её границах по состоянию на 2019 год.
Теперь сравним полученный результат с тем, что был найден ранее, при расчете по неверному алгоритму.
Было: 2 757,771439343673… кв. километров.
Стало: 2 757,771440594113… кв. километров.
Казалось бы, разница ничтожна: всего лишь в 1,25 квадратных метра! Однако, такая разница возникает не из-за округлений или погрешностей в расчетах, а из-за того, что Земля очень маленькая по сравнению с Солнцем, находится от него очень далеко, и красные касательные касаются Земли почти рядом с ее условными полюсами. На нашем рисунке, где масштабы не соблюдены, этого, конечно, не видно.
Но стоит нам изменить стартовые параметры, как разница в результатах будет более значительная.
Увеличим радиус Земли в 100 раз, до 637 100 км.
Уменьшим радиус Солнца в 100 раз, до 6 957 км.
Уменьшим расстояние от Земли до Солнца в 100 раз, до 1 495 978,70 км.
Подставим полученные значения в расчетные формулы и получим следующее.
При расчете по первому (неверному) алгоритму S = 27 577 714,3934… кв. километров.
При расчете по второму (моему) алгоритму S = 28 956 294,8228… кв. километров.
Как видите, разница стала более ощутимой.
Таким образом, мы убедились в том, что вести расчеты по первому принципу (делением площади сечения Земли диаметральной плоскостью на площадь сферы c радиусом, равным радиусу земной орбиты) нельзя.
И на десерт – несколько удивительных фактов о мощности Солнца.
Солнце излучает колоссальное количество радиации и теряет при этом свою массу: каждую секунду в результате термоядерных процессов 4,26 миллиона тонн солнечного вещества превращаются в лучистую энергию. Чтобы увезти такой груз на товарном поезде, понадобится 71 000 вагонов, в каждый из которых будет загружено 60 тонн. Длина такого состава будет равна 994 км.
Представьте себе, что мимо вас такой поезд проносится за одну секунду. 60 поездов в минуту. 3 600 поездов в час. И так постоянно: миллиарды лет в прошлом и миллиарды – в будущем. Вот с какой скоростью Солнце расходует свою массу! И тем не менее, для него это ничтожно мало и похудение Солнцу абсолютно не грозит: за один миллиард лет оно теряет таким образом всего лишь одну пятнадцатитысячную долю своей массы.
Полная мощность излучения Солнца составляет 3,83 х 10 (в 20 степени) МВт. Соответственно, плотность мощности излучения на его поверхности приблизительно равна 62,97 МВт на квадратный метр, чего достаточно для безостановочной постоянной работы в полную силу 10 000 бытовых электрических плит с четырьмя нагревательными элементами или 1 000 000 лампочек накаливания мощностью по 60 Вт каждая. На каждом квадратном метре!
За один год Солнце генерирует 33,57 х 10 (в 23 степени) МВт·час энергии. До верхних слоев атмосферы Земли доходит, как мы ранее установили, приблизительно одна двухмиллиардная часть, а именно 1,52 х 10 (в 15 степени) МВт·час. В среднем 53% излучения отражаются, рассеиваются и поглощаются атмосферой Земли, и только лишь 7,15 х 10 (в 14 степени) МВт·час достигает поверхности нашей планеты в течение одного года. Маловато будет?
Если всю эту энергию распределить равномерно во времени и по всей поверхности Земли, то на каждый квадратный метр придется всего лишь 0,16 кВт мощности (не стоит путать это значение с Солнечной постоянной – суммарной мощностью солнечного излучения, проходящего через единичную площадку, ориентированную перпендикулярно потоку, на расстоянии одной астрономической единицы от Солнца вне земной атмосферы, которая составляет 1,37 кВт на квадратный метр).
Полученной на поверхности Земли среднесуточной мощности 0,16 кВт на квадратный метр хватит, чтобы зажечь только лишь две с половиной лампочки. И тем не менее, в масштабах всей Земли эта энергия огромна.
Согласно справочным данным, мировое потребление всей энергии в 2008 году составило 143 000 000 ГВт·час (в это значение входит суммарно вся потребляемая человечеством и промышленностью энергия, получаемая на всех видах электростанций и от всех видов энергоресурсов и добываемого топлива). Так вот, суммарно солнечное излучение, достигшее поверхности Земли, приносит энергии в 5 000 раз больше, чем фактически расходуется во всем мире.
Для сравнения, самая мощная электростанция в России (Саяно-Шушенская ГЭС) имеет мощность 6 400 МВт, а годовая выработка электроэнергии на ней составляет 23 500 ГВт·час (так как станция работает приблизительно на 40 процентов от максимальной проектной мощности).
Количество фактически вырабатываемой станцией энергии меньше мирового потребления в 6 085 раз. Именно столько Саяно-Шушенских ГЭС потребовалось бы создать на нашей планете для обеспечения ее потребностей, если бы на Земле больше не было других электростанций и источников энергии. Выходит, что Солнце дает нам на поверхности Земли энергии в 30 425 000 раз больше, чем вырабатывает Саяно-Шушенская ГЭС!
Однако, использование человечеством энергии Солнца пока ничтожно мало. По состоянию на 2017 год, суммарная установленная электрическая мощность всех солнечных электростанций в России составляла всего 75,20 МВт, то есть 0,03% от мощности всех электростанций нашей страны, вместе взятых. В США и странах Европы солнечную энергию используют куда более активно, но все равно несоизмеримо меньше, чем другие виды энергоносителей.
Несмотря на то, что солнечная энергия бесплатна и экологически чиста, существуют факторы, сдерживающие развитие этого вида энергетики: фотоэлементы весьма дороги, а плотность потока солнечного излучения на поверхности Земли такова, что придется строить поистине гигантские сооружения для получения мощных электростанций.
Поскольку в среднем на один квадратный метр поверхности Земли приходится 0,16 кВт мощности солнечной энергии, то для построения солнечной электростанции такой же мощности, как и фактическая мощность Саяно-Шушенской ГЭС, необходимо будет всплошную укрыть фотоэлементами поле площадью 17 квадратных километров. И это при условии, что КПД таких солнечных батарей составит 100 процентов.
Но в реальности на сегодняшний день мы имеем средний КПД фотоустановок около 15-20 процентов. И тогда, с учетом такой производительности, чтобы перевести всю энергетику Земли на солнечную, под установку фотоэлементов потребуется выделение территории площадью около 600 000 кв. километров (при равномерном распределении электростанций по всей Земле, по разным ее широтам). Это сравнимо с площадью всей Украины (извините, но вместе с Крымом).
Поэтому строить такие электростанции целесообразно в районах с наибольшей инсоляцией – в широтах, близких к экватору, где реальное значение поступающей на поверхность Земли мощности в дневное время в ясную погоду может достигать 0,8-0,9 кВт на квадратный метр, что позволит более эффективно использовать энергию Солнца и сократить площадь необходимой для строительства территории.
Так сможем ли мы научиться эффективно использовать энергию Солнца и спасти Землю от экологической катастрофы, до которой остался один шаг? На этот вопрос я ответа уже найти не могу.
Буду рад видеть ваши вопросы, комментарии и замечания.
P.S. Эта статья – уникальный контент, который не был откуда-либо скопирован, а был создан автором с нуля. На подбор материалов, проверку фактов, математические расчеты, создание графики, написание статьи, редактирование, коррекцию, а также типографскую подготовку к публикации было затрачено около 60 часов времени. Если эта работа заинтересовала вас, вы можете отблагодарить автора, отослав ему посильную сумму на Яндекс Деньги 4100189981909.
Какую мощность излучения имеет Солнце?
Любая лампочка, излучающая свет, характеризуется мощностью излучения. Эта величина измеряется в ваттах, она определяет количество энергии (или тепла), выделяемого телом в единицу времени. Какова же мощность нашего Солнца?
Общую мощность электромагнитного излучения звезды, выделяемого ее в космическое пространство называют светимостью. Полная мощность излучения Солнца, то есть его светимость равна 3,828•1026 Ватт (~3,75⋅1028 Люмен). Это значит, что наша звезда светит примерно также мощно, как триллион триллионов лампочек мощностью 380 Вт! Это невероятно огромное значение. У многих атомных электростанций, например, у Запорожской АЭС, мощность одного реактора составляет 1ГВт. Получается, что Солнце вырабатывает за одну секунду столько же энергии, сколько выработает миллион атомных реакторов за 12 000 лет круглосуточной и беспрерывной работы.
Надо отметить, что до нашей планеты доходит только одна миллионная тепла, излучаемого Солнцем. Но именно эта энергия обеспечивает жизнь на Земле. Без солнечного света температура на нашей планете была бы не выше, чем, например, на Плутоне, где она равна –220°С.
Энергия в нашем светиле выделяется в ходе термоядерных реакций, топливом для которых является водород. При этом каждую секунду Солнце расходует более 4 млн тонн водорода. Из-за этого температура звезды составляет порядка 6000° С. Откуда же звезда берет этот водород? Он находился в ней ещё в тот момент, когда Солнце впервые вспыхнуло в космосе 4,6 млрд лет назад. С тех пор звезда просто сжигает свои запасы. Примерно через 5 млрд лет водород почти закончится.
Но это не значит, что Солнце погаснет. Оно начнет сжигать гелий, и при этом светило на время резко увеличится в размерах. Меркурий и Венера будут поглощены Солнцем. Естественно, что на Земле станет так жарко, что она будет абсолютно непригодна для жизни.
Однако ещё через некоторое время закончится и гелий, и тогда наша звезда постепенно потухнет и превратится в белого карлика. После этого Солнце будет медленно, в течение миллиардов лет остывать.
Список использованных источников
• https://pikabu.ru/story/pro_moshchnost_solntsa_5485141 • http://bog5.in.ua/problems/volkenshtejin/thermo%20rad/volkenshtejin%20z18%202.html • https://ru.wikipedia.org/wiki/Солнце
Пришелец Инопланетянович
Если не оставишь коммент, то я приду за тобой!!!
Оставить коммент
Не нашли, то что искали? Используйте форму поиска по сайту
Понравилась статья? Оставь комментарий и поделись с друзьями
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,939 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
