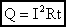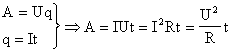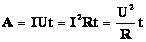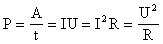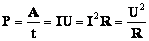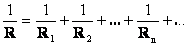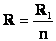Мощность при параллельном и последовательном соединении резисторов
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при параллельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
- Свойства и технические характеристики резисторов
- Мощность при последовательном соединение
- Мощность при параллельном соединение
Свойства и технические характеристики резисторов
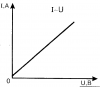
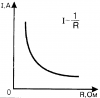
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное.
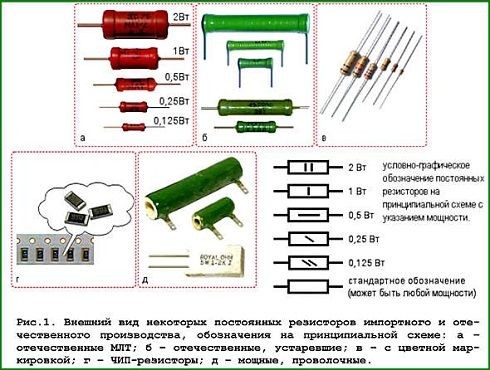
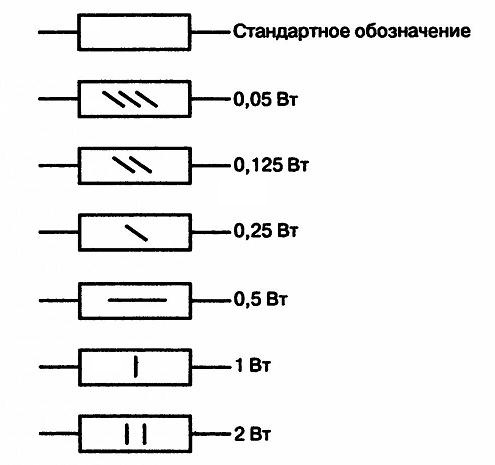
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
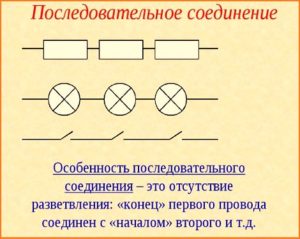
Для соединения резисторов в схемах используются три разных способа подключения – параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
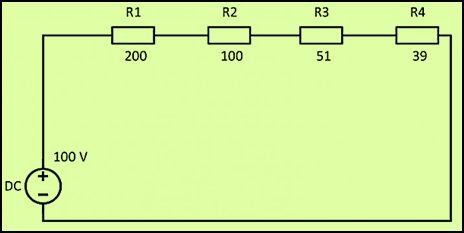
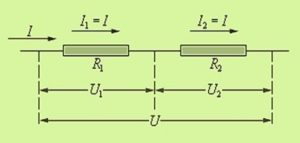
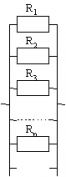
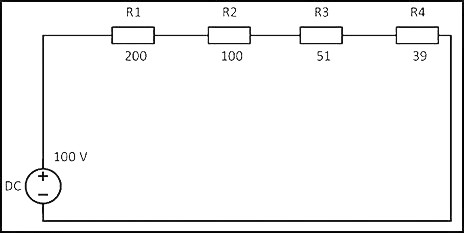
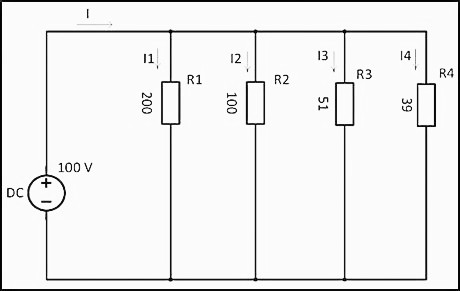
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
- P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
- P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
- P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при параллельном соединение
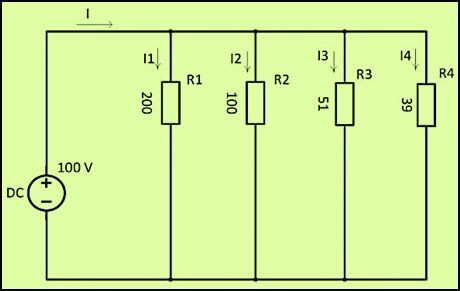
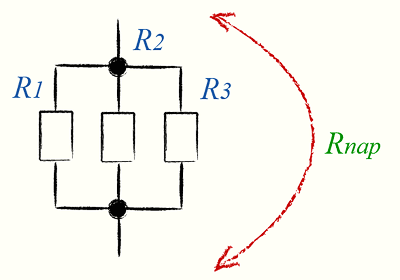
При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов: P1 = U 2 /R1 = 100 2 /200 = 50 Вт; P2 = U 2 /R2 = 100 2 /100 = 100 Вт; P3 = U 2 /R3 = 100 2 /51 = 195,9 Вт; P4 = U 2 /R4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и параллельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
Последовательное и параллельное соединение резисторов
Напряжение при последовательном и параллельном соединении резисторов
Сопротивление при последовательном и параллельном соединении резисторов
Параллельное соединение резисторов
Последовательное и параллельное соединение проводников
Как определяется мощность цепи при последовательном соединении?
Как распределяется мощность при последовательном соединении?
Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…
Как распределяются напряжения на резисторах при последовательном соединении?
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома: Т. е чем большее сопротивление резистора, тем большее напряжение на него падает.
Какие физические величины сохраняются при последовательном соединении конденсаторов?
Последовательное соединение конденсаторов
заряды одинаковы, складываются величины, обратные емкости.
Какой формулой для мощности удобнее пользоваться при расчете цепи с последовательно соединенными резисторами?
Формулу Q = I2Rt удобно применять, когда сила тока в проводниках одинакова, то есть когда они соединены последовательно (рис. 58.1). Q1/Q2 = R1/R2. Формулу Q = (U2/R)t удобно применять, когда напряжение на концах проводников одинаково, то есть когда они соединены параллельно (рис.
Что происходит с мощностью при последовательном соединении?
Мощность при последовательном соединение
Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. … Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A.
Что такое мощность тока определение?
Мощность электрического тока — это отношение произведенной им работы ко времени в течение которого совершена работа.
Как складываются сопротивления при параллельном соединении?
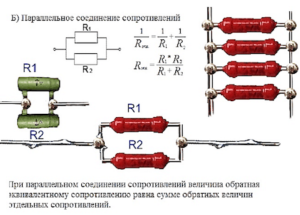
Из закона Ома и первого и второго правил Кирхгофа следует: При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей. При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.
Как найти R при параллельном соединении?
Общее сопротивление цепи при параллельном соединении проводников определяется по формуле: 1 R = 1 R 1 + 1 R 2 . Обратное значение общего сопротивления равно сумме обратных значений сопротивлений отдельных проводников. Для проверки формулы можно использовать омметр.
Как распределяется ток в цепи?
Ток через цепь равен сумме токов через каждый из проводников, образующих цепь; Напряжение на выводах цепи равно напряжению на любом из проводников, образующих цепь.
Какая физическая величина одинакова при последовательном соединении?
При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов.
Какие физические величины бывают одинаковыми при параллельном соединении проводников?
Какие физические величины сохраняются при последовательном соединении проводников? … При последовательном соединении сила тока во всех резисторах одинакова, а общее напряжение равно сумме напряжений на каждом из проводников. Общее сопротивление цепи равно сумме сопротивлений всех резисторов.
Какое сопротивление проводников называется последовательным?
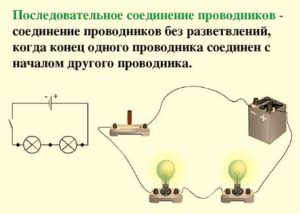
1. Какое сопротивление проводников называют последовательным? … Соединение проводников называется последовательным, если конец одного проводника соединяется с началом другого.
Как определить суммарную мощность?
Определите мощность источника питания.
- Мощность равна произведению силы тока на напряжение, то есть 1 Вт = 1 А х 1 В. Формула: Р = I х V. …
- Например, если сила тока равна 3 А, а напряжение равно 110 В, то мощность равна: 3 х 110 = 330 Вт. …
- Вот почему внесистемной единицей измерения мощности является вольт-ампер.
Как рассчитать мощность зная ток и напряжение?
Формула расчета мощности электрического тока
Согласно закону Ома, сила тока(I) пропорциональна напряжению(U) и обратно пропорциональна сопротивлению(R), а мощность(P) рассчитывается как произведение напряжения и силы тока. Исходя из этого, ток в участке сети рассчитывается: I = P/U.
Закон Ома для участка цепи. Закон Джоуля — Ленца. Работа и мощность электрического тока. Виды соединения проводников.
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению этого участка.
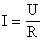
Выполняется для металлов и электролитов.
Закон Джоуля — Ленца.
Дж. Джоуль (1841—1843) Э. X. Ленц (1842—1843) независимо друг от друга экспериментально установили
В электрической цепи происходит преобразование энергии упорядоченного движения заряженных частиц в тепловую. Согласно з-ну сохранения энергии работа тока равна количеству выделившегося тепла.
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток:
Работа и мощность электрического тока.
Работа электрического тока:
Мощность электрического тока (работа в единицу времени):
В электричестве иногда применяется внесистемная единица работы — кВт . ч (киловатт-час).
1 кВт . ч = 3,6 . 10 6 Дж.
Виды соединения проводников.
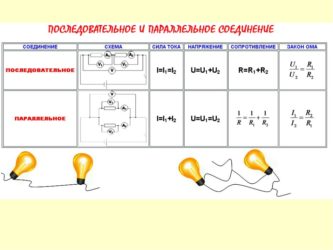
Последовательное соединение.
1. Сила тока во всех последовательно соединенных участках цепи одинакова:
I1=I2=I3=. =In=.
2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке:
U=U1+U2+. +Un+.
3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка:
R=R1+R2+. +Rn+.
Если все сопротивления в цепи одинаковы, то:
R=R1 . N
При последовательном соединении общее сопротивление увеличивается (больше большего).
Параллельное соединение.
1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках.
2. Напряжение на всех параллельно соединенных участках цепи одинаково:
U1=U2=U3=. =Un=.
3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению):
Если все сопротивления в цепи одинаковы, то:
При параллельном соединении общее сопротивление уменьшается (меньше меньшего).
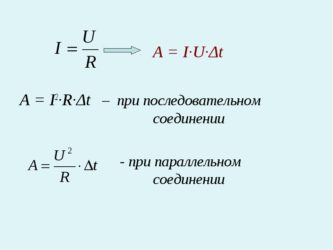
4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках:
5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках:
P=P1+P2+. +Pn+.
6. Т.к. силы тока во всех участках одинаковы, то: U1:U2. Un. = R1:R2. Rn.
Для двух резисторов: 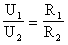
4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках:
A=A1+A2+. +An+.
т.к. 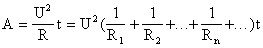
5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках:
P=P1+P2+. +Pn+.
6. Т.к. напряжения на всех участках одинаковы, то:
Для двух резисторов: 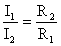
Резистор и сопротивление
Каталог
Показать каталог
- Arduino и совм. платы
- Raspberry
- Наборы Arduino
- Платы расширения
- Модули
- Радиомодули
- Bluetooth
- RFID
- Wi-Fi, Ethernet, GPS, GSM
- Звук и видео
- Свет
- Память и RTC
- Генераторы сигналов
- Расширения
- Термоэлектрические
- Датчики
- Газа
- Климатические
- Механического воздействия
- Пространства
- Света и цвета
- Тактильные
- Холла и тока
- Реле
- Двигатели
- Коллекторные
- Бесколлекторные
- Сервоприводы
- Шаговые
- Драйверы
- Механика
- Платформы
- Колеса
- Замки
- Радиоконструкторы
- Радиокомпоненты
- Резисторы
- Постоянные
- Потенциометры
- Варисторы
- Термисторы
- Фоторезисторы
- Конденсаторы
- Диоды
- Светодиоды
- Стабилитроны
- Диодные мосты
- Транзисторы
- Биполярные
- IGBT
- Полевые | MOSFET
- Стабилизаторы
- Предохранители
- Индуктивность
- Резонаторы
- Тиристоры
- Резисторы
- Дисплеи и индикаторы
- Макетные платы
- Паечные
- Беспаечные
- Провода и шлейфы
- Кабели и переходники
- Адаптеры, разъемы и штекеры
- Микроконтроллеры и микросхемы (IC)
- Программаторы и преобразователи
- Управление и ввод
- Элементы питания
- Аккумуляторы и батареи
- Зарядные устройства
- Отсеки и коннекторы
- Преобразователи и блоки питания
- BMS платы
- Сетевые фильтры
- Измерительные приборы
- Мультиметры и щупы
- Тестеры
- Вольтметры / Амперметры
- USB-нагрузка
- Всё для пайки
- Паяльники и паяльные наборы
- Оборудование для пайки
- Расходные материалы
- Изоляторы
- Светодиодная продукция
- Светодиодные ленты
- Светодиодные модули
- Контроллеры
- Кабели и клипсы
- Гирлянды
- Инструменты и материалы
- Инструменты
- Корпуса и крепления
- Магниты
- Расходные материалы
- Органайзеры и пакеты
- Кулеры
- Карты памяти и ридеры
Резистор и сопротивление
Теория
КОМПОНЕНТЫ
- Адресуемая светодиодная лента
- Геркон
- Диод
- Зуммер
- Кнопка
- Кварцевый резонатор
- Конденсатор
- Макетная плата
- Резистор
- Реле
- Светодиод
- Светодиодные индикаторы
- Сервопривод
- Транзистор
ARDUINO
- Что такое Arduino?
- Среда разработки Arduino IDE
- Онлайн-сервис TinkerCAD – эмулятор Arduino
- Сравнение плат Arduino. Какую выбрать?
- Как прошить плату Arduino с помощью другой Arduino (ArduinoISP)
RASPBERRY
ИНТЕРФЕЙСЫ ПЕРЕДАЧИ ДАННЫХ
1 кОм = 1000 Ом,
1 МОм = 1000 кОм,
1 ГОм = 1000 МОм
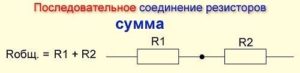
Последовательное соединение резисторов
Это справедливо и для большего количества соединённых последовательно резисторов:
Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.
При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.
Мощность при последовательном соединении
R = 200 + 100 + 51 + 39 = 390 Ом
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять
I = U/R = 100 В/390 Ом = 0,256 A
На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле:
P = I 2 x R = 0,256 2 x 390 = 25,55 Вт
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощности, то общая Р составит:
Робщ = 13,11 + 6,55 + 3,34 + 2,55 = 25,55 Вт
Параллельное соединение резисторов
Расчет параллельного сопротивления двух параллельно соединённых резисторов R1 и R2 производится по следующей формуле:
Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:
Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.
Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.
Мощность при параллельном соединении
1/R = 1/200 + 1/100 + 1/51 + 1/39 ≈ 0,06024 Ом
R = 1 / 0,06024 ≈ 16,6 Ом
Используя значение напряжения 100 В, по закону Ома рассчитывается сила тока
I = U/R = 100 В x 0,06024 Ом = 6,024 A
Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом
P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт
Расчет силы тока для каждого резистора выполняется по формулам:
На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов:
P1 = U 2 /R1 = 100 2 /200 = 50 Вт;
P2 = U 2 /R2 = 100 2 /100 = 100 Вт;
P3 = U 2 2/R3 = 100 2 /51 = 195,9 Вт;
P4 = U 2 2/R4 = 100 2 /39 = 256,4 Вт
Если сложить полученные мощности, то общая Р составит:
Робщ = 50 + 100 + 195,9 + 256,4 = 602,3 Вт
Последовательное и параллельное соединение
Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей – проводников.
Для начала давайте вспомним, что такое проводник? Проводник – это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м 2
l – длина проводника, м
Более подробно об этом я писал здесь.
Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.

Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
Если бы у нас еще были резисторы, соединенные параллельно, то для них
В этом случае, сила тока в цепи будет равна:

Задача
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение
Воспользуемся формулами, которые приводили выше.
Если бы у нас еще были резисторы, соединенные параллельно, то для них
Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи
2-ой способ найти I
Чтобы найти Rобщее мы должны воспользоваться формулой
Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
I=U/Rобщее = 10/1,25=8 Ампер.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при параллельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения — параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I2 x R = 0,2562 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I2 x R1 = 0,2562 x 200 = 13,11 Вт;
- P2 = I2 x R2 = 0,2562 x 100 = 6,55 Вт;
- P3 = I2 x R3 = 0,2562 x 51 = 3,34 Вт;
- P4 = I2 x R4 = 0,2562 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при параллельном соединение
При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом: P = I2 x R = 6,0242 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов: P1 = U2/R1 = 1002/200 = 50 Вт; P2 = U2/R2 = 1002/100 = 100 Вт; P3 = U2/R3 = 1002/51 = 195,9 Вт; P4 = U2/R4 = 1002/39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и параллельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
Содержание
- 1 Расчет мощности при последовательном соединении — Все об электричестве
- 1.1 Последовательное соединение
- 1.2 Применение
- 1.3 Параллельное соединение
- 1.4 Работа тока
- 1.5 Мощность тока
- 1.6 Влияние схемы соединения на новогоднюю гирлянду
- 1.7 Последовательное и параллельное соединение для конденсаторов
- 1.8 Смешанное соединение проводников
- 1.9 Теперь используем формулу расчета сопротивления:
- 2 Параллельное и последовательное соединение проводников: теория, формулы, подключение и расчет силы тока
- 2.1 Взаимная зависимость электрических величин
- 2.2 Схемы с несколькими проводниками
- 2.3 Параллельное соединение проводников
- 2.4 Последовательное соединение
- 2.5 Смешанное соединение
- 2.6 Ответ на задачу о елочной гирлянде
- 3 Последовательное и параллельное соединение ламп
- 3.1 Последовательное соединение ламп накаливания
- 3.2 Вывод:
- 3.3 Параллельное соединение ламп
- 4 Суммарная мощность при параллельном соединении. Расчет результирующего сопротивления при последовательно-параллельном соединении
- 4.1 Соединяем последовательно
- 4.2 Включаем параллельно
- 5 Мощность при параллельном и последовательном соединении резисторов
- 5.1 Свойства и технические характеристики резисторов
- 5.2 Мощность при последовательном соединение
- 5.3 Мощность при параллельном соединение
Расчет мощности при последовательном соединении — Все об электричестве
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединение
При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
Применение
Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой.
Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка.
Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Параллельное соединение
В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
Работа тока
Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:
А = I х U х t, где А – работа тока, t – время течения по проводнику.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:
А=I х (U1 + U2) х t
Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:
А = А1+А2
Мощность тока
При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:
Р=U х I
После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:
Р=Р1 + Р2
Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
Влияние схемы соединения на новогоднюю гирлянду
После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.
При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.
Последовательное и параллельное соединение для конденсаторов
При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
qобщ= q1 = q2 = q3
Для определения напряжения на любом конденсаторе, необходима формула:
U= q/С
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
С= q/(U1 + U2 + U3)
Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:
1/С= 1/С1 + 1/С2 + 1/C3
Немного иначе рассчитывается параллельное соединение конденсаторов.
Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
С= (q1 + q2 + q3)/U
Это значение рассчитывается как сумма каждого прибора в схеме:
С=С1 + С2 + С3
Смешанное соединение проводников
В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.
Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.
Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Теперь используем формулу расчета сопротивления:
- Первая формула для последовательного вида соединения.
- Далее, для параллельной схемы.
- И окончательно для последовательной схемы.
Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.
Источник: https://contur-sb.com/raschet-moschnosti-pri-posledovatelnom-soedinenii/
Параллельное и последовательное соединение проводников: теория, формулы, подключение и расчет силы тока
Практически каждому, кто занимался электрикой, приходилось решать вопрос параллельного и последовательного соединения элементов схемы.
Некоторые решают проблемы параллельного и последовательного соединения проводников методом «тыка», для многих «несгораемая» гирлянда является необъяснимой, но привычной аксиомой.
Тем не менее, все эти и многие другие подобные вопросы легко решаются методом, предложенным еще в самом начале XIX века немецким физиком Георгом Омом. Законы, открытые им, действуют и поныне, а понять их сможет практически каждый.
Для того чтобы выяснить, как то или иное соединение проводников повлияет на характеристики схемы, необходимо определиться с величинами, которые характеризуют любую электрическую цепь. Вот основные из них:
- Электрическое напряжение, согласно научному определению, это разность потенциалов между двумя точками электрической цепи. Измеряется в вольтах (В). Между клеммами бытовой розетки, к примеру, оно равно 220 В, на батарейке вольтметр покажет 1,5 В, а зарядное устройство вашего планшета или смартфона выдает 5 В. Напряжение бывает переменным и постоянным, но в нашем случае это несущественно.
- Электрический ток – упорядоченное движение электронов в электрической цепи. Ближайшая аналогия – ток воды в трубопроводе. Измеряется в амперах (А). Если цепь не замкнута, ток существовать не может.
- Электрическое сопротивление. Величина измеряется в омах (Ом) и характеризует способность проводника или электрической цепи сопротивляться прохождению электрического тока. Если продолжить аналогию с водопроводом, то новая гладкая труба будет иметь маленькое сопротивление, забитая ржавчиной и шлаками – высокое.
- Электрическая мощность. Эта величина характеризует скорость преобразования электрической энергии в любую другую и измеряется в ваттах (Вт). Кипятильник в 1000 Вт вскипятит воду быстрее стоваттного, мощная лампа светит ярче и т.д.
Взаимная зависимость электрических величин
Теперь необходимо определиться, как все вышеперечисленные величины зависят одна от другой. Правила зависимости несложны и сводятся к двум основным формулам:
Здесь I – ток в цепи в амперах, U – напряжение, подводимое к цепи в вольтах, R – сопротивление цепи в омах, P – электрическая мощность цепи в ваттах.
Предположим, перед нами простейшая электрическая цепь, состоящая из источника питания с напряжением U и проводника с сопротивлением R (нагрузки).
Поскольку цепь замкнута, через нее течет ток I. Какой величины он будет? Исходя из вышеприведенной формулы 1, для его вычисления нам нужно знать напряжение, развиваемое источником питания, и сопротивление нагрузки. Если мы возьмем, к примеру, паяльник с сопротивлением спирали 100 Ом и подключим его к осветительной розетке с напряжением 220 В, то ток через паяльник будет составлять:
220 / 100 = 2,2 А.
Какова мощность этого паяльника? Воспользуемся формулой 2:
2,2 * 220 = 484 Вт.
Хороший получился паяльник, мощный, скорее всего, двуручный. Точно так же, оперируя этими двумя формулами и преобразуя их, можно узнать ток через мощность и напряжение, напряжение через ток и сопротивление и т.д. Сколько, к примеру, потребляет лампочка мощностью 60 Вт в вашей настольной лампе:
60 / 220 = 0,27 А или 270 мА.
Сопротивление спирали лампы в рабочем режиме:
220 / 0,27 = 815 Ом.
Схемы с несколькими проводниками
Все рассмотренные выше случаи являются простыми – один источник, одна нагрузка. Но на практике нагрузок может быть несколько, и соединены они бывают тоже по-разному. Существует три типа соединения нагрузки:
- Параллельное.
- Последовательное.
- Смешанное.
Параллельное соединение проводников
В люстре 3 лампы, каждая по 60 Вт. Сколько потребляет люстра? Верно, 180 Вт. Быстренько подсчитываем сначала ток через люстру:
180 / 220 = 0,818 А.
А затем и ее сопротивление:
220 / 0,818 = 269 Ом.
Перед этим мы вычисляли сопротивление одной лампы (815 Ом) и ток через нее (270 мА). Сопротивление же люстры оказалось втрое ниже, а ток — втрое выше. А теперь пора взглянуть на схему трехрожкового светильника.
Схема люстры с тремя лампами
Все лампы в нем соединены параллельно и подключены к сети. Получается, при параллельном соединении трех ламп общее сопротивление нагрузки уменьшилось втрое? В нашем случае — да, но он частный – все лампы имеют одинаковые сопротивление и мощность. Если каждая из нагрузок будет иметь свое сопротивление, то для подсчета общего значения простого деления на количество нагрузок мало. Но и тут есть выход из положения – достаточно воспользоваться вот этой формулой:
1/Rобщ. = 1/R1 + 1/R2 + … 1/Rn.
Для удобства использования формулу можно легко преобразовать:
Rобщ. = (R1*R2*… Rn) / (R1+R2+ … Rn).
Здесь Rобщ. – общее сопротивление цепи при параллельном включении нагрузки. R1 … Rn – сопротивления каждой нагрузки.
Почему увеличился ток, когда вы включили параллельно три лампы вместо одной, понять несложно – ведь он зависит от напряжения (оно осталось неизменным), деленного на сопротивление (оно уменьшилось). Очевидно, что и мощность при параллельном соединении увеличится пропорционально увеличению тока.
Последовательное соединение
Теперь настала пора выяснить, как изменятся параметры цепи, если проводники (в нашем случае лампы) соединить последовательно.
Последовательно соединенная нагрузка
Расчет сопротивления при последовательном соединении проводников исключительно прост:
Rобщ. = R1 + R2.
Те же три шестидесятиваттные лампы, соединенные последовательно, составят уже 2445 Ом (см. расчеты выше). Какими будут последствия увеличения сопротивления цепи? Согласно формулам 1 и 2 становится вполне понятно, что мощность и сила тока при последовательном соединении проводников упадет. Но почему теперь все лампы горят тускло? Это одно из самых интересных свойств последовательного подключения проводников, которое очень широко используется. Взглянем на гирлянду из трех знакомых нам, но последовательно соединенных ламп.
Последовательное соединение трех ламп в гирлянду
Общее напряжение, приложенное ко всей цепи, так и осталось 220 В. Но оно поделилось между каждой из ламп пропорционально их сопротивлению! Поскольку лампы у нас одинаковой мощности и сопротивления, то напряжение поделилось поровну: U1 = U2 = U3 = U/3.
То есть на каждую из ламп подается теперь втрое меньшее напряжение, вот почему они светятся так тускло. Возьмете больше ламп – яркость их упадет еще больше.
Как рассчитать падение напряжения на каждой из ламп, если все они имеют различные сопротивления? Для этого достаточно четырех формул, приведенных выше. Алгоритм расчета будет следующим:
- Измеряете сопротивление каждой из ламп.
- Рассчитываете общее сопротивление цепи.
- По общим напряжению и сопротивлению рассчитываете ток в цепи.
- По общему току и сопротивлению ламп вычисляете падение напряжения на каждой из них.
Хотите закрепить полученные знания? Решите простую задачу, не заглядывая в ответ в конце:
В вашем распоряжении есть 15 однотипных миниатюрных лампочек, рассчитанных на напряжение 13,5 В. Можно ли из них сделать елочную гирлянду, подключаемую к обычной розетке, и если можно, то как?
Смешанное соединение
С параллельным и последовательным соединением проводников вы, конечно, без труда разобрались. Но как быть, если перед вами оказалась примерно такая схема?
Смешанное соединение проводников
Как определить общее сопротивление цепи? Для этого вам понадобится разбить схему на несколько участков. Вышеприведенная конструкция достаточно проста и участков будет два — R1 и R2,R3. Сначала вы рассчитываете общее сопротивление параллельно соединенных элементов R2,R3 и находите Rобщ.23. Затем вычисляете общее сопротивление всей цепи, состоящей из R1 и Rобщ.23, соединенных последовательно:
- Rобщ.23 = (R2*R3) / (R2+R3).
- Rцепи = R1 + Rобщ.23.
Задача решена, все очень просто. А теперь вопрос несколько сложнее.
Сложное смешанное соединение сопротивлений
Как быть тут? Точно так же, просто нужно проявить некоторую фантазию. Резисторы R2, R4, R5 соединены последовательно. Рассчитываем их общее сопротивление:
Rобщ.245 = R2+R4+R5.
Теперь параллельно к Rобщ.245 подключаем R3:
Rобщ.2345 = (R3* Rобщ.245) / (R3+ Rобщ.245).
Ну а дальше все очевидно, поскольку остались R1, R6 и найденное нами Rобщ.2345, соединенные последовательно:
Rцепи = R1+ Rобщ.2345+R6.
Вот и все!
Ответ на задачу о елочной гирлянде
Лампы имеют рабочее напряжение всего 13.5 В, а в розетке 220 В, поэтому их нужно включать последовательно.
Поскольку лампы однотипные, напряжение сети разделится между ними поровну и на каждой лампочке окажется 220 / 15 = 14,6 В. Лампы рассчитаны на напряжение 13,5 В, поэтому такая гирлянда хоть и заработает, но очень быстро перегорит. Чтобы реализовать задумку, вам понадобится минимум 220 / 13,5 = 17, а лучше 18-19 лампочек.
Схема елочной гирлянды из миниатюрных ламп накаливания
Источник: https://220v.guru/fizicheskie-ponyatiya-i-pribory/tok-provodnikov-v-parallelnom-i-posledovatelnom-soedinenii.html
Последовательное и параллельное соединение ламп
Здравствуйте, уважаемые читатели сайта sesaga.ru. Сегодня мы рассмотрим практичные схемы последовательного и параллельного соединения ламп накаливания.
В статье схемы подключения трех и более ламп я рассказывал про параллельное соединение, а вот про последовательное упустил. В этой статье мы рассмотрим оба вида соединений используемых в быту.
Пойдем от простого к сложному. Обыкновенная лампа на принципиальных схемах обозначается таким образом:
Следующий момент Вы должны понять и запомнить:
Соединительные провода на схемах показываются линиями. Места соединения трех и более проводов показываются точками, а если провода пересекаются без соединения, то в месте их пересечения точка не ставится.
На рисунке ниже показано, когда провода просто пересекаются, то есть проходят рядом и не касаются друг друга, и когда провода уже соединены между собой — об этом говорит точка, стоящая в пересечении.
А теперь рассмотрим виды соединений:
Последовательное соединение ламп накаливания
Последовательное соединение ламп накаливания в домашнем быту используется редко. В свое время я подключал две лампы последовательно у себя в подъезде, но это был единичный случай.
Тут ситуация была такая, что подъездная лампа перегорала с периодичностью в один месяц, и надо было что-то делать.
Обычно, в таких случаях лампу включают через диод, чтобы она питалась пониженным напряжением 110В и долго служила. Вариант проверенный, но при этом сама лампа мерцает, да и светит в полнакала.
Когда же стоят две последовательно, то они так же питаются пониженным напряжением 110В, не мерцают, долго служат, светят и потребляют энергии как одна. Причем их можно развести по разным углам помещения, что тоже плюс.
Но повторюсь – это редкий случай.
Посмотрите на рисунок ниже. Здесь изображены две схемы последовательного соединения ламп накаливания. В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.
Здесь в линии коричневого цвета, лампы HL1 и HL2 соединены последовательно – одна за другой. Поэтому такое соединение называют последовательным.
Если подать напряжение питания 220В на концы L и N, то загорятся обе лампы, но гореть они будут не в полную силу, а в половину накала. Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.
Поэтому при последовательном соединении двух ламп напряжение 220В будет делиться пополам, и составит 110В для каждой.
На следующем рисунке показаны три лампы соединенные последовательно.
На этой схеме напряжение на каждой лампе составит около 73 Вольт, так как будет делиться уже между тремя лампами.
Так же примером последовательного соединения могут служить новогодние гирлянды. Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.
Например, берем лампочки, рассчитанные на 6,3 Вольта и делим их на 220 Вольт. Получается 35 штук. То есть, чтобы сделать одну лампу на напряжение 220В, нам нужно соединить последовательно 35 штук с напряжением питания 6,3 Вольта.
P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.
Как Вы знаете, у гирлянд есть один недостаток. Перегорает одна из ламп, например, канала зеленого цвета, значит, не горит канал зеленого цвета. Тогда мы идем на базар, покупаем лампочки зеленого цвета, а потом дома по одной вынимаем, вставляем новую, и пока не заработает канал, перебираем его весь.
Вывод:
Недостатком последовательного соединения является то, что если выйдет из строя хоть одна из ламп, гореть не будут все, так как нарушается электрическая цепь.
А вторым недостатком, как Вы уже догадались, является слабое свечение. Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.
Параллельное соединение ламп
Параллельным соединением называют такое соединение, где все элементы электрической цепи, в данном случае лампы накаливания, находятся под одним и тем же напряжением. То есть получается, что каждая лампа, своими контактами, подключена и к фазе и к нулю. И если перегорит любая из ламп, то остальные будут гореть. Именно такое соединение ламп, рассчитанных на напряжение питания 220В, используется в домашнем быту, и не только.
На следующем рисунке так же изображено параллельное соединение. Здесь все три лампы соединены в одном месте. Еще такое соединение называют «звезда»
Бывают моменты, что когда именно из одной точки нужно развести проводку в разные направления.
Кстати, именно «звездой» делают разводку по квартире при монтаже розеток.
Ну вот в принципе и все. И как всегда по традиции ролик о последовательном и параллельном подключении ламп
Теперь я думаю, у Вас не должно возникнуть проблем с последовательным и параллельным соединением ламп.
Удачи!
Источник: https://sesaga.ru/posledovatelnoe-i-parallelnoe-soedinenie-lamp.html
Суммарная мощность при параллельном соединении. Расчет результирующего сопротивления при последовательно-параллельном соединении
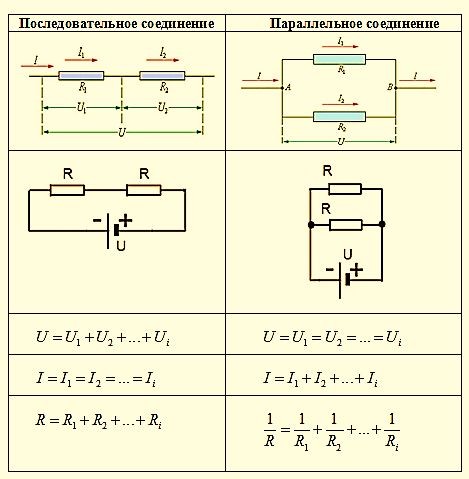
Это хотя и довольно простая тема, но очень важная. Правила всего два: при последовательном соединении складываются сопротивления резисторов, а при параллельном складываются их проводимости, которые, по определению из главы /, есть величины, обратные сопротивлению (см. рис. 5.3).
Понять, почему правила именно таковы, можно, если рассмотреть течение токов в обоих случаях — при последовательном соединении ток I через резисторы один и тот же, поэтому падения напряжения на них складываются, что равносильно сложению сопротивлений. При параллельном соединении, наоборот, равны падения напряжений U, а складывать приходится токи, что равносильно сложению проводимостей.
Если вы не поняли вышесказанное, то посидите над рис. 5.3 с карандашом и бумагой и выведите выражения закона Ома для каждого из случаев — и все станет на свои места.
Рис. 5.3. Последовательное и параллельное соединение резисторов
Из этих определений вытекает несколько практических правил, которые полезно заучить:
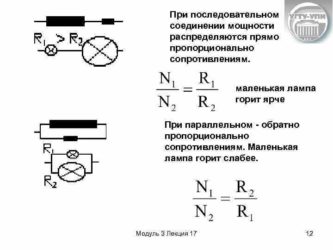
При последовательном соединении:
Пара резисторов имеет сопротивление всегда больше, чем сопротивление резистора с большим номиналом (правило «больше большего»);
Если номиналы резисторов равны, то суммарное сопротивление ровно вдвое больше каждого номинала;
Если номиналы резисторов различаются во много раз, то общее сопротивление примерно равно большему номиналу (типичный случай упоминался в главе 1: в примере на рис. 1.4 мы игнорируем сопротивление проводов, так как оно много меньше сопротивления резисторов);
При параллельном соединении:
Пара резисторов имеет сопротивление всегда меньше, чем сопротивление резистора с меньшим номиналом (правило «меньше меньшего»);
Если номиналы резисторов равны, то суммарное сопротивление ровно вдвое меньше каждого номинала;
Если номиналы резисторов различаются во много раз, то общее сопротивление примерно равно меньшему номиналу (это также можно проиллюстрировать на примере рис. 1.4, где мы игнорируем наличие вольтметра, включенного параллельно R2, так как его сопротивление намного больше сопротивления резистора).
Знание этих правил поможет вам быстро оценивать схему, не занимаясь алгебраическими упражнениями и не прибегая к помощи калькулятора. Даже если соотношение сопротивлений не попадает под перечисленные случаи, результат все равно можно оценить «на глаз» с достаточной точностью.
При параллельном соединении, которое представляет большую сложность при расчетах, для такой оценки нужно прикинуть, какую долю меньшее сопротивление составляет от их арифметической суммы- приблизительно во столько раз снизится их общее сопротивление по отношению к меньшему. Проверить это легко: пусть одно сопротивление имеет номинал 3,3 кОм, второе — 6,8 кОм.
В соответствии с изложенным мы будем ожидать, что общее сопротивление должно быть на 30% меньше, чем 3,3 кОм, то есть 2,2 кОм (3,3 составляет примерно одну треть от суммы 3,3+6,8, то есть общее сопротивление должно быть меньше, чем 3,3, на треть от этого значения, равную 1,1 — в результате и получаем 2,2).
Если мы проверим результат, полученный такой прикидкой в уме, точным расчетом, то мы получим в результате очень близкое значение 2,22 кОм.
В большинстве случаев нам такой точности и не требуется — помните, что и сами сопротивления имеют разброс по номиналу, и в большинстве обычных схем допуски на номиналы стандартных компонентов могут быть довольно велики (по крайней мере, в правильно составленных схемах).
Если же схема в некоторых случаях должна все же иметь какие-то строго определенные параметры, то с помощью стандартных компонентов вы все равно этого не добьетесь — параметры будут «гулять» (в пределах допусков, естественно) от дуновения ветерка из форточки, и в таких случаях надо применять прецизионные резисторы и конденсаторы, а во времязадающих цепях использовать кварцевые резонаторы.
Но составлять схему так, чтобы она теряла работоспособность от замены резистора 1 кОм на резистор 1,1 кОм — не наш метод!
Вычисление сопротивления и мощности при параллельном и последовательном соединении резисторов. (10+)
Расчет параллельно / последовательно соединенных резисторов, конденсаторов и дросселей
Параллельное или последовательное соединение (включение) применяется обычно в нескольких случаях. Во-первых, если нет резистора номинала. Во-вторых, если есть потребность получить резистор большей мощности.
В-третьих, Если необходимо точно подобрать номинал детали, а устанавливать подстроечник нецелесообразно из соображений надежности. Большинство радиодеталей имеют допуски. Чтобы их компенсировать, например для резистора, последовательно с большим резистором устанавливают меньший в разы.
Подбор этого меньшего резистора позволяет получить точно нужное значение сопротивления.
Соединяем последовательно
= += [Сопротивление первого резистора, кОм] * [Сила тока, мА] 2 / 1000= [Сопротивление второго резистора, кОм] * [Сила тока, мА] 2 / 1000Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 1 кОм, 4 Вт.
Включаем параллельно
1 / (1 / [Сопротивление первого резистора, кОм] + 1 / [Сопротивление второго резистора, кОм])Эта формула интуитивно понятна, да и формально может быть выведена из следующего соображения. При заданном напряжении на резисторах через каждый из них независимо идет ток, равный напряжению, деленному на сопротивление. Итоговое сопротивление равно напряжению, деленному на суммарный ток. В формулах значение напряжения счастливым образом сокращается, и получается приведенная формула.[Мощность, рассеиваемая первым резистором, Вт] = [Напряжение на резисторах, В] 2 / [Сопротивление первого резистора, кОм] / 1000[Мощность, рассеиваемая вторым резистором, Вт] = [Напряжение на резисторах, В] 2 / [Сопротивление первого резистора, кОм] / 1000Получается, что из двух резисторов по 500 Ом на 2 Вт можно сделать один на 250 Ом, 4 Вт.К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости , чтобы быть в курсе.Если что-то непонятно, обязательно спросите!
Понятия и формулы
Последовательно-параллельное, или смешанное, соединение представляет собой сложное соединение трех и более сопротивлений. Результирующее сопротивление при смешанном соединении рассчитывается поэтапно с применением формул расчета сопротивлений при последовательном и параллельном соединениях.
Примеры
Сначала заменим параллельно соединенные сопротивления r2 и r3 результирующим сопротивлением r(2-3):
r(2-3)=(r2∙r3)/(r2+r3)=(10∙20)/30=6,6 Ом.
Результирующее сопротивление всей схемы r=r1+r(2-3)=5+6,6=11,6 Ом.
Рис. 1.
2. Какой ток протекает по цепи (рис. 2) в случаях разомкнутого и замкнутого P? Как изменяется напряжение на сопротивлении r2 в обоих случаях?
Рис. 2.
а) Рубильник разомкнут. Результирующее сопротивление последовательно включенных сопротивлений r1 и r2
r(1-2)=r1+r2=25 Ом.
Ток I(1-2)=U/r(1-2) =100/25=4 А.
Падение напряжения на сопротивлении r2
U2=I(1-2)∙r2=4∙5=20 В.
б) Рубильник замкнут. Результирующее сопротивление параллельно включенных сопротивлений r1 и r3
r(1-3)=(r1∙r3)/(r1+r3)=(20∙10)/(20+10)=200/30=6,6 Ом.
Общее сопротивление всей схемы r=r(1-3)+r2=6,6+5=11,6 Ом.
Ток I=U/r=100/11,6=8,62 А.
Падение напряжения на сопротивлении r2 в этом случае равно: U2=I∙r2=8,62∙5=43,25 В.
Во втором случае ток увеличился в результате подключения параллельного сопротивления R3. Больший ток создает большее на сопротивлении r2.
3. Каким должно быть rд, чтобы две параллельно соединенные лампы на напряжение 120 В и ток 0,2 А могли быть включены в сеть напряжением U=220 В (рис. 3)?
Рис. 3.
Напряжение на лампах должно быть равно 120 В. Остальное напряжение (100 В) падает на дополнительном сопротивлении rд. Через сопротивление rд проходит ток двух ламп I=0,4 А.
По закону Ома rд=Uд/I=100/0,4=250 Ом.
4. Электронные лампы с напряжением накала 1,2 В и током накала 0,025 и 0,05 А подключены последовательно к источнику постоянного тока напряжением 4,5 В. Какими должны быть добавочное сопротивление rд и к лампе, имеющей меньший ток накала (рис. 4)?
Рис. 4.
Сопротивления в схеме должны быть подобраны так, чтобы протекал ток накала второй лампы I=0,05 А. Напряжение на нитях накаливания электронных ламп будет равно 1,2+1,2=2,4 В. Вычтя эту величину из напряжения батареи, получим величину падения напряжения на добавочном сопротивлении rд: Uд=4,5-2,4=2,1 В.
Отсюда дополнительное сопротивление rд=(Uд)/I=2,1/0,05=42 Ом.
Ток накала 0,05 А не должен весь протекать через нить первой электронной лампы. Половина этого тока (0,05-0,025=0,025 А) должна пройти через шунт r. Напряжение на шунте такое же, как и на нити лампы, т. е. 1,2 В. Отсюда сопротивление шунта равно: r=1,2/0,025=48 Ом.
5. Каковы результирующие сопротивление цепи и ток в ней в схеме на рис. 5?
Рис. 5.
Прежде всего, определим результирующее сопротивление параллельно соединенных сопротивлений:
r(1-2)=(r1∙r2)/(r1+r2)=(2∙4)/(2+4)=8/6=1,3 Ом;
r(4-5)=(r4∙r5)/(r4+r5)=(15∙5)/(15+5)=75/20=3,75 Ом.
Результирующее сопротивление цепи равно:
r=r(1-2)+r3+r(4-5)=1,3+10+3,75=15,05 Ом.
Результирующий ток при напряжении U=90,5 В
I=U/r=90,5/15,05=6 А.
Рис. 6.
Результирующая проводимость параллельно включенных сопротивлений
1/r(3-4-5) =1/r3 +1/r4 +1/r5 =1/5+1/10+1/20=7/20 сим;
r(3-4-5)=20/7=2,85 Ом.
Сопротивление цепи из r1 и r2 равно:
r(1-2)=r1+r2=15+5=20 Ом.
Результирующая проводимость и сопротивление между точками А и В соответственно равны: 1/rAB =1/r(3-4-5) +1/r(1-2) =7/20+1/20=8/20 сим; rAB=20/8=2,5 Ом.
Результирующее сопротивление всей схемы r=rAB+r6=2,5+7,5=10 Ом.
Результирующий ток I=U/r=24/10=2,4 А.
Напряжение между точками А и В равно напряжению источника U за вычетом падения напряжения на сопротивлении r6
UAB=U-I∙r6=24-(2,4∙7,5)=6 В.
На это напряжение включено сопротивление r4, поэтому ток, проходящий через него, будет равен:
I4=UAB/r4 =6/10=0,6 А.
Сопротивления r1 и r2 имеют общее падение напряжения UAB, поэтому ток, проходящий через сопротивление r1, равен:
I1=UAB/r(1-2) =6/20=0,3 А.
Падение напряжения на сопротивлении r1
Ur1=I1∙r1=0,3∙15=4,5 В.
7. Каковы результирующее сопротивление и ток в схеме на рис. 7, если напряжение источника U=220 В?
Рис. 7.
Начинаем с контура, расположенного справа от узлов 3 и 3. Сопротивления r7, r8, r9 соединены последовательно, поэтому
r(7-8-9)=r7+r8+r9=30+40+20=90 Ом.
Параллельно этому сопротивлению включено сопротивление r6, поэтому результирующее сопротивление в узле 3 и 3 (разрез a)
ra=(r6∙r(7-8-9))/(r6+r(7-8-9))=(20∙90)/(20+90)=1800/110=16,36 Ом.
Последовательно с сопротивлением ra включены сопротивления r4 и r5:
r(4-5-a)=10+20+16,36=46,36 Ом.
Результирующее сопротивление в узлах 2 и 2 (разрез b)
rb=(r(4-5-a)∙r3)/(r(4-5-a)+r3)=(46,36∙30)/(46,36+30)=1390,8/76,36=18,28 Ом.
Результирующее сопротивление всей цепи r=r1+rb+r2=40+18,28+10=68,28 Ом.
Результирующий ток I=U/r=220/68,28=3,8 А.
Источник: https://homele.ru/electrician/total-power-with-parallel-connection-calculation-of-the-resulting-resistance-in-a-seriesparallel-connection/
Мощность при параллельном и последовательном соединении резисторов
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением.
Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при параллельном и последовательном соединении резисторов будет различной.
Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора.
Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом.
Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения — параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A.На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I2 x R = 0,2562 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I2 x R1 = 0,2562 x 200 = 13,11 Вт;
- P2 = I2 x R2 = 0,2562 x 100 = 6,55 Вт;
- P3 = I2 x R3 = 0,2562 x 51 = 3,34 Вт;
- P4 = I2 x R4 = 0,2562 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при параллельном соединение
При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом: P = I2 x R = 6,0242 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов: P1 = U2/R1 = 1002/200 = 50 Вт; P2 = U2/R2 = 1002/100 = 100 Вт; P3 = U2/R3 = 1002/51 = 195,9 Вт; P4 = U2/R4 = 1002/39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и параллельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
Источник: https://electric-220.ru/news/moshhnost_pri_parallelnom_i_posledovatelnom_soedinenii_rezistorov/2016-10-31-1102
На чтение 7 мин. Просмотров 7.2k. Опубликовано 18.05.2020
Ни одна электрическая схема не обходится без резисторов. Что это такое, для чего он нужен и какими способами их подключают в электрическую цепь рассмотрим подробно.
Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.
- С левого края – левый.
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.
При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.
Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Последовательное подключение
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.
При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.
Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Какая мощность тока при последовательном и параллельном соединении
Определение мощности отдельного резистивного элемента производится по формуле
P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.
Мощность при параллельном соединении
Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где
- R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
- I – сила тока в цепи.
При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.
Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.
Мощность при последовательном соединении
Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где
- R – рассчитанное нами сопротивление для определенной схемы;
- U – падение напряжения на данном резистивном элементе.
Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.
Как правильно рассчитать сопротивление
Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где
- U – падение напряжение на конкретном резистивном элементе;
- I – ток, протекающий через него.
При последовательном соединении
Для двух элементов считаем Rобщ = R1+R2.
Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.
При параллельном соединении
Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).
Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле
Rобщ = 1/(1/R1+1/R2+1/R3+…+1/Rn).
Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.
Как рассчитать сложные схемы соединения резисторов
Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.

- R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
- R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
- R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.
Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.
Преобразование «звезда-треугольник»
Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:
- «звезда» – соединение трех ветвей с одним общим узлом;
- «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.
Справка: Узел – точка, в которой соединяются три и более проводника электрической цепи.
Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».
Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».
RA = RAB RAC/(RAB+RAC+RDC).
Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.
RAB=(RARB+RARC+RBRС)/RC
О разнице подключения звезда и треугольник читайте здесь.
Чему равна сила тока в цепи при параллельном соединении резисторов
Согласно правилу Кирхгофа ток, поступающий в узел, равен току, выходящему из узла, – величина тока до группы параллельных резисторов и после нее должна быть неизменной.
Ток в группе параллельных резисторов распределяется по цепи в зависимости от их номинала, после прохождения через сопротивления суммируется в узле и выходит из него неизменным I = I1+I2+I3+…+In.
Как определить величину эквивалентного сопротивления при последовательном соединении резисторов
Справка: Эквивалентом сопротивления называется замена части схемы, состоящей из нескольких резистивных элементов, одним элементом.
Для последовательного соединения эквивалентное сопротивление равно сумме сопротивлений резисторов, включенных в группу, для расчета применяется формула Rэкв = R1+R2+…+Rn.
Например: Нужно посчитать эквивалентное сопротивление данной схемы.

Выделяем первую группу из последовательно соединенных элементов – R2, R3, R4.
Считаем сопротивление Rобщ1 = R2+R3+R4.
Выделяем вторую группу из последовательных элементов R1, R5, R6.
Считаем сопротивление Rобщ2 = R1+R5+R6.
Получаем величину двух эквивалентных сопротивлений Rобщ1 и Rобщ2, соединенных параллельно.
Делаем расчет всей схемы Rэкв= Rобщ1× Rобш2/ (Rобщ1+ Rобщ2).
Зная способы соединения и формулы расчета можно рассчитать любую сложную схему соединения резистивных элементов, однако существует множество онлайн калькуляторов, которые сделают это быстрей человека, достаточно только ввести нужные параметры компонентов схемы.
| Закон Ома для участка цепи. | ||
|
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению этого участка. Выполняется для металлов и электролитов. |
|
|
|
Закон Джоуля – Ленца. Дж. Джоуль (1841—1843) Э. X. Ленц (1842—1843) независимо друг от друга экспериментально установили |
|
|
|
В электрической цепи происходит преобразование энергии упорядоченного движения заряженных частиц в тепловую. Согласно з-ну сохранения энергии работа тока равна количеству выделившегося тепла. |
|
|
|
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток: |
|
|
|
Работа и мощность электрического тока. |
||
|
Работа электрического тока: |
|
|
|
Мощность электрического тока (работа в единицу времени): |
|
|
|
В электричестве иногда применяется внесистемная единица работы – кВт.ч (киловатт-час). |
1 кВт.ч = 3,6.106 Дж. |
|
|
Виды соединения проводников. |
||
|
Последовательное соединение. 1. Сила тока во всех последовательно соединенных участках цепи одинакова: I1=I2=I3=…=In=… 2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке: U=U1+U2+…+Un+… 3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка: R=R1+R2+…+Rn+… Если все сопротивления в цепи одинаковы, то: R=R1. N При последовательном соединении общее сопротивление увеличивается (больше большего). |
Параллельное соединение. 1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках. I=I1+I2+…+In+… |
|
|
2. Напряжение на всех параллельно соединенных участках цепи одинаково: U1=U2=U3=…=Un=… 3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению): Если все сопротивления в цепи одинаковы, то: При параллельном соединении общее сопротивление уменьшается (меньше меньшего). |
||
|
4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. A=I2Rt=I2(R1+R2+…+Rn+…)t. 5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. силы тока во всех участках одинаковы, то: U1:U2:…:Un:… = R1:R2:…:Rn:… Для двух резисторов: |
4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. 5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. напряжения на всех участках одинаковы, то: I1R1= I2R2=…= I3R3=… Для двух резисторов: |