Как найти мощность в резисторе физика

Как найти мощность в резисторе физика

Мощность переменного тока

  • Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

  • Мощность тока через резистор

  • Мощность тока через конденсатор

  • Мощность тока через катушку

  • Мощность тока на произвольном участке

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть U и I — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени dt — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины U и I можно считать постоянными в течение интервала dt.

Пусть за время dt через наш участок прошёл заряд dq = Idt (в соответствии с правилом выбора знака для силы тока заряд dq считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

dA = Udq = UIdt.

Мощность тока P — это отношение работы электрического поля ко времени, за которое эта работа совершена:

P= I_0 frac{displaystyle dA}{displaystyle dt vphantom{1^a}} = UI. (1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: P > 0. Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: P < 0. Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

к оглавлению ▴

Мощность тока через резистор

Пусть переменный ток I = I_0 sin omega t протекает через резистор сопротивлением R. Напряжение на резисторе, как нам известно, колеблется в фазе с током:

U = IR = I_0 R sin omega t = U_0 sin omega t.

Поэтому для мгновенной мощности получаем:

P = UI= U_0 I_0 sin^2 omega t = P_0 sin^2 omega t. (2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение P_0 нашей мощности связано с амплитудами тока и напряжения привычными формулами:

P_0=U_0 I_0 = I_0^2 R = frac{displaystyle U_0^2}{displaystyle R vphantom{1^a}}.

На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой 50 Гц, т. е. за секунду совершается 50 колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между 0 и P_0. Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение P_0/2?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно 1/2.

Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно 1/2

Итак, для среднего значения bar{P} мощности тока на резисторе имеем:

bar{P}= frac{displaystyle P_0}{displaystyle 2 vphantom{1^a}} = frac{displaystyle U_0 I_0}{displaystyle 2 vphantom{1^a}} = frac{displaystyle I_0^2 R}{displaystyle 2 vphantom{1^a}} = frac{displaystyle U_0^2}{displaystyle 2R vphantom{1^a}}. (3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

bar{U}= frac{displaystyle U_0}{displaystyle sqrt(2) vphantom{1^a}}, bar{I}= frac{displaystyle I_0}{displaystyle sqrt(2) vphantom{1^a}}. (4)

Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

bar{P}=bar{U} bar{I} = bar{I}^2 R = frac{displaystyle bar{U}^2}{displaystyle R vphantom{1^a}}.

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения U, а затем к источнику переменного напряжения с таким же действующим значением U, то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые 220 вольт из розетки — это действующее значение напряжения бытовой электросети.

к оглавлению ▴

Мощность тока через конденсатор

Пусть на конденсатор подано переменное напряжение U = U_0 sin omega t. Как мы знаем, ток через конденсатор опережает по фазе напряжение на pi:

I = I_0 sin left ( omega t + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = I_0 cos omega t.

Для мгновенной мощности получаем:

P = UI = U_0 I_0 sin omega t cos omega t = frac{displaystyle 1}{displaystyle 2 vphantom{1^a}}U_0 I_0 sin2 omega t = P_0 sin2 omega t.

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть, 0 < t < T/4. Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, T/4 < t < T/2. Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, T/2 < t < 3T/4. Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, 3T/4 < t < T. Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

к оглавлению ▴

Мощность тока через катушку

Пусть на катушку подано переменное напряжение U = U_0 sin omega t. Ток через катушку отстаёт по фазе от напряжения на pi/2:

I = I_0 sin left ( omega t - frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = -I_0 cos omega t.

Для мгновенной мощности получаем:

P = UI = -U_0 I_0 sin omega t cos omega t = -frac{displaystyle 1}{displaystyle 2 vphantom{1^a}}U_0 I_0 sin2 omega t = -P_0 sin2 omega t.

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

к оглавлению ▴

Мощность тока на произвольном участке

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение U = U_0 sin omega t.

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз alpha. Мы записывали это так:

I = I_0 sin(omega t - alpha).

Тогда для мгновенной мощности имеем:

P = U_0 I_0 sin omega t sin(omega t - alpha). (5)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:

sin x sin y = frac{displaystyle 1}{displaystyle 2 vphantom{1^a}} (cos (x-y) - cos (x+y)).

В результате получим:

P = U_0 I_0 frac{displaystyle 1}{displaystyle 2 vphantom{1^a}} ( cos alpha - cos (2 omega t - alpha)). (6)

Но среднее значение величины cos (2 omega t - alpha) равно нулю! Поэтому средняя мощность оказывается равной:

bar{P} = U_0 I_0 frac{displaystyle 1}{displaystyle 2 vphantom{1^a}} cos alpha. (7)

Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

bar{P} = bar{U} bar{I} cos alpha.

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем alpha = 0, и мы приходим к формуле (3). Для конденсатора и катушки alpha = pi/2, и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы cos alpha у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Мощность переменного тока» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

как найти мощность на каждом резисторе



Ученик

(205),
на голосовании



13 лет назад

Голосование за лучший ответ

VVW MAMAY

Просветленный

(41320)


13 лет назад

Нечеткий вопрос…. непонятный…. если имеется ввиду мощность конкретно рассеиваемая на каждом резисторе к-либо ус-ва. . -то или вычислением ( элементарная физика )-теоретическим или по практическим результатам измерений …если вы имеете ввиду просто конкретное усторойство- то по габаритам и маркирове деталей- надо смотреть каталоги на эту элементную базу…. и по ней можно определить максимальную мошность которую может выдержать каждый резистор без изменеия его параметров….

Источник

Резистор – это один из главных радиоэлементов, у которого есть целый ряд важнейших параметров. Сегодня речь пойдет о мощности рассеивания, ведь этот параметр отвечает за надежную и стабильную работу любого резистора.

Как рассчитать мощность рассеивания резистора

Что такое мощность и рассеиваемая мощность

Для начала давайте освежим в памяти, что такое мощность постоянного тока, для этого следует вспомнить очень простую формулу:

Как рассчитать мощность рассеивания резистора

Из выше представленного выражения вполне ясно, что мощность зависит от таких величин как напряжение и ток.

Если мы рассмотрим реальную схему, то в процессе ее работы через резисторы, расположенные в схеме, будет протекать ток определенной величины, а так как они (резисторы) обладают определенным сопротивлением, то под действием тока на резисторе будет выделяться тепло. Это тепло и есть та мощность, которая рассеивается на резисторе.

Так вот, если мы в схему установим резистор с меньшей мощностью рассеивания, чем это требуется, то резистор будет перегреваться. Это приведет к его быстрому выходу из строя.

Поэтому очень важно соблюдать следующее правило: заменяемый резистор должен соответствовать по мощности рассеивания сгоревшему резистору, либо этот параметр должен быть больше, но никак не меньше.

Все выпускаемые резисторы соответствуют стандартному ряду, который выглядит так:

Как рассчитать мощность рассеивания резистора

1. 0,125 Вт, 0,25 Вт, 0,5 Вт, 1 Вт, 2 Вт, и более

Обычно, соблюдается следующее правило: чем больший размер у резистора, тем на большую рассеиваемую мощность он рассчитан.

Давайте рассмотрим пример. Допустим нам нужно установить резистор с сопротивлением 100 Ом, а ток через него будет протекать 0,1 Ампер.

Для того, чтобы рассчитать требуемую мощность рассеивания нашего резистора воспользуемся следующей формулой:

Как рассчитать мощность рассеивания резистора

Итак, получается, что в данном примере нам потребуется резистор с мощностью рассеивания в один Ватт.

Примечание. Для стабильной и надежной работы следует обязательно брать резистор с запасом по мощности рассеивания. Это позволит обеспечить требуемую надежность и долговечность работы схемы.

Но что делать, если вы не знаете, какой ток будет протекать через резистор. Для расчета требуемой мощности рассеивания можно воспользоваться уже другой формулой:

Как рассчитать мощность рассеивания резистора

Все вышеперечисленное справедливо для того случая, когда нужно заменить единичный резистор, но довольно часто в схемах можно найти так называемой составной резистор (несколько резисторов соединены параллельно, последовательно или же смешанно).

Итак, давайте для начала рассмотрим последовательное соединение.

При последовательном соединении через резисторы будет протекать одинаковый ток. И получается если нам нужно найти замену резистору на 100 Ом, через который протекает ток в 0,1 А и он рассчитан на мощность рассеивания в 1 Вт, его можно заменить двумя последовательно соединенными резисторами на 80 Ом и 20 Ом.

Если воспользоваться выше представленными формулами и рассчитать на какую мощность должен быть рассчитан каждый резистор, то получим следующий результат:

R1 – 20 Ом (0,2 Вт)

R2 – 80 Ом (0,8 Вт)

Как рассчитать мощность рассеивания резистора

Теперь смотрим таблицу со стандартным рядом и выбираем ближайший наибольший номинал. Получается, что в нашем случае подойдут резисторы с мощностью рассеивания R1 – 0.5 Вт, R2 – 1 Вт.

При параллельном же соединении учитывайте тот факт, что через резистор с меньшим сопротивлением будет течь больший ток.

Смешанное соединение на практике практически не используется.

Как рассчитать мощность рассеивания резистора

Как обойтись без расчетов

В принципе можно обойтись без формул и подсчетов, достаточно следовать следующему правилу:

Мощность каждого резистора, который входит в составляемую цепь (параллельную или последовательную) должен быть равен мощности рассеивания заменяемого резистора. Проще говоря, если вы хотите заменить резистор на 1 Вт составным резистором, то каждый из них должен быть не менее 1 Вт по мощности рассеивания.

Это все, что я хотел вам рассказать о расчете мощности рассеивания резистора и правилах его замены. Если статья оказалась вам полезна, то оцените ее лайком и спасибо за ваше внимание!

Источник

Мощность резистора

Как рассчитать мощность резистора?

Мощность рассеивания резистора
Мощность рассеивания резистора

У резистора есть довольно важный параметр, который целиком и полностью влияет на надёжность его работы. Этот параметр называется мощностью рассеивания. Он уже упоминался в статье о параметрах резистора.

Сама по себе мощность постоянного тока рассчитывается по простой формуле:

Формула мощности постоянного тока

Здесь, P(Вт) – мощность;

U(В) – напряжение;

I(А) – ток.

Как видим, мощность зависит от напряжения и тока. В реальной цепи через резистор протекает определённый ток. Поскольку резистор обладает сопротивлением, то под действием протекающего тока резистор нагревается. На нём выделяется какое-то количество тепла. Это и есть та мощность, которая рассеивается на резисторе.

Если в схему установить резистор меньшей мощности рассеивания, чем требуется, то резистор будет нагреваться и в результате сгорит. Поэтому, если в схеме нужно заменить резистор мощностью 0,5 Ватт, то ставим на 0,5 Ватт и более. Но никак не меньше!

Каждый резистор рассчитан на свою мощность. Стандартный ряд мощностей рассеивания резисторов состоит из значений:

  • 0,125 Вт

  • 0,25 Вт

  • 0,5 Вт

  • 1 Вт

  • 2 Вт

  • Более 2 Вт.

Чем больше резистор по размерам, тем, как правило, на большую мощность рассеивания он рассчитан.

Резисторы разной мощности

Допустим, у нас есть резистор с номинальным сопротивлением 100 Ом. Через него течёт ток 0,1 Ампер. На какую мощность должен быть рассчитан этот резистор?

Тут нам потребуется формула. Выглядит она так:

Формула: Сопротивление - Мощность

Здесь, P(Вт) – мощность;

R(Ом) – сопротивление цепи (в данном случае резистора);

I(А) – ток, протекающий через резистор.

Все расчёты следует производить, строго соблюдая размерность. Так, если сопротивление резистора не 100 Ом, а 1 кОм, то в формулу нужно подставить значение в Омах, т.е. 1000 Ом (1 кОм = 1000 Ом). Тоже правило касается и других величин (тока, напряжения).

Рассчитаем мощность для нашего резистора:

Расчёт мощности резистора

Мы получили мощность 1 Ватт. Теперь небольшое отступление.

В реальную схему необходимо устанавливать резистор с мощностью в полтора – два раза выше рассчитанной.

Поэтому нам подойдёт резистор мощностью 2 Вт (см. стандартный ряд мощностей резисторов).

Также есть и другая формула для расчёта мощности. Она применяется в том случае, если неизвестен ток, который протекает через резистор.

Формула расчёта мощности через напряжение и сопротивление

Всё бы хорошо, но в жизни бывают случаи, когда применяется последовательное или параллельное соединение резисторов. Как рассчитать мощность рассеивания для каждого из резисторов в последовательной или параллельной цепи?

Допустим, нам требуется заменить резистор сопротивлением 100 Ом. Протекающий через него ток равен 0,1 Ампер. Следовательно, мощность этого резистора 1 Ватт.

Для его замены можно применить два соединённых последовательно резистора сопротивлением 20 Ом и 80 Ом. На какую мощность должны быть рассчитаны эти резисторы?

Для последовательной цепи действует одно правило. Через последовательно соединённые резисторы течёт один и тот же ток. Теперь применим формулу для расчёта мощности и получим, что мощность рассеивания резистора на 20 Ом должна быть равна 0,2 Вт, а резистора на 80 Ом – 0,8 Вт. Выбираем резисторы согласно стандартному ряду мощностей:

R1 – 20 Ом (0,5 Вт);

R2 – 80 Ом (1 Вт)

Как видим, если сопротивления резисторов будут разные, то и мощность на них будет выделяться разная.

Мощность, рассеивающаяся на резисторе, зависит в первую очередь от тока, который течёт через данный резистор. А ток зависит от сопротивления резистора. Поэтому, если вы соединяете последовательно резисторы разных номиналов, то и рассеивающаяся мощность распределиться между ними.

Это обстоятельство необходимо учитывать при самостоятельном конструировании электронных самоделок иначе при неправильном подборе резисторов может получиться так, что на одном резисторе выделиться больше мощности, чем на другом, и он будет работать в тяжёлом температурном режиме.

Чтобы не ломать голову и не рассчитывать мощность каждого в отдельности резистора, можно поступать так:

Мощность каждого резистора, входящего в составляемую нами цепь (параллельную или последовательную) должна быть равна мощности заменяемого резистора. Иными словами, если нам надо заменить резистор, мощностью 1 Вт, то каждый из резисторов для его замены должен иметь мощность не менее 1 Ватта. На практике это самое быстрое и эффективное решение.

Для параллельного соединения резисторов нужно учитывать, что через резистор с меньшим сопротивлением протекает больший ток. Следовательно, и мощности на нём будет рассеиваться больше.

Главная » Радиоэлектроника для начинающих » Текущая страница

Также Вам будет интересно узнать:

  • Научись паять! Минимальный наборчик для пайки.

  • Научись паять! Подготовка и уход за паяльником.

Источник

Содержание материала

  1. Что такое мощность резистора
  2. Нагрев детали в зависимости от сопротивления
  3. Как рассчитать мощность резистора в схеме
  4. Параметры резисторного элемента
  5. Формула скорости потребления энергии резистором
  6. Для чего он нужен
  7. Как определить мощность резистора
  8. Как рассчитать мощность рассеивания резистора

Что такое мощность резистора

Мощность определяется как произведение силы тока на сопротивление: P = I * R и измеряется в ваттах (закон Ома). Рассеиваемая мощность резистора — это максимальный ток, который сопротивление может выдерживать длительное время без ущерба для работоспособности. То есть, этот параметр надо выбирать для каждой схемы отдельно — по максимальному рабочему току.

Как определить мощность резистора по внешнему виду

Как определить мощность резистора по внешнему виду: надо знать соответствие размеров и мощностей

Физически рассеиваемая мощность резистора — это то количество тепла, которое его корпус может «отдать» в окружающую среду и не перегреться при этом до фатальных последствий. При этом, нагрев не должен слишком сильно влиять на сопротивление резистора.

Нагрев детали в зависимости от сопротивления

Выбирая подходящий резистор, обязательно надо обращать внимание на температурный диапазон, при котором возможна корректная эксплуатация детали. Она всегда указывается изготовителем. Чтобы резистор не вышел из строя, необходим своевременный выход теплоты в атмосферу. Элемент не должен перегреваться. Чем холоднее воздух (в рамках допустимого диапазона), тем дольше имеет шанс прослужить компонент. Нельзя позволять, чтобы поблизости от резистора скапливалось избыточное тепло.

Когда температурный показатель достигает своего максимума в рамках диапазона, на сопротивлении начинается процесс выгорания верхнего маркируемого слоя. В таком случае необходимо принимать меры по снижению температуры, иначе у изделия выгорит наполнение, отвечающее за сопротивляемость, и оно станет полностью непригодным к дальнейшей эксплуатации.

Если детали с требуемой размерностью под конкретную схему не обнаружилось, можно использовать вариант с превосходящим значением, если он подходит собираемому устройству. Резисторы, чьи данные по мощности не дотягивают до требуемых, применять в такой ситуации допустимо, только объединив их последовательно. Вообще знание эффектов параллельно и последовательно связанных резисторных элементов пригодится в ситуации, если под рукой не оказалось детали с идеально подходящими параметрами.

Как рассчитать мощность резистора в схеме

Чтобы рассчитать мощность резисторов в схеме, кроме сопротивления (R) необходимо знать силу тока (I). На основании этих данных можно рассчитать мощность. Формула обычная: P = I² * R. Квадрат силы тока умножить на сопротивление. Силу тока подставляем в Амперах, сопротивление — в Омах.

Если номинал написан в килоомах (кОм) или мегаомах (мОм),  его переводим в Омы. Это важно, иначе будет неправильная цифра.

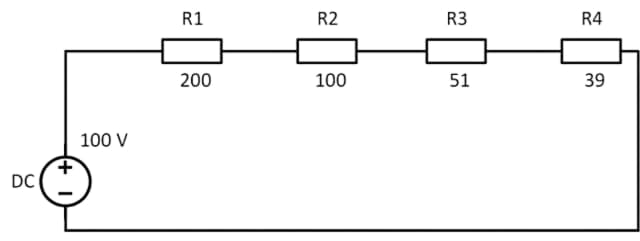
Схема последовательного соединения резисторов

Схема последовательного соединения резисторов

Для примера рассмотрим схему на рисунке выше. Последовательное соединение сопротивлений характерно тем, что через каждый отдельный резистор цепи протекает одинаковый ток. Значит мощность сопротивлений будет одинаковой. Последовательно соединенные сопротивления просто суммируется: 200 Ом + 100 Ом + 51 Ом + 39 Ом = 390 Ом. Ток рассчитаем по формуле: I = U/R. Подставляем данные: I = 100 В / 390 Ом = 0,256 А.

По расчетным данным определяем суммарную мощность сопротивлений: P = 0,256² * 390 Ом = 25,549 Вт.  Аналогично рассчитывается мощность каждого из резисторов. Например, рассчитаем мощность резистора R2 на схеме. Ток мы знаем, его номинал тоже. Получаем: 0,256А² * 100 Ом = 6,55 Вт. То есть, мощность этого резистора должна быть не ниже 7 Вт. Брать с более низкой мощностью точно не стоит — быстро перегорит. Если позволяет конструктив прибора, то можно поставить резистор большей мощности, например, на 10 Вт.

Есть резисторы серии МЛТ, в которых мощность рассе

Есть резисторы серии МЛТ, в которых мощность рассеивания тепла указана сразу после названия серии без каких-либо букв. В данном случае — МЛТ-2 означает, что мощность этого экземпляра 2 Вт, а номинал 6,8 кОм.

При параллельном подключении расчет аналогичен. Нужно только правильно рассчитать ток, но это тема другой статьи. А формула расчета мощности резистора от типа соединения не зависит.

Параметры резисторного элемента

Сопротивление резистора — формула для рассчета

К числу ключевых параметров данной группы деталей относятся:

  • сопротивление компонента;
  • допуск (степень вариативности номинального сопротивления) – может принимать значения до 20%;
  • ТКС – изменение сопротивляемости при нагреве или охлаждении воздуха на 1 градус (целесообразно, чтобы элементы одной электроцепи имели идентичное значение показателя);
  • мощность, показывающая, какое количество тепловой энергии может быть выделено в пространство при условии сохранения корректного функционирования элемента.

Важно! На то, сколько энергии будет рассеивать компонент, влияет его размер. Натренированный глаз способен к визуальному определению значения по габаритам резистора. Корреляция с величиной связана с тем, что когда ток течет через элемент с большим значением площади поверхности, теплота отдается в пространство с большей скоростью (если речь идет о воздухе).

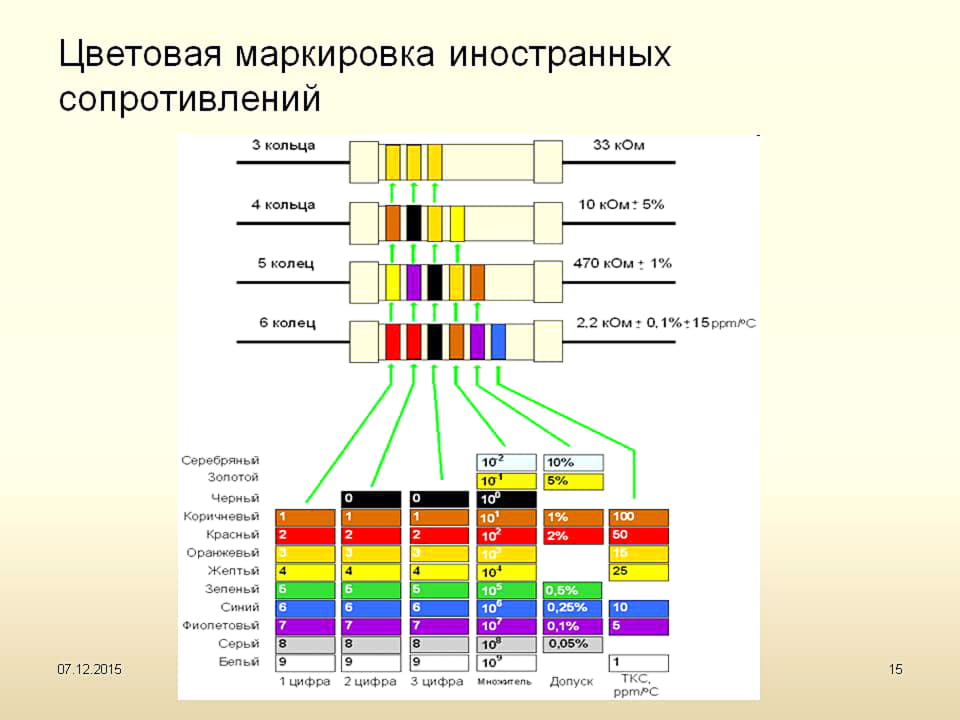
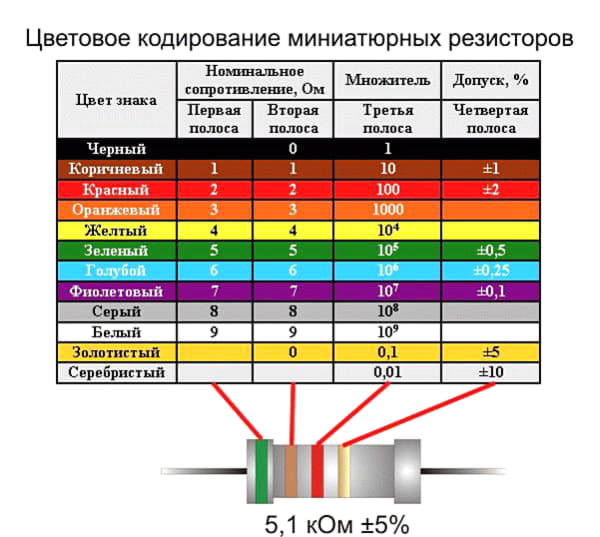
Миниатюрные смд компоненты снабжаются маркировкой из полосок разного цвета. Расшифровку цветового кода можно посмотреть онлайн (например, на сайте производителя). Зачастую она дается и в прилагаемой технической документации.

Цветовая кодировка миниатюрных деталей

Формула скорости потребления энергии резистором

кВа в кВт — как правильно перевести мощность

Количество энергии, генерируемой в виде тепла на единицу объема элемента, можно найти по формуле:

w = E2* ϭ=E*j,

где Е – напряженность поля, j – его плотность, а ϭ – электрическая проводимость среды.

Для чего он нужен

Резистор предназначен для оказания сопротивления проходящему через систему току. Применяется в различных областях. Назначение устройства может быть следующим:

  • «Переделка» токовой энергии в напряжение (или обратно);
  • Ограничение поступающей силы до нужного уровня;
  • Создание разделителей (например, в измеряющих устройствах);
  • Решение специализированных проблем (например, снижение влияния радиопомех).

Важно! Самый простой вариант применения прибора – работа светодиода. Собственное сопротивление элемента слишком мало. Без ограничителя – резистора – проходящий ток моментально выведет элемент из строя.

Светодиод

Светодиод

Как определить мощность резистора

Существует два способа определить уровень сопротивления той или иной модели – размер и формула.

Понять, как определить мощность конкретного резистора по внешнему виду, несложно – для этого установлены стандарты. Установленным габаритам стараются соответствовать все производители электротехнических деталей. В СССР были созданы таблицы, согласно которым мощность устройств регулировалась по длине и диаметру.

Важно! На элементах российского производства и некоторых зарубежных аналогах (сопротивлением в 1Вт и больше) значение мощности указывается на внешнем корпусе с помощью цифр. На иностранных устройствах другого уровня сопротивления дополнительно печатают букву «W».

Маркировка

Маркировка

Важно! На некоторых элементах импортного производства могут стоять другие обозначения. Это возможно, если производитель отказывается применять общепринятые стандарты.

Кроме этого – при определении мощности резистора по внешнему виду важно помнить, что стандарты отечественных моделей несколько выше (идентичные российские модели немного крупнее).

Вам это будет интересно   Формулировка и определение закона Ома

Мощность тока, выделяющаяся на резисторе, также определяется по специальной формуле. В качестве основы используется закон Ома, уравнение имеет следующий вид:

R = U / I, в которой R – сопротивление, U – напряжение в точках вывода В, I – сила тока на заданном участке.

Важно! Электротехнические платы редко содержат один элемент. Чаще платы содержат множество составляющих, соединяющихся последовательно или параллельно.

Последовательная сцепка означает, что выход одного элемента соединяется с входом следующего – один за другим. Для расчета, используют онлайн-калькуляторы или следующую формулу мощности тока, выделяющегося на резисторе:

R123 = R1 + R2 + R3.

Элементов в формуле должно быть столько, сколько сопротивлений содержит электрическая схема.

Параллельное соединение означает, что резисторы соединяются парно, а формула выглядит следующим образом:

R = (R1 * R2) / ( R1 + R2).

Схема с резистором

Схема с резистором

Результат обычно меньше, чем значение самого маломощного элемента в системе. В некоторых схемах применяют смешанное соединение. Расчет применяется поэтапно – сначала вычисляют последовательные, затем параллельные. Результат складывается и получается итоговое сопротивление технической платы.

Как рассчитать мощность рассеивания резистора

Вот мы и узнали, что мощность тока в резисторе рассчитывается по формуле. В реальной цепочке(последовательной или параллельной) через резисторные элементы протекает ток. Поскольку резистор имеет сопротивление, то под влиянием проходящего тока резисторный компонент греется. На нём выделяется немного тепловой энергии. Это и есть та мощность, которая рассеивается на резисторном элементе.

Если в электросхему вмонтировать резистор с мощностью меньше, чем надо, то резисторный компонент в итоге сгорит из-за перегрева. Поэтому, если в схеме требуется заменить резисторное устройство мощностью 0,5 Вт, то устанавливает на 0,5 Ватт и больше. Каждый резисторный компонент рассчитан на конкретные показатели мощности. Типовой ряд мощностей рассеивания резисторных компонент состоит из значений:

  • 0,125 В.
  • 0,25 В.
  • 0,5 В.
  • 1 Ватт.
  • 2 Ватт.
  • Более 2 Ватт.

Чем крупнее резистор, тем, он мощнее. К примеру, у нас есть резисторный элемент с сопротивлением 100 Ом. Через него течет ток 0,1 Ампер. Как вычислить его хар-ки мощности? Тут потребуется сопротивление резистора формула:

P(Вт) – мощность;

R(Ом) – сопротивление цепочки (а точнее резистора);

I(А) – ток.

Все расчёты необходимо выполнять, помня про размерность, даже связанные с площадью. Определим показатели мощности для нашего резисторного компонента: на выходе, получается мощность 1 Ватт. Здесь подойдёт резисторный компонент мощностью 2 В. Мощность резистора должна быть равна мощности заменяемого.

Теги

Источник

Добавить комментарий